Геомагнетизм и аэрономия, 2022, T. 62, № 4, стр. 411-425

Эволюция вертикального токового слоя в холловской плазме солнечной хромосферы в зависимости от направления тока

Л. М. Алексеева^1, *, С. П. Кшевецкий^2, 3, **

¹ Научно-исследовательский институт ядерной физики им. Д.В. Скобельцына Московского государственного университета им. М.В. Ломоносова (НИИЯФ МГУ)
г. Москва, Россия

² Балтийский федеральный университет им. И. Канта (БФУ им. И. Канта)
г. Калининград, Россия

³ Институт физики атмосферы им. А.М. Обухова РАН (ИФА РАН)
г. Москва, Россия

^* E-mail: l.m.alekseeva@yandex.ru
^** E-mail: spkshev@gmail.com

Поступила в редакцию 01.07.2021
После доработки 29.11.2021
Принята к публикации 27.01.2022

EDN: QHEVTO
DOI: 10.31857/S0016794022030026

Полный текст (PDF)

Аннотация

Теоретически изучены последствия поступления слабого магнитного поля в верхнюю хромосферу Солнца. В начальный момент плазма принимается неподвижной и всюду имеющей температуру 50 000 К, поле состоит из двух прилегающих друг к другу одинаковых разнополярных магнитных областей с вертикальной зоной контакта. Численно решена полностью самосогласованная 2D-система нелинейных столкновительных уравнений одножидкостной резистивной магнитогидродинамики с учетом эффекта Холла и теплопроводности. Установлено, что в ходе совместной эволюции поля и плазмы пограничный ток, направленный вверх, чаще принимает форму тонкого токового слоя и дольше существует в этом виде, чем пограничный ток, направленный вниз. Однако при токе вниз преобразование энергии магнитного поля в энергию упорядоченных потоков хромосферной плазмы идет эффективнее. В предположении медленного изменения величин по вертикали аналитически найдена область значений параметров, где, независимо от общего вида магнитных неоднородностей, токи вниз деградируют (размываются), а токи вверх резко увеличивают свою плотность. Принципиальная разница в поведении токов возникает в том случае, когда омическая диссипация и снос силовых линий из-за их частичной вмороженности оказывают меньшее влияние на изменения магнитного поля, чем эффект Холла в присутствии градиента плотности плазмы, создаваемого силой тяжести. Показано, что минимальная высота, где реализуется этот случай чистой градиентно-холловской эволюции магнитного поля, соответствует нижней границе короны. Высказано предположение, что омическая диссипация самопроизвольно образующихся концентрированных токов способствует нагреву короны.

1. ВВЕДЕНИЕ

Несмотря на интенсивность изучения надфотосферных слоев Солнца, неясной остается природа таких важных явлений как нагрев короны, ускорение солнечного ветра, возникновение хромосферных вспышек и др. Полагают, что их существование может быть связано с почти еще не изученными механизмами мелкомасштабной солнечной активности. Современные аппараты дают возможность видеть хромосферу Солнца как бы “через лупу” вплоть до неоднородностей размером в ~100 км. Однако наблюдаемую картину трудно интерпретировать на основе подходов, разработанных в крупномасштабной физике Солнца. Действительно, “через лупу” видна крайне динамичная среда, плотно заполненная массой движущихся и меняющихся неоднородностей. Некоторые из них существуют какое-то время как правильные образования, однако эти транзиентные структуры мало походят на стоящие по отдельности объекты, изучаемые крупномасштабной физикой Солнца (как-то: пятна, шлемовидные структуры и пр.). Наблюдаемое в хромосфере скорее напоминает развившиеся неустойчивости сплошной среды.

Наши работы направлены на выявление причинно-следственных связей в мелкомасштабной активности хромосферы. Предлагаемый подход исходит из двух положений. Первое – что плазма надфотосферных слоев Солнца структурируется поступающим снизу, через фотосферу, магнитным полем. Второе – что плазме с магнитным полем присущи неустойчивости, а их обстоятельно изучали в рамках лабораторной плазмофизики.

Мы решаем задачи с начальными условиями для полностью самосогласованной системы нелинейных уравнений классической столкновительной магнитогидродинамики (МГД). Начальные условия соответствуют появлению в плазме магнитного поля того или иного вида. Численно отыскивая решение, мы исследуем его на устойчивость. Для интерпретации форм и поведения возникающих неустойчивостей используется сопоставление с разработками лабораторной плазмофизики. Проведенное этим путем исследование позволяет связать конкретный вид поступившей в верхнюю хромосферу магнитной конфигурации с формами возникающих вследствие этого поступления образований (модификациями ее самой в ходе совместной эволюции с плазмой, результатами развития неустойчивостей и пр.). Знание такой связи будет помогать в расшифровке наблюдательного материала. С другой стороны, в дальнейшем – когда таких нелинейных расчетов с разными типовыми магнитными полями накопится много – можно будет составить представление об аномальных коэффициентах переноса в хромосферной плазме в конкретных ситуациях.

Согласно современным оценкам, 95% магнитного потока, поступающего снизу из фотосферы, не доходят до короны [Прист, 1985; Aschwanden, 2004]. Это значит, что находящаяся между фотосферой и короной хромосфера заполнена разнообразными, в основном горизонтальными, магнитными полями. Так что типичной структурой в верхней хромосфере Солнца должны быть токовые слои (ТС) той или иной ширины и протяженности, соответствующие зонам контакта различных горизонтальных магнитных полей, а в области токов обычно и проявляют себя плазменные неустойчивости. Поэтому нас интересует класс решений вида ТС. В цикле работ по физике хромосферы [Алексеева, 2006; Алексеева и Кшевецкий, 2011, 2013, 2019; Alekseeva and Kshevetskii, 2015] и в данной статье в качестве начальной выбрана магнитная конфигурация, состоящая из двух одинаковых прилегающих друг к другу разнополярных магнитных областей.

Решение 2D-задачи с начальными условиями ведется в предположении, что силовые линии магнитного поля представляют собой горизонтальные параллельные прямые, вдоль которых нет изменений физических величин. Лабораторным аналогом выбранной конфигурации является плоский пинч, и, как и он, она демонстрирует перетяжечную и изгибную неустойчивости. Но в природной плазме пинч эволюционирует иначе, чем в лаборатории, что порождает не замечаемые в лабораторных установках транзиентные формы. Показано [Алексеева и Кшвецкий, 2011], что пограничный токовый слой (аналог лабораторного плазменного столба с током) может утоньшаться (сжиматься) вдоль всей длины даже при полной начальной сбалансированности магнитного и газового давлений, когда градиент их суммы всюду ноль. Не менее неожиданно, что это целостное по длине сжатие создается перетяжечной неустойчивостью (в лаборатории создающей одну или серию перетяжек, из-за чего и возникло ее название). Причина в том, что в природной плазме отсутствуют электроды. Порождаемые первичной перетяжкой разнонаправленные потоки плазмы коллинеарно электрическому току уходят вдоль всей зоны контакта магнитных областей за пределы магнитной конфигурации. В результате пограничная зона, опустошаясь, сжимается. Соответствующий ей слой тока (ТС), вообще говоря, становится очень тонким токовым слоем (ТТС). Конфигурация реагирует на бернуллиевское падение газового давления в местах наибольшей скорости, и первичная перетяжка раздваивается. После этого направленная к центру конфигурации пара потоков создает вблизи него область повышенной плотности плазмы, своего рода плазмоид.

Если ТС горизонтален, то в дальнейшем он порождает характерную симметричную крестообразную фигуру [Алексеева и Кшевецкий, 2011; Alekseeva and Kshevetskii, 2015]. В расчетах с $\beta \sim 1.5{\kern 1pt} - {\kern 1pt} 2.3$ процесс прослежен вплоть до взрыва – явления вспышечного характера, когда за время 0.1 с или меньше вдруг резко увеличивается кинетическая температура [Alekseeva and Kshevetskii, 2015]. Если ТС вертикален, то плазмоид смещается вдоль него вниз – тонет.

(Отметим, что возникающий ТТС интересен не только как транзиентная структура, открывающая цепь названных превращений, но и сам по себе. Например, ТТС важен в связи с пересоединением. Оно не проявляет себя при нашем подходе, поскольку при пересоединении на одной и той же силовой линии создается разная скорость плазмы, что запрещено принятой 2D-геометрией. Однако выявление физических условий возникновения ТТС дает возможность опосредованно судить о возможности пересоединения).

Из теории лабораторных плазменных каналов известно, что в холловской плазме самопроизвольно и крайне легко возникают резкие скачки магнитного поля или, другими словами, ТТС (см. пионерские труды [Брушлинский и Морозов, 1974; Морозов и Соловьев, 1974], а также работы [Алексеева, 1980; Брушлинский и Ратникова, 1995, 1997; Alekseeva, 1999] и ссылки в этих изданиях). Это явление, в принципе, представляет большой интерес для физики солнечной атмосферы, где, благодаря нарастанию разреженности, роль эффекта Холла с высотой неизбежно приобретает важность. Классические уравнения столкновительной МГД с учетом эффекта Холла были применены к описанию хромосферной плазмы в работе [Goodman, 2005] (отметим содержащийся в ней исчерпывающий список литературы). Автор задал распределение магнитного поля в виде ТС и поперечный слою поток вещества на бесконечности; затем из стационарной системы уравнений нашел остальные величины. Его расчеты показали, что в хромосфере внутри ТС могут существовать вкрапления плазмы с корональными параметрами. Кроме того, было обстоятельно рассмотрено, как внесение поля и потока меняет коэффициенты переноса. (Следуя названным выше плазмофизическим работам, мы всюду используем полностью самосогласованную систему классических столкновительных уравнений МГД).

Ниже речь идет о свойствах вертикального ТТС. Как показывают предыдущие работы [Алексеева, 2006; Алексеева и Кшевецкий, 2019], выполненные с учетом эффекта Холла и силы тяжести для случая слабого магнитного поля, при токе вверх ТТС может также зафиксировать себя в стационарном (квазистационарном) состоянии. Это происходит, если эффект Холла влияет на изменения магнитного поля намного (заметно) сильнее, чем эффект вмороженности. Установлено также, что возникновение ТТС становится типичным явлением на большой высоте. Приуроченность ТТС к верхней границе хромосферы, где из-за разреженности плазмы эффект Холла сильнее, выглядит парадоксальной, поскольку ранее проведенное моделирование [Алексеева и Кшевецкий, 2019] показало, что, с одной стороны, в бесхолловской плазме за образование ТТС отвечает перетяжечная неустойчивость, а с другой – что именно эффект Холла эту перетяжечную неустойчивость подавляет. Отсюда возникает вопрос о существовании какого-то не известного пока механизма генерирования ТТС самим эффектом Холла.

Для ответа на него в настоящей работе сначала путем численного моделирования исследуются закономерности эволюции начального ТС в присутствии эффекта Холла. Показано, что действительно, благодаря эффекту Холла в ходе эволюции ТС может образоваться вертикальный ТТС. Однако происходит это не всегда. В случае, когда по границе соседствующих разнополярных одинаковых магнитных областей ток течет вниз (а не вверх, как было в предыдущих работах) начальный токовый слой под влиянием эффекта Холла, наоборот, размывается и деградирует. Во второй части статьи этот вывод аналитически обобщен на случай начальных магнитных конфигураций произвольного вида; плазма при этом для простоты считается изотермической, а магнитное поле медленно меняющимся по вертикали. Показано, что нижняя граница солнечной короны соответствует высоте, где разреженность солнечной атмосферы становится достаточной для того, чтобы эффект Холла стал определяющим образом влиять на эволюцию магнитных полей, поступивших через фотосферу.

2. УРАВНЕНИЯ И ПОСТАНОВКА ЗАДАЧИ

Будем считать плазму верхней хромосферы столкновительной и квазинейтральной. Примем, что она состоит из протонного и электронного газов с одинаковым парциальным давлением и температурой. Рассмотрим слой с характерным значением температуры плазмы ${{T}_{*}}$ и, соответственно, характерным значением высоты однородной атмосферы

(1)

$H = {{k{{T}_{*}}} \mathord{\left/ {\vphantom {{k{{T}_{*}}} {(g{{m}_{i}})}}} \right. \kern-0em} {(g{{m}_{i}})}},$

где k – постоянная Больцмана; g – ускорение силы тяжести; m_i – масса протона. Характерную для слоя концентрацию одного вида частиц обозначим ${{N}_{*}}.$

С приходом того или иного магнитного поля в этом слое начнут происходить согласованные между собою изменения поля и состояния плазмы. Величины ${{T}_{*}}$, ${{N}_{*}}$ и B₀, где B₀ – характерное значение модуля магнитного поля в начальный момент, дают базовый набор независимых размерных параметров для теоретического описания этой ко-эволюции. (К набору надо добавить еще и g, если речь идет об астрофизической плазме вообще.) Учтем, что для общей ориентировки в физической ситуации хорошо подходит (безразмерная) величина характерного плазменного параметра

(2)

${{\beta }_{{*0}}} = \frac{{8\pi k{{N}_{*}}{{T}_{*}}}}{{B_{0}^{2}}},$

и в качестве базовых параметров возьмем тройку ${{T}_{*}}$, ${{N}_{*}}$ и β_*0, которая эквивалентна тройке ${{T}_{*}}$, ${{N}_{*}}$ и B₀, т.к.

(3)

${{B}_{0}} = \beta _{{*0}}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}\sqrt {8\pi k{{N}_{*}}{{T}_{*}}} .$

Используем полностью самосогласованную систему классических уравнений одножидкостной МГД с учетом эффекта Холла, магнитной вязкости и теплопроводности [Брагинский, 1963; Брушлинский и Морозов, 1974]. Предполагая, что силовые линии магнитного поля суть горизонтальные параллельные прямые, вдоль них нет изменений физических величин и отсутствуют компоненты всех векторов, кроме магнитного поля, ограничимся поиском ее двумерного решения. Соответствующая 2D МГД-система уравнений [Брушлинский и Морозов, 1974], куда мы ввели еще силу тяжести, имеет вид¹ ¹:

(4)

$\begin{gathered} \rho \left( {\frac{{\partial {\mathbf{v}}}}{{\partial t}} + \left( {{\mathbf{v}} \cdot \nabla } \right){\mathbf{v}}} \right) = - \nabla \left( {P + \frac{{{{B}^{2}}}}{2}} \right) - \frac{{{{\beta }_{{*0}}}}}{2}\rho {{e}_{g}}, \\ {{e}_{g}} \equiv - \frac{{\mathbf{g}}}{g}, \\ \end{gathered} $

(5)

$\frac{{\partial \rho }}{{\partial t}} + {\text{div}}\rho {\mathbf{v}} = 0,\,\,\,\,P = \frac{{{{\beta }_{{*0}}}}}{2}\rho T,\,\,\,\,\gamma = {5 \mathord{\left/ {\vphantom {5 {3,}}} \right. \kern-0em} {3,}}$

(6)

$\begin{gathered} \frac{{\partial {\mathbf{B}}}}{{\partial t}} = {\text{rot}}\left[ {{\mathbf{v}} \times {\mathbf{B}}} \right] - {\text{rot}}\Theta {\kern 1pt} {\mathbf{j}} + \frac{\xi }{2}\left[ {\nabla \frac{1}{\rho } \times \nabla ({{B}^{2}} + P)} \right], \\ {\mathbf{j}} = {\text{rot}}{\mathbf{B}}, \\ \end{gathered} $

(7)

$\begin{gathered} \frac{{{{\beta }_{{*0}}}}}{{2\left( {\gamma - 1} \right)}}\rho \left( {\frac{{\partial T}}{{\partial t}} + \left( {{\mathbf{v}} \cdot \nabla } \right)T} \right) + P{\text{\;div\;}}{\mathbf{v}} = \\ = {\text{div\;{\rm K}}}\nabla T + \Theta {\kern 1pt} {{j}^{2}} + \\ + \,\,\frac{\xi }{2}\left[ {\frac{{{{\beta }_{{*0}}}}}{{2\left( {\gamma - 1} \right)}}\left( {{\mathbf{j}} \cdot \nabla T} \right) + P~{\text{div}}~\frac{{\mathbf{j}}}{\rho }~} \right]. \\ \end{gathered} $

Входящие в уравнения величины (их обозначения общепринятые) обезразмерены здесь подобно тому, как это сделано впервые в работе [Брушлинский и Морозов, 1974] и применено во всех наших работах. За единицу плотности выбрана величина ${{\rho }_{*}} \equiv {{m}_{i}}{{N}_{*}},$ за единицу длины – высота однородной атмосферы H. Комбинации ${{B_{0}^{2}} \mathord{\left/ {\vphantom {{B_{0}^{2}} {\left( {4\pi } \right)}}} \right. \kern-0em} {\left( {4\pi } \right)}}$ и

${{v}_{{{\text{*}}0}}} \equiv {{{{B}_{0}}} \mathord{\left/ {\vphantom {{{{B}_{0}}} {\sqrt {4\pi {{\rho }_{*}}} }}} \right. \kern-0em} {\sqrt {4\pi {{\rho }_{*}}} }}$

используются как единицы, соответственно, газового давления и скорости плазмы. Соответственно, ${{t}_{{{\text{*}}0}}} \equiv {H \mathord{\left/ {\vphantom {H {{{v}_{{{\text{*}}0}}}}}} \right. \kern-0em} {{{v}_{{{\text{*}}0}}}}}$ оказывается единицей времени, а ${{c{{B}_{0}}} \mathord{\left/ {\vphantom {{c{{B}_{0}}} {\left( {4\pi H} \right)}}} \right. \kern-0em} {\left( {4\pi H} \right)}}$ – единицей плотности электрического тока; c – скорость света. В роли коэффициентов уравнений выступают безразмерная константа (указывающая на присутствие эффекта Холла в плазме; исходя из вида, назовем ее холловским параметром разреженности плазмы)

(8)

$\xi = \frac{c}{{eH}}\sqrt {\frac{{{{m}_{i}}}}{{4\pi {{N}_{*}}}}} ,$

а также локальные (безразмерные же) магнитная вязкость Θ и теплопроводность Κ, зависящие от единственной функции $T$ = T(x, z, t):

(9)

$\Theta \equiv \frac{{{{c}^{2}}}}{{4\pi \sigma H{{{v}}_{{*0}}}}} = {{\theta }_{*}}\beta _{{*0}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}{{T}^{{ - {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}},\,\,\,\,{\text{{\rm K}}} = {{\kappa }_{*}}\beta _{{*0}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}{{T}^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}$

(e – заряд позитрона; σ – проводимость плазмы). Постоянные безразмерные множители ${{\theta }_{*}}$ и ${{\kappa }_{*}}$ представляют собою комбинации общефизических констант и базисных размерных газовых параметров ${{T}_{*}}$ и ${{N}_{*}}$ рассматриваемого хромосферного слоя (вид ${{\theta }_{*}}$ и ${{\kappa }_{*}}$ возникает из стандартных классических формул плазменной газодинамики [Прист, 1985; Спитцер, 1965; Aschwanden, 2004; Balescu, 1988] при обезразмеривании уравнений – подробнее см. в любой из работ [Алексеева и Кшевецкий, 2011, 2019; Alekseeva and Kshevetskii, 2015]). Отметим еще полезное для интерпретации проводимого исследования соотношение ${\xi \mathord{\left/ {\vphantom {\xi \Theta }} \right. \kern-0em} \Theta } \cong {{\omega }_{e}}{{\tau }_{e}},$ где ω_e – частота ларморовского вращения электрона; τ_e – временнóй интервал его столкновений с протонами [Брушлинский и Морозов, 1974].

Воспользуемся декартовой системой координат (x, y, z), ось z которой направлена вертикально вверх, ось y совпадает по направлению с B₀ в магнитной отсчетной точке, а ось x выбрана так, чтобы получилась правая тройка базисных векторов. В этом случае

${\mathbf{B}} = \left( {0,B,0} \right),\,\,\,\,{\mathbf{v}} = \left( {{{v}_{x}},0,{{v}_{z}}} \right),\,\,\,\,{\mathbf{j}} = \left( {{{j}_{x}},0,{{j}_{z}}} \right),\,\,\,\,\frac{\partial }{{\partial y}} = 0.{\text{\;}}$

Поскольку электрический ток ${\mathbf{j}} = {\text{rot}}~{\mathbf{B}},$ имеем

${\mathbf{j}} = - \frac{{\partial B}}{{\partial z}}{{{\mathbf{e}}}_{x}} + \frac{{\partial B}}{{\partial x}}{{{\mathbf{e}}}_{z}},$

так что, отметим, в принятой 2D-геометрии линии уровня величины B являются одновременно и линиями электрического тока.

Обратим внимание, что влияние эффекта Холла на изменения магнитного поля осуществляется через третий член правой части уравнения динамики магнитного поля (6) – назовем этот член “градиентно-холловским”, чтобы не упускать из виду, что и при малых значениях ξ (т.е. и в сравнительно плотном хромосферном слое) плазма будет вести себя как холловская, если только градиенты величин достаточно резки и ориентированы подходящим образом. Присутствие этого члена в системе уравнений (4)–(7) нарушает ее симметрию относительно замены B → (–B). Из-за этого две одинаковые по виду и отличающиеся только знаком B магнитные конфигурации, оказавшиеся в холловской плазме хромосферы, вызовут разный ход совместной эволюции (ко-эволюции) магнитного поля и плазмы² ².

Следуя выводам работы [Алексеева и Кшевецкий, 2019], рассмотрим две разнополярные магнитные области, расположенные рядом друг с другом по горизонтали. Мы изучим последствия поступления поля

(10)

$\begin{gathered} {{\left. {B\left( {x,z} \right)} \right|}_{{t{\kern 1pt} = {\kern 1pt} 0}}} = - \left[ {1 + \zeta \exp \left( { - \zeta } \right)} \right]\operatorname{th} (bX), \\ \zeta \equiv {{{{Z}^{2}}} \mathord{\left/ {\vphantom {{{{Z}^{2}}} {z_{k}^{2}}}} \right. \kern-0em} {z_{k}^{2}}}, \\ \end{gathered} $

где $X \equiv x - {{x}_{c}},$ $Z \equiv z - {{z}_{c}},$ ${{x}_{c}} = {{{{x}_{{{\text{max}}}}}} \mathord{\left/ {\vphantom {{{{x}_{{{\text{max}}}}}} {2,}}} \right. \kern-0em} {2,}}$ ${{z}_{c}} = {{{{z}_{{{\text{max}}}}}} \mathord{\left/ {\vphantom {{{{z}_{{{\text{max}}}}}} {2,}}} \right. \kern-0em} {2,}}$ ${{x}_{{{\text{max}}}}} = 0.207,$ ${{z}_{{{\text{max}}}}} = 2.8,$

что соответствует направлению тока вниз в контактном токовом слое между областями, имеющем резкость b и протяженность z_k. Такое поле лишь знаком отличается от уже исследованного в работе [Алексеева и Кшевецкий, 2019]. Плазму в начальный момент считаем всюду неподвижной и имеющей одинаковую по всей расчетной области температуру, так что

(11)

${{\left. {v\left( {x,z} \right)} \right|}_{{t{\kern 1pt} = {\kern 1pt} 0}}} = 0,\,\,\,\,{{\left. {T\left( {x,z} \right)} \right|}_{{t{\kern 1pt} = {\kern 1pt} 0}}} = 1.$

Там, где нет магнитного поля, плотность распределена по закону Больцмана

(12)

${{\rho }_{{{\text{G\;}}}}} = \exp \left[ {\left( {{{ - Z} \mathord{\left/ {\vphantom {{ - Z} H}} \right. \kern-0em} H}} \right)} \right]{\text{,}}$

что в условиях (11) по второму соотношению (5) соответствует давлению ${{P}_{{\text{G}}}} = {\text{\;}}{{{{\beta }_{{{\text{*}}0{\text{\;}}}}}{{\rho }_{{\text{G}}}}} \mathord{\left/ {\vphantom {{{{\beta }_{{{\text{*}}0{\text{\;}}}}}{{\rho }_{{\text{G}}}}} 2}} \right. \kern-0em} 2}.$ Пусть в начальный момент газовое и магнитное давления всюду сбалансированы, так что

(13)

${{\left. {P\left( {x,z} \right)} \right|}_{{t{\kern 1pt} = {\kern 1pt} 0}}} = {{P}_{{\text{G}}}}\left( Z \right) - \frac{{{{{\left. {B{{{\left( {x,~z} \right)}}^{2}}} \right|}}_{{t{\kern 1pt} = {\kern 1pt} 0}}}}}{2},$

(14)

${{\left. {\rho \left( {x,z} \right)} \right|}_{{t{\kern 1pt} = {\kern 1pt} 0}}} = 2~\frac{{{{{\left. {P\left( {x,z} \right)} \right|}}_{{t{\kern 1pt} = {\kern 1pt} 0}}}}}{{{{\beta }_{{*0~}}}}}.$

Поставленную задачу Коши (4)–(7) с начальными условиями (10)–(14) решим путем численного моделирования.

3. МОДЕЛИРОВАНИЕ. ДОСТОИНСТВО МЕТОДА

Наша расчетная область охватывает 280 км по горизонтали и 3920 км по вертикали сеткой 80 × × 247 узлов соответственно. При доступной в таком моделировании резкости b магнитной конфигурации (10) градиентно-холловский член будет ощутим в (6) лишь при работе с достаточно разреженной плазмой. Учитывая, что хромосфера, по современным источникам [Priest, 2014], может простираться вплоть до высоты 15 000 км, будем иметь в виду ее верхний слой; концентрацию протонов в нем рассчитаем, исходя из того [Demoulin and Klein, 2000], что в нижнем слое полностью ионизованной хромосферы эта величина составляет $~{{10}^{{15}}}$ м^–3 (это слои Π^II и Π^I по терминологии работы [Алексеева и Кшевецкий, 2019]). С заданием размерного параметра ${{T}_{*}}$ = = 50 000 К, а ${{\beta }_{{*0}}} = 7.5$ определятся величины всех параметров и множителей в задаче Коши (4–7, 10–14).

Решение задачи проводится численным конечно-разностным консервативным методом, который был специально разработан для солнечной плазмы и воплощен в программе PLASMAT [Кшевецкий, 2013]. Формулы численного интегрирования по своей структуре напоминают формулы метода Лакса–Вендроффа, но на первом полушаге применяются неявные аппроксимации. Метод аппроксимирует уравнения со вторым порядком точности по времени и пространству. Для аппроксимации пространственных производных используются центральные разности, поэтому схема не обладает численной вязкостью (аналогично [LeVeque, 1992; Thomas and Roe, 1993]). Особенностью метода является его способность автоматически строить обобщенные негладкие решения, начиная с момента, когда решение со временем теряет гладкость. Поэтому мы можем сравнительно долго отслеживать ход совместной эволюции плазмы и магнитного поля – начиная от гладких начальных распределений физических величин и включая стадию, когда под влиянием нелинейных процессов возникают и действуют резкие неоднородности (фронты, мелкомасштабная турбулентность и т.п.).

Более того, при работе данного алгоритма сеточные возмущения нарастают медленно. На временнóм интервале их малости они играют роль возмущений, которые провоцируют развитие физических неустойчивостей, свойственных данной магнитной конфигурации. Так, магнитное поле, в начальный момент, согласно (10), антисимметричное относительно оси X = 0, в точном решении (4–7, 10–14) должно было бы таким и оставаться, однако при численном решении таковым не остается, поскольку развивается изгибная неустойчивость, присущая этой конфигурации как плоскому пинчу. Поэтому в нашем моделировании, как и в реальной природе, процесс, соответствующий точному решению задачи Коши (4–7, 10–14), подвергаясь возмущениям, проявляется вместе со своими (физическими) неустойчивостями. Таким образом, решая задачу путем численного моделирования, мы одновременно исследуем ее решение на устойчивость.

4. РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ И ИХ АНАЛИЗ

При названных выше значениях базовых параметров ${{N}_{*}},~{{T}_{*}},{{\beta }_{{*0}}}$ размерная единица скорости и размерная единица времени составляют, соответственно, ${{v}_{{*0}}} = 10.5$ км/с и ${{t}_{{*0}}}$ = 2.2 мин. Моделирование отражает (~4.4–5.3)-минутные эволюции областей. Представив при описании результатов безразмерное время t величиной τ ≡ t/0.008, мы следим за ко-эволюцией поля и плазмы вплоть до значений τ = ∼250–300. Как и в работе [Алексеева и Кшевецкий, 2019] (где рассматривались конфигурации с током вверх при их вертикальной протяженности z_k = 0.34 в выражении (10) для начального магнитного поля), решения здесь получены для резкости b ≡ αq, где

(15)

$q = 130,\,\,\,\,\alpha = \frac{1}{2},\,\,\,\,\frac{1}{{1.5}},\,\,\,\,1,\,\,\,\,1.5,\,\,\,\,2,$

однако теперь ток на вертикальной оси конфигурации направлен вниз.

Обнаружено, что при одних и тех же ξ, Θ, Κ в задаче (4–7, 10–14) свойства решений с пограничным током вверх (ТС↑) и вниз (ТС↓) неодинаковы.

4.1. Разная способность токов вверх и токов вниз создавать тонкие токовые слои

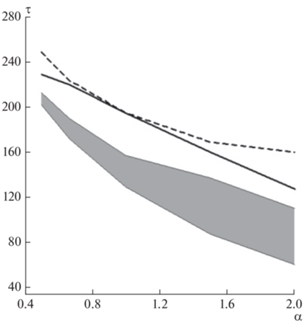
Бросается в глаза неодинаковая способность ТС↑ и ТС↓ создавать транзиентные структуры в виде тонкого токового слоя (ТТС) – соответственно, тонкого токового слоя с током вверх (ТТС↑) и тонкого токового слоя с током вниз (ТТС↓). Прекращение существования ТТС мы определяли по моменту появления первых признаков развития на нем изгибной неустойчивости. В ходе эволюции ТС↓ позже и на более короткое время приобретают вид ТТС↓ (рис. 1).

Рис. 1.

Время существования транзиентной структуры вида ТТС в зависимости от резкости α магнитной конфигурации: для ТТС↑ – интервал между нижней и верхней границами заштрихованной области; для ТТС↓ – интервал между жирной сплошной и пунктирной кривыми.

4.2. Различие транзиентных форм при эволюции ТС↑ и ТС↓

Эволюция ТС↑ идет монотонно вплоть до момента появления изгибной неустойчивости, тогда как эволюция ТС↓ на начальном этапе имеет хаотически колебательный характер.

О пространственном распределении магнитного поля удобно судить по полутоновым артам; напомним, что в принятой 2D-геометрии линии одинаковых значений B соответствуют линиям электрического тока (рис. 2). На картах тоже видна зависимость хода эволюции поля от направления начального тока. К тому времени (см. положение экстремумов на рис. 2а, 2б и 3а, 3б), когда ТС↑, сузившись, становится ТТС↑, ТС↓ демонстрирует даже некоторое утолщение (экстремумы расходятся на большее расстояние), но позже и он образует ТТС↓ (рис. 3в, 3г).

Рис. 2.

Полутоновые карты распределения начального магнитного поля ${{\left. {\mathbf{B}} \right|}_{{\tau = 0}}}$ в перпендикулярной вектору B плоскости для α = 1.5 при ТС↑ (а) и ТС↓ (б). Светлые (темные) тона соответствуют B > 0 (B < 0), интенсивность цвета отражает величину B. На каждой карте тонкими линиями нанесены контуры уровней ±1, ±0.8, ±0.6, ±0.4, ±0.2, 0 величины B (в принятой двумерной геометрии они же одновременно являются линиями электрического тока). Яркая белая точка отмечает местоположение минимума величины, яркая черная – максимума. Изображение растянуто в 4.4 раза по горизонтали. Толстые черные линии ограничивают область, которую мы будем воспроизводить на аналогичных картах ниже.

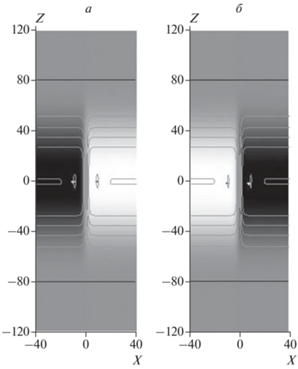
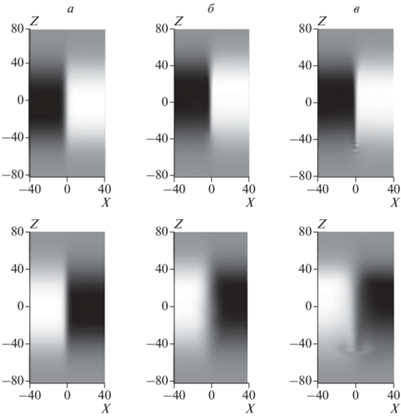
Рис. 3.

Полутоновые карты распределения B в перпендикулярной вектору B плоскости для ТС↑ (вверху) и для ТС↓ (внизу) в четыре момента времени, соответствующие ординатам точек на рис. 1 при значении абсциссы α = 1.5 (на том же рисунке) у двух огибающих заштрихованной области, а также у жирной сплошной и пунктирной кривых: τ = 87 (а), τ = 137 (б), τ = 160 (в) и τ = 169 (г). Светлые (темные) тона соответствуют B > 0 (B < 0), интенсивность цвета отражает величину |B|. Яркая белая (черная) точка отмечает местоположение минимума (максимума) величины B. Представлена центральная часть счетной области. Изображение растянуто в 4.4 раза по горизонтали.

Под ТТС↑ располагается дополнительная четкая структура в виде свисающего “хобота” или “ствола” какого-то оружия (верхние рис. 3в, 3г; возможно, с этим явлением связаны сообщения СМИ о неких “искусственных объектах”, “откачивающих энергию” из Солнца или “стреляющих” в него [Алексеева и Кшевецкий, 2013]). Под ТТС↓ мы видим нечто вроде наконечника стрелы (нижние рис. 3в, 3г).

4.3. “Бесхолловские” черты в эволюции ТС↓

Наличие “стрелы” (или “всплеска”, если стрела недостаточно развилась) является зримым свидетельством действия перетяжечной неустойчивости. Действительно, как говорилось в п. 1, первичная перетяжка в природных условиях астрофизической плазмы через некоторое время раздваивается, благодаря чему в область между перетяжками подкачивается вещество. В конфигурациях с горизонтальной осью получившийся плазмоид в дальнейшем оказывается сердцевиной, симметричной относительно обеих осей крестообразной структуры [Алексеева и Кшевецкий, 2011; Alekseeva and Kshevetskii, 2015]. Когда ось вертикальна, плазмоид (видимый на картах как серое пятно на оси из-за близости B к нулю внутри него – см. нижние рис. 3в, 3г) тонет, создавая “стрелу”/“всплеск” под магнитной конфигурацией. Однако все эти образования в полной мере генерируются полями пинчевого типа лишь при отсутствии эффекта Холла, поскольку последний действует в сторону подавления перетяжечной неустойчивости (см. в работе [Алексеева и Кшевецкий, 2019] рис. 7, 8 и комментарий к ним). Таким образом, наш численный эксперимент приводит к выводу, что в абсолютно одинаковых условиях ТС↓ в меньшей степени испытывает действие эффекта Холла, чем ТС↑.

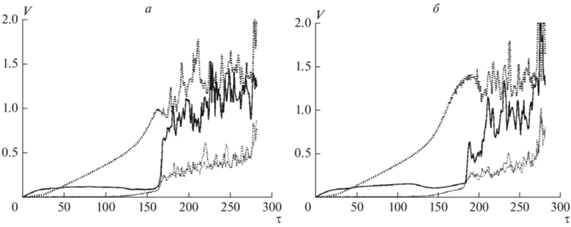
Еще одно “бесхолловское” качество свойственно ТС↓. По сравнению с ТС↑, при ТС↓ магнитная энергия эффективнее превращается в энергию упорядоченного движения плазмы (рис. 4). Основное различие наблюдается в скорости вертикального движения вниз (ср. жирные пунктирные кривые на панелях а, б рис. 4). Повышенная скорость вниз в случае ТС↓ связана с тонущим плазмоидом и говорит о действии порождающей его перетяжечной неустойчивости, развитию которой в случае ТС↑ мешает эффект Холла.

Рис. 4.

Эволюция скоростного поля для случая ТС↑ (а) и ТС↓ (б). Экстремальные по расчетной области значения V компоненты v_x (пара тонких кривых) и v_z (пара жирных) как функции времени τ. Сплошные кривые представляют максимумы значений соответствующих компонент скорости, пунктирные – абсолютные значения минимумов.

4.4. Контрольный численный эксперимент

Проведенное моделирование выявило разнообразные отличия эволюции ТС↑ и ТС↓ в холловской плазме хромосферы. Однако осталось неясным, каким образом эффект Холла эту разницу создает. Мы не можем непосредственно выявить специфику собственного воздействия эффекта Холла на эволюцию B простым повторением численного решения системы (4)–(7) при “отключении” всех членов правой части уравнения (6), кроме градиентно-холловского члена с ξ (далее для краткости, холловского): наша система полностью самосогласована, и поэтому заранее нет оснований пренебрегать другими членами по сравнению с холловским. Чтобы отделить действие эффекта Холла от других факторов, приходится привлекать комплекс результатов ранее проведенных исследований.

В работе [Алексеева, 2006] стационарное решение системы (4)–(7), записанной для ${{\kappa }_{*}}$ → ∞ в (7) (изотермичной плазмы) и произвольных значений остальных параметров, найдено аналитически путем разложения в ряд (4)–(7) по обратным степеням большого ${{\beta }_{{*0}}}$ в предположении медленных изменений величин вдоль вертикали

(16)

${\partial \mathord{\left/ {\vphantom {\partial {\partial z}}} \right. \kern-0em} {\partial z}} \ll {\partial \mathord{\left/ {\vphantom {\partial {\partial x.}}} \right. \kern-0em} {\partial x.}}$

Оказалось, что стационарное решение всегда соответствует токовому слою с током вверх. В качестве условия существования решения выступил такой набор параметров, при котором холловский член в правой части уравнения (6) значительно превосходит конвективный член, отвечающий за вмороженность магнитного поля (или кратко: магнитное поле оказывается над-конвективным). Исходя из установленного набора значений параметров, (квази)стационарное решение удалось получить в контрольном численном эксперименте работы [Алексеева и Кшевецкий, 2019], несмотря на то, что плазма уже не была изотермичной, а соотношение (16) выполнялось только в центральной части счетной области.

Очевидно, стационарность над-конвективного решения означает, что в (6) омические потери уравновешены действием холловского члена, последний же пропорционален величине ξ. Проведя численный эксперимент с бóльшим значением $\xi {\text{,}}$ чем было при квазистационарности, мы увидим, как выглядит нестационарная эволюция в над-конвективном над-омическом режиме – т.е. под преимущественным влиянием холловского члена в (6). Рисунок 5 представляет результаты численного эксперимента со значением $\xi $ в 1.3 раза бóльшим, чем использованное в работе [Алексеева и Кшевецкий, 2019] при получении квазистационарного решения. Оказывается (рис. 5а, 5б), что собственное воздействие эффекта Холла на совместную эволюцию поля и плазы выражается в том, что начальный ТС↑ становится тоньше и превращается в ТТС↑, тогда как начальный ТС↓, наоборот, деградирует, увеличивая толщину. Но затем его толщина снова становится меньше, что вместе с формированием слабого всплеска под ТС↓ (рис. 5в) говорит о нарастании влияния конвективного члена (усилении роли вмороженности) в более позднюю стадию эволюции.

Рис. 5.

Магнитное поле, моделируемое в ходе численного эксперимента по выявлению характера собственного воздействия эффекта Холла на поле и плазму, при ТС↑ (верхний ряд) и при ТС↓ (нижний) в разные моменты времени: $\tau = 0$ (a); $\tau = 130$ (б); $\tau = 260$ (в).

4.5. Интерпретация результатов численного моделирования

Подведем итог. Изменения B (рис. 2, 3 ) происходят под влиянием всех трех членов, составляющих правую часть уравнения (6): конвективного, омического и градиентно-холловского. Конвективный член делает возможной перетяжечную неустойчивость, в природной плазме она вызывает сужение начального токового слоя по всей его длине (п. 1). При ТС↑ такое же сужающее действие оказывает градиентно-холловской член. Тогда как в случае ТС↓ эти два фактора конкурируют. Отсюда наблюдаемые в наших численных экспериментах явления: немонотонность эволюции ТС↓ (п. 4.2), схожие с бесхолловскими результаты развития ТС↓ (п. 4.3, 4.4) и редкость создания ТТС↓ по сравнению с ТТС↑ (п. 4.1).

5. АНАЛИТИЧЕСКОЕ ИССЛЕДОВАНИЕ СПЕЦИФИКИ ПОВЕДЕНИЯ МАГНИТНОГО ПОЛЯ В ХОЛЛОВСКОЙ ПЛАЗМЕ ХРОМОСФЕРЫ

Путем аналитического исследования мы покажем, что таким же образом эффект Холла меняет магнитные конфигурации разных видов. В отличие от (15), теперь рассматриваем произвольные значения резкости горизонтальных изменений поля (мы сохраним для нее обозначение q); а высоту далее имеем в виду не только большую (ср. п. 3).

5.1. Случай изотермической плазмы

Для простоты представим себе, что плазма изотермична. Тогда уравнение ее состояния в (5) приобретает вид

$P = \left( {{{{{\beta }_{{*0}}}} \mathord{\left/ {\vphantom {{{{\beta }_{{*0}}}} 2}} \right. \kern-0em} 2}} \right)\rho {\text{.}}$

Соответственно, безразмерная газодинамическая скорость звука $s = \sqrt {{{{{\beta }_{{*0}}}} \mathord{\left/ {\vphantom {{{{\beta }_{{*0}}}} 2}} \right. \kern-0em} 2}} .$ Мы имеем дело с поступившими в хромосферу магнитными полями, для которых важны газовые характеристики окружающей среды. Эта ситуация соответствует достаточно большим значениям β, а значит, и большой газодинамической скорости звука s. При таком ее значении ρ и v будут быстро подстраиваться под изменяющееся магнитное поле, так что их можно считать квазистационарными. Полная система уравнений (4)–(7) для плазмы в присутствии силы тяжести при этом получает вид:

(17)

$\rho w = - \nabla \left( {{{s}^{2}}\rho + {{{{B}^{2}}} \mathord{\left/ {\vphantom {{{{B}^{2}}} 2}} \right. \kern-0em} 2}} \right) - {{s}^{2}}\rho {{e}_{g}},\,\,\,\,{{e}_{g}} \equiv - \frac{g}{g},$

(18)

${\text{div}}\rho {\mathbf{v}} = 0,$

(19)

$\frac{{\partial {\mathbf{B}}}}{{\partial t}} = {{\nu }_{{*0}}}\Delta {\mathbf{B}} + {\text{rot}}\left[ {{\mathbf{v}} \times {\mathbf{B}}} \right] + \xi \left[ {\nabla \frac{1}{\rho }\,\, \times \nabla \frac{{{{B}^{2}}}}{2}} \right].$

Здесь $w = \left( {{\mathbf{v}}\nabla } \right){\mathbf{v}}.$ Магнитная вязкость в уравнении динамики магнитного поля (19)

(20)

${{\nu }_{{*0}}} = {{\left. \Theta \right|}_{{T{\kern 1pt} \equiv {\kern 1pt} {{T}_{*}}}}}{\kern 1pt} ,$

согласно (9), постоянна в силу изотермичности плазмы.

5.2. Разложение системы уравнений по степеням s^–2

Систему (17)–(19) можно разложить по степеням малой величины (s^–2). Из уравнения (17) видно, что главным членом разложения ρ является Больцмановское распределение плотности

(21)

${{\varrho }^{{(0)}}} = \exp \left( { - z} \right).$

Пусть магнитное поле (и связанные с ним величины) характеризуется наличием горизонтальных градиентов, больших по сравнению с вертикальными, так что, аналогично (16),

(22)

$\frac{\partial }{{\partial x}} \sim q \gg \frac{\partial }{{\partial z}} \sim 1,$

где q – некоторая большая величина (вообще говоря, это некая функция медленной координаты z, не меняющая своего порядка при дифференцировании). Непосредственно по структуре уравнения непрерывности (18) видно, что v_z ~ qv_x. Привлекая z-компоненту уравнения Эйлера (17), убеждаемся, что

(23)

${{v}_{z}}\sim B$

(напомним, что B ∼ 1 согласно принятой нормировке). Другая компонента уравнения Эйлера позволяет определить поправку к плотности плазмы, связанную с внесением в среду магнитного поля. Об этой поправке мы дальше не говорим, поскольку она не вошла в главный член разложения интересующего нас градиентно-холловского члена уравнения (19) динамики магнитного поля

(24)

$\frac{{\partial {\mathbf{B}}}}{{\partial t}} = {{\nu }_{{*0}}}\Delta {\mathbf{B}} + {\text{rot}}\left[ {{\mathbf{v}} \times {\mathbf{B}}} \right] + \xi \left[ {\nabla \frac{1}{{{{\rho }^{{(0)}}}}} \times \nabla \frac{{{{B}^{2}}}}{2}} \right].$

5.3. Задача о (чистой) градиентно-холловской эволюции магнитного поля и ее решение

Согласно уравнению (24), изменения B со временем происходят под действием трех факторов: омической диссипации (первый член правой части уравнения), конвективного сноса частично вмороженных силовых линий (второй член) и эффекта Холла в сочетании с градиентом плотности, создаваемым силой тяжести (третий, градиентно-холловский, член). Характер изменений B под действием диссипации и сноса хорошо известен. Для выявления специфики влияния эффекта Холла на магнитное поле в присутствии силы тяжести рассмотрим случай, когда первый и второй члены в правой части (24) много меньше третьего и ими можно пренебречь (при каких параметрах такое возможно, выяснится ниже). Тогда

(25)

$\frac{{\partial B}}{{\partial t}} = \alpha B\frac{{\partial B}}{{\partial x}}~,\,\,\,\,\alpha = \frac{\xi }{{{{\varrho }^{{(0)~}}}}}$

(отметим, что координата z входит в получившееся уравнение лишь неявно через коэффициент α). Пусть в начальный момент t = 0

(26)

$B = {{\Phi }}\left( {x,~z} \right),$

где ${{\Phi }}$ – некоторая (гладкая) функция, зависимость которой от аргументов удовлетворяет условию (22). Медленную зависимость от z мы в дальнейшем всюду подразумеваем, но в формулах указывать не будем. Однако в напоминание о ней производную Φ по оставшейся (быстрой) пространственной переменной x будем обозначать как частную – штрихом наверху вместе с указанием быстрой переменной в нижнем индексе.

Уравнение (25) представляет собой неприведенный вид известного уравнения Хопфа, описывающего формирование разрывов (в частности, ударных волн), опрокидывание фронтов и т.п. в ходе эволюции изначально гладких начальных распределений некоторой физической величины [Зайцев и Полянин, 2003], в данном случае, B.

Замена переменной τ = αt приводит задачу Коши (25), (26) к виду

(27)

$\frac{{\partial B}}{{\partial \tau }} - B\frac{{\partial B}}{{\partial x}} = 0,$

(28)

$B = {{\Phi (}}x{\text{)}},\,\,\,\,\tau = 0.$

Интегрируя характеристическую систему

(29)

$\frac{{d\tau }}{1} = \frac{{dx}}{{ - B}} = \frac{{dB}}{0}$

квазилинейного уравнения в частных производных первого порядка (27), найдем его общее решение

(30)

$B = {{C}_{1}},\,\,\,\,x + {{C}_{1}}\tau = {{C}_{2}},$

где C₁, C₂ – постоянные интегрирования. Подстановка (30) в начальное условие (28), предварительно представленное в параметрическом виде

(31)

$\tau = 0,\,\,\,\,x = \eta ,\,\,\,\,B = \Phi \left( \eta \right),$

определяет постоянные ${{C}_{1}} = \Phi \left( \eta \right),$ ${{C}_{2}} = \eta $ для задачи Коши (27), (28). Внося их в (30), получаем ее решение в параметрическом виде

(32)

$B = \Phi \left( \eta \right),$

(33)

$x = \eta - \Phi \left( \eta \right)~\tau .$

Каждая характеристика (33) соответствует определенному значению параметра $\eta $ – иначе говоря, “быстрой” горизонтальной координате той или иной точки начального профиля B. Из (32) следует неизменность значений B вдоль характеристики.

5.4. Свойства градиентно-холловской эволюции магнитного поля

Еще до конкретизации вида Φ найденное решение позволяет сделать ряд выводов о свойствах градиентно-холловской эволюции (далее, ГХЭ) магнитного поля в хромосферной плазме:

А. Экстремальные значения B не меняются со временем.

Б. На участке с ненулевыми значениями Φ(η) при $\Phi _{\eta }^{{\text{'}}} > 0$ точка профиля, соответствующая большему $\eta $, будет догонять точку с меньшим $\eta $ и профиль будет становиться все круче. При ${{\Phi }}_{\eta }^{{\text{'}}} < 0$ она будет отставать, отчего профиль с течением времени становится более пологим. Эти изменения профиля магнитного поля B в ходе чистой ГХЭ весьма наглядны: они напоминают наблюдаемые на земном ландшафте изменения внешнего вида песчаной дюны под действием ветра. Отсюда ясно, что при поступлении магнитного поля в верхнюю хромосферу характер будущей его эволюции определяется знаком производной его начального профиля по горизонтальной переменной – иначе говоря, знаком вертикальной компоненты начального тока. Локальный электрический ток, направленный вверх, будет со временем увеличивать свою плотность, тогда как ток, текущий вниз, будет ее уменьшать. Или кратко: ток вверх эволюционирует в сторону создания тонкого токового слоя, а ток вниз деградирует.

В. Нейтральные точки начального профиля (где B = 0) в ходе ГХЭ не меняют своего местоположения в пространстве.

Г. Таким образом, нейтральная плоскость внутри токового слоя остается неподвижной. Согласно сказанному в п. Б, токовый слой сужается к ней, если ток течет вверх, и расширяется, когда ток направлен вниз.

Д. Поведение обостряющихся профилей “магнитных дюн” мы можем отслеживать лишь до того времени, пока они не станут слишком крутыми, ибо вслед за этим произойдет потеря однозначности решения (по наглядной аналогии с дюнами можно сказать, что крутой склон профиля опрокинется или обрушится)³ ³. Интервал времени до момента потери однозначности, т.е. до совпадения точек x для параметров η₁ и η₂ равен значению

$\tau = {{\tau }_{ + }}$

в точке пересечения соответствующих характеристик (33), т.е.

(34)

${{\tau }_{ + }} = \frac{{{{\eta }_{2}} - {{\eta }_{1}}}}{{\Phi \left( {{{\eta }_{2}}} \right) - \Phi \left( {{{\eta }_{{1о}}}} \right)}}$

При крутых профилях, меняющихся в соответствии с (22), на участках с $\Phi _{\eta }^{{\text{'}}} > 0$ разница η₂ – η₃ остается небольшой, и выражение (34) можно записать через производную. Соответственно, определится интервал времени, в течение которого решение задачи (25), (26) сохраняет однозначность во всех точках профиля,

(35)

${{\left( {{{\tau }_{ + }}} \right)}_{{{\text{min}}}}} = {1 \mathord{\left/ {\vphantom {1 {{{{[\Phi _{x}^{'}]}}_{{{\text{max}}}}}}}} \right. \kern-0em} {{{{[\Phi _{x}^{'}]}}_{{{\text{max}}}}}}}.$

5.4.1. Примеры эволюции конкретных магнитных полей

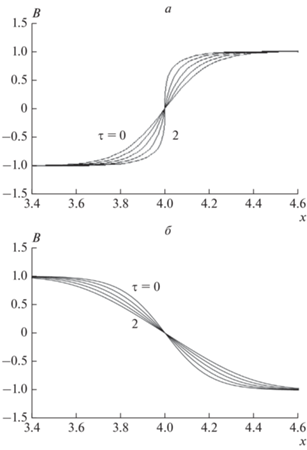
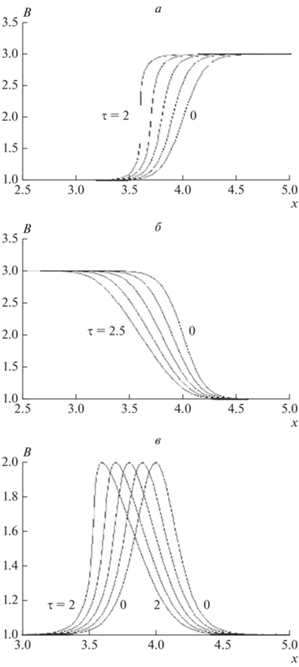
По рисункам 6, 7 можно видеть, что “магнитные дюны”, определенные решением задачи Коши (17)–(19), при различных профилях (26) начального магнитного поля ${{\left. B \right|}_{{t{\kern 1pt} = {\kern 1pt} 0}}} = \Phi \left( {x,~z} \right)~$ ведут себя так, как при ветре со стороны больших значений x вели бы себя земные дюны: они меняют положение по x в координатном пространстве, уменьшая крутизну склона или, наоборот, увеличивая ее (в пределе вплоть до опрокидывания).

Рис. 6.

Магнитное поле B в моменты времени τ = 0, 0.5, 1, 1.5, 2 (для второго из перечисленных далее случаев распределения также и в момент τ = 2.5) при различных формах начального профиля Φ(u), где u = 5(y – 4): (а) $\Phi = \operatorname{th} u + 2$ (ток направлен вверх); (б) ${{\Phi }} = - \operatorname{th} u + 2$ (ток направлен вниз); (в) ${{\Phi }} = {{\left[ {\operatorname{ch} u} \right]}^{{ - 2}}} + 1]$ (одиночный “горб”).

5.5. Область проявления ГХЭ магнитных полей в чистом виде

Мы рассмотрели чистую (над-диссипативную, над-конвективную) ГХЭ магнитного поля, которая возникает, когда уравнение (24) динамики B принимает вид (25). С учетом соотношений (22), (23) можно сказать, что это происходит при

(36)

$\xi q \gg 1,\,\,\,\,\xi q \gg {{\nu }_{{*0}}}{{q}^{2}}.$

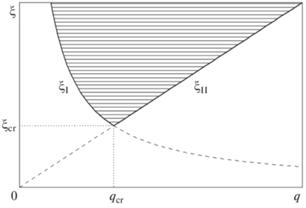
Включая сюда условно еще пограничное состояние, будем считать областью чистой ГХЭ область

(37)

$\xi \geqslant {{\xi }_{{\text{I}}}} \equiv {{q}^{{ - 1}}},$

(38)

$\xi \geqslant {{\xi }_{{{\text{II}}}}} \equiv {{\nu }_{{*0}}}q.$

Соответственно, в заштрихованной области рис. 8 возможна чистая ГХЭ магнитных полей с той или иной резкостью q пространственного распределения. Минимальному значению холловского параметра разреженности ξ = ξ_cr соответствует единственное значение $q = {{q}_{{{\text{cr}}}}},$ где

(39)

${{\xi }_{{{\text{cr}}}}} = \nu _{{*0}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}},\,\,\,\,~{{q}_{{{\text{cr}}}}} = \nu _{{*0}}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}.$

Критические величины ξ_cr и q_cr зависят от величины характерного магнитного поля B₀, которое входит через магнитную вязкость. Переписав (20) в эквивалентном виде

(40)

${{\nu }_{{{\text{*}}0}}} = {{\theta }_{*}}\beta _{{{\text{*}}0}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}},~$

(41)

${{\theta }_{*}} = {{\theta }_{{\text{*}}}}({{T}_{*}}) = \frac{{{{c}^{2}}}}{{4\pi {{\sigma }_{*}}H}}\sqrt {\frac{{{{m}_{i}}}}{{2k{{T}_{*}}~}}} ,$

получим

(42)

${{\xi }_{{{\text{cr}}}}} = \theta _{*}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}\beta _{{{\text{*}}0}}^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}},$

(43)

${{q}_{{{\text{cr}}}}} = \theta _{*}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}\beta _{{{\text{*}}0}}^{{ - {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}~ = \frac{1}{{{{\xi }_{{{\text{cr}}}}}}}.$

Таким образом, холловский параметр разреженности ξ, определенный выражением (8), указывает область хромосферных высот, где поступающие снизу магнитные поля с данными значениями параметров β_*0 и q в дальнейшем будут вести себя как “магнитные дюны”.

Рис. 7.

Магнитное поле токового слоя в моменты времени τ = 0, 0.5, 1, 1.5, 2 при начальных профилях Φ(u), где u = 5(y – 4): (а) $\Phi = \operatorname{th} u$ (ток вверх); (б) ${{\Phi }} = - \operatorname{th} u$ (ток вниз).

Рис. 8.

Область (заштрихована) проявления свободной градиентно-холловской эволюции на плоскости (q, ξ).

5.6. Самопроизвольный переход ГХЭ в другие режимы

При токе вверх его слой со временем становится тоньше (п. 5.4Б). В волновом пространстве – т.е. по резкости q – этот процесс соответствует удалению от левой предельной кривой ξ = ξ_I на рис. 8. Поэтому эволюция поля приобретает со временем все более над-конвективный характер. Стремление профиля к опрокидыванию (п. 5.4Д) означает, что у любой части магнитной неоднородности с током вверх q → ∞. Это значит, что у этой части магнитной неоднородности q неизбежно через какое-то время начнет соответствовать правой предельной кривой ξ = ξ_II, где в изменениях магнитного поля начинают главенствовать омические потери. Таким образом, тонкий токовый слой с током вверх, возникающий в процессе ГХЭ, на поздней ее стадии будет отдавать свою энергию на нагрев плазмы. Какой именно получится эта передача, на основе знания лишь о чистой ГХЭ сказать нельзя – тем более, что итог передачи должен зависеть от конкретного вида начальной магнитной конфигурации. Вообще же омическая диссипация создает диффузию тока, и она должна препятствовать процессу дальнейшего утоньшения тонкого токового слоя. Последнее утверждение согласуется с выводом работы [Алексеева, 2006] о том, что в условиях хромосферы возможно самоподдержание стационарного очень тонкого токового слоя, где действие эффекта Холла в поле силы тяжести уравновешивает омические потери – и такая структура имеет место исключительно при токе вверх.

При токе вниз идет уширение токовой области, что в волновом пространстве соответствует движению q по абсциссе рис. 8 влево. Ближе становится левая предельная кривая ξ = ξ_I и влияние сноса линий (вмороженности) на эволюцию магнитного поля становится не менее важным, чем градиентно-холловское воздействие. В пределе процесс будет развиваться по законам обычной идеальной магнитогазодинамики, где нет учета эффекта Холла и магнитной вязкости.

5.7. Проявления чистой ГХЭ и нижняя граница солнечной короны

Как уже говорилось (пп. 5.4, 5.6), хромосфера Солнца, из-за присутствия разнообразных магнитных неоднородностей, будет быстро создавать тонкие токовые слои с током вверх, получая затем от них дополнительный нагрев на высотах, отвечающих ξ ≥ ξ_cr на рис. 8. В связи с этим стоит обратить внимание на следующее обстоятельство.

Вблизи нижней границы спокойной короны имеем табличные значения ${{T}_{*}} = 2 \times {{10}^{6}}$ K, ${{N}_{*}} = {{10}^{{14}}}$ м^–3 [Demoulin and Klein, 2000]. Подставляя эти величины в безразмерные соотношения (8), (42), получим соответственно $\xi = 3.8 \times {{10}^{{ - 7}}}$ и $~{{\xi }_{{{\text{cr}}}}} = 4.3 \times {{10}^{{ - 7}}}{{\beta }^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}}.$ По существу, это совпадающие числа (при не слишком слабых магнитных полях), и в такой плазме уже возможна чистая ГХЭ магнитных полей. Величина q_cr соответствует горизонтальному размеру (полуширине) неоднородности ${{\lambda }_{{{\text{cr}}}}}\sim {{\beta }^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}} \times 30$ м. Согласно (35), время опрокидывания для нее составляет ${{\tau }_{ + }}\sim {{\beta }^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} \times 5$ мин. Как показывает рис. 8, с увеличением высоты диапазон размеров неоднородностей, способных вести себя как “магнитные дюны”, расширяется. Таким образом, газовые параметры нижней границы короны соответствуют нижней границе области выявленных “магнитных дюн”.

6. ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Аналитическое исследование (п. 5), проведенное для изотермической плазмы показало, что, благодаря чистой ГХЭ магнитного поля, в верхней хромосфере Солнца вертикальные токи как бы “редактируются”: токи, текущие вниз, деградируют, а токи вверх, наоборот, увеличивают свою плотность. Вывод касался начальных магнитных неоднородностей с горизонтальными размерами λ > λ_cr, для которых на высотах ξ > ξ_cr омическая диссипация и снос поля из-за частичной вмороженности менее существенны, чем ГХЭ (рис. 8).

Однако найденные закономерности проявили себя и в нашем численном эксперименте (п. 4), где плазма уже была неизотермической, а магнитное поле подвергалось воздействию магнитной вязкости и сноса. При сносе есть перетяжечная неустойчивость, а в природной плазме она сама генерирует ТТС – независимо от того, какой знак имеет ток (п. 1). И, тем не менее, эксперимент показывает, что чаще возникают и дольше существуют ТТС↑, чем ТТС↓ (п. 4.1), что указывает на присутствие ГХЭ как части общего эволюционного процесса. Эта частичная ГХЭ создает различие во внешнем виде транзиентных образований (п. 4.2). Ее самоустранением (5.6) при токе вниз объясняется установление со временем “бесхолловских” черт эволюции магнитного поля в холловской плазме (пп. 4.3, 4.4), монотонность и немонотонность установления тонких токовых слоев (пп. 4.2, 4.5).

Сходство результатов, полученных аналитически и путем численного моделирования, говорит о том, что мы правильно понимаем поведение магнитного поля в среде с убывающей плотностью и что ГХЭ магнитного поля должна проявлять себя в атмосфере Солнца как в чистом виде (п. 5), так и частично (п. 4). В последнем случае к ее действию может примешиваться возникновение тонких токовых слоев, обусловленных перетяжечной неустойчивостью в природной плазме.

7. ВЫВОДЫ

Путем численного моделирования мы установили, что в плазме верхних слоев хромосферы при вертикальной зоне контакта поступивших снизу разнополярных магнитных областей со слабым горизонтальным полем пограничный ток, направленный вверх, чаще развивается в тонкий токовый слой и потом дольше существует в таком виде, чем это происходит при пограничном токе вниз. Соответственно ток в виде тонкого токового слоя чаще уходит из хромосферы в корону, чем приходит туда из короны. Однако при пограничном токе вниз преобразование поступившей магнитной энергии в энергию упорядоченных потоков хромосферной плазмы идет эффективнее, чем при токе, текущем вверх (разница исчезает с переходом процесса в хаотическую стадию).

Неодинаковые для тока вверх и вниз изменения в контактной зоне обусловлены действием эффекта Холла при наличии вертикального градиента плотности плазмы. Можно сказать, что магнитное поле частично совершает градиентно-холловскую эволюцию (мы учитываем, что оно одновременно с тем эволюционирует еще под влиянием диссипации и сноса веществом силовых линий).

Что представляет собою градиентно-холловская эволюция в чистом виде, мы выяснили путем аналитического исследования случая начальных магнитных полей, медленно меняющихся по вертикали. Оказывается, когда определяющим для динамики конкретной конфигурации поля становится присутствие эффекта Холла, магнитное поле начинает эволюционировать особым, специфическим образом. Профиль каждой магнитной неоднородности (величина магнитного поля как функция горизонтальной координаты) ведет себя подобно профилю песчаной дюны на земном ландшафте: он движется, и при этом один его склон становится все более пологим, а другой приобретает крутизну. “Выполаживается” склон, которому соответствует электрический ток, направленный вниз; увеличивает крутизну склон – где ток вверх. В хромосфере есть критический уровень разреженности плазмы, когда эволюция полей в виде “магнитных дюн” становится возможной сначала лишь для одного, критического масштаба неоднородности магнитного поля. Однако диапазон масштабов эволюционирующих таким образом неоднородностей становится шире с увеличением высоты. Отмечено, что в атмосфере Солнца критический уровень разреженности реализуется при табличных значениях температуры и плотности плазмы, соответствующих нижней границе спокойной короны. В связи с этим ставится вопрос, не проявляет ли себя эволюция магнитных неоднородностей по типу “магнитных дюн” в нагреве короны.

Список литературы

− Алексеева Л.М. О физической природе анодного взрыва в плазменном канале // Письма в ЖТФ. Т. 6. Вып. 21. С. 1310–1312. 1980.
− Алексеева Л.М. Эффект Холла как причина появления токовых слоев в астрофизической плазме // Письма в астрон. журн. Т. 32. № 4. С. 307–315. 2006.
− Алексеева Л.М., Кшевецкий С.П. О структурировании солнечной надфотосферной плазмы плоскосимметричным пинч-эффектом // Астрофиз. бюлл. Т. 66. № 1. С. 76–86. 2011.
− Алексеева Л.М., Кшевецкий С.П. Магнитогидродинамическая эволюция плазмы в зоне контакта противоположно направленных магнитных полей и “искусственные объекты” в солнечной атмосфере // Изв. Крымской астрофиз. обс. Т. 109. № 3. С. 155–164. 2013.
− Алексеева Л.М., Кшевецкий С.П. Вертикальные токовые слои в солнечной хромосферной плазме с эффектом Холла. Численное моделирование // Геомагнетизм и аэрономия. Т. 59. № 5. С. 547–561. 2019.
− Брагинский C.И. Явления переноса в плазме // Вопросы теории плазмы. В. 1. С. 183–272. 1963.
− Брушлинский К.В., Морозов А.И. Расчет двумерных течений плазмы в каналах / Вопросы теории плазмы. В. 8. Ред. М.А. Леонтович. М.: Атомиздат. С. 88–163. 1974.
− Брушлинский К.В., Ратникова Т.А. Численная модель приэлектродной неустойчивости в каналах плазменных ускорителей // Физика плазмы. Т. 21. № 9. С. 784–790. 1995.
− Брушлинский К.В., Ратникова Т.А. Холловские поправки к расчету течения плазмы в приэлектродных слоях коаксиальных каналов // Физика плазмы. Т. 23. № 2. С. 126–130. 1997.
− Зайцев В.Ф., Полянин А.Д. Справочник по дифференциальным уравнениям с частными производными первого порядка. М.: Физматлит, 416 с. 2003.
− Кшевецкий С.П. Математическая программа для моделирования эволюции полностью ионизированной плазмы PLASMAT. Свидетельство о государственной регистрации № 2 013 618 823. 2013.
− Морозов А.И., Соловьев Л.С. Стационарные течения плазмы в магнитном поле // Вопросы теории плазмы. В. 8. С. 3–87. 1974.
− Прист Э.Р. Солнечная магнитогидродинамика. М.: Мир, 592 с. 1985.
− Спитцер Л. Физика полностью ионизованного газа. М.: Мир, 212 с. 1965.
− Alekseeva L.M. Effective gravity due to the Hall effect and quasi-acoustic–gravity waves in accelerated plasma flows // J. Plasma Phys. V. 61. № 5. P. 671–699. 1999.
− Alekseeva L.M., Kshevetskii S.P. Numerical MHD simulation of the coupled evolution of plasma and magnetic field in the solar chromosphere. I. Gradual and impulsive energisation // Solar Phys. V. 290. № 11. P. 3295–3318. 2015.https://doi.org/10.1007/s11207-015-0788-7
− Aschwanden M.J. Physics of the Solar corona: An introduction. Berlin: Springer, 842 p. 2004.
− Balescu R. Transport processes in plasmas. V. 1. Amsterdam: Elsevier. 1988.
− Demoulin P., Klein K.-L. Structuring of the solar plasma by the magnetic field / Transport and Energy Conversion in the Heliosphere / Lecture Notes in Physics. V. 553. Eds. J.P. Rozelot, L. Klein, J.-C. Vial. Berlin: Springer. P. 1–99. 2000.
− Goodman M.L. Self-consistent magnetohydrodynamic modeling of current sheet structure and heating using realistic descriptions of transport processes // Astrophys. J. V. 632. P. 1168–1175. 2005.
− LeVeque R.J. Numerical methods for conservation laws. 2nd edn. Birkhäuser, Basel. 1992.
− Priest E. Magnetohydrodynamics of the Sun. Cambridge: Cambridge University Press, 560 p. 2014.
− Thomas J.P., Roe P.L. Development of non-dissipative numerical schemes for computational aeroacoustics // AIAA 11th Computational Fluid Dynamics Conference, Technical Papers 2, Orlando, FL, 906. ADS. 1993.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Геомагнетизм и аэрономия

Архивы выпусков Информация о журнале Отправить рукопись в журнал