1. На главную
  2. Электронные версии
  3. Геомагнетизм и аэрономия
  4. T. 62, № 3, 2022

Геомагнетизм и аэрономия, 2022, T. 62, № 3, стр. 275-282

Зависимость возникновения коронального выброса от исходной длины эруптивного протуберанца

Б. П. Филиппов *

Институт земного магнетизма, ионосферы и распространения радиоволн им. Н.В. Пушкова РАН (ИЗМИРАН)
г. Москва, г. Троицк, Россия

* E-mail: bfilip@izmiran.ru

Поступила в редакцию 17.11.2021
После доработки 19.12.2021
Принята к публикации 27.01.2022

Полный текст (PDF)

Аннотация

Анализируется модель эрупции магнитного жгута, концы которого жестко закреплены в фотосфере. Длинные и короткие жгуты демонстрируют различные сценарии эрупции при прочих равных условиях. Короткие жгуты ускоряются быстро, но кратковременно, и довольно легко могут быть остановлены на сравнительно небольшой высоте, приводя к так называемым несостоявшимся эрупциям. Эрупция длинного жгута вероятнее приведет к его подъему на большую высоту и формированию коронального выброса. Такая тенденция прослеживается в реальных наблюдениях эруптивных явлений на Солнце.

1. ВВЕДЕНИЕ

Солнечные вспышки, эрупции протуберанцев/волокон и корональные выбросы являются главными наблюдаемыми проявлениями спорадической солнечной активности [Филиппов, 2007]. Наблюдаемые различными методами и разными инструментами, они демонстрируют внезапное выделение огромной энергии, по всей видимости, запасенной в магнитном поле солнечной короны. Возможно, все три явления представляют собой различные стороны одного и того же физического процесса, который еще не до конца понят, и не все его аспекты доступны для наблюдений [Harrison, 1995, Forbes, 2000; Zhang et al., 2001; Priest and Forbes, 2002].

Протуберанцы состоят из вещества, которое гораздо плотнее плазмы окружающей короны. Чтобы поддерживать их на значительной высоте, нужна какая-то внешняя сила, и ее может обеспечить только магнитное поле короны. Несмотря на небольшую степень ионизации вещества протуберанцев, его проводимость достаточно высока для того, чтобы препятствовать движению поперек силовых линий. Чтобы вещество находилось в устойчивом равновесии необходимо, чтобы силовые линии были вогнутыми, образуя ямки, служащие ловушками для плотной плазмы. В ранних моделях протуберанцев полагалось, что подобная структура поля создается изначально подфотосферными источниками [Menzel, 1951; Kippenhahn and Schluter, 1957]. Позднее было предложено, что необходимую структуру могут обеспечить электрические токи, протекающие в короне [Kuperus and Raadu, 1974; van Tend and Kuperus, 1978]. Наличие коронального электрического тока может проявляться в виде аркады петель со сдвинутыми вдоль центральной оси основаниями [Antiochos et al., 1994; DeVore and Antiochos, 2000; Aulanier et al., 2002], которая в своем развитии может превратиться в магнитный жгут, состоящий из цилиндрически спиральных силовых линий [Chen, 1989; Lin et al., 1998; Titov and Demoulin, 1999; Amari et al., 2000; Low, 2001; Kliem and Török, 2006; Zuccarello et al., 2012].

Причину эрупции протуберанцев видят в превышении корональным током некоторого критического значения, за которым следует развитие неустойчивостей и потеря равновесия. Одной из основных причин, инициирующих эрупции, считается винтовая или изгибная неустойчивость (kink instability), хорошо известная по изучению лабораторных пинчей [Кадомцев, 1963; Török et al., 2004]. Условием ее начала является превышение углом закручивания силовой линии на длине трубки порогового значения (условие Крускала – Шафранова). Правда, эта неустойчивость может быть триггером, но не движущей силой эрупции, поскольку, несмотря на значительные изгибы токовой трубки, ось симметрии всей структуры остается на прежнем месте. Другая неустойчивость, которая связана с равновесием тока во внешнем поле, более перспективна для обеспечения эрупции. Она развивается при большом градиенте внешнего поля, удерживающего ток от увеличения размеров его контура. В двумерных моделях эта неустойчивость связана с катастрофической потерей равновесия [Молоденский и Филиппов, 1987; Priest and Forbes, 1990; Forbes and Isenberg, 1991; Forbes and Priest, 1995; Longcope and Forbes, 2014], после которого равновесие невозможно. В случае тороидальной трубки такая неустойчивость получила название “тороидальной неустойчивости” [Осовец, 1958; Bateman, 1978; Kliem and Török, 2006].

В данной работе мы рассмотрим особенности эрупции магнитных жгутов с концами, закрепленными в фотосфере. Будет показано, что сценарии эрупции жгутов при прочих равных условиях зависят от их первоначальной длины, точнее расстояния между зафиксированными в фотосфере концами.

2. МОДЕЛЬ РАВНОВЕСИЯ ЖГУТА С ЗАКРЕПЛЕННЫМИ КОНЦАМИ

В ряде исследований эруптивных явлений на Солнце использовалась модель магнитного жгута в короне в виде сегмента тора с концами, зафиксированными в фотосфере (рис. 1), с различными допущениями и приближениями [Chen, 1989; Cargill et al., 1994; Isenberg and Forbes, 2007; Olmedo and Zhang, 2010; Filippov, 2020, 2021]. Наиболее строгий и последовательный подход был применен Isenberg and Forbes [2007], которые вывели точные аналитические выражения для магнитного поля, производимого электрическим током, протекающим по сегменту окружности. Однако формулы эти довольно громоздкие, выражающиеся через неполные эллиптические интегралы первого и второго рода, и в любом случае требуют численных расчетов, поэтому ниже мы будем использовать исходные выражения для поля в квадратурах и численное интегрирование.

Рис. 1.

Схематическое представление магнитного жгута в короне в виде сегмента тора с концами, зафиксированными в фотосфере.

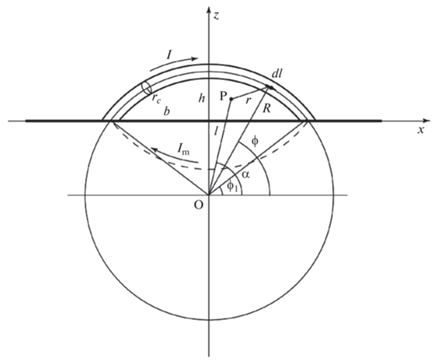
Магнитное поле внутри жгута с круговым сечением радиуса rc полагается линейным бессиловым (linear force-free field) [Lundquist, 1951; Lin et al., 1998]. Предполагается, что ось жгута все время остается в одной и той же вертикальной плоскости y = 0 и сохраняет форму сегмента окружности радиуса

(1)
$R = \frac{{{{b}^{2}} + {{h}^{2}}}}{{2h}},$
где b – половина расстояния между концами жгута, а h – высота вершины дуги (апекса). Внешнее поле моделируется линейным диполем m, расположенным на глубине d под фотосферой, с горизонтальной компонентой

(2)
${{B}_{e}} = \frac{{m\left[ {{{y}^{2}} - {{{(z + d)}}^{2}}} \right]}}{{{{{\left[ {{{y}^{2}} + {{{(z + d)}}^{2}}} \right]}}^{2}}}}.$

Выбор двумерного внешнего поля, не зависящего от координаты x, объясняется тем фактом, что фотосферные поля под волокнами имеют гораздо больший масштаб вдоль линии раздела полярностей, над которыми располагаются волокна, чем в поперечном направлении. С учетом того, что ось жгута остается в плоскости y = 0, в выражении (2) остается только зависимость от z.

Для максимальной простоты мы будем рассматривать уравнение движения только для элемента единичной длины на вершине петли

(3)
$M\frac{{{{d}^{2}}h}}{{d{{t}^{2}}}} = {{F}_{R}} + {{F}_{{\operatorname{Im} }}} + {{F}_{B}} + {{F}_{g}} + {{F}_{d}},$
где M – масса отрезка волокна единичной длины; FR – сила, растягивающая жгут по большому радиусу R тора из-за самодействия электрического тока вследствие кривизны оси; FIm – сила диамагнитного воздействия фотосферы на корональный ток, эквивалентная отталкиванию тока от своего изображения (“зеркального тока”, показанного штриховой линией на рис. 1); FB – сила взаимодействия коронального тока с внешним магнитным полем (2); Fg – сила тяжести; Fd – сила торможения из-за сопротивления окружающей среды.

Выражение для радиальной силы, растягивающей тороидальный жгут, было выведено Шафрановым [Шафранов, 1963]

(4)
${{F}_{R}} = \frac{{{{I}^{2}}}}{{{{c}^{2}}R}}\left[ {\ln \left( {\frac{{8R}}{{{{r}_{c}}}}} \right) - \frac{3}{2} + \frac{{{{l}_{i}}}}{2}} \right],$
где I – величина тороидального электрического тока; rc – радиус поперечного сечения тора; li – внутренняя самоиндукция жгута на единицу длины. Последняя зависит от распределения тока внутри трубки и li = 1 для внутреннего линейного бессилового поля [Lundquist, 1951; Lin et al., 1998; Isenberg and Forbes, 2007].

Третий и четвертый член в правой части (3) очевидно выражаются как

(5)
${{F}_{B}} = \frac{I}{c}{{B}_{e}}$
и
(6)
${{F}_{g}} = Mg\frac{{R_{ \odot }^{2}}}{{{{{(h + {{R}_{ \odot }})}}^{2}}}},$
где g – ускорение свободного падения на уровне фотосферы (на расстоянии ${{R}_{ \odot }}$ от центра Солнца).

Магнитное поле сегмента кольцевого тока в точке P (рис. 1) может быть найдено согласно закону Био и Савара интегрированием вдоль дуги l [Ландау и Лифшиц, 2005]

(7)
${{{\mathbf{B}}}_{I}} = \frac{I}{c}\int\limits_{{{\phi }_{1}}}^{{{\phi }_{2}}} {\frac{{d{\kern 1pt} {\mathbf{l}} \times {\mathbf{r}}}}{{{{r}^{3}}}}} ,$
где r – радиус-вектор от элемента дуги d l до точки P; ϕ1 и ϕ2 – угловые координаты концов дуги. Имеется только одна y-компонента поля в плоскости дуги
(8)
${{B}_{I}} = \frac{I}{c}\int\limits_{{{\phi }_{1}}}^{{{\phi }_{2}}} {\frac{{\left[ {{{R}^{2}} - Rl\cos (\alpha - \phi )} \right]d\phi }}{{{{{\left( {{{R}^{2}} + {{l}^{2}} - 2Rl\cos (\alpha - \phi )} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}} ,$
где все переменные понятны из рис. 1. Поскольку начало оси z помещено на фотосферу
(9)
${{l}^{2}} = {{x}^{2}} + {{(R - h + z)}^{2}},\,\,\,\,\sin \alpha = \frac{{R - h + z}}{l}.$
То же самое выражение (8) можно использовать для вычисления поля зеркального тока BIm с заменой l на lm:
(10)
$l_{m}^{2} = {{x}^{2}} + {{(R - h - z)}^{2}},\,\,\,\,\sin {{\alpha }_{m}} = \frac{{R - h - z}}{{{{l}_{m}}}}{\kern 1pt} {\kern 1pt} .$
Тогда

(11)
${{F}_{{\operatorname{Im} }}} = \frac{I}{c}{{B}_{{\operatorname{Im} }}}(0,h).$

Тороидальный ток I изменяется за счет индукции во время быстрой эволюции магнитного жгута. Зависимость величины тока от высоты вершины дуги может быть найдена из сохранения полоидального магнитного потока между фотосферой и осью жгута

(12)
${{\Phi }_{p}} = {{\Phi }_{I}} + {{\Phi }_{s}} = \frac{I}{c}{{L}_{e}} + \int\limits_S {({{B}_{e}} + {{B}_{{\operatorname{Im} }}}){\kern 1pt} ds} = {\text{const,}}$
где S – площадь между жгутом и фотосферой, а Le – внешняя самоиндукция дуги, которая для тока тонкой трубки выражается как [Ландау и Лифшиц, 2005]
(13)
$\begin{gathered} {{L}_{e}} = \int\limits_0^\Delta {\int\limits_{{{\omega }_{0}}}^\Delta {\frac{{R\cos \omega }}{{2\sin \frac{\omega }{2}}}} } {\kern 1pt} {\kern 1pt} d\omega {\kern 1pt} 'd\omega = \\ = 2R\Delta \left( {\ln {\text{tg}}\frac{\Delta }{4} + 2\cos \frac{\Delta }{2} + \ln \frac{{8R}}{{{{r}_{c}}}} - 2} \right), \\ \end{gathered} $
где
(14)
$\begin{gathered} \Delta = 2\arcsin \frac{b}{R},\,\,\,\,{\text{если}}\,\,\,\,h < b, \\ \Delta = 2\pi - 2\arcsin \frac{b}{R},\,\,\,\,{\text{если}}\,\,\,\,h \geqslant b \\ \end{gathered} $
и
(15)
${{\omega }_{0}} \approx \frac{{{{r}_{c}}}}{{2R}}.$
Интеграл (13) вычисляется вдоль корональной части контура, потому что вследствие условия вмороженности магнитного поля в фотосферу вектор-потенциал остается постоянным на поверхности фотосферы при эволюции жгута и не влияет на индукционные изменения тока [Isenberg and Forbes, 2007].

Радиус сечения жгута rc тоже меняется при его перемещении. Для внутреннего линейного бессилового поля, сохранение тороидального магнитного потока внутри трубки влечет обратную зависимость радиуса сечения от величины тока [Lin et al., 1998]

(16)
${{r}_{c}} = {{r}_{{c0}}}\frac{{{{I}_{0}}}}{I}.$

Полоидальный магнитный поток Φs тоже будем находить численным интегрированием:

(17)
${{\Phi }_{s}}(b,h) = \int\limits_{ - {{b}_{l}}}^{{{b}_{l}}} {\int\limits_{{{z}_{1}}}^{{{z}_{2}}} {({{B}_{e}} + {{B}_{{\operatorname{Im} }}})dxdz} } ,$
где bl – полуширина площади между жгутом и фотосферой
(18)
${{b}_{l}} = \left\{ {\begin{array}{*{20}{c}} {b - {{r}_{c}},\,\,\,\,h \leqslant b} \\ {R - {{r}_{c}},\,\,\,\,h > b} \end{array}} \right.$
z1 – координата внутренней границы нижней части жгута при превышении сегментом половины окружности, а z2 – координата внутренней границы верхней части жгута

(19)
${{z}_{1}} = \left\{ \begin{gathered} 0,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left| x \right| \leqslant b \hfill \\ \frac{{{{h}^{2}} - {{b}^{2}} - {{{({{{({{b}^{2}} + {{h}^{2}})}}^{2}} - 4{{h}^{2}}{{x}^{2}})}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}{{2h}} + {{r}_{c}},\,\,\,\,\left| x \right| > b, \hfill \\ \end{gathered} \right.$
(20)
${{z}_{2}} = \frac{{{{h}^{2}} - {{b}^{2}} + {{{\left( {{{{({{b}^{2}} + {{h}^{2}})}}^{2}} - 4{{h}^{2}}{{x}^{2}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}{{2h}} - {{r}_{c}}.$

3. ЭРУПЦИЯ ЖГУТОВ РАЗЛИЧНОЙ ДЛИНЫ

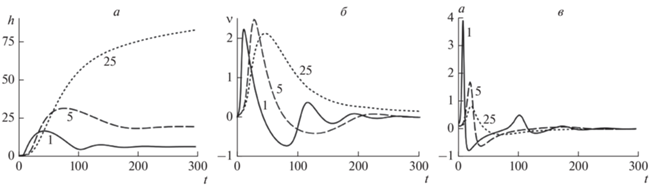
Рассмотрим зависимость каждого из слагаемых в правой части (3) (за исключением последнего) и их суммы от высоты апекса дуги для жгутов различной исходной длины. На рисунке 2 тонкими сплошными линиями показаны профили всех компонентов силы, действующей на апекс жгута, и сама суммарная сила (жирной сплошной линией) для значения b = d. Далее мы будем все линейные размеры указывать в единицах d – глубины залегания дипольного источника коронального магнитного поля, характеризующего масштаб этого поля в окрестностях жгута. Также жирными штриховыми линиями с длинным и коротким штрихом показаны профили суммарной силы для b = 5 и b = 25 соответственно.

Рис. 2.

Графики зависимости от высоты h суммарной силы F1 (сплошная жирная линия), действующей на элемент единичной длины на вершине дугообразного магнитного жгута (вся правая часть уравнения (3)), и ее компонентов (тонкие сплошные линии) для значения b = 1. Жирными штриховыми линиями с длинным и коротким штрихом показаны профили суммарной силы F5 и F25 для b = 5 и b = 25 соответственно. Высота h – в единицах d, силы – в произвольных безразмерных единицах.

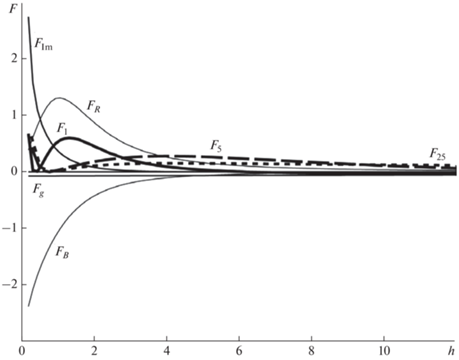
На малой высоте поле зеркального тока имеет большой градиент, поэтому сила взаимодействия коронального тока с внешним магнитным полем FB убывает с высотой медленнее, чем сила отталкивания от зеркального изображения FIm. Обе они уменьшаются и имеют, разумеется, противоположные знаки. Растягивающая радиальная сила FR мала на малой высоте, так как велик радиус кривизны оси жгута согласно выражению (1), но она быстро растет, достигая максимума при h = b, когда радиус кривизны оси R минимален. На больших высотах FR так же уменьшается, оставаясь доминирующей на большом интервале высот. Сила тяжести Fg выбрана малой по сравнению с электромагнитными силами на малой высоте, как это следует из оценки массы протуберанцев, электрического тока и коронального магнитного поля [Labrosse et al., 2010; Ballester, 1984; Куликова и др., 1986; Vrsnak et al., 1988; Srivastava et al., 1991; Forbes, 2000], однако она практически не меняется в интересующем нас интервале высот и может оказаться существенной или даже доминирующей на относительно большой высоте.

Исходное значение электрического тока подбиралось таким образом, чтобы кривая F(h) имела локальный экстремум (минимум) и касалась оси абсцисс на небольшой высоте. Очевидно, что эта точка касания соответствует неустойчивому равновесию, которое выливается в катастрофическую потерю равновесия, знаменующую начало эрупции жгута. Действительно, небольшое смещение от точки равновесия вниз приводит к появлению силы, направленной вверх, возвращающей жгут к равновесию, но смещение вверх тоже дает силу, направленную вверх, и толкает жгут дальше от точки равновесия.

Чем больше исходная длина жгута, тем более пологой становится кривая F(h). Критическая высота hc, т.е. точка касания кривой абсциссы, немного увеличивается с увеличением длины жгута. hc = 0.45 для b = 1, а для b = 5 и b = 25 – hc = 0.8 и hc = 0.85 соответственно. При этом значение критического тока, т.е. равновесного тока в критической точке, практически не зависит от длины жгута. По многочисленным наблюдениям эруптивных протуберанцев [McCauley et al., 2015] критическая высота составляет ~50 Мм. То есть глубина диполя обычно лежит в пределах 20–40 Мм.

Пересечение кривой F(h) оси абсцисс сверху вниз означает существование высокой точки устойчивого равновесия. В отсутствие силы тяжести, т.е. для “ненагруженного” жгута, ни одна из трех кривых F1, F5, F25 не пересекает ось абсцисс, так что эрупция каждого из них не прервется и будет “успешной”. Наличие даже небольшой массы, практически не влияющей на исходное равновесие, создает необходимое условие для остановки эрупции (failed eruption). Рассмотрим такую возможность подробнее, численно решая уравнение движения (3).

Очевидно, что в отсутствие диссипации жгут, достигнув верхней точки равновесия, будет осциллировать около нее с большой амплитудой, довольно резко “отскакивая” от области сильного поля около исходного положения равновесия и медленно возвращаясь с большой высоты. Чтобы предотвратить такое поведение, которое не наблюдается в эрупциях на Солнце, необходимо ввести диссипацию, описываемую последним членом в уравнении движения (3). Используем для простоты линейную зависимость силы сопротивления от скорости движения, соответствующую движению тела в вязкой жидкости при малых числах Рейнольдса [Ландау и Лифшиц, 2001]

(21)
${{F}_{d}} = - kv.$
Величину коэффициента k мы просто подбираем таким образом, чтобы избежать осцилляций с большой амплитудой. Возможна и квадратичная зависимость силы сопротивления от скорости, которая более типична для движения при больших значениях числа Рейнольдса. В действительности природа диссипации механических движений в солнечной короне не вполне ясна. Размерные оценки коэффициентов, обеспечивающих похожие на наблюдения результаты, отличаются от значений, следующих из формул гидродинамики на порядки [Zaitsev and Stepanov, 2018; Filippov, 2021].

На рисунке 3 показаны решения для трех жгутов с одинаковой массой на единицу длины и в одинаковых внешних условиях. Отличие только в исходной длине, расстоянии между зафиксированными в фотосфере концами жгута. Более короткие жгуты, действительно, останавливаются на высоте тем меньшей, чем короче жгут, а самый длинный продолжает подъем, хотя и с замедлением. Максимальное значение скорости, приобретаемой жгутом, примерно одинаково во всех трех случаях, но ускорение имеет более высокие и узкие пики для более коротких жгутов. Поэтому скорость длинных жгутов нарастает медленнее и дольше сохраняет большие значения, позволяя им достичь большей высоты и избежать остановки.

Рис. 3.

Зависимости высоты (а), скорости (б) и ускорения (в) полученные в результате решения уравнения движения (3) для трех значений длины жгута b = 1, b = 5 и b = 25. Высота h – в единицах d, скорость, ускорение и время – в произвольных безразмерных единицах.

4. ОБСУЖДЕНИЕ И ЗАКЛЮЧЕНИЕ

Модель эрупции магнитного жгута с концами, зафиксированными в фотосфере, демонстрирует различие сценариев эрупции для длинных и коротких жгутов при прочих равных условиях. Короткие жгуты ускоряются быстро, но кратковременно, и довольно легко могут быть остановлены на сравнительно небольшой высоте, производя так называемые несостоявшиеся эрупции. Эрупция длинного жгута вероятнее приведет к его подъему на большую высоту и формированию коронального выброса. Конечно, на динамику жгута влияет множество факторов: величина коронального поля, его структура, масса протуберанца, который “нагружает” жгут, однако такой параметр как исходная длина жгута перед эрупцией никогда не рассматривался в качестве критерия, позволяющего в какой-то мере прогнозировать развитие эруптивного процесса. Мы не ставили задачи определить критическое значение длины волокна, которое гарантирует успешность эрупции. Оно зависит и от массы протуберанца, и от величины аэродинамического торможения жгута в короне. Если первый параметр, в принципе, может быть измерен, например, спектроскопическими средствами, то второй остается весьма неопределенным. Оценки на основе гидродинамической теории дают значения, которые довольно плохо согласуются с наблюдениями затухания осцилляций плазменных образований в короне [Zaitsev and Stepanov, 2018; Filippov, 2021]. При параметрах, использованных для построения графиков на рис. 3, пороговое значение составляет ~10 d, или ~ 200–400 Мм. При принятой за единицу длины величине 20 Мм размерные значения для других параметров, показанных на графиках, можно получить, используя следующие масштабные коэффициенты: для силы – 4 × 1010 дн см–1, времени – 0.75 мин, скорости – 180 км с–1, ускорения – 5 × 104 см с–1.

Критическое значение электрического тока, при котором начинается эрупция, составляет 2 × × 1010 А, а начальный радиус поперечного сечения жгута в этой точке rc0 = 2 Мм. Коэффициент торможения принят k = 90 г см–1 с–1, что почти на порядок больше оценки, приведенной в работе [Zaitsev and Stepanov, 2018], и примерно на два порядка меньше использованного в работе [Filippov, 2021].

Если обратиться к результатам наблюдения эрупций на Солнце, то можно убедиться, что, действительно, эрупции длинных волокон, как правило, сопровождаются корональными выбросами, а эрупции коротких – нередко заканчиваются остановкой в нижней короне, но при этом чаще связаны со вспышечными проявлениями.

В работе [Sinha et al., 2019] анализируется выборка из 33 эруптивных явлений, наблюдавшихся в 2012–2016 гг. Среди них отмечаются события, которые сопровождались только вспышкой, только корональным выбросом или и тем, и другим. Эруптивных волокон, связанных только со вспышками и не сопровождавшихся корональными выбросами зафиксировано немного, всего 4. Средняя длина таких волокон до эрупции (расстояние между основаниями эруптивной петли) оставляла 130 Мм. Эрупций волокон, связанных только с корональными выбросами, наблюдалось вдвое больше – 8. Их средняя длина – ~350 Мм, почти втрое больше. Остальные события, самые многочисленные, были связаны как с выбросами, так и вспышками. Длина волокон в них варьируется в широких пределах от 80 до 450 Мм при среднем значении 215.

В исследовании 16 несостоявшихся эрупций, наблюдавшихся вблизи максимума 24-го солнечного цикла, отмечается расстояние между основаниями петель эруптивных протуберанцев тоже в 130 Мм [Filippov, 2020]. С другой стороны, средняя длина волокон, которые примерно в тот же период приводили к формированию быстрых корональных выбросов (5 событий) – 333 Мм, а тех, что сопровождались медленными выбросами (тоже 5 событий), 350 Мм.

Таким образом, тенденция к тому, что более длинные волокна имеют более благоприятную перспективу “породить” корональные выбросы прослеживается в реальных наблюдениях эруптивных явлений на Солнце. Хотя множество дополнительных и не менее важных факторов, которые не всегда легко учесть, делает проблему заблаговременного прогнозирования геоэффективных событий на Солнце по доступным в настоящее время измерениям параметров их “прародительских” областей еще далекой от окончательного решения.

Мы использовали свойства модели для анализа результатов наблюдений эрупций нескольких десятков волокон вне активных областей. Большинство из них относится к так называемому промежуточному типу (intermediate filaments) [Engvold, 2015]. Они располагаются между активными областями или противоположными полярностями старых, распавшихся активных областей и имеют некоторые признаки, характерные для двух крайних типов протуберанцев: спокойных (quiescent prominences), расположенных преимущественно выше широты 50°, и протуберанцев активных областей, находящихся внутри активных областей в непосредственной близости от пятен (active region prominences). Модель может быть применена и к последним, и в этом случае с ее помощью можно будет оценивать эффективность вспышечной активности, но это уже предмет другой статьи.

Список литературы

  1. – Кадомцев Б.Б. Гидромагнитная устойчивость плазмы / Вопросы теории плазмы. Вып. 2. Ред. М.А. Леонтович. М.: Госатомиздат. С. 132–176. 1963.

  2. – Куликова Г.Н., Молоденский М.М., Старкова Л.И., Филиппов Б.П. Токи в активной области HR16927 по данным Hα. Солнечные данные. № 10. Л.: Наука. С. 60–65. 1986.

  3. – Ландау Л.Д., Лифшиц Е.М. Гидродинамика. М.: Физматлит, 736 с. 2001.

  4. – Ландау Л.Д., Лифшиц Е.М. Электродинамика сплошных сред. М.: Физматлит, 656 с. 2005.

  5. – Молоденский М.М., Филиппов Б.П. Быстрое движение волокон в солнечных активных областях. II // Астрон. журн. Т. 64. № 5. С. 1079–1087. 1987.

  6. – Филиппов Б.П. Эруптивные процессы на Солнце. М.: Физматлит, 216 с. 2007.

  7. – Осовец С.М. Плазменный виток в электромагнитном поле / Физика плазмы и проблема управляемых термоядерных реакций. Т. 2. Ред. М.А. Леонтович. М.: изд. АН СССР. С. 238–241. 1958.

  8. – Шафранов В.Д. Равновесие плазмы в магнитном поле / Вопросы теории плазмы. Вып. 2. Ред. М.А. Леонтович. М.: Госатомиздат. С. 92–131. 1963.

  9. – Amari T., Luciani J., Mikic Z., Linker J. A twisted flux rope model for coronal mass ejections and two-ribbon flares // Astrophys. J. V. 529. № 2. L49–L52. 2000.

  10. – Antiochos S.K., Dahlburg R.B., Klimchuk J.A. The magnetic field of solar prominences // Astrophys. J. V. 420. № 1. P. L41–L44. 1994.

  11. – Aulanier G., DeVore C. R., Antiochos S. K. Solar prominence merging // Astrophys. J. V. 646. № 2. P. 1349–1357. 2002.

  12. – Ballester J.L. // A note on magnetic fields and elrctric currents in solar prominences // Solar Phys. V. 94. P. 151–154. 1984.

  13. – Bateman G. MHD Instabilities. Cambridge, MA: Massachusetts Institute of Technology, 270 p. 1978.

  14. – Cargill P.J, Chen J., Garren D.A. // Oscillations and evolution of curved current-carrying loops in the solar corona // Astrophys. J. V. 423. № 2. P. 854–870. 1994.

  15. – Chen J. Effects of toroidal forces in current loops embedded in a background plasma // Astrophys. J. V. 338. № 1. P. 453–470. 1989.

  16. – DeVore C.R., Antiochos S.K. Dynamical formation and stability of helical prominence magnetic fields // Astrophys. J. V. 539. № 2. P. 954–963. 2000.

  17. – Engvold O. Description and classification of prominences / Solar Prominences. Eds. J.-C. Vial, O. Engvold. Cham, Switzerland: Springer International Publishing. P. 31–60. 2015. https://doi.org/10.1007/978-3-319-10416-4

  18. – Filippov B. Failed prominence eruptions near 24 cycle maximum // Monthly Not. Roy. Astron. Soc. V. 494. P. 2166–2177. 2020. https://doi.org/10.1093/mnras/staa896

  19. – Filippov B., Mass of prominences experiencing failed eruptions // Publ. Astron. Soc. Australia. V. 38. e018. 2021. https://doi.org/10.1017/pasa.2021.14

  20. – Forbes T.G., Isenberg P.A. A catastrophe mrchanism for coronal mass ejections // Astrophys. J. V. 373. № 1. P. 294–307. 1991.

  21. – Forbes T.G. A review on the genesis of coronal mass ejections // J. Geoph. Res. V. 105. № A10. P. 23 153–23 166. 2000.

  22. – Forbes T.G., Priest E. Photospheric Magnetic Field Evolution and Eruptive Flares // Astrophys. J. V. 446. № 1. P. 377–389. 1995.

  23. – Harrison R. A. The nature of solar flares associated with coronal mass ejection // Astron. Astrophys. V. 304. P. 585–594. 1995.

  24. – Isenberg P.A., Forbes T.G. A three-dimensional line-tied magnetic field model for solar eruptions // Astrophys. J. V. 670. № 2. P. 1453–1466. 2007.

  25. – Kippenhahn R., Schluter A. Eine Theorie der solaren Filamente // Zitschr. Astrophys. V. 43. P. 36 –62. 1957.

  26. – Kliem B., Török T. Torus instability // Phys. Rev. Lett. V. 96. № 25. 255002. 2006.

  27. – Kuperus M., Raadu M.A. The support of prominences formed in neutral sheets // Astron. Astrophys. V. 31. P. 189–193. 1974.

  28. – Labrosse N., Heinzel P., Vial J.-C., Kucera T., Parenti S., Gunar S., Schmieder B., Kilper G. Physics of solar prominences: I-spectral diagnostics and non-LTE modelling // Space Sci. Res. V. 151. P. 243–332. 2010.

  29. – Longcope D.W., Forbes T.G. Breakout and tether-cutting eruption models are both catastrophic (sometimes) // Solar Phys. V. 289. 2091–2122. 2014.

  30. – Lin J., Forbes T.G., Isenberg P.A., Démoulin P. The effect of curvature on flux-rope models of coronal mass ejections // Astrophys. J. V. 504. № 2. P. 1006–1019. 1998.

  31. – Low B.C. Coronal mass ejections, magnetic flux ropes, and solar magnetism // J. Geophys. Res. V. 106. P. 25 141–25 164. 2001.

  32. – Lundquist S. On the stability of magneto-hydrostatic fields // Phys. Rev. V. 83. P. 307–311. 1951.

  33. – McCauley P.I., Su Y.N., Schanche N., Evans K.E., Su C., McKillop S., Reeves K.K. Prominence and filament eruptions observed by the solar dynamics observatory: statistical properties, kinematics, and online catalog // Solar Phys. V. 290. P. 1703–1740. 2015. https://doi.org/10.1007/s11207-015-0699-7

  34. – Menzel D.H. Magneto-hydrostatics and solar prominences // Astron. J. V. 56. № 1. P. 135–135. 1951.

  35. – Olmedo O., Zhang J. Partial torus instability // Astrophys. J. V. 718. № 1. P. 433–440. 2010. https://doi.org/10.1088/0004-637X/718/1/433

  36. – Priest E.R., Forbes T.G. Magnetic field evolution during prominence eruption and two-ribbon flares // Solar Phys. V. 126. № 2. P. 319–350. 1990.

  37. – Priest E.R., Forbes T.G. The magnetic nature of solar flares // Astron. Astrophys. Rev. V. 10. P. 313–377. 2002.

  38. – Sinha S., Srivastava N., Nandy D. Solar filament eruptions as precursors to flare-CME events: Establishing the temporal connection // Astrophys. J. V. 880. № 2. 84. 2019.

  39. – Srivastava N., Ambastha A., Bhatnagar A. Evolution of helically twisted prominence structures of March 11, 1979 // Solar Phys. V. 133. P. 339–355. 1991.

  40. – Titov V.S., Demoulin P. Basic topology of twisted magnetic configurations in solar flares // Astron. Astrophys. V. 351. P. 707–720. 1999.

  41. – Török T., Kliem B., Titov V S. Ideal kink instability of a magnetic loop equilibrium // Astron. Astrophys. V. 413. P. L27–L30. 2004.

  42. – van Tend W., Kuperus M. The development of coronal electric current system in active regions and their relation to filaments and flares // Solar Phys. V. 59. № 1. P. 115–127. 1978.

  43. – Vrsnak B., Ruzdjak V., Brajsa R., Dzubur A. Structure and stability of prominence with helical structure // Solar Phys. V. 116. P. 45–60. 1988.

  44. – Zaitsev V.V., Stepanov A.V. Prominence activation by increase in electric current // J. Atmos. Sol.-Terr. Phys. V. 179. P. 149–153. 2018.

  45. – Zhang J., Dere K.P., Howard R.A., Kundu M.R., White S.M. On the temporal relationship between coronal mass ejections and flares // Astrophys. J. V. 559. № 1. P. 452–462. 2001.

  46. – Zuccarello F.P., Meliani Z., Poedts S. Numerical modeling of the initiation of coronal mass ejections in active region NOAA 9415 // Astrophys. J. V. 758. № 2. 117. 2012.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Геомагнетизм и аэрономия

Архивы выпусков Информация о журнале Отправить рукопись в журнал