Геомагнетизм и аэрономия, 2022, T. 62, № 2, стр. 144-154
Статистически-вероятностные характеристики чисел Вольфа и их временнЫ́х производных
С. В. Яковлева 1, *, С. В. Старченко 1, **
1 Институт земного магнетизма, ионосферы и распространения радиоволн
им. Н.В. Пушкова РАН (ИЗМИРАН)
г. Москва, г. Троицк, Россия
* E-mail: svyakov@inbox.ru
** E-mail: sstarchenko@mail.ru
Поступила в редакцию 28.02.2021
После доработки 26.08.2021
Принята к публикации 24.09.2021
- EDN: PNTLUP
- DOI: 10.31857/S001679402202016X
Аннотация
Предложен результат статистически-вероятностного исследования среднегодовых чисел Вольфа W и их временны́х производных W '. Он состоит в том, что вероятностное распределение W преимущественно экспоненциальное с наиболее вероятным значением, равным 18, при среднеквадратичном 100, медианном 65 и среднем 79. Меньше от нормального распределения отклоняются W ' с наиболее вероятным значением –12/год, медианным –6.1/год, средним –0.02/год, среднеквадратичным 33/год, минимумом –74/год и потенциально недостоверным максимумом 112/год. Отношения средних величин согласуются с характерными временами роста/падения активности в 2.6/3.7 лет и 11-летней цикличностью. Даны оценки полувековой периодичности и скорости течений (~1 м/с), поддерживающих динамо.
1. ВВЕДЕНИЕ
Изучение огромного разнообразия статистических и вероятностных свойств солнечных пятен имеет богатую историю от, например, работ [Витинский, 1973; Витинский и др., 1986] до, например, работ [Priest, 2014; Clette et al., 2014; Frick et al., 2020]. Важнейшими исследованными свойствами являются такие, как правило Гневышева–Оля GO2 (положительная корреляция между интенсивностью четных циклов и интенсивностью нечетных циклов) и эффект Вальдмайера W2 (антикорреляция между временами нарастания цикла солнечных пятен и их амплитуд). Эти и другие известные статистически-вероятностные свойства подробно рассмотрены, например, в работах [Ogurtsov and Lindholm, 2011; Akaniru and Onuchukwu, 2017].
В этой работе мы ставим перед собой более простые задачи определения таких базовых статических характеристик временнóго ряда, которым в известных нам работах практически не уделялось внимания, поскольку все известные нам авторы были, в основном, сконцентрированы на статистически-вероятностных закономерностях, связанных с прогнозированием солнечной активности. К малоисследованным же базовым величинам, в частности, относятся разнообразные средние, пиковые и наиболее вероятные значения чисел Вольфа W.
Ряд среднегодовых чисел Вольфа W (c 1700 г.) можно скачать в его последней версии v2 по ссылке (http://sidc.oma.be/silso/datafiles). Из этого ряда нетрудно получить и ряд численных оценок временны́х производных dW/dt ≡ W ', который непосредственно характеризует вариации солнечной активности. Эти вариации, насколько нам известно, практически не изучались совсем. Мы будем признательны, если читатель укажет нам работы, перекрывающие этот, представляющийся нам весьма существенным, пробел.
Некоторые результаты исследований, частично подобных нашему исследованию, впрочем, вполне могут быть согласованы с этой работой. Так, центральная для нас, вероятностная функция распределения W многократно [Abdel-Rahman and Marzouk, 2018; Shibaev and Ishkov, 2012; Noble and Wheatland, 2011; Журавлев и Летуновский, 2010, 2011; Ишков и Шибаев, 2006; Barnes et al., 1980] использовалась преимущественно для прогнозирования, исходя частично из некоторой теории и частично из практики. Мы же собираемся получить эту функцию не только для W, но и для W ', опираясь исключительно на известные данные. При этом потенциально могут быть верифицированы некоторые из упомянутых теорий.
Спектральный и вейвлет-анализ [Sokoloff et al., 2020; Frick et al., 2020; Petrovay, 2020; Duhau and Jager, 2020; Шибаев, 2017; Tanaka, 2010] в первую очередь выделяют 11-летнюю цикличность, затем ее гармоники, вплоть до одно-двухлетних, а также менее уверенно выделяются декадные и столетние гармоники. Поскольку отношение W к W ' дает характерное время, то соответствующие отношения усредненных статистических величин, как это будет показано далее, успешно воспроизводят наиболее значимую часть этих временны́х характеристик. Полученные характерные времена также используются для оценок эффективных конвективных скоростей, поддерживающих гидромагнитное динамо [Charbonneau, 2020; Кичатинов и Непомнящих, 2017; Starchenko, 1994], а их величина позволяет оценить глубину, на которой фактически генерируется магнитное поле солнечных пятен.
Таким образом, после краткого (и потому, безусловно, неполного) обзора современного состояния вопроса об исследованиях стандартных и при этом изначально не прогностических статистически-вероятностных свойств чисел Вольфа и их временны́х производных – мы констатируем, что эти свойства или характеристики практически не были исследованы. Поэтому первоочередной целью этой работы и является проведение, насколько нам оказалось по силам, детального статистически-вероятностного исследования чисел Вольфа и их вариаций. Попутно нами проводится и небольшое сравнительное эволюционное исследование этих чисел и вариаций, которое имеет некоторый прогностический потенциал.
При этом проводимые нами статистически-вероятностные исследования по методологии являются практически полностью поисковыми, поскольку они, прежде всего, нацелены на поиск гипотетических закономерностей для преимущественно неслучайных процессов. Поэтому представляется вполне адекватным проведенное далее поисковое исследование на основе короткого, но достаточно точного ряда W. Старченко и Яковлева [2019а; б; 2021] частично обосновали предлагаемую методику поисковых исследований в результате ее апробации на ряде значений глобальной геомагнитной энергии E и ее производной dE/dt, которые являются прямыми аналогами W и W '.
Именно для подобных предварительных исследований некоторого массива данных и создавались так называемые методы анализа экспериментальных данных или “поискового” анализа, введенные Tukey [1977]. Подобные процедуры обеспечивают наглядный обзор характера данных, предоставляют информацию о необычных распределениях и даже об ошибочных значениях в наборе данных. Два наиболее часто используемых инструмента такого анализа – диаграмма “стебель–листья” (“Stem and Leaf Plot”) и диаграмма размаха (“Box Plot”), см., например, в работах [Freund et al., 2010; Frigge et al., 1989; Bowley et al., 1902].
Представление в виде диаграммы стебель-листья (здесь и далее употребляем без кавычек) позволяет провести разделение данных на группы и выявить их детали и особенности. Диаграмма размаха (диаграмма “ящик с усами”) в удобной форме показывает медиану (или, если нужно, среднее), нижний и верхний квартили, минимальное и максимальное значение выборки, а также выбросы.
Безусловно, современные статистические пакеты программ позволяют автоматически строить не только вышеописанные диаграммы, но и многие другие наглядные представления, которые преимущественно вне зоны нашего интереса. Однако, в этой работе, авторы постарались несколько модифицировать эти диаграммы с целью дать максимально детальное представление об исследуемых объектах. Фактически на диаграммах стебель-листья представлена каждая реализация. А кроме стандартных или “пакетных” величин выявлены как редко используемые (но значимые – типа локально наиболее вероятных величин) статистические величины, так и отмечены важные физические состояния (например – максимумы и минимумы активности). Разумеется, столь существенная детализация достигнута благодаря относительно коротким рядам, что обернулось “негладким” представлением графических материалов.
2. ИСХОДНЫЕ ДАННЫЕ
Мы используем среднегодовые числа Вольфа W с 1700 по 2020 гг., как было указано выше, в версии v2 из (http://sidc.oma.be/silso/datafiles). Временны́е производные dW/dt ≡ W ' получены на ту же середину года, что и W, посредством взятия среднего от производной слева и справа. Это простейшее усреднение производной, надеемся, несколько сглаживает изначальные ошибки, проистекающие из наблюдательного и договорного определения W.
На рисунке 1 представлена эволюция чисел Вольфа и их производных, которые и являются исходными данными для нашего статистического анализа. Интересно отметить, что почти всюду максимум в производной проявляется примерно за два года до максимума в числах, а минимум в производных – за примерно три года до минимума в числах. Это обстоятельство очевидным образом может быть использовано в прогнозировании солнечной активности.
Рис. 1.
Эволюция чисел Вольфа W и их временны́х производных W ' = dW/dt за 1700–2020 гг. Правая вертикальная ось в 1/год для W ', левая безразмерная – для W. Также приведены огибающие кривые для всех максимумов и минимумов.
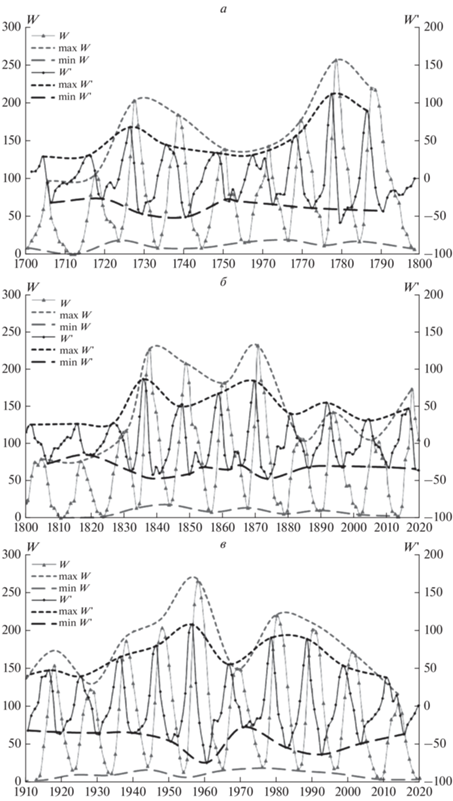
Также на рис. 1 представлены огибающие кривые, которые построены посредством последовательного сглаженного (опция в программе Excel) соединения точек, соответствующих максимумам и минимумам чисел W и производных W '. Эти огибающие кривые выглядят квазигармоническими, и можно попытаться оценить их характерные периоды. Сделать эту оценку удобнее, используя рис. 2. Он содержит только эти огибающие кривые и соответствующие им усредненные линии, которые задают базовые уровни для отсчета гармонических колебаний. На рис. 2 наиболее ярко соответствующая периодичность проявляется для максимумов (W max и W ' max). Грубо оценить длительность периодов можно по количеству локальных экстремумов. Для определенности будем учитывать только экстремумы, достаточно отстоящие от соответствующей усредненной величины, которая представлена горизонтальной линией. Получаем 7 локальных максимумов и 8 минимумов для W max, а для W' max – 6 максимумов и 9 минимумов. Итого в среднем имеем 7.5, что дает период в годах по самоочевидной формуле: (2020–1700)/(7.5–1) ≈ 50.
Рис. 2.
Огибающие кривые и усредненные величины (горизонтальные линии) для максимальных и минимальных значений чисел Вольфа W и производных W '.
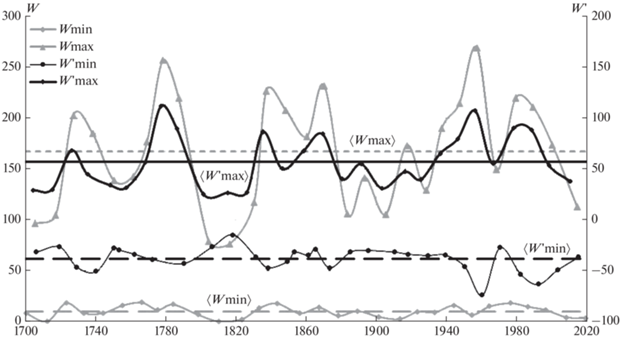
Особо выделяются доминирующие (как в W, так и в W ') максимумы около 1780 и 1956 годов. Их разделяет 176 лет, и эти фактически 150–200 лет являются самой долговременной, но весьма грубой оценкой гармонического периода в исходных данных.
3. ВИЗУАЛИЗАЦИЯ СТАТИСТИКИ ЧИСЕЛ ВОЛЬФА W
Для статистического анализа мы, прежде всего, сортируем исходные числа Вольфа (W) в количестве 321 (см. предыдущий раздел) так, чтобы они расположились от меньшего значения к большему. Затем статистически визуализируем все эти отсортированные W в табл. 1 как диаграмму стебель-листья или исходно – “Stem and Leaf Plot”, см., например, [Freund et al., 2010]. По сути, это гистограмма, представленная не графически, а в цифровом виде. В качестве “стебля” S, расположенного в левом крайнем столбце табл. 1, мы последовательно с шагом +10 на каждую строчку вверх используем соответствующие десятичные разряды, идущие от 0 до 260. Каждая строка табл. 1, или “ветка”, заполнена цифрами, или “листьями”, D, которые принимают значения от 0 до 9. Подчеркиванием отмечены “листья”, соответствующие минимумам солнечной активности, а жирным шрифтом выделены максимумы. Таким образом, каждый “лист” не только визуализирует конкретную реализацию числа Вольфа по простой (округленной до целых) формуле W = S + D, но и позволяет оценить его относительное статистическое или вероятностное распределение, как в целом, так и внутри каждой “ветки”.
Таблица 1.
Диаграмма стебель-листья для чисел Вольфа W
| Стебель S | Ветки (строки) с листьями (цифры D | W = S + D) | n | M |
|---|---|---|---|
| 260+ | 2 9 | 2 | 266 |
| 250+ | 7 Q3 + 1.5R | 1 | 257 |
| 240+ | |||
| 230+ | 2 | 1 | 232 |
| 220+ | 00 5 7 | 4 | 223 |
| 210+ | 0 15 8 9 | 5 | 215 |
| 200+ | 1 3 3 8 | 4 | 204 |
| 190+ | 1 1 2 3 3 7 9 | 7 | 194 |
| 180+ | 2 3 3 5 5 | 5 | 184 |
| 170+ | 0 2 447 8 | 6 | 174 |
| 160+ | 2 4 6 8 8 9 9 | 7 | 167 |
| 150+ | 0 0 4 4 9 | 5 | 153 |
| 140+ | 1 23 3 7 8 8 9 | 8 | 145 |
| 130+ | 0 0 0 1 3 3 3 5 5 5 6 6 8 9 | 14 | 134 |
| 120+ | 2 2 2 2 3 4 6 Q3 | 7 | 123 |
| 110+ | 0 1 1 2 3 3 4 5 5 6 7 7 9 | 13 | 114 |
| 100+ | 0 0 0 2 3 3 3 4 5 5 66 6 6 6 7 7 8 9 | 19 | 104 |
| 90+ | 0 0 1 1 4 4 5 7 8 8 9 9 | 12 | 95 |
| 80+ | 0 0 1 1 1 3 4 5 6 6 6 8 9 | 13 | 84 |
| 70+ | 0 0 0 2 3 4 4 5 5 5 6 6 6 8 8 8 9 9 9 9 | 20 | 75 |
| 60+ | 0 0 0 0 1 1 3 3 3 3 4 5 Q2 | 5 6 7 7 7 7 8 8 9 | 21 | 64 |
| 50+ | 1 1 1 3 3 4 4 4 4 5 7 7 8 8 8 9 9 | 17 | 55 |
| 40+ | 0 0 0 0 1 2 3 3 4 4 4 4 5 5 5 6 7 7 8 9 | 20 | 44 |
| 30+ | 1 1 3 3 3 4 5 5 5 6 7 7 8 8 9 9 9 | 17 | 35 |
| 20+ | 0 0 0 0 0 1 1 2 2 2 3 3 4 4 4 5 5 5 5 7 7 7 7 7 8 8 8 9 Q1 | 28 | 24 |
| 10+ | 00 0 0 1 1 1 1 22 2 3 3 3 3 4 4 55 5 66 6 6 7 7 7 7 8 8 8 8 8 8 89 9 9 | 38 | 15 |
| 0+ | 00 0 22 2 3 44 4 5 5 5 6 6 6 77 7 8888 8 9 9 9 | 27 | 5 |
| Всего: | 321 |
Так, наиболее вероятной является “ветка” 10+, поскольку в ней наибольшее число реализаций – 38 (столбец с количеством реализаций по каждой ветке озаглавлен n). Средняя по этой ветке величина W = 15 отражает усредненную по веткам наиболее вероятную величину (столбец, озаглавленный M – среднеарифметические числа W по веткам). Внутри же этой “ветки” наиболее вероятным будет W = 18, так как ему соответствует наибольшее количество реализаций – семь. Поскольку внутри всех остальных “веток” количество повторяющихся реализаций с одним и тем же D не превышает пяти, то естественно считать W = 18 (приблизительно – из-за округления до целых в табл. 1) наиболее вероятным и для всех реализаций. Соответствующие ему “листья” мы пометили крупным шрифтом и курсивом. Уточнив (возвращаясь к исходным неокругленным до целых данным) среднее по всем этим семи выделенным реализациям, далее будем использовать его как наиболее вероятную величину числа Вольфа k(W) = 18.3.
Перейдем теперь к более качественным, но при этом весьма наглядным и понятным графическим анализам, которые представлены на рис. 3 как гистограмма и диаграмма размаха. Под гистограммой здесь и далее подразумевается ступенчатая функция распределения вероятностей. Высота каждого столбца гистограммы (или эквивалентно – безразмерное значение каждой ступеньки функции распределения) получается из соответствующей строки – ветки в табл. 1 – посредством деления количества реализаций n, или “листьев” внутри “ветки”, на общее количество (321) реализаций и на фиксированную (10) ширину каждой ступеньки, или столбца, гистограммы. При этом очевидным образом, выполняется и нормировочное условие – интеграл (или площадь затемненной на рис. 3 области) гистограммы по числам Вольфа от 0 до 270 равен 1.
Рис. 3.
Ступенчатая функция распределения вероятности реализаций, или гистограмма, (отложена по вертикальной оси) и диаграмма размаха (Box Plot) для чисел Вольфа W (отложены по горизонтальной оси). Все оси и средние значения количества пятен над столбцами гистограммы – безразмерные. Методом наименьших квадратов построена экспоненциальная зависимость (сплошная линия), аппроксимирующая гистограмму с достоверностью R2 = 0.8581. Для сравнения приведена функция нормального распределения в виде кривой (штриховая линия) с тем же средним и дисперсией, что и у гистограммы.
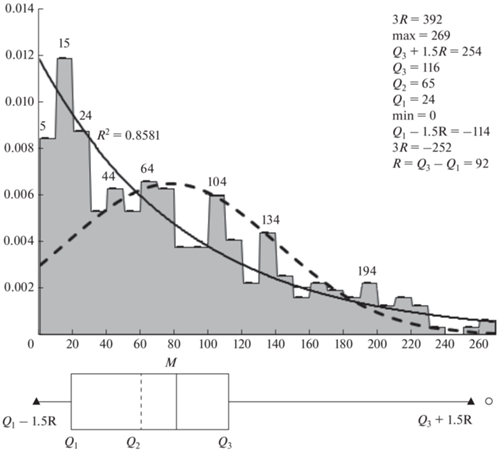
Для сравнения на гистограмму (рис. 3) нанесено нормальное распределение (штриховая кривая) с тем же средним (M) и той же дисперсией, что и у этой гистограммы. Основная причина сильного отклонения полученного распределения (представленного гистограммой) от этого нормального распределения в том, что наиболее вероятное по ветке W = 15 (над 2-м слева столбцом) значительно меньше среднеарифметического M = 78.5 и медианного MDN = 65.3. Подобные статистические параметры скорее присущи экспоненциальному распределению. И действительно – экспоненциальное распределение (непрерывная кривая) с ошибкой менее 15% аппроксимирует полученное распределение. Также бросается в глаза “изрезанность” и “дискретность” гистограммы, когда ее столбцы весьма существенно и нерегулярно отклоняются от гладких кривых. Это, по-видимому, в первую очередь обусловлено недостаточной длиной временнóго ряда, а также возможно указывает на тенденцию к формированию выделенных значений.
Для еще более наглядной интерпретации наших статистических результатов представим, следуя Freund et al. [2010], диаграмму размаха (оригинальное название “Box Plot”, или “ящик с усами”). Она расположена в нижней части рис. 3. Первый квартиль в масштабе исследуемой величины Q1, или “левая грань ящика”, (см. также табл. 1) задает границу 25% первых реализаций; второй (вертикальная штриховая линия), равный медианной величине Q2 = MDN, – половину, а третий Q3 – 75%. Для построения распределений вне “ящика” вычисляется размах меж квартилями R = Q3 – Q1, который примерно равен двум сигма (2σ), или удвоенной дисперсии. Слева от “ящика”, образованного квартилями: внешняя граница R1 = Q1 – 3R, внутренняя (до нее, собственно, и дотягиваются “усы”, обозначенные горизонтальными полосами) – R2 = Q1 – 1.5R, а справа: внутренняя граница R3 = Q3 + 1.5R и внешняя R4 = Q3 + 3R. Заполненные кружочки – это выбросы за внешнюю границу, а пустые – за внутреннюю границу. В нашем случае есть выбросы только за внутреннюю границу. При этом непропорционально длинный правый “ус” и весьма малая наиболее вероятная величина W хорошо соответствуют вышеописанному экспоненциальному распределению. Выявление же статистической и возможно связанной с ней физической природы такого распределения явно потребует отдельной более детальной работы, а здесь мы ограничимся его констатацией.
4. ВИЗУАЛИЗАЦИЯ СТАТИСТИКИ ДЛЯ ПРОИЗВОДНЫХ W ′
Построим по аналогии с предыдущим разделом диаграмму стебель-листья для производных W ' (см. табл. 2). Существенное отличие – наличие отрицательных величин, количество которых примерно на треть превышает количество положительных величин W '. При этом среднеарифметическое M = −0.015 по всем W ′ настолько мало по модулю, что в пределах возможной ошибки его можно считать нулевым. Это является следствием того, что члены последовательности Wi глобально ограничены. Сумма всех последовательных $W_{i}^{'},$ рассчитанных по алгоритму, использованному в данной статье, по i от 1 до N (=321 в нашем частном случае, что соответствует общему количеству чисел Вольфа, см. первую строку “Все” табл. 3 далее) равна (WN + WN – 1 – W1 – W2)/2. Очевидно, в общем случае, при делении на N → ∞ в пределе получаем 0. А то, что количество отрицательных реализаций преобладает, свидетельствует об общеизвестном превышении (на те же примерно 1/3) времени падения активности над временем ее роста.
Таблица 2.
Диаграмма стебель-листья для производных от чисел Вольфа W '
| Стебель S | Ветки (строки) с листьями (цифры D | W ' = S ± D) | n | M |
|---|---|---|---|
| 110+ | 2 | 1 | 112.2 |
| 100+ | 2 | 1 | 107.6 |
| 90+ | 0 0 7 Q3 + 1.5R | 3 | 92.5 |
| 80+ | 0 5 7 9 | 4 | 84.9 |
| 70+ | 1 1 | 2 | 71.0 |
| 60+ | 1 5 7 8 9 | 5 | 66.1 |
| 50+ | 0 3 4 4 5 5 5 6 7 9 | 10 | 54.8 |
| 40+ | 0 0 1 2 3 4 5 7 8 8 9 | 11 | 44.2 |
| 30+ | 0 0 0 1 1 1 1 2 2 2 4 4 4 6 8 8 8 9 9 9 9 9 | 22 | 34.5 |
| 20+ | 0 0 0 1 1 3 3 4 4 4 4 4 4 4 5 5 5 6 6 6 7 7 7 8 9 Q3 | 25 | 24.2 |
| 10+ | 0 0 0 1 2 3 3 4 4 4 4 5 6 6 7 7 7 7 8 8 9 9 9 | 23 | 14.9 |
| 0+ | 0 0 1 1 2 2 2 2 33 3 44 4 4 55 7 7 7 888 8 8 9 9 9 9 | 29 | 4.9 |
| 0– | 111 1 1 12 23 3 4 4 4 4 4 4 4 5 5 5 5 6 6 6 6 7 7 7 8 8 9 9 9 9 Q2 | 34 | –5.2 |
| –10– | 0 0 0 0 1 1 1 222 2 2 2 2 2 2 2 3 3 3 3 3 4 4 4 5 5 5 5 5 6 6 6 6 6 6 6 6 7 7 7 7 7 7 8 8 8 9 9 | 49 | –14.2 |
| –20– | 0 0 0 0 0 0 0 0 1 1 1 1 1 2 2 3 3 3 4 4 4 4 5 5 5 5 6 6 7 7 7 8 8 8 8 9 9 9 Q1 | 38 | –23.8 |
| –30– | 0 0 0 0 0 0 1 1 1 1 1 2 2 2 2 2 2 2 2 2 3 4 4 4 4 4 5 5 5 5 6 6 7 7 7 7 7 8 8 9 9 9 | 42 | –33.6 |
| –40– | 0 1 1 1 2 3 4 4 6 7 7 8 9 | 13 | –44.1 |
| –50– | 1 1 1 3 4 8 | 6 | –53.0 |
| –60– | 4 | 1 | –63.6 |
| –70– | 4 | 1 | –74.4 |
| –80– | Q1 – 1.5R | ||
| Всего: | 320 |
Примечание: Обозначения соответствуют обозначениям в примечании к табл. 1.
Наиболее вероятная величина k(W ′) = −12.025 здесь определяется весьма уверенно, поскольку в наиболее вероятной ветке –10 этому k соответствует 10 “листьев” с D = 2. В целом наблюдается более “простая” и даже в заметной степени “стандартная” для случайных процессов статистическая структура в W ' по сравнению с W. Для ее более наглядного анализа построим гистограмму и диаграмму размаха для W ' на рис. 4.
Рис. 4.
Ступенчатая функция распределения вероятности реализаций, или гистограмма, (отложена по вертикальной безразмерной оси) и диаграмма размаха (Box Plot) для производных от чисел Вольфа W ' (отложены по горизонтальной оси в 1/год). Значения над столбцами гистограммы – в 1/год. Приведена, для сравнения, функция нормального распределения в виде кривой с тем же средним и дисперсией, что и у гистограммы.
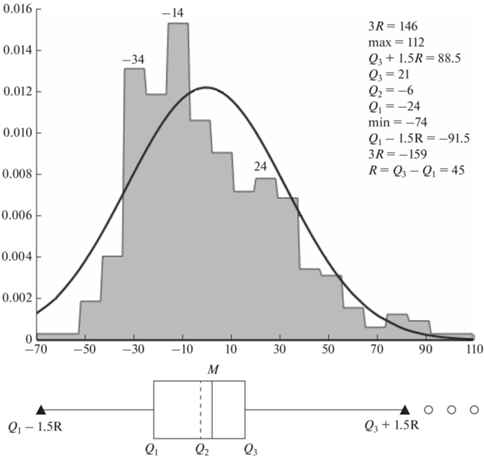
И действительно, как видно из гистограммы и “нормальной” кривой на рис. 4, распределение W ' заметно ближе к нормальному распределению по сравнению с W. Есть и заметные отличия от нормального распределения, которые наиболее наглядно выражаются существенными выбросами за “правый ус” диаграммы размаха.
Таким образом, как и для W выше, так и для W ', следует признать недостаточно достоверными максимальные значения, которые разумно частично исключить в рамках сравнительно простых статистических моделей. Другой важный результат – то, что W естественно моделировать преимущественно неким детерминистическим процессом, а для моделирования W ' необходимо в значительной степени учитывать полностью случайные процессы. Все эти обстоятельства могут оказаться существенным подспорьем в прогнозировании солнечной активности.
5. СВОДНАЯ СТАТИСТИКА И ХАРАКТЕРНЫЕ ВРЕМЕНА
Сводные статистические результаты по числам Вольфа и их производным представлены в табл. 3. Реализации для положительных и отрицательных значений W ' рассмотрены также и раздельно для отдельных исследований времен роста и падения активности. Для самих чисел Вольфа W мы также специально выделили те, которые соответствуют эпохам роста W ' ≥ 0 и эпохам падения W ' < 0. При этом, как это очевидно из табл. 3, дисперсия выделенных таким образом величин W ' существенно меньше дисперсии всех величин. Это свидетельствует о том, что солнечная активность подразделяется на эпохи роста и падения.
Таблица 3.
Сводные статистические величины
| Числа Вольфа W | |||||||
|---|---|---|---|---|---|---|---|
| N | M | MDN | RMS | σ | MIN | MAX | |
| Все | 321 | 78.5 | 65.3 | 100.00 | 63.0 | 0 | 269.3 |
| W ′ ≥ 0 | 136 | 78.46 | 64.4 | 101.80 | 69.5 | 0 | 269.3 |
| W ′ < 0 | 184 | 78.94 | 66 | 98.99 | 55.8 | 0 | 227.3 |
| Производная W ′ | |||||||
| N | M | MDN | RMS | σ | MIN | MAX | |
| Все | 320 | –0.015 | –6.08 | 32.72 | 32.67 | –74.35 | 112.2 |
| W ′ ≥ 0 | 136 | 30.84 | 25.15 | 39.29 | 24.35 | 0.3 | 112.2 |
| W ′ < 0 | 184 | –22.82 | –20.73 | 26.85 | 14.16 | –74.35 | –0.75 |
Характерные времена T = W/W ' естественным образом получаем при делении средних значений чисел Вольфа на соответствующие средние производные. Для получения этих характерных времен мы далее используем усредненные статистические величины из табл. 3.
Основным временем является время, определенное по всем среднеквадратичным значениям:
(1)
${{T}_{{{\text{RMS}}}}} = ({{{\text{100}}} \mathord{\left/ {\vphantom {{{\text{100}}} {{\text{32}}{\text{.72}}}}} \right. \kern-0em} {{\text{32}}{\text{.72}}}})\,{\text{лет}} = {\text{3}}{\text{.06}}\,{\text{лет}}{\text{.}}$В эпохи роста при W ' ≥ 0 характерное среднеквадратичное время из табл. 3:
(2)
${{T}_{{{\text{RMS}} + }}} = ({{101.8} \mathord{\left/ {\vphantom {{101.8} {39.29}}} \right. \kern-0em} {39.29}})\,\,{\text{лет}} = 2.59\,{\text{лет}}.$(3)
${{T}_{{{\text{RMS}} - }}} = ({{98.99} \mathord{\left/ {\vphantom {{98.99} {26.85}}} \right. \kern-0em} {26.85}})\,{\text{лет}} = 3.69\,{\text{лет}}.$(4)
$\begin{gathered} {{T}_{{{\text{M}} - }}} = - {\kern 1pt} ({{78.94} \mathord{\left/ {\vphantom {{78.94} {22.82}}} \right. \kern-0em} {22.82}})\,{\kern 1pt} {\text{лет}} = - 3.46\,{\kern 1pt} {\text{лет}}, \\ {{T}_{{{\text{MDN}} - }}} = ({{66} \mathord{\left/ {\vphantom {{66} {20.73}}} \right. \kern-0em} {20.73}})\,{\kern 1pt} {\text{лет}} = - 3.18\,{\kern 1pt} {\text{лет}}. \\ \end{gathered} $(5)
$\begin{gathered} {{T}_{{{\text{M}} + }}} = ({{78.46} \mathord{\left/ {\vphantom {{78.46} {30.84}}} \right. \kern-0em} {30.84}})\,\,{\text{лет}} = 2.54\,\,{\text{года}}, \\ {{T}_{{{\text{MDN}} + }}} = ({{64.4} \mathord{\left/ {\vphantom {{64.4} {25.15}}} \right. \kern-0em} {25.15}})\,\,{\text{лет}} = 2.56\,\,{\text{года}}. \\ \end{gathered} $Декадное характерное время можно получить только из всех реализаций для MDN:
Умножая это время на 4, получим оценку периода ~43 лет, что согласуется с оценкой ~50 лет, приведенной в конце раздела 2 этой работы. Знак минус в (6) означает большую длительность соответствующих эпох падения при W ' < 0, когда уменьшается величина W по сравнению с эпохами роста при W ' > 0.6. ОБСУЖДЕНИЕ, ЗАКЛЮЧЕНИЕ И РЕЗУЛЬТАТЫ
Грубо оценим величину скорости конвекции делением полутолщины конвективной зоны (КЗ) на основное среднеквадратичное время из (1). Получается 1 м/с, что примерно соответствует глубинной части КЗ [Charbonneau, 2020; Кичатинов и Непомнящих, 2017]. Таким образом, подтверждается гипотеза о глубинном происхождении солнечных пятен [Кичатинов, 2019; Cameron et al., 2017; Рузмайкин и Старченко, 1987].
Аналогичную оценку можно получить и для преимущественно двух-трех годовых характерных времен, которые представлены в предыдущем разделе. В целом же для детальных спектральных исследований представляется актуальным непосредственный статистический анализ не только некоторых средних, но и всех доступных “мгновенных времен вариаций” W/W ' или “частот” W '/W, которыми мы планируем заняться в наших последующих работах.
Главным результатом этой работы мы считаем выявление преимущественно экспоненциального распределения вероятностей для чисел Вольфа, которое требует дальнейшей большой работы по его более детальному обоснованию и определению его физической природы. Частичное обоснование физических механизмов, приводящих к подобному распределению, было дано в серии работ Журавлева и Летуновского [2010, 2011]. Они показали, что основным “равновесным” вероятностным распределением является именно показательное распределение, которое близко к обсуждаемому в этой работе экспоненциальному распределению. Его можно интерпретировать как распределение по энергиям, если при действии этого механизма каждое появившееся пятно имеет некоторое слабо меняющееся среднее значение энергии.
Также важным нам представляется разрешить кажущееся, надеемся, противоречие между полученным нами почти экспоненциальным распределением чисел Вольфа W и преимущественно нормальным распределением их производных (W '). Возможно, это противоречие обусловлено принципиально негладкой зависимостью W от времени и соответствующей, по сути, существенно случайной процедурой взятия производной.
Сформулируем основные результаты представленной работы.
1. Проведено статистически-вероятностное исследование среднегодовых чисел Вольфа W и их временны́х производных W ' посредством детальных диаграмм стебель-листья, ступенчатых функций распределения (в виде гистограмм) и наглядных диаграмм размаха.
2. Существенное отклонение вероятностного распределения W от нормального определяется наиболее вероятным значением W, равным всего 18, при среднеквадратичном 100, медианном 65 и среднем 79. При этом экспоненциальное распределение хорошо аппроксимирует наше экспериментальное распределение вероятностей с погрешностью менее 15%.
3. Меньше от нормального распределения отклоняются W ' с наиболее вероятным значением ‒12/год, медианным –6.1/год, средним –0.015/год, среднеквадратичным 33/год, максимумом 112/год и минимумом –74/год.
4. Таким образом, эволюцию чисел Вольфа W естественно моделировать преимущественно неким процессом с экспоненциальным распределением, а для моделирования W ′ необходимо в значительной степени учитывать случайные процессы с нормальным распределением. Надеемся, что дальнейшие исследования прояснят суть столь существенной статистической разницы между исходной величиной и ее производной.
5. Как для W, так и для W ' следует признать недостаточно достоверными их максимальные (с учетом знака для W ') значения, которые разумно частично исключить в рамках сравнительно простых статистических моделей.
6. Отношения средних величин согласуются с характерными экспоненциальными временами роста/падения активности в 2.6/3.7 года, 11-летней гармонической цикличностью и скоростью в глубине конвективной зоны ~1 м/с.
7. Достаточно значимыми для проведения дальнейших работ представляются долговременные тенденции с гармоническими или периодическими временами около пятидесяти лет, и возможно существует некоторая периодичность в диапазоне 150–200 лет.
Список литературы
− Витинский Ю.И. Цикличность и прогнозы солнечной активности. Л.: Наука, 258 с. 1973.
− Витинский Ю.И., Копецкий М., Куклин Г.В. Статистика пятнообразовательной деятельности Солнца. М.: Физматлит, 294 с. 1986.
− Журавлев В.М., Летуновский С.В. Анализ долговременной эволюции активности Солнца на основе ряда чисел Вольфа. (I Методика) // Изв. вузов. Поволжский регион. Физико-математические науки. № 4. С. 120–129. 2010.
− Журавлев В.М., Летуновский С.В. Анализ долговременной эволюции активности Солнца на основе ряда чисел Вольфа. (II Результаты) // Изв. вузов. Поволжский регион. Физико-математические науки. № 4. С. 164–174. 2011.
− Ишков В.Н., Шибаев И.Г. Циклы солнечной активности: общие характеристики и современные границы прогнозирования // Изв. РАН. Сер. физ. Т. 70. № 10. С. 1439–1442. 2006.
− Кичатинов Л.Л. Распад крупномасштабного магнитного поля на трубки у основания конвективной зоны Солнца // Письма в астрон. журн. Т. 45. № 1. С. 45–54. 2019.
− Кичатинов Л.Л., Непомнящих А.А. Согласованная модель солнечного динамо и дифференциального вращения // Письма в астрон. журн. Астрономия и космическая астрофизика. Т. 43. № 5. С. 370–382. 2017.
− Рузмайкин А.А., Старченко С.В. Магнитные проявления Солнечного вращения // Астрон. журн. Т. 64. С. 1057–1065. 1987.
− Старченко С.В., Яковлева С.В. Спектры энергии и мощности потенциального геомагнитного поля с 1840 г. // Геомагнетизм и аэрономия. Т. 59. № 2. С. 258–264. 2019а.
− Старченко С.В., Яковлева С.В. Определение удельных временны́х вариаций энергии потенциального геомагнитного поля из модели IGRF // Геомагнетизм и аэрономия. Т. 59. № 5. С. 649–654. 2019б.
− Старченко С.В., Яковлева С.В. Двухвековая эволюция и статистика времен вариаций Энергии потенциального геомагнитного поля // Геомагнетизм и аэрономия. Т. 61. № 5. С. 661–671. 2021.
− Шибаев А.И. Долгосрочный прогноз солнечной активности по 150-летней гармонике и характеристикам циклов достоверной части ряда чисел Вольфа // Солнечная и солнечно-земная физика – 2017, Санкт-Петербург, Пулково, 9–13 октября. Отв.ред. А.В. Степанов и Ю.А. Наговицын. Санкт-Петербург: Изд-во ВВМ. С. 389–392. 2017.
− Abdel-Rahman H.I., Marzouk B.A. Statistical method to predict the sunspots number // NRIAG J. Astronomy and Geophysics. V. 7. P. 175–179. 2018.
− Akaniru A., Onuchukwu C.C. Statistical analysis of sunspot number and area // COOU Journal of Multidisciplinary Studies. V. 1. № 1. P. 107–121. 2017.
− Barnes J.A., Tryon P.V., Sargent H.H. Sunspot cycle simulation using random noise / The ancient Sun: fossil record in the earth, moon and meteorites. Eds. Pepin R.O., Eddy J.A., Merrill R.B. N.Y.: Pergamon Press. Geochim. Cosmochim. Acta Suppl. V. 13. P. 159–163. 1980.
− Bowley A.L. Elements of statistics. London: P.S. King, 336 p. 1902.
− Cameron R.H., Dikpati M., Brandenburg A. The global Solar dynamo // Space Sci. Rev. V. 210. P. 367–395. 2017.
− Charbonneau P. Dynamo models of the solar cycle // Living Rev. Sol. Phys. V. 7. № 1. P. 1– 91. 2020. https://doi.org/10.1007/s41116-020-00025-6
− Clette F., Svalgaard L., Vaquero J.M., Cliver E.W. Revisiting the Sunspot Number. A 400-year perspective on the solar cycle // Space Sci. Rev. V. 186. P. 35–103. 2014.
− Duhau S., Jager C. Solar dynamo modes of oscillations and the long-term prediction of solar activity // Phys. Astron. Int. J. V. 4(1). P. 34–58. 2020.
− Freund R.J., Mohr D.L., Wilson W.J. Statistical Methods. 3d ed. Salt Lake City, USA: Academic press. 800 p. 2010.
− Frick P., Sokoloff D., Stepanov R., Pipin V., Usoskin I. Spectral characteristic of mid-term quasi-periodicities in sunspot data // MNRAS. V. 491. P. 5572–5578. 2020.
− Frigge M., Hoaglin D., Iglewicz B. Some Implementations of the Boxplot // The American Statistician. V. 43. No 1. P. 50–54. 1989. https://doi.org/10.1080/00031305.1989.10475612
− Noble P.L., Wheatland M. S. Modeling the sunspot number distribution with a Fokker–Planck equation // The Astrophysical Journal. V. 732. No 1. P. 1–8. 2011.
− Ogurtsov M., Lindholm M. Statistical Effects in the Solar Activity Cycles during AD 1823–1996 // ISRN Astronomy and Astrophysics. 2011. https://doi.org/10.5402/2011/640817
− Priest E. Magnetohydrodynamics of the Sun. Cambridge: Cambridge University Press. 560p. 2014.
− Petrovay K. Solar cycle prediction // Living Rev. Sol. Phys. 17:2. 93 p. 2020. https://doi.org/10.1007/s41116-020-0022-z. arXiv:1907.02107
− Shibaev I., Ishkov V. Investigation of the Statistical Characteristics of Wolf Numbers Reliable Series: Signs of Solar Cycles Likelihood // Proc. 7th Scientific Conf. “Space, Ecology, Safety” – SES 2011, Sofia, Bulgaria, SRTI-BAS. P. 297–301. 2012.
− Sokoloff D.D., Shibalova A.S., Obridko V.N., Pipin V.V. Shape of solar cycles and mid-term solar activity oscillations // MNRAS. V. 497. № 4. P. 4376–4383. 2020.
− Starchenko S.V. Dynamo models with strong generation 1. Kinematic solution and axisymmetric \alpha^2\omega-dynamo // Geoph. Astroph. Fluid Dynamics. V. 77. C. 55–77. 1994.
− Tanaka M. Time series modelling of Annual Maximum Sunspot Numbers // Information Science and Applied Mathematics. V. 18. B.Ll.S. Senshu University. P. 19–32. 2010.
− Tukey J.W. Exploratory Data Analysis. Reading, Massachusetts, USA: Addison-Wesley Pub. Co. 712 p. 1977.
Дополнительные материалы отсутствуют.
Инструменты
Геомагнетизм и аэрономия


