Геомагнетизм и аэрономия, 2021, T. 61, № 6, стр. 683-693
Связь между длительностью и величиной ускорения корональных выбросов массы
А. Б. Струминский 1, *, И. Ю. Григорьева 2, Ю. И. Логачев 3, А. М. Садовский 1
1 Институт космических исследований РАН
г. Москва, Россия
2 Главная астрономическая обсерватория РАН
С.-Петербург, Россия
3 Научно-исследовательский институт ядерной физики им. Д.В. Скобельцына
Московского государственный университета им. М.В. Ломоносова
г. Москва, Россия
* E-mail: astrum@iki.rssi.ru
Поступила в редакцию 01.03.2021
После доработки 25.04.2021
Принята к публикации 27.05.2021
Аннотация
Исследуется вопрос о том, какая последовательность процессов на Солнце приводит к положительной обратной связи между движением и нагревом плазмы, ускорением электронов, а в итоге, к формированию корональных выбросов массы, ударных волн и ускорению протонов. Для этого проведен анализ солнечных событий, связанных с тремя импульсными вспышками: M2.9 6 июля 2012 г., X2.2 и X9.3 6 сентября 2017 г. и одной длительной вспышкой M3.7 7 марта 2011 г. Электроны ускорялись до релятивистских энергий во всех четырех вспышках, но две последние сопровождались корональными выбросами массы, ударными волнами и ускорением протонов с энергией >300 МэВ. Найдено два отличия вспышек без корональных выбросов массы. Первое отличие – были ограничены высотой, которая характерна для радиоизлучения 1415 МГц (верхняя хромосфера). Второе отличие – максимум меры эмиссии в них запаздывал относительно максимума температуры на время менее 2 мин. Если считать, что вспышка и корональные выбросы массы черпают энергию из одного резервуара, то время запаздывания можно рассматривать как характерное время ускорения корональных выбросов массы – существование дополнительного оттока энергии. Из теоретических оценок максимальной величины ускорения корональных выбросов массы, значений их минимальной и максимальной скорости следует возможный разброс времени ускорения корональных выбросов массы. Сравнения оценок и наблюдений показывает, что необходимая длительность ускорения для реализации межпланетного корональных выбросов массы была достигнута в событиях М3.7 7 марта 2011 г. и X9.3 6 сентября 2017 г.
1. ВВЕДЕНИЕ
Возможность детального исследования корональных выбросов массы (КВМ) появилась после запуска космического аппарата (КА) SOHO (Solar and Heliospheric Observatory), на борту которого находились ультрафиолетовый телескоп EIT (Extreme Ultraviolet Imaging Telescope) и коронограф LАSCO (Large Angle Spectrometric Coronagraph). Телескоп EIT позволяет наблюдать корональные структуры, а коронограф LASCO – движение КВМ в трех диапазонах от центра Солнца: С1 (1.1–3RS), С2 (1.5–6RS) и С3 (4–30RS). Первый случай EIT и LASCO наблюдений начала развития КВМ описан в работе [Dere et al., 1997].
Взаимосвязь между солнечными вспышками и КВМ с использованием данных LASCO C1 исследовалась в работе [Zhang et al., 2001], где было выделено три фазы развития КВМ – начальная, импульсного ускорения и равномерного распространения. Начальная фаза характеризуется медленным подъемом со скоростью менее 80 км/с в течение десятка минут перед солнечной вспышкой. Фаза импульсного ускорения длится от нескольких до десятков минут, хорошо совпадает со вспышкой в мягком рентгеновском (SXR) излучении и прекращается вблизи его максимума. Далее следует фаза распространения, которая характеризуется постоянной или медленно спадающей скоростью. Среди рассмотренных событий авторы выделили случай КВМ 6 ноября 1997 г., связанный со вспышкой X9.7, в котором не было начальной фазы, а величина ускорения КВМ составила ~7.3 км/с2. Представления о кинематике КВМ, сформулированные [Zhang et al., 2001], являются в настоящее время определяющими [например, Кузнецов, 2008].
К сожалению, LASCO C1 прекратил свою работу в 1998 г. Отсутствие наблюдений LASCO C1 удалось компенсировать с помощью других инструментов. Так в работе [Gallagher et al., 2003] для исследования импульсного ускорения КВМ, связанного со вспышкой X1.5 21 апреля 2002 г., были использованы изображения, полученные инструментами КА TRACE (Transition Region and Coronal Explorer). Авторы [Gallagher et al., 2003] отмечают, что в этом событии начало ускорения совпало с ростом жесткого рентгеновского (HXR) излучения с энергий >25 кэВ по данным RHESSI (Ramaty High Energy Solar Spectroscopic Imager), а наибольшее ускорение КВМ наблюдалось в максимуме HXR. Это подразумевает связь между ускорением нетепловых электронов во вспышке и силами, обеспечивающими ускорение КВМ.
Благодаря коронографам COR1 и COR2 STEREO (Solar Terrestrial Relations Observatory) удалось пронаблюдать вблизи поверхности Солнца КВМ, связанный с наземным возрастанием (ground level enhancement (GLE)) интенсивности космических лучей 17 мая 2012 г. [Gopalswamy et al., 2013]. Авторы этой работы определили, что ударная волна КВМ, отождествленная по началу радиовсплеска II типа, сформировалась на расстоянии 1.38 Rs (здесь Rs – радиус Солнца) от центра Солнца. Солнечные протоны GLE вышли в межпланетное пространство (МП) при положении КВМ на 2.32 Rs. Также c помощью приборов на борту КА STEREO-B [Gopalswamy et al., 2016] была исследована кинематика КВМ в залимбовом событии 23 июля 2012 г.
После запуска. КА SDO (Solar Dynamic Observatory) в 2010 г. стало возможным изучать КВМ в нижней короне Солнце с помощью инструмента AIA (Atmospheric Imaging Assembly). Новые и неожиданные результаты по кинематике КВМ и его связи с нетепловым излучением солнечной вспышки X2.8 13 мая 2013 г. получены в работе [Gou et al., 2020]. Впервые было показано, что КВМ был ускорен в двух различных фазах – импульсной, с максимальной величиной ускорения ~5 км/с2, и длительной, с величиной ускорения до 0.7 км/с2. Эти две фазы ускорения КВМ соответствовали двум различным эпизодам энерговыделения: первый – “стандартной” эрупции магнитного волокна, второй – постэруптивному энерговыделению в петлях большого масштаба и ускорению частиц, генерирующих нетепловое рентгеновское и гамма-излучение.
Необходимо отметить, что в событии 10 сентября 2017 г., по всей видимости, также было две фазы ускорения КВМ. Согласно результатам [Gopalswamy et al., 2018] максимальная величина ускорения КВМ 9.1 ± 1.6 км/с2 была в 15:58 UT при его положении на ~2.05 Rs и скорости 3114 ± ± 240 км/с, а ускорение КВМ прекратилось в 16:18 UT при скорости ~4191 ± 272 км/с. Действительно, если предположить, что КВМ ускорялся от начала регистрации радиоизлучения на 15.4 ГГц в 15:52 UT до его максимума в 15:58 UT, то скорость ~3114 км/с была достигнута за 6 мин, т.е. среднее ускорение было 8.7 км/с2 (импульсная фаза ускорения). Далее КВМ приобрел дополнительную скорость 1077 км/с за 20 мин, т.е. среднее ускорение стало на порядок меньше 0.9 км/с2 (длительная фаза ускорения). Этот факт был не замечен в работах [Gopalswamy et al., 2018, Veronig et al., 2018].
Объектом активного МГД-моделирования в 2018–2019 гг. стали солнечные вспышки X2.2 и X9.3 6 сентября 2017 г., которые произошли в одной и той же активной области с разницей по времени около 3 часов. Основной задачей было объяснить, используя современные МГД-модели и имеющиеся данные по магнитному полю, почему вспышка X9.3 привела к эрупции, а X2.2 нет [Liu et al., 2018; Inoue et al., 2018; Jiang et al., 2018; Zou et al., 2019]. Удалось показать, что во время замкнутой вспышки X2.2 и вплоть до эруптивной вспышки X9.3 происходило формирование магнитного жгута, увеличение его магнитного потока и скрученности [Liu et al., 2018]. Основное различие между состояниями жгута во время вспышек X2.2 и X9.3 заключалось в том, что в первом случае жгут не достиг порога тороидальной неустойчивости, а во втором случае его превзошел [Zou et al., 2019]. Несмотря на успехи МГД-моделирования эрупции волокон необходимо отметить, что эти расчеты не ведутся в реальном времени. Они не учитывают энерговыделение при пересоединении и возможную при этом обратную связь. Моделирование солнечных вспышек во всем их многообразии остается задачей будущего.
Какая последовательность процессов на Солнце приводит к положительной обратной связи между движением и нагревом плазмы, ускорением электронов, а в итоге, к формированию ударных волн и ускорению протонов? В поисках ответа на этот вопрос мы исследуем четыре солнечные вспышки, представляющие три разные области на диаграмме, которая связывает характеристики солнечных вспышек и солнечных протонных событий (СПС) [Cliver et al., 2019]. На этой диаграмме выделяются: 1) вспышки, вызванные исчезновением волокна, характеризующиеся слабым электромагнитным излучением, но мощными СПС; 2) вспышки и СПС с хорошей корреляцией параметров; 3) средние и большие вспышки без СПС. Вспышка M3.7 7 марта 2011 г. [Ackerman et al., 2014; Share et al., 2018] и вспышка X9.3 6 сентября 2017 г. [Sharykin and Kosovichev, 2018; Lysenko et al., 2018; Струминский и др., 2020а] попадают в первую и вторую группу событий, соответственно. В них происходило ускорение релятивистских электронов и протонов >100 МэВ, а в МП наблюдались КВМ и СПС. Чтобы выделить процессы непосредственно связанные с КВМ и ускорением протонов, мы рассматриваем две вспышки из третей группы: M2.9 6 июля 2012 г. [Altyntsev et al., 2017] и X2.2 6 сентября 2017 г. [Струминский и др., 2020а], в которых ускорялись релятивистские электроны, но в МП не было КВМ и СПС.
Основные характеристики четырех рассматриваемых событий представлены в табл. 1. Для возможности сравнения они рассматриваются относительно выбранного нуля времени – начала радиоизлучения на 15.4 ГГц по данным RSTN (Radio Solar Telescope Network). Такой выбор нулевого времени был обоснован ранее и уже использовался нами неоднократно [Струминский и др., 2020а, б; Struminsky et al., 2020]. Мы отмечаем два явных отличия вспышек без КВМ: 1) они не развивались на высотах менее той, которая характерна для радиоизлучения 1415 МГц (верхняя хромосфера); 2) максимум меры эмиссии относительно максимума температуры запаздывал на время менее 2 мин. Эти различия дают основу для оценок некоторых физических параметров, которые обсуждаются далее.
Таблица 1.
Основные характеристики четырех рассматриваемых событий
| А | 07.03.2011 г. 19:47 UT, M3.7 S22W67 |
06.07.2012 г. 01:38 UT, M2.9 S18W41 |
06.09.2017 г. 09:00 UT, Х2.2 S08W33 |
06.09.2017 г. 11:54 UT, X9.3 S08W33 |
|||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Б | –4 | +15 | +71 | –1 | +2 | +4 | –3 | +10 | +17 | –1 | +8 | +16 | |||||
| В | +21 | +26 | +1.5 | +2.5 | +9 | +11 | +3 | +9 | |||||||||
| Г | +13 | 2125 | Нет | Нет | +30 | 1571 | |||||||||||
| Д | 245 | +4 | +52 | 1415 | 0 | +2 | 1415 | +3 | +3 | 245 | +8 | +9 | |||||
| Е | 0 | +15 | 2400 | 0 | 0 | 620 | 0 | +9 | 1400 | 0 | +2 | 8100 | |||||
| Ж | ? | +7 | ? | Нет | Нет | +3 | +8 | +7 | |||||||||
Примечание: А – дата, нулевое время UT – начало излучения на 15.4 ГГц, балл и координаты вспышки, Б – начало, максимум и конец SXR вспышки (GOES); В – время Тmax, и ЕМmax; Г – время первого появления КВМ (LASCO_C2) и его средняя скорость (км/с); Д – наименьшая частота (МГц) регистрируемого радиоизлучения (Radio Solar Telescope Network (RSTN)), моменты начала и максимума; Е – момент и величина максимума излучения на 15.4 ГГц (СЕП); Ж – начало радио всплесков III, II и IV типов. Все времена даны в минутах относительно выбранного нулевого времени.
2. ФИЗИЧЕСКИЕ СООБРАЖЕНИЯ И ОЦЕНКИ
2.1. Модификация эффекта Нойперта
Хорошо известен и часто используется наблюдательный эффект Нойперта [Neupert, 1968] – временнóй профиль производной интенсивности SXR ($({{I}_{{{\text{SXR}}}}})$ подобен профилям интенсивности HXR (${{I}_{{{\text{HXR}}}}}$) и микроволнового (MW) излучения $({{I}_{{{\text{MW}}}}}).$ Если эффект Нойперта выполняется, то нагрев плазмы, излучающей SXR, происходит за счет энергии нетепловых электронов, генерирующих HXR и MW, а потери энергии не существенны. Однако это происходит не всегда.
На наш взгляд, имеет смысл учесть, что в приближении однотемпературной плазмы интенсивность SXR является произведением функции температуры $f\left( T \right)~$ на меру эмиссии $EM$ ${{I}_{{{\text{SXR}}}}} = f\left( T \right)EM.$ Тогда ее производная будет $\frac{{d{{I}_{{{\text{SXR}}}}}}}{{dt}}$ = $\frac{{df\left( T \right)}}{{dT}}\frac{{dT}}{{dt}}EM$ + $\frac{{dEM}}{{dt}}f\left( T \right),$ и можно рассматривать отдельно зависимости производной температуры от времени – ${{dT\left( t \right)} \mathord{\left/ {\vphantom {{dT\left( t \right)} {dt}}} \right. \kern-0em} {dt}}$ и производной меры эмиссии от времени ${{dEM\left( t \right)} \mathord{\left/ {\vphantom {{dEM\left( t \right)} {dt}}} \right. \kern-0em} {dt}},$ проанализировать их соотношения с интенсивностями с ${{I}_{{{\text{SXR}}}}}$ и ${{I}_{{{\text{HXR}}}}},$ выделить фазы преимущественного изменения T и EM. Эти идеи развивались в работе [Шарыкин и др., 2012].
Рентгеновские детекторы КА серии GOES измеряют поток SXR излучения в двух диапазонах длин волн 0.5–4 Å и 1–8 Å, по этим данным в приближении одной температуры вспышечной плазмы можно оценить температуру (Т) и меру эмиссии (ЕМ). Это стандартная процедура в пакете SolarSoft. Временны́е производные рассчитывались с помощью процедуры программы Origin 7.5. Ниже в разделе 3 на графиках, где приведены dT/dt и dEM/dt, их размерность составляет [106 МК/мин] и [1049 (см3 мин)–1], соответственно.
Представляется естественным связать падение температуры и рост меры эмиссии (увеличение объема и концентрации плазмы, излучающей SXR), с развитием и ускорением КВМ. Если считать, что вспышка и КВМ черпают энергию из одного резервуара, то время запаздывания максимума EM относительно максимума T можно рассматривать, как характерное время ускорения КВМ – существование дополнительного канала отвода энергии из области вспышки. Это соображение используется нами при анализе конкретных событий в разделе 3.
2.2. Ограничение по высоте и оценка магнитного поля
В предположении, что КВМ ускоряется локальным магнитным полем, максимальная скорость, которую может достичь КВМ равна локальной альвеновской скорости ${{V}_{{\text{A}}}} = {B \mathord{\left/ {\vphantom {B {{{{(4\pi {{m}_{p}}n)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}} \right. \kern-0em} {{{{(4\pi {{m}_{p}}n)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}.$ В короне над активной областью альвеновская скорость может достигать ~3000 км/с. С другой стороны, очевидно, что для отрыва от Солнца КВМ должен приобрести вторую космическую скорость – 618 км/с.
Предположим, что минимальная частота радиоизлучения, выходящего из вспышечной области, соответствует плазменной частоте νp = $ = ({{{{n}_{e}}{{e}^{2}}} \mathord{\left/ {\vphantom {{{{n}_{e}}{{e}^{2}}} {\pi {{m}_{e}}}}} \right. \kern-0em} {\pi {{m}_{e}}}}) \approx 8972n_{e}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}},$ то можно оценить электронов концентрацию. Отсюда, зная минимальную частоту радиоизлучения и скорость КВМ можно сделать оценку на минимальную величину магнитного поля, необходимую для ускорения КВМ.
Для концентрации электронов ${{n}_{e}}(1415\,\,{\text{МГц}})$ = $ = 2.49 \times {{10}^{{10}}}$ см–3 получаем альвеновскую скорость ${{V}_{{\text{A}}}}\,\,\left[ {{{{\text{км}}} \mathord{\left/ {\vphantom {{{\text{км}}} {\text{с}}}} \right. \kern-0em} {\text{с}}}} \right] = 13.8B\,\,\left[ {{\text{Гс}}} \right],$ т.е. магнитное поле должно быть больше $B > 44.8$ Гс для ${{V}_{{\text{A}}}} > 618~$ км/с, а для достижения максимальной скорости 3000 км/с магнитное поле должно быть на порядок выше $B > 217$ Гс. Отметим, что для КВМ 4 ноября 2003, скорость которого составляла 2700 км/с, из других соображений была получена оценка величины магнитного поля 200 Гс [Кузнецов, 2008].
Аналогично для ${{n}_{e}}(245\,\,{\text{МГц}}) = 7.47 \times {{10}^{8}}$ см–3; ${{V}_{{\text{A}}}} = 79.9B > 618$ км/с, соответственно минимальное магнитное поле может лежать в пределах $7.7 < B < 37.5$ Гс (второе значение B получено для альвеновской скорости 3000 км/с).
2.3. Ограничения по длительности и величине ускорения
Время достижения заданной скорости зависит от величины ускорения. Если существует максимальная величина ускорения, которое может быть реализовано, то она определяет минимальное время достижения некоторой заданной скорости. Оценкой величины максимального ускорения является выражение ${{a}_{{{\text{max}}}}} \approx {{V_{{\text{A}}}^{2}} \mathord{\left/ {\vphantom {{V_{{\text{A}}}^{2}} {2d}}} \right. \kern-0em} {2d}},$ где $d$ – характерный размер области ускорения КВМ [например, Green et al., 2018]. Очевидно, для достижения максимальной скорости необходимо иметь постоянную альвеновскую скорость на длине d. Так как величина ускорения ограничена локальной альвеновской скоростью, то она больше для минимальных значений d. В случае очень компактного источника, d < 105 км, ускорение может достигать величин порядка 10 км/с2, которые наблюдаются в наиболее мощных событиях [Green et al., 2018]. Считаем, что ускорение КВМ импульсным, если время его ускорения до заданной скорости сопоставимо с минимально возможным. Величина минимального ускорения определяется его возможной максимальной длительностью (начало движение с постоянной средней скоростью).
Выход КВМ в МП возможен только при достижении им второй космической скорости. Зная величину максимального ускорения 10 км/с2, получаем минимальное время ускорения межпланетного КВМ > 1 мин при старте с поверхности Солнца, а для достижения максимальной скорости длительность ускорения должна быть >5 мин.
Пусть КВМ начинает движение с ускорением $a = {\text{const}}$ из положения R0 в момент t0 со скоростью V0 = 0 и продолжает двигаться с постоянным ускорением до времени t. Далее КВМ двигается равномерно с $V = {\text{const}}.$ Скорость нам известна из линейной аппроксимации наблюдений положения КВМ коронографом LASCO, $R = \alpha + \beta t,$ т.е. $V = \beta ,$ $a = {\beta \mathord{\left/ {\vphantom {\beta {\left( {t - {{t}_{0}}} \right)}}} \right. \kern-0em} {\left( {t - {{t}_{0}}} \right)}}.$
Условие сшивки равномерного и ускоренного движения в момент t:
(1)
$\left\{ \begin{gathered} {{R}_{0}} + {{a{{{\left( {t - {{t}_{0}}} \right)}}^{2}}} \mathord{\left/ {\vphantom {{a{{{\left( {t - {{t}_{0}}} \right)}}^{2}}} 2}} \right. \kern-0em} 2} = \alpha + \beta t \hfill \\ a\left( {t - {{t}_{0}}} \right) = \beta {\kern 1pt} . \hfill \\ \end{gathered} \right.$(2)
$t = {{\left( {2{{R}_{0}} - 2\alpha - \beta {{t}_{0}}} \right)} \mathord{\left/ {\vphantom {{\left( {2{{R}_{0}} - 2\alpha - \beta {{t}_{0}}} \right)} \beta }} \right. \kern-0em} \beta }.$В расчетах мы будем использовать две величины R0: 1.1RS (нижняя граница LASCO C1) или 1.25RS (начало импульсного ускорения 6 ноября 1997 г., [Zhang et al., 2001]). Ниже на примере импульсной вспышки X9.3 6 сентября 2017 г. и длительной вспышки M3.7 7 марта 2011 г. будет показано, что наблюдения КВМ и условие сшивки достаточно точно фиксируют возможные значения длительности и величины ускорения.
3. АНАЛИЗ НАБЛЮДЕНИЙ И ОБСУЖДЕНИЕ
3.1 . Вспышки, не сопровождающиеся КВМ
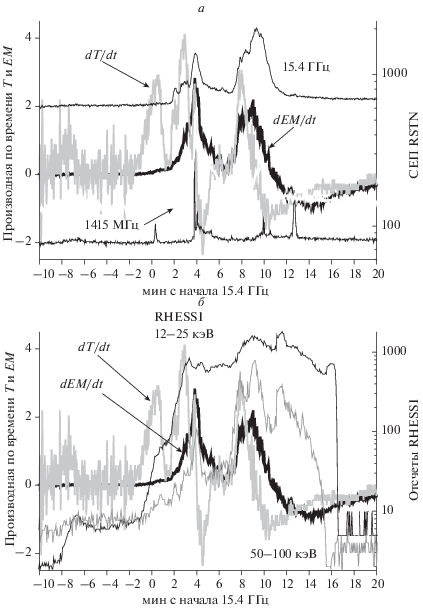
Вспышка M2.9 6 июля 2012 г. (рис. 1) – одна из самых коротких вспышек в SXR излучении, ее многоволновые наблюдения подробно рассмотрены в работе [Алтынцев и др., 2017]. Так как минимальная зарегистрированная частота радиоизлучения 1415 МГц (рис. 1а), то вспышка развивалась непосредственно в хромосфере и корональных высот (245 МГц) не достигла. Производная dT/dt показывает два эпизода нагрева (рис. 1). Первый не сопровождался ростом EM (нет хромосферного испарения), нагрев происходил за счет ускоренных электронов с мягким спектром (HXR <25 кэВ, рис. 1б). Второй связан с появлением релятивистских электронов (радиоизлучения на 15.4 ГГц). Он привел к Tmax на ~1.5 мин (90 с) и EMmax на ~2.7 мин (160 с). Запаздывание максимума EM составило ~1.2 мин (70 с), что очень близко к минимальному времени ускорения КВМ. При времени ускорения 70 с, величина ускорения, необходимая для достижения 618 км/с должна быть ~9 км/с2. Таким образом, в событии 6 июля 2012 г. просто могло не хватить времени для ускорения межпланетного КВМ даже в идеальных условиях, если бы вспышечные возмущения достигли корональных высот.
Рис. 1.
Сравнение временны́х профилей производной по времени температуры и меры эмиссии 06.07.2012 г., ноль 01:38 UT, M2.9. (а) – с потоком радиоизлучения на максимальной (15.4 Ггц) и минимальной (1415 МГц) зарегистрированных частотах; (б) – с потоком HXR излучения (RHESSI 12–25 кэВ, 50–100 кэВ).
Вспышка X2.2 6 сентября 2017 г. не поднялась выше хромосферы [Струминский и др., 2020а], радиоизлучение на частотах менее 1415 МГц не наблюдалось (рис. 2а). Производная dT/dt показывает три эпизода нагрева (рис. 2). Первый не сопровождался ростом EM (нет хромосферного испарения), нагрев происходил за счет ускоренных электронов с мягким спектром (HXR < 25 кэВ, рис. 2б). Два последующих эпизода нагрева связаны с ускорением релятивистских электронов (радиоизлучение на 15.4 ГГц, рис. 2а), это были независимые друг от друга эпизоды нагрева и хромосферного испарения (рис. 2). Задержка максимума EM относительно максимума T в обоих случаях была <2 мин. Таким образом, в событии X2.2 6 сентября 2017 г., по всей видимости, не были реализованы условия для ускорения КВМ, так как вспышечные возмущения не достигли корональных высот.
3.2. Вспышки, сопровождающиеся КВМ
На рисунке 3 показаны положения КВМ по данным LASCO в первый час после двух выбранных нами вспышек. Видно, что средняя скорость КВМ 7 марта 2011 г. была больше, чем 6 сентября 2017 г. Если использовать все положения КВМ, зафиксированные LASCO, и провести линейную аппроксимацию $R\left( t \right) = \alpha + \beta t,$ то ее параметры будут (α = 16 1418 ± 12 771 км и β = 2125 ± 24 км/с) и (α = ‒18 534 ± 146 643 км и β = 1569 ± 25 км/с), соответственно. Если же взять только первые два положения КВМ, то параметры аппроксимации будут (α = 244037 км и β = 1845 км/с) и (α = = ‒953 906 км и β = 2050 км/с). Так как две точки однозначно определяют прямую, то в последнем предложении α и β приведены без ошибок.
Рис. 3.
Положение КВМ по данным наблюдений SOHO LASCO С2 в событиях 07.03. 2011 г. M3.7 (черные квадраты) и 06.09. 2017 г. Х9.3 (открытые кружки), крестами показны наблюдения LASCO C1 06.11.1997 г. X9.7.
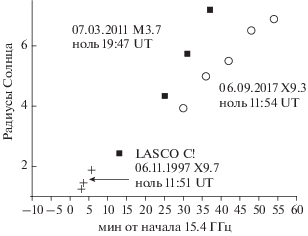
Здесь необходимо отметить, что КВМ 6 сентября 2017 г. появился в поле зрения LASCO на (+30 мин), т.е. на 17 мин позже относительно выбранного ноля времени, чем КВМ 7 марта 2011 (+13 мин). Это может свидетельствовать о том, что 7 марта 2011 г. КВМ продолжал ускоряться и после +25 мин (второго измеренного положения), а 6 сентября 2017 г. КВМ начал замедляться после +36 мин (второго измеренного положения). Не исключено, что оба КВМ могли на начальных этапах развиваться так же, как и КВМ 6 ноября 1997 г. (крестики на рис. 3), т.е. достигнуть максимальной скорости порядка 2000 км/c и далее замедляться. В этом случае должна была быть различной эффективность замедления корональных выбросов массы 7 марта 2011 г. и 6 сентября 2017 г.
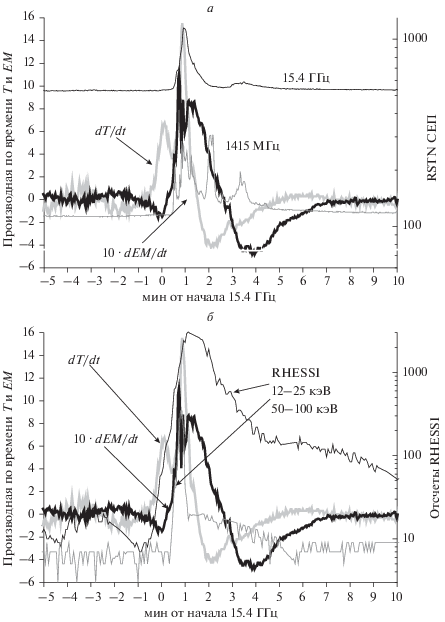
Вспышка X9.3 6 сентября 2017 г. (рис. 4) начала развиваться в хромосфере и достигла корональных высот примерно на +8 мин (начало излучения на 245 МГц, рис. 4а). Производная T показывает три эпизода нагрева, причем третий был на фазе спада температуры (рис. 4), а два последних эпизода из трех сопровождались непрерывным ростом меры эмиссии. Эта вспышка произошла в ночи КА RHESSI, поэтому для формирования представлений о развитии в ней нетепловых процессов нужно обращаться к данным других детекторов HXR излучения (KONUS WIND [Lysenko et al., 2018] или ACS SPI (Anti-Coincident Shield of Spectrometer on INTEGRAL) [Sharykin and Kosovovichev, 2018; Струминский и др., 2020а]. На рис. 4б производные T и EM сравниваются с темпом счета детектора ACS SPI. Значимое превышение над фоном ACS SPI видно примерно с –1 мин, т.е. с начала рентгеновской вспышки X9.3.
Рис. 4.
Сравнение временны́х профилей производной по времени температуры и меры эмиссии 06.09.2017 г., ноль 11:54 UT, Х9.3. (а) – с потоком радиоизлучения на максимальной (15.4 Ггц) и минимальной (245 МГц) зарегистрированных частотах; (б) – потоком HXR излучения (темп счета ACS SPI >150 кэВ за 50 мс, сглаженные средние за 1 мин). Стрелки показывают ожидаемые положения КВМ, наблюдения LASCO вне масштаба рисунка.
Стрелки на рис. 4б показывают две линейных аппроксимации положения КВМ (все точки или две точки наблюдения LASCO). Как и в случае вспышек без КВМ, здесь первый эпизод нагрева был на фазе роста SXR излучения и вызван ускоренными электронами с достаточно мягким спектром [Струминский и др., 2020а]. В последующих эпизодах нагрева уже значимо присутствовали релятивистские электроны (радиоизлучение на 15.4 ГГц). Вспышечная плазма прогрелась до максимальной температуры во втором эпизоде на +3 мин (182 с), а максимум меры эмиссии был достигнут на +8.6 мин (514 с). Таким образом, возможное время ускорения КВМ составило 5.5 мин (332 с). При величине ускорения близкой к предельной этого времени хватило бы для достижения скорости более 3000 км/с. Так как измеренные скорости были значительно меньше, то сценарий предельного ускорения не был реализован.
Оценим возможные времена ускорения КВМ для достижения наблюдаемых скоростей из условия сшивки (2) при R0 = 1.1RS (1.25RS) и t0 = = +3 мин (182 c). Если взять все точки LASCO, то подстановка численных значений в (2) даст t = = 1204 с = 20 мин (972 с = 16.2 мин), $t - {{t}_{0}} = 1022\,\,~{\text{с}}$ = = $17\,\,~{\text{мин}}\,\,\left( {790\,\,~{\text{с}} = 13.2\,\,{\text{мин}}} \right).$ Среднее ускорение будет 1.5 (2.0) км/с2 (1569 км/с разделить на 1022 с (790 с)), при таком среднем ускорении КВМ станет двигаться равномерно на 2.1RS. Заметим, что формальное окончание SXR вспышки было на +16 мин. Для того, чтобы альвеновская скорость была 1569 км/с на высоте, где плазменная частота равна 245 МГц, магнитное поле должно составлять 19 Гс.
Если взять только первые две точки LASCO С2, то подстановка численных значений в (1) даст t = 1506 с = 25 мин (1607 c = 26.7 мин), т.е. КВМ должен был двигаться равноускоренно почти до момента выхода в поле зрения LASCO С2. Время ускорения $t - {{t}_{0}} = 1324~\,\,{\text{c}}$ = 22 мин $\left( {1425\,\,{\text{с}} = 24\,\,{\text{мин}}} \right),$ а среднее ускорение будет равно 1.5 км/с2 (1.4 км/с2), при таком среднем ускорении КВМ станет двигаться равномерно на 3.0 (3.3) RS. Для того, чтобы скорость Альвена была на 2050 км/с на высоте, где плазменная частота равна 245 МГц, магнитное поле должно составлять 25 Гс.
Так как во вспышке M3.7 7 марта 2011 г. нет ярко выраженной импульсной фазы, то, по всей видимости, она была инициирована эрупцией волокна. Эта вспышка наиболее известна тем, что в ней впервые было измерено телескопом Fermi LAT длительное гамма-излучение >100 МэВ непосредственно из области вспышки [Ackerman et al., 2014; Share et al., 2018]. Мы исследовали вспышки, связанные с эрупцией волокна [например, Струминский и др., 2020б; Григорьева и др., 2020; Struminsky et al., 2020].
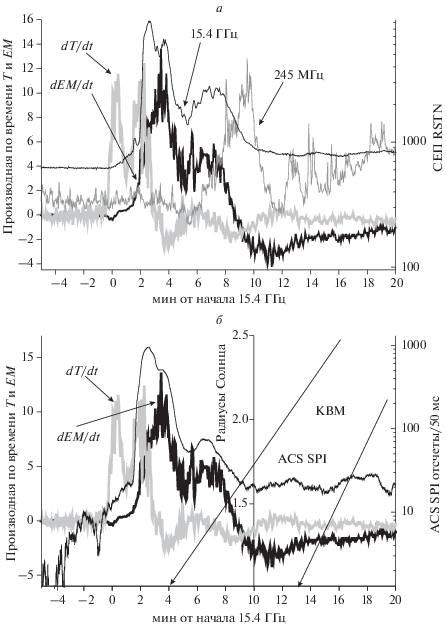
Температура и мера эмиссии во вспышке M3.7 7 марта 2011 г. росли длительное время, их временны́е производные не показали всплесков (рис. 5) с амплитудами характерными для импульсных вспышек (рис. 1, 2, 4). Производная температуры показала эффективный нагрев плазмы от начала роста HXR излучения 12–25 кэВ (рис. 5б) и примерно до +4 мин (начала радиоизлучения на 245 МГц, см. рис. 5а и табл. 1). Далее плазма нагревалась, но очень медленно. Видимый рост меры эмиссии начался с появлением радиоизлучения на 15.4 ГГц (рис. 5а).
Рис. 5.
Сравнение временны́х профилей производной по времени температуры и меры эмиссии 07.03.2011 г., ноль 19:37 UT, M3.7. (а) – с потоком радиоизлучения на максимальной (15.4 Ггц) и минимальной (245 МГц) зарегистрированных частотах; (б) – с потоком HXR излучения (RHESSI 12–25 кэВ, 50–100 кэВ). Стрела показывает ожидаемые положения КВМ, открытые кружки – данные наблюдений LASCO.
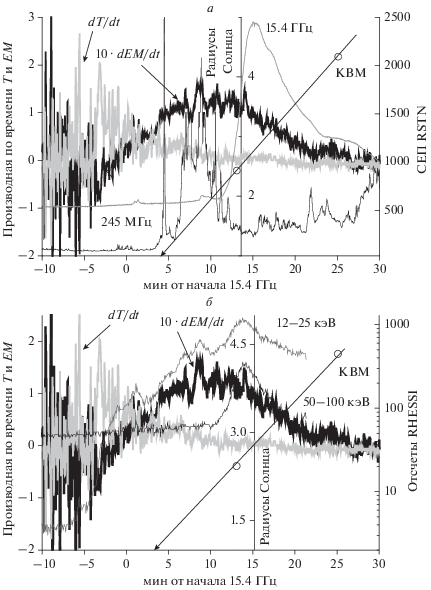
Cтрелка на рис. 5 показывает момент локализации КВМ на 1RS по линейной аппроксимации данных LASCO на +4.1 мин (245 с). Отметим, момент первого появления КВМ в поле зрения LASCO C2 был +13 мин (табл. 1). Обе аппроксимации (по всем или по двум точкам) дают одно время локализации на 1RS, но разные средние скорости (2126 ± 24 км/с и 1845 км/с). Это предполагает, что ускорение КВМ продолжалось и после +25 мин, на фазе спада SXR излучения. Из наблюдений микроволнового и HXR излучения, приведенных на рис. 5, следует, что КВМ начал ускоряться заведомо до основного возрастания интенсивности нетеплового излучения.
Для первых оценок длительности ускорения предположим, что КВМ начал движение на +4.2 мин (252 с), но не с 1.0 RS, а с R0 = 1.1 RS (1.25 RS). Подстановка численных значений для всех точек в (2) даст для t = 313 c = 5.2 мин (414 с = = 6.9 мин), время ускорения КВМ будет $t - {{t}_{0}} = 64\,\,{\text{с}}$ = $1.1~\,\,{\text{мин}}\,\,\left( {162\,\,{\text{с}} = 2.7\,\,{\text{мин}}} \right).$ Такие времена соответствуют среднему ускорению 33 (13) км/с2 (2126 км/с разделить на 64 с (162 с)). Если использовать аппроксимацию по двум точкам, то подстановка численных значений в (2) даст для t = 316 c = 5.3 мин (427 с = 7.1 мин), $t - {{t}_{0}} = 64\,\,{\text{с}}$ = $1.1~\,\,{\text{мин}}\,\,\left( {175\,\,{\text{с}} = 2.9\,\,{\text{мин}}} \right).$ Среднее ускорение будет 29 (10) км/с2 (1845 км/с разделить на 64 с (175 с)). Видно, что при таком выборе начального момента ускорения должен реализоваться предельный сценарий. Большая высота старта КВМ лучше согласуется с ожидаемым максимальным значением ускорения КВМ ~ 10 км/с2.
Для выполнения условия сшивки при меньших значениях среднего ускорения необходимо предположить более ранний момент ${{t}_{0}}$, пусть это будет выбранный нами 0 мин – начало роста радиоизлучения на 15.4 ГГц и меры эмиссии (рис. 5а), при R0 = 1.1 RS (1.25 RS). Подстановка численных значений в (2) для всех точек даст для t = $t - {{t}_{0}} = ~$ 569 c = 9.5 мин (666 с = 11.1 мин), а средние значения ускорения будут равны 3.7 (3.2) км/с2. Предположение о более раннем начале ускорения КВМ позволяет не рассматривать сценарий предельного ускорения КВМ. Равномерное движение должно начаться на 2 Rs. Для того, чтобы скорость Альвена была равна 2126 км/с на высоте, характерной для 245 МГц, магнитное поле должно быть B > 26 Гс.
Если использовать аппроксимацию для двух точек, то подстановка численных значений в (2) даст для t = $t - {{t}_{0}}$ = 569 c = 9.5 мин (676 с = 11.3 мин), т.е. среднее ускорение 3.3 (2.7) км/с2, что практически не отличается от случая всех точек. Равномерное движение могло начаться на 1.8 (2.1) Rs, но для выхода на среднюю скорость 2125 км/с необходимо доускорение после +25 мин. Магнитное поле в области ускорения должно быть B > 23 Гс, чтобы превысить 1845 км/с.
Таким образом, КВМ, связанный со вспышкой M3.7 7 марта 2011 г., эффективно ускорялся до максимумов HXR и MW излучения, а нетепловые процессы наиболее эффективно развивались уже на постэруптивной фазе, когда КВМ был на расстояниях >2Rs от центра, как это было в событии 13 мая 2013 г. [Gou et al., 2020]. По нашему мнению, именно на постэруптивной фазе вспышки происходит стохастическое ускорение протонов [Струминский и др., 2020а], генерирущих гамма-излучение >100 МэВ [Ackerman et al., 2014; Share et al., 2018].
4. ВЫВОДЫ
– Импульсные вспышки без КВМ ограничены по высоте плазменной частотой 1415 МГц (характерной для верхней хромосферы), задержка максимума меры эмиссии относительно максимума температуры <2 мин.
– Выполнены оценки необходимых величин магнитного поля на высотах характерных для излучения 1415 МГц и 245 МГц и минимального времени ускорения КВМ. В событиях без КВМ, вероятно, одна из этих необходимых величин не была достигнута.
– Из условия сшивки предполагаемого равноускоренного и наблюдаемого равномерного движения получены оценки величины и длительности ускорения для КВМ, связанных со вспышками M3.7 7 марта 2011 г. и X9.3 6 сентября 2017 г. Эти оценки свидетельствуют о том, что КВМ должны были ускоряться значительно дольше предполагаемого минимального времени.
– Полученные средние значения величины и длительности ускорения КВМ не противоречат ускорению КВМ в двух фазах – импульсной и длительной, как это непосредственно наблюдалось в событиях 13 мая 2013 г. [Gou et al. 2020] и 10 сентября 2017 г. [Gopalswamy et al., 2018].
– В рассмотренных случаях показано, что во вспышках наибольшие всплески HXR и MW излучения могут наблюдаться как до и во время импульсного ускорения КВМ (вспышка X9.3 6 сентября 2017 г.), так и после него (вспышка M3.7 7 марта 2011 г.). Это показывает, что процессы ускорения заряженных частиц во вспышках, вероятно, не зависят от величины ускорения КВМ.
– Не исключены возможности: 1) инициировать процессы пересоединения и ускорения нетепловых электронов подъемом магнитного жгута; 2) нарушить равновесие магнитного жгута вспышкой и спровоцировать КВМ. Событие 7 марта 2011 г. не исключает обе возможности.
– Если ускорение электронов и развитие КВМ совпадают по времени, то могут изменяться свойства мишени (число частиц и объем, в котором происходит взаимодействие электронов, т.е. температура и мера эмиссии). Это приводит к различным рентгеновским баллам вспышек.
Список литературы
– Григорьева И.Ю., Струминский А.Б., Шаховская А.Н. Длительные слабые вспышки С1.2: источник протонов и электронов // Геомагнетизм и аэрономия. Т. 60. № 6. С. 710–719. 2020.
– Кузнецов В.Д. Корональные выбросы массы / Плазменная Гелиогеофизика. Т. 1. Ред. Л.М. Зеленый и И.С. Веселовский. ФИЗМАТЛИТ. С. 81–95. 2008.
– Струминский А.Б., Григорьева И.Ю., Логачев Ю.И., Садовский А.М. Солнечные электроны и протоны в событиях 4–10 сентября 2017 г. и сопутствующие явления // Физика плазмы. Т. 46. № 2. С. 139–153. 2020а.
– Струминский А.Б., Логачев Ю.И., Григорьева И.Ю., Садовский А.М. Две фазы солнечных вспышек и стохастический механизм ускорения электронов и протонов // Астрофизика. Т. 63. № 3. С. 437–449. 2020б.
– Шарыкин И.Н., Cтруминский А.Б., Зимовец И.В. Энергетика и морфология мощных импульсных солнечных вспышек // Письма в АЖ. 2012. Т. 38. № 10. С. 751–760.
– Ackermann M., Ajello M., Albert A. et al. High-energy gamma-ray emission from solar flares: summary of FERMI large area telescope detections and analysis of two M-class flares // Astrophys. J. V. 787. L15 (13 pp). 2014. https://doi.org/10.1088/0004-637X/787/1/15
– Altyntsev A., Meshalkina N., Myshyakov I., Pal‘shin V., Fleishman G. Flare SOL2012-07-06: on the origin of the circular polarization reversal between 17 GHz and 34 GHz // Solar Phys. V. 292. № 9. P. 137–152. 2017.
– Cliver E.W., Kahler S.W., Kazachenko M., Shimojo M. The disappearing solar filament of 2013 September 29 and its large associated proton event: Implications for particle acceleration at the Sun // Astrophys. J. V. 877. L11 (17 pp). 2019. https://doi.org/10.3847/1538-4357/ab0e03
– Dere K.P., Brueckner G.E., Howard R.A. et al. EIT and LASCO observations of the initiation of a coronal mass ejection // Solar Phys. V. 175. P. 601–612. 1997.
– Gallagher P.T., Lawrence G.R., Dennis B.R. Rapid acceleration of a coronal mass ejection in the low corona and implications for propagation // Astrophys. J. V. 588. L53–L56. 2003.
– Gopalswamy N., Xie H., Akiyama S., Yashiro S., Usoskin I.G., Davila J.M. The first ground level enhancement event of solar cycle 24: direct observation of shock formation and particle release heights // Astrophys. J. V. 765: L30 (5 pp). 2013. https://doi.org/10.1088/2041-205/765/2/L30
– Gopalswamy N., Yashiro S., Thakur N., Mäkelä P., Xie H., Akiyama S. The 2012 July 23 backside eruption: an extreme energetic particle event? // Astrophys. J. V. 833. L216 (20 pp). 2016. https://doi.org/10.3847/1538-4357/833/2/216
– Gopalswamy N., Yashiro S., Mäkelä P., Xie H., Akiyama S., Monstein C. Extreme kinematics of the 2017 September 10 solar eruption and the spectral characteristics of the associated energetic particles // Astrophys. J. V. 863: L39 (6 pp). 2018. https://doi.org/10.3847/2041-8213/aad86c
– Gou T., Veronig A.M., Liu R. et al. Solar Flare–CME coupling throughout two acceleration phases of a fast CME // Astrophys. J. V. 897/ L36. 2020. https://doi.org/10.3847/2041-8213/ab9ec5
– Green L.M., Török T., Vršnak B., Manchester W., Veronig A. // The Origin, Early Evolution and Predictability of Solar Eruptions. // Space Sci. Rev. V. 214: L46 (52 pp). 2018. https://doi.org/10.1007/s11214-017-0462-5
– Inoue S., Shiota D., Bamba Y., Park S.-H. Magnetohydrodynamic modeling of a solar truption associated with an X9.3 flare observed in the active region 12673 // Astrophys. J. V. 867: L83 (8 pp). 2018. https://doi.org/10.3847/1538-4357/aae079
– Jiang C., Zou P., Feng X., Hu Q., Liu R., Vemareddy P., Duan A., Zuo P., Wang Y., Wei F. Magnetohydrodynamic simulation of the X9.3 flare on 2017 September 6: Evolving magnetic topology // Astrophys. J. V. 869. L13 (18 pp). 2018. https://doi.org/10.3847/1538-4357/aaeacc
– Liu L., Cheng X., Wang Y. Zhou Z., Guo Y. Cui J. Rapid buildup of a magnetic flux rope during a confined X2.2 class flare in NOAA AR 12673 // Astrophys. J. V. 867:L5 (8 pp). 2018. https://doi.org/10.3847/2041-8213/aae826
– Lysenko A.L., Anfinogentov S.A., Svinkin D.S., Frederiks D.D., Fleishman G.D..Gamma-ray emission from the impulsive phase of the 2017 September 06 X9.3 flare // Astrophys. J. V. 877. L145 (13 pp). 2019. https://doi.org/10.3847/1538-4357/ab1be0
– Neupert W.M. Comparison of solar X-ray line emission with microwave emission during flares // Astrophys. J. V. 153. L59–L64. 1968.
– Share G.H., Murphy R.J., White S.M., Tolbert A.K., Dennis B.R., Schwartz R.A., Smart D.F., Shea M.A. Characteristics of late-phase >100 MeV gamma-ray emission in solar eruptive events // Astrophys. J. V. 869 L182 (55 pp). 2018. https://doi.org/10.3847/1538-4357/aaebf7
– Sharykin I.N. Kosovichev A.G. Onset of photospheric impacts and helioseismic waves in X9.3 solar flare of 2017 September 6 // Astrophys. J. V. 864. L86 (13 pp). 2018. https://doi.org/10.3847/1538-4357/aad558
– Struminsky A.B., Logachev Yu.I., Grigorieva I.Yu., Sadovski A.M. Two types of gradual events: Solar protons and relativistic electrons // Geomagnetism and Aeronomy. V. 60. № 8. P. 1057–1066. 2020. https://doi.org/10.1134/S001679322008023X
– Veronig A.M., Podladchikova T., Dissauer K., Temmer M., Seaton D.B., Long D., Guo J., Vršnak B., Harra L. Kliem B. Genesis and impulsive evolution of the 2017 September 10 coronal mass ejection // Astrophys. J. V. 868. L107 (17 pp). 2018. https://doi.org/10.3847/1538-4357/aaeac5
– Zhang J., Dere K.P., Howard R.A., Kundu M.R., White S.M., On the temporal relationship between coronal mass ejections and flares // Astrophys. J. V. 559. № 1. P. 452–462. 2001.
– Zou P.G., Jiang C., Feng X., Zuo P., Wang Y., Wei F. A two-step magnetic reconnection in a confined X-class flare in solar active region 12673 // Astrophys. J. V. 870. L97 (8 pp). 2019. https://doi.org/10.3847/1538-4357/aaf3b7
Дополнительные материалы отсутствуют.
Инструменты
Геомагнетизм и аэрономия