Геомагнетизм и аэрономия, 2021, T. 61, № 4, стр. 418-427
Явления гистерезиса в жесткости обрезания космических лучей во время супербури 7–8 ноября 2004 г.
Н. Г. Птицына 1, *, О. А. Данилова 1, **, М. И. Тясто 1
1 Санкт-Петербургский филиал Института земного магнетизма,
ионосферы и распространения радиоволн им. Н.В. Пушкова РАН (СПб ИЗМИРАН)
г. Санкт-Петербург, Россия
* E-mail: nataliaptitsyna@ya.ru
** E-mail: md1555@mail.ru
Поступила в редакцию 21.11.2020
После доработки 11.01.2021
Принята к публикации 28.01.2021
Аннотация
Способность космических лучей проникать внутрь магнитосферы характеризуется жесткостью геомагнитного обрезания R, т.е. жесткостью, ниже которой поток частиц обрезан из-за магнитного экранирования. Во время магнитной бури топология магнитного поля изменяется, что влечет за собой вариации жесткости обрезания ΔR. В статье рассмотрена зависимость ΔRэф (вычисленных с помощью прослеживания траекторий частиц космических лучей в модельном магнитосферном поле) от параметров солнечного ветра, межпланетного магнитного поля и магнитосферы на разных фазах сильной магнитной бури 7–8 ноября 2004 г. Найдено, что траектория ΔRэф, т.е. последовательные значения, которые принимает ΔRэф в зависимости от исследуемых параметров, во время главной фазы не совпадает с траекторией в восстановительной фазе – формируются петли гистерезиса. Для связи ΔRэф с геомагнитным индексом Dst и скоростью солнечного ветра получены узкие петли гистерезиса, a с электромагнитными параметрами – широкие. Форма петель гистерезиса обнаруживает зависимость от широты наблюдения: с увеличением широты площадь петель для всех исследуемых параметров увеличивается.
1. ВВЕДЕНИЕ
Магнитная жесткость R (момент на единицу заряда) характеризует способность космических лучей (КЛ) проникать внутрь магнитосферы. Жесткость геомагнитного обрезания или геомагнитный порог – это жесткость, ниже которой поток частиц обрезан из-за магнитного экранирования. Во время магнитной бури геомагнитное экранирование уменьшается из-за уменьшения поля внутри магнитосферы как следствия формирования токовых систем – кольцевого тока, токов магнитопаузы и хвоста магнитосферы, а также продольных высокоширотных токов. В процессе эволюции бури топология магнитного поля изменяется, что влечет за собой изменение жесткости магнитного обрезания.
В многочисленных работах получено, что вариации геомагнитных порогов ΔR зависят от геомагнитной активности, параметров солнечного ветра и межпланетного магнитного поля ММП [Kanekal et al., 1998; Belov et al., 2003; Shimazu, 2009; Kress et al., 2010; Тясто и др., 2011; Tyssøy and Stadsnes, 2014; Adriani et al., 2016; Данилова и др., 2019; Птицына и др., 2019]. Однако результаты исследования зависимости ΔR от межпланетных параметров и индексов геомагнитной активности очень противоречивы: полученные зависимости различны для разных бурь и используемых подходов. Частично это может быть обусловлено тем обстоятельством, что интенсификация и распад токовых систем, которые контролируются поступлением в магнитосферу энергии солнечного ветра (СВ), происходят в различных режимах и на различных масштабах времени. Контроль ΔR параметрами гелио- и геомагнитосферы на разных фазах возмущения плохо изучен. Можно указать лишь несколько детальных исследований в этой области. Так, в работе [Adriani et al., 2016] найдены соответствующие коэффициенты корреляции для разных фаз умеренной бури 14 декабря 2006 г., а в работе [Птицына и др., 2020; Птицына и др., 2021] – для сильных бурь 20 ноября 2003 г. и 7–8 ноября 2004 г. В этих работах найдено, что взаимосвязь ΔR и параметров гелио- и геомагнитосферы различна на разных этапах эволюции магнитной бури, что приводит иногда к достаточно неожиданным суммарным эффектам на масштабе всей бури.
В работе [Птицына и др., 2021] было найдено, что на разных фазах бури наблюдается не только разная зависимость ΔR от варьируемого аргумента – параметров геомагнитной активности, СВ и параметров межпланетного магнитного поля (ММП), – но и от направления изменения аргумента. Траектории изменения жесткостей обрезания в зависимости от исследуемых параметров во время интенсификации бури (развитие токовых систем) не совпадали с траекториями на восстановительной фазе (распад токовых систем), что является признаком гистерезиса. В работе [Птицына и др., 2021] эти не отмеченные ранее явления гистерезиса были обнаружены для одной бури (в ноябре 2003 г.) и только для одной станции (Москва). Поэтому наличие этого эффекта для других магнитных возмущений, и для других станций (других широт) оставалось под вопросом.
Целями данной работы было: (i) проследить динамику изменений геомагнитных порогов ΔR в зависимости от динамики параметров межпланетной среды и геомагнитосферы во время эволюции магнитной бури 7–8 ноября 2004 г. для всех трех фаз бури; (ii) попытаться выявить явления гистерезиса, их характерные особенности, а также их пространственные зависимости, в частности, зависимости от широты.
2. МЕТОДЫ
Эффективные жесткости геомагнитного обрезания Rэф были рассчитаны методом прослеживания траекторий частиц КЛ в модельном магнитном поле [McCracken et al., 1962; Shea et al., 1965]. В качестве модели была использована магнитосферная модель Ts01 [Tsyganenko, 2002; Tsyganenko et al., 2003]. В этой модели основными источниками магнитного поля магнитосферы являются: симметричный и частичный круговые токи, система токов хвоста магнитосферы, продольные токи Биркеланда регионов 1 и 2, токи на магнитопаузе. В качестве входных параметров, определяющих влияние межпланетных условий на магнитосферу, используются Dst-вариация, плотность и скорость СВ, а также компоненты ММП.
Вариации жесткостей обрезания ΔRэф, полученные этим методом, определялись как разности между значениями жесткостей, рассчитанными для каждого часа в период бури, и жесткостями в спокойный период перед бурей. За спокойные (Dst ≈ 0) были взяты среднесуточные значения R 5 ноября 2004 года.
Коэффициенты корреляции k между ΔRэф и исследуемыми параметрами вычислялись для следующих станций: Токио (35.75° N, 139.72° E), Алматы (43.20° N, 76.94° E), Рим (41.90° N, 12.52° E), Иркутск (52.47° N, 104.03° E), Москва (55.47° N, 37.32° E) и Хобарт (42.90° S, 147.33° E). Станции выбирались на разных широтах таким образом, чтобы они в спокойное время охватывали большую полосу жесткостей обрезания R: Токио – 11.0 ГВ, Алматы – 6.18 ГВ, Рим – 6.1 ГВ, Иркутск – 3.25 ГВ, Москва – 2.12 ГВ, Хобарт – 1.76 ГВ.
Коэффициенты k и стандартные ошибки s были получены из анализа регрессионных уравнений отдельно по выборкам наблюдений для периодов каждой из трех фаз – предварительной, главной и восстановительной [Птицына и др., 2020].
3. ДАННЫЕ
Следующие данные использовались в качестве исходных: полное магнитное поле B, его компоненты Bz и By, электрическая компонента Ey, плотность N, скорость V, и давление P СВ, индексы Kp и Dst геомагнитной активности. Эти данные взяты на сайте (https://omniweb.gsfc.nasa.gov/ form/dx1.html).
В работе были использованы вариации жесткости обрезания ΔRэф и коэффициенты корреляции k с исследуемыми параметрами, полученные нами ранее в работе [Птицына и др., 2020]. Дополнительно были посчитаны k для корреляции ΔRэф и Ey компоненты электрического поля на всех трех фазах бури.
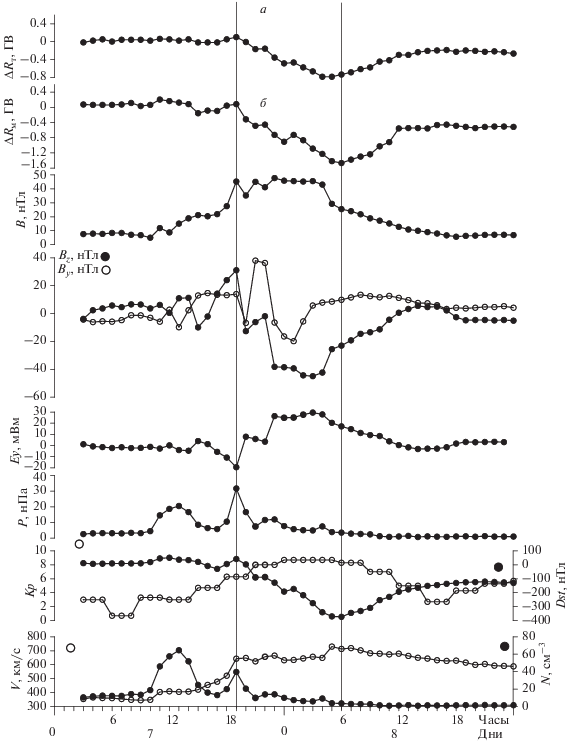
На рисунке 1 для 7–8 ноября 2004 г. на двух верхних панелях представлены значения ΔRэф для станций Токио (a) и Москва (б); на остальных панелях (сверху вниз) приведены изменения во времени B, Bz, By, Eу, N, P, Kp и Dst и V. Исходя из особенностей поведения во времени этих параметров, период магнитной бури 7–8 ноября 2004 г. был разбит на три фазы следующим образом: предварительная фаза бури, т.е. период перед бурей с 03:00 UT по 19:00 UT 7 ноября, главная фаза с 20:00 UT 7 ноября по 06:00 UT 8 ноября, фаза восстановления с 07:00 UT по 24:00 UT 8 ноября [Птицына и др., 2020].
Рис. 1.
Межпланетные параметры и индексы геомагнитной активности 7–8 ноября 2004 г. На верхней панели (сверху вниз) показаны изменения жесткостей обрезания ΔRэф для станций Токио (а) и Москва (б), полное магнитное поле B, его компоненты Bz и By, электрическая компонента Ey, давление P СВ, индексы Kp и Dst, плотность N, скорость V СВ. Вертикальными линиями отмечена главная фаза бури.
4. РЕЗУЛЬТАТЫ
4.1. Признаки гистерезиса
На рисунке 2 приведены диаграммы рассеяния между ΔRэф и Dst, V, Bz и B для ст. Москва на всех фазах бури. На этом рисунке точки для предварительной фазы бури показаны квадратиками, для главной – кружками, для восстановительной – треугольниками. На каждой панели рис. 2 приведены также коэффициенты корреляции k1, k2 и k3 для каждой из трех фаз бури между ΔRэф и исследуемыми параметрами. Кроме того, приведен линейный тренд для каждой фазы в виде прямых линий.
Рис. 2.
Диаграмма взаимосвязи ΔRэф с параметрами СВ, ММП и геомагнитной активности на ст. Москва для трех фаз бури 7–8 ноября 2004 г.: (1) – предварительная, (2) – главная, (3) – восстановительная. Стрелками указано направление течения времени при развитии бури. Коэффициенты корреляции k для трех фаз и линейные тренды также показаны.
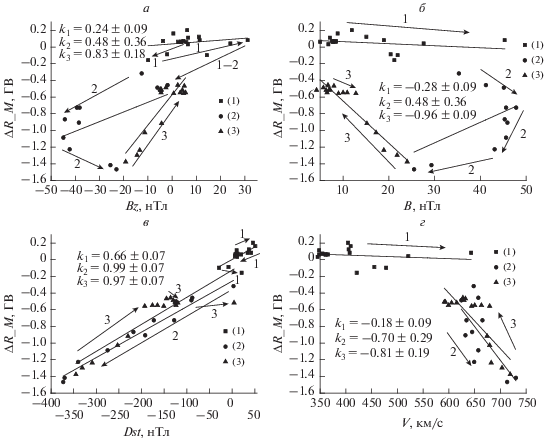
Рассмотрим рис. 2a, на котором показана связь между ΔRэф и Bz. Из рисунка видно, что Bz практически во время всей предварительной фазы было положительным и практически не влияло (k1 = 0.24) на поведение геомагнитного обрезания, так что ΔRэф оставалось вблизи нуля. Затем Bz сменило знак на отрицательный (7 ноября в 20:00 UT), определяя главную фазу, и после этого началось падение Rэф, которое продолжалось до 06:00 UT. После достижения максимума (–44.9 нТл) |Bz| начало уменьшаться и к концу главной фазы в 06:00 UT составило –23 нТл. При этом в течение всей главной фазы наблюдалось значительное падение Rэф, которое составило ΔRэф = –1.5 ГВ к концу фазы. Затем началось восстановление параметров. Линейные тренды точек сходятся к началу главной и концу восстановительной фаз. Видно, что траектория изменения значений ΔRэф (Bz) на восстановительной фазе не совпадает с траекториями на предварительной и главной фазах. Полученная зависимость ΔRэф (Bz) неоднозначна, она имеет петлеобразную форму: одно и то же значение ΔRэф получается при различных значениях Bz. Таким образом, рис. 2 позволяет проследить зависимость ΔRэф не только от значения варьируемого аргумента Bz, но и от направления изменения аргумента. Зависимость от направления изменения аргумента является признаком гистерезиса, т.е. в итоге, траектория изменения значений ΔRэф (Bz) формирует гистерезисную петлю. Эта петля является широкой, что иллюстрируется видом линейных трендов. Обратим внимание на то обстоятельство, что в данном случае коэффициенты корреляции для главной и восстановительной фаз существенно различаются: k2 = 0.48 ± 0.36 и k3 = 0.83 ± 0.18.
Рисунок 2а демонстрирует, что точки на диаграмме ΔRэф – Bz формируют кривую, свидетельствующую о нелинейности связи этих двух переменных. Из рисунка 2а видно, что во время главной фазы Bz меняется в пределах от –1.9 до –44.9 нТл в течение времени от 20:00 UT 7 ноября до 04:00 UT 8 ноября. В это время |ΔRэф| растет в прямой корреляции с ростом |Bz|, после чего с 04:00 UT |Bz| начинает уменьшаться, а |ΔRэф| продолжает расти вплоть до достижения минимального значения ΔR = –1.5 ГВ в максимуме бури.
Именно этим специфическим нелинейным поведением связи ΔRэф–Bz можно объяснить меньшую корреляцию между ΔRэф и Bz в главной фазе бури, чем в восстановительной.
Такого же типа нелинейная взаимосвязь прослеживается между ΔRэф и общим магнитным полем B. Для связи ΔRэф – B петля гистерезиса демонстрирует, что в 04 UT 8 ноября наблюдается изменение прямой пропорциональной зависимости на обратную. В этом случае, так же как и для Bz коэффициент корреляции в восстановительной фазе (k3 = –0.96 ± 0.09) по абсолютной величине существенно превышает коэффициент корреляции в главной фазе (k2 = 0.48 ± 0.36). Такая же петля гистерезиса образуется и для Ey (не показана на рис. 2, но видна на рис. 3в). То есть взаимосвязь ΔRэф со всеми электромагнитными параметрами формирует широкую однотипную петлю гистерезиса, которая указывает на резкое изменение режима взаимодействия с прямой пропорциональности на обратную в 04:00 UT 8 ноября.
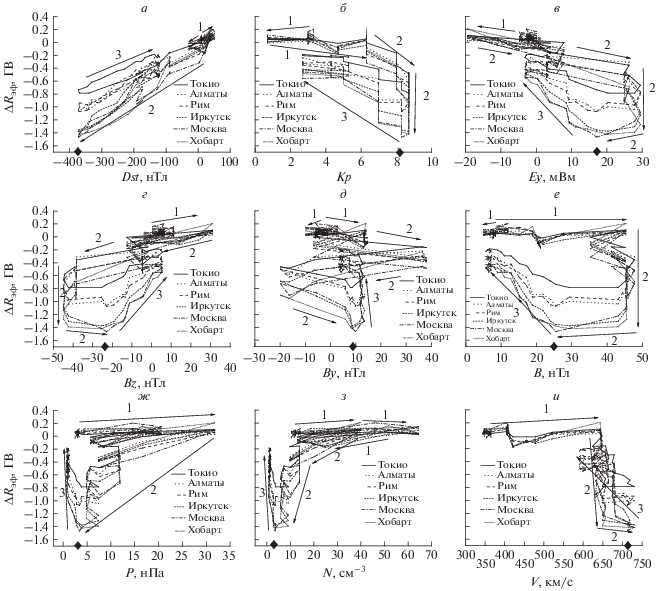
Рис. 3.
Петли гистерезиса для взаимосвязи ΔRэф с параметрами геомагнитной активности, ММП и СВ на разноширотных станциях. Три фазы бури: (1) – предварительная, (2) – главная, (3) – восстановительная. Стрелками указано направление течения времени при развитии бури. Черный ромбик на оси абсцисс указывает момент максимума бури, который совпадает с концом главной фазы.
Основная разница между образуемыми петлями на рис. 2а и 2б заключается в том, что для Bz изменения ΔRэф (Bz) происходят против часовой стрелки, а изменения ΔRэф (B) – по часовой стрелке. Для петли гистерезиса “по часовой стрелке” при фиксированном значении ΔR значение аргумента на главной фазе больше, чем на восстановительной. Для петли гистерезиса “против часовой стрелки” величина аргумента на главной фазе меньше, чем на восстановительной.
На рисунке 2в показана зависимость изменений ΔRэф от геомагнитного индекса Dst. Видно, что корреляция этих параметров на всех фазах бури очень высока, будучи максимальной в главной (k2 = 0.99 ± 0.07) и восстановительной фазах (k3 = = 0.97 ± 0.07). Видно, что в главной фазе по мере развития бури (развитие кольцевого тока) с уменьшением Dst до –373 нТл происходит падение ΔRэф до минимального значения –1.5 ГВ. Т.е максимальное падение жесткости обрезания наблюдается в максимуме бури. На фазе восстановления (распад кольцевого тока) с увеличением Dst, падение ΔRэф уменьшается. Видно, что точки главной фазы лежат близко к точкам восстановительной фазы, иногда перекрывая их. Однако траектории изменения значений ΔRэф (Dst) в главной и восстановительной фазах не совпадают, что можно видеть и при сравнении линейных трендов. Отсюда можно сделать вывод о том, что взаимосвязь ΔRэф и Dst обнаруживает признаки гистерезиса с характерной узкой петлей гистерезиса.
На рисунке 2г показана зависимость изменений ΔRэф от скорости СВ V. Видно, что падение ΔRэф происходит в прямой пропорциональности с ростом V: ΔRэф достигает минимума для этой бури (–1.5 ГВ) при росте V от 650 км/с в начале главной фазы до 750 км/с в конце. Здесь так же, как и для Dst, точки главной фазы расположены очень близко к точкам восстановительной фазы, в связи с чем траектории ΔRэф (V), так же как линейные тренды, лежат очень близко друг к другу, однако они не совпадают, формируя узкую петлю гистерезиса. Коэффициенты корреляции для главной и восстановительной фазы достаточно высоки и близки друг к другу (k2 = –0.70 ± 0.29, k3 = = ‒0.81 ± 0.19).
4.2. Зависимость петли гистерезиса от всех параметров и широты
В этом параграфе рассмотрим петли гистерезиса в зависимости от всех исследуемых параметров, а также от широты. Для этого на рис. 3 приведены диаграммы зависимости ΔRэф от Dst, Kp, Ey, Bz, By, B, V, N и P, где точки ΔR соединены во временнóй последовательности. Кроме того, диаграммы построены для всех шести разноширотных станций, данные которых взяты для исследования.
На рисунке 3 видно, что зависимость ΔRэф от параметров СВ и магнитосферы формирует петли гистерезиса для всех исследуемых параметров. Видно, что для Kp, B, Bz, Ey, N, и P петля гистерезиса достаточно широкая. Для Dst и V петли гистерезиса узкие (сравним с рис. 2). При этом зависимость ΔRэф от V носит не столь регулярный характер, как для остальных параметров, траектории восходящей и нисходящей ветви гистерезиса в некоторых местах пересекают друг друга. Менее регулярная картина видна также и для By. Тем не менее, полученные в результате кривые для V и By сохраняют отчетливые признаки гистерезиса.
Видно, что для петли гистерезиса на всех диаграммах рис. 3, кроме Bz и V (рис. 3г, 3и) обход цикла проходит по часовой стрелке. Что касается гистерезиса для By, то ситуация здесь более сложная – обход цикла на главной фазе начинается по часовой стрелке, а вторая половина главной фазы (с 04:00 UT) обходится против часовой стрелки, описывая s-образную кривую.
Обращает на себя внимание подобие петель гистерезиса для зависимости ΔRэф от Bz и Ey (рис. 3в и 3г), которые представляют собой очень похожие зеркально отраженные фигуры. Этот факт объясняется связью Ey = –VBz [Dungey, 1961].
Подобие петель гистерезиса видно также и на рис. 3ж и 3з. Это гистерезис, образованный связью ΔRэф с динамическими параметрами СВ N и P, которые также тесно связаны между собой. На этих рисунках видно, что в фазе восстановления идет резкое уменьшение падения ΔRэф, но при этом значения N и P практически не меняются, оставаясь около 0, которого они достигли вблизи максимума бури (рис. 1). Таким образом, плотность и давление СВ практически не участвуют в восстановительных процессах жесткости обрезания на восстановительной фазе бури.
На рисунке 3 видно, что верхняя часть каждой панели, та, которая соответствует подготовительной фазе бури, практически не изменяется с изменением широты. На этой фазе бури ΔRэф колеблется около 0, тем самым показывая, что исследуемые параметры, сами изменяясь в широких пределах, практически не влияют на жесткость обрезания. Причем это происходит на всех широтах и для всех параметров. С началом бури геометрия петель гистерезиса резко меняется, они начинают растягиваться в сторону увеличения широты наблюдений. Рисунок 3 демонстрирует тот факт, что петли гистерезиса группируются по признаку широты. В самой верхней точке диаграммы расположена петля гистерезиса для наиболее низкоширотной ст. Токио, затем две петли для среднеширотных станций Алмата и Рим, и ниже – петли для высокоширотных станций Москва, Иркутск и Хобарт. Таким образом, падение ΔRэф (увеличение |ΔRэф|) увеличивается пропорционально увеличению широты. Однако самое большое падение ΔRэф наблюдается практически на всех панелях не для самой высокоширотной ст. Xобарт, а для Москвы и Иркутска. Такая же зависимость ΔR от широты видна на рис. 1: амплитуда ΔRэф на низкоширотной ст. Токио меньше, чем на высокоширотной ст. Москва. То есть смещение петли гистерезиса по оси ординат к нижней точке происходит пропорционально увеличению широты. При этом не имеет значения для какого параметра СВ и магнитосферы сформирована петля, эта тенденция наблюдается на всех панелях рис. 3.
Для связи ΔRэф–Bz, ΔRэф–By и ΔRэф–V цикл гистерезиса обходится против часовой стрелки. Это означает, что значения Bz, By и V на главной фазе по абсолютной величине меньше, чем на восстановительной. Для остальных параметров цикл гистерезиса обходится по часовой стрелке.
4.3. Обсуждение результатов
В статье рассмотрена зависимость ΔRэф от параметров СВ, ММП и магнитосферы на разных фазах сильной магнитной бури 7–8 ноября 2004 г. Найдено, что эта взаимосвязь зависит от характера изменения этих параметров: траектория изменения ΔRэф в зависимости от исследуемых параметров во время развития токовых систем не совпадает с траекториями во время распада токовых систем. В процессе эволюции бури с развитием главной фазы и последующей восстановительной фазы исследуемые параметры гелио– и геомагнитосферы изменяются циклическим образом. В зависимости от их изменения в главной фазе происходит падение ΔRэф до минимального значения –1.5 ГВ, а в восстановительной фазе происходит его восстановление до значений, лежащих около 0. Причем возвращение к предбуревому состоянию проходит по другой траектории, чем рост во время главной фазы. Это является признаком гистерезиса. Мы выяснили также, что форма петель гистерезиса обнаруживает зависимость от широты: с увеличением широты петля растягивается на диаграмме вдоль оси ординат. Причем эта зависимость прослеживается для связи ΔRэф со всеми исследуемыми параметрами.
Явления гистерезиса во взаимосвязи изменений жесткостей обрезания КЛ и параметров гелио- и магнитосферы были получены в недавней работе [Птицына и др., 2021] для очень сильной бури 2003 г. на примере станции Москва. Сравнение признаков гистерезиса для обеих бурь обнаруживает общие черты. В частности, отмечены узкие петли для связи ΔRэф с геомагнитным индексом Dst и более широкие – с электромагнитными параметрами. Наиболее интересным фактом является подобие петель гистерезиса для южной компоненты поля Bz. В обоих случаях после начала бури значения |Bz| и |ΔRэф| увеличиваются в прямой пропорциональности друг от друга, но через 8 ч |Bz| начинает уменьшаться, а |ΔRэф| продолжает увеличиваться до конца главной фазы, т.е. прямая пропорциональная зависимость между |ΔRэф| и |Bz| сменяется обратной (2а этой статьи и рис. 2г в статье [Птицына и др., 2021]). В работе [Птицына и др., 2021] было найдено, что во время бури 2003 г. описанное нелинейное развитие связи ΔRэф с Bz происходило практически параллельно циклическому расширению–сужению области проникновения КЛ в магнитосферу, которое было установлено в работе [Ebihara et al., 2005] с помощью данных космических аппаратов DMSP, NOAA, и LANL. Было найдено, что проникновения частиц КЛ в магнитосферу в ноябре 2003 г. контролировалось продольными токами [Ebihara et al., 2005]. Аналогичное нелинейное поведение взаимосвязи ΔRэф с Bz в главной фазе бури 2004 г. позволяет предположить, что специфика этой связи и в этом случае, вероятно, определялась продольными токами. Из этого анализа также видно, что существенные изменения жесткостей обрезания в ответ на изменения параметров магнитосферы могут происходить на временны́х шкалах меньших, чем фаза бури.
Область проникновения заряженных космических частиц в различные секторы магнитосферы во время бури в апреле 1979 г. была рассмотрена с одновременным использованием данных ИСЗ Космос–900, Космос–1067 и ИНТЕРКОСМОС в работе [Сосновец и Тверская, 1986]. Было найдено, что кривые положения границ проникновения протонов с энергией >1 МэВ в главной и восстановительной фазах отличаются, то есть обнаруживаются признаки гистерезиса. При этом ширина петли гистерезиса для вечернего сектора больше и составляет 5°. Авторы работы [Сосновец и Тверская, 1986] связывают этот факт с формированием ассиметричного кольцевого тока, во время которого происходит дополнительная инжекция высокоэнергичных частиц в вечернем секторе.
Изменение жесткости обрезания в зависимости от параметров СВ и ММП тесно связано с динамикой взаимодействия СВ и магнитосферы и с передачей энергии от СВ магнитосфере. Гистерезис в зависимости ΔRэф от электромагнитных параметров, полученный нами, можно соотнести с результатами работы [Cai et al., 2009], в которой авторы рассмотрели 3D модель электромагнитных частиц, взаимодействующих с магнитосферой Земли, и исследовали стабильность такой системы. Авторы получили, что при циклическом изменении |Bz| от 0 до максимального значения и обратно, при достижении |Bz| некоторого критического значения магнитосфера резко сжимается и соответственно, внезапно меняется топология магнитного поля, что идентифицируется как признак пересоединения на дневной стороне. Получено, что при таком циклическом изменении Bz в какой-то момент времени система переходит из стабильного в нестабильное состояние, при этом происходит переход магнитного поля к форме с уменьшенной симметрией, в которой возникают диссипативные процессы, позволяющие поглощать излишек энергии, поступающей из СВ. По мнению авторов [Cai et al., 2009] это означает, что при передаче энергии СВ магнитосфере через диссипативные процессы некоторая часть этой энергии не восстанавливается. Размер магнитосферы и вся топология магнитного поля в процессе восстановительной фазы бури возвращаются к первоначальному состоянию, однако следуя другим путем, формируя тем самым петлю гистерезиса.
Можно заключить, что полученный нами гистерезис связан с тем фактом, что накопление энергии при развитии кольцевого тока на главной фазе бури и ее высвобождение на восстановительной фазе происходило не симметрично. Другие токовые системы, которые развиваются и затухают на разных временны́х масштабах, также могли вносить асимметричный вклад в процесс эволюции бури. Так как ширина петли гистерезиса определяется степенью симметрии/асимметрии процесса [Атабеков, 1957; Серенсен и др., 1975], то при взаимодействии КЛ с геомагнитным полем, а также с магнитными и динамическими параметрами межпланетной среды формируются петли гистерезиса разной ширины. Следует отметить, что площадь петли пропорциональна количеству энергии, которая теряется (переходит в тепло через диссипативные процессы) в ходе цикла гистерезиса [Красносельский и Покровский, 1983]. Таким образом, тот факт, что петля гистерезиса растягивается при переходе к более высоким широтам, т.е. ее площадь становится больше, свидетельствует, о том, что здесь действуют дополнительные диссипативные процессы, связанные с высокоширотными токовыми системами. Экспериментальные данные [Ермолаев и др., 2014] указывают на то, что буря 7–8 ноября 2004 г. характеризовалась чрезвычайно сильной геомагнитной активностью в авроральных и полярных широтах (более 2000 нТл согласно индексу AL). Существенное влияние высокоширотных токов на динамику очень сильных магнитных бурь во время главной и восстановительной фаз было продемонстрировано в работе [Левитин и др., 2014].
Эволюция токовых систем во время эволюции магнитной бури контролирует взаимодействие СВ и магнитосферы и, соответственно, определяет взаимосвязь жесткости обрезания КЛ и параметров магнитосферы, что отражается в характеристиках сформированных петель гистерезиса. Наши результаты свидетельствуют о том, что параметры гистерезиса действительно отражают изменения, происходящие в ΔRэф и параметрах гелио- и геомагнитосферы. Геометрия петли гистерезиса, ее вид, форма и/или площадь, по-видимому, могли бы служить информативным индексом взаимосвязи ΔRэф и параметров гелио- и геомагнитосферы. Однако вопрос о возникновении гистерезиса при взаимодействии КЛ и магнитосферы во время бури, связанного с развитием и эволюцией токовых систем, к настоящему времени не разработан. Для выяснения физической сути явлений, определяющих возникающий гистерезис и его характеристики, необходимо наличие гораздо большего статистического материала, чем дает исследование двух бурь. Мы предполагаем заняться накоплением и анализом такого материала в ближайшем будущем.
5. ЗАКЛЮЧЕНИЕ
Мы исследовали зависимость изменения жесткостей геомагнитного обрезания ΔRэф от параметров СВ, ММП и магнитосферы в процессе развития сильной магнитной бури 7–8 ноября 2004 г.
Получено, что ΔRэф зависит не только от варьируемого аргумента – параметров геомагнитной активности и межпланетной среды, но и от характера изменения аргумента. В процессе эволюции бури с развитием главной фазы и последующей восстановительной фазы исследуемые параметры гелио- и геомагнитосферы изменяются циклическим образом.
Установлено, что траектория ΔRэф, т.е. последовательные значения, которые принимает ΔRэф в зависимости от исследуемых параметров, во время развития токовых систем в главной фазе не совпадает с траекторией во время распада токовых систем в восстановительной фазе – формируются петли гистерезиса.
Найдено, что для связи ΔRэф с геомагнитными индексами и скоростью СВ V отмечены узкие петли, a с электромагнитными параметрами – широкие. Широта станции КЛ влияет на форму гистерезисной петли. Верхние точки на петле гистерезиса расположены практически одинаково для всех станций, в этих точках (перед бурей) |ΔRэф| ≈ 0, а нижняя точка на петле гистерезиса (максимум бури в конце главной фазы) – это максимум |ΔRэф|, который увеличивается с увеличением широты, растягивая петлю. В максимуме бури на низких широтах (ст. Токио) наблюдается максимальное падение жесткости обрезания ΔRэф ≈ –0.8 ГВ, а на высоких широтах (ст. Москва, Иркутск и Хобарт) ΔRэф достигает –1.5 ГВ. Эти значения определяют размер/площадь петли гистерезиса для исследуемой станции. Площадь гистерезиса в свою очередь, вероятно, определяет ту часть энергии СВ, поступающей в магнитосферу, которая теряется во время эволюции магнитной бури (интенсификация-релаксация).
Наши результаты свидетельствуют о том, что характеристики сформированных петель гистерезиса отражают специфику взаимодействия СВ и магнитосферы в процессе эволюции токовых систем во время исследуемой магнитной бури. Можно предположить, что полученный нами гистерезис связан с тем фактом, что накопление энергии при развитии кольцевого тока на главной фазе бури и ее высвобождение на восстановительной фазе происходило не симметрично, часть энергии не восстанавливалась. Другие токовые системы, которые развиваются и затухают на разных временны́х масштабах, также могли вносить асимметричный вклад в процесс эволюции бури.
Однако на данном этапе остается невыясненным, какая именно токовая система в общем случае стоит за полученными параметрами гистерезиса. Определение однозначных зависимостей ΔRэф от конкретной токовой системы на каждом этапе бури является сложной нерешенной задачей, так как к настоящему времени взаимодействие солнечного ветра и магнитосферы, которое контролирует вариации ΔRэф, еще плохо понято. Для выяснения физической сути явлений, определяющих возникающий гистерезис и его характеристики, в первую очередь необходимо наличие гораздо большего статистического материала. Мы предполагаем заняться созданием архива данных о гистерезисе по разным бурям и анализом этого материала в следующих работах.
Список литературы
– Атабеков Г.И. Теоретические основы электротехники. Линейные электрические цепи. СПб.: Лань, 592 с. 2009.
– Данилова О.А., Демина И.А., Птицына Н.Г., Тясто М.И. Картирование жесткости обрезания космических лучей во время главной фазы магнитной бури 20 ноября 2003 г. // Геомагнетизм и аэрономия. Т. 59. С. 160–167. 2019. https://doi.org/10.1134/S0016793219020051
– Ермолаев Ю.И., Зеленый Л.М., Застенкер Г.Н. и др. Солнечные и гелиосферные и магнитосферные возмущения в ноябре 2004 г. // Геомагнетизм и аэрономия. Т. 45. № 6. С. 324–332. 2014.
– Красносельский М.А., Покровский А.В. Системы с гистерезисом. М.: Наука, 271 с. 1983.
– Левитин А.Е., Дремухина Л.А., Громова Л.И., Птицына Н.Г. Генерация магнитного возмущения в период исторической магнитной бури в сентябре 1859 г.// Геомагнетизм и аэрономия. Т. 54. № 3. С. 324–332. 2014. https://doi.org/10.7868/S0016794014030110
– Птицына Н.Г., Данилова О.А., Тясто М.И., Сдобнов В.Е. Влияние параметров солнечного ветра и геомагнитной активности на вариации жесткости обрезания космических лучей во время сильных магнитных бурь // Геомагнетизм и аэрономия. Т. 59. № 5. С. 569–577. 2019. https://doi.org/10.1134/S0016793219050098
– Птицына Н.Г., Данилова О.А., Тясто М.И. Корреляция жесткости обрезания космических лучей с параметрами гелиосферы и геомагнитной активности на разных фазах магнитной бури в ноябре 2004 г. // Геомагнетизм и аэрономия. Т. 60. № 3. С. 281–292. 2020. https://doi.org/10.31857/S0016794020020145
– Птицына Н.Г., Данилова О.А., Тясто М.И., Сдобнов В.E. Динамика жесткости обрезания космических лучей и параметров магнитосферы во время различных фаз бури 20 ноября 2003 г. //Геомагнетизм и аэрономия. № 1. 2021. https://doi.org/10.31857/S0016794021010120
– Тясто М.И., Данилова O.A., Сдобнов В.E. Вариации жесткости геомагнитного обрезания космических лучей в период магнитосферных возмущений в мае 2005 г.: связь с межпланетными параметрами // Изв. РАН. Сер. физ. Т. 75. № 6. С. 857–859. 2011.
– Серенсен С.В., Когаев В.П., Шнейдерович Р.М. Несущая способность деталей машин. М.: Машиностроение, 354 с. 1975.
– Сосновец Э.Н., Тверская Л.В. Динамика кольцевого тока по данным о солнечных КЛ в магнитосфере // Геомагнетизм и аэрономия. Т. 26. № 1. С. 107–114. 1986.
– Adriani O., Barbarino G.C., Bazilevskaya G.N. et al. PAMELA’s measurements of geomagnetic cutoff variations during the 14 December 2006 storm // Space weather. V. 14. № 3. 2016. https://doi.org/10.1002/2016SW001364
– Belov A., Baisultanova L., Eroshenko E., Mavromichalaki H., Yanke V., Pchelkin V., Plainaki C., Mariatos G. Magnetospheric effects in cosmic rays during the unique magnetic storm on November 2003 // J. Geophys. Res. V. 110. A09S20. 2005. https://doi.org/10.1029/2005JA011067
– Cai D.S., Tao W., Yan X., Lembege B., Nishikawa K.I. Bifurcation and hysteresis of the magnetospheric structure with a varying southward IMF: Field topology and global three-dimensional full particle simulations // J. Geophys. Res: Space Physics. V. 114. № A12. 2009. https://doi.org/10.1029/2007JA012863
– Dungey J.W. Interplanetary magnetic field and the auroral zones // Phys. Rev. Lett. V. 6. P. 47–48. 1961. 2009. https://doi.org/10.1029/2007JA012863
– Ebihara Y., Fok M.-C., Sazykin S. Thomsen M.F., Hairston M.R., Evans D.S., Rich F.J., Ejiri M. Ring current and the magnetosphere–ionosphere coupling during the superstorm of 20 November 2003 // J. Geophys. Res. 2005. https://doi.org/10.1029/2004JA010924
– Kanekal S., Baker D., Blake J., Klecker B., Cummings J., Mewaldt R., Mason G., Mazur J. High–latitude energetic particle boundaries and the polar cap: A statistical study // J. Geophys. Res. V. 103. P. 9367–9372. 1998.
– Kress B.T., Mertens C.J., Wiltberger M. Solar energetic particle cutoff variations during the 29–31 October 2003 geomagnetic storm // Space Weather. V. 8. S05001. 2010.
– McCracken K.G., Rao U.R., Shea M.A. The trajectories of cosmic rays in a high degree simulation of the geomagnetic field // M.I.T. Tech. Rep. 77. Lab. Nucl. Sci. and Eng. Mass. Inst. of Technol. Cambridge. 146 p. 1962.
– Shea M.A., Smart D.F., McCracken K.G. A study of vertical cutoff rigidities using sixth degree simulations of the geomagnetic field // J. Geophys. Res. V. 70. P. 4117–4130. 1965.
– Shimazu H. Solar proton event and proton propagation in the earth’s magnetosphere // J. NICT. V. 1. P. 191–199. 2009.
– Tsyganenko N.A. A model of the near magnetosphere with a dawn–dusk asymmetry: 1. Mathematical structure // J. Geophys. Res. V. 107. A8. P. 1179. 2002. https://doi.org/10.1029/2001JA000219
– Tsyganenko N.A., Singer H.J., Kasper J.C. Storm–time distortion of the inner magnetosphere: How severe can it get? // J. Geophys. Res. V. 108. A5. 1209. 2003. https://doi.org/10.1029/2002JA009808
– Tyssøy H.N, Stadsnes J. Cutoff latitude variation during solar proton events: Causes and consequences // J. Geophys. Res.: Space Physics. V. 120. P. 553–563. 2014.
Дополнительные материалы отсутствуют.
Инструменты
Геомагнетизм и аэрономия


