Геомагнетизм и аэрономия, 2021, T. 61, № 4, стр. 468-477
Оценка планетарных индексов геомагнитной активности по данным отдельных магнитных обсерваторий российского сектора
В. Г. Петров 1, *, Е. И. Гамза 1, **
1 Институт земного магнетизма, ионосферы и распространения радиоволн
им. Н.В. Пушкова РАН (ИЗМИРАН)
г. Москва, г. Троицк, Россия
* E-mail: vpetrov@izmiran.ru
** E-mail: gamza@izmiran.ru
Поступила в редакцию 03.11.2020
После доработки 23.11.2020
Принята к публикации 28.01.2021
Аннотация
Исследованы связи между локальными индексами станций российского сектора и планетарными Ap-, Kp-индексами и возможности оценки планетарных индексов по значениям локальных. Показано, что локальные индексы западных российских обсерваторий позволяют достаточно хорошо оценить значения глобальных индексов. Оценка глобальных индексов по данным центральных и восточных станций российского сектора менее достоверна, но это может быть обусловлено отсутствием обсерваторий сети Kp, станций в этом секторе и недооценкой глобальной геомагнитной активности в 09–15 UT самим Kp-индексом.
1. ВВЕДЕНИЕ
Влияние геомагнитной активности (ГА) на практическую деятельность было обнаружено более 200 лет назад, когда начали внедряться линии телеграфной связи, и были замечены сбои в их работе во время магнитных бурь. В настоящее время с ГА связывают множество природных, технологических и биологических процессов. Однако для изучения и использования какого-либо явления необходимо иметь его определение и способы оценки интенсивности, т.е. научный подход невозможен без определения понятия геомагнитной возмущенности (ГА) и количественной оценки ее интенсивности – индексов геомагнитной активности. В работе [Афанасьева, 1954] дано следующее определение ГА: магнитная активность или возмущенность – это совокупность изменений магнитного поля Земли, вызываемых корпускулярным излучением Солнца. При расширенном толковании термина корпускулярного излучения с включением переносимого солнечным ветром магнитного поля это определение справедливо и с современной точки зрения. Одним из первых индексов для оценки ГА в этом смысле – К-индекс был предложен Дж. Бартельсом [Bartels et al., 1939] и утвержден резолюцией Международной ассоциации геомагнетизма и аэрономии (МАГ) в 1939 г. [IATME Bulletin, 1940].
K-индекс используется для количественной оценки уровня возмущенности магнитного поля в конкретной обсерватории в течение 3-часового интервала времени. Он определяется величиной изменения горизонтальной составляющей магнитного поля Земли, выраженной целым числом в диапазоне 0–9, причем 0 и 1 означает очень маленькие изменения, а 5 или более – геомагнитную бурю. Буква K происходит от немецкого слова “Kennziffer”, означающего “характерная цифра”, а методика вычисления К-индекса описана в работах [Bartels et al., 1939; Mayaud, 1980] и ряде других.
Проявление ГА зависит от местоположения точки наблюдения, поэтому для оценки планетарной ГА Бартельсом был предложен индекс планетарной ГА – Kp-индекс, вычисляемый как среднее взвешенное значение К-индексов ряда фиксированных обсерваторий [Bartels, 1955]. Авторы методики вычисления понимали, что амплитуда регистрируемого возмущения и значения локального K-индекса зависят от местного времени станции, проводящей измерения, и ввели промежуточный индекс Ks (standardized K-index) который получается из K-индекса введением к данным K-индекса каждой станции поправки. Эти поправки были статистически рассчитаны для каждой станции, каждого сезона и каждого 3-часового интервала так, чтобы максимально скомпенсировать наблюдаемую статистическую зависимость локального K-индекса от локального времени, и Kp получался уже усреднением этого стандартизованного Ks-индекса. Индексы Kp могут принимать 28 значений от 0 (очень спокойный интервал) до 9 (сильно возмущенный) с дробными частями, округленными до 1/3. Эти дробные значения могут обозначаться знаками “+” или “–”, например, значение Kp-индекса, равное 32/3, может обозначаться как 3.7, или 4–. Шкала для расчета K-индексов имеет почти логарифмический масштаб – увеличение индекса на единицу означает увеличение амплитуды вариаций приблизительно в два раза, поэтому арифметические операции (например, вычисление среднесуточного значения K или суммы K за сутки) с ним не имеет смысла, хотя, к сожалению, часто применяются. Для примера, сутки со значениями K-индекса 1 1 1 1 1 1 1 1 – это очень спокойный день, а со значениями 0 0 0 0 5 3 0 0 – это уже магнитная буря, хотя среднесуточное значение у них одно и тоже. Для таких операций предназначены локальные индексы А (обычно обозначаемые прописным а) и планетарный Ap, т.е. значения K, переведенные обратно в амплитуду вариаций в нТл по специальной единой для всех обсерваторий шкале.
В силу своей наглядности, длинного непрерывного ряда наблюдений с 1932 г. и понятного физического смысла [Mayaud, 1980], Kp-индекс стал широко использоваться для изучения, а затем и прогнозирования различных явлений в магнитосфере, ионосфере и на поверхности Земли. Например, в ионосферных исследованиях принято использовать Kp для параметризации ионосферных движений [Mats et al., 2015] и высыпаний энергичных частиц [Emery et al., 2008]. В магнитосферной физике установлена хорошая корреляция Kp с плотностью холодной плазмы в плазмосфере [Goldstein et al., 2014], плотностью горячей плазмы [Denton et al., 2016], положением плазмопаузы [Carpenter and Anderson, 1992], интенсивностью магнитосферной конвекции [Thomsen, 2004]. Многие модели магнитного поля в магнитосфере используют Kp в качестве входного параметра [Tsyganenko, 1989]. Kp также используется в моделях VLF [Agapitov et al., 2015] и ULF пульсаций [Ozeke et al., 2014)]. Авроральная зона, где наблюдаются полярные сияния и текут сильные авроральные электроструи, также расширяется к экватору по мере изменения интенсивности геомагнитной бури и увеличения значения Kp [Старков, 1994]. Другие примеры использования Kp приводятся в работе [Shprits et al., 2019].
Таким образом, Kp-индекс является очень важным индексом для диагностики и прогнозирования состояния многих параметров ионосферы и магнитосферы, и доступ к значениям Kp-индекса с минимальной задержкой существенен для многих прикладных задач. Предварительный Kp (https://www.swpc.noaa.gov/products/planetary-k-index, http://www-app3.gfz-potsdam.de/kp_index/ ql_bar.gif) доступен при наличии Интернета с задержкой от 3 до 6 ч, окончательное значение с задержкой до месяца. При отсутствии Интернета и доступа к сайтам Kp-индекса, он становится недоступным совсем.
В некоторых приложениях такая ситуация недопустима и возникает задача оценить значения Kp-индекса по данным К-индекса отдельной ближайшей обсерватории.
Знание текущего значения Kp-индекса необходимо для оценки текущих потоков электронов МэВ энергий в геосинхронных условиях, оценки состояния космических аппаратов и процессов накопления статического потенциала спутника [Heather et al., 2013], а также для определения интервалов времени, когда могут быть выполнены точные геомагнитные измерения.
Целью данной работы и является исследование возможности оценки значения планетарного Ap- и Kp-индексов по данным отдельной обсерватории российского сектора.
2. ОСОБЕННОСТИ ВЫЧИСЛЕНИЯ К-ИНДЕКСА
До появления цифровых магнитных измерений K-индексы вычислялись по аналоговым магнитограммам, и методика их вычисления была описана в работах [Bartels et al., 1939, Mayaud, 1967]. На основе этих методик позже были разработаны компьютерные методы вычисления K-индекса. На конференции МАГА в 1993 г. было одобрено и рекомендовано для использования четыре метода [IAGA news, 1993], их обзор и результаты сравнения с вычисленными вручную описаны в [Menvielle et al., 1995]. Наиболее известным и точным является метод линейной оценки, предложенный Финским метеорологическим институтом (FMI метод) [Jankowski et al., 1988; Pirjola et al., 1990] который мы и использовали.
Определяющим моментом при вычислении K-индекса на конкретной обсерватории является выбор значения вариации магнитного поля, при превышении которого K-индексу назначается максимальное значение равное 9, это значение обычно называется лимит К9 (иногда это значение обозначается L9). Граничные значения для меньших значений K-индекса однозначно устанавливаются по значению K9. Поскольку по самой идее K-индекс является характеристикой уровня геомагнитной возмущенности, а не места, где наблюдались вариации магнитного поля, то частотные распределения (вероятность наблюдения) данных значений K-индекса на разных обсерваториях, должны быть одинаковы [Bartels et al., 1939]. Это означает, что значения лимита K9 должно изменяться от обсерватории к обсерватории таким образом, что частота появления определенных уровней K за достаточно большой промежуток времени должна быть примерно одинакова во всех обсерваториях. В первую очередь значение K9 будет зависеть от геомагнитной широты обсерватории, но амплитуда наблюдаемых вариаций магнитного поля может зависеть и от величины индукционных токов в проводящей земле, поэтому выбранное по геомагнитной широте значение лимита K9 является предварительным и затем должно корректироваться по результатам сопоставления с данными ближайшей станции, имеющей утвержденное значение лимита K9 или с планетарным индексом геомагнитной активности Kp. Вопросы выбора правильного значения лимита K9 для отдельных обсерваторий и регионов были рассмотрены в работах [Regi et al., 2020; Hwang et al., 2013]. Для некоторых российских обсерваторий такое рассмотрение проведено в работе [Petrov and Krasnoperov, 2020], поэтому здесь на нем мы останавливаться не будем.
Исторически K-индекс долгое время вычислялся по данным аналоговых магнитометров с фотозаписью, которые регистрировали компоненту H, направленную вдоль местного магнитного меридиана и D (сейчас часто обозначаемую как Е в нТл, чтобы отличить от D в градусах), и все методики и значения лимитов были определены именно для НЕ-компоненты. Сейчас многие обсерватории проводят измерения (или преобразуют данные) в систему координат ХY с осью Х, направленной к географическому северу. Угол между направлениями X и H даже для среднеширотных станций может достигать нескольких десятков градусов. При переходе к измерениям XY-компоненты измеренные амплитуды вариаций изменяются и принятые лимиты K9 тоже могут измениться.
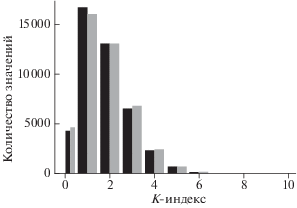
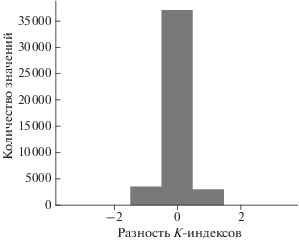
На рисунке 1 приведена гистограмма распределения числа случаев наблюдения различных значений К-индекса, вычисленных по НЕ- и XY-компонентам, для обс. Новосибирск. Эта обсерватория была выбрана для сравнения, так как значение склонения там достигает 35°. Для вычисления по XY число наблюдений малых значений K-индекса немного больше, а больших значений немного меньше, чем по НЕ. В соответствии с результатами работы [Petrov and Krasnoperov, 2020], это говорит о том, что значение лимита K9 при вычислении по XY нужно несколько увеличить и использовать 420 вместо 400. Этот вывод подтверждает и рис. 2, где показана гистограмма распределения разности значений K-индекса, вычисленных по XY- и НЕ-компонентам. В 80% случаев значения совпадают, а число случаев отклонения в одну или другую сторону достаточно близко. Небольшое превышение значений разности, равной –1 над +1 подтверждает упомянутую выше возможность небольшой корректировки K9 для вычисления по XY. Но эта разница незначительна и в дальнейшем мы будем вычислять K индекс по XY-компонентам, не делая преобразования к НЕ.
3. ОЦЕНКА AP- И KP- ИНДЕКСОВ ПО ДАННЫМ ОТДЕЛЬНОЙ СТАНЦИИ
Процедура выбора индивидуального лимита К9 для каждой обсерватории делает распределения значении К-индекса независимым от положения точки измерения, т.е. за достаточно большой интервал времени вероятность наблюдения конкретного значения K-индекса должна быть одинаковой для любой станции. Если это не так, то требуется изменение лимита K9 для данной станции. Однако амплитуда магнитных вариаций имеет максимальные значения в ночные часы местного времени, где наиболее сильны эффекты авроральных электроструй и продольных или токов растекания, замыкающих токи электроструй, и соответственно, в локальных K-индексах эффект местного времени хорошо заметен. При построении планетарного Kp-индекса разработчики индекса этот эффект учли и скомпенсировали его введением поправок в значения K-индекса станций, формирующих Kp, зависящих от местного времени каждой станции, и вычислением промежуточного Ks индекса, усреднением которого и получается Kp-индекс [Bartels et al., 1939].
Для получения оценки значения Kp-индекса по данным отдельной станции также необходимо ввести поправки, увеличивающие K-индекс конкретной станции в дневные часы и уменьшающие в ночные. Конечно, это не обеспечит усреднение по сети обсерваторий, определяющих Kp-индекс, но если процедура нормировки или стандартизации K-индекса работает удовлетворительно, то значение такого нормированного индекса должно быть примерно одно и то же и не зависеть от местного времени обсерватории, при этом эффект усреднения не должен быть сильным.
Определить эти поправки можно сопоставлением локальных и планетарных индексов отдельно для каждого временнóго интервала вычисления K-индекса. Иногда [Regi et al., 2020] такое сопоставление делается по значениям самого K-индекса, но учитывая, что само значение K-индекса является именно индексом, а не физической величиной, математические операции с ним физического смысла не имеют. В данной работе сопоставление выполнялось по значениям А- и Ap-индексов.
Сопоставление выполнялась в два этапа. Вначале по методике [Petrov and Krasnoperov, 2020] вычислялись значения лимита K9 для данной обсерватории, затем по методике FMI вычислялись А-индексы и считался коэффициент регрессии (Кreg) и корреляции (Kcor) между значениями локального А-индекса и планетарного Ap-индекса по всему имеющемуся набору данных. По найденному значению Kreg определялась поправка лимита K9 и вновь считался Kreg с новым лимитом K9. После этого Kreg по всему массиву оказывался близким к единице и вычислялся Kreg уже для каждого трехчасового интервала мирового времени. Такие расчеты были выполнены для всех среднеширотных российских обсерваторий, имеющих достаточно длинный ряд цифровых данных: Калининград (KLD), Москва (MOS), Борок (BOX) , Екатеринбург (ARS), Новосибирск (NVS), Иркутск (IRK), Якутск (YAK), Хабаровск (KHB), Магадан (MGD), Петропавловск (PET).
К сожалению, наличие цифровых данных по разным обсерваториям менялось от 4 до 19 лет и при малой статистике, особенно учитывая, что активность текущего солнечного цикла была мала, результаты для некоторых обсерваторий не очень надежны. В связи с небольшим интервалом наличия данных по обс. Калининград, они были дополнены данными обс. Хель (HLP). Сопоставление А- и K-индексов этих обсерваторий, расположенных на расстоянии ~80 км за пересекающийся интервал времени наблюдений, показало их очень высокую корреляцию (0.92) и разность их K-индексов никогда не превышала единицу, что позволило объединить их в один набор в дальнейшем обозначаемый как KLD(HEL). Для сопоставления А-индекса отдельной станции сети Kp, с Ap-индексом также были проведены расчеты для обс. Нимегк (NGK). Пример результатов расчета для обс. Москва приведен в табл. 1. В итоге для каждого интервала UT мы получили связь А = = Kreg*Ap + В. Поскольку коэффициент B достаточно мал (не более 5 нТл), то в дальнейшем для удобства мы будем приравнивать Kreg к отношению A/Ap.
Таблица 1.
Коэффициенты регрессии и корреляции А-индекса MOS c Ap-индексом
| Kreg | В | Kcor | Местное время | Мировое время |
|---|---|---|---|---|
| 1.131 | 4.096 | 0.893 | 0.8 | 22.5 |
| 0.923 | 3.277 | 0.879 | 3.8 | 1.5 |
| 0.687 | 3.059 | 0.879 | 6.8 | 4.5 |
| 0.57 | 4.288 | 0.859 | 9.8 | 7.5 |
| 0.759 | 4.712 | 0.825 | 12.8 | 10.5 |
| 1.169 | 3.633 | 0.875 | 15.8 | 13.5 |
| 1.51 | 3.348 | 0.875 | 18.8 | 16.5 |
| 1.415 | 3.971 | 0.877 | 21.8 | 19.5 |
Поскольку значение коэффициента регрессии Kreg определяется местным временем, на рис. 3 сведены эти значения для всех обсерваторий как функция местного времени (MLT). Общая закономерность – минимальное значение в 10–11 MLT, максимальное в 19–21 MLT хорошо видна, но разброс точек достаточно велик. Анализ этого отношения по данным отдельных станций выявляет ряд систематических изменений в ходе этого отношения в зависимости от долготы и широты станции. Видно, что положение минимума и максимума смещается с долготой в более поздние часы местного времени, причем, если долготы двух станций оказываются близкими, то положения экстремумов и общий ход оказывается одинаковым (см. MOS и BOX, KHB и MGD), т.е. этот сдвиг не является случайным. Также наблюдается зависимость разности максимальных и минимальных значений от широты – на более высокоширотных станциях эффект суточного хода более заметен. На рисунке 4 все значения Kreg сведены вместе.
Рис. 3.
Отношение локального А-индекса к планетарному Ap-индексу (коэффициент регрессии) как функция местного времени для ряда обсерваторий.
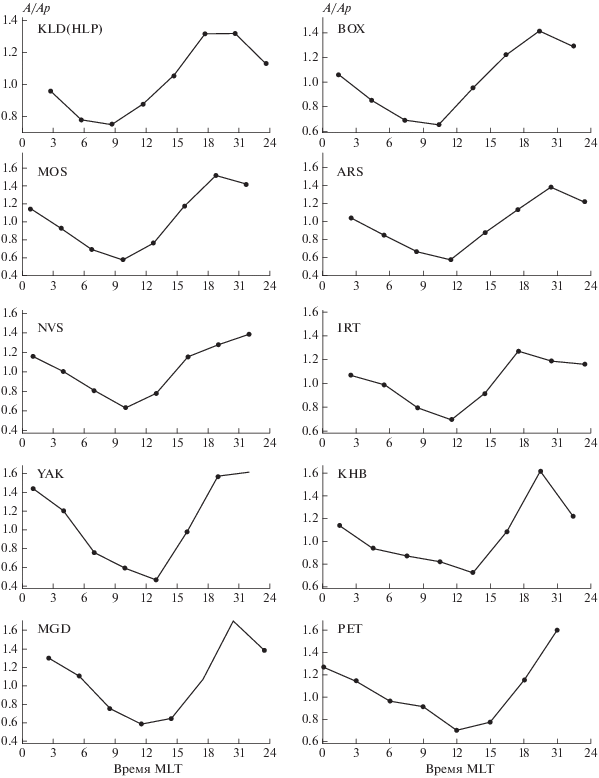
Рис. 4.
Значения A/Ap (коэффициент регрессии) для всех станций как функция местного времени. Черная кривая – сглаженные значения.
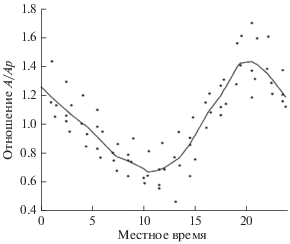
Используя известную (среднюю или индивидуальную для каждой станции) зависимость отношения амплитуды вариации магнитного поля А/Aр от MLT, можно ввести для каждого 3-часового интервала вычисления А-индекса поправку в значение лимита K9 (или в зарегистрированную вариацию XY, HE-компоненты), так, чтобы скомпенсировать такое суточное изменение амплитуды и убрать зависимость локального А-индекса от времени и вычислить нормированный (стандартизованный) А-индекс по данным отдельной станции. При хорошей нормировке значения такого нормированного А-индекса уже не будут зависеть от местного времени и осреднение по ряду станций не должно существенно изменить результат, т.е. такой нормированный А-индекс может использоваться как приближенное значение Ap-индекса.
В таблице 2 сведены данные о положении используемых станций и коэффициенты корреляции А-индекса без поправки на местное время (стандартный А-индекс) и с учетом поправки (нормированный А-индекс) с Ap-индексом. Из таблицы можно сделать следующие выводы:
Таблица 2.
Координаты станций и коэффициенты корреляции А-индекса станций c Ap-индексом
| КОД станции |
Долгота географическая |
Широта географическая |
Широта геомагнитная |
Коэффициент корреляции стандартный | Коэффициент корреляции нормированный |
|---|---|---|---|---|---|
| NGK | 12.7 | 52.1 | 48.0 | 0.884 | 0.911 |
| KLD(HLP) | 20.2 | 54.5 | 50.8 | 0.893 | 0.917 |
| BOX | 39.0 | 58.0 | 54.5 | 0.844 | 0.884 |
| MOS | 37.3 | 55.5 | 48.8 | 0.829 | 0.870 |
| ARS | 58.6 | 56.4 | 52.9 | 0.807 | 0.847 |
| NVS | 82.9 | 55.0 | 51.3 | 0.820 | 0.841 |
| IRT | 104.5 | 52.2 | 47.8 | 0.837 | 0.837 |
| YAK | 129.7 | 60.0 | 54.9 | 0.770 | 0.835 |
| KHB | 134.7 | 47.6 | 41.4 | 0.786 | 0.750 |
| MGD | 150.9 | 60.0 | 54.3 | 0.775 | 0.829 |
| PET | 158.3 | 53.0 | 46.7 | 0.794 | 0.771 |
1) А-индексы западных станций (NGK, KLD(HLP), BOX, MOS) имеют достаточно высокий коэффициент корреляции с Ap-индексом (0.893–0.844), а введение поправок на местное время заметно его увеличивает (0.917–0.884).
2) При увеличении долготы станции коэффициент корреляции уменьшается и эффект введения поправки на местное время также уменьшается.
Типичная ошибка вычисления самого коэффициента корреляции err = $\sqrt {{{(1 - {{r}^{2}})} \mathord{\left/ {\vphantom {{(1 - {{r}^{2}})} {(n - 2)}}} \right. \kern-0em} {(n - 2)}}} ,$ где r – значение коэффициента корреляции и n – количество пар точек наблюдения. В наших случаях ошибка вычисления коэффициента корреляции имеет значение 0.002–0.005 и можно утверждать, что в большинстве случаев введение нормировки достоверно улучшает оценку Ар по данным отдельной станции. Сделать количественную оценку качества приближения Ap-индекса по A-индексу сложно, в силу степенного характера A-индекса обычные оценки по стандартному отклонению σ не работают.
4. ОБСУЖДЕНИЕ
А-индексы более восточных станций систематически показывают меньший коэффициент корреляции с Ap, чем западные. На рисунке 5 показано расположение магнитных обсерваторий, данные которых используются при вычислении Kp и Ap-индексов. Видно, что из 13 используемых только 7 обсерваторий, т.е. более половины, расположены в Европе в очень узком долготном секторе, а в секторе 20°–150° Е таких обсерваторий вообще нет, и в интервале времени ~09–15 UT в ночном секторе, где наблюдаются максимальные амплитуды магнитных возмущений, нет ни одной Kp обсерватории.
Рис. 5.
Расположение магнитных обсерваторий, данные которых использованы при вычислении Kp- и Ap-индексов (http://isgi.unistra.fr/Images/reseau_Kp.jpg).
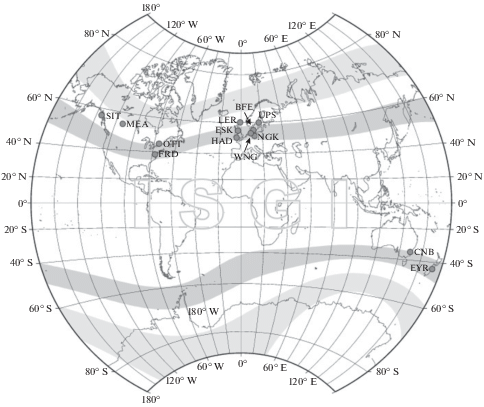
Конечно, введенная авторами Kp-индекса поправка на местное время через промежуточный Ks-индекс должна была скомпенсировать этот пропуск в долготном распределении используемых обсерваторий, но неизвестно насколько хорошо это получилось. Глобальная ГА в общем случае не должна зависеть от мирового времени. Даже если имеются UT-эффекты в ГА связанные, например, с суточным изменением угла наклона земного диполя к линии Солнце–Земля, то по методике построения Kp-индекса они исключаются введением индивидуальной поправки в K-индексы обсерваторий, формирующих Kp через использование Ks-индекса. В итоге статистически распределение значений Kp не должно зависеть от интервала UT.
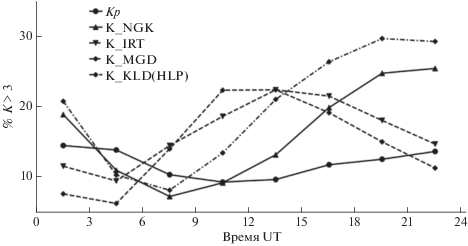
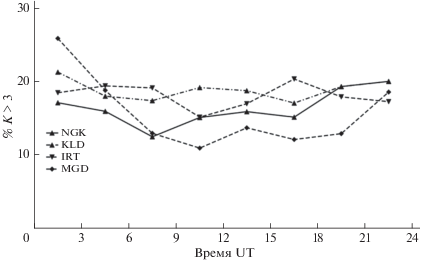
На рисунке 6 представлено число случаев наблюдения возмущенных значений (K > 3) в процентах от общего числа значений Kp и K-индексов ряда обсерваторий за период 2000–2019 гг. Видно, что в распределении Kp имеются систематические изменения с максимумом в 00–03 UT и минимумом в 09–15 UT. Если считать, что ГА не зависит от мирового времени, то в интервале 09–15 UT Kр-индекс не зарегистрировал 36% всех случаев с Kp > 3. На этом же рисунке приведено аналогичное распределение для европейской обс. NGK, входящую в сеть Kp и ряда российских обсерваторий. Максимальное число числа случаев наблюдения K-индекса > 3 для NGK и KLD(HLP) приходится на интервал примерно 22–01 UT, а минимальное на 07–10 UT мирового времени, что соответствует примерно 23–02 UT и 08–11 UT местного времени. При этом в дневном секторе регистрируется на 72% меньше интервалов со значением K-индекса > 3, чем в ночном. Это отражает известный факт, что сильные возмущения чаще наблюдаются в ночном секторе местного времени. Сравнивая суточную вариацию Kp- и K-индекса NGK, можно сделать вывод, что введение нормировки на локальное время в Kp и осреднение по ряду станций существенно уменьшает (с 72% до 36%) зависимость Kp от мирового времени, но не устраняет ее полностью.
Основной причиной наблюдаемого суточного хода в ГА по Kp-индексу может являться отсутствие в составе обсерваторий Kp-индекса, расположенных в секторе 20°–150° Е. Кривые суточного хода числа случаев K-индекса > 3 для обсерваторий IRT и MGD (рис. 6) показывают, что интервал времени с пониженной частотой регистрации сильных возмущений по Kp соответствует интервалу с повышенной частотой регистрации таких возмущений на станциях российского сектора. Их включение в состав обсерваторий, используемых для вычисления Kp-индекса, устранило бы провал в Kp. Это свидетельствует о том, что нормировка, используемая в Kp-индексе, недостаточно эффективно компенсирует уменьшение амплитуды магнитных возмущений в дневном секторе.
Для проверки эффективности предлагаемой методики нормировки магнитных возмущений для дневного сектора на рис. 7 приведены аналогичные графики, построенный по нормированному K-индексу (псевдо Kp). Регулярного суточного хода здесь уже не заметно, и частота появления случаев K > 3 меняется значительно меньше, чем на рис. 6, для NGK 36% вместо 70%, для KLD(HLP) 16% вместо 57%. Для восточных станций (MGD) вариация частоты наблюдения K > 3 от времени возрастает. Это может быть связано с ошибками самого Kp-индекса, по которому определялся нормировочный коэффициент в интервале 09–15 UT.
Рис. 7.
Число случаев наблюдения значений нормированного K-индекса >3 в зависимости от мирового времени.
Выполнить прямое сопоставление K и Kp-индексов непосредственно не удается, так как K-индекс может принимать 10 значений, а Kp – 28, и в связи с тем, что граничные значения в таблицах перевода K и Kp в А и Ap иногда не совпадают, однозначный перевод Kp- в K-индекс невозможен. Простая корреляция K и Kp смысла не имеет и в общем дает заметно меньшие коэффициенты корреляции (0.7–0.8) чем для А и Ap-индексов. Напоминаем, что основой для вычисления K-индексов является амплитуда вариации, т.е. фактически А-индекс, и перевод его в K-индекс и особенно в Kp, может существенно исказить соотношение между локальными и планетарными индексами. Таблицы, связывающие значения K- и А-индексов, хорошо известны [Заболотная, 2007]. В соответствии с этими таблицами, например, значение K = 7 присваивается интервалу со значением вариации A от 140–240 нТл, а Ap – с вариацией от 132–154 нТл соответствует Kp = 70, т.е. часть случаев Kp = 70 соответствует K = 7 (если амплитуда была >140), а часть K = 6 (А > 132, но <140). Вопросы сопоставления планетарного Kp и локального K-индексов требуют дальнейшего исследования. Возможные способы разрешения – либо полный переход к А-индексам, либо введение такой же 27 ступенчатой шкалы для локального K-индекса.
5. ВЫВОДЫ
Введение нормировки амплитуды вариации или лимита K9 для каждого UT интервала вычисления K-индекса позволяет с высокой достоверностью оценивать значения Ap- и Kp-индексов по данным российских станций, расположенных в западной части России.
Оценка значения Аp- и Kp-индексов по данным российских станций, расположенных в центральной и восточной части России, менее достоверна. Это, вероятно, является недостатком самих Ap- и Kp-индексов, основной вклад в которые дают станции европейского сектора, и поэтому он не полностью отражают глобальную геомагнитную активность в интервале 09–15 UT, когда в ночном секторе находятся российские станции.
Список литературы
– Афанасьева В.И. Справочник по переменному магнитному полю СССР. Ред. Афанасьева В.И., Л.: Гидрометеоиздат. 267 с. 1954.
– Заболотная Н.А. Индексы геомагнитной активности: Справочное пособие. М.: изд-во ЛКИ, 88 с. 2007.
– Старков Г.В. Математическое описание границ аврорального свечения // Геомагнетизм и аэрономия. Т. 34. № 3. С. 80–86. 1994.
– Agapitov O.V., Artemyev A.V., Mourenas D., Mozer F.S., Krasnoselskikh V. Empirical model of lower band chorus wave distribution in the outer radiation belt // J. Geophys. Res.: Space. V. 120. № 10. P. 425–442. 2015.
– Bartels J., Heck N., Johnston H. The Three-Hour-Range Index Measuring Geomagnetic Activity // Terrestrial Magnetism and Atmospheric Electricty. V. 4. P. 411–454. 1939.
– Bartels J. The stardandization index Ks, and planetary index Kp // IAGA Bulletin 12i. P. 88–101. 1955.
– Carpenter D.L., Anderson R.R. An ISEE/Whistler model of equatorial electron density in the magnetosphere // J. Geophys. Res. V. 97. P. 1097–1108. 1992. https://doi.org/10.1029/91JA01548
– Denton M.H., Henderson M.G., Jordanova V.K., Thomsen M.F., Borovsky J.E., Woodroffe J., Hartley D.P., Pitchford D. An improved model of electron and ion fluxes at geosynchronous orbit based on upstream solar wind conditions // Space Weather. V. 14. P. 511–523. 2016. https://doi.org/10.1002/2016SW001409
– Emery B., Coumans V., Evans D.S. et al., Seasonal Kp, solar wind, and solar flux variations in long-term single-pass satellite estimates of electron and ion auroral hemispheric power // J. Geophys. Res. V. 113, A06311. 2008. https://doi.org/10.1029/2007JA012866
– Goldstein J., Pascuale S.D., Kletzing C. et al. Simulation of Van Allen Probes plasmapause encounters // J. Geophys. Res. – Space. V. 119. P. 7464–7484. 2014. https://doi.org/10.1002/2014JA020252
– Heather A.E., Jörg-Micha J., McComas D.J. // Space Weather. V. 11(6). P. 339. 2013. https://doi.org/10.1002/swe.20053
– Hwang J., Hang-Pyo K., Young-Deuk P. J. Comparison of K-index Calculations between Several Geomagnetic Stations during IQDs and IDDs // Astron. Space Sci. V. 30(3) P. 169–174. 2013. https://doi.org/10.5140/JASS.2013.30.3.169
– IATME Bulletin. V. 11. P. 550, resolution 2. 1940
– Jankowski J.A., Ernst T., Sucksdorff C., Pirjola R., Rynö J. Experiences of a filter method and a standard curve method for determining K-indices // Ann. Geophys., V. 6. P. 589–593. 1988.
– Mats A., Dandouras I., Delcourt D. et al. The Earth: Plasma sources, losses, and transport processes // Space Sci. Rev. V. 192(1–4). P. 145–208. 2015. https://doi.org/10.1007/s11214-015-0187-2
– IAGA news. Computer derivation of K-Indices // IAGA news. № 32. P. 27–28. 1993.
– Mayaud P.N. Atlas des indices K / IAGA Bull., 21. Paris: IUGG Publ. Office, 113 p. 1967.
– Mayaud P. N. Derivation, meaning, and use of geomagnetic indices / Geophys. Monograph Ser. Washington DC: American Geophysical Union. 154 p. 1980. https://doi.org/10.1029/GM022
– Menvielle M., Papitashvili N., Häkkinen L., Sucksdorff C. Computer production of K indices: review and comparison of methods // Geophys. J. Int. V. 123. P. 866–886. 1995.
– Ozeke L.G., Mann I.R., Murphy K.R., Rae I.J., Milling D.K. Analytic expressions for ULF wave radiation belt radial diffusion coefficients // J. Geophys. Res. – Space. V. 119. P. 1587–1605. 2014. https://doi.org/10.1002/2013JA019204
– Petrov V.G., Krasnoperov R.I. The Aspects of K-index calculation at Russian geomagnetic observatories // Russian J. Earth Sciences. V. 20, ES6008. 2020. https://doi.org/10.2205/2020ES000724
– Pirjola R., Ryno J., Sucksdorff C. Computer production of K indices by a simple method based on linear elimination / Proc. Intern. Workshop on Geomagnetic Observatory Data Acquisition and Processing, Geophys. Publ. 15. Ed. K. Kauristie, C. Sucksdorff, H. Nevanlinna, p. 128. Helsinki: Finnish Meteorological Institute. 1990.
– Regi M., Bagiacchi P., DiMauro D., Lepidi S. Cafarel L. On the validation of K-index values at Italian geomagnetic observatories // Geosci. Instrum. Method. Data Syst. V. 9. P. 105–115. 2020.
– Shprits Y., Vasile R., Zhelavskaya I. Nowcasting and Predicting the Kp index Using Historical Values and Real-time Observations // Space Weather. V. 17. №. 8. P. 1219–1229. 2019. https://doi.org/10.1029/2018SW002141
– Thomsen M.F. Why Kp is such a good measure of magnetospheric convection // Space Weather. V. 2. S11044. 2004. https://doi.org/10.1029/2004SW000089
– Tsyganenko N.A. A magnetospheric magnetic field model with a warped tail current sheet // Planet. Space Sci. V. 37(1). P. 5–20. 1989.
Дополнительные материалы отсутствуют.
Инструменты
Геомагнетизм и аэрономия