Геомагнетизм и аэрономия, 2021, T. 61, № 1, стр. 3-7
Проявление сейсмоэффектов в ионосфере в дальней зоне от очага землетрясения
В. Ю. Белашов 1, *, Е. С. Белашова 2, О. А. Харшиладзе 3
1 Казанский (Приволжский) федеральный университет
г. Казань, Россия
2 Казанский национальный исследовательский технический университет им. А.Н. Туполева
г. Казань, Россия
3 Тбилисский государственный университет им. И. Джавахишвили
г. Тбилиси, Грузия
* E-mail: vybelashov@yahoo.com
Поступила в редакцию 19.04.2020
После доработки 22.06.2020
Принята к публикации 24.09.2020
Аннотация
На основе результатов теоретических исследований проявления сейсмической активности показано, что в результате воздействия на атмосферу и нейтральную компоненту ионосферы акустического импульса, вызванного поверхностной волной Рэлея, как в наземных экспериментах, так и в спутниковых наблюдениях на высотах F-области ионосферы могут регистрироваться возмущения вертикальной скорости нейтральной компоненты и электронной концентрации, что приводит к последующему формированию и эволюции в дальней зоне уединенной внутренней гравитационной волны (ВГВ) и возбуждению этой волной перемещающегося ионосферного возмущения (ПИВ) с соответствующими им характерными пространственными масштабами, распространяющих радиально от эпицентра под углами, близкими к горизонтали, со скоростями ∼200 мс−1. Рассмотрение 3-мерного случая с учетом всех значимых факторов (слабых нелинейности и дисперсии, диссипации и стохастических флуктуаций волнового поля) позволило уточнить полученные ранее другими авторами результаты и показало, что в дальней зоне от эпицентра землетрясения форма ионосферного отклика на сейсмическое событие существенно зависит от значений основных параметров ионосферы, определяющих ее дисперсионные характеристики, флуктуационные и диссипативные процессы в области распространения ВГВ и возбуждаемого ей ПИВ: это может быть и уединенное волновое возмущение, и волновой пакет с характерными масштабами ВГВ. При этом установлено, что имеют место как фазовый сдвиг ПИВ относительно фазы ВГВ (в пределах 0.5−5 мин), так и эффект релаксации в восстановлении электронной концентрации после прохождения солитона ВГВ. Полученные результаты анализа сейсмоионосферных пост-эффектов, выражающихся в формировании в дальней зоне солитоноподобных возмущений ВГВ и ПИВ и представляющих большой интерес, в частности, для лучшего понимания причинно-следственных связей в системе твердая земля–атмосфера–ионосфера, может использоваться для пеленгации эпицентров землетрясений и выделения сейсмообусловленных колебаний в спектре ионосферных флуктуаций.
1. ВВЕДЕНИЕ
Вопросы изучения эффектов в ионосферной плазме, обусловленных сейсмическими явлениями, привлекают пристальное внимание исследователей в связи с важностью этой проблемы не только для фундаментальной науки, но и для обеспечения безопасной жизнедеятельности населения сейсмоопасных регионов и на планете, в целом. При этом, наряду с изучением сейсмо-ионосферных явлений – предикторов сейсмической активности, важную роль по целому ряду причин играет исследование сейсмо-ионосферных пост-эффектов, например, с целью лучшего понимания причинно-следственных связей в системе твердая земля–атмосфера–ионосфера, для пеленгации эпицентров землетрясений, выделения сейсмообусловленных колебаний в спектре ионосферных флуктуаций и т.д.
Как известно, одна из первых попыток достаточно строгого теоретического изучения сейсмо-ионосферных эффектов, вызванных поверхностной рэлеевской волной, была предпринята Голицыным и Кляцкиным [1967], где эта задача решалась в 1-мерном линейном бездиссипативном приближении. Аналогичный подход, с учетом потерь, обусловленных слабой электропроводностью среды, был предпринят Павловым [1979]. Влияние слабой нелинейности на распространение в ионосфере вызванного землетрясением акустического импульса изучалось Павловым в работе [1986], однако и здесь был рассмотрен только 1-мерный случай. Трехмерная нестационарная задача сейсмического влияния на ионосферную плазму рассматривалась в работе Доильницыной и др. [1981], однако в данном исследовании авторы пренебрегали нелинейными эффектами. Таким образом, все известные нам исследования (см. достаточно полный обзор в работах [Белашов, 1990; Belashov and Vladimirov, 2005]) обладали теми или иными недостатками и, следовательно, полученные в них оценки степени влияния сейсмических событий на динамику ионосферной плазмы оказывались весьма приближенными. Более точные результаты могут быть получены при учете всех значимых факторов. Хорошим примером, при этом, могут служить теоретические оценки [Belashov, 1997a] для возбужденных рэлеевской волной внутренних гравитационных волн (ВГВ), в сравнении с результатами Павлова [1979].
В настоящей работе представлены результаты теоретического изучения проблемы с учетом слабых нелинейности и дисперсии, влияния диссипации и стохастических флуктуаций электронной концентрации, которые имеют место в ионосфере, в 3-мерной геометрии.
2. ОСНОВНЫЕ УРАВНЕНИЯ И АНАЛИЗ
Рассмотрим влияние возбуждаемого поверхностной волной Рэлея, вызванной землетрясением, волнового возмущения (импульса) на нейтральную компоненту атмосферы, и дальнейшее его распространение на ионосферных высотах близко к горизонтальной плоскости в дальней зоне от очага. Здесь “высокочастотные” акустические осцилляции затухают вследствие влияния дисперсионных эффектов, следствием чего является сдвиг спектрального максимума в более низкочастотную область − начинают преобладать колебания, относящиеся к ВГВ-ветви. Далее обсудим воздействие таких ВГВ на ионизованную компоненту ионосферной плазмы, а также влияние стохастических флуктуаций волнового поля на распространяющуюся волну.
Для описания движений нейтральной компоненты рассмотрим следующую систему уравнений газовой динамики [Belashov and Vladimirov, 2005]:
(1)
$\begin{gathered} {{\partial }_{t}}\rho {\kern 1pt} '\, + div\left[ {{{\rho }_{0}}(z){\mathbf{V}}} \right] = 0,\,\,\,\,{{\rho }_{0}}(z)\left[ {{{\partial }_{t}}{\mathbf{V}} + \left( {{\mathbf{V}}\nabla } \right){\mathbf{V}}} \right] = \\ = - \nabla p{\kern 1pt} '\, - \rho {\kern 1pt} 'g{{{\mathbf{e}}}_{z}} + \eta (z)\left[ {\frac{1}{3}\nabla div{\mathbf{V}} + {{\nabla }^{2}}{\mathbf{V}}} \right] + \\ + \,\,\varsigma (z)\nabla \left( {\nabla {\mathbf{V}}} \right),\,\,\,\,{{\partial }_{t}}p{\kern 1pt} '\,\, + \left( {{\mathbf{V}},\nabla {{p}_{0}}(z)} \right) = - {{c}^{2}}{{\rho }_{0}}(z)div{\mathbf{V}}, \\ \end{gathered} $Уравнения (1) не учитывают стохастических флуктуаций полей, и соответствующие члены будут нами введены в дальнейшем.
Первое граничное условие, аппроксимирующее поверхностную рэлеевскую волну на больших расстояниях от эпицентра, выберем в следующем виде:
(2)
${{\left. {{{V}_{z}}} \right|}_{{z = 0}}} = {{d}_{t}}Z(r{\kern 1pt} ',t),\,\,\,\,Z(r{\kern 1pt} ',t) = h(t)\exp \left[ {{{ - {{{(r{\kern 1pt} ')}}^{2}}} \mathord{\left/ {\vphantom {{ - {{{(r{\kern 1pt} ')}}^{2}}} {{{L}^{2}}}}} \right. \kern-0em} {{{L}^{2}}}}} \right],$Учитывая геометрию задачи, примем, что $k_{x}^{2} \gg k_{ \bot }^{2},$ $\left| {H{{k}_{x}}} \right| \ll 1,$ т.е. для нелинейных уединенных волн, распространяющихся под углами к горизонту, близкими к 90°, справедливо приближение Буссинеска. Тогда система уравнений (1) с учетом слабой нелинейности для скорости нейтральных частиц $u(t,r{\kern 1pt} ',z)$ = ${{\left. {V(t,r,z)} \right|}_{{x = \xi + {v}t}}}$ при ${{\partial }_{z}} = 0$ может быть редуцирована к одному уравнению пятого порядка [Белашов, 1990], с учетом члена, описывающего диссипативные эффекты вязкостного типа [Karpman and Belashov, 1991; Belashov and Vladimirov, 2005; Belashov and Belashova, 2015]:
(3)
$\begin{gathered} {{\partial }_{t}}u + \frac{{2\gamma - 1}}{{{{\gamma }^{2}}}}{{u}_{z}}{{\partial }_{\xi }}u - \sigma \partial _{\xi }^{2}u + 2\frac{{{{{(\gamma - 2)}}^{2}}}}{{{{\gamma }^{2}}}}{v}H\partial _{\xi }^{3} \times \\ \times \,\,\left[ {u + \frac{{{{{(\gamma - 2)}}^{2}}}}{{2{{\gamma }^{2}}}}\varepsilon {{H}^{2}}\partial _{\xi }^{2}u} \right] = \frac{{v}}{2}\int\limits_{ - \infty }^\xi {\partial _{y}^{2}ud\xi ,} \\ \end{gathered} $С учетом уединенных волн, перемещающихся под углами, близкими к горизонтали, уравнение непрерывности для электронной концентрации Ne в области F может быть записано в следующем виде [Белашов, 1990; Belashov and Vladimirov, 2005]:
(4)
$\begin{gathered} {{\partial }_{t}}{{N}_{e}} = {{\partial }_{z}}\left[ {\left( {{{\partial }_{z}}{{N}_{e}} + {{{{N}_{e}}} \mathord{\left/ {\vphantom {{{{N}_{e}}} {2{{H}_{i}}}}} \right. \kern-0em} {2{{H}_{i}}}}} \right){{D}_{0}}{{e}^{{{z \mathord{\left/ {\vphantom {z {{{H}_{i}}}}} \right. \kern-0em} {{{H}_{i}}}}}}}} \right. - \\ \left. { - \,\,{{u}_{z}}(1 - {{e}^{{ - \upsilon t{\kern 1pt} '}}})\sin I\cos I} \right] - \beta {{N}_{e}} + Q, \\ \end{gathered} $(5)
$\begin{gathered} {{N}_{e}}(u,t) = {{N}_{e}}(u,{{t}_{0}})\exp \left[ {\Im (u,t)} \right], \\ \Im (u,t) = \int\limits_{{{t}_{0}}}^t {g(u,t)dt} , \\ \end{gathered} $Как показано в работах [Белашов, 1990; Karpman and Belashov, 1991; Belashov and Vladimirov, 2005; Belashov and Belashova, 2015], в случае ε $ \ll $ −1 решения уравнения (3) при σ = 0 имеют вид классических алгебраических солитонов уравнения Кадомцева−Петвиашвили, поэтому в данном случае интеграл в правой части решения (5) может быть вычислен аналитически [ввиду громоздкости мы не приводим здесь аналитическую форму функционала $\Im (u,t)$]. Решение (5), описывающее перемещающееся ионосферное возмущение (ПИВ), при этом также будет иметь вид алгебраического солитона [Belashov, 1989; Белашов, 1990] (см. рис. 1). Если же, однако, $\varepsilon \to - 1$ или $\varepsilon \ll - 1$ при σ ≠ 0 требуется прибегнуть к численному интегрированию уравнения (3), поскольку для этих случаев его аналитические решения неизвестны. Результаты численного интегрирования уравнений (3), (5) при σ = 0 для типичных значений параметров области F и солитонных решений уравнения (3), описывающих возмущения, перемещающиеся со скоростями порядка 200 мс−1, были представлены в наших работах [Belashov, 1989; Белашов, 1990; Belashov and Vladimirov, 2005] (пример этих результатов см. на рис. 2). В данных работах было показано, что функция $N{\kern 1pt} '(u,t)$ в этом случае имеет волновой характер с нарастающей крутизной переднего фронта подобно ударной волне. При этом отмечается как фазовый сдвиг ПИВ относительно фазы ВГВ (в пределах 0.5−5 мин), так и эффект релаксации в восстановлении $N{\kern 1pt} '$ после прохождения солитона ВГВ. Эти эффекты нарастают с уменьшением ε, определяющим величину пространственной дисперсии. Как можно видеть из рис. 2, форма ионосферного отклика на сейсмическое событие существенно зависит от значений параметров ионосферы, определяемых величиной параметра $\varepsilon = {{ - {v}} \mathord{\left/ {\vphantom {{ - {v}} {{v}_{{\min }}^{{ph}}}}} \right. \kern-0em} {{v}_{{\min }}^{{ph}}}}$ в области распространения ВГВ и возбуждаемого ей ПИВ: это может быть и уединенное волновое возмущение, и волновой пакет.
Рис. 1.
Сейсмообусловленное ВГВ-возмущение в F-области ионосферы солитонного типа (и) при ε = −12 и соответствующее ему возмущение $N{\kern 1pt} '$ = $\left\{ {{{\left[ {{{N}_{e}}(u,t) - {{N}_{e}}(0,t)} \right]} \mathord{\left/ {\vphantom {{\left[ {{{N}_{e}}(u,t) - {{N}_{e}}(0,t)} \right]} {{{N}_{e}}(0,t)}}} \right. \kern-0em} {{{N}_{e}}(0,t)}}} \right\}$ × 100%.
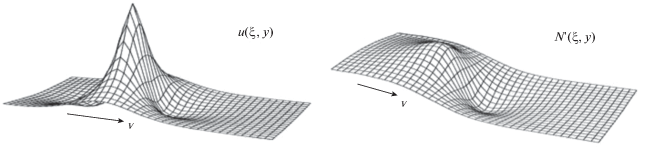
Рис. 2.
Профили ВГВ в дальней зоне от очага и возбуждаемых ими в ионосфере ПИВ электронной концентрации при у = 0: 1 – ВГВ; 2 – ПИВ ($N{\kern 1pt} '$) при ε = −1.2 (слева) и ε = −12 (справа).
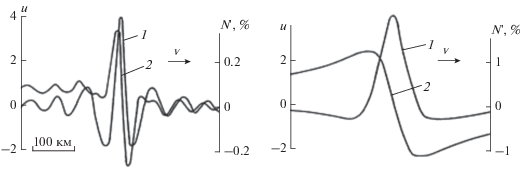
Рис. 3.
Эволюция в F-области ионосферы возбужденного рэлеевской волной солитона ВГВ с учетом диссипативных эффектов (σ = 1) при ε = −1.2: t = 0, 0.2.

Случай $\sigma \ne 0$ детально исследовался в работе [Karpman and Belashov, 1991], где было показано, что учет диссипативного члена приводит к экспоненциальному затуханию возмущения с уменьшением его амплитуды с декрементом $\Gamma (t)\sim \sigma .$ В этом случае также наблюдаются эффекты нарушения структуры и симметрии солитона ВГВ наряду с эффектом релаксации в восстановлении $N{\kern 1pt} '.$
При учете влияния стохастических флуктуаций волнового поля, практически всегда имеющих место на ионосферных высотах, на характер эволюции ПИВ, возбуждаемого рэлеевской волной, уравнение (3) должно быть дополнено членом $\kappa (t,r{\kern 1pt} ',z),$ описывающим такие флуктуации. Случай низкочастотных стохастических флуктуаций, когда допустимо принять $\kappa = \kappa (t)$ и считать $\varepsilon = 0$ в уравнении (3), детально исследовался аналитически в работе [Belashov, 1995], и все результаты, полученные там, могут быть легко перенесены на наше уравнение (3) с членом $\kappa = \kappa (t).$ Так, даже малые стохастические флуктуации волнового поля приводят к рассеянию возмущения при его распространении, при этом рассеивающийся ВГВ солитон уравнения (3) приобретает волновую структуру.
Однако в случае $\kappa = \kappa (t,r{\kern 1pt} ',z)$ аналитическое изучение этого процесса становится чрезвычайно сложным [Belashov et al., 2018], и мы использовали для этой цели численное моделирование. Полученные при этом результаты оказались качественно аналогичными случаю $\kappa = \kappa (t)$ [Belashov and Vladimirov, 2005; Belashov and Belashova, 2015]: здесь также наблюдается затухание осциллирующих решений и их разрушение со временем. Полученные нами оценки показали, что в F-области практически невозможно выделить возбуждаемый поверхностной рэлеевской волной ионосферный отклик для расстояний от эпицентра r $ \gg $ 12−13 L.
3. ЗАКЛЮЧЕНИЕ
В работе представлены результаты теоретических исследований проявления сейсмической активности в вариациях вертикальной скорости нейтральной компоненты и электронной концентрации на высотах F-области ионосферы. Рассмотрен 3-мерный случай с учетом слабых нелинейности и дисперсии, диссипации и стохастических флуктуаций волнового поля в ионосфере, что позволяет получить более точные результаты для дальней зоны от эпицентра землетрясения по сравнению с результатами ранее выполненных другими авторами работ. Исследованы сейсмо-ионосферные пост-эффекты, которые представляют большой интерес, в частности, для лучшего понимания причинно-следственных связей в системе твердая земля–атмосфера–ионосфера, для пеленгации эпицентров землетрясений, выделения сейсмообусловленных колебаний в спектре ионосферных флуктуаций и т.д. Рассмотрено воздействие импульсного возмущения в атмосфере, вызванного поверхностной волной Рэлея, на ионосферу и последующее формирование и эволюция в дальней зоне на высотах F-области ионосферы уединенной ВГВ и возбуждаемого ею ПИВ электронной концентрации.
Представленные результаты находятся в хорошем согласии с результатами, полученными в комплексных радиофизических экспериментах в периоды сейсмических событий на сети станций Дальневосточного региона России [Belashov, 1997b]. Важно также отметить, что возмущения, вызываемые в F-области ионосферы сейсмическими источниками, могут эффективно регистрироваться в экспериментах по доплеровскому зондированию ионосферы с учетом результатов, полученных в публикации [Белашов, 2018]. Подобного типа возмущения могут также наблюдаться в результате воздействия других источников импульсного типа, например, таких как извержения вулканов, запуски космических аппаратов и баллистических ракет, и мощные искусственные (подземные, наземные и атмосферные) взрывы [Row, 1967; Belashov, 1989; Drobzheva and Krasnov, 2003].
Список литературы
− Белашов В.Ю. Динамика нелинейных внутренних гравитационных волн на высотах F области ионосферы // Геомагнетизм и аэрономия. Т. 30. № 4. С. 637− 641. 1990.
− Белашов В.Ю. Аналитическое решение прямой и обратной задач в исследованиях внутренних гравитационных волн методом доплеровского сдвига частоты // Геомагнетизм и аэрономия. Т. 58. № 5. С. 651−653. 2018.
− Голицын Г.С., Кляцкин В.И. Колебания в атмосфере, вызванные движением земной поверхности // Изв. АН СССР. ФАО. Т. 3. № 10. С. 1044−1052. 1967.
− Доильницына Е.Г., Дробязко И.Н., Павлов В.А. О влиянии землетрясений на концентрацию электронов в слое F ионосферы // Геомагнетизм и аэрономия. Т. 24. № 7. С. 783−793. 1981.
− Карпман В.И. Нелинейные волны в диспергирующих средах. М.: Наука. 175 с. 1973.
− Павлов В.А. Воздействие землетрясений и извержений вулканов на ионосферную плазму // Изв. вузов. Радиофизика. Т. 22. С. 19−37. 1979.
− Павлов В.А. Акустический импульс над эпицентром землетрясения // Геомагнетизм и аэрономия. Т. 26. № 5. С. 807−815. 1986.
− Belashov V.Yu. Solitary electron density waves induced by the IGW’s solitons in the ionosphere // Proc. Intern. Symp. on EMC, Nagoya, Japan. N.Y.: IEEE, Inc. V. 1. P. 228. 1989.
− Belashov V.Yu. Dynamics of KP equation solitons in media with low-frequency wave field stochastic fluctuations // Phys. Lett. A. V. 197. P. 282−286. 1995.
− Belashov V.Yu. Seismogenic perturbations at heights of Ionosphere F Layer // Intern. Workshop on Seismo Electromagnetics (IWSE-97), Tokyo, Japan. Tokyo: NASDA. P. 225−233. 1997a.
− Belashov V.Yu. Some results of common analysis of ionospheric and seismic data obtained in the periods of seismic activity on the Russian North East station network // Intern. Workshop on Seismo Electromagnetics (IWSE-97), Tokyo, Japan. Tokyo: NASDA. P. 234−238. 1997b.
− Belashov V.Yu., Vladimirov S.V. Solitary waves in dispersive complex media. Theory, Simulation, Applications. Springer-Verlag: Berlin–Heidelberg–New York–Tokyo. 305 p. 2005.
− Belashov V.Yu., Belashova E.S. Dynamics of IGW and traveling ionospheric disturbances in regions with sharp gradients of the ionospheric parameters // Adv. Space Res. V. 56. P. 333−340. 2015.
− Belashov V.Yu., Belashova E.S., Kharshiladze O.A. Nonlinear wave structures of the soliton and vortex types in complex continuous media: Theory, simulation, applications / Lecture notes of TICMI. V. 18. Ed. G. Jaiani. Tbilisi: Tbilisi University Press. 90 p. 2018.
− Drobzheva Ya., Krasnov V. The acoustic field in the atmosphere and ionosphere caused by a point explosion on the ground // J. Atmos. Solar-Terr. Phys. V. 65. № 3. P. 369−377. 2003.
− Karpman V.I., Belashov V.Yu. Dynamics of two-dimensional solitons in weakly dispersive media // Phys. Lett. A. V. 154. № 3/4. P. 131−139. 1991.
− Row R.V. Acoustic-gravity waves in the upper atmosphere due to a nuclear detonation and an Earthquake // J. Geophys. Res. V. 72. № 5. P. 1599−1610. 1967.
Дополнительные материалы отсутствуют.
Инструменты
Геомагнетизм и аэрономия


