Геомагнетизм и аэрономия, 2019, T. 59, № 5, стр. 547-561

Вертикальные токовые слои в солнечной хромосферной плазме с эффектом Холла. Численное моделирование

Л. М. Алексеева^1, *, С. П. Кшевецкий^2, **

¹ Научно-исследовательский институт ядерной физики им. Д.В. Скобельцына Московского государственного университета им. М.В. Ломоносова (НИИЯФ МГУ)
г. Москва, Россия

² Балтийский федеральный университет им. И. Канта (БФУ им. И. Канта)
г. Калининград, Россия

^* E-mail: l.m.alekseeva@yandex.ru
^** E-mail: spkshev@gmail.com

Поступила в редакцию 07.09.2018
После доработки 01.12.2018
Принята к публикации 24.01.2019

DOI: 10.1134/S0016794019040035

Полный текст (PDF)

Аннотация

Путем численного решения 2D МГД-задачи (с постоянством физических величин вдоль прямых горизонтальных магнитных силовых линий) исследованы последствия поступления магнитного поля из нижележащих слоев в верхнюю хромосферу Солнца. Хромосферная плазма считается столкновительной, учитывается ее джоулева диссипация и теплопроводность; учтен также эффект Холла. Начальное магнитное поле характеризуется значением β = 1.5 и соответствует направленному вверх токовому слою конечной толщины. Выявлены случаи, когда совместная эволюция магнитного поля и плазмы приводит к формированию очень тонкого вертикального токового слоя, из которого по вертикали вниз истекает поток плазмы. Процесс оказался типичным для достаточно больших высот, где влияние эффекта Холла на эволюцию магнитного поля начинает превосходить влияние сноса поля из-за (частичной) вмороженности силовых линий. Образовавшийся тонкий токовый слой затем прекращает свое существование под действием пинчевых неустойчивостей (перетяжечной и/или изгибной). Пересоединение силовых линий не проявляет себя в условиях данного численного эксперимента из-за принятого постоянства физических величин (в том числе, скорости) на силовой линии. Соответственно, в природе описанные процессы следует рассматривать как альтернативные или дополнительные по отношению к обычно рассматриваемым сценариям пересоединения.

1. ВВЕДЕНИЕ

Надфотосферная часть солнечной атмосферы имеет структурированный вид, ее поведение весьма сложно. Отличие от простой сферически-симметричной газовой оболочки остывающего шара обусловлено присутствием магнитных полей. По современным оценкам, 95% магнитного потока, поступившего снизу из фотосферы, не доходят до короны [Прист, 1985; Aschwanden, 2004]. Таким образом заключенная между фотосферой и короной хромосфера заполнена разнообразными, в основном горизонтальными, магнитными полями. Именно она отличается большой динамичностью и крайним изобилием всевозможных неоднородностей, особенно мелкомасштабных. Физическая природа хромосферных явлений, как и их иерархия, остаются малоизученными.

Типичной структурой хромосферы должны быть токовые слои (ТС) той или иной ширины и протяженности, соответствующие зонам контакта различных магнитных областей. Токи в плазме обычно неустойчивы. Поэтому каждая такая зона контакта (или, что то же самое, контактный ТС), эволюционируя, может порождать различные – в том числе, очень мелкого масштаба – неоднородности магнитного поля и плазмы.

Целью настоящей работы является выявление и исследование сравнительно долгоживущих (транзиентных) структур, которые возникают при этой эволюции. Мы останавливаем внимание на тех случаях, когда транзиентной структурой оказывается особый вид мелкомасштабных магнитных неоднородностей – протяженные тонкие токовые слои (ТТС).

Случаи формирования ТТС интересны уже тем, что на ТТС возможна вспышечнообразная энергизация вещества. Огромное количество исследований показывает, что она может быть следствием магнитного пересоединения (см. работы [Сыроватский, 1957, Syrovatskii, 1971; Прист и Форбс, 2005; Зеленый, 2016; Leake et al., 2013; Ni et al., 2018] и ссылки там). Однако в хромосфере – с ее обилием контактных ТС – должен быть распространен также и другой, не связанный с пересоединением, вид вспышечноподобной активности. Его порождает нелинейное развитие пинчевой перетяжечной неустойчивости контактного ТС между разнополярными магнитными областями. В природной плазме (движению которой не мешают стенки, электроды и пр.) при этом формируется протяженный ТТС [Алексеева и Кшевецкий, 2011], что при некоторых параметрах процесса кончается внезапной и интенсивной энергизацией вещества вблизи центральной точки магнитной конфигурации [Alekseeva and Kshevetskii, 2015]. Мы исследуем здесь свойства ТТС как транзиентной структуры вместе с условиями, способствующими ее возникновению.

Некоторые свойства ТС между одинаковыми по величине разнополярными магнитными областями в столкновительной полностью ионизованной плазме хромосферы к настоящему времени уже известны. Они описаны в ряде теоретических исследований, где магнитное поле предполагалось горизонтальным, силовые линии считались параллельными прямыми, а физические величины – неизменными вдоль силовой линии; с этих же позиций проводится исследование хромосферы в настоящей работе. (Соответственно наше исследование и его результаты не имеют отношения к магнитному пересоединению, в результате которого силовая линия приобретает изогнутость, а скорость плазмы – изменения вдоль нее).

Случай, когда все величины зависят только от одной пространственной координаты, изучался в работе [Goodman, 2005]. Автор задал распределение величины магнитного поля в виде гиперболического тангенса и постоянный поток вещества поперек соответствующего ТС. Остальные величины были определены им из стационарных уравнений МГД, учитывающих эффект Холла и термоэлектрические явления. Расчеты показали, что в этих условиях внутри ТС располагается другая структура – диффузионный слой (diffusion region, DR), ширина которого меньше на несколько порядков ширины ТС. Интересно, что температура и плотность внутри DR соответствуют переходной области и нижней короне, на порядки отличаясь от значений в окружающей хромосферной плазме, температура которой вне токового слоя постепенно спадала до 20 000 К. Поддержание структуры в стационарном состоянии, несмотря на присутствие джоулевой диссипации, обеспечено заданным потоком вещества поперек токового слоя. В других работах, названных в этом разделе, свойства ТС установлены благодаря полученному (аналитически или численным путем) решению полностью самосогласованной системы двумерных столкновительных магнитогидродинамических (МГД) уравнений.

Численное решение системы с учетом скалярных электро- и теплопроводности плазмы при начальном распределении магнитного поля, соответствующем горизонтальному контактному ТС, было проведено для различных значений величины плазменного параметра $\beta = 1.2{\kern 1pt} - {\kern 1pt} 2.3.$ Оказалось, что определяющую роль на начальном этапе совместной эволюции магнитного поля и плазмы играет пинчевая перетяжечная неустойчивость. В природных условиях, где есть возможность выброса плазмы в виде коллинеарных току струй за пределы магнитной конфигурации, она приводит к сближению магнитных областей вплоть до образования однородного по длине ТТС, а при достаточно интенсивном ее развитии – к внезапному взрывообразному усилению выброса струй и сильной локальной энергизации плазмы [Алексеева и Кшевецкий, 2011; Alekseeva and Kshevetskii, 2015].

Ориентировочная попытка [Алексеева и Кшевецкий, 2013] численного решения аналогичной задачи с учетом силы тяжести и эффекта Холла для магнитной конфигурации с вертикальным ТС привела к обнаружению выброса вещества вниз, в виде цепочки сгустков по линии ТС (явление может создавать впечатление того “обстрела” Солнца “пулевой очередью”, который иногда обсуждают СМИ). В настоящей работе к этому прибавлено еще систематическое исследование физических причин, по которым в хромосфере Солнца разнополярные магнитные области, даже первоначально сбалансированные (когда сумма магнитного и газового давлений одинакова по пространству), порождают затем однородный по длине ТТС, существующий достаточно долго.

На возможность существования такого рода ТТС указывает найденное для слабого магнитного поля стационарное решение той же двумерной МГД-системы столкновительных уравнений; оно получено аналитически разложением по обратным степеням β в предположении значительно более быстрого изменения величин по горизонтали, чем по вертикали [Алексеева, 2006]. Решение имеет вид вертикального ТТС, стационарное существование которого в присутствии джоулевой диссипации обусловлено присутствием силы тяжести, эта же сила определяет направленность вверх электрического тока.

Ради сопоставления результатов моделирования с аналитически найденным стационарным решением мы для определенности будем рассматривать ток, текущий вверх.

2. ЧИСЛЕННЫЙ ЭКСПЕРИМЕНТ С ТЕКУЩИМ ВВЕРХ ТОКОМ

2.1. Строение хромосферы и план исследования

Плазму хромосферы будем считать водородной, полностью ионизованной и квазинейтральной. Пусть парциальные давления ее протонов и электронов (как и их температуры) равны друг другу, так что каждое составляет половину газового давления плазмы (то же относится и к температурам).

Рассматривается случай, когда плазма в начальный момент всюду имеет одинаковую температуру ${{T}_{*}}$ = 50 000 К. Характерное значение концентрации протонов ${{N}_{*}},$ которое может быть при такой температуре, зависит от представления о хромосфере в целом. Долгое время хромосферу воспринимали как тонкую оболочку и считали, что концентрацию частиц (протонов) в ней можно охарактеризовать одним значением ${{N}_{{\text{*}}}}.$ Однако позднее представления о толще хромосферы изменились. Оказалось, что хромосфера, во-первых, неоднородна и может включать в себя вкрапления в виде областей корональной плазмы [Gabriel, 1994; Schrijver, 2001; Aschwanden, 2004]. Во-вторых, толщина хромосферы может доходить до 15000 км [Priest, 2014].

При таком диапазоне высот концентрация частиц ${{N}_{{\text{*}}}}$ должна сильно отличаться вблизи нижней и верхней границ полностью ионизованной хромосферы – назовем соответствующие области нижним слоем Π^I и верхним слоем Π^II.

Наша расчетная область охватывает 280 км по горизонтали и 3920 км по вертикали сеткой 80 × × 247 узлов, соответственно. Мы выполним по серии расчетов по-отдельности для слоев Π^I и Π^II. В первой серии решение задачи с начальными условиями отыщем при значении $~{{N}_{*}} = N_{*}^{{\text{I}}} = {{10}^{{15}}}$ м⁻³, которое обычно приводится в связи с представлением о полностью ионизованной хромосфере как о тонкой оболочке [Demoulin and Klein, 2000]. (Поэтому само наше решение для слоя Π^I можно рассматривать, в частности, и как исследование в рамках бытующего ранее представления о тонкой хромосфере). Во второй серии расчетов, где имеется в виду слой Π^II, решение ищется при той же начальной температуре ${{T}_{*}},$ но при значении ${{N}_{{\text{*}}}} = N_{*}^{{{\text{II}}}},$ определенном по закону Больцмана для большей из высот. Сравнение результатов для Π^II и Π^I покажет, какие свойства хромосферных вертикальных токов обусловлены большей степенью разреженности плазмы.

2.2. Система уравнений, начальные и граничные условия, параметры

Итак, пусть в слой плазмы с характерными значениями температуры ${{T}_{*}}$ и концентрации протонов ${{N}_{{\text{*}}}}$ внесено горизонтальное магнитное поле характерной величины B₀ (эти три величины мы используем далее как базисные размерные единицы в процедуре обезразмеривания уравнений). О последствиях внесения на качественном уровне можно судить по величине характерного плазменного параметра (k – постоянная Больцмана):

(1)

${{\beta }_{{*0}}} = \frac{{8\pi k{{N}_{*}}{{T}_{*}}}}{{B_{0}^{2}}}.$

Для детального описания процесса мы привлечем полную одножидкостную МГД-систему столкновительных уравнений с учетом эффекта Холла, магнитной вязкости и теплопроводности [Брагинский, 1963; Брушлинский и Морозов, 1974]. Ограничимся случаем двумерной геометрии, считая, что вдоль линий магнитного поля физические величины не меняются, а сами линии представляют собой параллельные прямые, вдоль которых отсутствуют составляющие скорости и электрического тока. В дальнейшем мы будем использовать декартову систему координат (x, y, z), ось z которой направлена вертикально вверх, а ось y параллельна линиям горизонтального магнитного поля ${\mathbf{B}} = B\left( {x,~z} \right){{e}_{y}};$ соответственно, в ней ${{v}_{y}} = 0,$ ${{j}_{y}} = 0$ и все величины не меняются по y (обозначение здесь и дальше – общепринятые).

Предварительно обезразмерим входящие в уравнения величины подобно тому, как это сделано в работе [Брушлинский и Морозов, 1974]. Выберем за единицу плотности ${{\rho }_{{\text{*}}}} \equiv {{m}_{i}}{{N}_{*}}$ (здесь ${{m}_{i}}$ – масса протона), за единицу длины – высоту однородной атмосферы $H = {{k{{T}_{{\text{*}}}}} \mathord{\left/ {\vphantom {{k{{T}_{{\text{*}}}}} {\left( {g{{m}_{i}}} \right)}}} \right. \kern-0em} {\left( {g{{m}_{i}}} \right)}},$ где g – ускорение силы тяжести. Комбинации ${{B_{0}^{2}} \mathord{\left/ {\vphantom {{B_{0}^{2}} {\left( {4\pi } \right)}}} \right. \kern-0em} {\left( {4\pi } \right)}}$ и ${{{v}}_{{{\text{*}}0}}} \equiv {{{{B}_{0}}} \mathord{\left/ {\vphantom {{{{B}_{0}}} {\sqrt {4\pi {{\rho }_{{\text{*}}}}} }}} \right. \kern-0em} {\sqrt {4\pi {{\rho }_{{\text{*}}}}} }}$ используем как единицы газового давления и скорости плазмы, соответственно; ${{t}_{{{\text{*}}0}}} \equiv {H \mathord{\left/ {\vphantom {H {{{{v}}_{{{\text{*}}0}}}}}} \right. \kern-0em} {{{{v}}_{{{\text{*}}0}}}}}$ пусть будет единицей времени, а ${{c{{B}_{0}}} \mathord{\left/ {\vphantom {{c{{B}_{0}}} {\left( {4\pi H} \right)}}} \right. \kern-0em} {\left( {4\pi H} \right)}}$ – единицей плотности тока; c – скорость света.

Поскольку в настоящей работе речь идет о процессах в слоях Π^I и Π^II при одинаковом значении ${{{\beta }}_{{{\text{*}}0}}},$ выразим заодно ${{B}_{0}}$ и ${{{v}}_{{*0}}}$ через ${{\beta }_{{{\text{*}}0}}}$ и базисные газовые параметры ${{T}_{{\text{*}}}}$ и ${{N}_{{\text{*}}}}{\text{:}}$

(2)

${{B}_{0}} = \beta _{{*0}}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}\sqrt {8\pi k{{N}_{*}}{{T}_{*}}} ,$

(3)

${{{v}}_{{*0}}} = \beta _{{*0}}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}\sqrt {{{2k{{T}_{*}}} \mathord{\left/ {\vphantom {{2k{{T}_{*}}} {{{m}_{i}}}}} \right. \kern-0em} {{{m}_{i}}}}} ,$

отметив при этом, что значения ${{{v}}_{{*0}}}$ и ${{t}_{{{\text{*}}0}}}$ одинаковы для обоих слоев Π^I и Π^II.

Безразмерная система уравнений имеет вид [Брушлинский и Морозов, 1974]:

(4)

$\begin{gathered} \rho \left( {\frac{{\partial {\mathbf{v}}}}{{\partial t}} + \left( {{\mathbf{v}} \cdot \nabla } \right){\mathbf{v}}} \right) = - \nabla \left( {P + \frac{{{{B}^{2}}}}{2}} \right) - \frac{{{{\beta }_{{*0}}}}}{2}\rho {{{\mathbf{e}}}_{g}}, \\ {{{\mathbf{e}}}_{g}} \equiv - \frac{{\mathbf{g}}}{g}, \\ \end{gathered} $

(5)

$\frac{{\partial \rho }}{{\partial t}} + {\text{div}}\rho {\mathbf{v}} = 0,\,\,\,\,P = \frac{{{{\beta }_{{*0}}}}}{2}\rho T,\,\,\,\,\gamma = {5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0em} 3},$

(6)

$\begin{gathered} \frac{{\partial {\mathbf{B}}}}{{\partial t}} = {\text{rot}}\left[ {{\mathbf{v}} \times {\mathbf{B}}} \right] - {\text{rot}}\Theta {\mathbf{j}} + \frac{\xi }{2}\left[ {\nabla \frac{1}{\rho } \times \left( {{{B}^{2}} + P} \right)} \right], \\ {\mathbf{j}} = {\text{rot\;}}{\mathbf{B}}, \\ \end{gathered} $

(7)

$\begin{gathered} \frac{{{{\beta }_{{*0}}}}}{{2\left( {\gamma - 1} \right)}}\rho \left( {\frac{{\partial T}}{{\partial t}} + \left( {{\mathbf{v}} \cdot \nabla } \right)T} \right) + P{\text{div\;}}{\mathbf{v}} = \\ = {\text{div}}K\nabla T + \Theta {{j}^{2}} + \frac{\xi }{2}\left[ {\frac{{{{\beta }_{{*0}}}}}{{2\left( {\gamma - 1} \right)}}\left( {{\mathbf{j}} \cdot \nabla T} \right) + P~{\text{div}}~\frac{{\mathbf{j}}}{\rho }~} \right] \\ \end{gathered} $

(мы дополнительно учли еще силу тяжести).

Влияние эффекта Холла на динамику плазмы отражено присутствием безразмерной константы

(8)

$\xi = \frac{c}{{eH}}\sqrt {\frac{{{{m}_{i}}}}{{4\pi {{N}_{*}}}}} ,$

которая фигурирует лишь в уравнении динамики магнитного поля (6). Локальные магнитная вязкость ${\Theta }~$ и теплопроводность $K,$ зависящие от единственной функции T = T(x, z), определяются формулами

(9)

$\Theta = {{\theta }_{*}}\beta _{{*0}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}{{T}^{{ - {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}},\,\,\,\,K = {{\kappa }_{*}}\beta _{{*0}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}{{T}^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}},$

где ${{{\theta }}_{*}}$ и ${{\kappa }_{*}}$ – безразмерные множители, в которых, кроме общефизических констант, фигурируют лишь базисные газовые размерные параметры ${{T}_{{\text{*}}}}~$ и ${{N}_{{\text{*}}}}$ (Приложение: п2 и п3).

Пусть в момент t = 0 магнитное поле соответствует контактному ТС, имеющему протяженность ${{z}_{k}}$ и быстроту изменения в поперечном направлении, характеризующуюся величиной параметра b (его в дальнейшем будем для краткости называть резкостью):

(10)

${{\left. {B\left( {x,z} \right)} \right|}_{{t = 0}}} = \left[ {1 + \zeta \exp \left( { - \zeta } \right)} \right]\operatorname{th} \left( {bX} \right),\,\,\,\,\zeta \equiv {{{{Z}^{2}}} \mathord{\left/ {\vphantom {{{{Z}^{2}}} {z_{k}^{2}}}} \right. \kern-0em} {z_{k}^{2}}},$

где $X \equiv x - {{x}_{c}},$ $Z \equiv z - {{z}_{c}},$ ${{x}_{c}} = {{{{x}_{{{\text{max}}}}}} \mathord{\left/ {\vphantom {{{{x}_{{{\text{max}}}}}} 2}} \right. \kern-0em} 2},$ ${{z}_{c}} = {{{{z}_{{{\text{max}}}}}} \mathord{\left/ {\vphantom {{{{z}_{{{\text{max}}}}}} 2}} \right. \kern-0em} 2},$ ${{x}_{{{\text{max}}}}} = 0.207,$ ${{z}_{{{\text{max}}}}} = 2.8.$

Плазму в начальный момент считаем всюду неподвижной и имеющей одинаковую по всей расчетной области температуру:

(11)

${{\left. {{v}\left( {x,z} \right)} \right|}_{{t = 0}}} = 0,\,\,\,\,{{\left. {T\left( {x,z} \right)} \right|}_{{t = 0}}} = 1.$

Будем считать, что при t = 0 в тех местах счетной области, где нет магнитного поля, плотность плазмы распределена по закону Больцмана

(12)

${{\rho }_{{g{\text{\;}}}}} = \exp \left[ {\left( {{{ - Z} \mathord{\left/ {\vphantom {{ - Z} H}} \right. \kern-0em} H}} \right)} \right]{\text{,}}$

что соответствует давлению ${{P}_{g}} = {\text{\;}}{{{{\beta }_{{{\text{*}}0{\text{\;}}}}}{{\rho }_{g}}} \mathord{\left/ {\vphantom {{{{\beta }_{{{\text{*}}0{\text{\;}}}}}{{\rho }_{g}}} 2}} \right. \kern-0em} 2}.$ Пусть в начальный момент сумма газового и магнитного давления не меняется по пространству (есть баланс давлений)

(13)

${{\left. {P\left( {x,z} \right)} \right|}_{{t = 0}}} = ~{{P}_{g}}\left( Z \right) - \frac{{{{{\left. {B{{{\left( {x,~z} \right)}}^{2}}} \right|}}_{{t = 0}}}}}{2}~.$

Используя (5), имеем для плотности

(14)

${{\left. {\rho \left( {x,z} \right)} \right|}_{{t = 0}}} = 2~\frac{{{{{\left. {P\left( {x,z} \right)} \right|}}_{{t = 0}}}}}{{{{\beta }_{{*0~}}}}}.$

Постановка задачи не содержит никаких предположений о свойствах решения. Таким образом, моделирование у нас прямое: ставятся лишь начальные условия. Заметим, что впервые прямое моделирование для системы (4–7) было проведено в пионерской работе Брушлинского и Морозова [1974], рассматривающей движение в плазменных каналах.

Магнитное поле мы считаем простирающимся по горизонтали далеко за пределы расчетной области. Поэтому на боковых границах в качестве граничного условия потребуем обращения в нуль его производной по x. В вертикальном направлении все происходящее разворачивается глубоко внутри счетной области, поэтому на задании граничных условий для верхней и нижней ее границ мы останавливаться здесь не будем.

При выбранном значении ${{T}_{{\text{*}}}}$ = 50 000 К в обоих рассматриваемых слоях ${{\theta }_{*}} = 1.2 \times {{10}^{{ - 8}}}.$ В слое Π^I значение $\xi = {{\xi }^{{\text{I}}}} = 5 \times {{10}^{{ - 6}}},$ ${{\kappa }_{*}} = \kappa _{*}^{{\text{I}}} = 3.8 \times {{10}^{{ - 4}}}.$ Параметр ξ можно рассматривать как мерило разреженности среды. Для Π^II пусть $\xi = {{\xi }^{{{\text{II}}}}} = 400{{\xi }^{{\text{I}}}}$ (что соответствует высоте ~15 000 км). Согласно соотношению (8) и (Приложению: п3), $\kappa _{*}^{{{\text{II}}}}$ = $ = \kappa _{*}^{{\text{I}}}{{\left( {{{{{\xi }^{{{\text{II}}}}}} \mathord{\left/ {\vphantom {{{{\xi }^{{{\text{II}}}}}} {{{\xi }^{{\text{I}}}}}}} \right. \kern-0em} {{{\xi }^{{\text{I}}}}}}} \right)}^{2}}.$

2.3. Численный метод

Решение задачи проводится численным конечно-разностным консервативным методом, который был специально разработан для солнечной плазмы С.П. Кшевецким и воплощен в программе PLASMAT [Кшевецкий, 2013]. Формулы численного интегрирования по своей структуре напоминают формулы метода Лакса–Вендроффа, но на первом полушаге применяются неявные аппроксимации. Метод аппроксимирует уравнения со вторым порядком точности по времени и пространству. Для аппроксимации пространственных производных используются центральные разности, поэтому схема не обладает численной вязкостью (аналогично LeVeque [1992], Thomas and Roe [1993]). Особенностью метода является его способность строить обобщенные негладкие решения, что особенно важно в тех случаях, когда решение со временем теряет гладкость. Этим открывается возможность сравнительно долго отслеживать ход совместной эволюции плазмы и магнитного поля, начиная от гладких распределений физических величин вначале вплоть до состояния, когда под влиянием нелинейных процессов проявляют себя и действуют резкие неоднородности (фронты, мелкомасштабная турбулентность и т.п.) Метод универсален, первоначально он был развит и продолжает развиваться также в связи с задачами динамики земной атмосферы [Кшевецкий, 2006; Gavrilov and Kshevetskii, 2014; Gavrilov et al., 2015]. Компьютерная программа PLASMAT, применяемая для выполнения расчетов, существенно использует параллельные вычисления [Воеводин и др. 2012].

3. РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ

3.1. Общий обзор

Проведенный численный эксперимент относится к ситуации, когда при значении ${{\beta }_{{*0}}} = 7.5$ разнополярные магнитные области находятся рядом на одной высоте. Согласно выражениям (2, 3), размерная единица скорости и размерная единица времени составляют при этом, соответственно, ${{{v}}_{{*0}}} = 10.5$ км/с и ${{t}_{{*0}}}$ = 2.2 мин. Моделирование отражает ∼4.4–5.3 мин эволюции областей. Далее при описании результатов безразмерное время t будет предcтавлено величиной τ ≡ t/0.008, так что за эволюцией областей мы следим вплоть до значений τ $\sim $ 250–300. Решения получены для начальных конфигураций (10), имеющих вертикальную протяженность ${{z}_{k}} = 0.34$ и резкость b ≡ αq, где

(15)

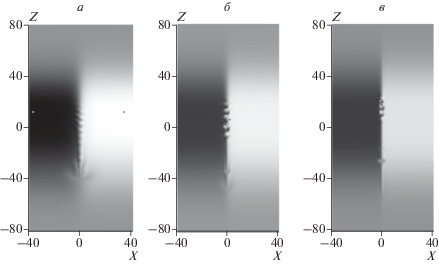
$q = 130;\,\,\,\,\alpha = \frac{1}{2},~\,\,\,\,\frac{1}{{1.5}},\,\,\,\,1,\,\,\,\,1.5,\,\,\,\,2,$

так что расстояние между разнополярными областями уменьшается с ростом α (рис. 1).

Рис. 1.

Полутоновые карты распределения начального магнитного поля ${{\left. {\mathbf{B}} \right|}_{{\tau = 0}}}$ в перпендикулярной вектору плоскости при α = 1/2 (а), α = 1 (б), α = 2 (в). Светлые (темные) тона соответствуют B > 0 (B < 0), интенсивность цвета отражает величину |B|; изображение растянуто в 4.4 раза в направлении от темной области к светлой. На каждой карте верхнего ряда тонкими светлыми линиями нанесены контуры уровней ±1, ±0.8, ±0.6, ±0.4, ±0.2, 0 величины B (в принятой двумерной геометрии они же одновременно являются линиями электрического тока), толстые черные линии ограничивают область, воспроизведенную на соответствующей нижней карте. На картах нижнего ряда яркая белая точка отмечает местоположение минимума величины, яркая черная – максимума. (Все далее используемые карты аналогичны нижним).

Поскольку у двумерного магнитного поля линии уровня совпадают с линиями электрического тока, по рис. 1 можно также судить о пространственном распределении тока в момент τ = 0. Исходный контактный ТС простирается на расстояние ${{z}_{k}}$ вдоль вертикальной оси симметрии $X = 0$ расчетной области. Плазма по бокам ТС имеет меньшую плотность, чем в области ТС, так как магнитное давление в начальный момент сбалансированно с газовым, согласно соотношению (13). В эксперименте мы видим, что в начале совместной эволюции состояния плазмы и магнитного поля область ТС уходит вниз по отношению к всплывающей периферии магнитной конфигурации.

В дальнейшем ход эволюции принимает более сложный характер, и он сложнее, чем тот, что предписан поставленной математической задачей Коши. Так, например, уравнения и условия нашей задачи (4−7, 10−11, 13−14) имеют определенную симметрию по отношению к центральной оси $X = 0,$ и таким же свойством симметрии должно обладать ее точное решение. Однако решение задачи, полученное путем численного моделирования, со временем приобретает асимметричные черты. Это связано с присутствием посторонних по отношению к задаче Коши внешних воздействий – сеточных возмущений. Они, нарастая со временем (но еще оставаясь малыми – напомним, что используемая нами программа позволяет длительно следить за процессом), провоцируют развитие физических неустойчивостей, свойственных данной магнитной конфигурации. Таким образом, смоделированное решение оказывается более содержательным с физической точки зрения, потому что и в реальности процесс, соответствующий точному решению задачи Коши, подвергаясь возмущениям, проявляется вместе со своими неустойчивостями. Исследуемая магнитная конфигурация (рис. 1) аналогична лабораторному (плоскому) Z-пинчу, и ей свойственны пинчевые неустойчивости: перетяжечная и изгибная. Последняя, являясь асимметричной по отношению к оси $X = 0,$ при своем развитии вносит асимметрию в результат численного моделирования.

Как известно, движение плазмы в основном обусловлено перетяжечной неустойчивостью, поскольку она сгущает силовые линии, увеличивая локальный градиент магнитного давления [Спитцер, 1965].

Развитие перетяжечной неустойчивости в астрофизических условиях имеет свою специфику: действие неустойчивости оказывается более сложным, чем обычное формирование локального сужения (перетяжки) или их последовательности, придающей области тока вид сцепленных сосисок (из-за чего неустойчивость нередко называют “сосисочной”). Усложнение связано с отсутствием электродов, которыми в лабораториях ограничена длина тока. Свободный выброс природной плазмы по линии ТС из области первичной перетяжки за пределы магнитной конфигурации создает падение газового давления (по закону Бернулли), заставляя магнитные поля сближаться вдоль всей длины ТС, даже если в начальный момент магнитное давление всюду было сбалансировано с газовым. Какие формы при этом последовательно будет принимать контактная зона между магнитными областями, определяется видом начальной конфигурации магнитного поля, его величиной и параметрами плазмы. Так, известно, что при параметрах моделирования, использованных в работах [Алексеева и Кшевецкий, 2011; Alekseeva and Kshevetskii, 2015], перетяжечная неустойчивость горизонтального контактного ТС конечной ширины через созданное ею скоростное поле преобразует сначала этот ТС в правильный ТТС, а затем сама же, взаимодействуя с этим скоростным полем, разрушает получившийся ТТС, превращая его в сложную крестообразную фигуру, которая остается симметричной вплоть до времени первых проявлений изгибной неустойчивости.

В настоящем численном эксперименте с вертикальным контактным ТС мы также наблюдали сначала развитие скоростного поля и уже затем появление изгибной неустойчивости. Изгибная неустойчивость имела возможность спокойного регулярного развития, порождая четкие эволюционирующие транзиентные структуры. Это легко понять: при выбранных параметрах эксперимента (протяженности тока ${{z}_{k}} = 0.34,$ большей по сравнению с ${{z}_{k}} = 0.17$ в указанных выше работах) первичной перетяжке труднее выбрасывать плазму из конфигурации, и перетяжечная неустойчивость развивается не так интенсивно.

Казалось бы, перетяжечной неустойчивости в условиях ослабленного выброса плазмы труднее сформировать однородный вертикальный ТТС, тем более, что плотность плазмы теперь меняется вдоль исходного ТС еще и из-за учитываемой силы тяжести. К тому же значение ${{\beta }_{{*0}}}$ здесь больше, чем в названных выше работах, что уменьшает роль магнитного поля и его неустойчивостей в изменении начального состояния поля и плазмы.

Однако такие ожидания оправдались лишь при моделировании слоя Π^I. У верхней границы хромосферы, в слое Π^II, напротив, формирование ТТС ярко проявило себя. Сравнив результаты моделирования в обоих слоях, мы выявим физическую причину распространенности ТТС на границе с короной.

3.2. Совместная эволюция поля и плазмы в (нижнем) слое Π^I

Заметим сразу, что в слое Π^I влияния эффекта Холла на поведение рассматриваемых конфигураций нет. Об этом свидетельствует сравнение результатов численного эксперимента с ξ и эксперимента, где ξ искусственно принято за нуль.

На временнóм промежутке наблюдения магнитная конфигурация существует как постепенно развивающаяся транзиентная структура. Для нее характерна направленная вниз “стрелка” в области попадания плазмы, текущей вдоль зоны ТС, в нижележащую неподвижную среду; позже к этому добавляется еще одна характерная черта – “насечка” на ТС, обусловленная спокойным развитием изгибной неустойчивости (рис. 2).

Рис. 2.

Магнитное поле B в слое Π^I в некоторый момент τ типичной стадии его эволюции в зависимости от начальной резкости α поля: α = 1/2 и τ = 259 (а); α = 1 и τ = 202 (б); α = 2 и τ = 163 (в).

Проявленность других черт транзиентной структуры монотонно зависит от величины α. Представление об этой вариативности дает сопоставление двух крайних случаев α = 1/2 и α = 2. В случае α = 1/2 наибольшей отдаленности магнитных областей появлению изгибной неустойчивости (“насечки”) предшествовали лишь слабые признаки развития перетяжечной неустойчивости в природной плазме: образования однородного ТТС не происходит (рис. 3а); разнонаправленная пара потоков вдоль ТС практически не проявляет себя, положение экстремумов продольной скорости указывает лишь на ускорение потока тонущей плазмы по мере своего движения вниз (рис. 3б, в).

Рис. 3.

Решение в слое Π^I при α = 1/2. Карты в момент τ = 201 для магнитного поля B (а) и вертикальной компоненты ${{{v}}_{z}}$ скорости (б); экстремальные по расчетной области значения ${{V}_{z}}$ скорости ${{{v}}_{z}}$ как функции времени τ: максимум (абсолютная величина минимума) – сплошная (точечная) кривая; жирная штрихпунктирная вертикаль – время визуального проявления изгибной неустойчивости на картах; горизонтальный отрезок толстой сплошной кривой отмечает время, когда наиболее интенсивное нисходящее движение плазмы приходится на головную часть направленного вниз потока (в).

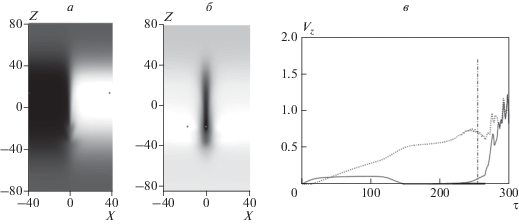
При α = 2 еще до проявления изгибной неустойчивости контактная зона, трансформируясь, стала настолько узкой, что на интервале τ = = 104–138 имела вид правильного ТТС с близко стоящими экстремумами B (рис. 4а). Появление ТТС, единственное при рассматриваемом наборе (15), связано с уже знакомым нам действием перетяжечной неустойчивости: она наиболее интенсивна при α = 2 из-за изначально тесного расположения магнитных областей – иначе говоря, из-за меньшего локального значения β возле вертикальной оси. Об этом говорят два параллельных току разнонаправленных потока плазмы, характерных для первичной перетяжки, которые мы видим на карте ${{{v}}_{z}}$ (рис. 4б) (хотя все же нисходящий поток развит сильнее, что связано с выпадением вниз более плотной плазмы, см. также рис. 4в).

Рис. 4.

Решение в слое Π^I при α = 2. Вид магнитного поля B во временнóм диапазоне τ = 104–138 (а); вертикальная компонента ${{{v}}_{z}}$ скорости при τ = 104 (б); экстремальные по расчетной области значения ${{V}_{z}}$ скорости ${{{v}}_{z}}$ как функции времени τ: максимум (абсолютная величина минимума) – сплошная (точечная) кривая; тонкая вертикальная точечная (штрихпунктирная) линия отмечает время возникновения (начало разрушения) ТТС; жирная штрихпунктирная вертикальная линия – время визуального проявления изгибной неустойчивости на картах; жирный горизонтальный штриховой отрезок показывает временнóй интервал существования “хобота” вне пределов конфигурации (в).

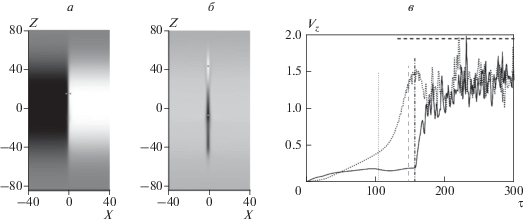
В заключение раздела сделаем замечание общего характера. Поскольку плазма в начальный момент была неподвижна, изменения величин экстремальных по расчетной области значений ${{V}_{z}}$ скорости ${{{v}}_{z}}$ позволяют удобным образом отслеживать временнóй ход превращения энергии магнитного поля в энергию вертикального движения плазмы. По виду графиков легко понять, в какой мере отличаются результаты численного эксперимента при разных значениях параметров. Зависимость экстремумов ${{V}_{z}}$ от времени показана на рис. 3в, 4в и им аналогичных ниже. На них дополнительно выделено еще несколько важных моментов. Если изменения конфигурации приводит к образованию ТТС, то тонкими вертикалями отмечается время его возникновения (сплошная линия) и время начала его разрушения (штрихпунктирная линия). За последнее принято время, когда в магнитной конфигурации с данным α на фоне правильного ТТС начинает проявлять себя изгибная неустойчивость; оно определялось как момент, когда максимум (минимум) магнитного поля оказывался при Х < 0 (Х > 0); проверка проводилась на каждом вычислительном шаге. Жирная штрихпунктирная вертикаль показывает время визуального возникновения изгибной неустойчивости (когда неустойчивость уже развита настолько, что становится заметной как “нарезка” на полутоновой карте магнитного поля). Практически в это же время “нарезка” появляется и на карте величины продольной скорости. Потом центральная часть конфигурации теряет свой правильный вид под влиянием мелкомасштабных флуктуаций, однако в целом пограничная зона между двумя магнитными областями продолжает выглядеть, как постепенно эволюционирующая транзиентная структура. Отметим здесь кратко внешние ее черты без уточнения, при каких α и в каком слое, Π^I или Π^II, они проявляются. “Стрелка” под ТС (вида изображенной на рис. 2) в ряде случаев превращается в удлиняющийся “хобот”; время, когда самая нижняя точка потока-хобота находится вне магнитной конфигурации, представлено толстым горизонтальным пунктирным отрезком – как на рис. 4в. (Заметим, что в какой-то области “хобота” иногда неясно проступают черты неразвитой крестообразной фигуры, описанной в работах [Алексеева и Кшевецкий, 2011; Alekseeva and Kshevetskii, 2015], которая в полной мере проявляется на горизонтальном токе при меньших характерных ${{\beta }_{{*0}}}$). Горизонтальным отрезком толстой сплошной кривой, как на рис. 3в, показано время, когда наиболее интенсивное движение плазмы приходится на головную часть направленного вниз потока.

3.3. Совместная эволюция поля и плазмы в (верхнем) слое Π^II

Эволюция начального контактного тока в разреженной плазме слоя Π^II качественно отличается от его эволюции в слое Π^I: здесь при всех рассмотренных значениях резкости α формируется однородный ТТС. Внешне он подобен тому, какой в слое Π^I мы наблюдали лишь в случае α = 2 (рис. 4а). Чем больше α, тем ближе к моменту τ = 0 появляется тонкий токовый слой и тем дольше, вообще говоря, он существует (рис. 5).

Рис. 5.

Время появления тонкого токового слоя (нижняя кривая) и время появления первых признаков прекращения его существования из-за появления изгибной неустойчивости (верхняя кривая) в зависимости от α.

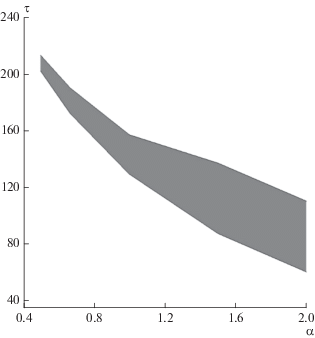
Верхняя кривая рисунка показывает время разрушения этого правильного ТТС под действием изгибной неустойчивости. Изгибная и перетяжечная неустойчивости (а последняя из них, как говорилось, сама способна создавать ТТС) обе свойственны Z-пинчу, при этом каждая из неустойчивостей по-своему зависит от α и от форм, которые принимает конфигурация с этим α во время своей эволюции. Сложность зависимости от разных обстоятельств, по-видимому, вносит вклад в некоторую изломанность верхней кривой. Однако вычленение закономерностей развития изгибной неустойчивости ради детального описания ее роли в разрушении ТТС выходит за рамки настоящей работы, поскольку для нас здесь важно образование самого ТТС. Поэтому далее обсуждать верхнюю кривую мы не будем.

Плавный ход нижней кривой заставляет думать о существовании в Π^II какой-то одной, общей для всех α, закономерной причины появления ТТС, которой не было в Π^I. Вид кривой наводит также на мысль, что в случае, когда начальный контактный ТС имеет достаточно большую резкость, он не будет меняться в течение какого-то интервала времени. Иначе говоря, поставленные нами начальные условия (10, 11; 13, 14) задачи Коши для уравнений (4–7) в этом предельном случае окажутся соответствующими ее стационарному или близкому ему точному решению.

Характерные транзиентные фигуры в слое Π^II с их удлинившимися “хоботами” (рис. 6) имеют более выразительный вид, чем в слое Π^I (рис. 2), что говорит об активизации динамических процессов в области контактного тока.

Рис. 6.

Магнитное поле B в слое Π^II на начальном этапе развития изгибной неустойчивости при значениях α = 1/2, τ = 250 (а); α = 1, τ = 185 (б); α = 2, τ = 144 (в).

В слое Π^II решительным образом изменяется характер конверсии магнитной энергии в энергию движения плазмы. В противоположность тому, что мы видели в Π^I (рис. 3в, 4в), в Π^II скоростное поле у конфигурации с малой резкостью (рис. 7а) почему-то оказывается более развитым, чем у конфигурации наибольшей резкости α = 2 (рис. 7б).

Рис. 7.

Экстремумы ${{V}_{z}}$ скорости ${{{v}}_{z}}$ в слое Π^II как функции времени при α = 1/2 (а) и α = 2 (б). Максимум (абсолютная величина минимума) – сплошная (точечная) кривая; тонкая вертикальная точечная (штрихпунктирная) линия отмечает время возникновения (начало разрушения) ТТС; жирная штрихпунктирная вертикаль – время визуального проявления изгибной неустойчивости на картах; жирным горизонтальным штриховым (сплошным) отрезком отмечен временнóй интервал существования “хобота” вне пределов конфигурации (интервал, когда наиболее интенсивное нисходящее движение плазмы приходится на головную часть направленного вниз потока).

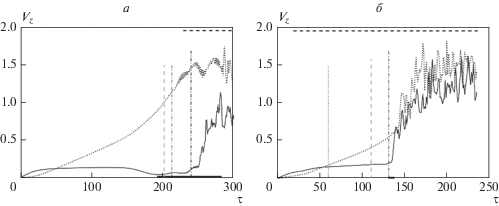
Случай α = 2 особо показателен. Большие значения ${{V}_{z}}$ в Π^I (рис. 4в) физически были обусловлены процессом развития перетяжечной неустойчивости, она же была там причиной формирования ТТС. Уменьшение ${{V}_{z}}$ в Π^II α = 2 говорит о том, что, во-первых, в слое Π^II есть какой-то физический фактор, способный (пусть частично) подавить перетяжечную неустойчивость в случае достаточно резкой конфигурации, а во-вторых, в слое Π^II , по-видимому, есть какой-то специфический (не связанный с перетяжкой) механизм формирования ТТС.

Самостоятельный интерес представляет тот факт, что в слое Π^II нисходящий поток выходит за пределы породившей его магнитной конфигурации, какое-то время имея максимальную величину скорости в головной части – на рис. 7 такие временны́е интервалы соответствуют сразу и штриховому и сплошному жирным горизонтальным отрезкам. Рисунок 7а показывает, что при этом достигается скорость V = 1.5, на рис. 7б мы видим V = 0.5. В размерных единицах, согласно (2), это составляет 15.75 и 5.25 км/с. Встретив на пути вниз какую-либо другую магнитную конфигурацию с горизонтальным электрическим током, такая вертикальная струя окажется потоком, который, по Goodman [2005], способен создавать внутри хромосферы вкрапления областей плазмы с корональными параметрами (см. ВВЕДЕНИЕ).

4. ИНТЕРПРЕТАЦИЯ И ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ. ВЫВОДЫ

Мы видели, что магнитное поле одного и того же вида, поступившее в нижнюю Π^I и верхнюю Π^II часть полностью ионизированной хромосферы, по-разному эволюционирует и по-разному конверсирует свою энергию в энергию плазмы. При этом решаемую задачу Коши (4–7; 10, 11; 13–14) для слоев Π^I и Π^II отличают только увеличенные в случае Π^II значения двух (зависящих от ${{N}_{*}}$) безразмерных констант: параметра холловской динамики ξ и множителя ${{\kappa }_{*}}$ в коэффициенте теплопроводности.

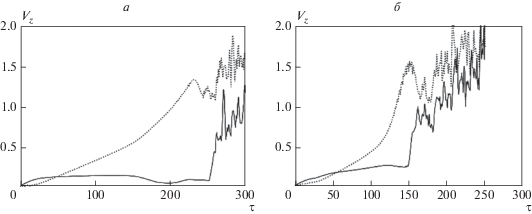
Проведенный нами численный эксперимент для Π^II при искусственно зануленном ξ выделяет влияние одной лишь увеличенной теплопроводности. В его результатах улавливается лишь тенденция изменения внешнего вида транзиентных структур при переходе от Π^I к Π^II. Отличие хода развития скоростного поля от реального заметно при наименьшей резкости магнитного поля (рис. 8а и 7а) и нарастает с ее увеличением, приобретая затем качественный характер (рис. 8б и 7б). Несходство результатов эксперимента при искусственной зануленности ξ с реальностью говорит о том, что эволюция и конверсия магнитного поля в слое Π^II находятся под влиянием эффекта Холла.

Рис. 8.

Временнóй ход величин экстремумов ${{V}_{z}}$ скорости ${{{v}}_{z}}$ в слое Π^II при искусственно отключенном эффекте Холла для α = 1/2 (а) и α = 2 (б). Максимум (абсолютная величина минимума) – сплошная (точечная) кривая; тонкая вертикальная точечная (штрихпунктирная) линия отмечает время возникновения (начало разрушения) ТТС. (Метки для характерных моментов отдельных процессов здесь не нанесены из-за искусственности случая).

Это проливает свет на причину распространенности ТТС в Π^II. В самом деле, известно, что у системы двумерных МГД уравнений типа (4–7) с учетом эффекта Холла и магнитной вязкости есть стационарное решение, отличительной чертой которого является наличие вытянутой области с очень большой плотностью электрического тока вдоль нее. Впервые такие слои концентрированного тока были замечены в устанавливающихся течениях при нахождении численного решения соответствующей задачи с начальными условиями для лабораторных плазменных каналов [Брушлинский и Морозов, 1974] (см. также работы [Брушлинский и Морозов, 1974; Брушлинский и Ратникова, 1995, 1997] и ссылки там). Анализ физической природы явления обнаружил его органическую связь с эффектом Холла [Морозов и Соловьев, 1974; Брушлинский и Морозов, 1974; Алексеева, 1980]. На примере частного случая сравнительно простого течения со специально подобранным соотношением числовых параметров аналитически показано, что за поддержание стационарного концентрированного тока в холловской плазме с магнитной вязкостью отвечает (по крайней мере, в этом случае) внешний фактор, создающий перепад плотности плазмы по линии концентрированного тока – для плазменного канала это разница газового давления на входе и выходе [Alekseeva, 1997, 1999]. Применительно к плазме солнечной хромосферы можно думать, что таким фактором может быть сила тяжести. Действительно, путем разложения в ряд по обратным степеням большого β и в предположении более быстрого изменения величин по горизонтали $x,$ чем по вертикали z, удается аналитически найти стационарное решение полностью самосогласованной системы (4−7), записанной для случая изотермической плазмы и постоянной магнитной вязкости [Алексеева, 2006]. Магнитное поле стационарного решения имеет вид

(16)

$B = \operatorname{th} \left[ {Q\left( {x - {{x}_{0}}} \right)} \right];$

(17)

$Q = \frac{\xi }{{2{\Theta }}}\frac{\partial }{{\partial z}}\left( {\frac{1}{{{{\rho }^{{\left( 0 \right)}}}}}} \right),\,\,\,\,Q \gg 1;$

скорость порядка

(18)

${v}\sim B$

противоположна направлению тока, нарастает книзу и вся сосредоточена в токовой области, так как возвратный поток широко распределен по пространству и скорость его незначительна. Зависимость ${{\rho }^{{\left( 0 \right)}}}\left( z \right),$ обусловленная силой тяжести, оказалась ответственной за существование этого направленного вверх тока резкости $Q \gg 1.$ Поиск решения велся в предположении многократного (в $K \gg 1$ раз) превосходства ξ-члена в правой части уравнения (6) над вторым конвективным членом; для краткости дальше будем называть этот режим (холловским) надконвективным. По получении решения величина $K$ конкретизовала себя как

(19)

$Q\xi \approx K \gg 1,$

что вместе с (17) и определило условия существования стационарного решения при заданных параметрах ξ и ${\Theta }$ плазмы.

С учетом (12), условия (17, 19) для слоев Π^I и Π^II соответственно дают вблизи $Z = 0$

(20)

$~{{Q}^{{\text{I}}}} = 76.08,\,\,\,\,{{K}^{{\text{I}}}} = 3.8 \times {{10}^{{ - 4}}},$

${{Q}^{{{\text{II}}}}} = 30{\kern 1pt} 400,\,\,\,\,{{K}^{{{\text{II}}}}} = 60.8.$

Величины ${{K}^{{\text{I}}}}$ и ${{K}^{{{\text{II}}}}}$ показывают, что при параметрах плазмы нижнего слоя Π^I стационарных концентрированных токовых слоев надконвективной природы не существует, тогда как в плазме верхнего слоя Π^II они есть. По величине ${{Q}^{{{\text{II}}}}}$ видно, что они представляют собою ТТС, но мы так называть их не будем, сохранив название ТТС для описания результатов полученного нами численного моделирования, свободного от перечисленных выше ограничений, наложенных при поиске аналитического решения.

Приведенные свойства аналитически найденного стационарного надконвективного концентрированного тока находят свою параллель в результатах проведенного нами моделирования.

1. Отметим, что начальное магнитное поле (10) численного эксперимента сходно по структуре со стационарным полем (16), но таковым не является, поскольку его характерная резкость q = 130 намного меньше резкости стационарной конфигурации: ${{Q}^{{{\text{II}}}}} \approx 200q.$ Однако стремление к стационарности при увеличении резкости заметно и в том диапазоне (15) резкости начального поля b ≡ αq, с которым мы работали (рис. 5).

2. Чем больше резкость начального условия, тем больше полученное для Π^II численное решение должно быть похожим на стационарное (определенное холловской надконвективностью). Это соображение подтверждается: в начале этого раздела мы отмечали, что с увеличением резкости зависимость развития скоростного поля от эффекта Холла нарастает.

3. В согласии с (20, 21), численное моделирование выявило присутствие ТТС именно в слое Π^II. Для слоя Π^I они не характерны. Лишь в варианте α = 2 проявил себя там ТТС, и он был связан со сравнительно сильным развитием перетяжечной неустойчивости из-за эффективно меньшего β.

4. Однако мы видели, что в слое Π^II перетяжечная неустойчивость при α = 2 не достигает такого развития, о чем свидетельствует меньшая величина продольной скорости (рис. 7б, 4в). Сравнение результатов эксперимента для реальной среды слоя Π^I (рис. 4в) с результатами для искусственно бесхолловской (рис. 8б) и реальной среды слоя Π^II (рис. 7б) показывает, что перетяжка подавлена именно эффектом Холла. Становится ясным физический механизм этого подавления: развитие перетяжек включает в себя продвижение к оси X = 0 “языков” плазмы с вмороженным в нее полем ${\mathbf{B}},$ а влияние вмороженности на изменения (6) магнитного поля в Π^II теперь уменьшено из-за конкурирующего влияния эффекта Холла на переходе к режиму холловской надконвективности.

5. Несмотря на ослабление в Π^II перетяжечной неустойчивости, которая в Π^I создавала ТТС при α = 2, ТТС есть при этом значении α в Π^II , что указывает на частично надконвективную природу ТТС на уровне высоты Π^II.

6. ТТС, которых не было при α ≠ 2 на уровне Π^I и которые появились в слое Π^II, тоже имеют частично надконвективную природу.

Таким образом, результаты проведенного моделирования показывают, что физической причиной разницы эволюции магнитного поля и конверсии его энергии в энергию плазмы в слоях Π^I и Π^II оказывается, пусть и частичная, надконвективность в слое Π^II процесса эволюции магнитного поля (имеющего достаточную резкость пространственного распределения) – когда явление “вмороженности” уступает по значимости холловскому воздействию на магнитное поле, проявляющемуся при наличии перепада плотности плазмы вдоль тока.

Заканчивая исследование, проведем контрольный численный эксперимент, чтобы при наших вычислительных возможностях (характерном q = 130) наглядно продемонстрировать роль надконвективности в создании длительно существующих токовых слоев. Для этого используем соотношения (17, 19) как критерий подобия надконвективных стационарных решений системы. Положив Q = q = 130 и задав некоторое достаточно большое значение $K,$ найдем из этих соотношений параметры $\xi = \xi _{K}^{q}$ и ${\Theta } = {\Theta }_{K}^{q}.$ Можно ожидать, что при этих их значениях решение задачи Коши (4−7; 10, 11; 13, 14) будет мало меняться со временем. Выполнив численный эксперимент, соответствующий $K = 5,$ убеждаемся, что изменения уменьшились, но остаются заметными. Можно проверить полученные нами в ходе работы представления о физической природе долго существующих ТС, попытавшись сделать решение задачи Коши еще менее изменчивым. Очевидно, надо взять значение $\xi ,$ несколько меньшее, чем $\xi = \xi _{5}^{q},$ чтобы вмороженность магнитного поля больше проявила себя. Тогда менее подавленная перетяжечная неустойчивость за некоторый промежуток времени после начала эксперимента успеет нивелировать разницу между скоростными полями (11) и (18), и моделируемая конфигурация, став более похожей на стационарное надконвективное решение (16−18), далее уже не будет изменяться. В варианте, изображенном на рис. 9, значение $\xi = \xi _{5}^{q}$ снижено в 2.5 раза. Мы видим, что ситуация стационарности действительно сохраняется в области ТС до тех пор, пока не приходят возмущения из области, в которой магнитное поле не является медленно меняющимся по Z и критерий подобия (17, 19) не работает.

Рис. 9.

Магнитное поле контрольного численного эксперимента для $\tau = 162$ (a); $\tau = 282$ (б); $\tau = 300$ (в).

Таким образом, возникновение вертикальных тонких токовых слоев в разреженном высотном хромосферном слое Π^II, где сильнее проявлен эффект Холла, физически объясняется тем, что в этом слое недиссипативные изменения магнитного поля в уравнении (6) связаны не только с вмороженностью силовых линий в плазму (через зависимость от скорости плазмы ${\mathbf{v}}$), но еще и с влиянием эффекта Холла (через зависимость от неоднородности распределения плотности плазмы по вертикали).

5. ЗАКЛЮЧЕНИЕ

Результаты численного моделирования нижнего и верхнего слоев полностью ионизированной части солнечной хромосферы указывают на возникновение и (в течение какого-то времени) последующее существование у верхней границы хромосферы очень тонких токовых слои с током, направленным вверх. Они рождаются в контактных зонах между разнополярными магнитными областями и обусловлены эффектом Холла. Поддержание стационарной картины электрического тока при диссипативном воздействии магнитной вязкости обеспечивает сила тяжести, создающая перепад плотности плазмы по высоте. Эти тонкие токовые слои аналогичны концентрированным токам, возникающим в лабораторных плазменных каналах с перепадом давлений между входом и выходом.

Попутно мы установили, что вертикальные зоны контакта разнополярных магнитных областей в полностью ионизированной части хромосферы выбрасывают плазму по вертикали вниз вдоль токового слоя. Уже за пределами магнитной конфигурации эти струи имеют скорость 5.25–15.75 км/с. Встречая на своем пути посторонние магнитные конфигурации с горизонтальным электрическим током, такие потоки вещества должны давать эффект, который был выявлен в работе [Goodman, 2005]. Он заключается в создании посреди толщи хромосферной плазмы вкрапленных областей, где плазма имеет корональные параметры, или, другими словами, приводит к фрагментарному виду солнечной хромосферы, о котором идет речь в работах [Gabriel, 1994; Schrijver, 2001; Aschwanden, 2004].

6. ФИНАНСИРОВАНИЕ РАБОТЫ

Работа выполнялась при поддержке Российского фонда фундаментальных исследований РФФИ грант № 17-05-00574 (примененные численный метод и компьютерная программа являются развитием метода и программы, созданных для моделирования атмосферных процессов, и содержат дополнительные блоки расчета электродинамических полей и токов).

7. БЛАГОДАРНОСТИ

Работа выполнена с использованием оборудования Центра коллективного пользования сверхвысокопроизводительными вычислительными ресурсами Московского государственного университета им. М.В. Ломоносова. Авторы глубоко признательны А.В. Гетлингу за постоянное внимание к работе, обсуждение ее результатов и ценные советы.

Список литературы

− Алексеева Л.М. О физической природе анодного взрыва в плазменном канале // Письма в ЖТФ. Т. 6. Вып. 21. С. 1310−1312. 1980.
− Алексеева Л.М. Эффект Холла как причина появления токовых слоев в астрофизической плазме // Письма в астрон. журн. Т. 32. № 4. С. 307–315. 2006.
− Алексеева Л.М., Кшевецкий С.П. О структурировании солнечной надфотосферной плазмы плоскосимметричным пинч-эффектом // Астрофиз. бюлл. Т. 66. № 1. С. 76–86. 2011.
− Алексеева Л.М., Кшевецкий С.П. Магнитогидродинамическая эволюция плазмы в зоне контакта противоположно направленных магнитных полей и “искусственные объекты” в солнечной атмосфере // Изв. Крымской астрофиз. обс. Т. 109. № 3. С. 155–164. 2013.
− Брагинский C.И. Явления переноса в плазме // Вопросы теории плазмы. В. 1. Ред. М.А. Леонтович. М.: Атомиздат. С. 183−272. 1963.
− Брушлинский К.В., Морозов А.И. Расчет двумерных течений плазмы в каналах // Вопр. теории плазмы. В. 8. Ред. М.А. Леонтович. М.: Атомиздат. С. 88−163. 1974.
− Брушлинский К.В., Ратникова Т.А. Численная модель приэлектродной неустойчивости в каналах плазменных ускорителей // Физика плазмы. Т. 21. № 9. С. 784–790. 1995.
− Брушлинский К.В., Ратникова Т.А. Холловские поправки к расчету течения плазмы в приэлектродных слоях коаксиальных каналов // Физика плазмы. Т. 23. № 2. С. 126–130. 1997.
− Воеводин Вл.В., Жуматий С.А., Соболев С.И., Антонов А.С., Брызгалов П.А., Никитенко Д.А., Стефанов К.С., Воеводин Вад. В. Практика суперкомпьютера “Ломоносов” // Открытые системы. М.: изд. дом “Открытые системы”. № 7. С. 36−39. 2012.
− Зеленый Л.М. Тонкие токовые слои: От работ Гинзбурга – Сыроватского до наших дней // УФН. Т. 186. № 11. С. 1153−1188. 2016.
− Кшевецкий С.П. Исследование разрушения вихря в стратифицированной жидкости // Журн. вычисл. математики. и мат. физики. Т. 46. № 11. С. 2081–2098. 2006.
− Кшевецкий С.П. Математическая программа для моделирования эволюции полностью ионизированной плазмы PLASMAT. Свидетельство о гос. регистрации № 2013618823. 2013.
− Морозов А.И., Соловьев Л.С. Стационарные течения плазмы в магнитном поле // Вопр. теории плазмы. В. 8. Ред. М.А. Леонтович. М.: Атомиздат. С. 3–87. 1974.
− Прист Э.Р. Солнечная магнитогидродинамика. М.: Мир, 592 с. 1985.
− Прист Э., Форбс Т. Магнитное пересоединение. Магнитогидродинамическая теория и приложения. М.: Физматлит, 592 с. 2005.
− Спитцер Л. Физика полностью ионизованного газа. М.: Мир, 212 с. 1965.
− Сыроватский С.И. Магнитная гидродинамика// УФН. Т. 62. С. 247–303. 1957.
− Alekseeva L.M. Generation of magnetic field by acceleration of Hall plasma and some consequences of this process / Proc. XXIII Internat. Conf. on Phenomena in Ionized Gases. Toulouse, France, 17–22 July 1997. V. 2. Ed. Bordage M.C., Gleizes A. Toulouse: University of Paul Sabatier. C. 156–157.
− Alekseeva L.M. Effective gravity due to the Hall effect and quasi-acoustic–gravity waves in accelerated plasma flows // J. Plasma Phys. V. 61. № 5. P. 671–699. 1999.
− Alekseeva L.M., Kshevetskii S.P. Numerical MHD simulation of the coupled evolution of plasma and magnetic field in the solar chromosphere. I. Gradual and impulsive energisation // Solar Phys. V. 290. № 11. P. 3295–3318. 2015.https://doi.org/10.1007/s11207-015-0788-7
− Aschwanden M.J. Physics of the solar corona: An introduction. Berlin: Springer, 842 p. 2004.
− Balescu R. Transport Processes in Plasmas. V. 1. Amsterdam: Elsevier, 350 p. 1988.
− Demoulin P., Klein K.-L. Structuring of the solar plasma by the magnetic field / Transport and energy conversion in the heliosphere. Lecture notes in physics. V. 553. Eds. Rozelot J.P., Klein L., Vial J.-C. Berlin: Springer. P. 1–99. 2000.
− Gabriel A.H. Some problems in understanding the solar corona / IAU Colloq. 144: Solar Coronal Structures. Eds. Rusin V., Heinzel P., Vial J.-C.. Tatranska Lomnica: Slovak Academy of Sciences. P. 1−9. 1994.
− Gavrilov N.M., Kshevetskii S.P. Three-dimensional numerical simulation of nonlinear acoustic-gravity wave propagation from the troposphere to the thermosphere // Earth Planets Space. V. 66. Paper 88. 2014.
− Gavrilov N.M., Kshevetskii S.P., Koval A.V. Verifications of the high-resolution numerical model and polarization relations of atmospheric acoustic-gravity waves // Geosci. Model Dev. V. 8. № 6. P. 1831–1838. 2015.
− Goodman M.L. Self-consistent magnetohydrodynamic modeling of current sheet structure and heating using realistic descriptions of transport processes // Astrophys. J. V. 632. P. 1168–1175. 2005.
− Kshevetskii S.P., Gavrilov N.M. Vertical propagation, breaking and effects of nonlinear gravity waves in the atmosphere // J. Atmos. Solar-Terr. Phys. V. 67. P. 1014–1030. 2005.
− Leake J.E., Lukin V.S., Linton M.G. Magnetic reconnection in a weakly ionized plasma// Phys. Plasmas. V. 20. I. 6. Article id. 061202 12 p. 2013.
− LeVeque R.J. Numerical methods for conservation laws. 2nd edn. Basel: Birkh¨auser, 1992.
− Ni L., Lukin V.S., Murphy N.A., Lin J. Magnetic reconnection in strongly magnetized regions of the low solar chromosphere // Astrophys. J. V. 852. I. 2. Article id. 95. 11 p. 2018.
− Priest E. Magnetohydrodynamics of the Sun. Cambridge: Cambridge University Press, 560 p. 2014.
− Schrijver C.J. The coronae of the Sun and solar-type stars (CD-ROM Directory: contribs/schrijv) / 11th Cambridge Workshop on Cool Stars, Stellar Systems and the Sun. V. CS-223. Eds. Garcia Lopez R.J., Rebolo R., Zapaterio Osorio M.R. San Francisco: Astr. Soc. P. P. 131–144. 2001.
− Syrovatskii S.I. Formation of current sheets in a plasma with a frozen-in strong magnetic field // Soviet Physics JETP. V. 33. № 5. P. 1727–1741. 1971.
− Thomas J.P., Roe P.L. Development of non-dissipative numerical schemes for computational aeroacoustics / AIAA 11th Computational Fluid Dynamics Conference, Technical Papers 2, Orlando, FL, 906. ADS. 1993.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Геомагнетизм и аэрономия

Архивы выпусков Информация о журнале Отправить рукопись в журнал