1. На главную
  2. Электронные версии
  3. Геомагнетизм и аэрономия
  4. T. 59, № 3, 2019

Геомагнетизм и аэрономия, 2019, T. 59, № 3, стр. 284-290

Модель потоков далекого ультрафиолетового излучения Солнца

А. А. Нусинов 1, *, Т. В. Казачевская 1, В. В. Катюшина 1

1 Институт прикладной геофизики им. Е.К. Федорова Росгидромета (ИПГ)
г. Москва, Россия

* E-mail: nusinov@mail.ru

Поступила в редакцию 22.01.2019
После доработки 23.01.2019
Принята к публикации 24.01.2019

Полный текст (PDF)

Аннотация

Развит подход к созданию модели спектра далeкого ультрафиолетового излучения Солнца в области длин волн, ответственной за диссоциацию молекулярного кислорода (115−242 нм). Модель основана на представлении о линейной зависимости потоков в излучения в интервалах шириной 1 нм от интенсивности в линии Лайман-альфа водорода (еe предполагается измерять фотометрами крайнего ультрафиолетового излучения на КА космического сегмента). Для каждого из этих интервалов получены коэффициенты линейной зависимости. Сравнение результатов модельных расчeтов с наблюдениями показалo, что погрешность модели не превышает 1−2%, что достаточно для целей расчeта состояния термосферы.

1. ВВЕДЕНИЕ

Солнечное излучение является наиболее важным фактором формирования верхней атмосферы. Из всего спектра излучения наиболее существенным для образования верхней атмосферы является ультрафиолетовое излучение Солнца. Воздействие излучения на верхнюю атмосферу приводит к ряду фотохимических процессов, прежде всего, диссоциации молекул кислорода. На высотах более ~120 км концентрации атомного и молекулярного кислорода сравниваются, а на высотах ~180 км концентрация атомного кислорода превосходит концентрацию также и молекул азота, и атомный кислород становится основным компонентом верхней атмосферы. Образование атомного кислорода почти всецело обусловлено диссоциацией молекул кислорода под воздействием ультрафиолетового излучения и процессами переноса. Порог диссоциации соответствует длине волны излучения λ = 242 нм [Окабе, 1981]. При длинах волн короче 104 нм происходит ионизация атмосферных газов, (см., например, [Иванов–Холодный и Михайлов, 1980]). Для этого участка спектра возникновением атомов кислорода можно пренебречь. Помимо диссоциации, поглощение в атмосфере далeкого ультрафиолетового излучения Солнца (ДУФ) приводит к ее нагреву (см., например, [Семенов и Шефов, 2005]). Важность учета вариаций потока ДУФ-излучения с уровнем активности при исследовании верхней атмосферы подчеркнута Woods and Lean [2007]: если при переходе от минимума солнечной активности к максимуму изменение температуры на высоте ~10 км составляет ~0.1 K, и ~1 K на 50 км, то на высотах ~500 км, в термосфере, изменения превышают 400 К. Таким образом, для моделирования основных процессов формирования верхней атмосферы требуется знание потоков в области 104−242 нм. В конечном счете, долговременные изменения верхней атмосферы обусловлены вариациями в этом диапазоне.

В последние два десятилетия мониторинг спектра излучения Солнца позволил детально исследовать характер воздействия вариаций излучения на верхнюю атмосферу (см., например, [Ermolli et al., 2013]) и на изменения атмосферного озона (например, [Merkel et al., 2011]).

Актуальным вопросом является проблема “оседания атмосферы”, т.е. существования систематического снижения плотности верхней атмосферы на фиксированных высотах (см., например, [Solomon et al., 2010]. Одним из возможных механизмов такого изменения является уменьшение интенсивности нагрева атмосферы и скорости диссоциации молекулярного кислорода вследствие снижения потока ДУФ. Модель излучения дает возможность проследить многолетние вариации ДУФ по архивным данным о входных параметрах в течение длительного времени, превышающего длительность эпохи спутниковых наблюдений, например, по ионосферным данным [Нусинов, 2004].

Моделирование потоков ДУФ при различных гелиофизических условиях существенно при решении некоторых практических задач, возникающих при разработке космической техники. В частности, необходим учет факторов воздействия, приводящих к деградации различных компонентов космических аппаратов, и определяемых, наряду с потоками ультрафиолетового излучения, например, фотоэлектронами, потоками ионов кислорода О+ и другими заряженными частицами низкой энергии, характеристики которой обусловлены состоянием верхней атмосферы.

Несмотря на актуальность проблемы создания достаточно точной и легко используемой модели ДУФ-излучения, адекватно описывающей как величины потоков излучения, так и их вариации для различных масштабов времени, до сих пор не существует моделей, надежно воспроизводящих потоки излучения в этом диапазоне при разных уровнях солнечной активности. Существует эталонный спектр для минимума активности в 2008 г. [Woods et al., 2009; Chamberlin et al., 2009], предложены методы расчета спектра для длин волн от 200 нм [Lean et al., 1997, 2005; Lean, 2000]. Модели NRLSSI [Lean, 2000] и SATIRE [Ball et al., 2011], в принципе, удовлетворяют изложенным выше требованиям, однако их использование затруднительно, поскольку для этого необходимо одновременное наблюдение солнечных пятен, площадей факельных площадок и Mg-индекса. Кроме того, в публикации [Yeo et al., 2015] отмечено, что модель NRLSSI дает существенно заниженные результаты по сравнению с надежными измерениями на SORCE.

2. ИСХОДНЫЕ ДАННЫЕ

При разработке модели необходимо, чтобы используемые данные удовлетворяли ряду требований. Во-первых, их вариации должны соответствовать наиболее широкому диапазону уровней солнечной активности, от минимального уровня до максимального. Данные должны быть получены одним и тем же прибором в течение цикла солнечной активности или за более длинный период. Однако, при длительных измерениях чувствительность приборов может заметно изменяться вследствие деградации датчиков (см., например, [Woods, 2008; Woods et al., 2018; Schmidtke, 2015]).

В настоящее время накоплен большой объем данных спутниковых наблюдений потоков солнечного излучения в этой области спектра. При этом во многих временны́х рядах сложно отличить долговременные изменения, обусловленные солнечной активностью, от эффектов деградации измерительных средств. Следует отметить, что изменение чувствительности со временем может быть немонотонным, как это наблюдалось, например, в измерениях аппаратурой ВУСС на КА “КОРОНАС-Ф” [Нусинов и др., 2009]. Исключение эффектов деградации возможно путем использования калибровки в полете, сравнивая текущие данные с калибровочными измерениями на ракетах или с эталонными (газоразрядные лампы или звезды) источниками. В последнее время удается исключить эффекты деградации аппаратуры с помощью усовершенствованных методов анализа данных [Woods et al., 2018].

В настоящее время наиболее надежными, охватывающими во времени весь солнечный цикл, являются данные, полученные в рамках проектов SORCE (Solar Radiation and Climate Experiment, 2003 г. по наст. время) и TIMED (Thermosphere, Ionosphere, Mesosphere, Dynamics, and Energetics, 2002 г. по наст. время). Спектральный диапазон SORCE (115−308 нм) полностью включает в себя все длины волн, соответствующие разрабатываемой модели, в то время, как диапазон TIMED (27−190 нм) содержит лишь часть заданного диапазона. Исходя из этого, для разработки модели приняты данные измерений SORCE, а данные TIMED использовались для проверки модели. Следует отметить, что такое использование данных оправдано, поскольку в обоих проектах использовались одни и те же методы калибровки.

3. РЕЗУЛЬТАТЫ АНАЛИЗА ДАННЫХ. МОДЕЛЬ ВАРИАЦИЙ ДУФ

Для анализа использовались среднесуточные данные измерений ДУФ аппаратурой SORCE/SOLSTICE [Sparn et al., 2005] в области 115−242 нм из базы данных LISIRD [Dewolfe et al., 2010]; рассматривались измерения, соответствующие более чем 5500 датам. Интернет-адрес базы данных: http://lasp.colorado.edu/lisird/. Исследовалась зависимость потоков фотонов в различных спектральных интервалах от потока в линии Lα (с длиной волны λ = 121.6 нм) при различных уровнях солнечной активности. Анализ показал, что при всех уровнях активности зависимость для любых длин волн близка к линейной. Примеры результатов анализа представлены на рис. 1 для двух интервалов длин волн: 130−131 нм и 200−201 нм. Из рисунка видно, что отклонения данных измерений от аппроксимирующих прямых невелики и не превышают нескольких процентов. Анализ показал, что аппроксимация с помощью полиномов более высокого порядка не приводит к сколько-нибудь заметному снижению погрешности аппроксимации.

Рис. 1.

Зависимость потоков квантов в интервале 130−131 нм (точки) и 200−201 нм (кружки) от потока в линии Лайман-альфа.

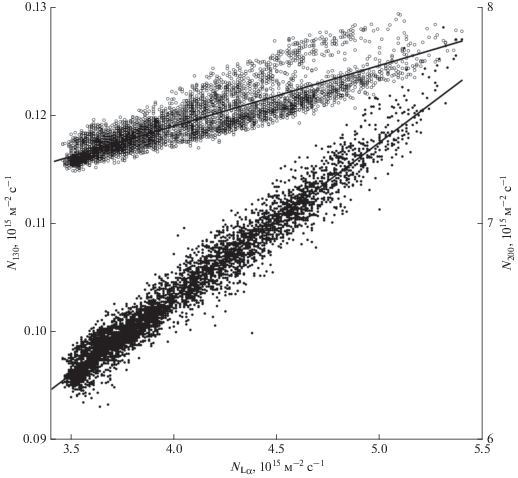
Прямые линии на рисунке соответствуют уравнению линейной регрессии

(1)
${{N}_{\lambda }} = {{10}^{{15}}}\left( {{{В }_{0}} + {{B}_{1}}{{N}_{{{\text{L}}\alpha }}}} \right),$
где Nλ в единицах м−2 с−1, а NLα – поток в лини Лайман-альфа в единицах 1015 м−2 с−1. Из рисунка видно, что отклонения от линий регрессии невелики и не превышают нескольких процентов при любых уровнях солнечной активности. Средняя величина отклонения ε данных измерений от результатов расчета по уравнению может быть оценена исходя из соотношения $\varepsilon = {1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0em} n}$ × × $\sum {\left( {{{\left| {\left( {{{N}_{{\lambda {\text{н }}}}} - {{N}_{{\lambda {\text{р }}}}}} \right)} \right|} \mathord{\left/ {\vphantom {{\left| {\left( {{{N}_{{\lambda {\text{н }}}}} - {{N}_{{\lambda {\text{р }}}}}} \right)} \right|} {{{N}_{{\lambda {\text{н }}}}}}}} \right. \kern-0em} {{{N}_{{\lambda {\text{н }}}}}}}} \right)} ,$ где n – число измерений, индексы “н” и “р” относятся к наблюдаемым и расчетным величинам. Анализ показал, что при использовании линейной регрессии погрешность ε для всех длин волн не превышает 2.1%, а среднее по длинам волн значение ε составляет ~0.8%.

Соотношение (1) вместе с входящими в него коэффициентами B0 и B1 составляет модель излучения. Коэффициенты регрессии определялись с помощью стандартных процедур статистического анализа и приведены в таблице 1 для всех интервалов длин волн λ.

Таблица 1.  

Коэффициенты регрессии модели

λ B0 B1 λ B0 B1 λ B0 B1
115−116 0.004255 0.001804 158−159 0.09262 0.009032 201−202 7.161 0.2759
116−117 0.009489 0.001171 159−160 0.09962 0.007214 202−203 7.16 0.2573
117−118 0.01697 0.008033 160−161 0.1091 0.008942 203−204 8.286 0.3016
118−119 0.0101 0.002357 161−162 0.1301 0.01041 204−205 9.194 0.343
119−120 0.01105 0.005337 162−163 0.1489 0.01266 205−206 9.529 0.3498
120−121 −0.01811 0.02848 163−164 0.1509 0.016 206−207 9.929 0.3641
121−122 0.003353 1.033 164−165 0.1584 0.02288 207−208 11.49 0.438
122−123 0.01356 0.006924 165−166 0.2813 0.02964 208−209 13.61 0.4286
123−124 0.008174 0.004624 166−167 0.2161 0.01449 209−210 20.51 0.4344
124−125 0.00567 0.003473 167−168 0.2168 0.02748 210−211 27.21 0.4651
125−126 0.007356 0.002591 168−169 0.2862 0.01855 211−212 33.28 0.5171
126−127 0.002345 0.00551 169−170 0.3833 0.0237 212−213 31.76 0.5343
127−128 0.006251 0.001672 170−171 0.4352 0.0296 213−214 28.9 0.4755
128−129 0.00537 0.001231 171−172 0.4313 0.03182 214−215 41.62 0.6306
129−130 0.00298 0.002255 172−173 0.4825 0.03339 215−216 33.98 0.6064
130−131 0.04721 0.01398 173−174 0.5088 0.02907 216−217 32.97 0.5731
131−132 0.01054 0.00156 174−175 0.6276 0.03549 217−218 32.2 0.5724
132−133 0.007355 0.001534 175−176 0.7735 0.0432 218−219 46.09 0.7713
133−134 0.00665 0.03015 176−177 0.8578 0.04277 219−220 48.56 0.8446
134−135 0.007007 0.001445 177−178 1.02 0.05821 220−221 48.39 0.8
135−136 0.01813 0.002713 178−179 1.155 0.06216 221−222 34.18 0.6375
136−137 0.01027 0.002021 179−180 1.144 0.0648 222−223 51.04 0.7784
137−138 0.01175 0.002049 180−181 1.401 0.1066 223−224 65.4 0.9615
138−139 0.01237 0.001856 181−182 1.573 0.1521 224−225 60.34 0.8618
139−140 0.001645 0.01301 182−183 1.727 0.09405 225−226 53.19 0.8435
140−141 0.01242 0.008466 183−184 1.856 0.1007 226−227 36.75 0.8083
141−142 0.01757 0.002667 184−185 1.646 0.08043 227−228 37.77 0.71
142−143 0.02024 0.002615 185−186 1.89 0.09092 228−229 54.84 0.8613
143−144 0.0227 0.003154 186−187 2.175 0.1116 229−230 46.99 0.6628
144−145 0.02234 0.003096 187−188 2.479 0.1192 230−231 57.22 0.8497
145−146 0.02411 0.003316 188−189 2.676 0.1255 231−232 49.24 0.7648
146−147 0.02969 0.004195 189−190 2.915 0.1496 232−233 53.23 0.7706
147−148 0.04167 0.004099 190−191 3.175 0.1391 233−234 44.28 0.7208
148−149 0.04137 0.004621 191−192 3.396 0.154 234−235 35.82 0.6185
149−150 0.03641 0.004487 192−193 3.666 0.1667 235−236 58.35 0.8059
150−151 0.04135 0.004978 193−194 2.913 0.1163 236−237 44.66 0.7614
151−152 0.04423 0.005683 194−195 4.689 0.2134 237−238 54.77 0.7777
152−153 0.04858 0.008902 195−196 4.584 0.2048 238−239 37.03 0.6956
153−154 0.05544 0.009558 196−197 5.22 0.2201 239−240 47.02 0.5688
154−155 0.07015 0.02243 197−198 5.308 0.221 240−241 43.47 0.5294
155−156 0.07628 0.01665 198−199 5.415 0.2117 241−242 51.46 0.5559
156−157 0.09533 0.01224 199−200 5.9 0.2353
157−158 0.08871 0.009998 200−201 6.448 0.249

4. ХАРАКТЕРИСТИКИ ВАРИАЦИЙ ДУФ ПО МОДЕЛЬНЫМ РАСЧЕТАМ

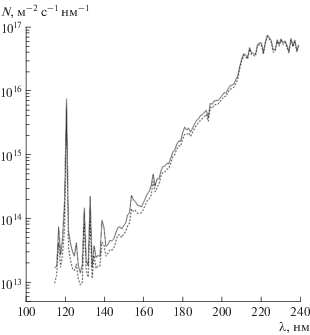
Модель позволяет получить значения потоков излучения во всех участках спектра рассматриваемого интервала 115 ≤ λ ≤ 242 нм. При этом могут быть использованы не только данные текущих измерений входного параметра NLα, но и архивные данные или его модельные оценки по каким-либо другим данным, например по индексу солнечного радиоизлучения F10.7 или по данным о критических частотах слоя Е ионосферы [Нусинов, 2004]. На рисунке 2 приведены модельные спектры, рассчитанные для максимального (сплошная линия) и минимального (штриховая линия) значений NLα, приведенных в базе данных LISIRD за период с 1947 по 2018 гг. (соответственно NLα = 3.31 × 1015 м−2 с−1 в 2018 г. и 7.12 × 1015 м−2 с−1 в 1947 г.).

Рис. 2.

Модельные спектры для экстремальных значений индекса NLα.

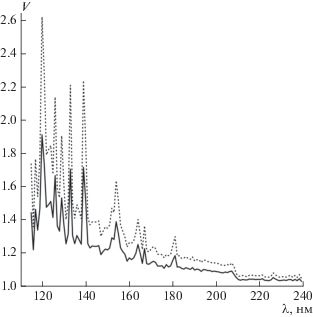
Из рисунка 2 видно, что при переходе от низкой солнечной активности к высокой потоки ДУФ почти не различаются в области спектра λ > 210 нм. Изменения заметно возрастают при переходе к более коротким длинам волн. Можно оценить максимальные значения изменчивости V (отношения потоков излучения для максимального и минимального уровня солнечной активности при заданной длине волны) по архивным данным LISIRD. Результаты модельных расчетов изменчивости потоков ДУФ при различных длинах волн представлены на рис. 3. Пунктирная линия соответствует приведенным выше значениям NLα за 1947−2018 гг. Ввиду инерционности процессов в верхней атмосфере отдельные экстремальные значения, приходящиеся на сравнительно короткие (одни или несколько суток) интервалы времени, вряд ли целесообразно использовать при модельных расчетах или оценках параметров верхней атмосферы. Сплошная линия на рис. 3 соответствует экстремальным величинам временнóго ряда, полученного путем вычисления скользящего среднего за три солнечных оборота (81 сут) суточных значений NLα (соответственно NLα = 3.5 × 1015 м−2 с−1 и 6.1 × 1015 м−2 с−1). Использование такого временнóго интервала типично при оценках состояния ионосферы и верхней атмосферы и приводит к более реалистичным оценкам вариаций. Как видно из рис. 3, интенсивность ДУФ-излучения может в циклах активности изменяться на десятки процентов, но при больших длинах волн изменения становятся незначительными и составляют при λ > 210 нм лишь ~4%.

Рис. 3.

Степень изменчивости спектра ДУФ в зависимости от длины волны. Пунктирная линия – для экстремальных суточных значений, сплошная линия для экстремальных значений NLα, средних за 3 солнечных оборота.

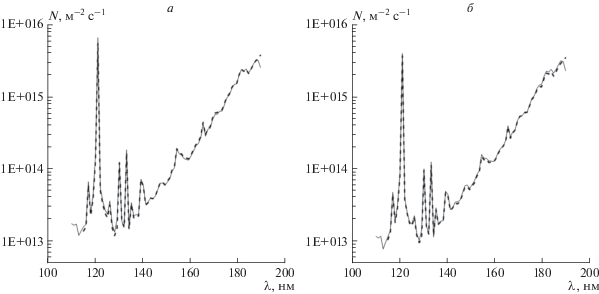
5. ПРОВЕРКА МОДЕЛИ НА ДАННЫХ АППАРАТУРЫ TIMED/SEE

Проверка модели проводилась с использованием данных измерений аппаратурой TIMED/SEE, калибровка которой, а также методы устранения эффектов деградации аналогичны используемым в аппаратуре SORCE/SOLSTICE (см., например, [Woods et al., 2005, 2018]. На рис. 4 приведены результаты сравнения модельных расчетов с измерениями на TIMED для эпох максимума и минимума солнечной активности в 23-м солнечном цикле. Видно, что для всего диапазона длин волн 115−190 нм результаты модельных расчетов практически совпадают с измерениями как при высокой, так и при низкой солнечной активности. Следует отметить, что уровень высокой активности приходится на период, когда измерения на SORCE, по которым разработана модель, еще не проводились. Можно полагать, что модель адекватно описывает изменения спектра ДУФ при любом уровне солнечной активности и в любом солнечном цикле.

Рис. 4.

Сравнение модельных расчетов с данными TIMED/SEE. (а) – вблизи максимума активности 21.02.2002 г.; (б) − вблизи минимума активности 21.02.2009 г. Сплошная линия – данные измерений, штриховая линия – расчет по модели.

6. ЗАКЛЮЧЕНИЕ

Основные результаты работы сводятся к следующему.

1. В итоге сопоставления потоков солнечного далекого ультрафиолетового излучения в спектральной области 115−242 нм, измеренных на космическом аппарате SORCE в течение 23−24-го циклов активности, выявлено, что вариации излучения во всех 1-нм интервалах этой области тесно связано с изменением интенсивности излучения в линии Lα (λ = 121.6 нм). Связь интенсивностей в отдельных интервалах с интенсивностью Lα близка к линейной при любом уровне солнечной активности, отклонения наблюдаемых величин потоков от линейной зависимости в среднем составляют ~1% при любых уровнях солнечной активности 23-го–24-го циклов.

2. Использование этой закономерности сделало возможной разработку модели спектра ДУФ, позволяющую рассчитать спектр в области 115−242 нм для любого уровня солнечной активности с погрешностью ~1−2%. Входным параметром для модели является интенсивность Lα, измерения которой проводятся в течение уже нескольких десятилетий. Использование модели позволяет рассчитать потоки солнечного ДУФ-излучения в 1-нм интервалах для любых уровней солнечной активности, а также и любых периодов времени, используя как данные текущих измерений потока в линии Lα, так и архивные данные. При отсутствии прямых измерений величина потока в этой линии может быть восстановлена с помощью архивных данных о традиционных индексах – числах солнечных пятен W, потока радиоизлучения F10.7 или по данным о критических частотах Е-слоя ионосферы.

7. БЛАГОДАРНОСТИ

Авторы выражают глубокую благодарность коллективу Лаборатории физики атмосферы и космического пространства (LASP) Университета Колорадо за предоставление данных измерений крайнего ультрафиолетового излучения Солнца.

Список литературы

  1. – Иванов-Холодный Г.С., Михайлов А.В. Прогнозирование состояния ионосферы. Л.: Гидрометиздат, 190 с. 1980.

  2. – Нусинов А.А. Ионосфера как природный детектор для исследования долговременных изменений потоков солнечного геоэффективного излучения // Геомагнетизм и аэрономия. Т. 44. № 6. С. 779–786. 2004.

  3. – Нусинов А.А., Казачевская Т.В., Катюшина В.В., Свидский П.М., Гонюх Д.А. Вариации потоков крайнего ультрафиолетового излучения с различными масштабами времени по измерениям на ИСЗ “КОРОНАС” (Эксперимент СУФР-СП-К и ВУСС-Л) / Солнечно-земная физика. Результаты экспериментов на спутнике КОРОНАС-Ф”. М.: Физматлит. …. с. 2009.

  4. – Окабе X. Фотохимия малых молекул. Пер. с англ. М.Д. Козьменко, Н.А. Садовского, ред. М.Г. Кузьмина. М.: Мир, 504 с. 1981.

  5. – Семенов А.И., Шефов Н.Н. Модель вертикального распределения концентрации атомарного кислорода в области мезопаузы и нижней термосферы // Геомагнетизм и аэрономия. Т. 45. № 6. С. 844−855. 2005.

  6. – Ball W.T., Unruh Y.C., Krivova N.A., Solanki S., Harder J.W. Solar irradiance variability: a six-year comparison between SORCE observations and the SATIRE model // Astron. Astrophys. V. 530. № A71. 2011.

  7. – Chamberlin P.C., Woods T.N., Crotser D.A., Eparvier F.G., Hock R.A., Woodraska D.L.-New, Higher Resolution Solar Extreme Ultraviolet (EUV) Irradiance Results for Solar Cycle Minimum Conditions on April 14, 2008 // Geophys. Res. Lett. V. 36. № 5. Cite ID L05102. 2009.

  8. – Dewolfe W.A.,Wilson A., Lindholm D.M., Pankratz C.K., Snow M.A., Woods T.N. Solar Irradiance Data Products at the LASP Interactive Solar IRradiance Data Center (LISIRD) // AGU 2010 GC21B-0881.

  9. – Ermolli I., Matthes K, Dudok de Wit T. et al. Recent variability of the solar spectral irradiance and its impact on climate modelling // Atmospheric Chemistry and Physics. V. 13. № 8. P. 3945−3977. 2013.

  10. – Lean J.L., Rottman G.J., Kyle H.L, Woods T.N., Hickey J.R., Puga L.C. Detection and parameterization of variations in solar mid and near ultraviolet radiation (200 to 400 nm) // J. Geophys. Res. V. 102. P. 29939−29956. 1997.

  11. – Lean J. Evolution of the Sun’s Spectral Irradiance since the Maunder Minimum // Geophys. Res. Lett. V. 27. P. 2425−2428. 2000.

  12. – Lean J., Rottman G., Harder J., Kopp G. SORCE contributions to new understanding of global change and solar variability // Solar Phys. V. 230. № 1. P. 7−53. 2005.

  13. – Merkel A.W., Harder J.W., Marsh D.R., Smith A.K., Fontenla J.M., Woods T.N. The impact of solar spectral irradiance variability on middle atmospheric ozone // Geophys.Res. Lett. V. 38. № 13. P. L13802−L13807. 2011.

  14. – Schmidtke G. Extreme ultraviolet spectral irradiance measurements since 1946 // History of Geo- and Space Sciences. V. 6. № 1. P. 3−22. 2015. https://doi.org/10.5194/hgss-6-3-2015

  15. − Solomon S.C., Woods T.N., Didkovsky L.V., Emmert J.T., Qian L. Anomalously low solar extreme-ultraviolet irradiance and thermospheric density during solar minimum // Geophys. Res. Lett. V. 37. L16103. 2010. https://doi.org/10.1029/ 2010GL044468

  16. – Sparn T.P., Rottman G., Woods T.N., Boyle B.D., Kohnert R., Ryan S., Davis R., Fulton R., Ochs W. The SORCE spacecraft and operations // Solar Phys. V. 230. P. 71–89. 2005.

  17. – Woods T.N., Eparvier F.G., Bailey S.M., Chamberlin P.C., Lean J., Rottman G.J., Solomon S.C., Tobiska W.K., Woodraska D.L. The Solar EUV Experiment (SEE): Mission overview and first results // J. Geophys. Res. V. 110. A01312. 2005. https://doi.org/10.1029/2004JA010765

  18. – Woods T.N., Lean J. Anticipating the next decade of Sun-Earth system variations // EOS, Transactions American Geophysical Union. V. 88. № 44. P. 457−458. 2007.

  19. – Woods T.N. Recent advances in observations and modeling of the solar ultraviolet and X-ray spectral irradiance // Adv. Space Res. V. 42. № 5. P. 895−902. 2008.

  20. – Woods T.N., Chamberlin P.C., Harder J.W., Hock R.A., Snow M., Eparvier F.G., Fontenla J., McClintock W.E., Richard E.C. Solar irradiance reference spectra (SIRS) for the 2008 Whole Heliosphere Interval (WHI) // Geophys. Res. Lett. 36. L01101. 2009. doi 101029/2008GL036373

  21. – Woods T.N., Eparvier F.G., Harder J., Snow M. Decoupling solar variability and instrument trends using the multiple same-irradiance-level (MuSIL) analysis technique // Solar Phys. V. 293. № 5. Id. 76. 21PP. 2018.

  22. – Yeo K.L., Ball W.T., Krivova N.A., Solanki S.K., Unruh Y.C., Morrill J. UV solar irradiance in observations and the NRLSSI and SATIRE-S models // J. Geophys. Res. Space. V. 120. P. 6055–6070. 2015. https://doi.org/10.1002/2015JA021277

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Геомагнетизм и аэрономия

Архивы выпусков Информация о журнале Отправить рукопись в журнал