Физика Земли, 2023, № 5, стр. 101-113
Геоэлектрическая интерпретация данных магнитного мониторинга в юго-западной части Байкала
Д. А. Орехова 1, *, И. В. Попова 1, **, С. М. Коротаев 1, М. С. Кругляков 2, Н. М. Буднев 3, В. Х. Кириаков 1, И. С. Москалев 4
1 Центр геоэлектромагнитных исследований Института физики Земли им. О.Ю. Шмидта РАН (ЦГЭМИ ИФЗ РАН)
г. Москва, Россия
2 University of Otago, Department of Physics
Dunedin, New Zealand
3 Иркутский государственный университет (ИГУ)
г. Иркутск, Россия
4 Институт солнечно-земной физики СО РАН (ИСЗФ СО РАН)
г. Иркутск, Россия
* E-mail: ordaal@gmail.com
** E-mail: popov7376@mail.ru
Поступила в редакцию 22.11.2022
После доработки 24.01.2023
Принята к публикации 07.02.2023
- EDN: VZRQMO
- DOI: 10.31857/S0002333723050083
Аннотация
Длительные градиентные магнитные измерения, которые проводятся в юго-западной части Байкала как сопровождающие эксперимент по глубоководному мониторингу вертикальной компоненты электрического поля, могут быть применены для целей изучения глубинного геоэлектрического разреза. В изучаемой области Байкал не может быть аппроксимирован двумерной моделью. Поэтому нами построена трехмерная геоэлектрическая модель озера и прилегающих территорий по имеющимся геолого-геофизическим данным. Однако этих данных не хватает в той области, где проводятся наши наблюдения. Уточнение верхней части разреза по градиентам магнитного поля на длинных базах осуществлено методом нейросетевой инверсии. Затем, на основании полученной базовой модели, строятся альтернативные модели отражающие известные гипотезы о строении глубинной части разреза Байкальского рифта – мантийный диапир и астеносферный выступ. Для них рассчитываются разности фаз между средним по базе градиентом поля и самим полем в базовой точке, а также разности фаз на концах этой базы как наиболее помехозащищенные градиентные функции. На основе сопоставления экспериментальных и модельных частотных кривых сделан вывод о наибольшей адекватности эксперименту модели мантийного диапира, по крайней мере, в юго-западной части Байкальской рифтовой зоны.
ВВЕДЕНИЕ
Продолжительные наблюдения вариаций магнитного поля и их градиентов на длинных базах были развернуты на суше в районе южной котловины оз. Байкал как дополнительные к данным выполняемого на базе Байкальской глубоководной нейтринной обсерватории длительного эксперимента по мониторингу вертикальной электрической компоненты поля Ez в водной толще для изучения и прогнозирования процессов в сопряженных геосферах [Коротаев и др., 2016; 2022; Korotaev et al., 2018]. Первоначальной целью этих наблюдений было подтверждение отсутствия в Ez теллурической составляющей, а также поиск возможных магнитных предвестников землетрясений. Однако достаточно сильные землетрясения происходят не часто, поэтому была поставлена задача использовать этот длительный мониторинг и для изучения глубинного геоэлектрического разреза. Геоэлектрическое приложение градиентов магнитных вариаций при глубинных исследованиях имеет преимущество над традиционным магнитовариационным профилированием (МВП), основанном на расчете типперов, поскольку на длинных периодах имеется существенная первичная вертикальная компонента поля, предположение об отсутствии которой является основой МВП. В градиентном подходе требуется лишь большая однородность первичного поля по сравнению с вторичным, что в средних широтах практически всегда выполняется. Иначе говоря, в градиентном подходе нарушение условия плоской волны (например, в суточной вариации) значительно менее драматично, чем в МВП.
Целью настоящей работы является получение информации о глубинном геоэлектрическом строении Байкальского рифта по данным длительных наблюдений градиентов магнитных вариаций на длинных, порядка 100 км, базах. Под длительными понимаются наблюдения, позволяющие использовать реализации длиной порядка месяца для достаточно достоверных спектральных оценок до суточного периода, и охватывающие различные сезоны (и годы) для проявления изменчивости поляризации суточной вариации.
СЕТЬ НАБЛЮДЕНИЙ
Сеть наземных наблюдений магнитного поля и его градиентов начала постепенно развертываться в окрестностях места глубоководного мониторинга Ez на Байкальской нейтринной обсерватории, начиная с 2012 г. Первоначальной задачей магнитных наблюдений была проверка предсказанного предварительным моделированием полного отсутствия в Ez теллурической составляющей, а перспективной – поиск магнитных эффектов процессов подготовки землетрясений. Последняя требовала достоверных оценок весьма медленных изменений поля, поэтому использовались абсолютные протонные (модульные) магнитометры. Попытка параллельного использования компонентного феррозондового магнитометра подтвердила правильность этого выбора. Измерение градиентов поля первоначально велось как на коротких (порядка 1 км), так и на длинных (порядка 100 км) базах. Однако опыт показал достаточную достоверность только длиннобазовых измерений. При переходе к задаче изучения геоэлектрического разреза, помимо наблюдений в окрестностях места глубоководного мониторинга, использовались данные низкочастотного индукционного магнитометра LEMI-419 на острове Ольхон (п. Узуры) обсерватории ИСЗФ СО РАН и стандартные данные магнитной обсерватории Иркутск (Патроны). Наконец, в 2021 г. специально для Байкальского эксперимента был разработан высокостабильный феррозондовый трехкомпонентный магнитометр DMC-1, три экземпляра которого были поэтапно установлены в районе исследований.
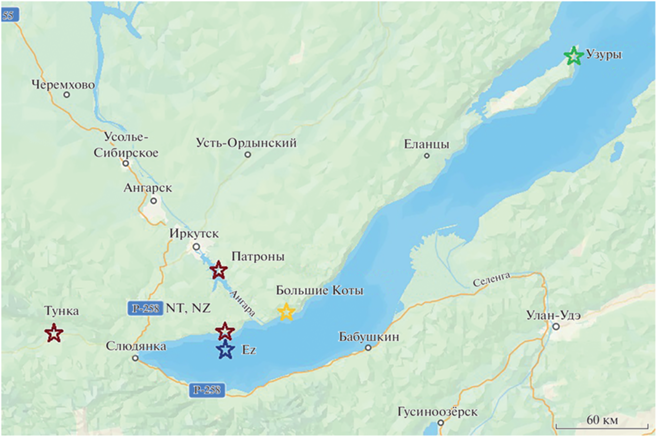
Расположение всех пунктов наблюдений показано на рис. 1. Использовались (необязательно синхронные между собой) данные модульного протонного магнитометра ММП-203 на космофизическом полигоне Долина Тунка (51.81 N, 103.07 E) и ММП-203 на побережье Байкала в районе нейтринной обсерватории (обозначение NT) (51.80 N, 104.42 E), а также трехкомпонентного феррозондового магнитометра DMC-1, установленного там же (обозначение NZ). Компонента Z магнитного поля наиболее чувствительна к геоэлектрическим неоднородностям, к тому же, из-за большого наклонения (73°), Z дает основной вклад в модуль T, поэтому из трех компонент для DMC-1 в расчете градиентов используется именно эта компонента. В качестве опорной синхронной точки наблюдений использовалась магнитная обсерватория Иркутск – Патроны (52.12 N, 104.45 E). Данные этих четырех станций, расположенных в юго-западной части Байкальского рифта, использовались при инверсии. При тестировании результатов моделирования, дополнительно к ним, использовались также данные Z станции Узуры, расположенной в средней части рифта (еще две станции DMC-1 начали работать в конце 2022 г. в пунктах Тунка и Большие Коты, но достаточный объем данных будет накоплен лишь через год). Горизонтальные магнитные компоненты использовались для определения поляризации поля при моделировании. Точка глубоководного мониторинга Ez (51.72° N, 104.42° E, глубина места 1367 м) играет контрольную роль – любая модель при любой поляризации должна удовлетворять экспериментальному факту отсутствия этой составляющей теллурического поля (точнее, теллурическая компонента Ez должна быть меньше экспериментально установленного порога ее обнаружимости: 5% полной горизонтальной компоненты Eτ [Korotaev et al., 2018]. Для всех рассматриваемых далее моделей это условие выполнено.
ОСОБЕННОСТИ ИНТЕРПРЕТАЦИИ
Разумеется, по столь ограниченной области наблюдений (рис. 1) нельзя самостоятельно построить региональную модель. Однако, пользуясь преимуществом большей длительности наблюдений по сравнению с обычными полевыми исследованиями, мы можем поставить задачу выбора между известными конкурирующими гипотезами о глубинном строении Байкальского рифта. Задача выбора из геоэлектрических моделей, отражающих эти гипотезы, модели, в наименьшей степени противоречащей эксперименту, может быть решена по ограниченному набору (длиннопериодных) данных. В работах [Korotaev et al., 2018; Орехова и др., 2017] мы уже ставили задачу оценки возможности выбора между моделями, отражающими эти известные в литературе конкурирующие гипотезы: гипотезой астеносферного выступа [Зорин, 1971; Gao et al., 1994; Логачев, 1999], гипотезой мантийного диапира [Крылов и др., 1981; Pospeev, 2012; Бердичевский и др., 1999] и гипотезой отсутствия того и другого [Грачёв, 1996; Мороз, Мороз, 2012; Мац и др., 2001; Розен и др., 2006; Эпов и др., 2012]. Было обнаружено, что модель астеносферного выступа явно противоречит эксперименту, а модели мантийного диапира и его отсутствия удовлетворительны, но экспериментально неразличимы. В дополнении к нашим предыдущим исследованиям, в которых выводы были сделаны на основе качественного сравнения частотных кривых градиентов магнитного поля, в настоящей работе мы используем количественный подход.
Котловина оз. Байкал находится в центральной части Байкальского рифта, разделяющего докембрийскую Сибирскую платформу и палеозойский Саяно-Байкальский складчатый пояс. Наши точки мониторинга в этом плане находятся в достаточно любопытной области – по разные стороны от шовной зоны и внутри нее. При этом в самой южной части оз. Байкал данная область никак не может быть аппроксимирована двумерной моделью. Поэтому по имеющимся априорным данным нами построена трехмерная региональная модель Байкальского региона в качестве стартовой для базовой геоэлектрической модели.
Расчеты показали, что значительное влияние на результаты расчетов магнитных полей оказывает верхняя часть модельного разреза (до глубины 35 км). В предшествующей работе [Korotaev et al., 2018] рассматривался достаточно обобщенный разрез до этой глубины. Теперь мы используем более детализированный разрез, построенный на основе синтеза опубликованных локальных интерпретаций электромагнитных зондирований в Байкальской рифтовой зоне и других априорных данных. К сожалению, в районе глубоководного мониторинга (юго-западная часть Байкала и прилегающая суша) таких зондирований ранее не проводилось. Поэтому вначале было решено найти параметры этой части модели, наилучшим образом соответствующие экспериментальным данным в районе наших пунктов измерений, с помощью нейросетевой (НС) инверсии. Были выбраны следующие параметры, оказывающие наиболее заметное влияние на функции электропроводности, определяемые по градиентам магнитного поля в районе мониторинга, а именно: удельные сопротивления фундамента под Байкалом и под пунктами измерений, осадочного слоя под Байкалом и наиболее крупных разломов вблизи наших точек. При этом геометрические параметры модели фиксировались.
Как показали численные эксперименты на предварительной модели Байкальского рифта [Орехова и др., 2017], из четырех функций электропроводности, которые можно определить из градиентных магнитных измерений, наиболее эффективны (в смысле отношения сигнал/шум) разность фаз между средним градиентом поля на длинной базе и полем на опорной обсерватории (∆ϕ), и, в несколько меньшей степени, разность фаз на концах этой базы (δϕ). Вопрос помехозащищенности был актуален вследствие заметного индустриального шума во всех полевых пунктах, особенно в районе нейтринной обсерватории.
Для модельного ряда, построенного на базе стартовой модели (без глубинной неоднородности) с вышеупомянутыми варьируемыми удельными сопротивлениями, рассчитывались наиболее помехозащищенные разности фаз Δϕ между разностью комплексных полей в точках мониторинга и в Патронах и полем в Патронах. При этом для каждой реализации (длительностью порядка месяца) на каждом периоде определялся эллипс поляризации. Модельная частотная кривая, соответствующая экспериментальной, рассчитывалась именно для этих эллиптических поляризаций. Для разных реализаций форма обеих кривых может меняться, но степень их близости к экспериментальной кривой не меняется [Korotaev et al., 2018]. Параметры окончательной базовой модели рассчитывались как результат нейросетевой инверсии на основе сопоставления экспериментальных и модельных частотных кривых в диапазоне периодов от 5.6 минуты до суток. Затем на основании этой базисной модели строились альтернативные модели, включающие мантийный диапир либо астеносферный выступ.
ОПИСАНИЕ БАЗОВОЙ МОДЕЛИ
Глубинные электромагнитные зондирования в окрестностях Байкальской рифтовой зоны начали проводиться с 1960-х годов. Однако основную информацию для уточнения верхней части разреза дали геофизические работы, проведенные за последние десятилетия в средней части Байкала [Глинский и др., 1989; Морозова и др., 1998; Мороз, Мороз, 2012; Семинский и др., 2012; Эпов и др., 2012; Поспеева и др., 2012; 2017; Терешкин, 2018; Шкиря и др., 2018]. Здесь рифтовая зона может быть аппроксимирована двумерной моделью. По результатам этих работ (МТЗ, ЗСБ) различными коллективами авторов были построены геоэлектрические профили, проходящие через акваторию Байкала и дальше в Прибайкалье и Забайкалье.
Литосфера в области байкальского рифта имеет блоковую структуру, и эти системы блоков по большей части вытянуты вдоль акватории оз. Байкал. Это дает основание для продления геоэлектрических структур, выделенных по данным исследований по профилям. Такие геоэлектрические профили, построенные различными коллективами, проходят вкрест простирания основных геологических структур, однако, как отмечено в этих работах, геоэлектрические блоки земной коры отличаются не только по химическому составу, но и по интенсивности проявления рифтогенных процессов. Таким образом, для преобразования этих двумерных разрезов в трехмерную модель Байкальской рифтовой зоны и окрестностей нами использовались как геологические карты, так и тектонические.
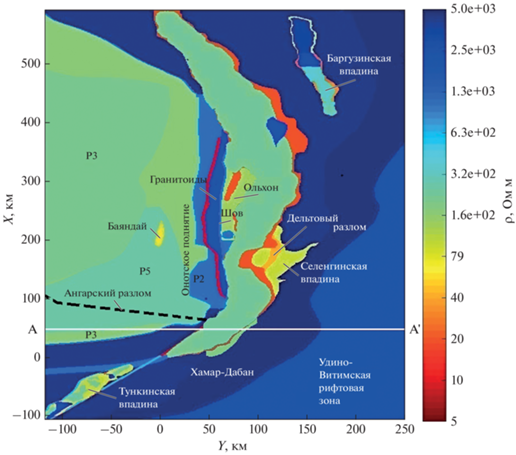
Итоговая базовая модель, показанная в плане на уровне земной поверхности на рис 2, включает в себя построенную по батиметрическим данным котловину оз. Байкал с удельным сопротивлением воды 200 Ом м и глубинами до 1640 м, а также осадочным обрамлением с мощностью до 4000 м [Мац и др., 2001], разбитым на три слоя. Разрез модели, соответствующий Сибирской платформе (за исключением Шарыжалгайского выступа, где на поверхность выходят архейские породы), содержит детализированный осадочный слой мощностью 2 км. Верхняя часть разреза включает сеть крупных разломов [Лунина и др., 2012], проходящих близ наших точек измерения, а также две кайнозойские долины: Тункинскую и Баргузинскую. Глубина заложения разломов 10 км, ширина, исходя из горизонтального шага сети в моделях: 3 км для береговых разломов, 7 км для Ангарского разлома. Удельное сопротивления фундамента под Байкалом у разных авторов оценивается по-разному (от 100 до 5000 Ом м), поэтому этот параметр включен в решение обратной задачи нейросетевым методом. Глубинная часть разреза содержит три проводящих слоя: 10–20/35, 35–50 и 170–230 км [Мороз, Мороз, 2012].
Рис. 2.
Горизонтальное сечение на уровне поверхности Земли, общее для всех моделей. AA' − вертикальное сечение моделей через район мониторинга, показанное на рис. 3.
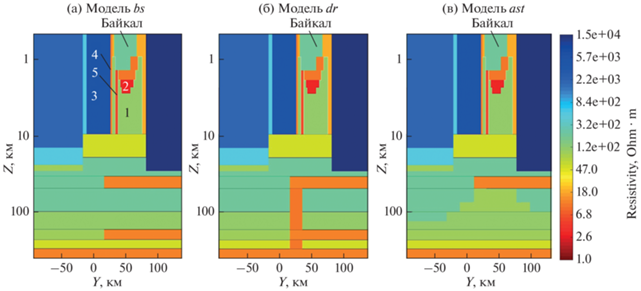
Альтернативы этой базовой модели (bs) включают в себя мантийный диапир (модель dr), то есть астеносферный слой, отделенный от основной астеносферы слоем “нормальной” мантии и соединенный с ней субвертикальным каналом, приуроченным к зоне сочленения Сибирской платформы и Байкальской складчатой области, или подъем астеносферного слоя под рифтовой зоной (модель аst). Вертикальные разрезы базовой модели и этих ее двух альтернатив представлены на рис. 3. Распределение удельных сопротивлений на земной поверхности является общим для всех моделей до глубин 35 км и является результатом решения обратной задачи, рассматриваемой ниже.
Рис. 3.
Вертикальные разрезы: (а) – базовой модели bs; (б) – модели с мантийным диапиром dr; (в) – модели с астеносферным выступом ast. Варьируемые параметры: 1 – фундамент под Байкалом; 2 – нижний осадочный слой под Байкалом; 3 – фундамент под районом мониторинга; 4 – береговой разлом (“предполагаемый” разлом по работе [Лунина и др., 2012]); 5 – Южно-Байкальский разлом, а также Ангарский разлом, показанный на рис. 2.
НЕЙРОСЕТЕВОЕ РЕШЕНИЕ ОБРАТНОЙ ЗАДАЧИ
В геоэлектрике успешно развиваются традиционные подходы к решению многомерной обратной задачи МТЗ [Mackie, Madden, 1993; Zhdanov, Tartaras, 2002]. Эти методы оправдывают себя, как правило, при низком уровне помех в данных и наличии достаточной априорной информации, а также требуют больших вычислительных мощностей. Однако они оказываются малоэффективными в условиях неполноты, разнородности и зашумленности данных, а также при необходимости обработки больших объемов данных многократно (например, в режиме мониторинга).
Во многих задачах геофизики в настоящее время успешно используются нейросетевые методы. В том числе нейронные сети успешно применяются для решения обратных задач, так как способны преодолевать ограничения, связанные с разнородностью, зашумленностью, неполнотой и большим объемом данных, например, в задачах оценки параметров двумерных [Шимилевич, Оборнев, 1999] и трехмерных геоэлектрических структур [Spichak, Popova, 2000]. Успешное использование нейронных сетей было также продемонстрировано при решении обратной задачи геоэлектрики с целью изучения разломной тектоники и других проводящих структур Кольского полуострова [Велихов и др., 2011; Григорьев и др., 2013].
Нейросетевой метод, основанный на алгоритме обратного распространения ошибки (МОРО) [Rumelhart et al., 1988], обычно используется в задачах аппроксимации функции. Такой подход предполагает наличие обучающей выборки и среди других НС методов относится к варианту “обучения с учителем”. Архитектура нейронной сети, на которой осуществляется реализация данного алгоритма, представляет собой, как правило, трехслойную сеть, состоящую из нейронов входного слоя, связанных с нейронами промежуточного слоя. Нейроны промежуточного слоя в свою очередь соединены с нейронами выходного слоя посредством связей, которым приписываются весовые коэффициенты. Для описанной выше архитектуры сети обучающая выборка состоит из пар векторов. Каждая пара включает входной и выходной векторы.
В нашем случае обучающая выборка была сформирована на основе стартовой базовой трехмерной геоэлектрической модели, описанной в предыдущем разделе, построенной с учетом имеющихся геофизических данных. Она включает в себя всю акваторию оз. Байкал с осадочным обрамлением, край Сибирской платформы, Саяно-Байкальский складчатый пояс и Тункинскую долину. Предложенная классобразующая структура описывается следующими шестью параметрами: удельными сопротивлениями фундамента под Байкалом, нижнего осадочного слоя под Байкалом, фундамента под точкой измерений на берегу, разлома под районом мониторинга на берегу, Южно-Байкальского разлома под Байкалом, идущего вдоль этого берега, и разлома близ обсерватории Патроны (Ангарского разлома). Для каждого из шести параметров был также определен дискретный набор значений (см. табл. 1) для расчета моделей, на которых затем обучалась нейронная сеть.
Таблица 1.
Значения параметров моделей, выбранных для создания обучающей выборки
| Элементы структуры | Ro min | Ro max | Ro доп |
|---|---|---|---|
| 1. Фундамент под Байкалом | 100 | 5000 | |
| 2. Нижний осадочный слой под Байкалом | 0.5 | 6 | |
| 3. Фундамент под районом мониторинга на берегу | 500 | 5000 | |
| 4. Береговой разлом | 1 | 10 | |
| 5. Южно-Байкальский разлом | 1 | 1000 | |
| 6. Ангарский разлом | 1 | 500 | 10 |
Модельные расчеты полей велись с использованием суперкомпьютеров МСЦ РАН по программе, реализующей метод интегральных уравнений [Kruglyakov, Kuvshinov, 2018]. При расчетах использовалась следующая сетка: по горизонтали в обоих направлениях 1000 м, по вертикали от 500 м для верхних 4 км и далее шаг увеличивался вплоть до 100 км в нижней части модели. При такой сетке каждая модель содержит более 6 млн. ячеек. Размеры наших моделей составили 400 км по вертикали, 306 км на 700 км по горизонтали. Для этих моделей рассчитывалась градиентная функция Δϕ – разность фаз [(mag – mag1) – mag1], где mag1 – вариация магнитного поля в опорной точке (обсерватория Иркутск), mag – в остальных точках. Рассматривались следующие девять периодов: сутки, ½ суток и далее в геометрической прогрессии до 5.6 мин.
Из рассчитанных функций были скомпонованы (NZ + NT + Tu) входные векторы для обучения нейронной сети, где под NZ подразумевается точка на побережье Байкала – расчет для компоненты Z магнитного поля, NT – та же точка, но расчет для модуля магнитного поля, Tu – полигон в Тункинской долине, модуль поля. На выход нейронной сети в созданной обучающей выборке подавались соответствующие им значения шести параметров модели. Таким образом, мы имеем ряд наборов, состоящих из значений функций магнитного поля на девяти частотах и соответствующих им значений макропараметров геоэлектрической среды, предназначенных для обучения нейронной сети. После того, как определены модельные наборы для обучения, нейронная сеть учится ставить в соответствие известным входным данным - известные выходные.
Структура нейронной сети в нашей задаче определяется шестью нейронами на выходе, каждый из которых соответствует определенному параметру модели, и 27 нейронами на входе, так как для девяти периодов мы имеем три точки (NZ, NT, Tu), то есть всего двадцать семь значений функций магнитного поля. Обучающая выборка состоит из 81 модели.
После создания обучающей выборки началось обучение трехслойной нейронной сети. Прямое распространение входного сигнала, представляющего значения функций магнитных полей, по такой сети происходило от слоя к слою. При этом каждый $j$-й нейрон последующего слоя получал от всех $k$-ых нейронов предыдущего слоя суммарный сигнал:
где: $u_{i}^{l}$ – выходной сигнал для $i$-го нейрона $l$-го слоя; $G$ – передаточная функция нейрона (например, гиперболический тангенс); $W_{{ij}}^{l}$ – коэффициенты связи между нейронами слоя $l$ – 1 и $l$; ${{x}_{j}}$ – состояние $j$-го нейрона слоя $l$ – 1.Для уже обученной сети выходной вектор представляет собой отклик сети, ожидаемый “учителем”, как результат подачи на входы НС значений входного вектора, и соответствует значениям описанных выше параметров классообразующей модели для данного обучающего примера. На самом деле в процессе обучения на выходах сети вычисляются значения, отличные от определенных “учителем” значений. Поэтому фактический отклик сравнивается с желаемым откликом сети и вычисляется ошибка. Суммарная среднеквадратичная ошибка по всем обучающим примерам представляет собой квадрат разности между “правильным” $u_{i}^{t}$ и действительным ${{u}_{i}}$ значениями выходных нейронов и равняется
где суммирование велось по всем $p$-ым обучающим примерам для всех нейронов $i$выходного слоя. Коэффициенты связи между слоями сети являются теми параметрами, которые определяют величину ошибки (2), поэтому суть процесса обучения состоит в подборе для каждой пары слоев матрицы связей нейронов ${{W}_{{ij}}}$ с целью ее минимизации. Значения коэффициентов связей устанавливаются стандартным МОРО с использованием на каждом шаге для каждой пары соседних слоев вычисляемого градиента ошибки:(3)
$\Delta W_{{ij}}^{{(n)}} = - \alpha \frac{{\partial Er}}{{\partial {{W}_{{ij}}}}} + \beta \Delta W_{{ij}}^{{(n - 1)}},$В отличие от процедуры обучения, которая требует многих шагов для прохождения сигнала по сети вперед и назад, процедура распознавания требует только одного прохода распознаваемого сигнала от входа к выходу и выполняется с установленными на этапе обучения коэффициентами связи, содержащими в себе “правила вывода”. При этом на выходе формируется конечный результат, который можно трактовать как результат инверсии данных в заданном классе моделей.
Выше уже было указано, что структура нейронной сети в нашей задаче определяется шестью нейронами на выходе и 27 нейронами на входе. Обучающая выборка состояла из 81 модели. Для такого соотношения числа входных, выходных нейронов и величины обучающей выборки важно было установить оптимальное число нейронов в промежуточном слое, которое влияет на достижение минимальных значений порога точности. Одновременно с изменением нейронов промежуточного слоя менялся порог достигаемой точности $eps$. С одной стороны, нейронную сеть нельзя было переобучить, так как тогда бы терялась ее способность к обобщению, а с другой стороны нужно было получить такую структуру сети, которая достигала бы минимального порога точности.
Кроме того, при распознавании нельзя ожидать, что распознаваемые реальные данные будут точно соответствовать тем, из которых состояла база данных и на которых обучалась нейронная сеть. Именно интерполяционные и экстраполяционные качества нейронных сетей позволяют распознавать данные, принадлежащие тому же классу моделей, на которых обучалась сеть, но не входящие в обучающую выборку. Существенно на эти свойства влияет выбор передаточной функции нейрона. Поэтому были обучены и протестированы нейронные сети с тремя передаточными функциями нейрона: линейной, сигмоидной (гиперболический тангенс) и логистической. После многочисленных расчетов была выбрана следующая архитектура нейронной сети: один скрытый слой нейронной сети типа многоуровневого персептрона и 20 нейронов в нем. Оказалось, что на скрытом и выходном слое лучше использовать логистическую функцию. Пороговая точность обучения была определена значением 0.11. Обучение результирующей нейронной сети заняло не более десяти минут. В дальнейшем необходимо увеличивать обучающую выборку за счет увеличения промежуточных значений параметров классообразующей модели для достижения лучшего результата обучения и распознавания нейронной сети.
После обучения нейронной сети, было проведено распознавание/инверсия на реальных данных и получены значения шести параметров, описывающих базовую модель, а именно следующие значения сопротивлений: 100.18 Ом м для фундамента под Байкалом; 2.63 Ом м для нижнего осадочного слоя под Байкалом; 5000.0 Ом м для фундамента под точкой измерений на берегу; 10.67 Ом м для наземного разлома; 4.83 Ом м для разлома под Байкалом и 254.06 Ом м для разлома под Патронами (Ангарского разлома).
РЕЗУЛЬТАТЫ СОПОСТАВЛЕНИЯ МОДЕЛЕЙ С ЭКСПЕРИМЕНТОМ
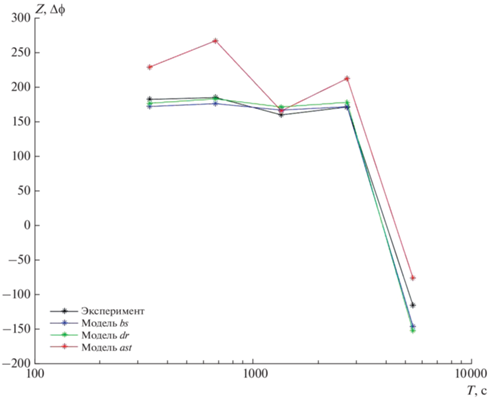
Для базовой модели (bs) с полученными параметрами, а также для построенных на ее основе альтернатив dr (мантийный диапир) и ast (астеносферный выступ) были рассчитаны градиентные фазовые функции Δϕ в точках измерения возле нейтринной обсерватории (NT и NZ) и на Тункинском полигоне, а также в пункте Узуры, не участвовавшем в нейросетевой инверсии. Этот пункт находится в средней части Байкала, вдали от района нашего мониторинга (рис. 1) и может служить для контроля общности наших выводов о глубинной структуре рифта.
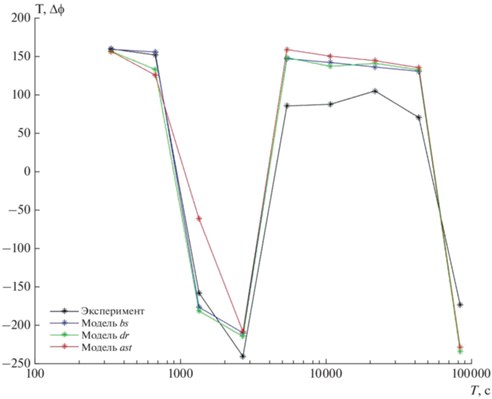
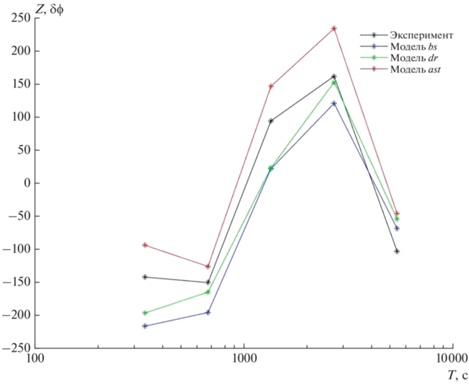
На рис. 4–рис. 6 показаны примеры сопоставления экспериментальных и модельных частотных кривых Δϕ. Видно, что во всех случая модель ast наихудшим образом соответствует эксперименту, особенно в п. Узуры. Модели dr и bs соответствуют лучше, но малоразличимы между собой.
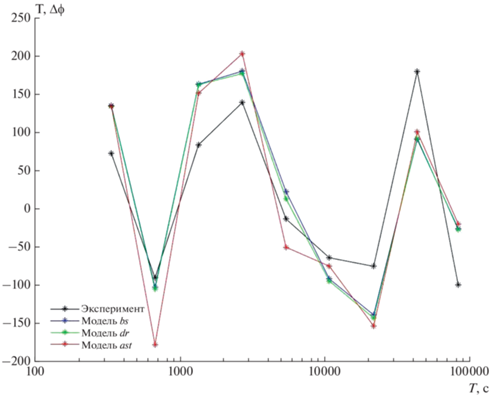
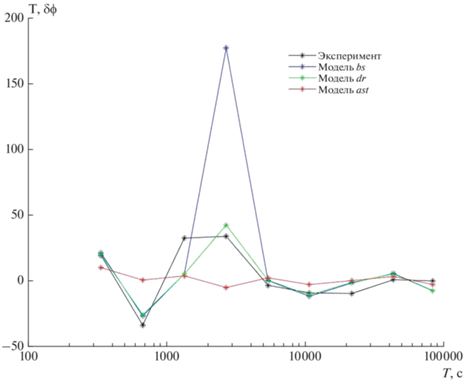
Другую функцию, δϕ (разность фаз [mag – mag1]) из-за ее большей уязвимости к помехам, удалось экспериментально определить только в Узурах и Тунке (рис. 7 и рис. 8). Эта функция подтверждает плохое соответствие эксперименту модели ast. Наилучшим соответствием обладает модель dr.
Сравним полученные кривые с использованием критерия достоверности различия. Рассмотрим отношения среднеквадратичных отклонений (СКО) экспериментальной и различных модельных кривых sdr/sbs и sast/sbs. sdr/sbs < 1 или sast/sbs < 1 свидетельствует в пользу моделей dr или ast соответственно; sdr/sbs > 1 и sast/sbs > 1 свидетельствует в пользу модели bs. Будем считать вывод надежным, если отклонение отношения от единицы будет не меньше 20%. Отметим, что выполнение этих неравенств является необходимым, но не достаточным условием выбора наиболее адекватной модели. Например, при малых, в среднем, сдвигах фаз частотные кривые могут быть близки по среднему уровню, но существенно отличаться по форме. В сомнительных случаях рассмотрим также отношение соответствующих корреляций экспериментальной и различных модельных кривых (знаки неравенств в свидетельствах будут обратными).
Начнем с наиболее надежно определяемой функции ∆φ (табл. 2).
Таблица 2.
Отношения среднеквадратичных отклонений экспериментальных и модельных частотных кривых ∆φ
| Отношения СКО | Узуры | NT | NZ | Тунка |
|---|---|---|---|---|
| sdr/sbs | 1.16 | 1.02 | 0.56 | 0.99 |
| sast/sbs | 3.25 | 1.34 | 1.31 | 1.13 |
Как видим, модель ast всюду является наихудшей. Модели dr и bs по нашему критерию являются неразличимыми всюду, кроме NZ, где модель dr оказалась достоверно наилучшей. Проверим эту особенность с помощью корреляций. rdr/rbs = = 2.69 > rast/rbs =–3.57, то есть действительно, модель dr наилучшая, а ast – наихудшая.
Подобным образом рассмотрим δφ в тех точках, где эту функцию удалось достаточно надежно определить (табл. 3).
Таблица 3.
Отношения среднеквадратичных отклонений экспериментальных и модельных частотных кривых δφ
| Отношения СКО | Узуры | Тунка |
|---|---|---|
| sdr/sbs | 0.83 | 0.22 |
| sast/sbs | 1.11 | 0.42 |
В Узурах по отношениям СКО формально наилучшей является модель ast, наихудшей – bs, но оба отношения недостаточно отличаются от 1 по критерию достоверности различия. Отношения корреляций rdr/rbs = 0.99, rast/rbs = 0.48, т.е. модели bs и dr неразличимы, модель аst – достоверно наихудшая. Наконец, в Тунке модель dr достоверно наилучшая, но судя по отношению sast/sbs, модель bs оказалась наихудшей в противоречии со всем предыдущим. Это как раз тот вышеупомянутый случай, когда критерий отношения s недостаточен, что легко видеть из рис. 8 (rbs = 0.66, rdr = 0.85, rast =0.14). В самом деле, отношения корреляций rdr/rbs = 1.29 и rast/rbs = 0.21 подтверждают, что наилучшей здесь является модель dr, а наихудшей, как и везде, модель ast.
ЗАКЛЮЧЕНИЕ
Можно констатировать, что модель астеносферного выступа явно не соответствует экспериментальным данным. Модель мантийного диапира на юго-западном конце Байкальского рифта (Тунка) минимально противоречит эксперименту. В юго-западной части Байкала (нейтринная обсерватория) это можно утверждать с меньшей уверенностью. Однако в центральной части рифта (Узуры) она пока экспериментально не различима от модели без глубинной неоднородности.
В дальнейшем эти выводы будут уточняться, в частности, благодаря расширению области мониторинга на п. Большие Коты (рис. 1), новым данным из пунктов Тунка и нейтринная обсерватория и увеличению обучающей выборки для нейросетевой инверсии.
Список литературы
Бердичевский М.Н, Ваньян Л.Л., Кошурников А.В. Магнитотеллурические зондирования в Байкальской рифтовой зоне // Физика Земли. 1999. № 10. С 3–25.
Велихов Е.П., Григорьев В.Ф., Жданов М.С., Коротаев С.М., Кругляков М.С., Орехова Д.А., Попова И.В., Терещенко Е.Д., Щорс Ю.Г. Электромагнитное зондирование Кольского полуострова мощным крайне низкочастотным источниками // Докл. РАН. Геофизика. 2011. Т. 438. № 3. С. 390–395.
Глинский Б.М., Дихтер И.Я., Зейгарник В.А. и др. Комплекс методических аппаратурных средств и результаты электромагнитных зондировании с мощным энергоисточником на Байкальском прогностическом полигоне // Докл. АН СССР. 1989. Т. 308. №1. С. 59–61.
Грачёв А.Ф. Основные проблемы новейшей тектоники и геодинамики северной Евразии // Физика Земли. 1996. № 12. С. 5–36.
Григорьев В.Ф., Коротаев С.М., Кругляков М.С., Орехова Д.А., Попова И.В., Терещенко Е.Д., Терещенко П.Е., Щорс Ю.Г. Результаты морского электромагнитного зондирования мощным удаленным источником в Кольском заливе Баренцева моря // Физика Земли. 2013. № 3. С. 75–86.
Зорин Ю.А. Новейшая структура и изостазия Байкальской рифтовой зоны и сопредельных территорий. М.: Наука. 1971. 167 с.
Коротаев С.М., Буднев Н.М., Сердюк В.О., Киктенко Е.О., Горохов Ю.В. Глубоководный электромагнитный мониторинг в Байкале – классический и неклассический аспекты // Вопросы естествознания. 2016. № 2. С. 41–53.
Коротаев С.М., Буднев Н.М., Сердюк В.О., Киктенко Е.О., Орехова Д.А. Байкальский глубоководный мониторинг – новые результаты // Физика Земли. 2022. № 5. С. 116–127.
Крылов С.В., Мандельбаум М.М., Мишенькин Б.П., Мишенькина З.Р., Петрик Г.В., Селезнев В.С. Недра Байкала (по сейсмическим данным). Новосибирск: Наука. 1981. 105 с.
Логачев Н.А. Главные структурные черты и геодинамика Байкальской рифтовой зоны // Физическая мезомеханика. 1999. Т. 2. № 1–2. С. 163–170.
Лунина О.В., Гладков А.С., Гладков А.А. Систематизация активных разломов для оценки сейсмической опасности // Тихоокеанская геология. 2012. Т. 31. С. 49–60.
Мац В.Д., Уфимцев Г.Ф., Мандельбаум М.М. Кайнозой Байкальской рифтовой впадины. Строение и геологическая история. Новосибирск: изд-во СО РАН, филиал “Гео”. 2001. 252 с.
Мороз Ю.Ф., Мороз Т.А. Глубинный геоэлектрический разрез Байкальского рифта // Вестник КРАУНЦ. Науки о Земле. 2012. № 2. Вып. 20. С. 114–126.
Морозова Г. М., Манштейн А. К., Ельцов И. Н. Глубинные электромагнитные зондирования с контролируемым источником в Байкальской рифтовой зоне. Геофизические методы изучения земной коры. Новосибирск: Объед. Ин-т геологии, геофизики и минералогии. 1998. С. 57–62.
Орехова Д.А., Кругляков М.С., Коротаев С.М., Буднев Н.М. Возможности выбора адекватной геоэлектрической модели Байкальского рифта по наблюдениям в районе эксперимента по глубоководному электромагнитному мониторингу // Актуальные проблемы науки Прибайкалья. 2017. Вып. 2. С. 150–159.
Поспеева Е.В., Витте Л.В., Потапов В.В. Геологическое истолкование результатов магнитотеллурического зондирования в Юго–Восточной части Байкальской рифтовой зоны // Интерэкспо Гео–Сибирь. 2012. №2. P. 3–8.
Поспеева Е.В., Потапов В.В., Витте Л.В. Магнитотеллурические зондирования в западно–забайкальском секторе Центрально–Азиатского складчатого пояса // Геология и геофизика. 2017. Т. 58. С. 157–175.
Розен О.М., Манаков А.В., Зинчук Н.Н. Сибирский кратон: формирование, алмазоносность. М.: Научный мир. 2006. 212 с.
Семинский К.Ж., Кожевников Н.О., Черемных А.В., Поспеева Е.В., Бобров А.А., Оленченко В.В., Тугарина М.А., Потапов В.В., Бурзунова Ю.П. Межблоковые зоны северо-западного плеча байкальского рифта: результаты геолого-геофизических исследований по профилю пос. Баяндай м. Крестовский // Геология и геофизика. 2012. Т. 53. С. 250–269.
Терешкин С.А. Первые результаты интерпретации данных МТЗ, записанных станциями VEGA в Прибайкалье за период 2014–2017 гг. Всероссийская конф. Геонауки. Иркутск: ИГТУ. 2018. С. 20–25.
Шимилевич М.И., Оборнев Е.А. Применение метода нейронных сетей для решения многопараметрических обратных задач магнитотеллурического зондирования аппроксимации обратных операторов в задачах электромагнитных зондирований // Изв. вузов. Геология и разведка. 1999. Т. 2. С. 102–106.
Шкиря М.С., Терёшкин С.А., Давыденко Ю.А., Петрищев М.С. Применение комплекса электромагнитных зондирований изучения электропроводности донных отложений озера Байкал. Всероссийская конф. ГеоБайкал. Иркутск: ИГТУ. 2018. С. 11–16.
Эпов М.И., Поспеева Е.В., Витте Л.В. Особенности состава и строения земной коры краевой части сибирского кратона (в зоне влияния рифтогенных процессов) по данным магнитотеллурических зондирований // Геология и геофизика. 2012. Т. 53. С. 380–398.
Gao S.P., Davis M., Liu H., Slack P., Zorin Y.A., Logatchev N.A., Kogan M., Burkholder P., Meyer R.P. Asymmetric upwarp of the asthenosphere beneath the Baikal rift zone, Siberia // J. Geophys. Res. 1994. V. 99. P. 15319–15330.
Korotaev S.M., Budnev N.M., Serdyuk V.O., Orekhova D.A., Kruglyakov M.S., Kiktenko E.O., Mirgazov R.R., Zurbanov V.L., Gorohov J.V., Ryabov E.V. Baikal electromagnetic experiment // Atmospheric and Oceanic Physics. 2018. V. 54. № 11. P. 1569–1594.
Kruglyakov M, Kuvshinov A. Using high-order polynomial basis in 3-D EM forward modelling based on volume integral equation method // Geophysical J. International. 2018. V. 213. P. 1387–1401.
Mackie R.I., Madden T.R. Three-dimensional magnetotelluric inversion using conjugate gradients // J.Geophys. 1993. V. 115. P. 215–229.
Pospeev A.V. The velocity structure of the upper mantle and regional deep thermodynamics of the Baikal rift zone // Geodynamics & Tectonophysics. 2012. V. 3. № 4. P. 377–383.
Rumelhart D., McClelland J., the PDP Research Group. Parallel Distributed Processing Cambridge: MIT Press. 1988. P. 547.
Spichak V., Popova I. Artificial neural network inversion of magnetotelluric data in terms of three-dimensional earth macroparameters // Geophys. J. Int. 2000. V. 142. P. 15–26.
Zhdanov M., Tartaras E. Inversion of multi-transmitter 3-D electromagnetic data based on the localized quasi-linear approximation // Geophys. J. 2002. V. 148. P. 506–519.
Дополнительные материалы отсутствуют.