Физика Земли, 2023, № 5, стр. 13-23
Определение эффективной электропроводности флюидонасыщенного керна по данным компьютерной томографии
М. И. Эпов 1, 2, Э. П. Шурина 2, 3, Д. В. Добролюбова 2, 3, А. Ю. Кутищева 2, 3, С. И. Марков 2, 3, *, Н. В. Штабель 2, 3, Е. И. Штанько 2, **
1 Сибирский научно-исследовательский институт геологии, геофизики и минерального сырья
г. Новосибирск, Россия
2 Институт нефтегазовой геологии и геофизики им. А.А. Трофимука СО РАН
г. Новосибирск,, Россия
3 Новосибирский государственный технический университет
г. Новосибирск, Россия
* E-mail: MarkovSI@ipgg.sbras.ru
** E-mail: mik_kat@ngs.ru
Поступила в редакцию 09.12.2022
После доработки 13.04.2023
Принята к публикации 13.04.2023
- EDN: WCBZVZ
- DOI: 10.31857/S0002333723050046
Аннотация
Предложена методика определения эффективной удельной электропроводности образцов горных пород при использовании их цифровых моделей. Модифицированный алгоритм реконструкции внутренней структуры образца по данным неразрушающих визуализирующих исследований керна позволяет построить релевантную дискретную модель, с высокой точностью аппроксимирующую поровое пространство. В отличие от существующих подходов, восстановленная дискретная геометрическая модель образца гетерогенной среды является иерархической и ориентирована на применение параллельных вычислительных схем многомасштабных конечноэлементных методов для прямого математического моделирования электромагнитных процессов. Приводятся результаты решения задачи об определении эффективной удельной электропроводности флюидонасыщенных образцов горных пород и их сравнение с данными лабораторных экспериментов.
ВВЕДЕНИЕ
Терригенные горные породы характеризуются сложной внутренней структурой, для которой свойственны иерархичность и многомасштабность, возникающие вследствие длительных процессов осадконакопления [Li et al., 2021]. Большинство из них обладают выраженной анизотропией и большим контрастом физических свойств составляющих частей. Значения последних могут значительно варьироваться в зависимости от внешних природных и техногенных факторов: колебаний температуры, сейсмических эффектов [Борисов и др., 2017; Zhang, Yoshino, 2020], а также механических воздействий при разработке месторождений [Khurshid, Afgan, 2022].
На транспортные свойства горных пород влияет эффект масштаба. Так, например, горные породы могут быть высоко проницаемыми в масштабе развитой сети микротрещин и каверн, но при этом на масштабе пласта могут быть слабопроницаемыми или даже непроницаемыми.
На практике детальный учет приведенных выше структурных и физических особенностей существенно затруднен, поэтому для их описания применяют эффективные модели и оценки физических свойств пласта [Durmaz, 2004; Эпов и др., 2012]. Процедура получения эффективных характеристик неоднородных сред называется гомогенизацией [Durmaz, 2004; Жиков и др., 1993].
Разведка и разработка нефтегазовых залежей включает этап изучения кернов, в ходе которого определяется пористость, микротрещиноватость и флюидонасыщение [Буторин, 2015; Чусовитин и др., 2016; Шишлов, Губаева, 2012].
Для получения релевантных данных о физических свойствах керна выполняется широкий спектр лабораторных исследований, в том числе и трудоемких. При контактных методах исследования свойств породы нарушается целостность и разрушаются образцы. Поэтому перспективным видится применение численного моделирования с использованием технологии цифрового керна [Воробьев и др., 2018].
Процедура численного моделирования физических процессов в таких средах базируется на технологии апскейлинг (upscaling) или “укрупнения” модели [Aarnes et al., 2007; Tabarovsky, Epov, 2021]. Она предполагает исследование эффективных свойств репрезентативных объемов горной породы на разных масштабах: от керна до нефтегазоносного пласта [Brandt, 2010]. Корректное определение свойств керна – первый этап апскейлинга.
Технология цифрового керна предполагает, что информация о внутренней структуре образца горной породы представлена в виде некоторого набора цифровизированных данных о ней: изображений компьютерной томографии, электронной микроскопии шлифов и т.д. [Zhu, 2019]. Наиболее информативной с точки зрения изучения внутренней микроструктуры керна является микрофокусная и нанофокусная рентгеновская томография, применяемая для изучения образцов в масштабе сантиметров и миллиметров [Воробьев и др., 2018]. На этом масштабе можно изучать трещиноватость, кавернозность и микропористость образцов.
Процедура численной гомогенизации на цифровом керне состоит из следующих этапов: построение дискретной модели керна (требования к ней определяются изучаемыми физическими процессами и применяемыми методами численного моделирования); численное моделирование физических процессов, протекающих в образце; вычисление эффективной характеристики по результатам последнего.
Можно выделить несколько подходов к построению цифровой дискретной модели керна. Один из них – создание идеализированной модели типа “pore-network” [Dong, Blunt, 2009; Qingrong et al., 2016; Jia et al., 2007; Xu et al., 2022], описывающей пористую среду как набор узлов и соединяющих их каналов без учета геометрических характеристик пор. Такие модели обеспечивают сохранение связности порового пространства и ориентированы на гидродинамические приложения [Jia et al., 2007]. Для их построения используется априорная информация о пористости среды или эмпирические соотношения между размерами пор и каналов. Для реализации такого подхода не требуется высокого разрешения или малого шага сканирования изображений.
Для построения полной дискретной модели, учитывающей геометрические особенности образца, применяются либо стохастические методы восстановления структуры [Zhang et al., 2021], либо прямые методы, которые используют в качестве исходных данных изображения высокого разрешения и обеспечивают достаточно точную аппроксимацию сложных границ различных фазовых составляющих гетерогенной среды [Ju et al., 2002; Schaefer et al., 2007; Lorensen, Cline, 1987; Cong et al., 2005].
Для численного моделирования физических процессов в гетерогенных средах со сложной структурой наиболее часто применяются метод конечных элементов и его многомасштабные модификации [Hou, Efendiev, 2009]. Это связано с возможностью их адаптации к особенностям решаемой задачи без редуцирования исходной модели. Математический аппарат этих методов позволяет разрабатывать алгоритмы и вычислительные схемы для решения прикладных задач без введения в модель дополнительных параметров, не имеющих физического смысла [Hattori et al., 2017; Jiang et al., 2014; Bao et al., 2014; Zhou et al., 2016; Li et al., 2016].
Эффективность конечноэлементных методов определяется требованиями к дискретной модели, построение которой осуществляется на первом этапе: необходимо сеточное разбиение, аппроксимирующее множество внутренних границ. Использование многомасштабного подхода обусловливает введение сеточной иерархии в соответствии с иерархией функциональных пространств. Проблема построения сеточной дискретизации гетерогенной среды на основе ее цифровых изображений достаточно хорошо изучена [Zhang et al., 2021; Ju et al., 2002; Schaefer et al., 2007; Lorensen, Cline, 1987; Cong et al., 2005]. Необходимо отметить, что построение иерархического сеточного разбиения на основе цифровых изображений гетерогенных сред в литературе не рассматривалось.
Для построения сеточных разбиений при использовании цифровых изображений наиболее широко применяются методы, основанные на выделении изоповерхностей, аппроксимирующих внутренние границы. К ним относятся: методы марширующих кубов/тетраэдров (Marching Cubes/Tetrahedra) [Lorensen, Cline, 1987; Cong et al., 2005]; дуального оконтуривания (Dual Contouring), [Ju et al., 2002; Schaefer et al., 2007] и поверхностных сетей (Surface Nets) [Gibson, 1999]. Для построения трехмерного сеточного разбиения в области с выделенными изоповерхностями используются алгоритмы Делоне [Du, Wang, 2006] или продвигаемого фронта [Schreiner et al., 2006]. В расширенных методах шагающих кубов (Extended Marching Cubes) и дуального оконтуривания нет необходимости в явном построении изоповерхностей, поскольку внутренние границы учитываются в первичном разбиении [Zhang et al., 2010]. Адаптивное сеточное разбиение получается рекурсивным локальным измельчением элементов исходного разбиения по мере приближения к внутренним границам [Liang, Zhang, 2013]. Основным недостатком подходов типа шагающих кубов является наличие элементов низкого разрешения как на выделенной изоповерхности, так и в результирующей трехмерной сетке. Поэтому их применение сочетается с использованием алгоритмов оптимизации сеток [Ströter et al., 2022]. Также важным требованием является сохранение связности порового пространства в результирующих сеточных разбиениях, поскольку это оказывает значительное влияние на корректное вычисление эффективных транспортных характеристик среды [Liu et al., 2016].
Некоторые алгоритмы построения таких сеточных аппроксимаций реализованы в коммерческом и свободно распространяемом ПО. Среди основных коммерческих программных продуктов следует назвать Avizo [Avizo …], Simpleware [Simpleware …], Materialise Mimics [Materialise …] и GeoDict [GeoDict …]; среди свободно распространяемых – 3D Slicer [3D Slicer …], ITKsnap [Yushkevich, Gerig, 2017] и FIJI (на основе ImageJ) [Schindelin et al., 2012]. Готовые коммерческие и свободно распространяемые программные пакеты позволяют работать с ограниченным набором геометрических и физических характеристик неоднородностей в исследуемом объекте [Jovanović, Jovanović, 2010].
Ранее авторами предложено вводить иерархию сеточных разбиений, которая позволяет точнее аппроксимировать внутренние особенности объекта и ориентирована на многомасштабные модификации метода конечных элементов для решения задач различной физической природы [Шурина и др., 2018]. Также было разработано и реализовано программное обеспечение для решения задачи о распределении скалярного электрического потенциала в областях со сложной внутренней структурой гетерогенным методом конечных элементов [Шурина и др., 2017]. В работе исследована возможность применения разработанных программных комплексов для определения эффективной удельной электропроводности оцифрованных реальных кернов и их сравнения с экспериментально измеренной.
Метод численной гомогенизации основан на применении иерархических адаптированных сеточных разбиений и прямого численного моделирования при использовании неконформных конечно-элементных аппроксимаций. Предлагаемый комбинированный подход решает основную проблему применения цифровых двойников кернов при математическом моделировании физических процессов: сохраняется достаточная точность аппроксимации внутренних границ и значительно сокращается время решения прямой задачи за счет ориентированности гетерогенного многомасштабного метода конечных элементов на параллельные вычисления.
АЛГОРИТМ ПЕРЕХОДА ОТ ПОСЛЕДОВАТЕЛЬНОСТИ ПОСЛОЙНЫХ ИЗОБРАЖЕНИЙ К ДИСКРЕТНОМУ АНАЛОГУ ОБРАЗЦА
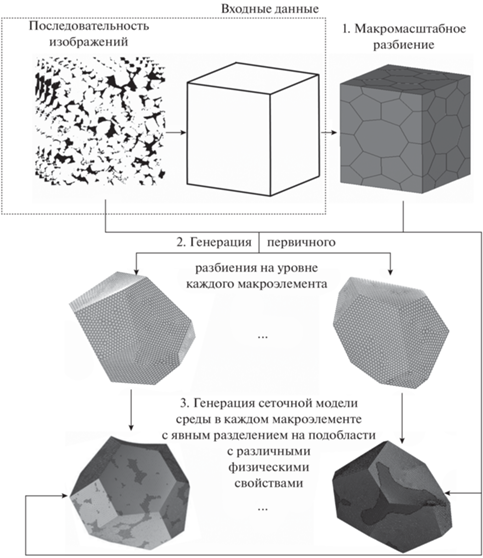
Для выполнения прямого моделирования в физическом образце необходимо перейти от последовательности послойных цифровых изображений его внутренней структуры к дискретному аналогу, учитывающему микроструктуру среды. Основная идея предлагаемого алгоритма отражена на рис. 1.
В качестве входных данных выступает набор изображений в градациях серого, от которого необходимо перейти к набору сегментированных изображений с конечным числом подобластей ${{\Omega }_{i}},\,\,i = 1,N$, и функцией интенсивности цвета, постоянной внутри каждой подобласти: $\forall (x,y) \in {{\Omega }_{i}},$ $p(x,y) = {\text{const}}$.
Проблема сегментации изображений сама по себе является достаточно затратной и в рамках этой работы она подробно не рассматривалась. Заметим, что в настоящее время основными способами ее решения являются алгоритмы на основе порогового критерия [Tuller et al., 2013] или нейронных сетей и машинного обучения [Tang et al., 2020]. В работе использован первый из них.
Следующий этап – построение макроэлементного разбиения расчетной области. Форма макроэлемента выбирается в соответствии с особенностями рассматриваемой среды, ее внутренней структуры и внешней геометрии. В самом общем случае макроэлемент представляет собой полиэдр.
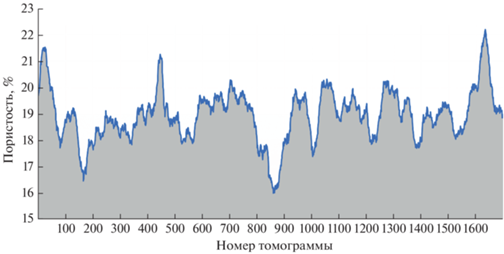
Для кернов осадочных пород характерно, как правило, незначительное изменение концентрации включений в отдельных подобластях. На рис. 2 приведен пример распределения относительной поверхностной концентрации пор на сегментированных сканах. В масштабе всей выборки эта величина колеблется от 16 до 22% в отдельных срезах. Таким образом, представляется целесообразным строить регулярное макроразбиение без учета внутренних особенностей среды. В случае, если число неоднородностей в области невелико или они достаточно крупные, этим этапом можно пренебречь и перейти к следующему в масштабах всей области. Решение о введении макроразбиения осуществляется также в зависимости от реализуемого далее конечноэлементного алгоритма для прямого моделирования физического процесса.
Рис. 2.
Распределение относительной поверхностной концентрации пор в отдельных сечениях образца (номер томограммы).
Неоднородности внутри каждого элемента макроразбиения учитываются на уровне его разбиения на тетраэдры – микроразбиения. Отметим, что микроразбиения между макроэлемементами являются несогласованными, что позволяет эффективно применить технологии параллельного программирования.
ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ПРОСТРАНСТВЕННОГО РАСПРЕДЕЛЕНИЯ ЭЛЕКТРИЧЕСКОГО ПОТЕНЦИАЛА
Рассмотренный выше алгоритм позволяет формировать иерархические сеточные разбиения, адаптированные для современных многомасштабных вариаций метода конечных элементов. Для оценки применимости и качества сеточных разбиений вычислим пространственное распределение электростатического потенциала в образце под действием постоянной разности потенциалов.
Рассмотрим трехмерную расчетную область $\Omega = \bigcup\nolimits_{m = 0}^M {{{\Omega }_{m}}} $, где M – число подобластей с различной электропроводностью.
Тогда для численного моделирования необходимо решить эллиптическую однородную краевую задачу с неоднородными краевыми условиями Дирихле на основаниях образца и с однородными условиями Неймана на боковой поверхности:
(1)
$ - {\text{div}}\left( {\sigma \left( {\mathbf{x}} \right){\text{grad}}\,u\left( {\mathbf{x}} \right)} \right) = 0\,\,\,\,{\text{в}}\,\,\,\,\Omega = \bigcup\limits_{m = 0}^M {{{\Omega }_{m}}} ,$(2)
${{\left. {u\left( {\mathbf{x}} \right)} \right|}_{{{\text{bottom}}}}} = {{u}_{d}},\,\,\,\,{{\left. {u\left( {\mathbf{x}} \right)} \right|}_{{{\text{top}}}}} = {{u}_{u}},$(3)
${{\left. {\frac{{\partial u\left( {\mathbf{x}} \right)}}{{\partial {\mathbf{n}}}}} \right|}_{{{\text{side}}}}} = 0,$(4)
${{\left. {u\left( {\mathbf{x}} \right)} \right|}_{{{{{\left( {{{\Omega }_{n}} \cap {{\Omega }_{m}}} \right)}}^{ + }}}}} = {{\left. {u\left( {\mathbf{x}} \right)} \right|}_{{{{{\left( {{{\Omega }_{n}} \cap {{\Omega }_{m}}} \right)}}^{ - }}}}},\,\,\,\,\forall n,m \in M,$(5)
$\begin{gathered} \sigma \left( {\mathbf{x}} \right)\,{{\left. {\frac{{\partial u\left( {\mathbf{x}} \right)}}{{\partial {\mathbf{n}}}}} \right|}_{{{{{\left( {{{\Omega }_{n}} \cap {{\Omega }_{m}}} \right)}}^{ + }}}}} = \sigma \left( {\mathbf{x}} \right)\,{{\left. {\frac{{\partial u\left( {\mathbf{x}} \right)}}{{\partial {\mathbf{n}}}}} \right|}_{{{{{\left( {{{\Omega }_{n}} \cap {{\Omega }_{m}}} \right)}}^{ - }}}}}, \\ \forall n,m \in M, \\ \end{gathered} $Сетки, получаемые по последовательности послойных изображений, являются иерархическими, причем на верхнем уровне иерархии они представляют согласованное нерегулярное разбиение на полиэдры произвольной формы, на нижнем уровне каждого макроэлемента – тетраэдральное согласованное нерегулярное разбиение. Поскольку тетраэдральные разбиения двух соседних полиэдров в общем случае могут быть не согласованы по общей границе, то для решения задачи (1)–(5) применим гетерогенный многомасштабный метод конечных элементов на полиэдральных носителях (FE-HMM) [Шурина и др., 2017; Weinan, Engquist, 2003]. Его основной идеей является разделение всего пространства решения на сумму двух подпространств: макроподпространство, учитывающее эффективные свойства макросреды, и микроподпространство, которое отражает все структурные микроособенности. Для построения подпространств используются соответствующие уровни иерархии сеточного разбиения.
Определим вариационную постановку на макроуровне для задачи (1)–(5) следующим образом: найти $u\left( {\mathbf{x}} \right) \in {{V}_{0}}\left( \Omega \right) + {{u}_{d}} + {{u}_{u}}$ такую, что
(6)
$\begin{gathered} \int\limits_\Omega {\sigma \left( {\mathbf{x}} \right)\nabla u\left( {\mathbf{x}} \right) \cdot \nabla v\left( {\mathbf{x}} \right)d\Omega } = 0, \\ \forall v\left( {\mathbf{x}} \right) \in {{V}_{0}}\left( \Omega \right), \\ \end{gathered} $(7)
$\begin{gathered} V\left( \Omega \right) = \left\{ {u,v \in {{L}^{2}}\left( \Omega \right):\,\left( {u,v} \right) = \frac{{}}{{}}} \right. \\ \left. { = \int\limits_\Omega {uvd\Omega } ,\,\,\,{{{\left\| u \right\|}}^{2}} = \int\limits_\Omega {{{u}^{2}}d\Omega } } \right\}, \\ \end{gathered} $(8)
${{V}_{0}}\left( \Omega \right) = \left\{ {u \in V\left( \Omega \right):{{{\left. u \right|}}_{{\partial \Omega }}} = 0\,} \right\}.$Введем на полиэдральном сеточном разбиении $P\left( \Omega \right)$ набор неполиномиальных функций формы $\phi _{k}^{{}}\left( {\mathbf{x}} \right)$, ассоциированных с узлами сетки $k = \overline {1,K} $. На тетраэдральных разбиениях $T\left( {{{p}_{i}}} \right)$, $i = \overline {1,N} $ также определим линейные лагранжевы базисные функции $\varsigma _{g}^{i}\left( {\mathbf{x}} \right)$, $g = \overline {1,{{G}^{i}}} $. Более подробно формирование базисных функций в гетерогенном многомасштабном методе конечных элементов для полиэдральных носителей изложено в работе [Шурина и др., 2017].
Тогда искомое решение $u\left( {\mathbf{x}} \right)$ представим в виде:
(9)
${{u}^{H}}\left( {\mathbf{x}} \right) = \sum\limits_{k = 1}^K {{{q}_{k}}{{\phi }_{k}}\left( {\mathbf{x}} \right) = \sum\limits_{k = 1}^K {{{q}_{k}}\sum\limits_{i = 1}^N {\sum\limits_{g = 1}^{{{G}^{i}}} {r_{g}^{{i,k}}\varsigma _{g}^{i}} } } } \left( {\mathbf{x}} \right).$Введенные наборы функций формы и базисных функций образуют дискретные гильбертовы подпространства: $V_{0}^{H}\left( {P\left( \Omega \right)} \right)$ – дискретное подпространство гильбертова пространства $V_{0}^{{}}\left( \Omega \right)$ (8), определенное на полиэдральном макроразбиении $P\left( \Omega \right)$, $V_{0}^{h} = \sum\nolimits_{i = 1}^N {V_{0}^{h}\left( {T\left( {{{p}_{i}}} \right)} \right)} $ – дискретное подпространство гильбертова пространства $V_{0}^{{}}\left( \Omega \right)$ (8), определенное на микроразбиении $T\left( {{{p}_{i}}} \right)$. Тогда дискретная вариационная постановка FE-HMM примет вид: найти ${{u}^{H}}\left( {\mathbf{x}} \right) \in V_{0}^{H}\left( {P\left( \Omega \right)} \right) \oplus $ $ \oplus \,\,V_{0}^{h} + {{u}_{d}} + {{u}_{u}}$ такое, что
(10)
$\begin{gathered} \int\limits_\Omega {{{\sigma }^{H}}\left( {\mathbf{x}} \right)\nabla {{u}^{H}}\left( {\mathbf{x}} \right) \cdot \nabla {{v}^{H}}\left( {\mathbf{x}} \right)d\Omega } = 0, \\ \forall {{v}^{H}}\left( {\mathbf{x}} \right) \in V_{0}^{H}\left( {P\left( \Omega \right)} \right) \oplus V_{0}^{h}, \\ \end{gathered} $На основе проведенных прямых расчетов пространственного распределения скалярного электрического потенциала внутри образца можно вычислить его эффективную удельную электропроводность, используя закон Ома. Значение эффективной электропроводности рассчитывается по формуле:
(11)
${{\sigma }_{{{\text{eff}}}}} = \frac{{{{I}^{{{\text{total}}}}}L}}{{S({{u}_{u}} - {{u}_{d}})}},$В сечениях образца, ортогональных оси OZ, полный ток Itotal, протекающий через сечение S, вычисляется следующим образом:
где электропроводность $\sigma $ является функцией пространственных координат.
ВЕРИФИКАЦИЯ АЛГОРИТМОВ НА СИНТЕТИЧЕСКОМ ОБРАЗЦЕ
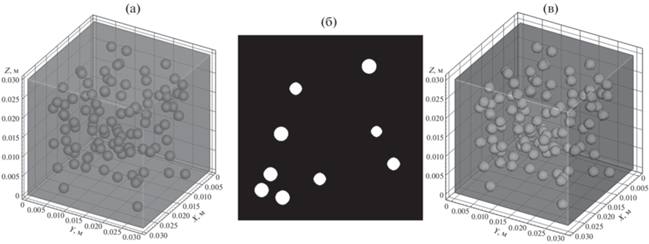
Верификация алгоритмов выполнена на синтетическом параллелепипедальном образце с известной внешней и внутренней геометрией (рис. 3). Реализованные численные алгоритмы построения сеточных разбиений и решения прямой и обратной задачи электростатики ориентированы на образцы параллелепипедальной и цилиндрической формы, которые преимущественно используются для изучения микроструктуры керна средствами КТ-томографии. Для описания его внутренней структуры сгенерирована последовательность послойных изображений (рис. 3б). Размеры образца: 0.03 × 0.03 × 0.03 м. Образец содержит 100 сферических включений (радиус 0.0012 м).
Рис. 3.
(а) – Модельный образец со сферическими включениями; (б) – пример изображения из последовательности “сканов”, скан № 417, соответствует сечению образца z = 0.02085 м; (в) – реконструированная внутренняя структура образца.
Для приведенной на рис. 3а геометрии известна объемная доля включений V* = 2.68%. Рассчитанная для реконструированной по набору послойных изображений объемная доля включений VNum = 2.64%. Таким образом, относительная погрешность аппроксимации объемной доли включений составляет 1.58%. Удельная площадь поверхности для данной геометрии S* = 1.810 ×10–3 м2, рассчитанная удельная площадь включений SNum = = 1.760 × 10–3 м2, относительная погрешность аппроксимации составляет 2.76%.
Удельная электропроводность скелета в образце σm = 10–6 См/м. При использовании построенной сеточной модели выполнен расчет эффективной удельной электропроводности σeff по формуле (11). Включения заполнены флюидом с удельной электропроводностью σin = 6.369 См/м. Рассчитанная по формуле Максвелла–Гарнетта [Снарский и др., 2007] эффективная удельная электропроводность σeff = 1.087 × 10–6 См/м, численно определенная по формуле (11) эффективная удельная электропроводность образца σeff_num = = 1.088 × 10–6 См/м. Относительная погрешность определения эффективной удельной электропроводности составляет 0.16%. Отметим, что она меньше относительной погрешности округления объемной доли пор и их удельной поверхности.
РАСЧЕТ ЭФФЕКТИВНОЙ УДЕЛЬНОЙ ЭЛЕКТРОПРОВОДНОСТИ РЕАЛЬНОГО КЕРНА ПО ПОСЛЕДОВАТЕЛЬНОСТИ ПОСЛОЙНЫХ КТ-ИЗОБРАЖЕНИЙ
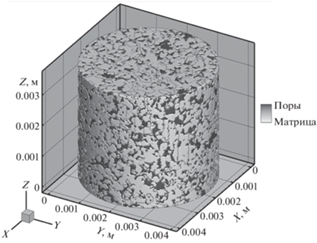
Пакет сканов содержит 1800 изображений цилиндрического образца Berea Sandstone с известной пористостью 20.90%. Разрешение каждого из цифровых изображений 1900 × 1900 пикселей. Габаритные размеры цилиндрического образца: радиус R = 0.002 м, высота L = 0.036 м (рис. 4). Рассчитанная пористость составила 20.85% (относительная погрешность “восстановления” объема включений равна 0.2%).
На образце керна были выполнены экспериментальные лабораторные измерения удельной электропроводности с целью сравнения с рассчитанными эффективными характеристиками.
В ходе эксперимента измерения выполнялись на одном и том же образце керна, который последовательно насыщался двумя жидкостями с различной удельной электропроводностью σi (i = 1, 2): σ1 = 11.760 См/м и σ2 = 6.369 См/м. Удельная электропроводность матрицы σm = 10–6 См/м. Граничные условия для задачи (1)–(3) при расчете пространственного распределения электрического потенциала u(x) заданы следующим образом: ud = 0 (В), uu = 1 (В).
Расчеты эффективной электропроводности произведены по формуле (11) и приведены в табл. 1.
Таблица 1.
Расчетные данные
| Удельная электропроводность флюида, См/м | I total, А | uu, В | ud, В | S, м2 | L, м | σeff, См/м |
|---|---|---|---|---|---|---|
| 11.76 | 3.79 × 10–3 | 1 | 0 | 1.26 × 10–5 | 3.60 × 10–3 | 1.080 |
| 6.369 | 2.08 × 10–3 | 0.596 |
В табл. 2 приведено сравнение измеренных в лаборатории значений эффективной удельной электропроводности керна и результаты вычислительных экспериментов для двух различных насыщающих флюидов.
Таблица 2.
Измеренные и вычисленные значения эффективной удельной электропроводности для двух различных насыщающих растворов
| Удельная электропроводность флюида, См/м | Измеренная удельная электропроводность керна, См/м | Вычисленная удельная электропроводность керна, См/м | Относительное расхождение, % |
|---|---|---|---|
| σ1 = 11.76 | σm1 = 1.041 | σc1 = 1.080 | 3.75 |
| σ2 = 6.369 | σm2 = 0.675 | σc2 = 0.596 | 11.68 |
В табл. 3 показаны отношения измеренных и вычисленных контрастов.
Таблица 3.
Отношения измеренных и вычисленных удельных электропроводностей образца для двух насыщающих флюидов
| Контраст удельных электропроводностей флюидов σ1/σ2 | Контраст измеренных значений σm1/σm2 | Контраст вычисленных значений σc1/σc2 | |
|---|---|---|---|
| 1.846 | 1.542 | 1.811 | |
| Oжидаемыe соотношения | 1.000 | 1.000 | |
| Фактические соотношения | 0.835 | 0.980 | |
| Отклонение ожидаемых от фактических, % | 16.4 | 1.87 |
Предполагается, что при смене насыщающих флюидов геометрия порового пространства не изменяется. Из закона Ома следует, что отношение удельных электропроводностей керна, насыщенного разными флюидами, будет численно совпадать с отношением удельных электропроводностей флюидов:
Однако между этими величинами была установлена относительная разница: 16.4% для измеренных величин и 1.87% для рассчитанных эффективных характеристик. Относительная величина погрешности между вычисленными и измеренными величинами электропроводности составляют 3.75 и 11.68% для флюидов с σ1 = 11.76 См/м и σ2 = 6.369 См/м, соответственно.
Неточность восстановления внутренней структуры образца по серой гамме сканов – один из факторов, влияющих на точность вычисления эффективной удельной электропроводности. Глубина серого цвета исходных изображений составляет 16 бит, что соответствует изменению функции его интенсивности в диапазоне от 0 до 65 535. Разделение порового пространства на уровне каждого скана на скелет и включения выполняется согласно пороговому критерию. При этом исходные сканы в градациях серого не обладают достаточно высоким контрастом: подавляющая часть информации о различных областях лежит в сравнительно узком диапазоне изменения функции интенсивности цвета от 10 000 до 17 000 (только 10.7%). Это не позволяет достаточно точно определить пороговое значение для разделения изображения на области скелета и включений.
В приведенных выше расчетах пороговое значение функции интенсивности цвета принято равным 13000, при котором достигается наиболее близкая к измеренной пористость 20.85%. Она практически совпадает с измеренной величиной (относительная погрешность реконструкции относительного объема пор равна 0.2%). Из табл. 4 видно, что даже при небольшом изменении значения порога разделения фаз (от 12 600 до 13 220, 0.9% ширины всего диапазона) рассчитанная пористость изменяется в достаточно широком диапазоне от 19.65 до 22.11% (относительная разность 11.8%), что влияет на вычисленную эффективную электропроводность, расхождение которой с измеренной тогда варьируется в диапазоне от 0.77 до 21.79%.
Таблица 4.
Изменение вычисленной пористости и электропроводности цифрового образца при изменении значения порога разделения фаз
| Пороговое значение | Пористость, % | Вычисленная удельная электропроводность, См/м | Погрешность относительно измеренной удельной электропроводности σm2 = 0.675 См/м, % |
|---|---|---|---|
| 12 600 | 19.65 | 0.5279 | 21.79 |
| 13 000 | 20.85 | 0.5961 | 11.68 |
| 13 090 | 21.64 | 0.6417 | 4.93 |
| 13 220 | 22.11 | 0.6698 | 0.77 |
ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ
Расхождение результатов вычислительных экспериментов с экспериментальными данными не является критическим и может быть объяснено некорректностью входных данных.
Максимальное расхождение между вычисленным значением электропроводности и экспериментальными данными составило 11.68% для второго флюида. При этом отклонение ожидаемых соотношений от фактических для экспериментальных данных достигло 16.4% по результатам второго лабораторного эксперимента. Можно предположить, что по завершению первого эксперимента или при насыщении образца вторым флюидом нарушается геометрия порового пространства. Этот вывод косвенно подтверждается проведенным исследованием с варьированием порога разделения фаз на изображениях, где наиболее близкое значение эффективной удельной электропроводности к измеренному было получено для пористости 22% (исходные данные – образец Berea Sandstone с пористостью 20.9%).
Также дополнительную погрешность вносит недостаточная точность разделения фаз при использовании полуэмперического порогового критерия.
ЗАКЛЮЧЕНИЕ
В работе предложен и реализован комплексный подход к задаче определения эффективных свойств реальных образцов терригенных пород, внутренняя структура которых задана в виде последовательности послойных изображений, полученных методом неразрушающей визуализации. Реализован программный комплекс, включающий в себя следующие этапы: предварительная обработка входных данных (сегментация изображений в градациях серого на основе порогового критерия); построение иерархической дискретной модели, адаптированной для последующего применения современных многомасштабных модификаций метода конечных элементов; решение прямой задачи о распределении скалярного электрического потенциала при использовании построенной дискретной модели исследуемого образца; определение эффективной удельной электропроводности образца. Разработанный программный комплекс верифицирован на модельном образце с известной геометрией. Валидация выполнена путем сравнения с результатами лабораторного эксперимента.
Дальнейшее развитие связано с исследованием влияния нарушения непрерывности проводящих каналов в сеточном разбиении, построенном по дискретным изображениям сечений КТ, на вычисленные значения эффективных характеристик. Необходимо провести дополнительное исследование процедуры аппроксимации внутренней структуры образца микроуровневым сеточным разбиением с детальным изучением качества аппроксимации внутренних границ и степенью их влияния на расчетные эффективные физические свойства.
Список литературы
Борисов В.Е., Иванов А.В., Критский Б.В., Меньшов И.С., Савенков Е.Б. Численное моделирование задач пороупругости. Препринты ИПМ им. М.В.Келдыша. 2019. Т. 81. 36 с.
Буторин А.В. Строение продуктивного клиноформного пласта по данным сейсморазведки // Геофизика. 2015. Т. 1. С. 10–18.
Воробьев К.А., Воробьев А.Е., Тчаро Х. Цифровизация нефтяной промышленности: технология “цифровой” керн // Вестник евразийской науки. 2018. Т. 10. № 3. С. 72.
Жиков В.В., Козлов С.М., Олейник О.А. Усреднение дифференциальных операторов. М.: Физматлит. 1993. 464 с.
Снарский А. А., Безсуднов И. В., Севрюков В. А. Процессы переноса в макроскопически неупорядоченных средах: от теории среднего поля до перколяции. М.: ЛКИ. 2007. 304 с.
Чусовитин А., Тимчук А., Грачев С. Исследование геолого-технологической модели сложнопостроенного коллектора нефтегазовой залежи Самотлорского месторождения // Вестник Пермского национального исследовательского политехнического университета. Геология, нефтегазовое и горное дело. 2016. Т. 15. № 20. С. 246–260.
Шишлов С., Губаева Ф. Строение и условия формирования раннемелового продуктивного пласта БВ-8 Повховского нефтяного месторождения (Западная Сибирь) // Нефтегазовая геология. Теория и практика. 2012. Т. 7. № 2. С. 1–24.
Шурина Э.П., Добролюбова Д.В., Штанько Е.И. Специальные процедуры для работы с объектами со сложной внутренней структурой по стеку КТ-сканов // Cloud of Science. 2018. Т. 5. № 1. С. 40–58.
Шурина Э.П., Эпов М.И., Кутищева А.Ю. Численное моделирование порогов перколяции коэффициентов электропроводности // Вычислительные технологии. 2017. Т. 22. № 3. С. 3–15.
Эпов М.И., Шурина Э.П., Артемьев М.К. Численная гомогенизация электрических характеристик сред с контрастными мелкомасштабными включениями // Докл. РАН. 2012. Т. 442. № 1. С. 118–120.
Slicer [Электронный ресурс] URL: https://www.slicer.org (дата обращения 16.01.22).
Aarnes J., Kippe V., Lie K.-A., Rustad A. Modelling of multiscale structures in flow simulations for petroleum reservoirs. Geometric Modelling, Numerical Simulation, and Optimization. 2007. P. 307–360.
Avizo for Materials Science Thermo Fisher Scientific Inc. [Электронный ресурс] URL: https://www.fei.com/software/avizo-for-materials-science (дата обращения: 16.01.22).
Bao J., Fathi E., Ameri S. A coupled finite element method for the numerical simulation of hydraulic fracturing with a condensation technique // Engineering Fracture Mechanics. 2014. V. 131. P. 269–281.
Brandt A. Principles of systematic upscaling. Multiscale methods: bridging the scales in science and engineering. Ed. Jacob Fish. Oxford: 2010. Online: (дата обращения 28.08.2022).https://doi.org/10.1093/acprof:oso/9780199233854.003.0007
Cong A., Liu Y., Kumar D., Cong W., Wang G. Geometrical modeling using multiregional marching tetrahedral for bioluminescence tomography // SPIE Medical Imaging: Visualization, Image-Guided Procedures, and Display. International Society for Optics and Photonics. 2005. V. 5744. P. 756–764.
Dong H., Blunt M.J. Pore-network extraction from micro-computerized-tomography images // Phys. Rev. E 2009. V. 80. P. 036307.
Du Q., Wang D. Recent progress in robust and quality Delaunay mesh generation // J. Computational and Applied Mathematics. 2006. V. 195. № 1–2. P. 8–23.
Durmaz S. A numerical study on the effective thermal conductivity of composite materials. IZMIR. 2004. 240 p.
GeoDict Software [Электронный ресурс] URL: https://www.math2market.com/ (дата обращения 16.01.22).
Gibson S. F. F. Constrained elastic surface nets: Generating smooth models from binary segmented data. TR99. 1999. V. 24. 13 p.
Hattori G., Trevelyan J., Augarde C., Coombs W., Aplin A. Numerical simulation of Fracking in Shale Rocks: Current State and Future Approaches // Archives of Computational Methods in Engineering. 2017. V. 24. № 2. P. 281–317.
Hou T., Efendiev Y. Multiscale Finite Element Methods: Theory and Applications. B.: Springer. 2009. 241 p.
Jia L., Ross C.M., Kovscek A.R. A pore-network-modeling approach to predict petrophysical properties of diatomaceous reservoir rock // SPE Reservoir Evaluation & Engineering. 2007. V.10. № 6. P. 597–608.
Jiang Y., Zhao J., Li Y., Jia H., Zhang L. Extended Finite Element Method for Predicting Productivity of Multifractured Horizontal Wells // Mathematical Problems in Engineering. 2014. V. 2014. P. 1–10.
Jovanović J. D., Jovanović M. L. Finite element modeling of the vertebra with geometry and material properties retrieved from CT-Scan Data // Facta universitatis-series: Mechanical Engineering. 2010. V. 8. №. 1. P. 19–26.
Ju T., Losasso F., Schaefer S., Warren J. Dual contouring of hermite data // Proceedings of SIGGRAPH. 2002. P. 339–346.
Khurshid I., Afgan I. Geochemical investigation of electrical conductivity and electrical double layer-based wettability alteration during engineered water injection in carbonates // J. Petroleum Science and Engineering. 2022. V. 215. № A. 110627.
Li C., Wang D., Kong L. Mechanical response of the Middle Bakken rocks under triaxial compressive test and nanoindentation // International J. Rock Mechanics and Mining Sciences. 2021. V. 139. P. 104660.
Li L., Xia Y., Huang B., Zhang L., Li M., Li A. The Behaviour of Fracture Growth in Sedimentary Rocks: A Numerical Study Based on Hydraulic Fracturing Processes // Energies. 2016. V. 9. P. 1–28.
Liang X., Zhang Y. An octree-based dual contouring method for triangular and tetrahedral mesh generation with guaranteed angle range // Engineering with Computers. 2013. V. 30. № 2. P. 211–222.
Liu J., Pereira G.G., Liu Q., Regenauer-Lieb K. Computational challenges in the analyses of petrophysics using microtomography and upscaling: a review // Computers & Geosciences. 2016. V. 89. P. 107–117.
Lorensen W.E., Cline H.E. Marching cubes: A high resolution 3d surface construction algorithm // Computer Graphics (Proceedings of SIGGRAPH 87). 1987. V. 21. №. 4. P. 163–169.
Materialise Mimics Overview [Электронный ресурс] URL: http://www.materialise.com/en/medical/software/mimics (дата обращения 16.01.22).
Schaefer S., Ju T., Warren J. Manifold dual contouring // IEEE Transactions on Visualization and Computer Graphics. 2007. V. 13. № 3. P. 610–619.
Schindelin J. et al. Fiji: an open-source platform for biological-image analysis // Nature methods. 2012. V. 9. № 7. 676 p.
Schreiner J., Scheidegger C.E., Silva C.T. High-quality extraction of isosurfaces from regular and irregular grids // IEEE Transactions on Visualization and Computer Graphics. 2006. V. 12. № 5. P. 1205–1212.
Simpleware Software Solutions Synopsys, Inc. [Электронный ресурс] URL: https://www.synopsys.com/simpleware.html (дата обращения 16.01.22).
Ströter D., Mueller-Roemer J.S., Weber D., Fellner D.W. Fast harmonic tetrahedral mesh optimization // The Visual Computer. 2022. V. 38. P. 3419–3433.
Tabarovsky L.A., Epov M.I. Method of Upscaling and Downscaling Geological and Petrophysical Models to Achieve Consistent Data Interpretation of Different Scales. US Patient. Pub. № US2021/0165125 A1. Pub. Date: Jun. 3, 2021.
Tang D.G., Milliken K.L., Spikes K.T. Machine learning for point counting and segmentation of arenite in thin section // Marine and Petroleum Geology. 2020. V. 120. P. 104518.
Tuller M., Kulkarni R., Fink W. Segmentation of X-ray CT data of porous materials: A review of global and locally adaptive algorithms // Soil–water–root processes: Advances in tomography and imaging. 2013. V. 61. P. 157–182
Weinan E., Engquist B. The heterogeneous multiscale methods // Comm. Math. Sci. 2003. V. 1. №. 1. P. 87–132.
Xiong Q., Baychev T.G., Jivkov A.P. Review of pore network modelling of porous media: Experimental characterisations, network constructions and applications to reactive transport // J. Contaminant Hydrology. 2016. V. 192. P. 101–117.
Xu K., Wei W., Chen Y., Tian H., Xu S., Cai J. A Pore Network Approach to Study Throat Size Effect on the Permeability of Reconstructed Porous Media // Water. 2022. V. 14. № 1. 77 p.
Yushkevich P.A., Gerig G. ITK-SNAP: an intractive medical image segmentation tool to meet the need for expert-guided segmentation of complex medical images // IEEE pulse. 2017. V. 8. № 4. P. 54–57.
Zhang B., Yoshino T. Temperature-enhanced electrical conductivity anisotropy in partially molten peridotite under shear deformation // Earth and Planetary Science Letters. 2020. V. 530. P. 115922.
Zhang T., Xia P., Lu F. 3D reconstruction of digital cores based on a model using generative adversarial networks and variational auto-encoders // Journal of Petroleum Science and Engineering. 2022. V. 207. P. 109151.
Zhang Y., Hughes T.J.R., Bajaj C.L. An automatic 3D mesh generation method for domains with multiple materials // Computer methods in applied mechanics and engineering. 2010. V. 199. № 5–8. P. 405–415.
Zhou J., Zhang L., Braun A., Han Z. Numerical modeling and investigation of fluid-driven fracture propagation in reservoirs based on a modified fluid-mechanically coupled model in two-dimensional particle flow code // Energies. 2016. V. 9. P. 1–19.
Zhu L., Zhang C., Zhang Ch., Zhou X., Zhang Z., Nie X., Liu W., Zhu B. Challenges and prospects of digital core-reconstruction research // Geofluids. 2019. V. 2. P. 1–29.
Дополнительные материалы отсутствуют.