Доклады Российской академии наук. Математика, информатика, процессы управления, 2021, T. 499, № 1, стр. 67-72
ПОДАВЛЕНИЕ МУЛЬТИПЛИКАТИВНЫХ ШУМОВ В ИЗОБРАЖЕНИЯХ НА ОСНОВЕ ГРУППИРОВАНИЯ СХОЖИХ ОБЪЕКТОВ
В. Ф. Кравченко 1, 2, 3, *, В. И. Пономарев 4, **, академик РАН В. И. Пустовойт 2, 3, ***, Г. Аранда-Бохоргес 4, ****
1 Институт радиотехники и электроники
им. В.А. Котельникова Российской академии наук
Москва, Россия
2 Научно-технологический центр уникального приборостроения Российской академии наук
Москва, Россия
3 Московский государственный технический университет им. Н.Э. Баумана (национальный исследовательский университет)
Москва, Россия
4 Национальный Политехнический институт Мексики
Мехико, Мексика
* E-mail: kvf-ok@mail.ru
** E-mail: vponomar@ipn.mx
*** E-mail: vlad_pst@yahoo.com
**** E-mail: gibran.aranda.bionics@gmail.com
Поступила в редакцию 28.04.2021
После доработки 16.05.2021
Принята к публикации 26.05.2021
Аннотация
Впервые обоснована и реализована процедура фильтрации изображений, искаженных мультипликативным шумом. Процедура включает следующие этапы: формирование сходных структур в трехмерном пространстве (3D), гомоморфное преобразование, фильтрация изображения в 3D-пространстве дискретного косинусного преобразования (DCT), формирование статистической оценки изображения на основе группирования схожих структур, обратное гомоморфное преобразование и заключительный этап обработки, где корректируются погрешности и восстанавливаются контуры и детали изображений. Дана физическая интерпретация процедуры фильтрации в условиях мультипликативных шумов и разработана структурная схема подавления шумов. Моделирование предложенного метода подтвердило преимущество новой процедуры фильтрации в терминах общепризнанных критериев: оценки структурного индекса схожести, пикового отношения сигнал/шум и индекса сохранения контуров, а также и при визуальном сравнении профильтрованных изображений.
ВВЕДЕНИЕ
Улучшение качества деталей изображений в системах дистанционного зондирования и в медицинских исследованиях существенно усложнено вследствие влияния шумов различной природы, смазывания деталей и контуров. Сложная и меняющаяся структура реальных изображений не позволяет эффективно уменьшать влияние шумов и восстанавливать искаженные детали изображений, что часто приводит к неверным решениям в приложениях (визуализация объектов в дистанционном зондировании, распознавание образов, медицинская диагностика заболеваний, управление объектами, др.). Различные шумы, как мультипликативные, в частности спекл шумы, так и аддитивные, присутствуют в изображениях, полученных системами дистанционного зондирования, в ультразвуковой диагностике, а также в медицинских приложениях. Снижение интенсивности шумов в изображениях является обязательным элементом для улучшения визуализации контуров и мелких деталей и восстановлении структуры и качества изображений [1–12]. Ряд эффективных методов фильтрации основан на применении статистических процедур [1–7] совместно с использованием дисперсного представления изображений в базисах пространственных преобразований (DCT, различных вейвлет- и контурлет-функций, др.), которые позволяют улучшить визуализацию деталей и контуров, сохранить качество хроматических и структурных свойств [8–12].
Известные в литературе алгоритмы подавления шумов различной природы в изображениях, как правило, разработаны для конкретных шумов (мультипликативного, импульсного или аддитивного) и не позволяют осуществлять эффективную фильтрацию изображений, искаженных шумом сложной структуры, в частности мультипликативно-аддитивным шумом [2–4, 8–12]. Большинство известных алгоритмов требует априорных статистических данных о шумах и изображениях.
Здесь предложен и обоснован оригинальный подход в обработке изображений на основе использования идей изложенных в [1–7] в случае искажений мультипликативным спекл-шумом. Разработанный подход сочетает процедуры группирования 3D-структур, гомоморфной фильтрации, теорию статистических оценок и алгоритмы обработки изображений в дисперсном их представлении. Метод содержит четыре этапа: на первом этапе изображение сегментируется в ряд областей, в каждой из которых находятся объекты со схожими структурными свойствами. Внутри сегментированной области проводится группирование структур (лучей) из объектов со схожими свойствами на основе выбранного критерия подобия. На заключительном шаге первого этапа каждый луч объектов подвергается гомоморфному преобразованию (log), которое формирует новые структуры в 3D-пространстве. На втором этапе фильтрации лучи из 2D-объектов изображения в сегментах преобразуются на основе дискретного косинусного преобразования (DCT). Здесь сгруппированные схожие объекты образуют третью координату в дисперсном представлении изображения, что позволяет улучшить качество фильтрации. Второй этап обработки завершается обратным гомоморфным преобразованием (exp), формируя предварительную оценку изображения, необходимую для реализации последующего этапа. На третьем этапе обработки изображений реализуется новая статистическая оценка изображения с учетом корреляции между схожими сгруппированными участками в каждом луче изображения. На заключительном четвертом этапе проводится коррекция погрешностей предыдущих процедур, а также восстановление контуров и мелких деталей изображений.
Критериями, используемыми при сравнении предложенных алгоритмов с известными в литературе, являются: пиковое отношение сигнал–шум в децибелах (PSNR), оценка структурного индекса схожести (SSIM) и индекс сохранения контуров (EPI) [1–5, 8–12, 14].
Результаты многочисленных численных экспериментов в условиях различных интенсивностей шумов на изображениях из базы данных дистанционного зондирования подтверждают эффективность нового метода, позволяющего существенно уменьшить искажение изображений cпекл-шумами, восстанавливая мелкомасштабные детали и контуры изображений и улучшая качество изображений.
ПОСТАНОВКА ЗАДАЧИ И МЕТОД РЕШЕНИЯ
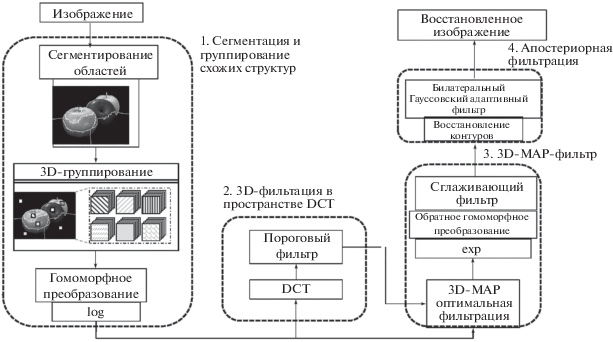
Предложенная процедура фильтрации включает в себя четыре основных этапа обработки, как показано на рис. 1.
Регистрируемое искаженное изображение S(i, j) в случае модели мультипликативно-аддитивного шума (ε(i, j) и n(i, j)), которая характерна для изображений дистанционного зондирования или сформированных ультразвуковыми датчиками при медицинской диагностике:
анализируется с целью формирования групп схожих объектов. На первом шаге на основе анализа гистограммы изображения оценивается количество кластеров со схожими структурными свойствами и проводится кластеризация областей по алгоритму (K-means). В каждом кластере реализуется поиск схожих блоков (block-matching: BM) и формируются 3D-образования из объектов со схожими структурами путем минимизации критерия подобия SAD:(2)
$\begin{gathered} \log [S(i,j)] \approx \log [\varepsilon (i,j)] + \log [R(i,j)] + \\ \, + n(i,j){\text{/}}[\varepsilon (i,j)R(i,j)]. \\ \end{gathered} $На втором этапе обработки изображение (2) фильтруется в 3D-пространстве дисперсного представления на основе DCT, где лучи схожих объектов формируют третью координату (рис. 1).
Преобразование, примененное к 3D-структурам, формирует в пространстве DCT массив данных $S(u,{v};l)$, который подвергается пороговой фильтрации. Здесь выделенные ранее кластеры изображения с плавным изменением интенсивности (α = 1) и области с контурами или мелкими деталями (α = 2) подвергаются пороговым ограничениям. Для каждой 3D-структуры реализуется ограничение коэффициентов в пространстве преобразования DCT:
(3)
$\hat {S}(u,v,l) = \left\{ \begin{gathered} S(u,v,l),\quad S(u,v,l) \geqslant T_{\alpha }^{{}}, \hfill \\ 0,\quad S(u,v,l) < {{T}_{\alpha }}, \hfill \\ \end{gathered} \right.$В дальнейшем к массиву данных $\hat {S}(u,v,l)$ применяется обратное преобразование (IDCT), формируя первую аппроксимацию блоков ${{\tilde {B}}_{l}}(i,j)$, $l = 1,..,K$.
На третьем этапе обработки существующая корреляция между схожими 2D-структурами в луче группирования используется при формировании оценок пикселей на основе статистического метода максимума функции апостериорной плотности вероятности (MAP). Оценка каждого пикселя определяется вычисляемой матрицей корреляции в сформированном после обратного преобразования луче схожих 2D-объектов ${{\tilde {B}}_{l}}(i,j)$, l = 1, …, K.
Функции плотностей вероятностей аппроксимируются гауссовскими:
Оценка MAP определяется одноименными пикселями в луче схожих объектов на основе критерия максимума функции апостериорной плотности вероятности так:
(4)
$\begin{gathered} \mathop {\max }\limits_{{{R}_{{3D}}}} p({{S}_{{3D}}}{\text{/}}{{R}_{{3D}}}) = \mathop {\max }\limits_{{{R}_{{3D}}}} {\kern 1pt} '\{ p({{S}_{{3D}}}{\text{/}}{{R}_{{3D}}}) \circ p({{R}_{{3D}}})\} \Rightarrow \\ \, \Rightarrow {{{\hat {R}}}_{{3D}}} = \frac{{{{A}^{T}}{{{\left\| K \right\|}}^{{ - 1}}}{{{\tilde {R}}}_{{3D}}}{\text{ }} - \frac{{{{{\bar {R}}}_{{3D}}}}}{{{{\sigma }^{2}}}}{\text{ }}}}{{{{A}^{T}}{{{\left\| K \right\|}}^{{ - 1}}}A - \frac{1}{{{{\sigma }^{2}}}}}}. \\ \end{gathered} $Здесь ${{\hat {R}}_{{3D}}}$ определяет оцениваемое значение пикселей в 3D-структуре, ${{\bar {R}}_{{3D}}}$ является средним значением вектора из массива зашумленных пикселей S3D в луче 2D-схожих структур, ${{\tilde {R}}_{{3D}}}$ определен блоками ${{\tilde {B}}_{l}}(i,j)$, которые сформированы на предыдущем этапе, а $\sigma $ определяется среднеквадратическим значением этих пикселей. На заключительном шаге этого этапа 3D-обработка завершается линейным сглаживанием с весами, которые зависят от дистанции SAD:
(5)
$\begin{gathered} \hat {R}(i,j) = {{\sum\limits_{l = 1}^K {{{{\hat {R}}}_{{3DMAP}}}(i,j;l)} {\text{ }}{{w}_{l}}} \mathord{\left/ {\vphantom {{\sum\limits_{l = 1}^K {{{{\hat {R}}}_{{3DMAP}}}(i,j;l)} {\text{ }}{{w}_{l}}} {\sum\limits_{l = 1}^K {{{w}_{l}}} }}} \right. \kern-0em} {\sum\limits_{l = 1}^K {{{w}_{l}}} }}, \\ {{w}_{l}} = 1 - SAD{\text{ }}[{{B}_{l}}(i,j),{{B}_{1}}(i,j)]. \\ \end{gathered} $На четвертом этапе фильтрации шумов производится коррекция эффектов предыдущих этапов, реконструируются сглаженные контуры и мелкие детали изображений с использованием билатеральной фильтрации и восстановления контуров (рис. 1). Здесь обработка определяется адаптивным билатеральным фильтром с двумя весовыми функциями гауссовского типа, где первая зависит от геометрического расстояния между пикселями, подлежащим фильтрации, и соседним в окне обработки, а вторая весовая функция вводит нелинейную обработку с весами, которые зависят от разности интенсивностей пикселей.
РЕЗУЛЬТАТЫ ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ
Свойства нового метода фильтрации спекл-шумов, названного DES-SP-MAP, а также известных наилучших по качеству алгоритмов [1, 8–12] были исследованы на основе стандартных численных критериев PSNR, SSIM и EPI, а также используя субъективный визуальный анализ профильтрованных изображений.
Значения критерия PSNR вычисляются по следующей формуле:
а величины SSIM критерия определяются так:(7)
${\text{SSIM}}\left( {R,\hat {R}} \right) = \frac{{(2{{\mu }_{R}}{{\mu }_{{\hat {R}}}} + {{C}_{1}})({{\sigma }_{{R\hat {R}}}} + {{C}_{2}})}}{{(\mu _{R}^{2} + \mu _{{\hat {R}}}^{2} + {{C}_{1}})(\sigma _{R}^{2} + \sigma _{{\hat {R}}}^{2} + {{C}_{2}})}}.$В формуле (7) ${{\mu }_{R}}$ и ${{\mu }_{{\hat {R}}}}$ определяют локальные средние для R и $\hat {R}$, соответственно; $\sigma _{R}^{2}$ и $\sigma _{{\hat {R}}}^{2}$ являются локальными значениями дисперсий для R и $\hat {R}$, и ${{\sigma }_{{R\hat {R}}}}$ – это локальная функция ковариации для R и $\hat {R}$. Константы cn выбираются такими, чтобы избежать нестабильности [14].
Индекс EPI [10–12] позволяет оценить количество контуров, которые сохраняются в обработанном изображении, что важно при фильтрации как изображений в дистанционном зондировании, так и медицинских изображений, где контуры несут информацию о подозрительных структурах, связанных с заболеванием. Критерий EPI определяется так:
(8)
$\begin{gathered} {\text{EPI}}\left( {R,\hat {R}} \right) = \\ \, = \frac{{\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {} } (\Delta R(i,j) - {{\mu }_{{\Delta R}}})(\Delta \hat {R}(i,j) - {{\mu }_{{\Delta \hat {R}}}})}}{{\sqrt {\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {} } {{{(\Delta R(i,j) - {{\mu }_{{\Delta R}}})}}^{2}}{{{(\Delta \hat {R}(i,j) - {{\mu }_{{\Delta \hat {R}}}})}}^{2}}} }}, \\ \end{gathered} $Изображения из базы данных дистанционного зондирования [13] были искажены мультипликативным шумом разной интенсивности (СКО шума: 0.02–0.10) и в дальнейшем обработаны алгоритмами. Представленные в табл. 1 величины PSNR, SSIM и EPI, это их усредненные значения по всем 12 изображениям из базы данных [13] в случае применения алгоритмов фильтрации L. Chen [8], Wang [9], Sun [10], S. Chen [11], Mullisa [12] и нового DES-SP-MAP, а также визуальный анализ рис. 2 подтверждают, что новый алгоритм превосходит лучшие из известных в широком диапазоне интенсивностей шумов. Эффективная фильтрация изображений SAR-05 SAR-06, в которых наблюдается много мелких деталей и контуров, и вариации интенсивности, подтверждает робастность предложенного метода для разных интенсивностей шумов (рис. 2).
Таблица 1.
Усредненные по 12 изображениям SAR значения PSNR, SSIM и EPI из базы данных [13] в случае применения алгоритмов фильтрации L. Chen, Wang, Sun, S. Chen, Mullisa и предложенного алгоритма DES-SP-MAP
| Фильтр | СКО | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.02 | 0.04 | 0.06 | 0.08 | 0.10 | 0.02 | 0.04 | 0.06 | 0.08 | 0.10 | 0.02 | 0.04 | 0.06 | 0.08 | 0.10 | |
| L. Chen [8] | 24.86 | 24.81 | 24.68 | 24.56 | 24.42 | 0.775 | 0.774 | 0.773 | 0.771 | 0.770 | 0.751 | 0.746 | 0.744 | 0.743 | 0.742 |
| Wang [9] | 23.41 | 23.28 | 23.10 | 22.92 | 22.71 | 0.652 | 0.651 | 0.649 | 0.648 | 0.646 | 0.678 | 0.669 | 0.667 | 0.665 | 0.664 |
| Sun [10] | 24.90 | 24.73 | 24.58 | 24.44 | 24.31 | 0.789 | 0.788 | 0.771 | 0.770 | 0.771 | 0.755 | 0.751 | 0.750 | 0.748 | 0.746 |
| S. Chen [11] | 24.04 | 23.92 | 23.77 | 23.57 | 23.39 | 0.725 | 0.710 | 0.696 | 0.695 | 0.693 | 0.704 | 0.704 | 0.703 | 0.702 | 0.700 |
| Mullisa [12] | 25.49 | 25.38 | 25.28 | 25.13 | 25.00 | 0.804 | 0.803 | 0.802 | 0.800 | 0.799 | 0.768 | 0.766 | 0.763 | 0.762 | 0.762 |
| Новый DES-SP-MAP |
26.21 | 25.84 | 25.67 | 25.51 | 25.41 | 0.813 | 0.810 | 0.809 | 0.807 | 0.806 | 0.799 | 0.797 | 0.796 | 0.796 | 0.793 |
| PSNR | SSIM | EPI | |||||||||||||
Рис. 2.
Профильтрованные изображения и инвертированные ошибки (увеличение в 3 раза): а – изображение SAR-05 (СКО = 0.08), обработанное новым фильтром DES-SP-MAP; б – изображение SAR-05 (СКО = 0.08), обработанное фильтром R. Wang; в – изображение SAR-06 (СКО = 0.1), обработанное новым фильтром DES-SP-MAP; г – изображение SAR-06 (СКО = 0.1), обработанное фильтром S. Chen. Следующие изображения в строках а–г – это увеличенная часть из предыдущего и инвертированные ошибки.

ВЫВОДЫ
Теоретическое обоснование и анализ физических результатов численного моделирования нового метода в фильтрации изображений в условиях их искажений спекл-шумом позволяют сделать ряд важных выводов:
1. Предложенный метод, который основан на дисперсном представлении данных (DCT), корреляции между схожими объектами и оптимальной оценке MAP, эффективно восстанавливает сложные структуры в изображениях.
2. Логарифмирование значений пикселей изображения позволяет преобразовать мультипликативную шумовую модель в аддитивную и реализовать фильтрацию с использованием дисперсных методов фильтрации.
3. 3D-фильтрация с весами, зависящими от степени схожести объектов, улучшает качество обработанных изображений.
4. Апостериорная обработка, использующая билатеральная фильтрацию и восстановление контуров в изображении, улучшает качество визуализации мелких деталей и контуров.
5. Новый метод подтвердил наилучшее качество как в значениях критериeв (PSNR, SSIM и EPI), так и при визуальном анализе профильтрованных изображений среди всех известных методов.
Список литературы
КравченкоВ.Ф., Пономарев В.И., Пустовойт В.И., Паласиос-Энрикес A. // Доклады РАН. Математика, информатика, процессы управления. 2020. Т. 494. С. 71–75.
Кравченко В.Ф., Пономарев В.И., Пустовойт В.И. // ДАН. 2018. Т. 481. № 4. С. 375–380.
Palacios-Enriquez A., Ponomaryov V., Reyes-Reyes R., Sadovnychiy S. // Circuits, System & Signal Proces. 2018. V. 37. № 12. P. 5389–5416.
Kravchenko V., Perez H., Ponomaryov V. Adaptive Signal Processing of Multidimensional Signals with Applications. M.: Fizmatlit, 2009.
Dabov K., Foi A., Katkovnik V., Egiazarian K. // IEEE Trans. Image Process. 2007. V. 16. № 8. P. 2080–2095.
Donoho D. L., Johnstone J. M. // Biometrika. 1994. V. 81. № 3. P. 425–455.
Verdoliva L., Gaetano R., Ruello G., Poggi G. // IEEE Geosci. Rem. Sens. Lett. 2015. V. 12. № 2. P. 314–318.
Chen L., Jiang X., Li Z., Liu X. // IEEE Trans. Geosci. Rem. Sens. 2020. V. 58. № 11. P. 7734–7752.
Wang R., He N., Wang Y., Lu K. // Multimedia Tools Appl. 2020. V. 79. P. 7633–7647.
Sun Y., Lei L., Guan D., Li X. // IEEE Trans. Geosci. Rem. Sens. 2021. V. 59. № 2. P. 1231–1249.
Chen S., Wang X., Xiao S. // IEEE Geosci. Rem. Sens. Lett. 2021. V. 18. № 4. P. 702–706.
Mullissa A. G., Marcos D., Tuia D., et al. // IEEE Trans. Geosci. Remote Sens. 2020. P. 1–15. https://doi.org/10.1109/TGRS.2020.3042694
Avolio S., Galli L., Passaro, D., et al. In: Proc. 2007 IEEE Int. Geosci. Remote Sens. Symp., Barcelona, 2007. P. 3874–3877. https://doi.org/10.1109/IGARSS.2007.4423690.
Wang Z., Bovik A. // IEEE Signal Process. Mag. 2009. V. 26. № 1. P. 98–117.
Дополнительные материалы отсутствуют.
Инструменты
Доклады Российской академии наук. Математика, информатика, процессы управления