Доклады Российской академии наук. Математика, информатика, процессы управления, 2020, T. 494, № 1, стр. 93-96

1. В заданном коридоре $Y \subset {{\mathbb{R}}^{3}}$ из точки ${{t}_{{\text{*}}}}$ в точку $t{\text{*\;\;}}({{t}_{{\text{*}}}},t{\text{*}} \in Y)$ движется объект t со скоростным поражающим миниобъектом m, способным двигаться прямолинейно и равномерно. В ${{\mathbb{R}}^{3}}$ имеется множество G, $G \cap Y = \phi $, являющееся замыканием открытого множества, препятствующее видимости и движению. Наблюдатель f, недружественный по отношению к объекту t, опасаясь миниобъекта, располагается вблизи выпуклого фрагмента границы $\partial G$ множества G, чтобы обеспечить возможность укрыться от m. Скорость ${{{v}}_{m}}$ миниобъекта m существенно превосходит скорости ${{{v}}_{f}},{{{v}}_{t}}$ наблюдателя и объекта, при этом ${{{v}}_{t}} > 0$.

Предположим, что находясь в точке ${{t}_{0}} \in Y$, объект обнаружил наблюдателя $f \notin Y$, демаскировавшего себя. Учитывая возможность немедленного запуска миниобъекта, наблюдатель выбирает фрагмент $S \subset \partial G$ с базовой точкой s ∈ S, за которым он может укрыться, за время ${{\tau }_{0}} = \mathcal{R}{\text{/}}{{{v}}_{m}}$, где $\mathcal{R} = \left\| {{{t}_{0}} - s} \right\|$. Одновременно с перемещением от базовой точки s в укрытие наблюдатель продолжает по мере возможности следить за движением объекта t. В предлагаемой модели объект и миниобъект m изображаются точками, а наблюдатель – шаром ${{V}_{\varepsilon }}\left( f \right)$ радиуса ε > 0, в центре f которого расположено средство наблюдения. Попадание миниобъекта в шар ${{V}_{\varepsilon }}\left( f \right)$ означает гибель наблюдателя.

Траектория объекта – это гладкая кривая $\mathcal{T} \subset Y$ (маршрут) в совокупности со скоростным режимом ${{{v}}_{t}}$ движения объекта по ней. Требуется выяснить возможности наблюдателя следить за объектом в безопасном для себя режиме, а объекта – уклониться от наблюдения на участке маршрута от момента прохождения объектом точки t₀ до момента полного укрытия наблюдателя.

В данной работе характеризуются маршруты или их части, по которым возможен скрытый от наблюдения проход объекта. Подобная задача для ${{\mathbb{R}}^{2}}$ решалась в [3]. Экстремальным задачам движения объекта в условиях слежения точечными наблюдателями посвящены работы [1, 2], см. также [4]. Модель с телесным наблюдателем ближе к реальности, но является более трудоемкой в связи с повышенной уязвимостью последнего.

2. Далее фрагмент S – связная открытая на $\partial G$ поверхность, являющаяся выпуклой, в каждой ее точке существует опорная к S плоскость. Наблюдатель f выбирает фрагмент S и свое начальное положение f₀ вблизи базовой точки s так, чтобы

1) видеть возможно бόльшую часть коридора Y;

2) расстояние $\rho \left( {{{t}_{0}},S} \right)$ было достаточно большим для обеспечения наблюдателю возможности укрыться от миниобъекта, стартовавшего из точки t₀;

3) ${\text{inf\;}}\{ {\text{||}}x - y{\text{||:\;}}x \in S,y \in Y\} > \varepsilon $;

4) существовал шар ${{V}_{\varepsilon }}\left( {\bar {f}} \right)$, удовлетворяющий включению

где есть конус с вершиной t₀, натянутый на S, а ${\text{conv}}({{t}_{0}} \cup S)$ – выпуклая оболочка объединения ${{t}_{0}} \cup S$.

Представляют интерес следующие два варианта расположения фрагмента S относительно t₀ и Y. В обоих вариантах предполагается существование плоскости $Q = {{Q}^{S}}$, содержащей точку t₀ и опорной к фрагменту S во внутренней для S базовой точке $s \in S \cap Q$. Пусть ${{y}_{s}} \in Y$ – ближайшая к s точка из Y. По условию выбора фрагмента S имеем ${\text{||}}s - {{y}_{s}}{\text{||}} < {\text{||}}s - {{t}_{0}}{\text{||}}$. Объект t движется по коридору Y от ${{t}_{{\text{*}}}}$ через точку t₀ в сторону точки y_s и далее к конечной точке t*. В варианте (см. рис. 1)

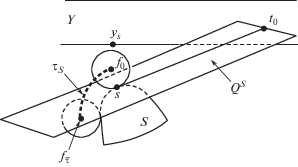
I) фрагмент S и точка y_s расположены по разные стороны от Q,

II) фрагмент S и точка y_s расположены по одну сторону от Q.

В обоих случаях начальное положение f₀ наблюдателя таково, что шар ${{V}_{\varepsilon }}\left( {{{f}_{0}}} \right)$ касается плоскости Q и поверхности S в точке s.

Траекторию движения центра шара ${{V}_{\varepsilon }}\left( {{{f}_{\tau }}} \right)$ при переходе наблюдателя из положения ${{V}_{\varepsilon }}\left( {{{f}_{0}}} \right)$ в положение ${{V}_{\varepsilon }}\left( {\bar {f}} \right)$ обозначим через ${{\mathcal{T}}_{S}}$. Естественно предположить, что траектория ${{\mathcal{T}}_{S}}$ лежит в плоскости Z, натянутой на точки ${{t}_{0}},{{f}_{0}},\bar {f}$ и $\rho \left( {{{f}_{\tau }},S} \right) = \varepsilon $ при $0 \leqslant \tau \leqslant \bar {\tau }$. Через τ_Q далее обозначаем значение временнόго параметра, при котором ${{f}_{{{{\tau }_{Q}}}}} \in Q$.

Предполагается, что наблюдатель из положения ${{V}_{\varepsilon }}\left( {{{f}_{0}}} \right)$ перемещается в положение ${{V}_{\varepsilon }}({{f}_{{{{\tau }_{Q}}}}})$, отслеживая движение объекта из точки ${{t}_{{\text{*}}}}$ в точку t₀. В момент прохождения объекта через точку t₀ и возможного запуска миниобъекта в направлении точки $s \in S$ наблюдатель стартует из точки ${{f}_{{{{\tau }_{Q}}}}}$ и за время $\bar {\tau } - {{\tau }_{Q}} \leqslant {{\tau }_{0}}$ на максимальной скорости уходит по траектории ${{\mathcal{T}}_{S}}$ в укрытие в точку ${{f}_{{\bar {\tau }}}}$.

Пусть ${{f}_{\tau }} \in {{\mathcal{T}}_{S}}$, ${{K}_{\tau }} = {\text{co}}\left( {{{f}_{\tau }},S} \right)$, ${{B}_{\tau }} = S \cap \partial {{K}_{\tau }}$. Ради простоты будем предполагать, что поверхность S является строго выпуклой, т.е. S не содержит прямолинейных отрезков. В этом случае множество ${{B}_{\tau }}$ является линией (см. рис. 2).

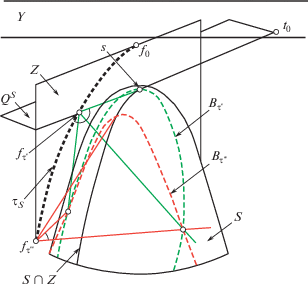
Пусть луч ${{l}_{\tau }}\left( b \right) = \left\{ {~b + \lambda \left( {b - {{f}_{\tau }}} \right){\text{:}}\,\lambda \geqslant 0} \right\},b \in {{B}_{\tau }}$, пересекается с Y, λ_Y = ${\text{sup}}\left\{ {\lambda {\text{:}}\,b + \lambda \left( {b - {{f}_{\lambda }}} \right) \in Y} \right\}$. Определим коническую поверхность:

и множество

Справедливы

Лемма 1. Пусть ${{\tau }_{Q}} \leqslant \tau {\kern 1pt} ' < \tau {\kern 1pt} '' < \bar {\tau }$, тогда ${{\mathcal{K}}_{{\tau '}}} \subset {{\mathcal{K}}_{{\tau ''}}}$.

Лемма 2. Отображения

являются непрерывными по Хаусдорфу.

Замечание 1. При отсутствии условия строгой выпуклости поверхности S отображение $\tau \to {{B}_{\tau }}$ является полунепрерывным сверху.

3. Множество траекторий $\mathcal{T} \subset Y$, соединяющих точку t₀ с поверхностью ${{k}_{{\bar {\tau }}}}$, обозначим через $\mathbb{T}$. Они соответствуют промежутку времени $\left[ {{{\tau }_{Q}},\bar {\tau }} \right]$ движения наблюдателя от ${{f}_{{{{\tau }_{Q}}}}}$ до выхода из зоны видимости миниобъекта. Для $\mathcal{T} \in \mathbb{T}$ возможны сегменты двух видов:

Пусть каждый из них максимален по вложению.

Опишем тактику движения объекта t от $\mathcal{T} \cap {{k}_{{\tau '}}}$ до $\mathcal{T} \cap {{k}_{{\tau ''}}}$ на отрезке времени ${{{\Delta }}_{\tau }} = [\tau {\kern 1pt} ',\tau {\kern 1pt} '']$. Скорость движения объекта t определяется скоростью движения конической поверхности k_τ, которая, в свою очередь, зависит от скорости движения наблюдателя f по траектории ${{\mathcal{T}}_{S}}$. При увеличении τ поверхность k_τ движется непрерывно от t₀ в сторону точки y_s. Наблюдателю не видны точки из множества $Y \cap {{\mathcal{K}}_{\tau }}$, поэтому в момент времени τ объект t, скрываясь от f, должен находиться во множестве $\mathcal{T} \cap {{\mathcal{K}}_{\tau }}$, в частности, принадлежать поверхности k_τ.

Если для любого $\tau \in {{{\Delta }}_{\mathcal{T}}}$ множество $\mathcal{T} \cap {{\mathcal{K}}_{\tau }}$ одноточечно, то движение объекта по маршруту $\mathcal{T} \cap {{{\Delta }}_{\mathcal{T}}}$ задается равенством $t = t\left( \tau \right) = \mathcal{T} \cap {{k}_{\tau }}$, т.е. t движется на временнόм промежутке ${{{\Delta }}_{\mathcal{T}}}$, не обгоняя k_τ, будучи невидимым для f, и его скорость движения равна

Если для некоторого отрезка $\left[ {{{\tau }_{1}},{{\tau }_{2}}} \right] \subset {{{\Delta }}_{\mathcal{T}}}$ множество $\mathcal{T} \cap {{k}_{\tau }}{\text{\;}}\left( {\tau \in \left[ {{{\tau }_{1}},{{\tau }_{2}}} \right]} \right)$ не является одноточечным, но одноточечно для ${{\tau }_{1}} - \delta ,~{{\tau }_{2}} + \delta $ при малых δ > 0, то объект, двигаясь по части маршрута $\mathcal{T}$, заключенного между ${{k}_{{{{\tau }_{1}}}}}$ и ${{k}_{{{{\tau }_{2}}}}}$, может лишь отстать от ${{k}_{\tau }}{\text{\;}}\left( {\tau \geqslant {{\tau }_{2}}} \right)$, оставаясь невидимым для f в силу леммы 1. Таким образом, указан способ выбора скоростного режима ${v}(t)$ объекта t на отрезке времени ${{{\Delta }}_{\mathcal{T}}}$. На временном отрезке Δ объект вынужден двигаться под наблюдением. Участок траектории $\mathcal{T}$ между точками t, t' будем обозначать через $\left[ {t,t{\kern 1pt} '} \right]$. Через Y° обозначается внутренность коридора Y.

Теорема 1. Пусть выпуклая поверхность $S \subset \partial G$, расположенная в позиции I), $\mathcal{T} \in \mathbb{T}$, тогда существуют $\tau {\text{*}},~\tau {\text{**}}~({{\tau }_{Q}} < \tau {\text{*}} \leqslant \tau {\text{**}} < \bar {\tau })$ такие, что на участках траектории $\left[ {t\left( {{{\tau }_{Q}}} \right),t\left( {\tau {\text{*}}} \right)} \right]$, $\left[ {t\left( {\tau {\text{**}}} \right),t\left( {\bar {\tau }} \right)} \right]$ возможно скрытое от наблюдателя движение объекта, в частности, движение $t\left( \tau \right) = \mathcal{T} \cap {{k}_{\tau }}$ со скоростью $dt{\text{/}}d\tau $.

Следствие. Пусть $\mathcal{T} \in \mathbb{T}$, D = $\{ [\tau {\kern 1pt} ';\tau {\kern 1pt} '']$ $ \subset $ $ \subset $ $[{{\tau }_{Q}},\bar {\tau }]\} $ – множество всех отрезков вида ${{{\Delta }}_{\mathcal{T}}}$ (см. (1)), включающее отрезки $[{{\tau }_{Q}},\tau {\text{*}}],[\tau {\text{**}},\bar {\tau }]$, тогда возможно скрытое от наблюдателя на отрезках из D движение объекта, его скорость ${{{v}}_{t}}$ на всей траектории $\mathcal{T}$ удовлетворяет неравенству (см. (2))

На оставшейся части отрезка $[{{\tau }_{Q}},\bar {\tau }]$ движение объекта происходит в условии наблюдения.

Теорема 2. Если S – выпуклая поверхность в позиции I) и $Y^\circ \cap {{k}_{\tau }} \ne \phi $ для всех $\tau \in \left[ {{{\tau }_{Q}},\bar {\tau }} \right]$, то скрытый от наблюдателя проход объекта t по маршруту $\mathcal{T} \in \mathbb{T}$ возможен тогда и только тогда, когда $\mathcal{T} \subset Y \cap \left( {\bigcup\limits_{{{\tau }_{Q}}}^{\bar {\tau }} {{{k}_{\tau }}} } \right)$.

Замечание 2. Если пересечение $\mathcal{T} \cap {{k}_{\tau }}$ одноточечно для любого $\tau \in \left[ {{{\tau }_{Q}},\bar {\tau }} \right]$, то объект может двигаться по правилу $t\left( \tau \right) = \mathcal{T} \cap {{k}_{\tau }}$. На участке многозначности пересечения $\mathcal{T} \cap {{k}_{\tau }}$ скорость движения может быть максимальной.

Теорема 3. Пусть S – выпуклая поверхность, расположенная в позиции II). Для любого маршрута $\mathcal{T} \in \mathbb{T}$ найдется точка $\tilde {t} \in \mathcal{T}$, $\tilde {t} \ne {{t}_{0}}$, $\tilde {t} \notin {{k}_{{\bar {\tau }}}}$ такая, что наблюдатель может отслеживать движение объекта на участке маршрута от t₀до $\tilde {t}$, и только на нем.

ИСТОЧНИК ФИНАНСИРОВАНИЯРабота выполнена в рамках исследований, проводимых в Уральском математическом центре.