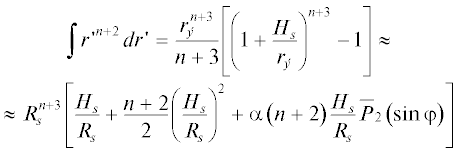Астрономический вестник, 2023, T. 57, № 6, стр. 532-543
Анализ эволюции Луны и возможной динамики ее недр
Н. А. Чуйкова a, *, Л. П. Насонова a, **, Т. Г. Максимова a
a Государственный астрономический институт им. П.К. Штернберга, МГУ
Москва, Россия
* E-mail: chujkova@sai.msu.ru
** E-mail: nason@sai.msu.ru
Поступила в редакцию 06.04.2023
После доработки 02.05.2023
Принята к публикации 17.05.2023
- EDN: DCIPBU
- DOI: 10.31857/S0320930X23060038
Аннотация
Для раннего этапа развития Луны определены топография ее поверхности и возможное распределение аномалий плотности в ее недрах. Найдено распределение аномалий силы притяжения и гравитационного потенциала в различных слоях верхней мантии, обусловленное гравитационным воздействием аномальных структур коры и мантии. Анализ полученных результатов приводит к выводу о возможности конвективных движений в расплавленных электропроводящих слоях коры и мантии, которые могли создать древнее магнитное поле. Для современного состояния плотностного строения Луны также определены гравитационные аномалии в различных слоях, которые могут привести к твердотельной конвекции в некоторых затвердевших областях Луны.
ВВЕДЕНИЕ
Анализ доставленных на Землю образцов лунного грунта позволил сделать некоторые выводы об эволюции Луны, наиболее полный обзор которых дан в книге (Жарков, 1983). Однако после 1994 г. исследования Луны продолжались сразу несколькими странами (Япония, Китай, Индия, США) в течение 2007–2013 гг. Были отправлены к Луне тяжелые спутники с научной аппаратурой, которые проделали огромную работу. В статье “Луна” из книги (Бережной и др., 2017, С. 65–105) довольно подробно изложены результаты современных исследований Луны с помощью тяжелых спутников и научной аппаратуры на них (1994–2013 гг.). В этой же статье есть и анализ эволюции Луны и возможной динамики ее недр на ранней стадии эволюции Солнечной системы на основе космических исследований. Кроме того, анализ эволюции Луны есть в книгах (Рускол, 1975; Сагитов, 1979; Галкин, 1988), а также в докладах на Московских международных симпозиумах по исследованиям Солнечной системы в 2017–2022 гг. Что же касается современных статей в рецензируемых журналах, посвященных той же тематике (Voropaev и др., 2021; Wu и др., 2019; Kuskov и др., 2019 и др.), то в них рассмотрены только вопросы эволюции Луны, однако вопросы динамики недр Луны в них не рассматривались.
АНОМАЛИИ ПОТЕНЦИАЛА И СИЛЫ ПРИТЯЖЕНИЯ В РАЗЛИЧНЫХ СЛОЯХ КОРЫ И МАНТИИ ЛУНЫ
Наши выводы об эволюции Луны и возможной динамике ее недр сделаны на основе анализа построенных карт аномалий потенциала и силы притяжения в различных слоях Луны (см. рис. 3–12). Расчет аномалий потенциала и силы притяжения делался в квадратичном приближении (Насонова, Чуйкова, 2007) на основе аномалий плотности в этих слоях (Чуйкова и др., 2020, рис. 4–8), полученных нами путем использования нового решения обратной задачи гравиметрии (Chujkova и др., 2014), проверенного нами для Земли.
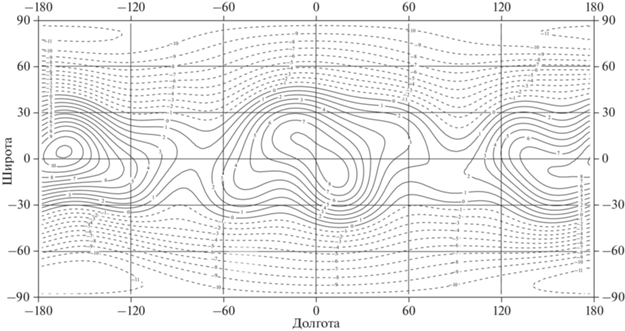
Рис. 1.
Высоты изостатически скомпенсированного рельефа Луны для ее раннего этапа развития. Сечение изолиний 0.5 км, диапазон изменения ((–6.6) – 3.9) км.
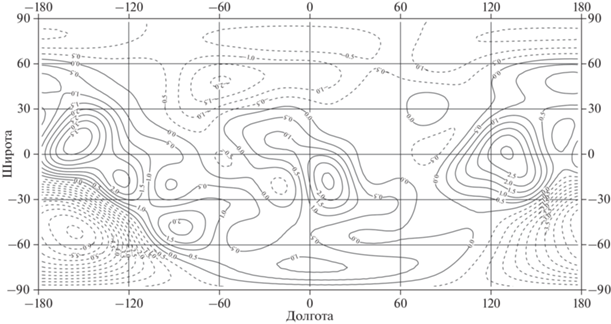
Рис. 2.
Распределение аномальных масс в коре на глубинах 0–10 км для раннего этапа развития Луны, приведенных к плотности простого слоя на средней глубине 2.71 км. Сечение изолиний 0.5 × 106 кг/м2. Диапазон изменений ((‒4.923) – 4.945) × 106 кг/м2.
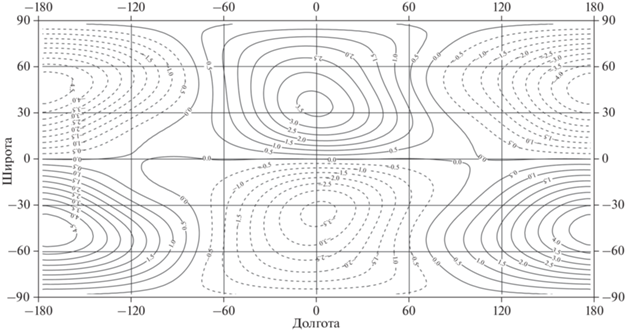
Рис. 3.
Относительные аномалии гравитационного потенциала на средней поверхности рельефа Луны при R1 = 1737.15 км. Сечение изолиний 2 × 10–5V0, V0 = g0R0,g0 = 1.62 м /c2, R0 = 1737.4 км. Диапазон изменений ((–27.8) – 28.3) × 10–5V0.
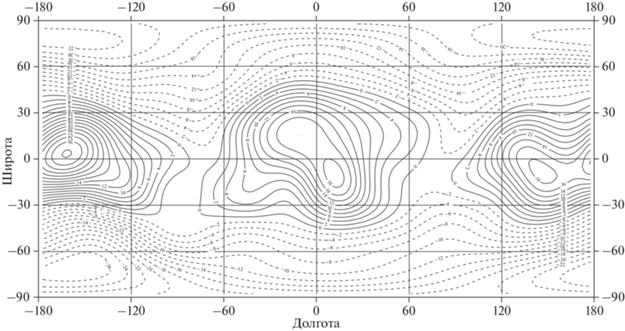
Рис. 4.
Относительные аномалии гравитационного потенциала в коре на средней глубине 2.71 км относительно R0. Сечение изолиний 2 × 10–5V0. Диапазон изменений ((–27.0) – 27.7) × 10–5V0.
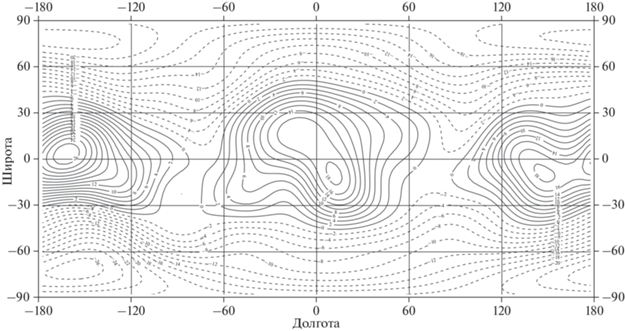
Рис. 5.
Относительные аномалии гравитационного потенциала в верхней мантии на средней глубине 91.1 км относительно R0. Сечение изолиний 2 × 10–5V0. Диапазон изменений ((–16.6) – 15.3) × 10–5V0.
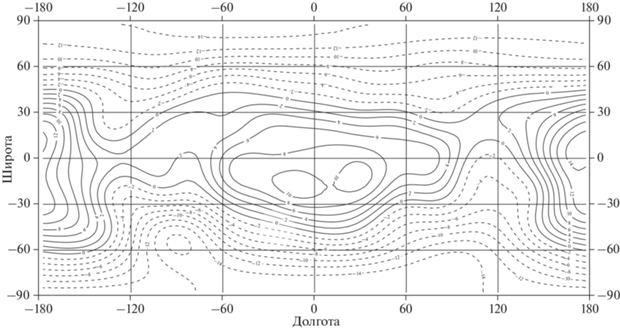
Рис. 6.
Относительные аномалии гравитационного потенциала в верхней мантии на средней глубине 156.8 км относительно R0. Сечение изолиний 2 × 10–5V0. Диапазон изменений ((–15.9) – 15.6) × 10–5V0.
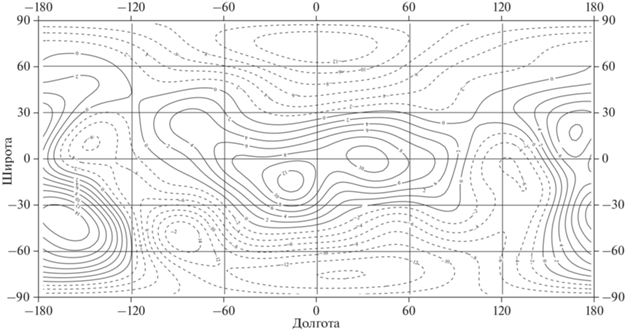
Рис. 7.
Относительные аномалии гравитационного потенциала на границе между верхней и нижней мантией на глубине 528.2 км относительно R0. Сечение изолиний 5 × 10–6V0. Диапазон изменений ((–33.2) – 38.4) × 10–6V0.
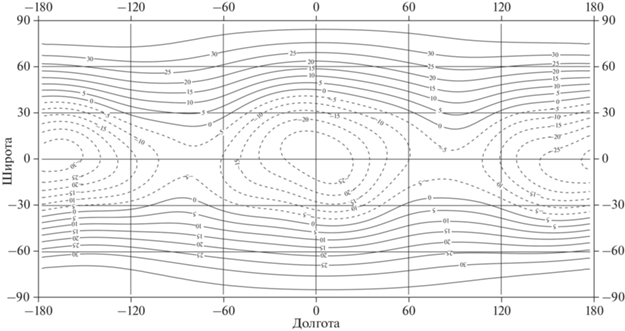
Рис. 8.
Относительные аномалии силы притяжения на средней поверхности рельефа Луны при R1 = 1737.15 км. Сечение изолиний 10–4g0. Диапазон изменений ((–13.6) – 14.1) × 10–4g0.
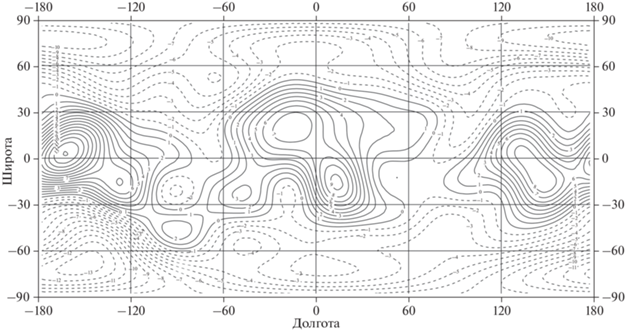
Рис. 9.
Относительные аномалии силы притяжения на внутренней поверхности простого слоя (см. рис. 2) на средней глубине 2.71 км относительно R0. Сечение изолиний 5 × 10–4g0. Диапазон изменений ((–32.4) – 43.6) × 10–4g0.
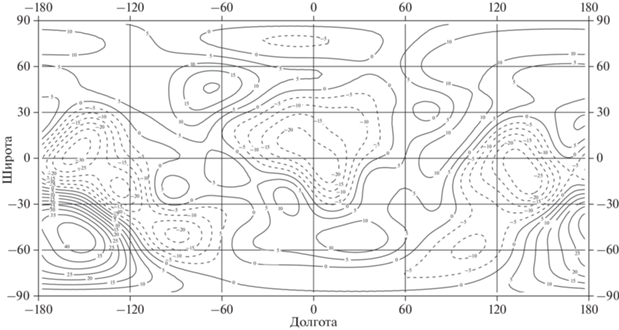
Рис. 10.
Относительные аномалии силы притяжения на внутренней поверхности простого слоя (рис. 4) на средней глубине 91.1 км относительно R0. Сечение изолиний 2 × 10–4g0. Диапазон изменений ((–26.5) – 23.2) × 10–4g0.
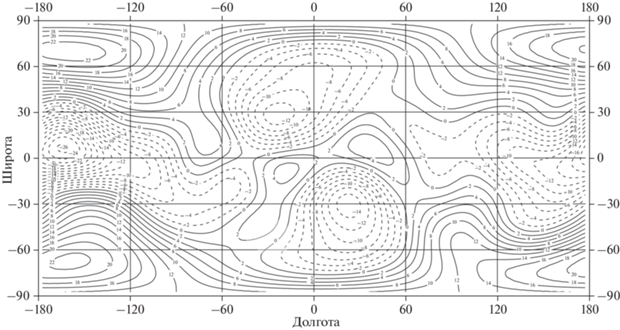
Рис. 11.
Относительные аномалии силы притяжения на внутренней поверхности простого слоя (рис. 5) на средней глубине 156.8 км относительно R0. Сечение изолиний 2 × 10–4g0. Диапазон изменений ((–11.2) – 14.5) × 10–4g0.
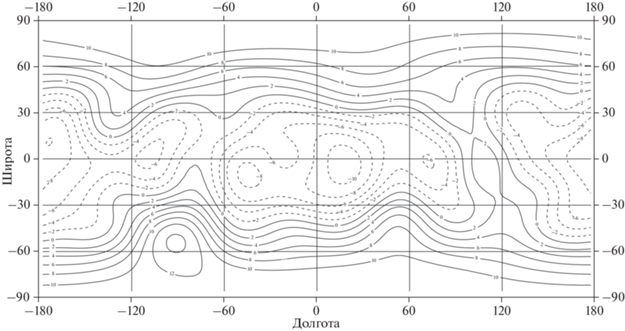
Рис. 12.
Относительные аномалии силы притяжения на внутренней поверхности границы средняя-нижняя мантия (рис. 7) на средней глубине 528.2 км относительно R0. Сечение изолиний 10–4g0. Диапазон изменений ((–11.9) – 11.2) × 10–4g0.
Полученные нами ранее (Чуйкова и др., 2020) аномальные плотностные структуры коры и мантии Луны вызывают аномалии как потенциала, так и силы притяжения в различных слоях коры и мантии, что могло привести к конвективным движениям в расплавленных электропроводящих слоях мантии, которые могли создать древнее магнитное поле. Анализ образцов грунта, доставленных с Луны, показал, что их магнетизм весьма разнороден для различных образцов (Жарков, 1983), что приводит к выводу о невозможности механизма гидромагнитного динамо для древней Луны.
В линейном приближении латерально распределенные аномальные массы представляются в виде простого слоя непрерывной плотности, распределенного на поверхности сферы. В этом случае между коэффициентами разложения аномалий плотности простого слоя по сферическим функциям и стоксовыми постоянными, обусловленными вкладом слоя, существует линейная связь (Дубошин, 1961):
$\Delta {{\sigma }_{s}}{{H}_{s}}\left( {\phi ,\lambda } \right) = \,\Delta {{\sigma }_{s}}\sum\nolimits_{n = 1}^N {\sum\nolimits_{m = 0}^n {\left( {\bar {A}_{{nm}}^{{(s)}}\cos m\lambda \, + \,\bar {B}_{{nm}}^{{(s)}}\sin m\lambda } \right)} } {{\overline P }_{{nm}}}\left( {\sin \phi } \right)$
– представление аномалий плотности простого слоя в виде разложения по нормированным сферическим функциям степени n ≤ N; $\Delta {{\sigma }_{1}}$, ${{H}_{1}}$ – средняя плотность и высоты эквивалентного (т.е. приведенного к однородной плотности $\Delta {{\sigma }_{1}}$ = 2.55 × × 103 кг/м3) рельефа относительно среднего радиуса ${{R}_{0}}$; Δσs = 0.35 × 103 кг/м3, Hs – средние скачки аномалий плотности на поверхностях компенсации рельефа и высоты поверхностей относительно среднего радиуса Rs; Δms= ΔσsHs – аномальные массы, распределенные в коре и в мантии и условно отнесенные к среднему радиусу Rs (согласно средней глубине изостатической компенсации, полученной в (Чуйкова и др., 2020)): $\left\{ {\begin{array}{*{20}{c}} {a_{{nm}}^{{(s)}}} \\ {b_{{nm}}^{{(s)}}} \end{array}} \right\}$ – коэффициенты разложения ${{h}_{s}} = \frac{{{{H}_{s}}\left( {\varphi ,\lambda } \right)}}{{{{R}_{s}}}}$ по нормированным сферическим функциям.
Суммарный вклад аномальных структур коры и мантии во внешний гравитационный потенциал и силу притяжения определяется тогда следующими выражениями:
(1)
$\Delta {{V}_{e}}\left( {r,\varphi ,\lambda } \right) = \frac{{f{{M}_{0}}}}{r}\sum\limits_{s = 1}^7 {\sum\limits_{n = 1}^N {{{{\left( {\frac{a}{r}} \right)}}^{n}}Y_{n}^{{(s)}}\left( {\varphi ,\lambda } \right)} } ,$(2)
$\begin{gathered} \Delta {{g}_{e}}\left( {r,\varphi ,\lambda } \right) = - \frac{{\partial {{V}_{e}}}}{{\partial r}} = \\ = \frac{{f{{M}_{0}}}}{{{{r}^{2}}}}\sum\limits_{s = 1}^7 {\sum\limits_{n = 1}^N {\left( {n + 1} \right){{{\left( {\frac{a}{r}} \right)}}^{n}}Y_{n}^{{\left( s \right)}}\left( {\varphi ,\lambda } \right)} } , \\ \end{gathered} $$\begin{gathered} Y_{n}^{{\left( s \right)}}\left( {\varphi ,\lambda } \right) = \\ = \sum\nolimits_{m = 0}^n {\left( {\Delta C_{{nm}}^{{(s)}}\cos m\lambda + \Delta D_{{nm}}^{{(s)}}\sin m\lambda } \right){{{\overline P }}_{{nm}}}\left( {\sin \varphi } \right)} , \\ \end{gathered} $
${{\overline P }_{{nm}}}\left( {\sin \varphi } \right)$ – нормированные по Каула присоединенные функции Лежандра (Чуйкова и др., 2006).
Аналогичным образом можно определить вклад этих же структур во внутреннее гравитационное поле в коре и в мантии. Так, при расчете аномалий гравитационного поля в верхней коре (при R1 < r < R0) вклад рельефа (s = 1) определяется формулами:
(3)
$\Delta {{V}_{i}}\left( {r,\varphi ,\lambda } \right) = \frac{{f{{M}_{0}}}}{{{{R}_{s}}}}\sum\limits_{n = 1}^N {{{{\left( {\frac{r}{{{{R}_{s}}}}} \right)}}^{n}}Y_{n}^{{(s)}}\left( {\varphi ,\lambda } \right)} ,$(4)
$\Delta {{g}_{i}}\left( {r,\kappa ,\lambda } \right) = - \frac{{f{{M}_{0}}}}{{R_{s}^{2}}}\sum\limits_{n = 1}^N {n{{{\left( {\frac{r}{{{{R}_{s}}}}} \right)}}^{{n - 1}}}Y_{n}^{{(s)}}\left( {\varphi ,\lambda } \right)} .$Вклад остальных слоев (s = 2–7) определяется формулами, аналогичными формулам (1) и (2), нужно только заменить их для внутреннего потенциала и силы притяжения:
(5)
$\Delta {{V}_{i}}\left( {r,\varphi ,\lambda } \right) = \frac{{f{{M}_{0}}}}{{\mathop R\nolimits_s }}\sum\limits_{s = 2}^7 {\sum\limits_{n = 1}^N {{{{\left( {\frac{r}{{\mathop R\nolimits_s }}} \right)}}^{n}}Y_{n}^{{(s)}}\left( {\varphi ,\lambda } \right)} } ,$(6)
$\begin{gathered} \Delta {{g}_{i}}\left( {r,\varphi ,\lambda } \right) = - {\text{ }}\frac{{\partial {{V}_{i}}}}{{\partial r}} = \\ = - \frac{{f{{M}_{0}}}}{{{{{\mathop R\nolimits_s }}^{2}}}}\sum\limits_{s = 2}^7 {\sum\limits_{n = 1}^N {n{{{\left( {\frac{r}{{\mathop R\nolimits_e }}} \right)}}^{{n - 1}}}Y_{n}^{{\left( s \right)}}\left( {\varphi ,\lambda } \right)} } , \\ \end{gathered} $(7)
${\text{где}}\,\,\left\{ {\begin{array}{*{20}{c}} {\Delta C_{{nm}}^{{(s)}}} \\ {\Delta D_{{nm}}^{{(s)}}} \end{array}} \right\} = \frac{3}{{2n + 1}}{{\left( {\frac{{{{R}_{s}}}}{{{{R}_{0}}}}} \right)}^{3}}\frac{{\Delta {{\sigma }_{s}}}}{{\overline \sigma }}\left\{ {\begin{array}{*{20}{c}} {a_{{nm}}^{{(s)}}} \\ {b_{{nm}}^{{(s)}}} \end{array}} \right\},$(8)
$\left\{ {\begin{array}{*{20}{c}} {a_{{nm}}^{{\left( s \right)}}} \\ {b_{{nm}}^{{\left( s \right)}}} \end{array}} \right\} = {{\left\{ {\begin{array}{*{20}{c}} {{{a}_{{nm}}}} \\ {{{b}_{{nm}}}} \end{array}} \right\}}_{1}} = \frac{1}{{{{R}_{s}}}}\left\{ {\begin{array}{*{20}{c}} {\overline A _{{nm}}^{{(s)}}} \\ {\overline B _{{nm}}^{{(s)}}} \end{array}} \right\}$В реальности массы рельефа и, тем более, аномальные массы, обусловленные скачком плотности
на границах слоев Луны, являются не простым сферическим слоем, а распределенными по
высоте относительно эллипсоида относимости 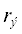 . В этом случае при представлении внешнего поля для s = 1.2 формулами (1) и (2) коэффициенты разложения определяются интегрированием по массам рельефа в квадратичном
приближении:
. В этом случае при представлении внешнего поля для s = 1.2 формулами (1) и (2) коэффициенты разложения определяются интегрированием по массам рельефа в квадратичном
приближении:
 $\begin{gathered} \left\{ {\begin{array}{*{20}{c}} {\Delta C_{{nm}}^{{(s)}}} \\ {\Delta D_{{nm}}^{{(s)}}} \end{array}} \right\} = \frac{{\Delta {{\sigma }_{s}}}}{{\left( {2n + 1} \right){{M}_{0}}}}\int\limits_{} {\int\limits_{} {\int\limits_{} {r{\kern 1pt} {{'}^{{n + 2}}}} {{{\bar {P}}}_{{nm}}}} } \times \\ \times \,\,(\sin \varphi {\kern 1pt} ')\cos m\lambda {\kern 1pt} 'r{\kern 1pt} '{\text{d}}\lambda {\kern 1pt} '{\text{d}}\sin \varphi {\kern 1pt} ',\,\,\,\,{\text{где}} \\ \end{gathered} $
$\begin{gathered} \left\{ {\begin{array}{*{20}{c}} {\Delta C_{{nm}}^{{(s)}}} \\ {\Delta D_{{nm}}^{{(s)}}} \end{array}} \right\} = \frac{{\Delta {{\sigma }_{s}}}}{{\left( {2n + 1} \right){{M}_{0}}}}\int\limits_{} {\int\limits_{} {\int\limits_{} {r{\kern 1pt} {{'}^{{n + 2}}}} {{{\bar {P}}}_{{nm}}}} } \times \\ \times \,\,(\sin \varphi {\kern 1pt} ')\cos m\lambda {\kern 1pt} 'r{\kern 1pt} '{\text{d}}\lambda {\kern 1pt} '{\text{d}}\sin \varphi {\kern 1pt} ',\,\,\,\,{\text{где}} \\ \end{gathered} $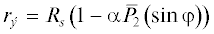 , $\alpha = \frac{2}{3}e \approx {{10}^{{ - 3}}}$, $e$ – сжатие эллипсоида относимости (для Луны e = 0).
, $\alpha = \frac{2}{3}e \approx {{10}^{{ - 3}}}$, $e$ – сжатие эллипсоида относимости (для Луны e = 0).
При учете квадратичных членов и эллипсоидальности поверхности относимости в формуле (8) возникают дополнительные члены, а именно
(9)
$\left\{ {\begin{array}{*{20}{c}} {a_{{nm}}^{{(s)}}} \\ {b_{{nm}}^{{(s)}}} \end{array}} \right\} = {{\left\{ {\begin{array}{*{20}{c}} {{{a}_{{nm}}}} \\ {{{b}_{{nm}}}} \end{array}} \right\}}_{1}} + \frac{{n + 2}}{2}{{\left\{ {\begin{array}{*{20}{c}} {{{a}_{{nm}}}} \\ {{{b}_{{nm}}}} \end{array}} \right\}}_{2}} + \alpha \left( {n + 2} \right){{\left\{ {\begin{array}{*{20}{c}} {{{a}_{{nm}}}} \\ {{{b}_{{nm}}}} \end{array}} \right\}}_{3}},$где первый член (индекс 1) соответствует коэффициентам разложения функции ${{h}_{s}}$ (т.е. линейному приближению), член с индексом 2 соответствует коэффициентам разложения функции ${{\left( {{{h}_{s}}} \right)}^{2}}$, а с индексом 3 – коэффициентам разложения функции ${{h}_{s}}{{\overline P }_{2}}\left( {\sin \varphi } \right).$ При расчете сил притяжения на эллипсоиде, подобно расположенном относительно эллипсоида относимости, коэффициенты, учитывающие эллипсоидальность (с индексом 3), в квадратичном приближении отсутствуют.
Аналогичным образом можно получить формулы и для внутреннего поля, где в выражениях (3), (4), (7) вместо (9) следует использовать формулу (10):
(10)
$\left\{ {\begin{array}{*{20}{c}} {a_{{nm}}^{{(s)}}} \\ {b_{{nm}}^{{(s)}}} \end{array}} \right\} = {{\left\{ {\begin{array}{*{20}{c}} {{{a}_{{nm}}}} \\ {{{b}_{{nm}}}} \end{array}} \right\}}_{1}} - \frac{{n - 1}}{2}{{\left\{ {\frac{{{{a}_{{nm}}}}}{{{{b}_{{nm}}}}}} \right\}}_{2}} + \alpha \left( {n - 1} \right){{\left\{ {\begin{array}{*{20}{c}} {{{a}_{{nm}}}} \\ {{{b}_{{nm}}}} \end{array}} \right\}}_{3}}.$Сравнивая формулы (6) совместно с (9) и (4) совместно с (10), мы видим, что вклад квадратичных членов во внешнюю и внутреннюю силу притяжения одинаков по знаку и отличается только множителем (n + 1) (n + 2) для внешнего поля и n(n – 1) для внутреннего. Вклад же линейных членов и членов, учитывающих эллипсоидальность, противоположен по знаку для внешней и внутренней сил притяжения.
Формулы, позволяющие выразить коэффициенты ${{\left\{ {{{a}_{{nm}}},{{b}_{{nm}}}} \right\}}_{2}}$, ${{\left\{ {{{a}_{{nm}}},{{b}_{{nm}}}} \right\}}_{3}}$ через ${{\left\{ {{{a}_{{nm}}},{\text{ }}{{b}_{{nm}}}} \right\}}_{1}}$, были получены нами путем математического моделирования символьных вычислений в математических пакетах компьютерной алгебры (Насонова, Чуйкова, 2007).
АНОМАЛЬНЫЕ СТРУКТУРЫ РЕЛЬЕФА И АНОМАЛЬНЫЕ МАССЫ В КОРЕ И МАНТИИ ЛУНЫ НА ГЛУБИНАХ 0–530 км
Определено возможное распределение аномалий плотности в недрах Луны. Для этой цели применено разработанное нами новое решение некорректной обратной задачи гравиметрии, проверенной для Земли и Марса. Суть его заключается в том, что на основе только космических данных о гравитационном поле и рельефе планеты однозначно определяются глубины изостатической компенсации для ряда гармоник разложения высот рельефа по сферическим функциям. Показано, что возможная изостатическая компенсация рельефа осуществляется в интервале глубин 0–530 км. Определены наиболее вероятные глубины компенсации в этом интервале на этих глубинах. Для остальных гармоник были выбраны два других варианта: компенсация на двух уровнях, первым из которых является средняя глубина коры в 2.7 км; возможные глубины для второго уровня определялись из анализа результатов, полученных для изостатически скомпенсированных гармоник (Чуйкова и др., 2020).
Для раннего этапа развития Луны ((4–4.57) × × 109 лет назад) нами были определены топография ее поверхности и возможное распределение плотности в ее недрах. Рис. 1 и рис. 2 соответствуют самому раннему периоду истории Луны, когда большая часть Луны была в расплавленном состоянии и силы плавучести превосходили силы вязкости. Распределения аномалий плотности в коре и мантии на глубинах (20–280, 528.2 км) (Чуйкова и др., 2020) соответствуют более позднему периоду, когда аномальные массы, соответствующие изостатической компенсации масс рельефа, из расплавленного состояния перешли в твердое состояние (т.е. отвердели). Для глубин больше 530 км, по-видимому, эта часть мантии соответствует более древним, не подверженным плавлению слоям Луны (Nakamura, 1983; Хаббард, 1987).
Что же касается приповерхностных отвердевших слоев Луны на глубинах 0–10 км, то очевидно, что они были разрушены ударами метеоритов и комет в более поздние времена и никак не компенсированы, а создают напряжения в теле Луны (Чуйкова и др., 2020). Исключение составляет бассейн Южный полюс – Эйткен, который, по-видимому, образован в результате удара крупного небесного тела в более раннее время (~4 × 109 лет назад) и изостатически скомпенсирован вплоть до средней глубины 238 км (Чуйкова и др., 2020). Кроме того, его падение, по-видимому, привело к повороту Луны относительно линии Земля–Луна, что могло привести к смещению к северу приливного горба Луны, образованного в ранние времена (рис. 2), и к изменению карты высот рельефа Луны (рис. 1) по сравнению с первоначальным временем (измененной к тому же к настоящему времени из-за ударов метеоритов и комет). Так, современные точные расчеты для высот рельефа относительно центра масс показывают смещение центра фигуры Луны относительно центра масс от Земли на расстояние 1774.0 м, смещение к западу на 730.7 м и смещение к северу на расстояние 238.1 м. Общее смещение Δr = 1933.2 м при φ = 7.1° и при λ = –158.5° з.д. (Чуйкова и др., 2019).
Распределение аномальных масс в коре на глубинах 20–50 км, в верхней мантии на глубинах 60–170 км, в переходном слое верхняя-средняя мантия на глубинах 190–280 км и на границе средняя-нижняя мантия на глубине 528.2 км приведено в статье (Чуйкова и др., 2020), см. рис. 4–8.
АНОМАЛИИ ГРАВИТАЦИОННОГО ПОТЕНЦИАЛА И СИЛЫ ПРИТЯЖЕНИЯ
На рис. 3–7 представлены карты аномалий потенциала V на различных глубинах.
На рис. 8–12 представлены карты аномалий силы притяжения g на различных глубинах.
Из сравнения рис. 3–12 видно, что различные регионы Луны имеют довольно различающиеся аномалии гравитационного поля на разных глубинах, что может привести к конвективным движениям в различных слоях Луны.
КОНВЕКТИВНЫЕ ДВИЖЕНИЯ И МАГНИТНЫЕ АНОМАЛИИ В КОРЕ И МАНТИИ ЛУНЫ
Конвективные движения возможны, если есть силы, вызывающие латеральные движения вещества. В газовых и жидких оболочках планет (и Солнца) в качестве таких сил выступают силы Кориолиса, возникающие при радиальных движениях в сферических оболочках. Во внутренних оболочках в качестве таких сил могут выступать латеральные аномалии гравитационного потенциала. В итоге возникают энергетически выгодные движения для тяжелых компонент субдукцирующего блока вниз к центру Луны (в силу действия закона гравитационной дифференциации), но и латеральные перемещения в сторону максимума потенциала, а для легких компонент плюма – движения в сторону минимума потенциала.
Построенные на основе полученных нами раньше аномалий плотности в различных слоях Луны (Чуйкова и др., 2020) карты аномалий силы притяжения и потенциала на различных глубинах (рис. 3–12) приводят к выводу о возможности конвективных движений в мантии Луны в ранние периоды истории Луны, когда большая часть Луны была в расплавленном состоянии. Так, латеральные движения (рис. 3–7) максимальны на поверхности и в верхнем слое коры (рис. 3, рис. 4), затем убывают в мантии и меняют свой знак при пересечении верхней и нижней мантии на глубине 528.2 км (рис. 7). Радиальные движения, обусловленные дифференциацией компонент вещества коры и мантии (рис. 8–12), аномалии скоростей которых максимальны в верхнем слое коры (рис. 9) и затем убывают в мантии и меняют свой знак при пересечении верхней и нижней мантии на глубине 528.2 км (рис. 12). Причем характер аномалий сильно меняется при пересечении различных границ в коре и мантии. Все это приводит к выводу, что локальные поля магнитных аномалий, обусловленные наличием электропроводящих веществ (например, железа) (Паркинсон, 1986), весьма разнородны в различных участках лунной коры и мантии, что соответствует анализу лунных образцов грунта.
Также интересно отметить, что расчет аномалий гравитационного потенциала в аномальных зонах показывает четкую корреляцию картины латерального распределения потенциала (рис. 6, рис. 7) с распределением аномальных масс на этих же глубинах. Это свидетельствует о том, что распределение аномальных масс слоя устойчиво к гравитационному воздействию аномальных масс на других уровнях и определяется потенциалом только масс слоя. Причем анализ аномалий притяжения между слоями (рис. 8, рис. 9), ответственных за вариации скорости дифференциации между слоями, приводит к выводу, что положительные аномалии плотности и потенциала поддерживаются за счет меньшей скорости дифференциации ниже слоя, а отрицательные аномалии – за счет меньшей скорости дифференциации выше слоя. Все это может свидетельствовать о том, что отклонения внутреннего строения Луны (а также планет) от равновесного, образовавшиеся в начальный период формирования Луны (а также планет), могут оставаться стабильными в течение долгого периода существования Солнечной системы, несмотря на стремление любой замкнутой системы к равновесному состоянию. Можно также отметить, что горизонтальная компонента скорости течения, обусловленная вариациями потенциала, максимальна в средних частях слоя и может только усиливать вариации плотности со временем, а вертикальная компонента максимальна вблизи границ слоев.
Что же касается современного состояния плотностного строения Луны, то неравномерное гравитационное поле может отражать флуктуации плотности, обусловленные твердотельной конвекцией в глубинных недрах Луны (Хаббард, 1987). Чтобы данные по тепловому потоку (Keihm, Langseth, 1977) пришли в согласие с сейсмическими данными (Nakamura, 1983), Хаббард предположил, что недра Луны до сих пор могут быть активными, несмотря на то, что над ними располагается мощная упругая литосфера.
Подробный анализ эволюции Луны дан в книге (Жарков, 1983). В истории эволюции Луны им выделены пять периодов. Первый период формирования макроструктуры лунных недр продолжался примерно 1.1 × 108 лет, начиная с момента образования Луны (4.57 × 109 лет назад) и закончился 4.46 × 109 лет назад. Следующий период завершился 3.86 × 109 лет назад и связан с началом образования круговых морей. Окончание периода датируется временем ударного образования Моря Дождей (3.86 × 109 лет назад). В этот период в Луне протекали разнообразные процессы, как эндогенные, так и экзогенные, которые привели к стабилизации Луны как планетного тела. Третий период в эволюции Луны длился примерно 108 лет ((4–3.9) × 109 лет назад) и связан с ударным образованием круговых бассейнов и завершился формированием материков. Четвертый период (от 3.9 × 109 до 3.16 × 109 лет назад) связан с заполнением лунных морей базальтовой лавой и завершился образованием масконов. Его особенностью является затухание тектонической активности Луны. В последующие периоды лик Луны не менялся за счет эндогенных процессов. Эрозия лунной поверхности в последние 3 × 109 лет обусловлена только метеоритной бомбардировкой, которая не стерла главных событий в жизни Луны. Жарков сделал также и подробный анализ приливной эволюции лунной орбиты (Жарков, 1983).
Полный анализ эволюции Луны и возможной динамики ее недр сделан в книге (Сагитов, 1979). В истории эволюции Луны выделяются три фазы: догеологическая (4.6 млрд лет назад произошла дифференциация пород в недрах Луны и образование первичной коры); магматическая (4.3 млрд лет назад образовался слой реголита от падения планетезималий; 4.0 млрд лет назад образовались впадины округлой формы (будущие круговые моря), обрамленные кольцевыми горами, по трещинам с глубин ~400 км изливался (3.8–3.2 млрд лет назад) расплавленный базальт, образуя моря и Океан Бурь). Высокая вулканическая активность закончилась 3.0 млрд лет назад, образовалась толстая литосфера с глубиной нижней границы ~1000 км.
Экзогенная фаза началась, когда ослабла роль внутренней энергии (за счет распада радиоактивных элементов). Затухала сейсмическая активность и началась метеоритная бомбардировка, но эндогенные процессы остались, только приуменьшилась их роль. Следы недавних лавовых излияний видны на валах поздних крупных кратеров. Признаки вулканизма наблюдались и в наши дни в виде выхода газов из недр в кратерах Тихо, Аристарх и других.
Аналогичный анализ эволюции Луны сделан также в книге (Галкин, 1988). Выводы Галкина опираются как на результаты анализа лунных образцов грунта, так и на замеры электромагнитных и гравитационных полей, теплового потока, скоростей сейсмических волн, наблюдения скоротечных явлений. Интенсивная конвекция в недрах Луны в прошлом могла быть источником магнитного поля, обнаруженного в лунных образцах. В настоящее время тектоническая жизнь Луны парализуется мощной литосферой. В разогретой астеносфере могут существовать конвективные потоки, но они слабы и в состоянии вызвать лишь редкие, слабые истечения газов. Однако открытие и изучение энергичных тектонических лунотрясений, наблюдения быстро проходящих явлений на поверхности, высокий тепловой поток и истечение инертных газов из недр Луны показали, что в лунных недрах еще идут активные процессы.
Некоторые наблюдатели отмечали изменение деталей поверхности в районе кратера Альфонс и выделение газа из центральной горки этого кратера. Указание на былую тектоническую активность служит знаменитая Прямая Стена в Море Облаков; этот 125-километровый уступ высотой 200–300 м, вероятно, образован при перемещении плит лунной коры (Бережной и др., 2017).
Следует отметить, что в статье (Кусков и др., 2018) приведены аргументы, которые отвергают возможное формирование Луны из вещества примитивной мантии Земли. Наиболее убедительные гипотезы образования Луны из некоторого первоначального роя частиц и тел, двигающихся по геоцентрической орбите, представлены в книге (Рускол, 1975).
ЗАКЛЮЧЕНИЕ
Полученные нами результаты свидетельствуют о том, что эволюция недр Луны за время ее существования в основном происходила в слоях Луны до глубины 530 км. Конвективные движения, обусловленные аномалиями гравитационного потенциала и силы притяжения в различных слоях мантии Луны, могли привести к локальным полям магнитных аномалий (Паркинсон, 1986). Сделанные выводы об эволюции Луны и возможной динамике ее недр основаны на результатах анализа образцов лунного грунта и гравитационного поля за 1969–1987 гг.
Итоги исследований других авторов отражены в докладах на Московских международных симпозиумах по исследованиям Солнечной системы в 2017–2022 гг. Однако в научных программах симпозиумов в основном представлены результаты анализа данных научной аппаратуры и планы освоения Луны и ее ресурсов в последующие годы. Проблемы эволюции Луны отражены только в нескольких докладах на симпозиуме в 2022 г. (Voropaev, Krivenko, 2022; Yongliao Zou и др., 2022; Kronrod и др., 2022), а также в докладах на симпозиумах: в 2017 г. (Kronrod и др., 2017; Gusev и др., 2017), в 2018 г. (Head, Vilson, 2018), в 2019 г. (Head, Vilson, 2019; Voropaev, Dnestrovsky, 2019). Кроме того, эти проблемы были рассмотрены в статьях (Voropaev и др., 2021; Wu и др., 2019; Kronrod и др., 2019), а также есть статьи других авторов в рецензируемых журналах (Kuskov и др., 2019; Wu и др., 2019; Zuber и др., 2013). Все результаты в этих статьях получены на основе данных о гравитационном поле и рельефе Луны. Однако вопросы динамики недр Луны в них не рассмотрены. По-видимому, наиболее подробной и точной для гравитационного поля Луны является современная модель (KA Grail mission), полученная по данным слежения системы спутник-спутник (Zuber и др., 2013).
Список литературы
Бережной А.А., Бусарев В.В., Ксанфомалити Л.В., Сурдин В.Г. (ред.-сост.), Холшевников К.В. Солнечная система. М.: Физматлит, 2017. 460 с.
Галкин И.Н. Внеземная сейсмология. М.: Наука, 1988. С. 102–124.
Дубошин Г.Н. Теория притяжения. М.: Физматгиз, 1961. С. 258–261.
Жарков В.Н. Внутреннее строение Земли и планет. М.: Наука, 1983. С. 396–404.
Кусков О.Л., Кронрод Е.В., Кронрод В.А. Геохимические ограничения на “холодные” и “горячие” модели внутреннего строения Луны: валовый состав // Астрон. вестн. 2018. Т. 52. № 6. С. 481–494.
Насонова Л.П., Чуйкова Н.А. Аномалии внешнего и внутреннего гравитационного поля изостатически уравновешенной коры Земли в квадратичном приближении // Вестн. Моск. ун-та. Сер. 3. Физ., астрон. 2007. № 6. С. 61–68.
Паркинсон У. Введение в геомагнетизм. М.: Мир, 1986. 528 с.
Рускол Е.Л. Происхождение Луны. М.: Наука, 1975. С. 130–153.
Сагитов М.У. Лунная гравиметрия. М.: Наука, 1979. С. 389–403.
Хаббард У. Внутреннее строение планет. М.: Мир, 1987. С. 174–195.
Чуйкова Н.А., Насонова Л.П., Максимова Т.Г. Аномалии внутреннего гравитационного поля в коре и верхней мантии Земли // Вестн. Моск. ун-та. Сер. 3. Физ., астрон. 2006. № 4. С. 48–56.
Чуйкова Н.А., Насонова Л.П., Максимова Т.Г. Определение глобальных плотностных неоднородностей и напряжений внутри Луны // Астрон. вестн. 2020. Т. 54. № 4. С. 325–336. (Chujkova N.A., Nasonova L.P., Maximova T.G. Determination of global density inhomogeneities and stresses inside the Moon // Sol. Syst. Res. 2020. V. 54. № 4. P. 295–306.)
Чуйкова Н.А., Родионова Ж.Ф., Максимова Т.Г., Гришакина Е.А. Анализ высот рельефа Луны и корреляционной связи рельефа с гравитационным полем; предварительные выводы о глобальных плотностных неоднородностях коры Луны // Астрон. вестн. 2019. Т. 53. № 3. С. 174–184. (Chujkova N.A., Rodionova Zh.F., Maximova T.G., Grishakina E.A. Analysis of lunar terrain altitudes and correlation links between the terrain and gravitational field; preliminary conclusions on the global density inhomogeneities of the lunar crust // Sol. Syst. Res. 2019. V. 53. № 3. P. 161–171.)
Chujkova N.A., Nasonova L.P., Maximova T.G. The new method to found the anomalous internal structute of terrestrial planets and its test on the Earth // IAG Symp. Ser. 2014. V. 144. Chapter 195. P. 209–219. Proc. 3rd Internat. Gravity Field Service (IGFS), Shanghai, China, June 30–July 6. 2014. https://doi.org/10.1007/978-3-319-39820-4.
Gusev A., Hanada H., Kosov A., Ping J., Vasilyev M. Spin-orbital evolution and interior of the Moon: past, modern, future // Abstracts of the Eight Moscow Sol. Syst. Symp. 2017. P. 268–270.
Head J., Vilson L. Lunar basaltic volcanic eruptions: gas releasenpatterns and variations in lava vesicularity: fissure, Mare flows, and ring moat dome structure (RMDS) morphology.
Abstracts of the Ninth Moscow Sol. Syst. Symp. 2018. P. 164–166.
Head J., Vilson L. Rethinking lunar mare basalt regolith formation: New concepts of lava flow protolith and evolution of regolith thickness and internal structure // Abstracts of the Tenth Moscow Sol. Syst. Symp. 2019. P. 103–106.
Keihm S.J., Langseth M.G. Lunar thermal regime to 300 km // Proc. 8th Lunar Sci. Conf. 1977. P. 499–514.
Kronrod E.V., Matsumoto K., Kuskov O., Kronrod V., et al. Lunar internal structure models consistent with seismic and selenodetic (GRAIL and LLR) data and thermodynamic constraints // Abstracts of the Eight Moscow Sol. Syst. Symp. 2017. P. 271–273.
Kronrod E.V., Kronrod V.A., Kuskov O.L. Thermal evolution of the Moon with geophysical constraints // Abstracts of the Thirteen Moscow Sol. Syst. Symp. 2022. P. 181–183.
Kuskov O.L., Kronrod E.V., Kronrod V.A. Effect of thermal state on the mantle composition and core size of the Moon // Geochem. Intern. 2019. V. 57. P. 605–620.
Nakamura Y. Seismic velocity structure of the lunar mantle // J. Geophys. Res. 1983. V. 88. P. 677–686.
Voropaev S.A., Dnestrovsky A.Yu. Features of the fossil tidal bulge formation for the early Moon // Abstracts of the Tenth Moscow Sol. Syst. Symp. 2019. P. 116–118.
Voropaev S.A., Dnestrovskii A.Yu., Marov M.Ya. Features of the fossil tidal bulge formation for the early Moon // Doklady Physics. Pleiades Publ., 2019. V. 64. P. 80–83.
Voropaev S.A., Nugmanov I.I., Dushenko N.V., Kuz’mina T.G., Korochantsev A.V., Senin V.G., Eliseev A., Jianguo Y. Relationship between the H5 chondrite composition, structure and mechanical properties from the example of NWA12370 and Pultusk // Sol. Syst. Res. 2021. V. 55. № 5. P. 409–419.
Voropaev S.A., Krivenko A.P. Some features of the early Moon’ degassing // Abstracts of the Thirteen Moscow Sol. Syst. Symp. 2022. P. 99–101.
Wu W.R., Liu J.Z., Tang Y.N.,Yu D.,Yu G.,Zhang J.H. China Lunar Exploration Program // J. Deep Space Exploration. 2019. V. 6(5). P. 405–416.
Zou Y.L., Liu J.Z., Lin Y.T., Du A.M., Jia Y.Z., Zhang J.H., Xu L.,Wang C. Studying lunar evolution based on comprehensive physical field exploration for International Lunar Research Station program // Abstracts Thirteen Moscow Sol. Syst. Symp. 2022. P. 129–131.
Zuber M.T., Smith D.E., Watkins M.M., Asmar S.W., Konopliv A.S., Lemoine F.G., Melosh H.J., Neumann G.A., Phillips R.J., Solomon S.C., Wieczorek M.A., Williams J.G., Goossens S.J., Kruizinga G., Mazarico E., Park R.S., Dah-Ning Yuan D.-N. Gravity field of the Moon from the Gravity Recovery and Interior Laboratory (GRAIL) mission // Science. 2013. V. 339. № 6120. P. 668–671. https://doi.org/10.1126/science.1231507
Дополнительные материалы отсутствуют.
Инструменты
Астрономический вестник