Астрономический вестник, 2023, T. 57, № 2, стр. 181-196
Избранные проблемы классической и современной небесной Механики и звездной динамики. II. Современные исследования
И. И. Шевченко a, b, *, А. В. Мельников c, В. Б. Титов a, Р. В. Балуев a, А. В. Веселова a, А. В. Кривов a, Д. В. Микрюков a, Д. В. Миланов a, А. А. Мюлляри a, И. И. Никифоров a, Н. П. Питьев a, Е. Н. Поляхова a, Л. Л. Соколов a, В. Ш. Шайдулин a
a Санкт-Петербургский государственный университет
Санкт-Петербург, Россия
b Институт прикладной астрономии РАН
Санкт-Петербург, Россия
c Главная (Пулковская) астрономическая обсерватория РАН
Санкт-Петербург, Россия
* E-mail: i.shevchenko@spbu.ru
Поступила в редакцию 30.05.2022
После доработки 24.06.2022
Принята к публикации 29.07.2022
- EDN: NWBVNT
- DOI: 10.31857/S0320930X2302007X
Аннотация
В обзоре освещены, в современном контексте приложений, важнейшие научные результаты, полученные учеными и выпускниками СПбГУ в области небесной механики и звездной динамики. Вторая часть обзора включает следующие темы: оценки и вычисление параметра MOID, проблемы астероидно-кометной опасности, пылевые комплексы в Солнечной системе, вращательная динамика спутников планет, циркумбинарная динамика, методы открытий и определения орбит экзопланет.
ВВЕДЕНИЕ
В обзоре освещены, в современном контексте приложений, важнейшие научные результаты ученых и выпускников СПбГУ в области небесной механики и звездной динамики; обзор разделен на тематические главы. В данной второй части обзора представлены современные исследования.
В 2024 г. будет отмечаться 300-летний юбилей Санкт-Петербургского университета. Авторы посвящают настоящий обзор этой знаменательной дате.
ОЦЕНКИ И ВЫЧИСЛЕНИЕ ПАРАМЕТРА MOID
Параметр MOID (Minimum Orbital Intersection Distance) представляет собой теоретико-множественное расстояние между двумя софокусными эллиптическими орбитами, то есть глобальный минимум (евклидова) расстояния между двумя точками, лежащими на разных орбитах. Необходимость нахождения MOID возникает, прежде всего, в исследованиях, связанных с астероидно-кометной опасностью. Задача быстрого и точного вычисления MOID приобретает также все большее значение при расчетах и оперативной корректировке орбит космических аппаратов в связи с быстрорастущим количеством космического мусора в околоземном пространстве.
С практической точки зрения основная трудность задачи вычисления MOID заключается в том, что она не имеет общего аналитического решения в явных функциях оскулирующих элементов. Возникает необходимость использования численных методов. С конца 1950-х годов – эпохи первых ИСЗ – тема быстрого и точного вычисления MOID стала актуальной; был предложен и реализован целый ряд методов вычисления MOID.
Принципиально новый подход к решению данной задачи,11 который приводит к точному значению MOID при малых затратах вычислительных ресурсов, был предложен в (Kholshevnikov, Vassiliev, 1999b): с использованием методов алгебраической геометрии было показано, что в общем случае задача сводится к нахождению нулей тригонометрического многочлена восьмой степени, или, что то же самое, нулей алгебраического многочлена шестнадцатой степени; данные нули соответствуют критическим точкам функции расстояния между орбитами. Эффективный алгоритм поиска указанных нулей описан и реализован в работе (Baluev, Mikryukov, 2019). Алгоритм следит за величиной численных ошибок, получаемых в результате вычислений, а также тщательно анализирует почти вырожденные случаи, в том числе практические случаи почти круговых и почти компланарных орбит. Проведенные Балуевым и Микрюковым (Baluev, Mikryukov, 2019) вычислительные тесты показали, что алгоритм обладает высокой надежностью и точностью, а также то, что, несмотря на дополнительные расходы времени, связанные с контролем ошибок, он претендует на звание одного из наиболее быстрых методов вычисления параметра MOID на настоящий момент. Представленный в работе (Baluev, Mikryukov, 2019) программный комплекс реализован на языке общего назначения C++ и размещен в сети Интернет в свободном доступе.
Метод Холшевникова и Васильева (Kholshevnikov, Vassiliev, 1999b) поиска критических точек функции расстояния в паре эллиптических орбит допускает обобщение на случай, в котором каждая орбита является произвольным коническим сечением (эллипс, парабола, гипербола). Это обобщение, включающее также тривиальные случаи прямолинейных орбит, рассматривается в работе (Baluyev, Kholshevnikov, 2005). Позже, на основании результатов этой работы Балуев (Baluev, 2021) модифицировал программный комплекс (Baluev, Mikryukov, 2019) с целью добавления в него случаев гиперболических орбит. В текущей версии данного программного комплекса каждая из орбит может являться либо эллиптической, либо гиперболической.22
Размеры современных каталогов (речь идет в первую очередь о каталогах малых тел Солнечной системы) требуют вычисления параметра MOID для чрезвычайно большого количества пар орбит. Однако задача нахождения MOID является актуальной, как правило, только для близких орбит. Вычисление расстояния между далекими орбитами обычно не представляет интереса.
Таким образом, возникает задача определения нижней оценки расстояния между орбитами. Если ее значение оказывается больше некоторого положительного числа δ, то и расстояние ρ (численное значение MOID) между орбитами также больше δ и такие орбиты в условиях рассматриваемой задачи (определяющих порог близости δ) могут считаться “далекими” друг от друга. Чтобы указанная оценка имела практический смысл для использования, она должна удовлетворять двум очевидным требованиям.
Во-первых, она всегда должна быть неотрицательной и обращаться в нуль тогда и только тогда, когда орбиты пересекаются. Рассмотрим простую нижнюю оценку ζ расстояния ρ между эллиптическими орбитами ${{\mathcal{E}}_{1}}$ и ${{\mathcal{E}}_{2}}$, определяемую формулой
(1)
$\rho ({{\mathcal{E}}_{1}},{{\mathcal{E}}_{2}}) \geqslant \zeta ({{\mathcal{E}}_{1}},{{\mathcal{E}}_{2}})\mathop = \limits^{{\text{def}}} \max \left\{ {{{q}_{1}} - {{Q}_{2}},{{q}_{2}} - {{Q}_{1}}} \right\}.$Здесь qk и Qk обозначают соответственно перицентрическое и апоцентрическое расстояния в орбите ${{\mathcal{E}}_{k}}$. Оценка (1), очевидно, справедлива для любых софокусных эллипсов, но положительна только тогда, когда апоцентр одного из них лежит к общему фокусу ближе, чем перицентр другого. Примером такой пары орбит является любая парная комбинация, составленная из восьми основных планет Солнечной системы. Но для случая Нептун–Плутон, а также для практически интересных случаев близких орбит оценка (1) не несет никакой информации, так как оказывается меньше нуля.
Во-вторых, вычисление оценки с точки зрения затрат машинных ресурсов должно быть задачей существенно более экономной, нежели расчет самого расстояния ρ. Оценка, представляющая собой относительно простую явную функцию орбитальных элементов, очевидно удовлетворяет этому требованию, поскольку для нахождения ρ требуется применение численных методов.33
Вопрос о существовании и построении оценки, удовлетворяющей указанным двум требованиям, был впервые рассмотрен в статье (Kholshevnikov, Vassiliev, 1999a). В этой работе проанализированы топологически различные конфигурации двух софокусных кеплеровых орбит и на основании этого анализа вводятся понятия коэффициентов зацепления для пары орбит. Построенные Холшевниковым и Васильевым коэффициенты зацепления являются непрерывными функциями оскулирующих элементов и в силу этого обстоятельства оказываются на практике удобными “индикаторами” близости орбит (см. подробности в указанной работе, а также в статье (Холшевников, Титов, 2007)). Изучение свойств коэффициентов зацепления орбит позволило Холшевникову и Васильеву наметить идею построения практически информативной нижней оценки расстояния ρ.
Данная идея получила развитие в работе (Mikryukov, Baluev, 2019), в которой авторы строят нижнюю оценку τ расстояния ρ для практически наиболее важного случая некомпланарных эллиптических орбит. Общая схема построения τ выглядит следующим образом. В плоскости орбиты ${{\mathcal{E}}_{k}}$ строится двумерное множество ${{\mathcal{H}}_{k}}$, содержащее целиком ${{\mathcal{E}}_{k}}$, после чего вычисляется расстояние между ${{\mathcal{H}}_{1}}$ и ${{\mathcal{H}}_{2}}$, которое и принимается за τ. Существенным является то, что множество ${{\mathcal{H}}_{k}}$ имеет простую геометрическую форму: его границы состоят лишь из отрезков прямой и лучей (рис. 1). Благодаря этому расстояние между ${{\mathcal{H}}_{1}}$ и ${{\mathcal{H}}_{2}}$ легко находится, так как оказывается равным расстоянию между двумя некоторыми скрещивающимися прямыми. Расстояние между этими прямыми, выражающееся простым и явным образом через элементы орбит, в итоге служит нижней оценкой τ величины ρ. Полученную оценку τ Микрюков и Балуев записали в виде
(2)
$\rho ({{\mathcal{E}}_{1}},{{\mathcal{E}}_{2}}) \geqslant \tau ({{\mathcal{E}}_{1}},{{\mathcal{E}}_{2}})\mathop = \limits^{{\text{def}}} C({{e}_{1}},{{e}_{2}},I)\sigma ({{\mathcal{E}}_{1}},{{\mathcal{E}}_{2}}).$Рис. 1.
Множество ${{\mathcal{H}}_{k}}$ (k = 1, 2), заключающее орбиту ${{\mathcal{E}}_{k}}$, выделено синим цветом. Пунктирная прямая a обозначает прямую пересечения орбитальных плоскостей. Множество ${{\mathcal{H}}_{k}}$ бесконечно и располагается симметрично относительно a; на рисунке показана его часть, лежащая вблизи прямой a и имеющая с a две общие точки B и C. Угол φ является убывающей функцией от эксцентриситета орбиты ${{\mathcal{E}}_{k}}$ и заключен в пределах 0 < φ ≤ 45○. При вращении прямой a вокруг притягивающего фокуса F угол φ не изменяется, то есть множество при этом вращении всегда остается подобным самому себе (изменяется лишь расстояние между точками B и C, принадлежащими ${{\mathcal{E}}_{k}}$). Метод построения ${{\mathcal{H}}_{k}}$ описан в работе (Mikryukov, Baluev, 2019). Рис. из работы (Mikryukov, Baluev, 2019), адаптировано.
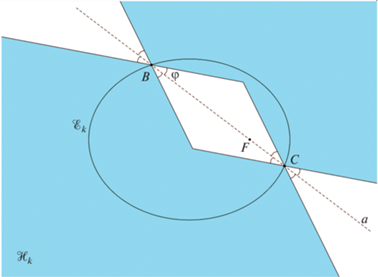
Здесь ek – эксцентриситет орбиты ${{\mathcal{E}}_{k}}$, I – угол между орбитальными плоскостями, а σ представляет собой незначительную модификацию одного из введенных Холшевниковым и Васильевым (Kholshevnikov, Vassiliev, 1999a) коэффициентов зацепления. Явный вид функций, записанных в правой части (2), приведен в работах (Kholshevnikov, Vassiliev, 1999a; Mikryukov, Baluev, 2019). Важным свойством функции σ является то, что она удовлетворяет неравенству
(3)
$\rho ({{\mathcal{E}}_{1}},{{\mathcal{E}}_{2}}) \leqslant \sigma ({{\mathcal{E}}_{1}},{{\mathcal{E}}_{2}}),$(4)
$\tau ({{\mathcal{E}}_{1}},{{\mathcal{E}}_{2}}) \leqslant \rho ({{\mathcal{E}}_{1}},{{\mathcal{E}}_{2}}) \leqslant \sigma ({{\mathcal{E}}_{1}},{{\mathcal{E}}_{2}}),$Практическая эффективность оценки τ исследовалась Микрюковым и Балуевым (Mikryukov, Baluev, 2019) с нескольких точек зрения. Прежде всего, были выполнены эксперименты по созданию каталога пар крупных объектов главного пояса с близкими орбитами.55 Применение оценки τ, благодаря которому производился отсев пар с заведомо далекими орбитами (и стало быть, для которых ρ не вычислялось), показало, что скорость построения каталога возрастает в несколько раз по сравнению с построением такого же каталога без использования τ. Микрюков и Балуев (Mikryukov, Baluev, 2019) также провели несколько экспериментов по анализу точности оценки τ – выяснялось насколько отношение τ/ρ оказывается близким к единице в различных случаях. Обнаружено, что для объектов главного пояса величина τ/ρ превышает значение 0.5 очень редко. Относительно большие значения τ/ρ, заключенные в пределах 0.4–0.5, наблюдаются, как правило, в парах с заметно вытянутыми орбитами или с большим взаимным наклоном орбитальных плоскостей. В такие пары часто входят астероиды семейств, например, семейства Венгрии. Обычными же для главного пояса являются относительно низкие значения τ/ρ из промежутка 0.05–0.2.
Функция τ существенным образом зависит от взаимного наклона орбитальных плоскостей. Чем меньше угол наклона, тем ближе к нулю τ. Это явление обусловлено тем, что идея построения оценки τ опирается на понятие скрещивающихся прямых (в предельном компланарном случае эти прямые пересекаются и расстояние между ними становится равным нулю, см. подробности в статье (Mikryukov, Baluev, 2019)). В чувствительности к углу между орбитальными плоскостями заключается основное объяснение того, почему для большинства объектов главного пояса (у которых орбиты расположены вблизи общей плоскости эклиптики) оценка τ имеет весьма низкую точность. Определяемая формулой (1) оценка ζ, в отличие от τ, свободна от указанной зависимости. Это означает, что в некоторых очевидных случаях – в особенности когда орбиты околокруговые, почти компланарные и имеют существенно различные размеры – оценка ζ может быть гораздо точнее оценки τ. Для иллюстрации этого эффекта Микрюков и Балуев приводят пример пары Земля–Марс, для которой ζ/ρ ≈ 0.978, τ/ρ ≈ 0.02 и пример пары Уран–Нептун, для которой ζ/ρ ≈ ≈ 0.996, τ/ρ ≈ 0.013.
ПРОБЛЕМЫ АСТЕРОИДНО-КОМЕТНОЙ ОПАСНОСТИ
В 80-е годы XX века началось интенсивное изучение динамики астероидов, которые могут угрожать Земле. Падение крупного метеорита под Челябинском в 2013 г. еще раз обратило внимание общественности на важность проблемы. В настоящее время исследованиям, связанным с астероидно-кометной опасностью, посвящено большое количество статей и книг, регулярно проводятся тематические конференции. Астероидно-кометная опасность – серьезнейшая междисциплинарная проблема.
В Трудах Всесоюзного совещания, проведенного в ИТА АН СССР в 1991 г., опубликована статья Холшевникова “Вероятность столкновения с объектом, движущимся по орбите соударения с Землей” (Холшевников, 1992). В материалах конференции “Астероидная опасность – 95” (ИТА РАН, 1995), была опубликована заметка Елькина и Соколова “О последовательных прохождениях АСЗ в окрестности Земли” (Елькин, Соколов, 1995), посвященная сближениям с Землей астероида перед соударением с ней. Показано, что такие сближения, как правило, должны иметь место. Тесные сближения астероида с Землей, предваряющие соударения с ней, позволяют обнаружить новые или потерянные опасные объекты и уточнить их орбиты, а также использовать эффект гравитационного маневра для экономного увода астероида от соударения. В работе (Холшевников и др., 2021) выявлена любопытная и важная тенденция: на траекториях, ведущих к соударению, сближения обычно более тесные, чем, например, на номинальных орбитах.
В 2004 г. был открыт астероид Апофис, впоследствии давший неоценимый материал для исследований различных аспектов астероидно-кометной опасности. Апофис – необычный астероид. Он отличается от других известных сближающихся с Землей астероидов прежде всего тем, что в течение долгого времени (более 15 лет) он был одним из наиболее опасных для Земли астероидов. Это обусловлено особенностями его орбиты, прежде всего установленным тесным сближением с Землей 13 апреля 2029 г. и последствиями этого сближения. Хотя в настоящее время Апофис считается практически безопасным для Земли, история исследований его возможных движений интересна и поучительна.
С 2006 по 2011 год Апофис находился далеко от Земли и поэтому практически не наблюдался, его орбита не уточнялась. В это время теоретически исследовались возможные (в соответствии с имевшимися тогда данными) траектории астероида. Основная цель – выделение и изучение опасных сценариев, ведущих к столкновению с Землей. В работе (Chesley, 2006) найдено несколько возможных соударений Апофиса с Землей: в 2036 г., 2037 г., и др. После уточнения орбиты в 2006 г. из них осталось возможным только соударение в 2036 г. Оно и его последствия тщательно исследовались.
Малое изменение орбиты до сближения ведет к ее большому изменению после сближения. Отсюда – потеря точности прогнозирования после тесного сближения, невозможность выделить только одну опасную траекторию. После одного–двух тесных сближений движение становится практически непредсказуемым. Земля изменяет гелиоцентрическую орбиту астероида при сближении; в частности, астероид может перейти на орбиту, резонансную с орбитой Земли. В этом случае через небольшое целое число лет они снова встретятся, в том числе возможно соударение. Это явление носит название “резонансный возврат”.
Резонансные возвраты Апофиса возможны не только после сближения с Землей в 2029 г., но и после сближения с ней в 2036 г. Если возможно соударение, возможны и тесные сближения. Исследования показали существование множества (несколько десятков) опасных сценариев, связанных с ними. Так, в работе (Соколов и др., 2008) с использованием метода точечных гравитационных сфер (ТГС) были обнаружены резонансные возвраты в 2037, 2038, 2039 (2 возврата) и 2040 (2 возврата) годах, при этом порождающие недетерминированные ТГС-траектории интерпретировались как квазислучайные движения, согласно определению Алексеева. С использованием численного интегрирования неупрощенных уравнений движения астероида было найдено возможное тогда соударение Апофиса с Землей в 2040 г. Остальные резонансные возвраты соответствуют тесным сближениям. Разработан метод, позволяющий обойти потерю точности, связанную с тесным сближением в 2029 г., при численном поиске возможных соударений астероидов с Землей. Там же исследовалось рассеяние возможных траекторий астероида после сближения в 2029 г.; показано, что свойства опасных траекторий практически не зависят от используемой модели движения планет и номинальной уточняемой орбиты астероида. Были получены оценки необходимого для предотвращения соударения с Землей изменения скорости астероида. Если удар по астероиду, меняющий его скорость, производится до сближения в 2029 г., требуемое изменение скорости может быть на 4 десятичных порядка меньше. Этот важный результат подтверждается в других работах (см., например, Ивашкин, Стихно, 2009).
Разработаны методы, алгоритмы и программы поиска возможных соударений (Petrov и др., 2018). В работе (Соколов и др., 2012) приводится наиболее подробный список соударений, связанных с резонансными возвратами после сближения в 2036 г. Характеристики соударений оказываются устойчивыми относительно малых изменений модели движения, что продемонстрировано в работе (Соколов и др., 2012).
Апофис сближается с Землей приблизительно каждые 7 лет, поэтому следующие его наблюдения проводились в 2012–2013 годах. Орбита была существенно уточнена, что привело, в частности, к исключению возможного соударения с Землей в 2036 г.; оно стало невозможным, как и связанные со сближением в 2036 г. резонансные возвраты. Однако еще в 2011 г. была установлена возможность ряда соударений, связанных с резонансными возвратами после сближения Апофиса с Землей в 2051 г. (Chesley, 2011). Тщательные исследования показали, что оставались возможными порядка сотни соударений в текущем столетии. Самое опасное – в 2068 г. с вероятностью около семи миллионных. Следует отметить, что такое большое число возможных тогда соударений, после уточнения орбиты, было неожиданным. Ожидали, что, скорее всего, Апофис после 2013 г. станет безопасным. Однако как раз совсем близко от его номинальной (тогда) орбиты располагалось сгущение областей, ведущих к соударениям.
Список возможных соударений Апофиса с Землей, связанный с резонансными возвратами после сближения в 2051 г., приведен в работе (Соколов и др., 2018). Он содержит 158 соударений в текущем столетии. Следующее сближение Апофиса с Землей, когда можно было проводить его наблюдения, произошло в 2020–2021 годах. На этот раз уточнение его орбиты, с использованием в том числе радиолокационных наблюдений, оказалось достаточным для того, чтобы признать Апофис безопасным для Земли, по крайней мере в ближайшие 100 лет.66
Исследованы возможные соударения и сближения с Землей многих других астероидов. Это, в частности, 2013 XK22, 2015 RN35, 2008 EX5 (Соколов и др., 2021), 2007 VK184, 2011 AG5 (Соколов и др., 2013) и другие. Большинство из них уже перестали быть опасными после уточнения их орбит из наблюдений, однако полученные свойства траекторий соударения и сближения и сейчас представляют определенную ценность.
Разработаны методы, алгоритмы и программы для нахождения возможных соударений и сближений астероидов с Землей, Луной и планетами. Поиск возможных соударений можно довольно эффективно проводить варьированием начальных данных на одномерном многообразии, если орбита известна достаточно точно (как в случае Апофиса). Положения ведущих к соударениям областей начальных данных образуют структуру фрактального типа, связанную с резонансными возвратами.
Изучены возможности предотвращения соударения с Землей Апофиса и других астероидов. В работе (Александрова и др., 2016) показано, что атомный взрыв после сближения с Землей до соударения с ней может безопасно разрушить астероид. Согласно (Батмунх и др., 2019), с использованием двигателей малой тяги возможен увод от соударения с Землей астероида умеренных размеров. Соколов и др. (2018) на примере астероида Апофис выявили возможность предотвращения множества соударений при ударном изменении скорости астероида с учетом эффекта гравитационного маневра.
В работе (Баляев, 2020) найдены астероиды с большими вероятностями соударений с Луной и планетами; позднее было показано, что астероиды с перигелийным расстоянием более 1.3 а. е., которые, согласно действующей терминологии, не являются “околоземными”, могут приближаться к Земле на расстояние менее 100 ее радиусов за время порядка 100 лет и даже сталкиваться с ней. Продолжение численных исследований возможных траекторий большого числа астероидов с известными орбитами представляет несомненный интерес, поскольку позволит выделить ранее неизвестные опасные для Земли объекты, в том числе не являющиеся в настоящее время “околоземными”.
ПЫЛЕВЫЕ КОМПЛЕКСЫ В СОЛНЕЧНОЙ СИСТЕМЕ
Новым актуальным научным направлением в астрономии в конце 1980-х годов стало исследование околопланетных и околоспутниковых пылевых комплексов в Солнечной системе. Одним из сигналов о существовании подобных комплексов послужила внезапная потеря связи с космическим зондом Фобос-2 в 1989 г. Примерно за неделю до запланированного сближения с Фобосом, 27 марта 1989 г., станция Фобос-2 не вышла на связь. Несколько часов спустя слабый сигнал был принят, но телеметрическую информацию извлечь не удалось. По характеру сигнала можно было только предположить, что аппарат не был стабилизирован и хаотично вращался. Дальнейшие попытки связаться со станцией оказались безуспешными, и 15 апреля 1989 г. они были прекращены. Было высказано предположение, что причиной могло оказаться столкновение станции с метеороидом миллиметрового размера.
Еще в 1971 г. Soter (1971) высказал гипотезу о существовании вокруг орбит Фобоса и Деймоса разреженных пылевых колец. Идея проста: лишенные атмосферы спутники подвергаются высокоскоростным ударам межпланетных метеороидов, в результате которых с поверхностей выбрасывается пыль, суммарная масса которой на 3–4 порядка превосходит массу ударника. Типичные скорости выброса больше скорости убегания с поверхностей спутников, но меньше скорости убегания от планеты в межпланетное пространство, поэтому пылинки оказываются на околопланетных орбитах, образуя пылевые кольца вокруг орбит родительских спутников. Стало ясно, что если такие кольца действительно существуют, концентрация частиц вдоль орбит Фобоса и Деймоса может быть достаточно высокой, и удар микрометеороида становится вполне вероятным сценарием того, что произошло с Фобосом-2. Однако истинная причина потери аппарата, скорее всего, так и останется не выясненной.
Первая модель пылевого тора вокруг орбиты Фобоса опубликована в работах (Кривов и др., 1991; Kholshevnikov и др., 1993). Далее обнаружились новые многочисленные аспекты задачи. Также и вопрос, есть ли кольца у Марса, оставался без ответа. В серии работ (Krivov, 1994; Krivov и др., 1996, 2006; Krivov, Hamilton, 1997; Krivov, Jurewicz, 1998; Makuch и др., 2005) изначальная модель тора Фобоса была дополнена моделью тора Деймоса, заметно уточнена и всесторонне обобщена. Так, были добавлены возмущения от сжатия Марса, а также давление солнечного излучения, существенно влияющее на частицы размером менее ~1 мм. Стало ясно, что динамика и распределение частиц различных размеров должны быть принципиально различными. Выяснилось, что кольца Фобоса и Деймоса должны сильно отличаться друг от друга (Krivov и др., 1996; Krivov, Hamilton, 1997). Тонкое, как бритвенное лезвие, и чрезвычайно разреженное кольцо Фобоса, скорее всего, трудно будет обнаружить, тогда как “пухлый” и более плотный тор Деймоса, состоящий из долгоживущих частиц, должен быть основным пылевым комплексом около Марса (Makuch и др., 2005).
Моделировались и предсказываемые облака непосредственно вокруг обоих спутников (Krivov, Jurewicz, 1998). Обсуждались возможности обнаружить и кольца, и околоспутниковые облака как при удаленных наблюдениях в рассеянном свете, так и с помощью пылевых детекторов на борту космических аппаратов, запускаемых к Марсу. Несмотря на все усилия, гипотетические кольца Марса до сих пор обнаружить не удалось. Одна из вероятных причин этого – плохо известное распределение выбрасываемых с поверхности спутников реголитных частиц по размерам (Krivov и др., 2006). Возможно, лишь незначительная доля пылинок выбрасывается в “динамически благоприятном” диапазоне размеров около 10–100 мкм, в котором – согласно моделям – они оказываются долгоживущими.
Дальнейшие попытки обнаружить марсианские кольца будут предприняты, например, в рамках японской космической экспедиции MMX (старт планируется в 2024 г.). Очевидно, что механизм микрометеоритной бомбардировки спутников Марса должен работать и для спутников других планет – по крайней мере достаточно маленьких, с низкой скоростью убегания. Соответственно, такие спутники должны быть окружены пылевыми облаками, а вокруг их орбит могут образовываться пылевые кольца (см., например, Dikarev и др., 2006). В серии работ (Krivov и др., 2003; Sremčević и др., 2003; 2005) была разработана аналитическая модель облака вокруг произвольного спутника, а в статье (Hamilton, Krivov, 1996) – выведены и решены гамильтоновы уравнения движения околопланетных частиц с учетом совместно действующих возмущений от сжатия планеты, светового давления, силы Лоренца и притяжения Солнца. Последняя модель оказалась особенно полезной. В ней рассматривается задача, которую можно назвать магнитофотогравитационной круговой ограниченной задачей трех тел. Гамильтониан задачи, по сути, представляет собой классическую постоянную Тиссерана, выраженную через планетоцентрические элементы и обобщенную на случай присутствия нескольких дополнительных возмущений. Разработанный аналитический метод впоследствии нашел неожиданные интересные приложения и в “непылевых” задачах – например, к динамике двойных астероидов (Hamilton, Krivov, 1997) и к движению искусственных спутников Земли с большим миделевым сечением или малой массы (Krivov и др., 1997; Krivov, Getino, 1997). Примером другой изящной теоретической задачи с потенциально широкой областью применения стало описание огибающей поверхности семейства траекторий изотропно выброшенных частиц. Результаты ее решения при различных предположениях об орбите родительского тела и положении точек выброса были опубликованы в цикле работ (Коблик, Холшевников, 1994; Холшевников, Орлов, 2000; Холшевников и др., 2003; Орлов, Холшевников, 2004; 2008; 2012; Orlov, Kholshevnikov, 2013). Исследовались и стохастические эффекты в движении околопланетных пылевых частиц (Spahn и др., 2003; Makuch и др., 2006).
Некоторые из описанных выше моделей были применены для описания известного с 1960-х годов кольца Е Сатурна – на тот момент крупнейшего из планетных колец и самого яркого околопланетного пылевого комплекса в Солнечной системе. Оно расположено в обширной зоне от 3 до 7.5–8 радиусов Сатурна и охватывает орбиты семи спутников планеты – от Мимаса до Дионы. Источником пылевого материала считается 250‑километровый Энцелад, движущийся ближе к внутреннему краю кольца. Дикарев и Кривов (1998) исследовали динамику частиц кольца Е Сатурна с учетом возмущений от светового давления Солнца, сжатия планеты, силы Лоренца за счет трех зональных гармоник магнитного потенциала планеты, а также сопротивления плазмы. На основе массового численного интегрирования уравнений движения отдельных частиц построена коллективная модель кольца Е, лучше согласующаяся с наблюдательными данными, чем предшествующие модели.
Дикареву (Dikarev, 1999) удалось обобщить модель на случай переменного электростатического заряда пылинки и учесть эффекты силы сопротивления плазмы. Предполагалось, что основной источник выброса частиц с Энцелада – микрометеоритная бомбардировка его поверхности. Позже, благодаря наблюдениям зонда Cassini (Srama и др., 2004), выяснилось, что это не так: пыль извергается активным “ледяным вулканом” в южной приполярной области спутника (Spahn и др., 2006a; 2006b).
Исследовалась также динамика выбросов со спутника Сатурна Гипериона (Banaszkiewicz, Krivov, 1997a; 1997b; Krivov, Banaszkiewicz, 2001a; 2001b). Движение этих частиц контролируется резонансом средних движений с Титаном и двумя негравитационными возмущающими силами – световым давлением и торможением в плазменной среде. Большая часть убегающих частиц либо оказывается свободной от резонанса из-за высоких начальных скоростей, либо высвобождается из “резонансного замка” двумя возмущающими силами. Орбиты, не запертые в резонансе, неустойчивы, и частицы испытывают многократные тесные сближения с Титаном. В результате заметная часть пылинок, покидающих сферу действия Гипериона, рано или поздно достигает атмосферы Титана. Приток пыли с Гипериона на Титан может быть существенным, сравнимым с притоком на Титан межпланетного вещества. Не исключено, что поступление водосодержащих частиц с Гипериона в атмосферу Титана может помочь в объяснении наблюдаемых там высоких концентраций молекул СО и СO2.
Проект (Thiessenhusen и др., 2002) был нацелен на исследование гипотетического разреженного пылевого облака в системе Плутон–Харон (другие спутники Плутона тогда еще не были открыты). Как и во многих других упомянутых выше системах, предлагается механизм выброса вещества с поверхностей вследствие сверхскоростных ударов микрометеороидов, в данном случае – приходящих из пояса Койпера. Однако динамика пылинок в системе Плутон–Харон будет иной, чем в пылевых поясах Марса, Юпитера и Сатурна. Негравитационные силы (сила Лоренца, световое давление и другие), не должны играть сколько-нибудь заметной роли, поскольку Плутон не имеет магнитного поля и плазмосферы и чрезвычайно удален от Солнца. С другой стороны, гравитационная часть задачи сложнее, чем в других системах: масса Харона всего в 8 раз уступает массе Плутона. Так как движение пылинок определяется притяжением обоих тел, можно ожидать грушевидной формы облака, по крайней мере, его более плотной части. Показано, что темп выброса пыли с поверхностей обоих тел сравним, но времена жизни у частиц с Харона внутри сферы Хилла системы Плутон–Харон значительно больше, чем у частиц с Плутона, вследствие чего пылинки с Харона преобладают. Ожидаемая оптическая толщина на несколько порядков ниже той, которая позволила бы наблюдать облако фотометрически. Однако концентрация пыли в облаке достаточно высока для того, чтобы обнаружить пыль детектором на борту космического аппарата, который может быть запущен к Плутону.
Параллельно с теоретическими исследованиями известных и предполагаемых пылевых структур предприняты интенсивные усилия по обнаружению еще не открытых комплексов наблюдательно. Эти усилия оказались небезуспешными. В результате анализа данных космического аппарата Galileo обнаружены пылевые облака вокруг трех спутников Юпитера – Европы, Ганимеда и Каллисто (Krüger и др., 1999; 2000; 2003), а также пылевые кольца низкой плотности между их орбитами (Krivov и др., 2002a). Тем самым был фактически открыт новый класс объектов Солнечной системы – пылевые оболочки спутников планет. Анализ другого подмножества данных Galileo привел к обнаружению ранее не известного слабого пылевого кольца Юпитера, простирающегося по меньшей мере от орбиты Европы до орбиты Каллисто (Krivov и др., 2002b). Хотя кольцо чрезвычайно разрежено и недоступно фотометрическим наблюдениям, на момент открытия оно стало самым большим из обнаруженных к тому времени планетных колец. Кроме того, оно стало первым из известных колец, источником которого являются не малые спутники, а спутники лунного размера.
ВРАЩАТЕЛЬНАЯ ДИНАМИКА СПУТНИКОВ ПЛАНЕТ
К настоящему времени у планет Солнечной системы обнаружено уже более двух сотен спутников.77 Исследование динамики этих небесных тел представляет значительный интерес с точки зрения понимания процессов формирования и эволюции Солнечной системы и планетных систем у других звезд. Во вращательной и орбитальной динамике спутников и спутниковых систем можно наблюдать как регулярное, так и хаотическое поведение. В настоящее время, помимо синхронного с движением по орбите вращения спутника относительного своего центра масс, у трех десятков спутников планет Солнечной системы установлено чрезвычайно быстрое (в несколько тысяч раз быстрее синхронного) вращение, а седьмой спутник Сатурна – Гиперион – находится в режиме хаотического, непредсказуемого вращения. Подробный обзор современного состояния исследований вращательной динамики спутников планет представлен в работе Мельникова и Шевченко (2022).
Синхронный с движением по орбите режим плоского (ось вращения ортогональна плоскости орбиты) вращения согласно теории (MacDonald, 1964) является наиболее вероятной финальной стадией долговременной приливной эволюции спутника. В работах Мельникова и Шевченко (2000; 2007), Мельникова (2001) и Куприянова и Шевченко (2006) была подробно рассмотрена возможность существования нескольких возможных режимов плоского синхронного вращения у известных спутников планет. Типичными представителями таких спутников являются пятый спутник Юпитера – Амальтея (Ю5), для нее в фазовом пространстве плоского вращательного движения существуют две моды синхронного резонанса, и шестнадцатый спутник Сатурна – Прометей (С16), у которого возможны три режима синхронного вращения. На рис. 2 приведена диаграмма “ω0 – e”, где ω0 = (3(B – A)/C)1/2 – параметр, характеризующий динамическую асимметрию формы спутника, A < B < C – главные центральные моменты инерции, e – эксцентриситет орбиты спутника. На диаграмме указаны области существования трех режимов плоского синхронного вращения, соответствующих, согласно (Мельников, Шевченко, 2000; 2007), синхронному α-резонансу, синхронному β-резонансу и бифуркационной моде синхронного резонанса αbif (см. подробнее Мельников, 2001). Для ряда спутников, у которых возможны несколько мод синхронного резонанса, была исследована устойчивость плоского синхронного вращения относительно наклона оси вращения (Мельников, Шевченко, 1998; 2000; 2007; Kouprianov, Shevchenko, 2005; Melnikov, Shevchenko, 2008). Устойчивость плоского синхронного вращения обусловливает возможность захвата спутника в ходе динамической эволюции в синхронный спин-орбитальный резонанс и долговременное нахождение спутника в нем. Определив на представленной на рис. 2 диаграмме положения известных спутников планет Солнечной системы, Мельников и Шевченко (Melnikov, Shevchenko, 2010) отметили, что значительная часть спутников попадает в область, где синхронный резонанс не существует. Согласно полученным выводам, указанные спутники вращаются либо много быстрее, чем синхронно с движением по орбите, либо, что менее вероятно, хаотично.
Рис. 2.
Диаграмма “ω0 – e”. Указаны области существования синхронного α-резонанса, синхронного β‑резонанса и бифуркационной моды синхронного резонанса – αbif. В белой области синхронный резонанс не существует. Красными точками обозначены спутники планет Солнечной системы, для которых известна величина ω0. Синими точками указаны положения спутников, для которых ω0 получена при помощи аппроксимации (Куприянов, Шевченко, 2006) на основе известной величины среднего радиуса фигуры спутника. Рис. из статьи (Melnikov, Shevchenko, 2010), адаптировано.
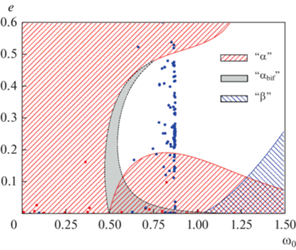
В работах Куприянова и Шевченко (Kouprianov, Shevchenko, 2005) и Мельникова, Шевченко (2007) был выполнен детальный статистический анализ данных о размерах и возможных значениях инерционных параметров известных спутников. Согласно наблюдаемой статистике большую часть спутников представляют малые спутники (средний радиус фигуры менее 300 км), обладающие существенно иррегулярной формой. Мельников и Шевченко (Melnikov, Shevchenko, 2010) рассмотрели задачу о типичных современных вращательных режимах спутников планет и показали, что большинство малых спутников находятся либо в регулярном (и более быстром, чем синхронное) вращении, либо вращаются хаотически. Теоретический вывод о весьма быстром вращении многих малых спутников подтверждают современные наблюдательные данные (Denk, Mottola, 2019).
Исследованию хаотической вращательной динамики спутников посвящены работы Девяткина и др. (2002), Melnikov, Shevchenko (2008; 2010) и Мельникова (2014; 2020). В работе Девяткина и др. (2002) проведено моделирование наблюдаемых кривых блеска и вращательной динамики Гипериона, в итоге был сделан вывод о хаотическом характере его вращения. Строго, путем вычисления характеристических показателей Ляпунова, этот вывод был подтвержден в работе (Melnikov, 2002). Величина ляпуновского времени (времени предсказуемой динамики) для хаотического вращения Гипериона составляет один–два месяца, как показывают численные (Melnikov, 2002; Kouprianov, Shevchenko, 2005) и теоретические оценки (Шевченко, 2002). Поэтому хаотическую динамику Гипериона можно непосредственно наблюдать и изучать на относительно коротких временных интервалах. На основе теории сепаратрисных алгоритмических отображений (Shevchenko, 1999) разработаны аналитические методы оценивания максимальных показателей Ляпунова (см. Шевченко, 2002; Shevchenko, 2020b).
Вопросы о возможности хаотического вращения других спутников планет Солнечной системы и особенностях, присущих хаотической вращательной динамике спутников, были детально рассмотрены в работах (Kouprianov, Shevchenko, 2005; Melnikov, Shevchenko, 2008; 2010; Мельников, 2014; 2020). В работах (Kouprianov, Shevchenko, 2005) и (Melnikov, Shevchenko, 2008) показано, что наблюдаемое хаотическое вращение в настоящее время возможно в динамике спутников Сатурна – Прометея (С16) и Пандоры (С17). Данный вывод подтверждается как малыми величинами ляпуновских времен для возможной хаотической вращательной динамики указанных спутников, так и близостью к неустойчивому состоянию режима плоского синхронного вращения для этих спутников. Посредством численных экспериментов было установлено (Melnikov, Shevchenko, 2008; Мельников, 2020), что у Прометея и Пандоры при хаотическом вращении имеет место эффект преимущественной ориентации наибольшей оси фигуры спутника по направлению на планету, поэтому хаотическое вращение спутника внешне может быть схоже с синхронным.
Недавно Мельников (2020) показал, что указанный эффект имеет место в возможной хаотической динамике спутников с малой величиной эксцентриситета орбиты (e < 0.005). Мельниковым (2014) была рассмотрена задача о возможности существования странного аттрактора в ходе приливной эволюции вращательного движения малых спутников. Странный аттрактор, движение на котором является хаотическим, формируется в окрестности синхронного резонанса в фазовом пространстве плоского вращательного движения спутника. Было показано (Мельников, 2014), что странный аттрактор может существовать в динамике Гипериона.
ЦИРКУМБИНАРНАЯ ДИНАМИКА
В связи с открытием в начале 10-х годов этого столетия циркумбинарных планетных систем (систем, в которых планеты обращаются вокруг центральной тесной двойной звезды) у звезд главной последовательности, существенную актуальность приобрели исследования циркумбинарной планетной динамики. Предметом исследований являются, в частности, устойчивость, архитектура и проблемы потенциальной обитаемости циркумбинарных планетных систем.
В работе (Shevchenko, 2015) построена теория, описывающая область хаотических орбит вокруг системы двух гравитационно связанных тел (двойной звезды, двойной черной дыры, двойного астероида). Если массовый параметр (отношение масс центральной двойной) выше некоторого порога, центральная непрерывная область хаоса проявляется благодаря перекрытию орбитальных резонансов, соответствующих целочисленным отношениям p : 1 между периодами обращения частицы и центральной двойной. В этой зоне имеет место неограниченная хаотическая орбитальная диффузия частицы, вплоть до ее выброса из системы. Оценено значение массового параметра μ, выше которого такая хаотическая зона присутствует универсально. Показано, что наблюдаемое разнообразие орбитальных бипланетных (двухпланетных) конфигураций у одиночных звезд и разнообразие циркумбинарных экзопланетных систем согласуются с существованием порогового значения μ: на эмпирической зависимости “массовый параметр центральной двойной μ – отношение орбитальных периодов Tout/Tin внешней планеты и центральной двойной” бипланетные системы все оказываются слева от вертикали (указывающей теоретический порог μ > 0.05 для появления центральной хаотической зоны), тогда как циркумбинарные системы находятся справа от нее. Очевидно полное отсутствие экзосистем с Tout/Tin < 5 при μ > 0.05, что согласуется с теорией: при μ > 0.05 формируется центральная хаотическая зона, где орбиты планет с любыми начальными эксцентриситетами подвержены неограниченной хаотической диффузии, вплоть до выброса планеты из системы. Таким образом, теория предсказывает существование порогового значения отношения масс центральной двойной для возникновения области глобального орбитального хаоса, что подтверждается современными данными наблюдений экзопланетных систем.
Попова и Шевченко (Попова, Шевченко, 2012; Popova, Shevchenko, 2013) провели исследование устойчивости и хаотической динамики планет в кратных звездных системах Kepler-16, -34 и -35. Для планет этих систем путем вычисления ляпуновских спектров движения были построены диаграммы устойчивости “перицентрическое расстояние – эксцентриситет”; они свидетельствуют, что планеты располагаются в резонансных ячейках на границах центральных хаотических областей (в пространстве орбитальных параметров), см. рис. 3 для системы Kepler-16.
Рис. 3.
Диаграмма устойчивости для системы Kepler-16 в координатах “перицентрическое расстояние – эксцентриситет”. Синим цветом выделена зона хаоса. Красный кружок – планета. Сплошные и прерывистые кривые указывают границы области хаоса и сепаратрисы резонансов согласно современным теоретическим моделям. Рис. из работы (Попова, Шевченко, 2016).
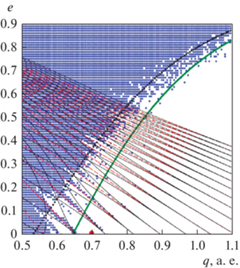
Данный феномен аналогичен явлению, хорошо известному в динамике Солнечной системы, а именно выживанию Плутона и плутино, находящихся в орбитальном резонансе 3 : 2 с Нептуном. Порядок центрального резонанса “занятой” резонансной ячейки увеличивается с увеличением массового параметра μ возмущающей двойной, так как увеличение μ сдвигает границу центральной хаотической области вовне. Таким образом, установлено, что в пространстве орбитальных параметров наблюдаемые циркумбинарные планеты располагаются на границах хаотических областей внутри резонансных ячеек фрактальных граничных зон.
Путем массовых численных экспериментов выявлены области хаотического движения на плоскости начальных условий “перицентрическое расстояние q – эксцентриситет e” планетных орбит (Попова, Шевченко, 2012). Исходя из аналитического критерия Shevchenko (2015) хаотичности планетных орбит в двойных звездных системах, построены теоретические кривые, описывающие глобальную границу области динамического хаоса вокруг центральной двойной. Согласно Shevchenko (2015), эти кривые описываются формулой
где(6)
$\Delta {{E}_{{{\text{cr}}}}} \approx A{{\mu }^{{2/5}}}{{q}^{{--1/10}}}{\text{exp}}\left( {--B{{q}^{{3/2}}}} \right),$На основе теории Mardling (2008), описывающей отдельные резонансные “зубцы” (соответствующие целым резонансам между орбитальными периодами планеты и двойной), в работе (Попова, Шевченко, 2012) построены локальные границы хаоса. Показано, что теоретические модели успешно описывают как глобальную, так и локальные границы “хаос–порядок” на построенных численно диаграммах устойчивости, что говорит об адекватности этих теорий и их эффективности в обеспечении аналитических критериев хаотичности планетных орбит.
Попова и Шевченко (Popova, Shevchenko, 2013) провели анализ возможных циркумбинарных конфигураций планетных систем у двойных звезд α Cen A-B и EZ Aqr A-C (одной из ближайших к нам двойных). На основе современных представлений о динамике и архитектуре циркумбинарных систем были определены наиболее вероятные орбиты циркумбинарных планет в этих системах. В случае EZ Aqr A-C циркумбинарная зона обитаемости располагается в интервале от ~0.033 до ~0.064 а. е. по радиусу от барицентра двойной, и планета в резонансной ячейке на границе центральной зоны хаоса может находиться в зоне потенциальной обитаемости. В работе дано полное аналитическое описание диаграмм устойчивости для циркумбинарных планетных систем.
Большой интерес представляют спиральные структуры в планетезимальных дисках. Демидова и Шевченко исследовали динамические возмущения протопланетного планетезимального циркумбинарного диска (диска вокруг двойной звезды) в эпоху, когда его газовая составляющая исчезает (Demidova, Shevchenko, 2015). Построена теория для вековой динамики планетезималей в циркумбинарных дисках в безгазовом случае. Продемонстрировано, как формируется циркумбинарная спиральная структура. Численно и аналитически изучена эволюция структуры в ходе распространения волны плотности по диску на вековой шкале времени. Выведены аналитические формулы, описывающие возникающие структурные особенности; они в точности согласуются с численно-экспериментальной картиной. Таким образом, построена аналитическая теория, описывающая спиральные структуры в планетезимальных дисках двойных звезд.
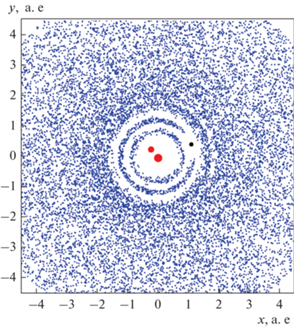
Демидова и Шевченко исследовали многополосные кольцевые структуры в планетезимальных дисках, обусловленные наличием планет (Demidova, Shevchenko, 2016; Демидова, Шевченко, 2018). Теоретически и путем численного моделирования показано, как планета в планетезимальном диске формирует в нем многополосную структуру, состоящую из нескольких колец вокруг центральной одиночной или двойной звезды, заполненных веществом или свободных от него. В наиболее яркой форме этот эффект проявляется в случае циркумбинарных дисков. Оценена предельная масса планеты, при которой система из многих колец сокращается до трехполосной: заполненного веществом коорбитального с планетой кольца и двух кольцеобразных полостей, положение которых соответствует орбитальным резонансам 2 : 1 и 1 : 2 с планетой. В рамках предложенной теории объяснена природа трехполосной структуры в диске HL Tau, присутствующей на изображениях, полученных комплексом радиотелескопов. Таким образом, установлены закономерности формирования кольцевых многополосных структур, обусловленных наличием планет, в планетезимальных дисках одиночных и двойных звезд. Проведено моделирование динамики остаточных дисков в циркумбинарных системах, открытых космическим телескопом Kepler; на его основе сделан вывод, что обнаружение циркумбинарных кольцеобразных структур при наблюдениях систем двойных звезд может быть свидетельством существования планет, формирующих эти структуры. На рис. 4 приведен пример кольцевой структуры в циркумбинарном диске с планетой, полученный путем численного моделирования.
Рис. 4.
Пример кольцевой структуры в циркумбинарном диске с планетой, полученный путем численного моделирования. Рис. из работы (Демидова, Шевченко, 2018).
С использованием методов теории симплектических отображений построена теория планетных хаотических зон в планетезимальных дисках, позволяющая аналитически оценивать основные параметры этих зон – радиальные размеры, скорости расчистки, ляпуновские шкалы времени (Shevchenko, 2020a; 2020b). Путем массовых численных экспериментов получены данные о свойствах планетных хаотических зон, согласующиеся с теорией (Демидова, Шевченко, 2020).
МЕТОДЫ ОТКРЫТИЙ И ОПРЕДЕЛЕНИЯ ОРБИТ ЭКЗОПЛАНЕТ
Ведущиеся сейчас активные исследования внесолнечных планетных систем затрагивают многие задачи небесной механики, касающиеся методов открытий и определения орбит экзопланет, их орбитальной динамики. Этим задачам посвящен ряд работ Балуева.
В работе (Baluev, 2008) рассматривались возможные орбитальные конфигурации планетной системы HD 37124. Проведен анализ всех имевшихся на тот момент наблюдательных данных, с учетом новой для того времени модели шума лучевой скорости (доплеровского дрожания звезды). Впервые для этой планетной системы была предложена интерпретация данных, указывающая на орбитальный резонанс 2 : 1. Впоследствии эта конфигурация была подтверждена независимой группой (Wright и др., 2011).
В работе (Baluev, 2011) рассматривалась резонансная планетная система GJ 876, которая была на тот момент одной из немногих систем, демонстрирующих наблюдаемые гравитационные возмущения. Впервые было показано наличие автокоррелированного (красного) доплеровского шума, с амплитудой порядка 2 м/с и временным параметром около 3 сут. Этот шум, вероятно, свидетельствует о пятенной активности звезды. С его учетом в рамках модели гауссовского случайного процесса была уточнена конфигурация планетной системы, в частности угол взаимного наклона орбит двух главных планет ограничен величиной 15°, а также показано, что орбита внутренней планеты близка к круговой. Кроме того, в этой работе был предложен быстрый метод фиттинга возмущенной орбитальной конфигурации, использующий уравнения чувствительности для вычисления частных производных лучевой скорости по параметрам модели (которые нужны в градиентных методах фиттинга).
В работе (Baluev, 2013b) пионерский метод учета коррелированного доплеровского шума получил дальнейшее развитие при анализе планетной системы GJ 581. Показано, что после такого учета (i) доплеровский сигнал ранее оспоренной планеты e выделяется в данных разных обсерваторий уверенно и независимо, (ii) сигналы гипотетических планет f и g, которые ранее заявлялись некоторыми группами, оказываются ложным эффектом красного шума, (iii) статистическая значимость сигнала планеты d становится пограничной. Таким образом, пример GJ 581 демонстрирует оба типа статистических ошибок, к которым может привести наличие красного шума: обнаружение ложных сигналов (ошибка первого рода) и необнаружение реально существующего (ошибка второго рода).
В работе (Baluev, Beaugé, 2014) исследовалась резонансная планетная система HD 82943. В доплеровских данных спектрографа CORALIE для этой системы обнаружена годичная систематическая ошибка, которая искажала прежние результаты анализа. В новой модели устойчивая орбитальная конфигурация соответствует трехпланетному резонансу 1:2:5, при этом две главные планеты (b, c) находятся вблизи состояния апсидальной коротации со значительными эксцентриситетами. При этом, если система пришла к данной конфигурации через адиабатическую миграцию, начиная от почти круговых орбит, то в какой-то период времени она должна была пройти состояние асимметричной апсидальной коротации. Это могло стать причиной катастрофических событий в системе, ранее заподозренных по аномальному содержанию лития-6 в атмосфере звезды (Israelian и др., 2001).
Существо описанных выше работ лежало зачастую не столько в плоскости исследования конкретных планетных систем, сколько в методологической плоскости. Например, сюда относится определение структуры доплеровского шума, когда шумовой компонент с нестандартными свойствами существенно искажает результаты анализа и итоговую модель планетной системы. Таким образом, значительную роль здесь играет разработка новых статистических методов моделирования, а также соответствующего программного обеспечения. В частности, следует упомянуть разработанный в СПбГУ пакет PlanetPack3 с открытым исходным кодом (Baluev, 2013a; 2018a). Он позволяет решать целый комплекс сложных и нестандартных задач статистической обработки наблюдений, в частности, выполнять самосогласованное моделирование доплеровских и фотометрических измерений, в том числе с использованием гравитационно-возмущенной модели планетной системы в рамках задачи N тел.
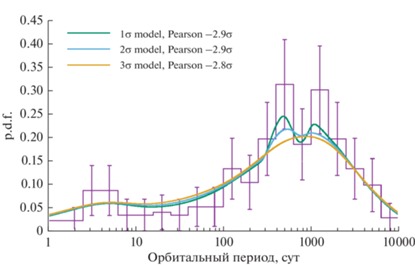
Самостоятельным ответвлением данной темы стало исследование не отдельных планетных систем, а экзопланетной статистики. В работе (Baluev, 2018b) представлена адаптация метода вейвлет-анализа для поиска значимых структур в одномерных статистических выборках. В последующей работе (Baluev, Shaidulin, 2018) эта методика применялась к выборке открытых экзопланет. В частности, была обнаружена статистически значимая группа (сгущение) планет-гигантов (с массой более примерно массы Сатурна), занимающая узкий интервал по орбитальному периоду около значения 1 года (см. рис. 5). Предположительно, она связана с эффектом ледяной аккумуляции в протопланетном диске, то есть этот результат можно считать наблюдательным подтверждением как самого существования данного эффекта, так и его значимости для процессов планетообразования.
Рис. 5.
Плотность распределения орбитальных периодов экзопланет, очищенная от шума методом вейвлет-анализа. Рис. из статьи (Baluev, Shaidulin, 2018).
Авторы благодарны рецензенту за полезные замечания. Работа Д.В. Микрюкова и И.И. Шевченко поддержана в рамках гранта РНФ № 22-22-00046.
Список литературы
Александрова А.Г., Галушина Т.Ю., Прищепенко А.Б., Холшевников К.В., Чечеткин В.М. О превентивном разрушении опасного астероида // Астрон. журн. 2016. Т. 39. № 6. С. 595–602.
Баляев И.А. Об ускорении численного интегрирования уравнений движения астероидов // Астрон. вестн. 2020. Т. 54. № 6. С. 567–576. https://doi.org/10.31857/S0320930X20330014. (Balyaev I.A. Acceleration of numerical integration of the equations of motion of asteroids // Sol. Syst. Res. 2020. V. 54. № 6. P. 557–566.)10.31857/S0320930X20330014
Батмунх Н., Оськина К.И., Санникова Т.Н., Титов В.Б., Холшевников К.В. Увод астероида с помощью двигателей малой тяги, направленной по трансверсали // Астрон. журн. 2019. Т. 96. № 11. С. 961–968.
Девяткин А.В., Горшанов Д.Л., Грицук А.Н., Мельников А.В., Сидоров М.Ю., Шевченко И.И. Наблюдения и теоретический анализ кривых блеска естественных спутников планет // Астрон. вестн. 2002. Т. 36. № 3. С. 269–281. (Devyatkin A.V., Gorshanov D.L., Gritsuk A.N., Melnikov A.V., Sidorov M.Yu., Shevchenko I.I. Observations and theoretical analysis of lightcurves of natural satellites of planets // Sol. Syst. Res. 2002. V. 36. № 3. P. 248–259.)
Демидова Т.В., Шевченко И.И. Моделирование динамики остаточных дисков в системах Кеплер-16, Кеплер-34 и Кеплер-35 // Письма в Астрон. журн. 2018. Т. 44. № 2. С. 140–147.
Демидова Т.В., Шевченко И.И. Долговременная динамика планетезималей в хаотических зонах планет // Письма в Астрон. журн. 2020. Т. 46. № 11. С. 827–836.
Дикарев В.В., Кривов А.В. Динамика и пространственное распределение частиц кольца Е Сатурна // Астрон. вестн. 1998. Т. 32. № 2. С. 147–163. (Dikarev V.V., Krivov A.V. Dynamics and spatial distribution of Saturn’s E ring particles // Sol. Syst. Res. 1998. V. 32. № 2. P. 128–143.)
Елькин А.В., Соколов Л.Л. О последовательных прохождениях АСЗ в окрестности Земли // Тез. докл. Всеросс. конф. с международным участием “Астероидная опасность – 95”. 23–25 мая 1995 г. Санкт-Петербург: ИТА РАН, МИПАО. 1995. Т. 2. С. 41.
Ивашкин В.В., Стихно К.А. О применении гравитационного воздействия на астероид Apophis для коррекции его орбиты // Докл. АН РАН. Сер. Механика. 2009. Т. 424. № 5. С. 621–626.
Коблик В.В., Холшевников К.В. Огибающая орбит изотропно выброшенных частиц // Вестн. СПбГУ. Сер. 1. 1994. Вып. 1. С. 98–102.
Кривов А.В., Соколов Л.Л., Холшевников К.В., Шор В.А. О существовании роя частиц в окрестности орбиты Фобоса // Астрон. вестн. 1991. Т. 25. № 3. С. 317–326. (Krivov A.V., Sokolov L.L., Kholshevnikov K.V., Shor V.A. On the existence of the swarm of particles around the Phobos orbit // Sol. Syst. Res. 1991. V. 25. № 3. P. 233–242.)
Куприянов В.В., Шевченко И.И. О форме и вращательной динамике малых спутников планет // Астрон. вестн. 2006. Т. 40. № 5. С. 428–435. (Kouprianov V.V., Shevchenko I.I. The shapes and rotational dynamics of minor planetary satellites // Sol. Syst. Res. 2006. V. 40. № 5. P. 393–399.)https://doi.org/10.1134/S0038094606050042
Мельников А.В. Бифуркационный режим синхронного резонанса в поступательно-вращательном движении несферических естественных спутников планет // Космич. исслед. 2001. Т. 39. № 1. С. 74–84.
Мельников А.В. Условия возникновения странных аттракторов во вращательной динамике малых спутников планет // Космич. исслед. 2014. Т. 52. № 6. С. 500–511.
Мельников А.В. Ориентация фигур малых спутников планет при хаотическом вращении // Астрон. вестн. 2020. Т. 54. № 5. С. 458–467. https://doi.org/10.1134/S0038094620050068. (Mel’nikov A.V. Orientation of figures of small planetary satellites during chaotic rotation // Sol. Syst. Res. 2020. V. 54. № 5. P. 432–441.)10.1134/S0038094620050068
Мельников А.В., Шевченко И.И. Об устойчивости вращательного движения несферических естественных спутников относительно наклона оси вращения // Астрон. вестн. 1998. Т. 32. № 6. С. 548–559. (Mel’nikov A.V., Shevchenko I.I. The stability of the rotational motion of nonspherical natural satellites with respect to tilting the axis of rotation // Sol. Syst. Res. 1998. V. 32. № 6. P. 480–490.)
Мельников А.В., Шевченко И.И. Об устойчивости вращения несферических естественных спутников в синхронном резонансе // Астрон. вестн. 2000. Т. 34. № 5. С. 478–486. (Mel’nikov A.V., Shevchenko I.I. On the stability of the rotational motion of nonspherical natural satellites in a synchronous resonance // Sol. Syst. Res. 2000. V. 34. № 5. P. 434–442.)
Мельников А.В., Шевченко И.И. Необычные режимы вращения малых спутников планет // Астрон. вестн. 2007. Т. 41. № 6. С. 521–530. (Mel’nikov A.V., Shevchenko I.I. Unusual rotation modes of minor planetary satellites // Sol. Syst. Res. 2007. V. 41. № 6. P. 483–491.)https://doi.org/10.1134/S0038094607060032
Мельников А.В., Шевченко И.И. Вращательная динамика и эволюция спутников планет Солнечной и экзопланетных систем // Астрон. вестн. 2022. Т. 56. № 1. С. 3–26. https://doi.org/10.31857/S0320930X22010042. (Melnikov A.V., Shevchenko I.I. Rotational dynamics and evolution of planetary satellites in the Solar and exoplanetary systems // Sol. Syst. Res. 2022. V. 56. № 1. P. 1–22.)10.31857/S0320930X22010042
Орлов С.А., Холшевников К.В. Пылевой тор III? Уравнения огибающей поверхности семейства траекторий изотропно выброшенных частиц с учетом движения узлов и перицентров // Вестн. СПбГУ. 2004. Сер. 1. Вып. 1. С. 112–119.
Орлов С.А., Холшевников К.В. Орбитальный пылевой тор как огибающая поверхность семейства траекторий изотропно выброшенных частиц // Астрон. вестн. 2008. Т. 42. № 2. С. 99–118. (Orlov S.A., Kholshevnikov K.V. The orbital dust torus as an enveloping surface of a family of trajectories of isotropically ejected particles // Sol. Syst. Res. 2008. V. 42. № 2. P. 91–110.)https://doi.org/10.1007/s11208-008-2001-0
Орлов С.А., Холшевников К.В. Пылевой тор, образованный выбросом частиц в апсидальных точках // Астрон. вестн. 2012. Т. 46. № 3. С. 223–234. (Orlov S.A., Kholshevnikov K.V. Dust torus produced by particles ejected in the apsidal points // Sol. Syst. Res. 2012. V. 46. № 3. P. 208–219.)https://doi.org/10.1134/S0038094612020098
Попова Е.А., Шевченко И.И. Планетная динамика в системе Alpha Centauri: диаграммы устойчивости // Письма в Астрон. журн. 2012. Т. 38. № 9. С. 652–659.
Попова Е.А., Шевченко И.И. Об устойчивости циркумбинарных планетных систем // Письма в Астрон. журн. 2016. Т. 42. № 6. С. 525–532.
Соколов Л.Л., Баляев И.А., Кутеева Г.А., Петров Н.А., Эскин Б.Б. Возможные соударения и сближения с Землей некоторых опасных астероидов // Астрон. вестн. 2021. Т. 55. № 1. С. 65–73. https://doi.org/10.31857/S0320930X21010084
Соколов Л.Л., Башаков А.А., Борисова Т.П., Петров Н.А., Питьев Н.П., Шайдулин В.Ш. Траектории соударения астероида Апофис с Землей в XXI веке // Астрон. вестн. 2012. Т. 46. № 4. С. 311–320. (Sokolov L.L., Bashakov A.A., Borisova T.P., Petrov N.A., Pitjev N.P., Shaidulin V.S. Impact trajectories of the asteroid Apophis in the 21st century // Sol. Syst. Res. 2012. V. 46. № 4. P. 291–300.)https://doi.org/10.1134/S0038094612040077
Соколов Л.Л., Башаков А.А., Питьев Н.П. Особенности движения астероида 99942 Apophis // Астрон. вестн. 2008. Т. 42. № 1. С. 54–65. (Sokolov L.L., Bashakov A.A., Pitjev N.P. Peculiarities of the motion of asteroid 99942 Apophis // Sol. Syst. Res. 2008. V. 42. № 1. P. 18–27.)https://doi.org/10.1007/s11208-008-1003-2
Соколов Л.Л., Борисова Т.П., Васильев А.А., Петров Н.А. Свойства траекторий соударения астероидов с Землей // Астрон. вестн. 2013. Т. 47. № 5. С. 441–447. https://doi.org/10.7868/S0320930X13040087 (Sokolov L.L., Borisova T.P., Vasil’ev A.A., Petrov N.A. Properties of collision trajectories of asteroids with the Earth // Sol. Syst. Res. 2013. V. 47. № 5. P. 408–413.)10.7868/S0320930X13040087
Соколов Л.Л., Петров Н.А., Васильев А.А., Кутеева Г.А., Шмыров А.С., Эскин Б.Б. О возможности увода астероида от соударений с Землей с использованием кинетического метода // Астрон. вестн. 2018. Т. 52. № 4. С. 343–350. https://doi.org/10.1134/S0320930X18040060 (Sokolov L.L., Petrov N.A., Vasil’ev A.A., Kuteeva G.A., Shmyrov A.S., Eskin B.B. On the possibility of deflecting an asteroid from collision with the Earth using the kinetic method // Sol. Syst. Res. 2018. V. 52. № 4. P. 338–346.)10.1134/S0320930X18040060
Холшевников К.В. Вероятность столкновения с объектом, движущимся по орбите соударения с Землей // Тр. Всесоюзного совещания “Астероидная опасность” 10–11 октября 1991 г. Санкт-Петербург / Ред. Сокольский А.Г. СПб: ИТА РАН, 1992. С. 95.
Холшевников К.С., Баляев И.А., Соколов Л.Л., Эскин Б.Б. Ретроспективный анализ орбит сталкивающихся с Землей астероидов // Вестн. СПбГУ. Сер. 1. Астрономия. 2021. Т. 8 (66). Вып. 3. С. 523–532.
Холшевников К.В., Орлов С.А. Пылевой тор I. Уравнения огибающей поверхности семейства траекторий изотропно выброшенных частиц // Вестн. СПбГУ. Сер. 1. 2000. Вып. 3. С. 118–123.
Холшевников К.В., Орлов С.А., Джазмати М.С. Пылевой тор III. Исследование огибающей поверхности семейства траекторий изотропно выброшенных частиц // Вестн. СПбГУ. Сер. 1. 2003. Вып. 4. С. 119–130.
Холшевников К.В., Титов В.Б. Задача двух тел: Учебное пособие. СПб: Изд-во СПбГУ, 2007. 180 с.
Шевченко И.И. О максимальных показателях Ляпунова хаотического вращения естественных спутников планет // Космич. исслед. 2002. Т. 40. № 3. С. 317–326.
Baluev R.V. Resonances of low orders in the planetary system of HD37124 // Celest. Mech. and Dyn. Astron. 2008. V. 102. P. 297–325.
Baluev R.V. Orbital structure of the GJ876 planetary system, based on the latest Keck and HARPS radial velocity data // Celest. Mech. and Dyn. Astron. 2011. V. 111. P. 235–266.
Baluev R.V. PlanetPack: a radial-velocity time-series analysis tool facilitating exoplanets detection, characterization, and dynamical simulations // Astron. and Comput. 2013a. V. 2. P. 18–26.
Baluev R.V. The impact of red noise in radial velocity planet searches: only three planets orbiting GJ581? // Mon. Notic. Roy. Astron. Soc. 2013b. V. 429. P. 2052–2068.
Baluev R.V. PlanetPack3: A radial-velocity and transit analysis tool for exoplanets // Astron. and Comput. 2018a. V. 25. P. 221–229.
Baluev R.V. Statistical detection of patterns in unidimensional distributions by continuous wavelet transforms // Astron. and Comput. 2018b. V. 23. P. 151–165.
Baluev R.V. Fast error-safe MOID computation involving hyperbolic orbits // Astron. and Comput. 2021. V. 34. id. 100440.
Baluev R.V., Beaugé C. Possible solution to the riddle of HD 82943 multi-planet system: the three-planet resonance 1 : 2 : 5? // Mon. Notic. Roy. Astron. Soc. 2014. V. 439. P. 673–689.
Baluyev R.V., Kholshevnikov K.V. Distance between two arbitrary unperturbed orbits // Celest. Mech. and Dyn. Astron. 2005. V. 91. № 3–4. P. 287–300.
Baluev R.V., Mikryukov D.V. Fast error-controlling MOID computation for confocal elliptic orbits // Astron. and Comput. 2019. V. 27. P. 11–22.
Baluev R.V., Shaidulin V.S. Fine-resolution wavelet analysis of exoplanetary distributions: hints of an overshooting iceline accumulation // Astrophys. and Space Sci. 2018. V. 363. id. 192.
Banaszkiewicz M., Krivov A.V. Hyperion as a Dust Source in the Saturnian System // Dynamics and Astrometry of Natural and Artificial Celestial Bodies / Eds Wytrzyszczak I., Lieske J.H., Feldman R.A. Dordrecht: Kluwer, 1997a. P. 171–176.
Banaszkiewicz M., Krivov A.V. Hyperion as a dust source in the Saturnian system // Icarus. 1997b. V. 129. P. 289–303.
Chesley S.R. Potential impact detection for Near-Earth asteroids: the case of 99942 Apophis (2004 MN4) // Asteroids, Comets, Meteors. Proc. IAU Symp. № 229. 2005. Cambridge Univ. Press, 2006. P. 215–228.
Chesley S.R. Asteroid impact hazard assessment over long time intervals // American Astronomical Society, AAS Meeting No. 219. 2011. Id.122.02.
Demidova T.V., Shevchenko I.I. Spiral patterns in planetesimal circumbinary disks // Astrophys. J. 2015. V. 805. id. 38.
Demidova T.V., Shevchenko I.I. Three-lane and multi-lane signatures of planets in planetesimal disks // Mon. Notic. Roy. Astron. Soc. 2016. V. 463. P. L22–L26.
Denk T., Mottola S. Studies of irregular satellites: I. Lightcurves and rotation periods of 25 Saturnian moons from Cassini observations // Icarus. 2019. V. 322 P. 80–102.
Dikarev V.V. Dynamics of particles in Saturn’s E ring: effects of charge variations and the plasma drag force // Astron. and Astrophys. 1999. V. 346. P. 1011–1019.
Dikarev V.V., Krivov A.V., Grüun E. Two stages of dust delivery from satellites to planetary rings // Planet. and Space Sci. 2006. V. 54. P. 1014–1023.
Hamilton D.P., Krivov A.V. Circumplanetary dust dynamics: effects of solar gravity, radiation pressure, planetary oblateness, and electromagnetism // Icarus. 1996. V. 123. P. 503–523.
Hamilton D.P., Krivov A.V. Dynamics of distant moons of asteroids // Icarus. 1997. V. 128. P. 241–249.
Israelian G., Santos N.C., Mayor M., Rebolo R. Evidence for planet engulfment by the star HD 82943 // Nature. 2001. V. 411. P. 163–166.
Kholshevnikov K.V., Krivov A.V., Sokolov L.L., Titov V.B. The dust torus around Phobos orbit // Icarus. 1993. V. 105. P. 351–362.
Kholshevnikov K.V., Vassiliev N.N. On linking coefficient of two Keplerian orbits // Celest. Mech. and Dyn. Astron. 1999a. V. 75. № 1. P. 67–74.
Kholshevnikov K.V., Vassiliev N.N. On the distance function between two Keplerian elliptic orbits // Celest. Mech. and Dyn. Astron. 1999b. V. 75. № 2. P. 75–83.
Kouprianov V.V., Shevchenko I.I. Rotational dynamics of planetary satellites: A survey of regular and chaotic behavior // Icarus. 2005. V. 176. P. 224–234.
Krivov A.V. On the dust belts of Mars // Astron. and Astrophys. 1994. V. 291. P. 657–663.
Krivov A.V., Banaszkiewicz M. Unusual origin, evolution and fate of icy ejecta from Hyperion // Planet. and Space Sci. 2001a. V. 49. P. 1265–1279.
Krivov A.V., Banaszkiewicz M. Dust influx to Titan from Hyperion // Collisional Processes in the Solar System / Eds Marov M.Ya., Rickman H. Astrophysics and Space Science Library. Dordrecht: Kluwer, 2001b. V. 261. P. 265–276.
Krivov A.V., Hamilton D.P. Martian dust belts: waiting for discovery // Icarus. 1997. V. 128. P. 335–353.
Krivov A.V., Jurewicz A. The ethereal dust envelopes of the Martian moons // Planet. and Space Sci. 1998. V. 47. P. 45–56.
Krivov A.V., Getino J. Orbital evolution of high-altitude balloon satellites // Astron. and Astrophys. 1997. V. 318. P. 308–314.
Krivov A.V., Feofilov A.G., Dikarev V.V. Search for the putative dust belts of Mars: The late 2007 opportunity // Planet. and Space Sci. 2006. V. 54. № 9–10. P. 871–878.
Krivov A.V., Krüger H., Grün E., Thiessenhusen K.-U., Hamilton D.P. A tenuous dust ring of Jupiter formed by escaping ejecta from the Galilean satellites // J. Geophys. Res. 2002a. V. 107. № E1. https://doi.org/10.1029/2000JE001434
Krivov A.V., Sokolov L.L., Dikarev V.V. Dynamics of Mars-orbiting dust: Effects of light pressure and planetary oblateness // Celest. Mech. Dynam. and Astron. 1996. V. 63. № 3–4. P. 313–339.
Krivov A.V., Sokolov L.L., Getino J. Orbital instability zones of balloon satellites // Dynamics and Astrometry of Natural and Artificial Celestial Bodies / Eds Wytrzyszczak I., Lieske J.H., Feldman R.A. Dordrecht: Kluwer, 1997. P. 361–366.
Krivov A.V., Sremčević M., Spahn F., Dikarev V.V., Kholshevnikov K.V. Impact-generated dust clouds around planetary satellites: spherically symmetric case // Planet. and Space Sci. 2003. V. 51. № 3. P. 251–269.
Krivov A.V., Wardinski I., Spahn F., Krüger H., Grün E. Dust on the outskirts of the Jovian system // Icarus. 2002b. V. 157. P. 436–455.
Krüger H., Krivov A.V., Hamilton D.P., Grün E. Detection of an impact-generated dust cloud around Ganymede // Nature. 1999. V. 399. P. 558–560.
Krüger H., Krivov A.V., Grün E. A dust cloud around Ganymede maintained by hypervelocity impacts of interplanetary micrometeoroids // Planet. and Space Sci. 2000. V. 48. P. 1457–1471.
Krüger H., Krivov A.V., Sremčević M., Grün E. Impact-generated dust clouds surrounding the Galilean moons // Icarus. 2003. V. 164. P. 170–187.
MacDonald G.J.F. Tidal friction // Rev. Geophys. and Space Phys. 1964. V. 2. P. 467–541.
Makuch M., Brilliantov N.V., Sremčević M., Spahn F., Krivov A.V. Stochastic circumplanetary dynamics of rotating non-spherical dust particles // Planet. and Space Sci. 2006. V. 54. P. 855–870.
Makuch M., Krivov A.V., Spahn F. Long-term dynamical evolution of dusty ejecta from Deimos // Planet. and Space Sci. 2005. V. 53. P. 357–369.
Mardling R. Resonance, chaos and stability: The three-body problem in astrophysics // Lect. Notes Phys. 2008. V. 760. P. 59–96.
Mikryukov D.V., Baluev R.V. A lower bound of the distance between two elliptic orbits // Celest. Mech. and Dyn. Astron. 2019. V. 131. № 6. id. 28.
Melnikov A.V. Modelling of lightcurves of minor planetary satellites // Тр. ИПА РАН. 2002. Вып. 8. С. 131–132.
Melnikov A.V., Shevchenko I.I. On the rotational dynamics of Prometheus and Pandora // Celest. Mech. and Dyn. Astron. 2008. V. 101. № 1–2. P. 31–47.
Melnikov A.V., Shevchenko I.I. The rotation states predominant among the planetary satellites // Icarus. 2010. V. 209. P. 786–794.
Orlov S.A., Kholshevnikov K.V. Dust torus formed by particles ejected from a celestial body at an arbitrary point of its elliptic orbit // Celest. Mech. and Dyn. Astron. 2013. V. 116. P. 35–52.
Petrov N., Sokolov L., Polyakhova E., Oskina K. Predictions of asteroid hazard to the Earth for the 21st century // AIP Conf. Proc. 2018. V. 1959. id. 040012.
Popova E.A., Shevchenko I.I. Kepler-16b: safe in a resonance cell // Astrophys. J. 2013. V. 769. P. 152–158.
Shevchenko I.I. The separatrix algorithmic map: Application to the spin-orbit motion // Celest. Mech. and Dyn. Astron. 1999. V. 73. P. 259–268.
Shevchenko I.I. Adiabatic chaos in the Prometheus–Pandora system // Mon. Notic. Roy. Astron. Soc. 2008. V. 384. № 3. P. 1211–1220.
Shevchenko I.I. Chaotic zones around gravitating binaries // Astrophys. J. 2015. V. 799. Id. 8.
Shevchenko I.I. Lyapunov and clearing timescales in planetary chaotic zones // Astron. J. 2020a. V. 160. Id. 212.
Shevchenko I.I. Dynamical Chaos in Planetary Systems. Springer Nature, 2020b. 401 p.
Soter S. Report of Center for Radiophysics and Space Research No 462. 1971. Ithaca, NY: Cornell Univ.
Srama R., Ahrens T.J., Altobelli N., Auer S., Bradley J.G., Burton M., Dikarev V.V., Economou T., Fechtig H., Gőrlich M., and 34 co-authers. The Cassini Cosmic Dust Analyzer // Space Sci. Rev. 2004. V. 114. № 1–4. P. 465–518.
Spahn F., Albers N., Hörning M., Kempf S., Krivov A.V., Makuch M., Schmidt J., Seiŝ M., Sremčević M. E ring dust sources: Implications from Cassini’s dust measurements // Planet. and Space Sci. 2006a. V. 54. № 9–10. P. 1024–1032.
Spahn F., Krivov A.V., Sremčević M., Schwarz U., Kurths J. Stochastic forces in circumplanetary dust dynamics // J. Geophys. Res. 2003. V. 108 (E4). https://doi.org/10.1029/2002JE001925
Spahn F., Schmidt J., Albers N., Hörning M., Makuch M., Seiŝ M., Kempf S., Srama R., Dikarev V., Helfert S., Moragas-Klostermeyer G., Krivov A.V., Sremčević M., Tuzzolino A.J., Economou Th., Grün E. Cassini dust measurements at Enceladus and implications for the origin of the E ring // Science. 2006b. V. 311. P. 1416–1418.
Sremčević M., Krivov A.V., Spahn F. Impact-generated dust clouds around planetary satellites: asymmetry effects // Planet. and Space Sci. 2003. V. 51. P. 455–471.
Sremčević M., Krivov A.V., Spahn F. Impact-generated dust clouds around planetary satellites: model versus Galileo data // Planet. and Space Sci. 2005. V. 53. P. 625–641.
Thiessenhusen K.-U., Krivov A.V., Krüger H., Grün E. A dust cloud around Pluto and Charon // Planet. and Space Sci. 2002. V. 50. P. 79–87.
Wright J.T., Veras D., Ford E.B., Johnson J.A., Marcy G.W., Howard A.W., Isaacson H., Fischer D.A., Spronck J., Anderson J., Valenti J. The California planet survey. III. A possible 2 : 1 resonance in the exoplanetary triple system HD 37124 // Astrophys. J. 2011. V. 730. id. 93.
Дополнительные материалы отсутствуют.
Инструменты
Астрономический вестник


