Астрономический журнал, 2022, T. 99, № 3, стр. 239-249
Численная модель для исследования протонных полярных сияний на Марсе
А. Г. Жилкин 1, *, Д. В. Бисикало 1, В. И. Шематович 1
1 Институт астрономии Российской академии наук
Москва, Россия
* E-mail: zhilkin@inasan.ru
Поступила в редакцию 22.10.2021
После доработки 26.11.2021
Принята к публикации 26.11.2021
- EDN: BUDMGV
- DOI: 10.31857/S0004629922030070
Аннотация
В работе представлены гибридная и МГД модели обтекания Марса плазмой солнечного ветра, при помощи которых рассчитываются поток протонов солнечного ветра и граница индуцированной магнитосферы. Эти параметры являются входными для кинетической Монте-Карло модели воздействия потока протонов невозмущенного солнечного ветра на дневную атмосферу Марса. Ее предполагается использовать для определения потоков энергии и энергетических спектров атомов водорода, проникающих в дневную верхнюю атмосферу через границу индуцированной магнитосферы. Полученные характеристики позволяют оценить параметры авроральных протонных явлений, открытых недавно в верхней атмосфере Марса. Полученные характеристики позволяют проводить расчеты авроральных протонных свечений, наблюдавшихся в верхней атмосфере Марса при помощи спектрографа IUVIS на борту КА MAVEN. Сравнение результатов этих расчетов с наблюдениями открывает уникальную возможность уточнения свойств атмосферы и магнитного поля Марса, а также расширяет способы определения параметров солнечного ветра.
1. ВВЕДЕНИЕ
У Марса отсутствует собственное глобальное магнитное поле и лишь в южном полушарии наблюдается относительно слабая остаточная намагниченность коры планеты, и, соответственно, его верхние атмосфера и ионосфера напрямую взаимодействуют с плазмой солнечного ветра. Главной особенностью взаимодействия плазмы солнечного ветра [1] с немагнитными планетами является формирование полости в солнечном ветре, так называемой индуцированной магнитосферы. Индуцированная магнитосфера является препятствием для сверхзвукового потока плазмы и, следовательно, перед планетой должна формироваться головная (отошедшая) ударная волна. Возле подсолнечной точки индуцированная магнитосфера отделена от плазмы солнечного ветра магнитным барьером, областью с увеличенным магнитным полем [2].
Магнитный барьер формируется посредством суперпозиции межпланетного магнитного поля (ММП), вмороженного в поток солнечного ветра и полей электрических токов, индуцированных в проводящих слоях планетной ионосферы. На внешней стороне давление магнитного поля барьера уравновешивается динамическим давлением плазмы солнечного ветра, а на внутренней стороне – тепловым давлением ионосферной плазмы. Внутренняя граница магнитного барьера примерно соответствует границе индуцированной магнитосферы. Индуцированная магнитосфера наполнена ионами планетного происхождения. Планетные ионы присутствуют также и в областях термализованного солнечного ветра (magnetosheath) и невозмущенного солнечного ветра. Головная ударная волна вызывает замедление потока солнечного ветра от сверхзвуковой к дозвуковой скорости (см., напр., [1]). Граница между замедленным потоком солнечного ветра и индуцированной магнитосферой, часто называемая границей индуцированной магнитосферы (IMB), не полностью препятствует проникновению плазмы солнечного ветра в атмосферу. Гирорадиусы частиц солнечного ветра достаточно велики по сравнению с размерами IMB, что позволяет частицам плазмы двигаться по спирали вдоль сжатого магнитного поля и непосредственно взаимодействовать с верхними слоями марсианской атмосферы. Это уникальное свойство малого размера индуцированной магнитосферы позволяет протонам и альфа-частицам солнечного ветра проникать в атмосферу Марса.
Низкая гравитация Марса приводит к образованию протяженной нейтральной короны атомарного водорода далеко за пределами границы индуцированной магнитосферы (см., напр., [3]). Следствием этого фактора является то, что вероятности реакции обмена зарядами (перезарядки) между протонами солнечного ветра и атомами короны становятся значительными. В реакции перезарядки протон солнечного ветра захватывает электрон от экзосферного атома и становится энергетическим нейтральным атомом водорода (ENA-H). Кроме того, протоны планетарного происхождения, ускоренные в плазменной среде, также могут подвергаться реакции перезарядки с экзосферными атомами. ENA-H сохраняют скорость исходного иона из-за очень малых потерь энергии в процессе перезарядки по сравнению с его кинетической энергией, и они больше не испытывают действия электромагнитных полей, т.е. проникают через границу индуцированной магнитосферы непосредственно в атмосферу Марса. Кинетическая энергия ENA-H на порядки превышает локальную энергию гравитации вокруг Марса, и таким образом ENA-H движутся в пространстве почти по прямой линии (см., напр., обзор [4]).
Протонные авроральные явления, такие как протонная аврора – измеренный при помощи спектрографа IUVIS на борту КА MAVEN избыток свечения атомарного водорода в линии Ly$\alpha $ [5], наблюдаются [6] на дневной стороне Марса и вызываются проникающими в атмосферу потоками ENA-H – атомов водорода с высокими кинетическими энергиями, образующихся за счет перезарядки протонов солнечного ветра в водородной короне Марса [5, 6]. В данной работе для исследования авроральных протонных явлений использованы разработанные ранее гибридная и МГД модели обтекания Марса плазмой солнечного ветра, которые позволяют рассчитать структуру плазменной оболочки Марса, в частности, расположение отошедшей ударной волны и границы индуцированной магнитосферы. Поток протонов солнечного ветра после отошедшей ударной волны и граница IMB являются необходимыми входными данными для кинетической Монте-Карло модели [7, 8] высыпания в верхнюю атмосферу планеты протонов и атомов водорода с высокими кинетическими энергиями. Далее, эта кинетическая модель используется для изучения перезарядки протонов солнечного ветра в протяженной водородной короне Марса и позволяет получить спектры атомов водорода [8], проникающих в атмосферу через границу индуцированной магнитосферы Марса. Рассчитанные энергетические спектры потока атомов водорода используются в качестве верхнего граничного условия при исследовании [7] высыпания атомов водорода с высокими энергиями в верхнюю атмосферу, что и позволяет провести сопряженное моделирование за счет совместного использования гибридных/МГД и кинетических моделей наблюдаемых характеристик протонных авроральных явлений в верхней атмосфере Марса.
В следующем разделе представлено описание МГД и гибридной моделей, а также результаты соответствующих расчетов структуры плазменной оболочки Марса. В Заключении сформулированы основные выводы по работе.
2. ОПИСАНИЕ МОДЕЛИ ДЛЯ РАСЧЕТА ПЛАЗМЕННОЙ ОБОЛОЧКИ МАРСА
2.1. МГД модель
Рассмотрим задачу обтекания Марса плазмой солнечного ветра. В приближении идеальной магнитной гидродинамики структура течения определяется следующей системой уравнений:
(2)
$\frac{{\partial{ \vec {v}}}}{{\partial t}} + \left( {\vec {v} \cdot \nabla } \right)\vec {v} = - \frac{{\nabla P}}{\rho } - \frac{{\vec {B} \times (\nabla \times \vec {B})}}{{4\pi \rho }} + \vec {g} + \vec {f},$(3)
$\frac{{\partial{ \vec {B}}}}{{\partial t}} = \nabla \times \left( {\vec {v} \times \vec {B}} \right),\quad \nabla \cdot \vec {B} = 0,$(4)
$\frac{{\partial \varepsilon }}{{\partial t}} + \left( {\vec {v} \cdot \nabla } \right)\varepsilon + \frac{P}{\rho }\nabla \cdot \vec {v} = Q,$Вычисления проводились в декартовой системе координат, начало которой располагалось в центре планеты. Ось $x$ направлена от центра Солнца к центру Марса, ось $y$ – вдоль орбитального движения планеты, а ось $z$ – вдоль ее оси собственного вращения.
Для задания параметров солнечного ветра в окрестности Марса мы использовали МГД модель ветра из работы [9]. Были использованы следующие значения: концентрация протонов ${{n}_{{\text{w}}}} = 3.1$ см–3, температура ${{T}_{{\text{w}}}} = 1.3 \times {{10}^{5}}$ К, скорость ${{v}_{{\text{w}}}} = 407$ км/с. Считалось, что в расчетной области вектор скорости ${{\vec {v}}_{{\text{w}}}}$ имеет только $x$-компонент, соответствующий радиальной скорости ${{{v}}_{r}}$ солнечного ветра. Азимутальным компонентом скорости ${{v}_{\varphi }}$, как собственным (3.3 км/с), так и обусловленным орбитальным вращением планеты (24.1 км/с), мы пренебрегали. Магнитное поле солнечного ветра ${{\vec {B}}_{{\text{w}}}}$ в окрестности Марса имеет как радиальный ${{B}_{r}}$, так и азимутальный ${{B}_{\varphi }}$ компонент. Для этих величин мы использовали значения ${{B}_{r}} = 9.4 \times {{10}^{{ - 6}}}$ Гс = 0.94 нТл, ${{B}_{\varphi }} = - 1.5 \times $ $ \times \;{{10}^{{ - 5}}}$ Гс = $ - 1.5$ нТл. Соответствующая индукция магнитного поля ${{B}_{{\text{w}}}} = 1.8 \times {{10}^{{ - 5}}}$ Гс = 1.8 нТл. В непосредственной окрестности Марса все эти величины можно считать постоянными. Отметим, что в использованной модели солнечного ветра в плоскости эклиптики вертикальный компонент магнитного поля ${{B}_{z}}$ отсутствует вследствие экваториальной симметрии. Он может возникать, например, в случае отклонения параметров солнечного ветра от экваториальной симметрии.
Скорость звука в плазме солнечного ветра в окрестности Марса составляет величину ${{c}_{{\text{w}}}} = $ $ = \sqrt {2{{k}_{{\text{B}}}}{{T}_{{\text{w}}}}{\text{/}}{{m}_{{\text{p}}}}} = 46.3$ км/с, где ${{k}_{{\text{B}}}}$ – постоянная Больцмана, ${{m}_{{\text{p}}}}$ – масса протона. Фактор 2 учитывает тот факт, что солнечный ветер состоит из полностью ионизованной водородной плазмы. В самом деле, полное давление солнечного ветра определяется суммой парциальных давлений ионов и электронов. Пренебрегая небольшим вкладом $\alpha $-частиц, можно считать, что средний молекулярный вес плазмы ветра равен 1/2, что как раз и соответствует фактору 2 в использованном выражении для скорости звука в ветре. Число Маха ${{v}_{{\text{w}}}}{\text{/}}{{c}_{{\text{w}}}} = 8.8$ и, следовательно, обтекание Марса солнечным ветром происходит в сверхзвуковом режиме. Альфвеновская скорость ${{u}_{{\text{w}}}} = $ $ = {{B}_{{\text{w}}}}{\text{/}}\sqrt {4\pi {{\rho }_{{\text{w}}}}} = 21.9$ км/с, где плотность ${{\rho }_{{\text{w}}}} = {{m}_{{\text{p}}}}{{n}_{{\text{w}}}}$. Отсюда альфвеновское число Маха ${{v}_{{\text{w}}}}{\text{/}}{{u}_{{\text{w}}}} = 18.6$ и, следовательно, обтекание Марса солнечным ветром происходит в существенно сверхальфвеновском режиме. Эти оценки, в частности, указывают на то, что вокруг Марса должна возникать ударная волна.
Поскольку предполагалось, что планета является идеально проводящим шаром, то магнитное поле солнечного ветра проникать в область $r < {{R}_{{{\text{Mars}}}}}$ не может. Это означает, что в модели необходимо учитывать наведенное магнитное поле Марса, которое экранирует поле ветра. Для описания этого поля можно использовать аналитическое решение задачи о магнитном поле идеально проводящего шара, помещенного в однородное внешнее магнитное поле. Как известно (см., напр., [10]), вне шара такое поле является дипольным. Поэтому в области $r \geqslant {{R}_{{{\text{Mars}}}}}$ можно написать
(7)
${{\vec {B}}_{{{\text{Mars}}}}} = \frac{{{{\mu }_{{{\text{Mars}}}}}}}{{{{r}^{3}}}}\left[ {3(\vec {d} \cdot \vec {n})\vec {n} - \vec {d}} \right],$Моделирование проводилось в двумерной расчетной области $ - 5{{R}_{{{\text{Mars}}}}} \leqslant x,y \leqslant 5{{R}_{{{\text{Mars}}}}}$ с числом ячеек $512 \times 512$. Для численного решения уравнений (1)–(5) была использована разностная схема Роу-Эйнфельдта-Ошера для магнитной гидродинамики, детали которой описаны в работе [11] (см. также монографию [12]).
В начальный момент времени вся расчетная область вне планеты ($r > {{R}_{{{\text{Mars}}}}}$) заполнялась солнечным ветром. Граничные условия задавались следующим образом. На расстоянии ${{R}_{{{\text{Mars}}}}}$ от центра устанавливалась твердая граница, на которой были заданы постоянные граничные условия. На участках внешних границ, через которые солнечный ветер втекал в расчетную область, граничные условия задавались постоянными с учетом использованных параметров ветра. На участках, через которые вещество покидало расчетную область, поддерживались условия свободного вытекания. Характерным динамическим временем задачи является ${{t}_{0}} = {{R}_{{{\text{Mars}}}}}{\text{/}}{{v}_{{\text{w}}}} = 8.3$ с. Моделирование проводилось до достижения квазистационарного решения, когда основные параметры течения переставали существенно изменяться со временем. Это составляет примерно 50–100 характерных времен.
Для сравнения мы провели три расчета для моделей с параллельным, перпендикулярным и наклонным магнитным полем без учета ионосферы, когда дополнительные источники $S$, $\vec {f}$ и $Q$ отсутствуют. В первом случае магнитное поле ветра задавалось равным ${{B}_{x}} = {{B}_{{\text{w}}}}$, ${{B}_{y}} = 0$ и, следовательно, вектор ${{\vec {B}}_{{\text{w}}}}$ оказывался параллельным вектору скорости ${{\vec {v}}_{{\text{w}}}}$. Во втором случае мы задавали ${{B}_{x}} = 0$, ${{B}_{y}} = - {{B}_{{\text{w}}}}$ и вектор ${{\vec {B}}_{{\text{w}}}}$ оказывался перпендикулярным вектору скорости ${{\vec {v}}_{{\text{w}}}}$. В третьем случае задавалось полное магнитное поле ветра ${{B}_{x}} = {{B}_{r}}$, ${{B}_{y}} = {{B}_{\varphi }}$. Результаты соответствующих расчетов для параллельного и перпендикулярного магнитного полей демонстрируют рис. 1 и 2, где представлены распределения плотности (цвет, изолинии), скорости (стрелки) и магнитного поля (линии) в орбитальной плоскости Марса. Планете соответствует закрашенный кружок.
Рис. 1.
Распределения плотности (цвет, изолинии), скорости (стрелки) и магнитного поля (линии) в орбитальной плоскости Марса для модели с параллельным (слева) и перпендикулярным (справа) к вектору скорости магнитным полем. Плотность выражена в единицах ${{\rho }_{{\text{w}}}}$. Закрашенный кружок соответствует радиусу Марса.
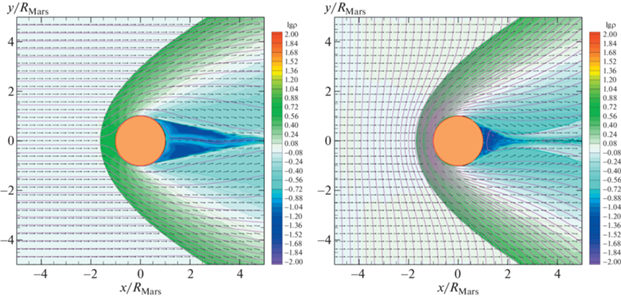
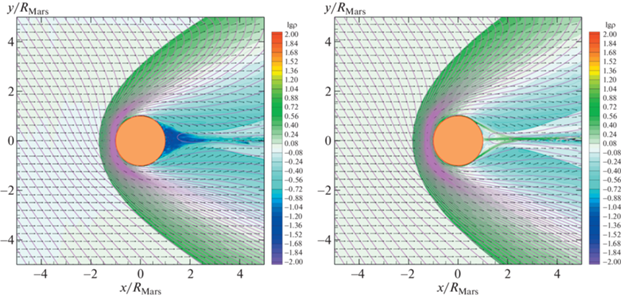
Рис. 2.
Распределения плотности (цвет, изолинии), скорости (стрелки) и магнитного поля (линии) в орбитальной плоскости Марса для модели без учета (слева) и с учетом (справа) водородной короны. Плотность выражена в единицах ${{\rho }_{{\text{w}}}}$. Закрашенный кружок соответствует радиусу Марса.
Во всех трех моделях вокруг планеты формируется ударная волна. В подсолнечной точке она находится от поверхности Марса на расстоянии ${{H}_{{{\text{sh}}}}} = 2070$ км в первом случае, ${{H}_{{{\text{sh}}}}} = 2380$ км во втором случае и ${{H}_{{{\text{sh}}}}} = 2275$ км в третьем. Как видно, расстояние до ударной волны оказывается минимальным в случае продольного поля и максимальным в случае перпендикулярного поля. В случае наклонного поля она занимает промежуточное положение. Следует иметь в виду, что в трехмерном случае положения ударных волн могут немного измениться (см., напр., [13]). Поэтому полученные значения величин ${{H}_{{{\text{sh}}}}}$ следует рассматривать как оценочные.
На ночной стороне формируется разреженная область, ограниченная тангенциальным разрывом, на котором развивается неустойчивость Кельвина-Гельмгольца. В результате за планетой тянется турбулентный шлейф. Во второй и третьей моделях (правая панель на рис. 1 и левая панель на рис. 2) в результате схождения потоков при обтекании планеты ветром формируются дополнительные ударные волны вдоль турбулентного шлейфа. В первой модели (левая панель на рис. 1) этот эффект в расчетной области выражен слабее, поскольку проявляется на более далеких расстояниях. В трехмерном приближении структура течения на ночной стороне планеты будет отличаться от картины, полученной в двумерном приближении, за счет изменения конфигурации сходящихся потоков. В частности, это касается структуры и интенсивности дополнительных ударных волн.
Обтекание Марса солнечным ветром приводит к возникновению магнитного барьера, который проявляется в виде области сгущения магнитных силовых линий. Магнитосфера Марса создается наведенным полем. Поэтому магнитопаузе соответствует граница магнитного барьера, которая, впрочем, не является четко выраженной и определяется весьма приближенно. В первой модели (параллельное поле) положение магнитопаузы вообще не определяется, поскольку в продольном направлении течение имеет газодинамический характер.
Для более точного определения положения магнитопаузы необходимо учесть в расчетах вещество ионосферы Марса. Тогда границе магнитопаузы будет соответствовать поверхность контактного разрыва (ионопауза), разделяющая плазму ветра и ионосферы [14]. Ионосфера Марса формируется процессами ионизации, происходящими в атмосфере [15]. Во внутренних частях атмосферы могут возникать тяжелые ионы. Самые верхние слои атмосферы Марса состоят из атомарного водорода и, начиная с высоты примерно 200 км, формируют водородную корону. Ионизация нейтрального водорода приводит к появлению соответствующих ионов, которые также участвуют в формировании общей картины течения. Ионосферный водород можно учесть в МГД модели с помощью включения дополнительных источников $S$, $\vec {f}$ и $Q$ в правые части уравнений (1)–(4).
Распределение концентрации атомов водорода в протяженной короне Марса можно задавать при помощи модели Чемберлена [16] для планетной изотермической экзосферы,
(8)
$n[{\text{H}}] = {{n}_{0}}\exp \left[ { - \frac{{G{{M}_{{{\text{Mars}}}}}}}{{c_{T}^{2}}}\left( {\frac{1}{{{{R}_{{{\text{Mars}}}}}}} - \frac{1}{r}} \right)} \right],$(9)
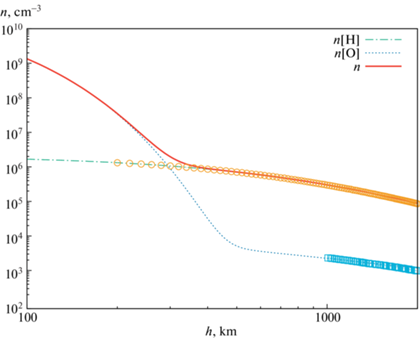
${{c}_{T}} = \sqrt {\frac{{{{k}_{{\text{B}}}}{{T}_{{\text{n}}}}}}{{{{m}_{{\text{p}}}}}}} = 1.22\;{\text{км/с}},$Распределение атомарного водорода $n[{\text{H}}]$ в короне Марса, полученное по формуле (8), представлено на рис. 3 штрихпунктирной линией. Данные из работы [3] показаны кружками. Видно, что аналитическое решение для стационарной изотермической атмосферы хорошо соответствует экспериментальным данным. Поэтому для описания водородной короны в нашей модели мы будем использовать выражение (8).
Рис. 3.
Модельные высотные профили концентрации атомарного водорода $n[{\text{H}}]$ (штрихпунктирная линия) и кислорода $n[{\text{O}}]$ (пунктирная линия) в короне Марса. Полная концентрация $n = n[{\text{H}}] + n[{\text{O}}]$ показана сплошной линией. Данные измерений показаны кружками (водород [3]) и квадратиками (кислород [17]).
Функция ионизации нейтрального водорода может быть записана в виде:
где $\nu \approx {{10}^{{ - 7}}}$ Гц – частота фотоионизации, $k \approx 1$ – эффективность фотоионизации. Оптическая толщина определяется выражением(12)
$\tau = \frac{\sigma }{{\cos \chi }}\int\limits_r^\infty \,n[{\text{H}}](r{\kern 1pt} ')dr{\kern 1pt} ',$Величина $\vec {f}$ в уравнении движения (2) описывает силу трения ионов водорода с нейтральными атомами водорода в стационарной короне:
где частота столкновений ${{\nu }_{{{\text{in}}}}} = {{k}_{{{\text{in}}}}}n[{\text{H}}]$, ${{k}_{{{\text{in}}}}} = 1.7 \times $ $ \times \;{{10}^{{ - 9}}}\;{\text{с}}{{{\text{м}}}^{3}}\;{{{\text{с}}}^{{ - 1}}}$ [18]. Наконец, эффекты нагрева-охлаждения определяются работой силы трения (13) и обменом энергией с нейтральными атомами водорода (см., напр., [19]):(14)
$Q = {{\nu }_{{{\text{in}}}}}{{\vec {v}}^{2}} + \frac{1}{2}{{\nu }_{{{\text{in}}}}}\frac{{{{k}_{{\text{B}}}}}}{{{{m}_{{\text{p}}}}}}\left( {T - {{T}_{{\text{n}}}}} \right).$(15)
$\varepsilon = \frac{3}{2}\frac{{{{k}_{{\text{B}}}}}}{{{{m}_{{\text{p}}}}}}T,\quad {{\varepsilon }_{{\text{n}}}} = \frac{3}{2}\frac{{{{k}_{{\text{B}}}}}}{{{{m}_{{\text{p}}}}}}{{T}_{{\text{n}}}},$(16)
$\frac{1}{2}{{\nu }_{{{\text{in}}}}}\frac{{{{k}_{{\text{B}}}}}}{{{{m}_{{\text{p}}}}}}\left( {T - {{T}_{{\text{n}}}}} \right) = - \frac{1}{3}{{\nu }_{{{\text{in}}}}}\left( {{{\varepsilon }_{{\text{n}}}} - \varepsilon } \right).$Результат расчета модели с учетом водородной короны Марса представлен на правой панели рис. 2. Структура течения на дневной стороне практически не изменилась. Образовавшийся ионосферный слой оказывается достаточно тонким. Однако на ночной стороне планеты область разрежения заполняется ионосферным водородом. Турбулентный шлейф вещества также состоит в основном из ионосферного водорода. В целом эти эффекты являются слабо выраженными из-за низкой плотности водородной короны. Более корректная модель помимо ионов водорода должна включать также и тяжелые ионосферные ионы. Однако аккуратный учет ионов различных сортов в рамках одножидкостной магнитной гидродинамики провести нельзя. Для этого необходимо рассмотреть более общие модели.
2.2. Гибридная модель
Приведенные выше результаты расчетов потоков высыпающихся в верхнюю атмосферу Марса атомов водорода с высокими энергиями на основе одножидкостной магнитной гидродинамики для описания процессов перезарядки протонов солнечного ветра с протяженной водородной короной планеты [3] показали, что этого явно недостаточно. Поэтому для более корректного и детального расчета этих процессов нами была разработана гибридная модель [20]. В основе модели лежат уравнения движения отдельных ионов (кинетическая часть) и квазигидродинамические уравнения для безмассовой электронной жидкости и нейтрального компонента (квазигидродинамическая часть). Использование приближения безмассовой электронной жидкости обусловлено тем, что масса электронов мала по сравнению с массами ионов и нейтралов. Из уравнения движения электронного компонента в этом приближении можно выразить напряженность электрического поля, которое возникает за счет движения электронов в магнитном поле и градиента давления электронов (батарейный эффект). Ионы различных типов рассматриваются в приближении независимых частиц. Иными словами, в гибридной модели сама ионная среда считается бесстолкновительной. Кроме того, в силу приближения безмассовой электронной жидкости столкновениями ионов с электронами также можно пренебречь. Однако в модели учитываются столкновения ионов с нейтралами. При этом нейтральный компонент рассматривается в квазигидродинамическом приближении.
Система уравнений, на которой основана гибридная модель, может быть записана в следующем виде:
(18)
$\frac{{d{{{\vec {u}}}_{s}}}}{{dt}} = \vec {g} + \frac{{{{e}_{s}}}}{{{{m}_{s}}}}\left[ {\vec {E} + \frac{1}{c}\left( {{{{\vec {u}}}_{s}} \times \vec {B}} \right)} \right] - {{\nu }_{{{\text{ns}}}}}\left( {{{{\vec {u}}}_{s}} - {{{\vec {v}}}_{{\text{n}}}}} \right),$(19)
${{q}_{{{\text{ion}}}}} = \sum\limits_\alpha \,{{e}_{\alpha }}{{n}_{\alpha }},\quad {{\vec {j}}_{{{\text{ion}}}}} = \sum\limits_\alpha \,{{e}_{\alpha }}{{n}_{\alpha }}{{\vec {v}}_{\alpha }},$(20)
${{n}_{{\text{e}}}} = \frac{{{{q}_{{{\text{ion}}}}}}}{e},\quad {{\vec {v}}_{{\text{e}}}} = \frac{1}{{{{q}_{{{\text{ion}}}}}}}\left( {{{{\vec {j}}}_{{{\text{ion}}}}} - \frac{c}{{4\pi }}\nabla \times \vec {B}} \right),$(21)
$\vec {E} = - \frac{1}{c}\left( {{{{\vec {v}}}_{{\text{e}}}} \times \vec {B}} \right) - \frac{{\nabla {{P}_{{\text{e}}}}}}{{{{q}_{{{\text{ion}}}}}}},\quad {{P}_{{\text{e}}}} = {{K}_{{\text{e}}}}n_{{\text{e}}}^{\gamma },$(22)
$\frac{{\partial{ \vec {B}}}}{{\partial t}} = \nabla \times \left( {{{{\vec {v}}}_{{\text{e}}}} \times \vec {B}} \right),\quad \nabla \cdot \vec {B} = 0.$Численный алгоритм в целом соответствует работам [20, 21], но адаптирован к нашей задаче и состоит из нескольких последовательных этапов. В его основе лежат разностные схемы второго порядка для уравнений движения ионов (17) и (18), а также циклическая схема с перешагиванием для решения уравнения индукции (22). Для расчета средних величин, характеризующих ионный компонент (концентрация ${{n}_{\alpha }}$, средняя скорость ${{\vec {v}}_{\alpha }}$, плотность заряда ${{q}_{{{\text{ion}}}}}$, плотность тока ${{\vec {j}}_{{{\text{ion}}}}}$), необходимо некоторым образом просуммировать вклады каждой частицы в данной ячейке расчетной сетки. Это соответствует известному методу частиц в ячейке. Для расчета весовых коэффициентов в каждой ячейке мы использовали функции распределения частицы первого порядка (кусочно-линейные функции). Похожая гибридная численная модель применялась в аналогичной задаче в работах [18, 22–28].
В расчетах, проведенных в рамках гибридной модели, мы учитывали частицы трех сортов: протоны солнечного ветра, ионы водорода H+ и ионы кислорода O+. Для описания формирования ионов водорода мы использовали подход, рассмотренный в предыдущем разделе. Формирование ионов кислорода происходит в процессе фотоионизации нейтральных атомов кислорода. Распределение концентрации атомарного кислорода можно описать на основе трех компонентов: внутренняя атмосфера, внешняя атмосфера и экзосфера [29]. Можно использовать следующее выражение [18]:
(23)
$\begin{gathered} n[{\text{O}}] = {{n}_{1}}\exp \left( {\frac{{{{r}_{1}} - h}}{{{{H}_{1}}}}} \right) + {{n}_{2}}\exp \left( {\frac{{{{r}_{2}} - h}}{{{{H}_{2}}}}} \right) + \\ + \;{{n}_{3}}\frac{{{{r}_{3}}}}{{{{H}_{3}} + h}}, \\ \end{gathered} $В расчетах использовалась трехмерная сетка, состоящая из $50 \times 50 \times 50$ ячеек. Отметим, что в гибридной модели мы не можем корректным образом проводить расчеты в двумерном приближении, как это делалось выше в МГД моделях. Это обусловлено тем, что даже в случае плоского движения скорость электронов ${{\vec {v}}_{{\text{e}}}}$ (20) и напряженность электрического поля $\vec {E}$ (21) будут иметь вертикальные компоненты. В результате гибридная модель оказывается гораздо более ресурсоемкой. В нашем случае число частиц в конце счета составляло более 2.3 млн.
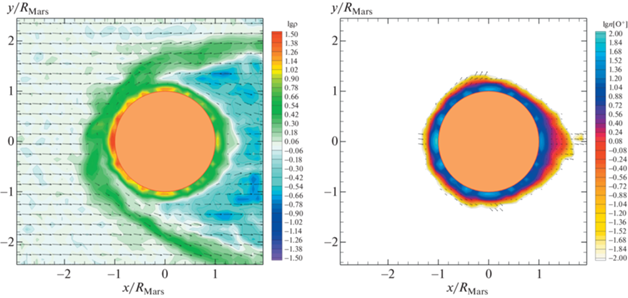
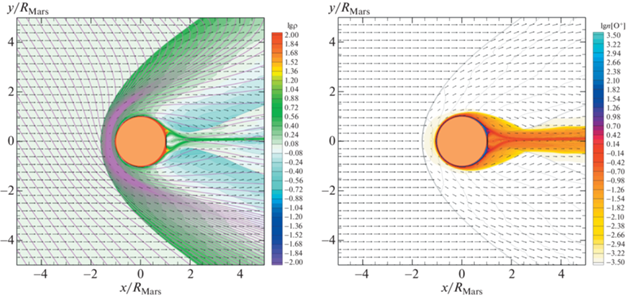
Результат расчета, проведенного в рамках гибридной модели, представлен на рис. 4. На левой панели показаны распределения плотности $\rho $ (цвет, изолинии) и средней массовой скорости $\vec {v}$ (стрелки) в орбитальной плоскости Марса. На правой панели показаны распределения концентрации $n[{{{\text{O}}}^{ + }}]$ (цвет) и средней скорости $\vec {v}[{{{\text{O}}}^{ + }}]$ (стрелки) ионов кислорода O+. Как и в МГД моделях, в результате взаимодействия солнечного ветра с планетой вокруг нее устанавливается ударная волна. В подсолнечной точке высота ударной волны достигает ${{H}_{{{\text{sh}}}}} = 2040$ км, что неплохо согласуется с МГД моделью. Учет ионосферы, состоящей из ионов водорода и кислорода, приводит к формированию ионопаузы, отделяющей ионосферную плазму от плазмы ветра. Ее положение в подсолнечной точке можно оценить величиной ${{H}_{{{\text{mp}}}}} = 1020$ км. Однако из-за грубой сетки эти оценки являются весьма приближенными. В целом можно сказать, что результат расчета соответствует МГД моделям, но высокая ресурсоемкость гибридной модели не позволяет проследить мелкие детали.
Рис. 4.
Распределения в орбитальной плоскости Марса плотности (цвет, изолинии) и средней массовой скорости (стрелки) (слева), а также концентрации (цвет) и средней скорости (стрелки) ионов кислорода O+ (справа), полученные в гибридной модели. Плотность выражена в единицах ${{\rho }_{{\text{w}}}}$. Закрашенный кружок соответствует радиусу Марса.
2.3. Многокомпонентная МГД модель
Для получения более детальной картины течения в окрестности Марса с учетом ионосферных ионов нами была разработана также модель промежуточного типа, основанная на приближении многокомпонентной (многожидкостной) магнитной гидродинамики. В этой модели используются уравнения для массовых величин (плотности $\rho $, средней массовой скорости $\vec {v}$ и удельной внутренней энергии $\varepsilon $), уравнение индукции для магнитного поля $\vec {B}$, а также уравнения непрерывности для отдельных компонентов плазмы. Для исследования структуры течения в окрестности Марса этот подход неоднократно применялся другими авторами [30–34].
Отдельные компоненты (ионы различных сортов) плазмы будем помечать индексом $\alpha $. Будем считать, что средние скорости ${{\vec {v}}_{\alpha }}$ и температуры ${{T}_{\alpha }}$ всех компонентов являются одинаковыми [30]. Тогда уравнения непрерывности для каждого компонента сорта $\alpha $ можно записать в виде:
(24)
$\frac{{\partial {{\rho }_{\alpha }}}}{{\partial t}} + \nabla \cdot \left( {{{\rho }_{\alpha }}\vec {v}} \right) = {{S}_{\alpha }},$(26)
$\frac{\partial }{{\partial t}}\left( {\rho {{\xi }_{\alpha }}} \right) + \nabla \cdot \left( {\rho {{\xi }_{\alpha }}\vec {v}} \right) = {{S}_{\alpha }}.$Для полной ионной плотности
получаем уравнение (1), где полная функция источника Уравнения движения (2), индукции (3) и энергии (4) для массовых величин сохраняют свой прежний вид с учетом силы трения (13) и функции нагрева-охлаждения (14). Плотность $\rho $, давление $P$, внутренняя энергия $\varepsilon $ и температура $T$ удовлетворяют уравнению состояния идеального газа(29)
$P = \frac{{{{k}_{{\text{B}}}}}}{{\mu {{m}_{{\text{p}}}}}}\rho T,\quad \varepsilon = \frac{{{{k}_{{\text{B}}}}T}}{{\mu {{m}_{{\text{p}}}}(\gamma - 1)}},$Для численного решения этих уравнений был использован недавно разработанный нами аналог разностной схемы Роу-Эйнфельдта-Ошера для многокомпонентной магнитной гидродинамики. Расчеты проводились при тех же параметрах сетки и расчетной области, как и для случая чистой магнитной гидродинамики.
Результат расчета представлен на рис. 5. На дневной стороне структура течения осталась прежней. Сформировались ударная волна и магнитный барьер. Толщина ионосферного слоя увеличилась по сравнению с тем, что было нами получено в рамках МГД моделирования. Это достигается за счет учета в многокомпонентной модели ионов кислорода. На ночной стороне планеты турбулентный шлейф вещества становится гораздо более плотным. На правой панели рис. 5 показано распределение концентрации ионов кислорода $n[{{{\text{O}}}^{ + }}]$. Плотная ионосферная оболочка формируется вокруг планеты. Часть ионов кислорода сносится солнечным ветром в турбулентный шлейф. Вокруг потока вещества на ночной стороне также формируются ударные волны. Однако снова заметим, что в трехмерном приближении структура и интенсивность этих дополнительных ударных волн могут существенно измениться.
Рис. 5.
Распределения плотности (цвет, изолинии), скорости (стрелки) и магнитного поля (линии) в орбитальной плоскости Марса для модели без учета (слева) и с учетом (справа) водородной короны. Плотность выражена в единицах ${{\rho }_{{\text{w}}}}$. Закрашенный кружок соответствует радиусу Марса.
В подсолнечной точке высота ударной волны ${{H}_{{{\text{sh}}}}} = 1890$ км. Толщина ионопаузы, отделяющей ионосферную плазму Марса от плазмы ветра, в подсолнечной точке можно оценить величиной ${{H}_{{{\text{mp}}}}} = 700$ км. Найденные параметры ударной волны и ионопаузы неплохо согласуются с результатами, полученными в рамках магнитной гидродинамики и гибридной модели. Однако картина течения получается намного более детализированная, чем в гибридной модели. Таким образом, можно сказать, что модель многокомпонентной магнитной гидродинамики позволяет совместить достоинства обеих моделей.
3. ЗАКЛЮЧЕНИЕ
В наших предыдущих исследованиях [8], выполненных при помощи кинетической Монте-Карло модели, были получены численные оценки влияния наблюдаемых изменений содержания атомарного водорода в протяженной короне Марса на эффективность перезарядки протонов невозмущенного солнечного ветра и определены параметры и свойства процесса высыпания образующихся при перезарядке энергетических нейтральных атомов водорода – ЭНА-Н в дневную атмосферу Марса, что позволило детально исследовать протонные авроральные явления на Марсе. Установлено, что значение эффективности перезарядки изменяется в интервале 4–8% для выявленных в наблюдениях вариаций лучевой концентрации атомарного водорода в короне Марса, а энергетический спектр проникающих через границу индуцированной магнитосферы в атмосферу Марса атомов водорода идентичен спектру невозмущенных протонов солнечного ветра. Для анализа проникновения потока энергичных частиц солнечного ветра в верхнюю атмосферу Марса использована модификация кинетической Монте-Карло модели, разработанной ранее для анализа данных измерений приборов MEX/ASPERA-3 на борту космического аппарата (КА) Mars Express и MAVEN/SWIA на борту КА MAVEN [7, 8].
В работе представлены гибридная и МГД модели обтекания Марса плазмой солнечного ветра, при помощи которых рассчитываются входные параметры (поток протонов солнечного ветра и граница IMB) для кинетической Монте-Карло модели воздействия потока протонов невозмущенного солнечного ветра на дневную атмосферу Марса. Одножидкостная МГД модель позволяет учесть только ионы водорода, чего явно недостаточно для моделирования структуры ионосферной оболочки Марса. В рамках гибридной модели можно учитывать ионы различных сортов. Однако из-за ее относительно высокой ресурсоемкости трудно достичь пространственного разрешения, позволяющего проследить мелкие детали. Сравнение результатов расчетов, проведенных в рамках представленных в работе моделей, показало, что модель многокомпонентной МГД совмещает достоинства одножидкостной МГД и гибридной моделей. Поэтому в дальнейшем нами предполагается развитие именно этого подхода.
Используя рассчитанные входные данные, в последующих исследованиях при помощи кинетической Монте-Карло модели будут определены потоки энергии и энергетические спектры атомов водорода, проникающих в дневную верхнюю атмосферу через границу индуцированной магнитосферы и получены оценки параметров авроральных протонных явлений [5, 6], наблюдаемых в верхней атмосфере Марса при помощи спектрографа IUVIS на борту КА MAVEN. Сравнение результатов таких расчетов с наблюдениями открывает уникальную возможность уточнения свойств атмосферы и магнитного поля, а также изучения авроральных явлений на Марсе [35].
Список литературы
F. Nagy, D. Winterhalter, K. Sauer, T. E. Cravens, et al., Space Sci. Rev. 111, 33 (2004).
E. Dubinin, M. Fraenz, J. Woch, E. Roussos, et al., Space Sci. Rev. 126, 209 (2006).
M. S. Chaffin, J. Y. Chaufray, D. Deighan, N. M. Schneider, et al., J. Geophys. Res. Planets 123(8), 2192 (2018).
Y. Futaana, J.-Y. Chaufray, H. T. Smith, P. Garnier, et al., Space Sci. Rev. 162, 213 (2011).
A. Hughes, M. Chaffin, E. Mierkiewicz, J. Deighan, S. Jain, N. Schneider, M. Mayyasi, and B. Jakosky, J. Geophys. Res. Space Physics 124(12), 10.533 (2019).
J. Deighan, S. K. Jain, M. S. Chaffin, X. Fang, et al., Nature Astron. 2, 802 (2018).
V. I. Shematovich, D. V. Bisikalo, J.-C. Gerard, and B. Hubert, Astron. Rep. 63, 835 (2019).
V. I. Shematovich, D. V. Bisikalo, and A. G. Zhilkin, Astron. Rep. 65, 203 (2021).
E. J. Weber and L. Davis, Jr., Astrophys. J. 148, 217 (1967).
Л. Д. Ландау, Е. М. Лифшиц, Электродинамика сплошных сред (М.: Физматлит, 2003).
А. Г. Жилкин, А. В. Соболев, Д. В. Бисикало, М. М. Габ-деев, Астрон. журн. 96(9), 748 (2019).
Д. В. Бисикало, А. Г. Жилкин, А. А. Боярчук, Газодинамика тесных двойных звезд (М.: Физматлит, 2013).
Д. В. Бисикало, А. А. Боярчук, В. М. Чечеткин, О. А. Кузнецов, Д. Молтени, Астрон. журн. 76, 905 (1999).
J. S. Halekas, R. J. Lillis, D. L. Mitchell, T. E. Cravens, et al., Geophys. Res. Lett. 42, 8901 (2015).
Mazelle, D. Winterhalterm, K. Sauer, J. G. Trotignon, et al., Space Sci. Rev. 111, 115 (2004).
J. W. Chamberlain, Planet. Space Sci. 11, 901 (1963).
A. Rahmati, T. E. Cravens, A. F. Nagy, J. L. Fox, et al., Geophys. Research Lett. 41, 4812 (2014).
Bößwetter, T. Bagdonat, U. Motschmann, and K. Sauer, Ann. Geophysicae 22, 4363 (2004).
Б. Н. Гершман, Динамика ионосферной плазмы (М.: Наука, 1974).
A. P. Matthews, J. Comput. Phys. 112, 102 (1994).
T. Bagdonat and U. Motschmann, J. Comput. Phys. 183, 470 (2002).
H. Shimazu, Earth, Planets and Space 51, 383 (1999).
H. Shimazu, J. Geophys. Res. 106(A5), 8333 (2001).
E. Kallio and P. Janhunen, J. Geophys. Res. 106(A4), 5617 (2001).
E. Kallio and P. Janhunen, J. Geophys. Res. 107(A3), 1035 (2002).
E. Kallio, K. Liu, R. Jarvinen, V. Pohjola, and P. Janhunen, Icarus 206, 152 (2010).
X.-D. Wang, M. Alho, R. Jarvinen, E. Kallio, S. Bara-bash, and Y. Futaana, J. Geophys. Res. Space Physics 121, 190 (2016).
X.-D. Wang, M. Alho, R. Jarvinen, E. Kallio, S. Bara-bash, and Y. Futaana, J. Geophys. Res. Space Physics 123, 8730 (2018).
J. L. Fox and A. B. Hac, Icarus 204, 527 (2009).
Y. Ma, A. F. Nagy, I. V. Sokolov, and K. C. Hansen, J. Geophys. Res. 109(A7), id. A07211 (2004).
Y. J. Ma, X. Fang, A. F. Nagy, C. T. Russell, and G. Toth, J. Geophys. Res. Space Physics 119, 1272 (2014).
C. Dong, Y. Ma, S. W. Bougher, G. Toth, et al., Geophys. Res. Lett. 42, 9103 (2015).
C. Dong, S. W. Bougher, Y. Ma, G. Toth, et al., J. Geophys. Res. Space Physics 120, 7857 (2015).
Y. J. Ma, C. T. Russell, X. Fang, Y. Dong, et al., Geophys. Res. Lett. 42, 9113 (2015).
J.-C. Gerard, B. Hubert, B. Ritter, V. I. Shematovich, and D. V. Bisikalo, Icarus 321, 266 (2019).
Дополнительные материалы отсутствуют.
Инструменты
Астрономический журнал


