Астрономический журнал, 2020, T. 97, № 10, стр. 849-857
Солнечный квадруполь в тензорном описании
А. С. Шибалова 1, 2, *, В. Н. Обридко 1, Д. Д. Соколов 1, 2, В. В. Пипин 3
1 Институт земного магнетизма, ионосферы и распространения радиоволн им. Н.В. Пушкова РАН
Москва, Россия
2 Московский государственный университет им. М.В. Ломоносова
Mосква, Россия
3 Институт солнечно-земной физики СО РАН
Иркутск, Россия
* E-mail: as.shibalova@physics.msu.ru
Поступила в редакцию 05.03.2020
После доработки 29.06.2020
Принята к публикации 30.06.2020
Аннотация
В работе исследуются циклические вариации квадрупольного компонента магнитного поля Солнца в рамках тензорного описания. Результаты согласуются с классическим описанием квадруполя с помощью сферических функций, а математический аппарат тензорной алгебры позволяет сравнивать наблюдаемые изменения магнитного квадруполя и изменения, предсказываемые теориями магнитного динамо. Мы пришли к выводу, что свойства квадруполя могут быть достаточно хорошо описаны моделями солнечного динамо, предполагающими отклонения от дипольной симметрии без независимого возбуждения мод квадрупольной симметрии.
1. ВВЕДЕНИЕ
Особый интерес для теории динамо представляет поведение двух первых гармоник магнитного поля Солнца – нечетной и четной гармоник, т.е. диполя и квадруполя. Дело в том, что в конвективной оболочке, строго симметричной относительно солнечного экватора, могут возбуждаться магнитные поля двух типов – нечетные и четные относительно солнечного экватора. При этом дифференциальное вращение и зеркальная асимметрия движений, а также меридиональная циркуляция не перемешивают эти поля.
В частности, в простейших моделях солнечного динамо квадрупольный момент, как и более высокие моменты четного порядка в точности равны нулю. Сравнительно небольшим изменением гидродинамики сферической оболочки можно получить модели, в которых генерируются магнитные поля квадрупольной, а не дипольной симметрии (см. [1] и приведенные там ссылки). Естественно думать, что могут встречаться звезды, в которых работает динамо именно этого типа, но соответствующие уверенные наблюдательные данные пока отсутствуют. В принципе механизм динамо может производить и магнитные поля смешанной четности (mixed parity solutions) (напр., [2]), возможно, именно так работало солнечное динамо в конце минимума Маундера (см. [3, 4] и приведенные там ссылки).
Магнитное поле Солнца, несомненно, имеет моды не только дипольной, но и квадрупольной симметрии. В принципе, можно было бы рассматривать представление о том, что солнечное динамо постоянно дает решения со смешанной четностью, только вклад квадрупольных мод был аномально высок в конце минимума Маундера. Однако возможна и другая, гораздо менее обременительная для теории, точка зрения, согласно которой моды квадрупольного типа создаются просто потому, что Солнце не идеально симметрично относительно солнечного экватора.
Существует два метода описания квадрупольного компонента магнитного поля. Один из них опирается на представление в виде суммы сферических функций, коэффициенты в которой находятся путем решения уравнения Лапласа. Второе описание использует тензорное представление. Оба описания имеют свои преимущества и недостатки. Описание на языке сферических функций, коэффициентов Гаусса и следующего далее выделения полюсов квадруполя более просто и привычно при анализе солнечных наблюдений. Однако описание на языке тензора квадрупольного момента необходимо, например, при исследовании свойств солнечного ветра. Такое описание в особенности полезно при сопоставлении со свойствами вектора дипольного момента. Отметим, что и вектор, и тем более тензор могут и, как показывают наблюдения, действительно бывают в определенные моменты времени не ориентированы вдоль оси вращения Солнца. В контексте задач солнечного ветра это значит, что при таких ориентациях естественно ожидать сложной конфигурации токовых слоев в солнечной магнитосфере (см., напр., [5]).
В данной работе мы изучим циклические вариации тензора квадруполя на Солнце и сопоставим их с характеристиками поведения основных характерных точек (полюсов) квадруполя. Описание квадрупольных компонентов на языке полюсов дано в недавней работе [6].
2. КВАДРУПОЛЬНЫЙ МОМЕНТ
Разложение потенциала магнитного поля по сферическим функциям (радиальная часть – по модели PFSS (Potential Field with Source Surface [7])) выглядит следующим образом [7]:
(1)
$\begin{gathered} \Psi = \sum\limits_{l = 0}^\infty \,\sum\limits_{m = 0}^l \,{{R}_{l}}(r)P_{l}^{m}(cos\theta ) \times \\ \times \;({{g}_{{lm}}}cosm\varphi + {{h}_{{lm}}}sinm\varphi ), \\ \end{gathered} $(2)
${{R}_{l}} = {{R}_{0}}\frac{{{{{\left( {\tfrac{{{{R}_{0}}}}{r}} \right)}}^{{l + 1}}}\left[ {1 - {{{\left( {\tfrac{r}{{{{R}_{s}}}}} \right)}}^{{2l + 1}}}} \right]}}{{l + 1 + l{{{\left( {\tfrac{{{{R}_{0}}}}{{{{R}_{s}}}}} \right)}}^{{2l + 1}}}}}.$(3)
$\begin{gathered} {{B}_{\theta }} = - \sum\limits_{l,m} \,\frac{{\partial P_{l}^{m}}}{{\partial \theta }}({{g}_{{lm}}}cosm\varphi + {{h}_{{lm}}}sinm\varphi ) \times \\ \, \times ({{({{R}_{0}}{\text{/}}r)}^{{l + 2}}} + {{(r{\text{/}}{{R}_{s}})}^{{l - 1}}}{{c}_{l}}), \\ \end{gathered} $Нас интересуют квадрупольные компоненты магнитного поля, которым соответствуют члены с $l = 2$. Выпишем в явном виде часть суммы, соответствующую этим слагаемым:
(4)
$\begin{gathered} {{\Psi }_{q}} = \left( {\frac{3}{2}co{{s}^{2}}\theta - \frac{1}{2}} \right){{g}_{{02}}} + \\ + \;\sqrt 3 sin\theta cos\theta ({{g}_{{21}}}cos\varphi + {{h}_{{21}}}sin\varphi ) + \\ + \;\frac{3}{{\sqrt {12} }}si{{n}^{2}}\theta ({{g}_{{22}}}cos(2\varphi ) + {{h}_{{22}}}sin(2\varphi )). \\ \end{gathered} $(6)
$f(r) = {{{{{\left( {\frac{{{{R}_{0}}}}{r}} \right)}}^{{l + 2}}}\left[ {1 - {{{\left( {\frac{r}{{{{R}_{s}}}}} \right)}}^{{2l + 1}}}} \right]} \mathord{\left/ {\vphantom {{{{{\left( {\frac{{{{R}_{0}}}}{r}} \right)}}^{{l + 2}}}\left[ {1 - {{{\left( {\frac{r}{{{{R}_{s}}}}} \right)}}^{{2l + 1}}}} \right]} {\left[ {l + 1 + l{{{\left( {\frac{{{{R}_{0}}}}{{{{R}_{s}}}}} \right)}}^{{2l + 1}}}} \right].}}} \right. \kern-0em} {\left[ {l + 1 + l{{{\left( {\frac{{{{R}_{0}}}}{{{{R}_{s}}}}} \right)}}^{{2l + 1}}}} \right].}}$(7)
$\begin{gathered} {{D}_{{11}}} = \frac{3}{{\sqrt {12} }}{{g}_{{22}}} - \frac{1}{2}{{g}_{{20}}};\quad {{D}_{{12}}} = \frac{3}{{\sqrt {12} }}{{h}_{{22}}}; \\ {{D}_{{13}}} = \frac{{\sqrt 3 }}{2}{{g}_{{21}}};\quad {{D}_{{22}}} = - \frac{3}{{\sqrt {12} }}{{g}_{{22}}} - \frac{1}{2}{{g}_{{20}}}; \\ {{D}_{{23}}} = \frac{{\sqrt 3 }}{2}{{h}_{{21}}};\quad {{D}_{{33}}} = {{g}_{{20}}}. \\ \end{gathered} $Поворотом системы координат этот тензор можно привести к диагональному виду, так что значения диагональных компонентов диагонализированного тензора можно рассматривать как полуоси эллипсоида, положение которого в пространстве определяется углами, образуемыми осями эллипсоида с осями исходной системы координат. По этим осям направлены собственные векторы тензора квадрупольного момента, а длины осей являются его собственными значениями ${{\lambda }_{i}}$, которые можно найти из векового уравнения
(8)
${\text{det}}\left\| {\begin{array}{*{20}{c}} {{{D}_{{11}}} - \lambda }&{{{D}_{{12}}}}&{{{D}_{{13}}}} \\ {{{D}_{{21}}}}&{{{D}_{{22}}} - \lambda }&{{{D}_{{23}}}} \\ {{{D}_{{31}}}}&{{{D}_{{32}}}}&{{{D}_{{33}}} - \lambda } \end{array}} \right\| = 0,$(9)
$\begin{gathered} ({{D}_{{11}}} - {{\lambda }_{i}})x_{1}^{i} + {{D}_{{12}}}x_{2}^{i} + {{D}_{{13}}}x_{3}^{i} = 0, \\ {{D}_{{21}}}x_{1}^{i} + ({{D}_{{22}}} - {{\lambda }_{i}})x_{2}^{i} + {{D}_{{23}}}x_{3}^{i} = 0, \\ {{D}_{{31}}}x_{1}^{i} + {{D}_{{32}}}x_{2}^{i} + ({{D}_{{33}}} - {{\lambda }_{i}})x_{3}^{i} = 0, \\ \end{gathered} $Найденные значения можно наглядно представить в виде трех векторов, отложенных от начала координат (координаты собственных векторов при этом задают направление, а модуль собственного значения – длину вектора). Далее будем называть такие векторы полуосями тензора. Интерес для исследования представляют изменение во времени длин осей и их положения в пространстве.
Как видно, эта процедура сводится к пересчету по несложным, хотя и громоздким формулам. Однако ее применение в приложении к интересующим нас вопросам оказывается нетривиальным. Дело в том, что нас интересует временная эволюция квадрупольного момента, а для ее изучения необходимо зафиксировать порядок осей тензора. Изменение порядка соответствующих собственных векторов отражает фиктивный поворот квадрупольного момента, не связанный с реальным изменением магнитного поля. При решении векового уравнения (8) возникает неопределенность в определении порядка его корней, поскольку три корня кубического уравнения можно в принципе расположить в любой последовательности. Наша задача состоит в выборе физически осмысленной нумерации.
В качестве первого приближения решения собственные значения располагались по убыванию. Для дальнейшего построения порядка осей мы пользуемся тензорными свойствами квадрупольного момента. При наличии оси симметрии одна из главных осей тензора совпадает по направлению с этой осью. При этом она оказывается также “выделенной” своей длиной по отношению к двум оставшимся (этот случай действительно часто встречается в изучаемой базе данных), при этом два собственных значения велики по модулю и достаточно близки друг к другу, а третье существенно меньше. Трудность состоит к том, что два близких по модулю собственных значения при эволюции во времени даже за счет случайных погрешностей измерения могут меняться местами, что при формальной интерпретации результатов приводит к нефизическому выводу о частых и существенных перестройках тензора квадрупольного момента. Для того, чтобы устранить этот артефакт, достаточно потребовать сохранения ориентации базиса собственных векторов. В принципе, это можно сделать программным образом, но при имеющемся объеме данных оказывается, что это проще сделать вручную.
Дополнительная проблема появляется из-за того, что собственное значение может менять знак. Напомним, что абсолютное собственное значение мы интерпретируем как длину оси, тогда появление знака “–” может означать изменение направления оси на противоположное, поэтому процедура поиска находит то один, то другой конец одной и той же оси, а в формально найденных значениях координат собственных векторов остаются нефизические скачки. Скачок на $90^\circ $ возникает в случае, когда изменяется направление одной или всех трех осей, скачок на $180^\circ $ – если изменяется направление двух осей. Эти скачки тоже оказывается проще устранить вручную.
3. РЕЗУЛЬТАТЫ
Мы вычислили тензор квадрупольного момента начиная с 1976 г., с этого времени уже имеются необходимые нам коэффициенты Гаусса (рис. 1).
Рис. 1.
Временнóе поведение собственных значений тензора квадрупольного момента. Собственные значения упорядочены по величине и далее по соображениям непрерывности во времени.

На рис. 1 показаны зависимости осей эллипсоида от времени (модель PFSS). Оказывается, что два собственных значения с наибольшим по абсолютной величине собственным значением имеют противоположные знаки. В силу принятой системы нумерации они получают обозначения ${{\lambda }_{1}}$ и ${{\lambda }_{3}}$. Длины двух больших осей эллипсоида (см. рис. 2) близки по величине и хорошо скоординированы (коэффициент корреляции $0.92$). Третья ось эллипсоида гораздо меньше по величине и практически не скоррелирована c двумя другими (см. рис. 3), коэффициент корреляции здесь $0.45$.
Рис. 2.
Соотношение двух больших по модулю собственных значений ${{\lambda }_{1}}$ и ${{\lambda }_{3}}$. Прямая показывает корреляционную зависимость.

Рис. 3.
Соотношение собственных значений ${{\lambda }_{1}}$ и ${{\lambda }_{2}}$ (соответствующих большой и малой осям тензора). Прямая показывает корреляционную зависимость.

Длины больших осей тензора квадрупольного момента тесно связаны с уровнем солнечной активности, определяемым по числу солнечных пятен (рис. 4), которое, в свою очередь, отражает поведение компонента магнитного поля, имеющего дипольную симметрию (источник данных по солнечным пятнам: WDC-SILSO, Royal Observatory of Belgium, Brussels). На рис. 5 показано положение точки пересечения первой оси тензора с единичной сферой для небольшого промежутка времени (1976–1978 гг.). Видно, что на малых временах ось совершает случайные блуждания в небольшой области единичной сферы. Поскольку Солнце вращается дифференциально, для описания долговременного поведения осей тензора необходимо фиксировать систему отсчета, в которой измеряется долгота. Естественно, мы пользуемся кэррингтоновской системой отсчета. Долговременное поведение большей оси тензора показано на рис. 6 (изменение гелиографической долготы в течение четырех солнечных циклов).
Рис. 4.
Соотношение длины большей оси квадрупольного момента (${{\lambda }_{1}}$, изрезанная кривая) и числа солнечных пятен ($SSN$, более плавная кривая).

Рис. 5.
Траектории точки пересечения оси ${{\lambda }_{1}}$ с поверхностью единичной сферы, 1976–1978 гг.

Рис. 6.
Диаграмма изменения долготы одной из осей тензора. Полярный угол соответствует долготе, по радиусу отложено время (шкала вынесена слева от диаграммы).

Сравнение приведенного выше описания поведения осей тензора и полюсов квадруполя показывает, что оба описания дают в целом одну и ту же картину эволюции квадрупольного магнитного поля (см. более подробно [6]), однако они отличаются в деталях. Для того, чтобы показать это различие, на рис. 7 показано уклонение по долготе $\Delta \theta $ соответствующих осей тензора квадрупольного момента и полюса квадруполя. Видно, что большие отклонения встречаются, но в целом значения отклонения близки к нулю. Возникновение больших отклонений полюса от положения главной оси связано с тем, что квадруполь все же не полностью можно описать как простой четырехполюсник.
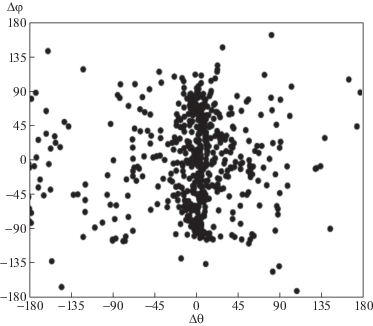
Рис. 7.
Отклонение гелиографических долгот большей оси тензора квадрупольного момента и соответствующего полюса квадруполя как функция времени.

Мы вычислили также, насколько отличаются широты полюса и соответствующей оси тензора, и сравнили эти отклонения ($\Delta \varphi $) с соответствующими отклонениями долготы. На рис. 8 показано отклонение одноименных осей тензора и квадруполя как по широте, так и по долготе. Видно, что долготы полюса и оси в среднем гораздо ближе друг к другу, чем соответствующие широты. По-видимому, это связано с тем, что скорость вращения квадруполя не совсем совпадает с кэррингтоновской скоростью вращения, это различие не постоянно во времени, причем скорости вращения оси тензора и полюса тоже могут не совпадать в данный момент.
Видно, что несмотря на хорошее совпадение долгот, широты осей квадруполя и тензора никак не связаны друг с другом. Ось, соединяющая положительные полюса квадруполя, отстоит по долготе от оси, соединяющей отрицательные полюса, на $\pi {\text{/}}2$, но по широте эти оси наклонены друг другу на сильно флуктуирующий угол.
4. ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ
Отметим еще раз, что описания квадрупольного момента на языке полюсов четырехполюсника и на языке тензора квадрупольного момента близки друг к другу, но не тождественны. Эти различия связаны, конечно, как с неполнотой представления о четырехполюснике, так и с неизбежными наблюдательными погрешностями. Конечно, в задачах, не требующих отказа от наглядного языка полюсов четырехполюсника, нет необходимости переходить на менее наглядный тензорный язык, но при желании и необходимости это можно сделать.
Представляется интересным выяснить, насколько вытекающая из наблюдательных данных картина эволюции квадрупольного магнитного поля согласуется с теоретическими представлениями о солнечном динамо. Мы уже отмечали в [6], что наблюдательные данные не вынуждают нас рассматривать модели динамо с генерацией квадрупольного магнитного поля, независимой от генерации дипольного магнитного поля. С другой стороны, кажется, феноменология квадруполя вполне вписывается в представления о более-менее случайных отклонениях от дипольной симметрии. Поэтому кажется не очень существенным, с какой именно моделью динамо в сферической конвективной оболочке звезды солнечного типа мы проводим сравнение, лишь бы эта модель допускала отклонения от симметрии дипольного типа и не предписывала бы независимое возбуждение квадрупольных мод. В качестве такой модели мы, более-менее произвольно, избираем модель из работы [10] (модель солнечного асимметричного динамо с супердиффузией, см. также [11]). Конечно, в этом сравнении не приходится ожидать буквального совпадения флуктуаций в наблюдениях и в теории, а речь может идти лишь о сопоставлении тенденций. Соответствующее сопоставление проведено на рис. 9. В обоих случаях ярко выражен 11-летний цикл с накладывающимися на него случайными (и, возможно, квазипериодическими) колебаниями. В целом наблюдательная и теоретическая кривые похожи друг на друга настолько, насколько это допускает естественная вариабельность солнечного цикла.
Рис. 9.
Сопоставление вариаций длины первой оси тензора квадрупольного момента по данным наблюдения (сплошная линия) и модели динамо (пунктир).

Напомним, что в выбранной модели динамо квадрупольный компонент магнитного поля возбуждается в результате диффузионного распада биполярных активных областей. Кроме того, необходимо учесть, что модель описывает динамо процесс в мелком сферическом слое и процесс образования биполярных активных областей локализован в той же области. При наложении динамо волн тороидального магнитного поля это может приводить к тому, что в минимумах активности параметры модели, описывающие пятнообразование, могут сильно флуктуировать и это дает вариации фазы минимумов. Это хорошо видно на рис. 9 при сравнении теоретической и наблюдательной кривой. Также следует заметить, что данная модель описывает квазистационарный магнитный цикл без существенных долговременных вариаций. Промежуток для сравнения с наблюдениями выбран достаточно случайно. Более длинный ряд наблюдений даст возможность сопоставить долговременные вариации параметров квадруполя с моделями динамо, в которых тоже необходимо предусмотреть такую возможность.
Работа поддержана проектом РФФИ 18-02-00085.
Список литературы
D. Moss, S. H. Saar, and D. Sokoloff, Monthly Not. Roy. Astron. Soc. 388, 416 (2010).
A. Brandenburg, F. Krause, R. Meinel, D. Moss, and I. Tuominen, Astron. and Astrophys. 213, 411 (1989).
D. Sokoloff and E. Nesme-Ribes, Astron. and Astrophys. 288, 293 (1994).
I. G. Usoskin, R. Arlt, E. Asvestari, E. Hawkins, et al., Astron. and Astrophys. 581, id. A95, 19 (2015).
R. A. Kislov, O. V. Khabarova, and H. V. Malova, Astrophys. J. 875, id. 281 (2019).
V. N. Obridko, D. D. Sokoloff, B. D. Shelting, A. S. Shi-balova, and I. M. Livshits, Monthly Not. Roy. Astron. Soc. 492, 5582 (2020).
J. T. Hoeksema, The Solar Magnetic Field Since 1976, http://wso.stanford.edu .
J. T. Hoeksema, Adv. Space Res. 11, 15 (1991).
X. Zhao and J. T. Hoeksema, Solar Phys. 151, 91 (1994).
V. V. Pipin and A. G. Kosovichev, Astrophys. J. 867, id. 145 (2018).
P. Frick, D. Sokoloff, R. Stepanov, V. Pipin, and I. Usos-kin, Monthly Not. Roy. Astron. Soc. 491, 5572 (2020).
Дополнительные материалы отсутствуют.
Инструменты
Астрономический журнал