1. На главную
  2. Электронные версии
  3. Акустический журнал
  4. T. 69, № 6, 2023

Акустический журнал, 2023, T. 69, № 6, стр. 756-764

Особенности уменьшения уровня звука экранами Т-образного профиля

А. И. Комкин a, *, Р. Н. Мусаева a

a Московский государственный технический университет им. Н.Э. Баумана
105005 Москва, ул. 2-я Бауманская 5, Россия

* E-mail: akomkin@mail.ru

Поступила в редакцию 27.02.2023
После доработки 03.04.2023
Принята к публикации 16.05.2023

Полный текст (PDF)

Аннотация

Исследованы акустические характеристики экранов Т-образного профиля на основе конечно-элементного моделирования. Установлено, что эффективность уменьшения уровня звука данным экраном связана не только с дифракцией, но также и с интерференцией звука на передней и задней кромках экрана. Показано, что интерференция звука на задней кромке экрана, в отличие от интерференции звука на передней кромке, влияет на звуковое поле только на небольших расстояниях от задней поверхности экрана. Проанализировано влияние на эти процессы частоты звука и геометрических размеров экрана.

Ключевые слова: шумозащитный экран, Т-образный профиль, дифракция, интерференция, моделирование

ВВЕДЕНИЕ

К числу основных средств защиты от шума относятся акустические экраны. Их используют для защиты как от транспортного шума, так и от шума различного оборудования. Для улучшения эффективности шумозащитных экранов без увеличения их высоты стали предлагать изменения в конструкцию экрана, прежде всего его верхней кромки. Такой подход основывался на том, что наличие на этой кромке двух или более дифрагирующих ребер позволит улучшить шумозащитные свойства экрана. Был проведен значительный объем исследований экранов и их характеристик, в том числе и исследования, посвященные модификации его верхней кромки. Новые конструкции барьеров были впервые предложены Виртом [1], Мэем и Османом [2] и вызвали значительное количество работ, посвященных исследованиям экранов с различными конфигурациями их верхней кромки, например, [3–7]. Обстоятельный обзор публикаций, связанных с историей развития данного направления, представлен в [8, 9].

Существует несколько теоретических методов оценки акустических характеристик экранов, основанных на теории дифракции, которые стали предметом всестороннего обзора Ли и Вонга [10]. Они дают довольно громоздкие выражения даже для простейших конфигураций экранов, что затруднило их широкое применение на практике. Хотя, например, для случая круглой насадки на верхней кромке экрана было получено аналитическое решение задачи [11–14]. В качестве альтернативы для оценки эффективности экранов в инженерной практике широко применяется эмпирическая формула Маекавы [15], полученная им на основе обширных экспериментальных данных. К настоящему времени эта формула неоднократно корректировалась [10]. Хотя формула Маекавы проста в использовании, она справедлива для случая тонкого, абсолютно жесткого, полубесконечного экрана и потому, как правило, является только грубым инструментом при инженерном проектировании экранов.

Исходя из этого в настоящее время и в ближайшем будущем основными инструментами для анализа характеристик акустических экранов, помимо экспериментального, станут численные методы. Их реализация требует меньше ресурсов, а кроме того, они обладают большими возможностями, связанными, например, с учетом подстилающей поверхности, на которой размешается экран, толщины экрана, свойств материала экрана, конфигурации его верхней кромки. Наиболее распространенным численным методом расчета экранов сложной формы является метод граничных элементов, который начал использоваться с этой целью практически одновременно с появлением такого рода экранов [16]. К настоящему времени имеется очень много работ, посвященных расчетам экранов этим методом, например, [5, 17, 18]. В [19] проведена верификация аналитических и численных расчетов с экспериментальными результатами. Наряду с методом граничных элементов численные расчеты экранов проводят и методом конечных элементов. Сравнение вычислительной эффективности этих двух методов при решении акустических задач приведено в [20]. Применительно к расчету экранов показано [21], что оба метода приводят практически к одинаковым результатам. Примеры использования метода конечных элементов для решения такого рода задач представлены в [22, 23].

Из всего многообразия экранов со сложной конфигураций верхней кромки одним из наиболее популярных объектов исследования являются экраны Т-образного профиля [24–32]. В этих работах исследовался широкий круг вопросов, связанных с определением влияния на эффективность таких экранов конфигурации верхней кромки, наличия на ней звукопоглощающего материала. В [31] даже исследовались Т-образные экраны с размещенной на них системой активного гашения шума. Кроме того, в этих исследованиях оценивалась зависимость эффективности такого экрана от частоты звука и расположения расчетной точки за экраном. Вместе с тем, следует отметить, что при этом практически не рассматривались вопросы, связанные с физической стороной дела и посвященные механизмам формирования звукового поля за экраном Т-образного профиля. Исключение составляет, пожалуй, работа [30], в которой на основе проведенных численных расчетов делается вывод, что на эффективность таких экранов оказывает влияние и интерференция звука. В этой работе путем численных расчетов была проверена гипотеза об эквивалентности Т-образного экрана прямому экрану эквивалентной толщины и установлена ее неправомерность. Спектр звукового давления в расчетной точке за экраном оказался совсем не таким плавным, как у толстого прямого экрана, а гораздо более неравномерным. Таким образом, требуется более детальное исследование акустических процессов, происходящих в такого рода экранах, как сделано, например, в [33], где исследовался экран с негладкой передней поверхностью.

Данная работа является дальнейшим развитием исследований экранов с насадками на верхней кромке [34] и посвящена выявлению на основе конечно-элементного моделирования механизмов уменьшения уровня звука экраном Т-образного профиля.

КОНЕЧНО-ЭЛЕМЕНТНАЯ МОДЕЛЬ ЭКРАНА

Для исследования влияния профиля экрана на его акустическую эффективность и выявления закономерностей дифракции звука на таком экране было проведено численное моделирование экрана в программном пакете COMSOL Multiphysics. При этом использовалась двумерная (2D) конечно-элементная модель экрана. Расчетная область ограничивалась окружностью радиусом 40 м. Граничные условия на окружности, ограничивающей расчетную область, соответствовали согласованной нагрузке с импедансом Z = $\rho с = 411.6$ Па с/м, где ρ – плотность воздуха, c – скорость звука в воздухе. В центре окружности, определяющей расчетную область, располагался точечный источник звука, который с учетом 2D моделирования являлся, по сути, линейным источником и характеризовался интенсивностью I (Вт/м). В конечно-элементной модели использовалось неравномерное разбиение на тетраэдры. При этом для обеспечения приемлемой точности вычислений на длине волны, соответствующей верхней граничной частоте 1000 Гц рассматриваемого частотного диапазона, укладывалось четыре конечных элемента максимального размера.

При моделировании рассматривались две конфигурации экрана: прямой экран и экран с Т-образным профилем (рис. 1). Экраны рассматривались тонкими и абсолютно жесткими. Кроме того, для упрощения последующего анализа наличие подстилающей поверхности, на которую опирается экран, не учитывалось, т.е. экраны рассматривались полубесконечными. Экраны определялись эффективной высотой h, а Т-образный экран характеризовался еще и размером l. Положение верхней кромки экрана относительно источника звука определялось углом α. Эффективность снижения шума Т-образным экраном оценивалась по отношению к прямому экрану с помощью такого показателя как вносимые потери IL, которые при этом определялись соотношением:

$IL = {{L}_{{\text{I}}}} - {{L}_{{\text{Т}}}}\left[ {{\text{дБ}}} \right],$
где LI и LТ – уровни звукового давления в расчетной точке соответственно с прямым и Т-образным экранами.

Рис. 1.

Конфигурации (а) – T-образного и (б) – прямого экранов.

РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ

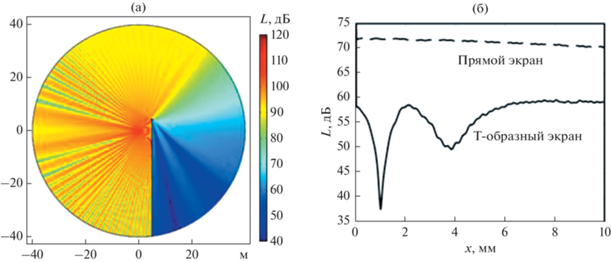
Одним из достоинств исследования акустики экранов численными методами является возможность получения разнообразной информации о характеристиках звукового поля в окрестности экрана, например картины распределения звукового давления в рассматриваемой расчетной области, которые могут дать наглядное представление о происходящих в ней физических процессах. Такого рода расчеты показывают [34], что независимо от вида экрана в пространстве перед экраном наблюдается сложная интерференционная картина, связанная с отражением падающей на переднюю плоскость экрана звуковой волны. Напротив, картина распределения звукового давления в пространстве за экраном существенно зависит от вида экрана. Для прямого экрана без насадки в этой зоне наблюдается плавное снижение звукового давления по мере приближения к задней поверхности экрана, связанное с дифракцией звука на его верхней кромке. Для экрана Т-образного профиля распределение звукового давления за экраном более сложное, связанное с наличием узких секторов с низким уровнем звукового давления (рис. 2а), что также может быть обусловлено процессом интерференции. Эти особенности наглядно иллюстрируются на рис. 2б, где для сравнения приведены графики изменения звукового давления за экраном вдоль продольной оси х для прямого экрана и экрана Т-образного профиля.

Рис. 2.

(а) – Картина распределения звукового давления в расчетной области с экраном и (б) – зависимость звукового давления за экраном вдоль продольной оси х на частоте 800 Гц.

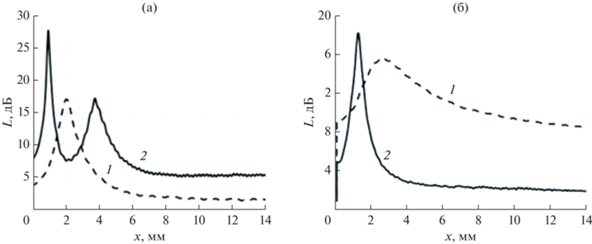
Чтобы выявить особенности дифракции звука на экране Т-образного профиля, были рассчитаны вносимые потери IL для такого экрана. Так как эти вносимые потери вычисляются по отношению к прямому экрану, то фактически они определяют, насколько изменение формы экранa повышает его эффективность. На рис. 3 для угла α = 40° представлены зависимости IL от расстояния х от расчетной точки R до задней поверхности экрана. Видно, что с изменением расстояния х эффективность насадки может претерпевать существенные изменения. На некоторых расстояниях имеет место значительный рост (локальный пик) эффективности. Положение этого пика зависит от частоты звука. С ростом частоты форма кривой эффективности усложняется и может содержать уже два локальных экстремума. Характерной особенностью такого рода кривых является то, что наблюдаемые экстремумы сосредоточены в ближней области за экраном, при х < 8 м. При больших х кривые эффективности выравниваются и практически перестают зависит от х. Следует отметить, что установившиеся значения вносимых потерь на больших расстояниях от экрана зависят как от частоты, так и от геометрических размеров экрана. Эти зависимости не так просты и очевидны, как для прямого экрана, снижение звукового давления за которым возрастает с увеличением высоты экрана и частоты звуковой волны. Для Т-образного экрана все оказывается сложнее. Так, если для экрана c h = 4.5 м и l = 0.5 м (рис. 3а) установившееся значение IL увеличивается с ростом частоты, то для экрана с вдвое меньшими значениями этих параметров (рис. 3б) все происходит наоборот: на низкой частоте эффективность насадки больше, чем для высокой. Отметим, что отношение l/h в этих двух конфигурациях экранов было одинаковым: l/h = 0.1.

Рис. 3.

Зависимость эффективности Т-образного экрана от положения расчетной точки при α = 40° для экранов c (а) – h = 4.5 м, l = 0.5 м и (б) – h = 2.25 м, l = 0.25 м на частотах 400 (1) и 800 Гц (2).

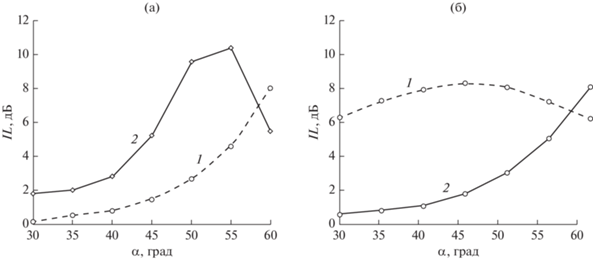
Далее были рассчитаны установившиеся значения вносимых потерь IL на больших расстояниях от экрана (х = 15 м), и получены зависимости этих значений от угла α, определяющего положение экрана относительно источника звука. Для двух рассмотренных выше конфигураций Т-образного экрана такие зависимости представлены на рис. 4. Как видим, эти зависимости в значительной степени зависят как от геометрических параметров экрана, так и от частоты звука. Для первой конфигурации экрана (рис. 4а) на частоте 400 Гц вносимые потери IL плавно возрастают с увеличением угла α, а на вдвое большей частоте IL изменяются более сложным образом: сначала IL также плавно возрастают, а затем, достигая некоторого максимума, начинают снижаться. Но в целом IL на более высокой частоте значительно больше, чем на низкой. Для второй конфигурации экрана картина кардинально меняется (рис. 4б). Здесь уже плавное возрастание IL с ростом α происходит на частоте 800 Гц, а на вдвое меньшей частоте зависимость IL от угла α не столь существенна, и IL максимальны при α = 45°. В целом, для этой конфигурации, наоборот, вносимые потери на низкой частоте выше, чем на высокой.

Рис. 4.

Зависимость эффективности Т-образного экрана от угла α для экранов c (а) – h = 5 м, l = 0.5 м и (б) – h = 2.25 м, l = 0.25 м на частотах 400 (1) и 800 Гц (2).

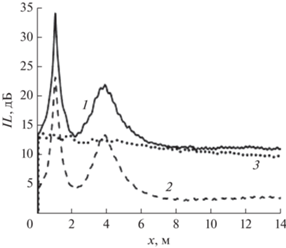
Особенности уменьшения уровня звука Т-образным экраном можно выявить, учитывая, что такой экран можно рассматривать как совокупность двух Г-образных экранов, один из которых развернут по направлению к источнику шума. На рис. 5 представлены зависимости IL от координаты расчетной точки х для таких экранов с h = 4.5 м и l = 0.5 м при α = 70°. Как и следовало ожидать, наибольшей эффективностью обладает Т-образный экран. Эффективность развернутого к источнику звука Г-образного экрана на больших расстояниях х приближается к эффективности Т-образного экрана, но не содержит характерных для последнего пиков эффективности на малых расстояниях от экрана. Отсюда следует, что если нас, в первую очередь, интересует эффективность экрана на больших расстояниях от его задней поверхности, то в этом случае вместо Т-образного экрана без потери эффективности можно использовать развернутый к источнику Г-образный экран. В противоположность этому, эффективность обращенного к расчетной точке Г-образного экрана имеет те же локальные пики эффективности на малых расстояниях, как и Т-образный экран, но на больших расстояниях его эффективность заметно ниже, чем у двух других экранов. Следовательно, при небольшом удалении расчетной точки эффективность Т-образного экрана определяется физическими процессами, происходящими на его задней кромке. Появляющиеся здесь локальные пики эффективности обусловлены, по-видимому, тем, что в расчетной точке происходит интерференция звука, который непосредственно после дифракции на задней кромке экрана попадает в расчетную точку, со звуком, который после дифракции сначала отражается от задней поверхности экрана и только потом попадает в расчетную точку. Наоборот, на большом удалении расчетной точки от экрана эффективность Т-образного экрана определяется процессами, происходящими на его передней кромке, обращенной к источнику звука. То обстоятельство, что эта эффективность помимо частоты существенно зависит от угла α, и эта зависимость может содержать некоторые локальные максимумы (рис. 4), позволяет предположить, что при этом также имеет место интерференция звука, но уже на передней кромке Т-образного экрана.

Рис. 5.

Эффективность Т-образного (1), Г-образного (2) и развернутого Г-образного (3) экранов при α = = 70° на частоте 800 Гц.

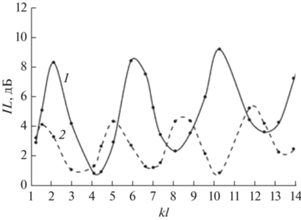
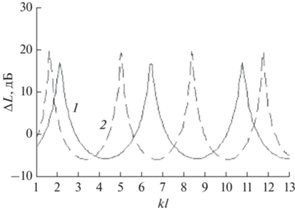
Для того чтобы подтвердить справедливость этого предположения, были проведены дополнительные расчеты для Г-образного экрана, обращенного к источнику звука. Определялись вносимые потери IL такого экрана как функции угла α при различных значениях l и на различных частотах f, когда расчётная точка соответствовала х = 15 м. Оказалось, что получаемые при этом графики зависимостей IL(α) практически совпадали при одинаковых значениях безразмерного числа kl, где k – волновое число, k = 2πf/c. Это позволило перестроить полученные результаты расчетов, получив для различных углов α графические зависимости IL(kl). Такие графики для рассматриваемого экрана при двух углах α представлены на рис. 6. Они показывают, что эффективность такого экрана является сложной функцией kl с ярко выраженными максимумами и минимумами.

Рис. 6.

Эффективность развернутого Г-образного экрана как функция kl при α = 40° (1) и α = 20° (2).

Положение максимумов на графиках зависит от угла α, так что с уменьшением α эти максимумы смещаются влево, соответствуя меньшим значениям kl. Вместе с тем, для каждого α значения kl, соответствующие максимумам вносимых потерь IL, связаны рядом нечетных чисел. Так, значение kl для первого максимума отличается от значения kl для второго максимума в три раза, значение kl для третьего максимума больше значения kl для первого максимума в пять раз и т.д. Например, как следует из рис. 6, при α = 40° первые три максимума IL соответствуют значениям kl равным 2, 6 и 10, а при α = 20° максимумы IL в первом приближении равны 1.7, 5, 8.5 и 11.9.

АНАЛИЗ ЧИСЛЕННЫХ РЕЗУЛЬТАТОВ

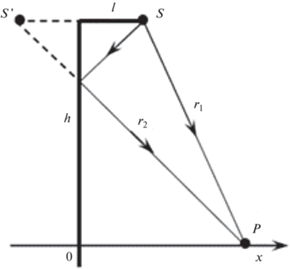
Для анализа формирования ближнего звукового поля за экраном, которое по нашим предположениям обусловлено проявлением в этой области интерференционных процессов, была рассмотрена модель Г-образного экрана, представленная на рис. 7. В этой модели не учитывается положение истинного источника звука, которое мы при проведении численных расчетов определяли углом α. В этой модели точечный источник звука S расположен на задней кромке экрана, а звуковое давление в расчетной точке является суперпозицией волн, одна из которых, р1, приходит по прямому лучу от источника S, а вторая, р2, по лучу, отраженному от поверхности экрана, что эквивалентно наличию мнимого источника S'. Правомерность такого подхода обусловлена тем, что, как показывают приведенные выше результаты численных расчетов (рис. 3а, 5), положение пиков вносимых потерь IL в малой степени зависит от угла α, хотя зависимость их амплитуды от угла α значительна. Нас в последующем качественном анализе и будет интересовать прежде всего положение пиков в ближней зоне за экраном, а не их амплитуда.

Рис. 7.

Расчетная схема для оценки интерференции звуковых волн в области за экраном.

Если предположить, что поверхность экрана является абсолютно жесткой, то звуковое давление в расчетной точке в такой модели определится выражением:

(1)
${{P}_{\Sigma }} = {{P}_{1}} + {{P}_{2}} = \frac{A}{{{{r}_{1}}}}{{e}^{{ - ik{{r}_{1}}}}} + \frac{A}{{{{r}_{2}}}}{{e}^{{ - ik{{r}_{2}}}}},$
где A – некоторая постоянная, определяющая интенсивность точечного источника, k – волновое число, r1 = [h2 + (x – l)2]1/2, r2 = [h2 + (x + l)2]1/2.

Интерференция в расчетной точке будет определяться как отношением путей r1/r2, так и их разностью ∆r = r2 − r1. Ее влияние на звуковое поле в расчетной точке определим по аналогии с вносимыми потерями в логарифмических единицах соотношением:

(2)
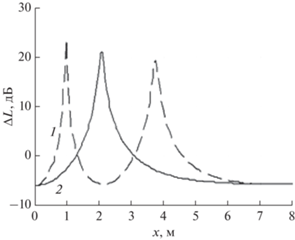
$\begin{gathered} \Delta L = 10\lg ([{{{{{\left| {{{P}_{1}}} \right|}}^{2}}} \mathord{\left/ {\vphantom {{{{{\left| {{{P}_{1}}} \right|}}^{2}}} {{{{\left| {{{P}_{\Sigma }}} \right|}}^{2}}}}} \right. \kern-0em} {{{{\left| {{{P}_{\Sigma }}} \right|}}^{2}}}}]{\text{ }} = \\ = - 10\lg [1 + 2({{{{r}_{1}}} \mathord{\left/ {\vphantom {{{{r}_{1}}} {{{r}_{2}}}}} \right. \kern-0em} {{{r}_{2}}}})\cos (k\Delta r) + {{({{{{r}_{1}}} \mathord{\left/ {\vphantom {{{{r}_{1}}} {{{r}_{2}}}}} \right. \kern-0em} {{{r}_{2}}}})}^{2}}]. \\ \end{gathered} $

На рис. 8 представлена зависимость расчетного параметра ΔL от расстояния до расчетной точки, полученная для экрана с h = 4.5 м и l = 0.5 м. Сравнение представленных на этом рисунке данных с результатами численных расчетов (рис. 3а) показывает их хорошее соответствие друг другу, что в первую очередь относится к значениям координат х, определяющих пиковые (максимальные) значения IL и ΔL, которые на обоих графиках практически совпадают. Это подтверждает сделанное выше предположение о том, что наблюдаемые на приведенных графиках значительные колебания вносимых потерь IL в ближней зоне за T-образным экраном обусловлены интерференцией звука в этой области.

Рис. 8.

Изменение уровня звукового давления за экраном из-за интерференции звука на частоте 400 (1) и 800 Гц (2).

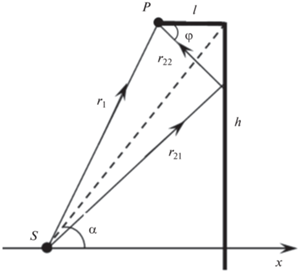
Далее с помощью модели экрана, представленной на рис. 9, было рассмотрено формирование звукового поля перед экраном, у его передней кромки, за счет наличия в этой области интерференционных процессов. При этом, как и ранее, положение точечного источника звука S характеризуется углом α, а расчетная точка Р располагается у передней кромки экрана. Звуковое давление в расчетной точке Р является суперпозицией двух волн, одна из которых приходит туда по прямому лучу от источника звука S, а вторая по лучу, отраженному от передней поверхности экрана. Для описания звукового поля здесь также могут использоваться формулы (1)–(2) с тем отличием, что входящие в эти формулы величины r1 и r2 определяются выражениями:

$\begin{gathered} {{r}_{1}} = {{\left[ {{{h}^{2}} + {{{\left( {{h \mathord{\left/ {\vphantom {h {{\text{tg}}\alpha }}} \right. \kern-0em} {{\text{tg}}\alpha }}--l} \right)}}^{2}}} \right]}^{{1/2}}},\,\,\,\,{{r}_{2}} = {{r}_{{21}}} + {{r}_{{22}}}, \\ {{r}_{{21}}} = {{\left[ {{{{\left( {{h \mathord{\left/ {\vphantom {h {{\text{tg}}\alpha }}} \right. \kern-0em} {{\text{tg}}\alpha }}} \right)}}^{2}} + {{{\left( {h--l{\text{tg}}\varphi } \right)}}^{2}}} \right]}^{{1/2}}}, \\ {{r}_{{22}}} = l{{[\left( {1 + {\text{t}}{{{\text{g}}}^{2}}\varphi } \right)]}^{{1/2}}},\,\,\,{\text{ tg}}\varphi = {{\left( {{1 \mathord{\left/ {\vphantom {1 {{\text{tg}}\alpha }}} \right. \kern-0em} {{\text{tg}}\alpha }} + {l \mathord{\left/ {\vphantom {l h}} \right. \kern-0em} h}} \right)}^{{ - 1}}}. \\ \end{gathered} $
Рис. 9.

Расчетная схема для оценки интерференции звуковых волн в области перед экраном.

На рис. 10 представлена зависимость ΔL от безразмерного параметра kl, полученная при тех же расчетных параметрах, что и при численном моделировании (рис. 6). Сравнение результатов аналитических и численных расчетов показывает, что в обоих случаях характер кривых и положения максимумов на них совпадают. Одинаковы и тенденции в зависимости этих кривых от угла α: с увеличением угла α положения максимумов смещаются к более высоким значениям kl, так что сами графические зависимости становятся более растянутыми.

Рис. 10.

Изменение уровня звукового давления на передней кромке экрана при α = 40° (1) и α = 20° (2).

Заметим, что в предельном случае, когда α → 0, величина ∆r → 2l, а отношение (r1/r2) → 1. Тогда, как следует из (2), появление максимумов функции ΔL (kl) соответствует условию cos(2kl) = − 1, которое приводится к виду: kl = (2n + 1)π/2, где n = 0, 1, 2…. Следовательно, первый максимум в этом предельном случае соответствует kl = π/2, а последующие максимумы определяются рядом нечетных чисел, что согласуется с данными, представленными на рис. 6 и 10.

Конечно, имеют место и отличия в результатах численных и аналитических расчетов. Так, численные расчеты показывают, что с увеличением угла α существенно возрастает и размах колебаний функции IL(kl), а также то, что имеется некоторый тренд возрастания среднего значения вносимых потерь с ростом kl. Очевидно, что эти эффекты обусловлены наличием дифракции звука на Т-образном экране, что не учитывается в рассмотренной простой аналитической модели. В целом, проведенный анализ позволяет сделать заключение, что наблюдаемая при расчетах существенная зависимость установившихся значений вносимых потерь IL в дальней зоне за T-образным экраном от угла α и параметра kl обусловлена наличием интерференции звука на передней кромке этого экрана.

ЗАКЛЮЧЕНИЕ

Численное моделирование Т-образного экрана показало, что для такого экрана помимо дифракционных процессов существенное значение имеют и процессы интерференции звука, протекающие в пространстве как перед экраном, так и за экраном. При этом пространство за экраном можно разделить на две зоны. В ближней зоне, ограниченной расстоянием порядка 8 м от задней поверхности экрана, существенное значение имеет интерференция звука на задней кромке экрана, что приводит к появлению в этой зоне локальных пиков эффективности экрана. Положение этих пиков является функцией координаты х, существенно зависит от частоты звука и геометрических параметров Т-образного экрана, но практически не зависит от положения источника звука относительно экрана. В дальней зоне, при расстояниях от задней поверхности экрана больших 8 м, эффективность Т-образного экрана заданной конфигурации для данной частоты звука остается практически постоянной, не зависящей от координаты х. Вместе с тем значение этой постоянной существенно зависит от частоты звука, конфигурации экрана, а также положения источника звука. Показано, что такие вариации установившегося значения эффективности экрана в дальней зоне являются периодической функцией безразмерного параметра kl. Они являются следствием интерференции звука на передней кромке Т-образного экрана.

Список литературы

  1. Wirt L.S. The control of diffracted sound by means of thnadners (shaped noise barriers) // Acustica. 1979. V. 42. № 2. P. 73–88.

  2. May D.N., Osman M.M. Highway noise barriers-new shapes // J. Sound Vib. 1980. V. 71. № 1. P. 73–101.

  3. Cohn L.F., Harris R.A., Rolfer R.L., Duncan D.L., Woosley R.L. Special noise barrier // Transportation research record. 1993. V. 1416. P. 69–74.

  4. Watts G.R., Crombie D.H., Hothersall D.C. Acoustic performance of new designs of traffic noise barriers: Full scale tests // J. Sound Vib. 1994. V. 177. № 3. P. 289–305.

  5. Fujiwara K., Hothersall D.C., Kim Ch. Noise barriers with reactive surfaces // Appl. Acoust. 1998. V. 53. № 4. P. 255–272.

  6. Ishizuka T., Fujiwara K. Performance of sound barriers with various edge shapes and acoustical conditions // Appl. Acoust. 2004. V. 65. № 2. P. 125–141.

  7. Okubo T., Yamamoto K. Simple prediction method for sound propagation behind edge-modified barriers // Acoust. Sci. & Tech. 2007. V. 28. № 1. 7–15.

  8. Samuels S., Ancich E. Recent developments in the design and performance of road traffic noise barriers // Acoust. Australia. 2001. V. 29. № 2. P. 73–78.

  9. Ekici I., Bougdah H. A review of research on environmental sound barriers // Build. Acoust. 2003. V. 10. № 4. P. 289–323.

  10. Li K.M., Wong H.Y. A review of commonly used analytical and empirical formulae for predicting sound diffracted by a thin screen // Appl. Acoust. 2005. V. 166. № 1. P. 45–76.

  11. Fujiwara K., Furuta N. Sound shielding efficiency of a barrier with a cylinder at the edge // Noise Control Eng. J. 1991. V. 37. № 1. P. 5–11.

  12. Mozer M., Volz R. Improvement of sound barriers using headpieces with finite acoustic impedance // J. Acoust. Soc. Am. 1999. V. 106. № 6. P. 3049–3060.

  13. Миронов М.А., Урусовский И.А. Затухающие волны в тени цилиндра // Акуст. журн. 2002. Т. 48. № 5. С. 661–665.

  14. Урусовский И.А. Дифракция звука на экране с веерной насадкой // Акуст. журн. 2013. Т. 59. № 1. С. 86–95.

  15. Maekawa Z. Noise reduction by screens // Appl. Acoust. 1968. V. 1. № 3. P. 157–173.

  16. Seznec R. Diffraction of sound around barriers: use of the boundary elements technique // J. Sound Vib. 1980. V. 73. № 2. P. 195–209.

  17. Hothersall D.C., Chandler-Wilde S.N., Hajmirzae M.N. Efficiency of single noise barriers // J. Sound Vib. 1991. V. 146. № 2. P. 303–323.

  18. Egan C.A., Chilekwa V., Oldham D.J. An investigation of the use of top edge treatments to enhance the performance of a noise barrier using the boundary element method // Proc. ICSV13. 2006. Vienna, Austria.

  19. Gerges S.N.Y., Calza A.J. Acoustic barriers: Analytical methods, Boundary element method and experimental verification // Build. Acoust. 2002. V. 9. № 3. P. 167–190.

  20. Bolejko R., Dobrucki A. FEM and BEM computing costs for acoustical problems // Arch. Acoust. 2006 V. 31. № 2. P. 193–212.

  21. Fard S.M.B., Kessissoglou N., Samuels S., Burgess M. Numerical study of noise barrier designs // Proc. Acoust. 2013. Victor Harbor, Australia.

  22. Kulkina V., Komkin A. Study of acoustic characteristics of noise barriers // MATEC Web of Conf. ASO-2020. V. 320. № 00030.

  23. Комкин А.И., Назаров Г.М. Особенности дифракции звука на звукопоглощающем экране // Акуст. журн. 2021. Т. 67. № 3. С. 303–307.

  24. Hajek J.J., Blaney C.T. Evaluation of T-profile noise barriers // Transp. Research Record, 1984. V. 983. P. 8–17.

  25. Hothersall D.C., Crombie D.H., Chandler-Wilde S.N. The performance of T-profile and associated noise barriers // Appl. Acoust. 1991. V. 32. P. 269–287.

  26. Hasebe M. Sound reduction by a T-profile noise barrier // J. Acouct. Soc. Japan. (E). 1995. V. 16. № 3. P. 173–179.

  27. Defrance J., Jean P. Integration of the efficiency of noise barrier caps in a 3D ray tracing method. Case of a T-shaped diffracting device // Appl. Acoust. 2003. V. 64. P. 765–780.

  28. Monazzam M., Lam Y. Performance of T-shape barriers with top surface covered with absorptive quadratic residue diffusers // Appl. Acoust. 2008. V. 69. P. 93–109.

  29. Oldman D., Egan C. A parametric investigation of the performance of T-profiled highway noise barriers and the identification of a potential predictive approach // Appl. Acoust. 2011. V. 72. № 11. P. 803–813.

  30. Okubo T., Yamamoto K. Equivalence in diffraction-reducing efficiency between T-profile and thick barrier against road traffic noise // Acoust. Sci. & Tech. 2013. V. 34. № 4. P. 277–283.

  31. Fan R., Su Z., Cheng L. Modeling, analysis, and validation of an active T-shaped noise barrier // J. Acoust. Soc. Am. 2013. V. 134. № 3. P. 1990–2003.

  32. Monazzam M.R., Abbas M., Yazdanirad S. Performance Evaluation of T-Shaped Noise Barriers Covered with Oblique Diffusers Using Boundary Element Method // Arch. Acoust. 2019. V. 44. № 3. P. 521–531.

  33. Yang C., Pan J., Cheng L. A mechanism study of sound wave-trapping barriers // J. Acoust. Soc. Am. 2013. V. 134. № 3. P. 1961–1969.

  34. Комкин А.И., Мусаева Р.Н. Моделирование акустических экранов с различной конфигурацией верхней кромки // Сб. трудов XXXIV сессии РАО. М.: ГЕОС, 2022. С. 1124–1128.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Акустический журнал

Архивы выпусков Информация о журнале Отправить рукопись в журнал