Акустический журнал, 2022, T. 68, № 6, стр. 647-669

1. ВВЕДЕНИЕ

Проблема излучения шума турбулентными струями до сих пор не имеет общепринятого теоретического решения [1–3]. Причиной этого является, в первую очередь, нерешенность фундаментальной проблемы турбулентности. Кроме того, задача осложняется тем, что в турбулентной струе лишь малая часть гидродинамических пульсаций является эффективным источником шума, и в настоящее время нет общепринятого ответа на вопрос о том, какая составляющая турбулентных пульсаций в струе несет ответственность за генерацию шума.

Для определения звукового излучения струи в настоящее время широко применяются вихреразрешающие численные методы (LES). В этих расчетах удается определить многие важные характеристики турбулентных пульсаций в струе, в том числе и излучаемый ими шум [4–6]. Результаты численных расчетов имеют большое практическое значение и служат серьезной поддержкой в исследовании шума струи, но сами по себе они не дают понимания механизмов генерации звукового излучения турбулентными сдвиговыми потоками, которое необходимо для разработки методов снижения шума.

Основным направлением теоретического анализа процесса генерации шума турбулентными течениями является создание низко-порядковых моделей источников звука, в которых вместо решения полных уравнений газовой динамики делается попытка выделить основные факторы, ответственные за излучение звука турбулентностью. Разработка таких моделей опирается на те или иные гипотезы о механизмах шумообразования, корректность которых проверяется сравнением с экспериментом. В работах, связанных с моделированием источников звука, можно выделить несколько основных направлений. Одно из них основано на предположении о том, что основным источником звука являются крупномасштабные линейные возмущения среднего течения струи (волны неустойчивости Кельвина–Гельмгольца) [7–9]. При этом в качестве области течения, где происходит возбуждение волн неустойчивости, рассматриваются как кромка сопла [10], так и весь объем турбулентного потока [11, 12]. Следует отметить, что в дозвуковых струях волновые пакеты возмущений являются неэффективными излучателями звука, поскольку для таких пакетов лишь экспоненциально малая часть пространственно-временного спектра волнового пакета попадает в область сверхзвуковых фазовых скоростей, определяющую звуковое излучение. Кроме того, эти экспоненциально малые “сверхзвуковые хвосты” спектра очень чувствительны к форме волнового пакета, что делает оценку их вклада в шум струи в случае дозвуковых скоростей сильно зависящей от плохо прогнозируемых деталей самого пакета. Другое направление исследований основано на представлении о том, что основной вклад в генерацию звука дает мелкомасштабная турбулентность. Несмотря на то, что до сих пор отсутствует полная физическая модель мелкомасштабных источников звука, этот подход служит основой большого числа исследований и расчетов шума струи, например [13–19]. Отметим еще комбинированные модели, в которых предполагается, что в разных диапазонах частот и скоростей доминируют крупномасштабные или мелкомасштабные механизмы генерации шума [20–22]. Следует отметить также модели, в которых в качестве крупномасштабных возмущений, отвечающих за излучение звука, рассматриваются нелинейные крупные вихри. В частности, в работах [23, 24] рассматривается комбинированное излучение от собственных колебаний крупномасштабных вихрей и мелкомасштабных источников шума и оценивается их относительный вклад в шум для тонально возбужденной струи.

В настоящей работе проводится исследование механизма акустического излучения струи в рамках концепции мелкомасштабных источников шума. В работах этого направления стандартным подходом является метод акустических аналогий, основанный на разделении механизмов генерации и распространения звуковых возмущений. При этом исходные уравнения сплошной среды преобразуются к уравнениям, в левой части которых выделен оператор распространения, описывающий линейные возмущения системы, а остальные члены перенесены в правую часть уравнений и трактуются как источник, динамика которого может быть описана независимым образом. Метод акустической аналогии был впервые предложен Лайтхиллом [1], который использовал в качестве оператора распространения обычное волновое уравнение. Однако, при использовании аналогии Лайтхилла для описания шума струи возникают проблемы с моделированием направленности излучения. Это связано с тем, что в области малых углов к оси струи существенную роль играет эффект рефракции. В аналогии Лайтхилла члены уравнения, ответственные за рефракцию, отнесены в правую часть к источникам, для которых обычно используются упрощенные модели с эмпирической оценкой параметров. В этом случае учет эффекта рефракции оказывается затруднительным. Поэтому для моделирования излучения во всем диапазоне углов используются более сложные акустические аналогии, в которых эффект рефракции включен в оператор распространения. На этом пути был предложен ряд акустических аналогий, среди которых следует упомянуть аналогии Филипса [25], Лилли [26], Хоу [27], Голдстейна [15] и др.

Необходимо заметить, что метод акустических аналогий содержит в себе ряд проблем теоретического характера, связанных с разделением системы на две части, одна из которых (источник) описывается как случайное поле, обеспечивающее накачку другой части системы (оператор распространения). Стохастизация процесса, т.е. описание сложной детерминированной системы методами вероятностного анализа является общим подходом при описании турбулентности ([28, 29] и др.). Но в отличие от классической однородной и изотропной турбулентности, турбулентность в сдвиговом течении характеризуется наличием неоднородного среднего течения, обладающего гидродинамическими (вихревыми) степенями свободы. Если эти гидродинамические степени свободы включены в оператор распространения, то они могут возбуждаться источниками, что приводит к некоторым вторичным эффектам, существенно влияющим на звуковое излучение.

Одной из таких проблем является то, что среди собственных решений оператора распространения могут содержаться решения, соответствующие неустойчивости Кельвина–Гельмгольца. В этом случае возникает вопрос о том, какому условию должна удовлетворять функция Грина оператора распространения: условию ограниченности или причинности. Так, например, первоначальный вариант аналогии Голдстейна [15], где использовалась функция Грина, получаемая с условием ограниченности, позже был модифицирован с учетом условия причинности так, что функция Грина стала включать вклад волн неустойчивости Кельвина–Гельмгольца [11]. Однако, в дальнейшем были высказаны возражения против использования функции Грина с условием причинности при описании источников звука в струе [30]. Проблема неустойчивых мод в линейном операторе, описывающем распространение звуковых волн, возникает также при разработке численных методов, поскольку наличие таких мод приводит к неустойчивости численной схемы. Это заставляет использовать различные методы демпфирования численных схем [14] или переходить к другим аналогиям, не имеющим неустойчивых собственных решений [31].

Еще одна важная проблема метода акустических аналогий касается так называемого “сдвигового шума”. Именно эта проблема является предметом исследования настоящей работы. Необходимо отметить, что термин “сдвиговый шум” принято использовать в различных значениях в зависимости от используемой акустической аналогии [32]. Впервые этот термин появился, по-видимому, при описании источников шума в струе с помощью аналогии Лайтхилла. В этой аналогии звуковой источник включает квадратичные и линейные по возмущениям скорости члены. Вклад первых был отнесен к собственному шуму турбулентности, а вторых – к сдвиговому шуму. Анализ собственной и сдвиговой составляющих шума струи в аналогии Лайтхилла проводился, в частности, в работах [33–37]. Впоследствии термин “сдвиговый шум” стали использовать применительно к акустическим аналогиям, в которых все линейные по возмущениям члены перенесены в левую часть. Это касается, в частности уравнения Лилли. В этом случае использовалось другое определение, согласно которому к источникам сдвигового шума были отнесены члены в правой части уравнения, имеющие коэффициенты, пропорциональные средней завихренности. Сравнение двух альтернативных представлений о сдвиговом шуме в рамках аналогий Лайтхилла и Лилли проводилось в работе [32], посвященной оценке шума струи на основе уравнения Лилли.

Сдвиговый шум является существенной составляющей в суммарном шуме струи, а в некотором диапазоне параметров эта составляющая может доминировать. В частности, это касается области низких частот, а также излучения источников, расположенных в области течения с большими градиентами скорости, например, на начальном участке струи. Это определяет важность вопроса о том, насколько модели, предсказывающие сдвиговый шум, соответствуют реальному процессу излучения звука турбулентными течениями. Однако, несмотря на это, сама постановка проблемы сдвигового шума была подвергнута критике в работах [14, 38 ]. Приведенные аргументы состоят в том, что хотя уравнение Лилли и содержит в правой части члены, пропорциональные средней завихренности, но оно само является результатом преобразований линеаризованных уравнений Эйлера с нелинейной правой частью, в которых нет такого рода членов. Отсюда был сделан вывод о том, что разделение источников шума на две составляющие в уравнении Лилли не отражает физической природы генерации шума, а является искусственным следствием математических преобразований. Одновременно с этим Голдстейном была предложена акустическая аналогия [15], в которой была реализована идея использования линеаризованных уравнений Эйлера в качестве оператора распространения с нелинейными членами в качестве источника. Работы Морриса [14, 38] и разработка аналогии Голдстейна, одновременно с успешным внедрением численных методов в задачах расчета шума струи, по-видимому, послужили причиной прекращения серьезных усилий в направлении решения проблемы сдвигового шума. Поэтому последующие работы, связанные с использованием акустических аналогий, были в основном связаны с численной и экспериментальной оценкой характеристик случайного поля источников в рамках аналогии Голдстейна.

Однако, в действительности, переход от уравнения Лилли к аналогии Голдстейна лишь маскирует, но не решает проблему сдвигового шума, за которой стоит физическая проблема взаимодействия звуковых источников с линейными колебаниями сдвигового течения. В этом можно убедиться на примере рассмотренной в настоящей работе (раздел 3) модельной задачи об излучении звукового поля точечным квадрупольным источником в плоскопараллельном слое смешения. В этой задаче исходные уравнения не содержат членов, пропорциональных завихренности, но такой член появляется в решении, что связано с тем, что при помещении квадрупольного источника в сдвиговое течение пространственные составляющие квадруполя оказываются в областях течения с различной средней скоростью. В результате решение имеет две составляющие, одна из которых является собственным излучением источника, а другая пропорциональна градиенту скорости в сдвиговом потоке. Вторая составляющая связана с возбуждением источником вихревых возмущений сдвигового потока и в соответствии с этим интерпретируется как сдвиговое излучение. В таком понимании сдвиговый шум не зависит от математических преобразований, а определяется наличием гидродинамических степеней свободы в линейном операторе распространения, используемом в акустической аналогии.

Помимо проблем, связанных с оператором распространения, важным вопросом является моделирование источников в правой части акустической аналогии. При моделировании источников обычно принимается ряд предположений об их пространственной структуре и динамике, одно из которых касается порядка мультипольности звуковых источников в струе. Этот вопрос до настоящего времени вызывает споры по причине того, что распределенное поле источников может быть записано различными эквивалентными способами. Так, например, поле дипольных источников эквивалентно полю монополей, связанному с диполями оператором дивергенции. Аналогичная связь существует между квадрупольным и дипольным представлениями поля источников. Эта неоднозначность послужила причиной создания ряда моделей звукового излучения струи, в которых в качестве источников рассматривались мультиполи разного порядка: монополи [13], диполи [14] или квадруполи [11, 16, 17]. Выбор порядка мультипольности источников, зависит, в первую очередь, от предназначения модели. В частности, для предсказания одноточечных характеристик звукового поля струи вполне достаточна наиболее простая модель монопольных источников. Однако, для предсказания корреляционных характеристик звукового поля учет квадрупольности звуковых источников является существенным [18]. В настоящей работе выбирается квадрупольное представление источников, что необходимо для анализа азимутальных гармоник звукового излучения струи.

При разработке и использовании моделей квадрупольных источников проблемой является необходимость задания большого количества параметров корреляции компонент тензора второго ранга, определяющего источник звука в правой части. Принятое в настоящей работе предположение об изотропности квадрупольных источников позволяет существенно уменьшить количество эмпирических параметров. Основанием для этого предположения служит то, что видимое отсутствие сферической симметрии излучения струи может быть связано не с неизотропностью источника, а с эффектами конвекции и рефракции. В то же время, сам процесс генерации звука мелкомасштабными источниками может иметь при этом изотропный характер. Предположение об изотропности источников использовалось ранее при построении моделей звуковых источников в работах [39–42]. Однако, имевшиеся тогда данные акустических измерений не могли служить надежной базой для проверки этой гипотезы. Измерения азимутальных гармоник звукового излучения, используемые в настоящей работе, позволяют вернуться к этому вопросу на новом уровне. Анализ этих данных свидетельствует о том, что турбулентность, отвечающая за звуковое излучение струи, обладает свойством изотропности. Подтверждение этой гипотезы открывает новые возможности для использования результатов, полученных в классической теории турбулентности [28, 43], применительно к струйным турбулентным течениям. В настоящей работе используется также представление звукового источника в струе на основе дифференциального уравнения Ланжевена с дельта-коррелированной правой частью. Этот метод, основанный на анализе измерений пульсаций скорости в турбулентной струе [44], использовался ранее для моделирования звуковых источников в работах [17, 45]. Физическая трактовка такого представления состоит в том, что элементарные события в вихревой динамике, ответственные за излучение звука, представляют собой быстрые “вспышки” возмущений со сравнительно более медленной дальнейшей эволюцией. Именно это быстрое начало гидродинамических процессов выделяется, как источник звука, на фоне других процессов, определяющих энергию турбулентных пульсаций, но не эффективных с точки зрения генерации шума. Использование такого представления звуковых источников позволило существенно упростить оценку звукового излучения, уменьшив кратность интегрирования по объему турбулентного течения.

Важным вопросом при моделировании звукового излучения струи является постановка прямой или обратной задачи. В отличие от прямой задачи, в которой параметры источников выражаются через характеристики гидродинамических пульсаций, в обратной задаче источники определяются по излучаемому ими звуковому полю. Хотя обратная задача, вообще говоря, не имеет однозначного решения, этот метод является эффективным инструментом в тех случаях, когда затруднен доступ к прямым измерениям источников или неясным является сам механизм излучения. В турбулентных струях большая часть гидродинамических пульсаций не эффективна с точки зрения генерации звукового излучения, и только лишь малая их часть имеет отношение к генерации шума. Поэтому прямая оценка параметров источников звука по измерениям гидродинамических пульсаций в струе затруднительна, и в этом случае, по мнению авторов, более уместным является подход, основанный на постановке обратной задачи определения источников по излучаемому ими полю. В случае успеха, такой подход дает новую нетривиальную информацию о структуре турбулентности в сдвиговых потоках и, в особенности, ее излучающей части.

Решение обратной задачи должно опираться на эксперимент, по возможности достаточно нетривиальный для того, чтобы сравнение модели с данными измерений служило серьезным основанием в пользу того или иного представления источников. В контексте этой проблемы предлагается использовать измерения шума струи, включающие направленности азимутальных мод в полосах частот [46], выполненные с помощью решетки из 6 микрофонов по методу азимутальной декомпозиции [46, 47]. Такой метод позволяет выделить в акустическом поле струи отдельные азимутальные гармоники, что по сравнению с измерениями суммарного звукового сигнала обеспечивает более жесткий отбор моделей звуковых источников.

Настоящая работа имеет следующую структуру. В разделе 2 приводятся основные уравнения, используемые в рассматриваемой акустической аналогии. В качестве оператора распространения используются линеаризованные уравнения Эйлера для изэнтропического потока, а источником является квадрупольное поле, представляющее собой нестационарную часть тензора напряжений Рейнольдса.

В разделе 3 рассматривается модельная задача об излучении звука точечным квадруполем в двумерном слое смешения, в которой проявляются основные особенности, связанные с эффектом сдвигового излучения. Анализ решения этой задачи позволяет выделить в звуковом поле две составляющие, имеющие различный механизм генерации и определяемые, как собственное и сдвиговое излучение источника. Показано, что появление сдвиговой компоненты шума, амплитуда которой пропорциональна завихренности среднего течения, связано с возбуждением источником вихревых возмущений.

В разделе 4 определяются корреляционные характеристики случайного поля источников в струе с учетом свойств квадрупольности источников и их изотропности. В разделе 5 находятся функции Грина квадрупольных источников в квазиоднородной струе круглого сечения, которые будут далее использоваться в интеграле свертки при вычислении звукового поля. В разделе 6 выводятся соотношения, определяющие спектральную мощность азимутальных гармоник звукового излучения струи. В разделе 7 описаны данные измерений шума турбулентной струи, полученные с помощью решеток микрофонов методом азимутальной декомпозиции звуковых сигналов.

В разделе 8 проводится анализ моделируемого звукового поля и его сравнение с данными эксперимента. Показано, что в звуковом поле струи так же, как и в модельной задаче, рассмотренной в разделе 3, можно выделить две компоненты, собственную и сдвиговую, которые по-разному зависят от параметров среднего течения. Сравнение модели с данными акустических измерений показывает, что модель способна описать сложную картину направленности азимутальных гармоник при достаточно простых предположениях о структуре звукового источника, но лишь в том случае, если в модели учитывается только собственный шум струи, а сдвиговая часть отброшена. Тем самым делается важный вывод, что учет сдвиговой составляющей приводит к серьезному рассогласованию модели с данными измерений.

В разделе 9 рассмотрены возможные причины выявленного несоответствия модели звукового излучения струи данным акустических измерений в части сдвиговой компоненты шума, а также некоторые варианты решения этой проблемы. На примере модельной задачи об источнике в 2-мерном слое смешения показано, что малая модификация среднего течения, физически согласующаяся с представлением о самих звуковых источниках и об их возникновении, приводит к исчезновению сдвиговой компоненты в звуковом излучении. Таким образом, сдвиговая компонента шума оказывается чувствительной к локальной структуре поля завихренности на малых масштабах. Это означает, что несоответствие модели данным измерений может быть связано с некорректным приближением среднего поля при описании процесса излучения звука, и тогда решением проблемы мог бы быть учет локальной структуры поля завихренности в модели источников.

Рассмотрен также другой подход к решению проблемы сдвигового шума, который состоит в использовании акустических аналогий, в которых оператор распространения описывает неактивную среду, отвечающую только за распространение акустических возмущений, но не имеющую гидродинамических степеней свободы. При использовании таких акустических аналогий сдвиговый шум не возникает, и соответствие модели данным измерений достигается без искусственного исключения сдвиговой компоненты из суммарного звукового излучения.

2. АКУСТИЧЕСКАЯ АНАЛОГИЯ

Рассматривается акустическая аналогия, в которой все линейные по возмущениям члены включены в оператор распространения, а нелинейные члены трактуются как источник. Для описания процесса звукового излучения будем использовать уравнения Эйлера с условием изэнтропичности

где ${\mathbf{v}}$ – поле скорости, плотность ${{\rho }}$ и давление $p$ связаны соотношением $d{{\rho }} = \frac{1}{{{{с}^{2}}}}dp$, $c$ – скорость звука.

Представим основные переменные в виде суммы средних полей скорости, давления и плотности ${{{\mathbf{V}}}_{0}},{{\rho }_{0}},{{p}_{0}}$ и нестационарных возмущений ${\mathbf{v}}{\kern 1pt} ',\rho {\kern 1pt} {\text{'}},p{\kern 1pt} '$. Используя локально-однородное приближение для возмущений, будем пренебрегать неоднородностью среднего течения струи в осевом направлении. В соответствии с этим ${{p}_{0}} = {\text{const}}$, $\nabla {{{\mathbf{V}}}_{0}} = 0$. Будем также рассматривать случай изотермической струи, для которой средняя плотность постоянна, т.е. ${{{{\rho }}}_{0}} = {\text{const}}$. В этом случае из (2.1), (2.2) получим уравнения для нестационарных возмущений:

где ${{c}_{0}}$ – скорость звука среднего течения, ${{T}^{{ij}}} = {{{{\rho }}}_{0}}\left( {v{\kern 1pt} {{'}^{i}}v{\kern 1pt} {{'}^{j}} - \overline {v{\kern 1pt} {{'}^{i}}v{{{\kern 1pt} }^{{'j}}}} } \right)$ – нестационарная часть тензора напряжений Рейнольдса, ${\text{M}}$ – число Маха течения струи.

Уравнения (2.3)–(2.5) будем использовать как основные уравнения рассматриваемой акустической аналогии. При этом левые части уравнений (2.3), (2.4) описывают распространение возмущений, а правые части трактуются как источник. Далее будем опускать знак штриха при обозначении возмущений. Для струи со скоростью V = 120 м/с, акустические измерения которой используются для сравнения с моделью, величина ${{{\text{M}}}^{2}}$ мала и составляет около 0.12. На основании этого будем пренебрегать членами порядка $O\left( {{{{\text{M}}}^{2}}} \right)$ в правой части уравнений и описывать источник как квадрупольное поле.

3. ТОЧЕЧНЫЙ КВАДРУПОЛЬ В ДВУМЕРНОМ СЛОЕ СМЕШЕНИЯ

Прежде чем переходить к моделированию шума струи, рассмотрим особенности излучения звука источниками в сдвиговом течении на простом примере точечного квадруполя в двумерном слое смешения. Анализ сдвиговой компоненты излучения в этой простой задаче позволит понять проблемы, возникающие при моделировании шума струи на основе метода акустических аналогий.

Рассмотрим 2-мерный сдвиговый поток с х-компонентой средней скорости потока $\,{{V}_{0}}\left( y \right)$, где ось х направлена в направлении потока (рис. 1). Будем полагать, что слой смешения имеет постоянную завихренность ${{\Omega }_{0}}$ и занимает область $ - d < y < d$. Вне слоя смешения скорость потока ${{V}_{0}} = 0$ при $y > d$ и ${{V}_{0}} = {\text{const}}$ при $y < d$.

Рассматриваются линейные возмущения течения, которые возбуждаются точечным квадрупольным источником вида

где $\delta \left( {\mathbf{r}} \right) = \delta \left( x \right)\delta \left( y \right)$ – двумерная дельта-функция.

Возмущения описываются уравнениями (2.3)–(2.5). Применяя к этим уравнениям преобразование Фурье по времени и координате x и исключая возмущения скорости и плотности, получим уравнение для возмущений давления:

где $\bar {\omega } = \omega - \alpha \,{{V}_{0}}\left( y \right)$.

Ограничимся случаем низкоскоростного течения, ${\text{M}} \to 0$, и тонкого слоя смешения, $\alpha d \ll 1$. В этом случае решение уравнения (3.2) с условием излучения при $y > d$ имеет вид

где $\gamma = \sqrt {{{\alpha }^{2}} - {{k}^{2}}} $, $k = {\omega \mathord{\left/ {\vphantom {\omega {{{c}_{0}}}}} \right. \kern-0em} {{{c}_{0}}}}$. Применяя обратное преобразование Фурье по x и взяв интеграл методом перевала, получим в дальнем поле, $kr \gg 1$, где $r = \sqrt {{{x}^{2}} + {{y}^{2}}} $, $\theta = {\text{arccos}}\left( {{x \mathord{\left/ {\vphantom {x r}} \right. \kern-0em} r}} \right)$.

Полученное решение содержит в себе два слагаемых. Первое слагаемое совпадает с выражением для звукового поля квадрупольного источника в покоящейся среде и представляет собой собственное излучение источника. Второе слагаемое пропорционально завихренности сдвигового потока, в соответствии с чем определяется как сдвиговая компонента звукового излучения.

Отметим, что при уменьшении скорости потока сдвиговый член исчезает, если частота $f$ фиксирована, но при постоянном числе Струхаля ${\text{Sh}} = \frac{{f\,d}}{{{{V}_{0}}}}$ сдвиговое и собственное излучение имеют один порядок при сколь угодно малых скоростях течения. Эта особенность предельного перехода ${\text{M}} \to 0$ связана с различием в условиях излучения для квадруполя в покоящейся среде и в сдвиговом потоке. Источник, находящийся в сдвиговом потоке, не только сам непосредственно излучает звуковые волны, как это происходит в покоящейся среде, но помимо этого возбуждает в потоке возмущения завихренности, которые, в свою очередь, являются источником вторичного звукового излучения. Для того чтобы в этом убедиться, определим вклад возмущений завихренности в интеграл квадрупольного момента, определяющий звуковое излучение при ${\text{M}} \to 0$. Квадрупольный момент будем вычислять в соответствии с формулой Меринга, которая в двумерном случае имеет вид [48]

где ${\mathbf{\Omega }}{\kern 1pt} $ – возмущение завихренности. Для течений с малыми числами Маха интеграл (3.5) определяется в приближении несжимаемого течения. В этом случае возмущения завихренности находятся из уравнения Гельмгольца с источником в правой части где ${{f}^{i}} = \frac{{\partial {{T}^{{ij}}}}}{{\partial {{r}^{j}}}}$, ${{T}^{{ij}}}$ определяется выражением (3.1), возмущения скорости ${\mathbf{v}}$ выражаются через возмущения завихренности $\Omega {\kern 1pt} $ интегралом Био‑Савара.

Из (3.6) следует, что для слоя смешения с постоянной завихренностью возмущения завихренности локализованы на той линии тока, где расположен точечный источник, а также на краях слоя смешения, где среднее поле завихренности ${{\Omega }_{0}}$ имеет разрыв. Вычисляя возмущения завихренности из уравнения (3.6) и подставляя их в интеграл (3.5), получим вклад в квадрупольный момент возмущений завихренности на линии расположения источника, $y = 0$,

а также вклад возмущений завихренности на краях слоя смешения, $y = \pm \,d$,

Складывая (3.7) и (3.8), получим суммарный квадрупольный момент вихревых возмущений, создаваемых точечным квадрупольным источником,

Можно видеть, что интеграл квадрупольного момента (3.9) содержит два слагаемых, одно из которых соответствует точечному квадруполю (3.1) и определяет собственный шум источника, а другое возникает в результате взаимодействия источника со сдвиговым потоком.

Таким образом, звуковое излучение квадрупольного источника в сдвиговом потоке обладает характерной особенностью, которая состоит в появлении сдвиговой компоненты шума, амплитуда которой пропорциональна завихренности среднего течения. Причиной появления сдвиговой компоненты излучения является возбуждение источником вихревых возмущений в сдвиговом потоке. В разделе 8 мы увидим, что звуковое излучение струи, моделируемое на основе акустической аналогии, также содержит в себе сдвиговую составляющую, пропорциональную градиенту скорости в сдвиговом течении.

4. КОРРЕЛЯЦИОННЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНОГО ПОЛЯ ИСТОЧНИКОВ

Перейдем теперь к моделированию шума турбулентной струи с использованием линеаризованных уравнений Эйлера (2.3)–(2.5) в качестве оператора распространения возмущений и с квадрупольным источником, определяемым правой частью уравнения (2.3). Метод акустических аналогий предполагает описание источников звука как случайного поля с характеристиками, определяющими пространственные и временные масштабы турбулентных возмущений, отвечающих за излучение звука, а также их конвективную скорость. Эти представления позволили в прошлом, обобщая экспериментальные данные, получать общую эффективность излучения звука турбулентной струей в широком диапазоне скоростей от М = 0.5 до М = 4 [49]. С развитием вычислительных методов возник интерес в построении замкнутой полуэмпирической теории шума струи, в которой характеристики звукового излучения определяются пространственно-временной корреляционной функцией турбулентных пульсаций. Среди работ, посвященных моделированию излучения струи на языке корреляционных функций, необходимо, в первую очередь, отметить работу [13]. В этой работе для источников звука была предложена пространственно-временная корреляционная функция:

где ${{V}_{0}}$ – скорость конвекции звуковых источников, ${{\tau }_{0}}$ и ${{l}_{0}}$ – временной и пространственный масштабы корреляции, $x,y,z$ – декартовы координаты с осью z вдоль оси струи. Вид этой функции был выбран на основе имевшихся в то время измерений корреляций возмущений скорости и предположения об аналогии между характеристиками вторых и четвертых моментов поля скорости. Позднее это предположение было подтверждено непосредственными измерениями корреляционных функций для компонент тензора Рейнольдса [44]. В связи с успешностью подхода, предложенного в работе [13], корреляционные функции вида (4.1) неоднократно использовались в дальнейшем для моделирования источников шума в струе (см., например, [16, 17]).

Характерной особенностью корреляционной функции (4.1) является излом в форме “клюва” (разрыв производной) при ${{z}_{1}} = {{z}_{2}}$. Как показано в работе [38], именно эта особенность дает возможность получить широкополосный спектр акустического излучения турбулентной струи, что не удается сделать при использовании корреляционной функции, имеющей гладкую гауссовскую форму. Возникает вопрос о том, какая динамика источников звука может быть ответственна за эту особенность в корреляционной функции. В работе [45] было показано, что случайная переменная $\xi \left( {{\mathbf{r}},t} \right)$ с корреляционной функцией (4.1) может быть представлена как решение уравнения Ланжевена

где правая часть $\eta \left( {{\mathbf{r}},t} \right)$ представляет собой случайное поле с корреляционной функцией, имеющей простую гауссовскую форму

Таким образом, для описания поля источников вместо плотности источников $\xi \left( {{\mathbf{r}},t} \right)$ может быть выбрана альтернативная случайная переменная ${{\eta }}\left( {{\mathbf{r}},t} \right)$, что оказывается важным для анализа динамических процессов, лежащих в основе генерации аэродинамического шума. При малом пространственном масштабе ${{l}_{0}}$ поле ${{\eta }}\left( {{\mathbf{r}},t} \right)$ представляет собой пространственно-временной белый шум. Такое представление означает, что случайное поле звуковых источников с корреляционной функцией (4.1) можно трактовать как сумму некоррелированных элементарных процессов, каждый из которых представляет собой случайный “всплеск” возмущений с их последующей конвекцией и затуханием.

Аналогичное представление плотности источников $\xi $ через интенсивность их рождения ${{\eta }}$ было использовано в работе [17], где эти переменные были связаны более общим интегральным уравнением, описывающим различную динамику источников в зависимости от ядра интеграла. В частности, если эта динамика представляет собой простое затухание, то интегральное уравнение сводится к уравнению Ланжевена (4.2). Вместе с тем, использование более общего представления позволило провести в [17] сравнение различных вариантов динамики звуковых источников. В частности, было показано, что звуковое излучение определяется, в первую очередь, быстрым процессом рождения источников и слабо зависит от последующей, сравнительно более медленной динамики.

В настоящей работе с учетом квадрупольного характера звукового поля плотность источников описывается симметричным тензором второго ранга ${{T}^{{ij}}}\left( {{\mathbf{r}},t} \right)$ c нулевым следом, который в общем случае записывается в виде

где $D_{n}^{{ij}}$ – набор детерминированных линейно-независимых базисных квадрупольных полей, амплитуды ${{\xi }_{{\left( n \right)}}}\left( {{\mathbf{r}},t} \right)$ представляют собой случайные поля, удовлетворяющие уравнению Ланжевена где ${{{\mathbf{V}}}_{0}}$ – скорость конвекции источников, совпадающая со средней скоростью течения в точке их локализации, параметр $\varepsilon = \tau _{0}^{{ - 1}}$ характеризует скорость потери корреляции возмущений. Таким образом, при описании поля звуковых источников мы переходим от квадрупольного поля (4.4), характеризующего плотность источников, к полю характеризующему интенсивность рождения возмущений, ответственных за излучение звука.

В настоящей работе используется условие изотропности квадрупольного поля ${{Q}^{{ij}}}$, в соответствии с которым (см. Приложение А) будем предполагать, что поля ${{\eta }_{{\left( n \right)}}}\left( {{\mathbf{r}},t} \right)$ взаимно не коррелированы и имеют одинаковые характеристики, а базисные квадруполи $D_{n}^{{ij}}$ имеют вид (А2). Спектральную плотность полей ${{\eta }_{{\left( n \right)}}}\left( {{\mathbf{r}},t} \right)$ по аналогии с (4.3) запишем в виде

Предполагая пространственный масштаб корреляции ${{l}_{0}}$ малым, перепишем выражение (4.7) в виде

где $\delta \left( {\mathbf{r}} \right)$ – пространственная дельта-функция.

Выражения (4.4), (4.5), (4.8) определяют случайное поле квадрупольных источников в модели звукового излучения струи.

5. ФУНКЦИЯ ГРИНА

Найдем решение системы уравнений (2.3)–(2.5), правая часть которой определяется выражениями (4.4), (4.5), а интенсивность рождения источников имеет вид ${{\eta }_{{\left( n \right)}}} = \delta \left( {{\mathbf{r}} - {{{\mathbf{r}}}_{s}}} \right)\exp \left( { - i\omega t} \right)$. Поскольку такие решения будут использоваться в интеграле свертки при вычислении звукового поля, будем их называть функциями Грина ${{G}_{{\left( n \right)}}}\left( {{\mathbf{r}},{{{\mathbf{r}}}_{s}},\omega } \right)$ для n-ого базисного квадруполя.

При вычислении функций Грина будем использовать локально-однородное приближение. Это означает, что при вычислении звукового поля от точечного квадрупольного источника будем пренебрегать неоднородностью течения струи в осевом направлении, принимая локальные характеристики среднего поля в том сечении, где расположен источник. Однако, при вычислении звукового поля от всей струи будем вычислять интеграл по всей области источников, взяв в каждом поперечном сечении струи функцию Грина, вычисленную именно для этого сечения.

Определим цилиндрические координаты $\rho ,\varphi ,z$ с осью z, совпадающей с осью струи. Применяя к уравнениям (2.3)–(2.5) преобразование Фурье по φ и z и исключая из этих уравнений возмущения скорости и плотности, получим уравнение для возмущений давления

где $\bar {\omega } = \omega - \alpha \,{{V}_{0}}\left( \rho \right)$, ${{V}_{0}}\left( \rho \right)$ – z-компонента средней скорости. Источник в правой части уравнения (5.1) определяется из соотношений где $q\left( {{\mathbf{r}},\omega } \right) = {{\bar {\omega }}^{2}}\nabla \left( {\frac{1}{{{{{\bar {\omega }}}^{2}}}}{\mathbf{f}}} \right)$, декартовы компоненты ${{f}^{i}} = \frac{{\partial {{T}^{{ij}}}}}{{\partial {{r}^{j}}}}$.

Будем полагать, что ${{V}_{0}}\left( \rho \right) = {{V}_{{{\text{jet}}}}} = {\text{const}}$ при $\rho < {{\rho }_{1}}$, слой смешения с заданной переменной средней скоростью ${{V}_{0}}\left( \rho \right)$ находится в интервале ${{\rho }_{1}} < \rho < {{\rho }_{2}}$, ${{V}_{0}}\left( \rho \right) = 0$ при $\rho > {{\rho }_{2}}$. Предполагается, что источник находится внутри слоя смешения в точке с координатой $\rho = {{\rho }_{s}}$. Решение задачи находится из условий конечности в нуле, непрерывности на границах слоя смешения $\rho = {{\rho }_{1}},\;\rho = {{\rho }_{2}}$, условия излучения при $\rho \to \infty $ и условия ограниченности решения для исключения из решения волн неустойчивости.

Решение этой задачи для точечного квадрупольного источника вида ${{T}^{{ij}}} = D_{n}^{{ij}}\delta \left( {{\mathbf{r}} - {{{\mathbf{r}}}_{s}}} \right)\exp \left( { - i\omega t} \right)$ приведено в Приложении Б, где звуковое поле в области вне струи $\rho > {{\rho }_{2}}$ представлено в виде

где $H_{m}^{{\left( 1 \right)}}$ – функция Ганкеля порядка $m$, $\gamma = \sqrt {{{\alpha }^{2}} - {{k}^{2}}} $, $k = {{{\omega \mathord{\left/ {\vphantom {\omega c}} \right. \kern-0em} c}}_{0}}$, $n$ – номер базисного квадруполя, функции направленности $F_{{\left( n \right)\;m}}^{{}}$ для тонкого слоя смешения определены выражениями (Б10).

Для того чтобы перейти от решения (5.3) к функции Грина задачи, используем уравнение (4.5), связывающее плотность звуковых источников ${{\xi }_{{\left( n \right)}}}$ с интенсивностью их рождения ${{\eta }_{{\left( n \right)}}}$. Применяя к этому уравнению Фурье-преобразование по времени и координате z, получим

Из (5.4) следует, что Фурье-компоненты функции Грина связаны с (5.3) множителем ${{\left( { - i{{{\bar {\omega }}}_{s}} + \varepsilon } \right)}^{{ - 1}}}$, где ${{\bar {\omega }}_{s}} = \omega - \alpha \,{{V}_{0}}\left( {{{\rho }_{s}}} \right)$, т.е.

Используем обратное преобразование Фурье по z-координате:

В дальнем поле интеграл (5.6) вычисляется методом перевала:

где $r = \sqrt {{{\rho }^{2}} + {{{\left( {z - {{z}_{s}}} \right)}}^{2}}} $, $\theta = \arccos \left( {\frac{{z - {{z}_{s}}}}{r}} \right)$, ${{M}_{s}} = $ $ = {{{{{{V}_{0}}\left( {{{\rho }_{s}}} \right)} \mathord{\left/ {\vphantom {{{{V}_{0}}\left( {{{\rho }_{s}}} \right)} c}} \right. \kern-0em} c}}_{0}}$, ${{\tau }_{0}} = {{\varepsilon }^{{ - 1}}}$. Это выражение для функции Грина будет далее использоваться при вычислении дальнего звукового поля от квадрупольных источников в струе.

6. СПЕКТРАЛЬНАЯ ПЛОТНОСТЬ АЗИМУТАЛЬНЫХ ГАРМОНИК ЗВУКОВОГО ИЗЛУЧЕНИЯ

Звуковое поле, создаваемое гармоническим квадрупольным источником ${{Q}^{{ij}}}\left( {{\mathbf{r}},\omega } \right) = {{\eta }_{{\left( n \right)}}}\left( {{\mathbf{r}},\omega } \right)D_{n}^{{ij}}$, запишем через свертку плотности источников с функцией Грина

где ${{G}_{{\left( n \right)}}}\left( {{\mathbf{r}},{\mathbf{r}}{\kern 1pt} ',\omega } \right)$ – функция Грина для n-ого базисного квадруполя, определенная выражением (5.7). Соответственно, для случайного источника с взаимным спектром (4.8) взаимная спектральная плотность звукового излучения имеет вид

В осесимметричной струе пульсации должны описываться полями, инвариантными относительно вращения вокруг оси струи. В соответствии с этим спектральная плотность (4.8) не зависит от азимутального угла φ, т.е. $A\left( {{\mathbf{r}}{\kern 1pt} ',\omega } \right) = A\left( {\rho {\kern 1pt} ',z{\kern 1pt} ',\omega } \right)$. Кроме того, вследствие осевой симметрии функция Грина зависит только от разницы азимутальных углов ${{\varphi }_{1}} - \varphi {\kern 1pt} '$, а ее разложение в ряд Фурье имеет вид

Подставляя (6.3) в (6.2) и интегрируя по углу $\varphi {\kern 1pt} '$, получим:

где коэффициенты Фурье

Выражения (6.4), (6.5) определяют взаимный спектр звукового поля для каждого базисного квадруполя. С учетом взаимной некоррелированности амплитуд ${{\eta }_{{\left( n \right)}}}\left( {{\mathbf{r}},t} \right)$ взаимный спектр суммарного звукового поля от источника (4.6) имеет вид

где индекс n в скобках обозначает номер соответствующего базисного квадруполя, спектры ${{S}_{{p\;\left( n \right)\;m}}}$ находятся из интеграла (6.5).

В настоящей работе мы будем рассматривать автоспектры звукового поля, выражения для которых следуют из (6.5), (6.6) при ${{{\mathbf{r}}}_{1}} = {{{\mathbf{r}}}_{2}}$:

Подставляя функцию Грина (5.7) в (6.8), получим спектральную плотность азимутальных гармоник дальнего звукового поля

В настоящей работе рассматривается дальнее звуковое поле струи, которое имеет слабую чувствительность к пространственному распределению источников. С учетом этого сделаем некоторые упрощения модели, ограничив область локализации источников. Будем полагать, что источники расположены в конце начального участка в сечении с координатой ${{z}_{s}} = 6D$, где D – диаметр сопла, на окружности с координатой ${{\rho }_{s}}$, определяемой из условия ${{V}_{0}}\left( {{{\rho }_{s}}} \right) = 0.65{{V}_{{{\text{jet}}}}}$. В соответствии с этим для распределения мощности источников будем использовать выражение $A\left( {\rho ,z} \right) = {{A}_{0}}{{\Delta }_{\rho }}{{\Delta }_{z}}\delta \left( {\rho - {{\rho }_{s}}} \right)\delta \left( {z - {{z}_{s}}} \right)$, где ${{\Delta }_{\rho }},\;{{\Delta }_{z}}$ – величины реального разброса источников по радиальной и осевой координате. Тогда суммарная спектральная мощность источников в струе запишется в виде

Используя локальность распределения источников, проинтегрируем (6.9). В результате получим спектральную мощность m-ой азимутальной гармоники звукового излучения

где r и θ отсчитываются от конца начального участка струи. Выражение (6.11) дает направленности азимутальных гармоник звукового излучения струи и будет далее использоваться для сравнения с экспериментом.

Время потери корреляции в конце начального участка струи оценим, как ${{\tau }_{0}} \sim {D \mathord{\left/ {\vphantom {D {{{V}_{{{\text{jet}}}}}}}} \right. \kern-0em} {{{V}_{{{\text{jet}}}}}}}$ [50]. Из этой оценки следует, что член $\tau _{0}^{{ - 2}}{{\omega }^{{ - 2}}}$ в (6.9) является существенным при низких частотах ${\text{Sh}} < 0.2$, в то время как для более высоких частот им можно пренебречь.

7. ДАННЫЕ ИЗМЕРЕНИЙ АЗИМУТАЛЬНЫХ ГАРМОНИК В ЗВУКОВОМ ПОЛЕ СТРУИ

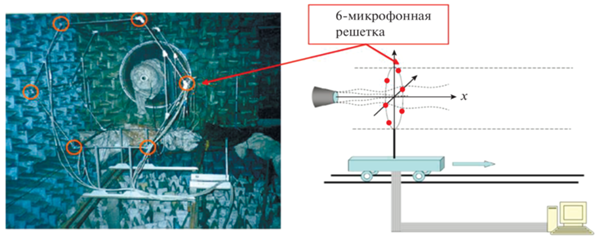
Используемые в настоящей работе данные акустических измерений были получены методом азимутальной декомпозиции ADT (Azimuthal Decomposition Technique). Этот экспериментальный метод был предложен в [47] специально для измерения азимутальных компонент звукового излучения аэродинамических источников шума. Схема эксперимента представлена на рис. 2. Метод основан на предварительном модальном разложении акустических сигналов на микрофонах до усреднения данных. Акустические сигналы на круговой решетке из 6 микрофонов представляются в виде ряда Фурье

где интегралы аппроксимируются суммой по 6 точкам расположения микрофонов. С использованием этих формул из результатов измерений оцениваются спектральные плотности коэффициентов ряда (7.1). Коэффициенты ряда (7.1) связаны с коэффициентами используемого в моделировании ряда Фурье $p\left( \varphi \right) = \sum\nolimits_{m = - \infty }^\infty {{{p}_{m}}\exp \left( {im\varphi } \right)} $ соотношениями ${{p}_{0}} = {{a}_{0}}$, ${{p}_{m}} = p_{{ - m}}^{*} = \frac{1}{2}\left( {{{a}_{m}} - i{{b}_{m}}} \right)$ при $m \ne 0$. Соответственно, для спектральных плотностей этих коэффициентов справедливы соотношения ${{S}_{{p\;m}}}\left( \omega \right) = \frac{1}{2}{{S}_{{а\;m}}}\left( \omega \right)$ при $m \ne 0$, ${{S}_{{p\;0}}}\left( \omega \right) = {{S}_{{а\;0}}}\left( \omega \right)$

В эксперименте [46] получены спектральные плотности азимутальных гармоник $m = 0,1,2$ для различных расстояний от решетки микрофонов до сопла. Характерные направленности гармоник для струи ${{V}_{{{\text{jet}}}}} = 120\;\;{{\text{м}} \mathord{\left/ {\vphantom {{\text{м}} {\text{с}}}} \right. \kern-0em} {\text{с}}}$ в диапазоне частот 800 < < f < 1050 Гц (число Струхаля Sh = 0.3 соответствует максимуму спектра звукового излучения струи) представлены на рис. 3. Можно видеть, что направленности азимутальных гармоник имеют сложную форму, необходимость предсказания которой дает хорошую базу для отбора приемлемых моделей звукового излучения струи.

8. СРАВНЕНИЕ МОДЕЛИ С ДАННЫМИ ЭКСПЕРИМЕНТА

Сравним направленности моделируемого звукового поля с данными эксперимента, приведенными в разделе 7. В рассматриваемом диапазоне частот 800 < f < 1050 Гц длина звуковой волны $\lambda \approx 0.4\;{\text{м}}$ много больше области, занимаемой источниками, размер которой равен диаметру сопла $D \approx 0.04\;{\text{м}}$. Это дает возможность ограничиться главными членами по малому параметру $k{{\rho }_{s}}$.

Рассмотрим, прежде всего, моделируемое звуковое поле в предельном случае ${{V}_{{{\text{jet}}}}} = 0$, т.е. без учета влияния потока. В этом случае выражение (6.11) соответствует полю точечного изотропного квадруполя в покоящейся среде, а главные члены по малому параметру $k{{\rho }_{s}}$ в выражениях (Б10) для безразмерных направленностей имеют вид:

Набор направленностей ${{F}_{{\left( n \right)m}}}$, представленный в (8.1), показывает, что при отсутствии течения каждый базисный квадруполь в главном приближении по параметру $k{{\rho }_{s}}$ отвечает за излучение только одной азимутальной гармоники. При этом квадруполь n = 1 излучает нулевую гармонику, квадруполи n = 2, 3 – первую гармонику, квадруполи n = 4, 5 – вторую гармонику.

Подставляя (8.1) в (6.11), получим направленности азимутальных гармоник звукового излучения. Сравнение результатов моделирования с данными измерений для струи ${{V}_{{{\text{jet}}}}} = 120\;{{\text{м}} \mathord{\left/ {\vphantom {{\text{м}} {\text{с}}}} \right. \kern-0em} {\text{с}}}$, представленное на рис. 4, показывает, что даже в простейшем варианте без учета влияния потока модель качественно отражает сложные формы направленности трех основных азимутальных гармоник. Отличие модели и эксперимента проявляется, прежде всего, в том, что в данных акустических измерений можно видеть усиление звука в направлении вниз по потоку, а в модели это усиление отсутствует, поскольку не учитываются эффекты конвекции источников и рефракции звука на среднем течении.

Рассмотрим далее влияние потока на моделируемое звуковое излучение. Это влияние имеет двоякий характер. Прежде всего, эффекты рефракции и конвекции приводят к изменению направленности звукового излучения. Кроме того, появляется дополнительная составляющая, пропорциональная градиенту средней скорости в слое смешения, которую мы так же, как в разделе 2, будем называть сдвиговой компонентой шума.

Используя выражение (6.11), вычислим вклады базисных квадруполей в азимутальные гармоники звукового излучения с учетом среднего течения струи со скоростью ${{V}_{{{\text{jet}}}}} = 120$ м/с. Для того чтобы оценить влияние рефракции, рассмотрим сначала “усеченную” модель, в которой учитываются вклады в излучение только тех членов ${{F}_{{\left( n \right)\;m}}}$, которые приведены в (8.1). С учетом влияния скорости струи выражения (8.1) преобразуются к виду:

где $\bar {\omega }_{{{\text{in}}}}^{{}} = \omega \left( {1 - {{M}_{{{\text{jet}}}}}\cos \theta } \right)$, $\bar {\omega }_{s}^{{}} = \omega \left( {1 - {{M}_{s}}\cos \theta } \right)$, ${{C}_{0}} = \frac{{\bar {\omega }_{{{\text{in}}}}^{2}}}{{\omega _{{}}^{2}}}$, ${{C}_{1}} = \frac{1}{2}\left( {\frac{{\bar {\omega }_{{{\text{in}}}}^{2}}}{{\omega _{{}}^{2}}} + 1} \right)$.

Подставляя (8.2) в (6.11), определим направленности азимутальных гармоник для “усеченной” модели. Сравнение результатов вычислений с данными измерений представлено на рис. 5. Можно видеть очень хорошее соответствие этой модели экспериментальным данным.

Однако, как отмечалось выше, влияние потока не ограничивается изменением формы направленностей ${{F}_{{\left( n \right)m}}}$, приведенных в (8.2). В звуковом излучении появляются также сдвиговые члены, которые нарушают соответствие базисных квадруполей азимутальным гармоникам. В частности, в азимутальную гармонику m = 0 вклад дает не только базисный квадруполь n = 1, но также и n = 2. Вычисляя из (Б10) соответствующую безразмерную направленность, получим

Эта составляющая отсутствует для источника в покоящейся среде, но дает соизмеримый с другими составляющими вклад в области частот $\omega \sim {{\Omega }_{0}}$. Более того, эта составляющая может доминировать в звуковом излучении в области низких частот, а также для источников, локализованных в начальном участке струи, где слой смешения является тонким. На рис. 6 представлены вклады базисных квадруполей n = 1 и n = 2 в гармонику m = 0, вычисленные из выражения (6.11) с величиной завихренности, соответствующей концу начального участка. Мы видим, что даже для этой области струи, где ширина слоя смешения достигает величины порядка диаметра сопла, базисный квадруполь n = 2 дает вклад в звуковое излучение, который существенно превышает экспериментальные значения. Для того чтобы привести модель в соответствие с экспериментом в отношении гармоники m = 0, необходимо было бы уменьшить амплитуду квадруполя n = 2, отказавшись от предположения об изотропности источника. Однако, в этом случае также уменьшится вклад этого квадруполя в гармонику m = 1, где в свою очередь возникнет рассогласование модели с экспериментом.

Из выражений (Б10) можно видеть, что сдвиговые члены, пропорциональные средней завихренности, возникают также и для квадруполей n = 4, 5, которые с учетом этих членов дают вклады не только в гармонику m = 2, как в случае отсутствия потока, но также и в гармонику m = 1.

Таким образом, в звуковом излучении струи можно выделить две составляющие, имеющие различную зависимость от параметров струи (скорости и градиента скорости). Эти две составляющие мы будем определять как собственный и сдвиговый шумы струи. К собственному шуму струи мы отнесем ту часть звукового излучения, на которую среднее течение оказывает влияние через эффекты рефракции и конвекции, но которая не включает в себя членов, пропорциональных градиенту средней скорости. К сдвиговому шуму мы отнесем составляющую, пропорциональную градиенту средней скорости в сдвиговом течении. Как было показано в разделе 2, появление сдвиговой компоненты шума связано с тем, что оператор распространения, описывающий линейные возмущения среднего течения, имеет не только акустическую степень свободы, отвечающую за распространение звуковых волн, но обладает также гидродинамическими (вихревыми) степенями свободы. Возбуждаемые источниками вихревые моды генерируют вторичное звуковое излучение, обладающее характеристиками сдвиговой компоненты шума.

Сравнение модели с данными акустических измерений позволяет сделать вывод о том, что модель способна описать сложную картину направленности азимутальных гармоник при простых предположениях о структуре звукового источника, но лишь в том случае, если в модели учитывается только собственный шум струи (рис. 5). При этом совпадение формы направленности трех главных гармоник служит подтверждением квадрупольного характера излучения. А совпадение по амплитудам трех азимутальных гармоник при выборе единственного амплитудного множителя подтверждает правильность гипотезы об изотропности источников. В то же время звуковое излучение, определяемое в рамках выбранной акустической аналогии, включает в себя не только собственную, но также сдвиговую компоненту, учет которой приводит к серьезному рассогласованию модели с данными измерений (рис. 6). Полученные результаты могут означать, что модель источников звука правильно учитывает основные факторы, влияющие на процесс генерации звука, но при этом ошибочно предсказывает наличие сдвиговой компоненты, которая, по-видимому, отсутствует в излучении реальной турбулентной струи.

9. ОБСУЖДЕНИЕ

Рассмотрим возможные причины выявленного несоответствия модели звукового излучения струи данным акустических измерений в части сдвиговой компоненты шума, а также некоторые варианты решения этой проблемы. Прежде всего, заметим, что модель излучения звука источниками в среднем завихренном течении является идеализацией реального процесса генерации звука в турбулентной струе. Картина среднего течения возникает только при усреднении реального турбулентного течения, в котором поле завихренности распадается на отдельные вихри так, что акустические возмущения распространяются на фоне нестационарного поля нелинейных гидродинамических пульсаций. Описание этого процесса является исключительно сложной задачей. Поэтому используется приближение среднего поля, в соответствии с которым распространение звуковых волн происходит на фоне среднего завихренного течения. Описанное приближение схематически изображено на рис. 7, где излучение звука мелкомасштабным вихрем происходит в одном случае на фоне “газа” других вихрей, а во втором случае на фоне среднего поля завихренности.

Замена поля турбулентных пульсаций средним течением является удобным приемом в задачах распространения звука. Однако активность среды, связанная с порождением первичным источником вихревых возмущений, делает эту процедуру неоднозначной. Проблема в том, что воздействие точечного источника на поле завихренности максимально в окрестности источника, так что вклад в сдвиговый шум от вихрей в малой окрестности источника имеет тот же порядок, что и вклад вихрей в остальной области течения. Поэтому сдвиговая компонента шума оказывается чувствительной к тому, как осуществляется предельный переход к среднему полю в окрестности источника.

Для того чтобы это показать, рассмотрим модификацию модельной задачи, рассмотренной в разделе 2. Сделаем поправку к среднему течению, предполагая, что в тонкой полосе $ - h < y < h$ в окрестности источника завихренность ${{\Omega }_{0}}\left( y \right)$ равна нулю, а в оставшейся части слоя смешения завихренность постоянна. Соответственно профиль средней скорости ${{V}_{0}}\left( y \right)$ изменится так, что в полосе $ - h < y < h$ поле скорости будет постоянным (рис. 8). Найдем решение такой задачи, а затем сделаем предельный переход $h \to 0$. Так же, как в задаче раздела 2, ограничимся случаем низкоскоростного течения и тонкого слоя смешения.

С учетом модификации среднего течения вместо (7.2) получим следующее уравнение для возмущений давления:

где $\pi \left( y \right) = 1$ при $ - h < y < h$, $\pi \left( y \right) = 0$ при $y < - h$ или $y > h$, $h \to 0$. Поправочный член $\pi \left( y \right)$, выражающий изменение поля средней скорости, обнуляет член уравнения с градиентом скорости в полосе $ - h < y < h$.

Модификация среднего течения в малой окрестности источника оказывает существенное влияние на величины разрывов давления и производной давления в точке расположения источника, которые определяют решение. В результате получим решение уравнения (9.1) при $y > d$, которое с учетом условия излучения имеет вид

где $\gamma = \sqrt {{{\alpha }^{2}} - {{k}^{2}}} $, $k = {\omega \mathord{\left/ {\vphantom {\omega {{{c}_{0}}}}} \right. \kern-0em} {{{c}_{0}}}}$. Применяя обратное преобразование Фурье по x и вычислив интеграл методом перевала, получим при $kr \gg 1$где $r = \sqrt {{{x}^{2}} + {{y}^{2}}} $, $\theta = {\text{arccos}}\left( {{x \mathord{\left/ {\vphantom {x r}} \right. \kern-0em} r}} \right)$.

Мы видим, что решение (9.3), в отличие от (3.4), не содержит сдвиговой компоненты. Таким образом, малая модификация среднего течения приводит к полному исчезновению сдвиговой компоненты звукового излучения. Это означает, что приближение среднего поля при моделировании мелкомасштабных источников звука в рассматриваемой системе является неоднозначным и зависит от локальной структуры поля завихренности на малых масштабах вихрей, ответственных за излучение.

Этот результат показывает, что несоответствие модели звукового излучения струи данным измерений может быть связано с некорректным приближением среднего поля для этой системы. В этом случае решением проблемы мог бы быть учет локальной структуры поля завихренности в турбулентной струе, которой позволил бы правильно учитывать условия излучения звука мелкомасштабной турбулентностью.

Возможен также другой подход к решению проблемы сдвигового шума при описании звукового излучения струи. Он состоит в том, чтобы использовать другую акустическую аналогию, такую, в которой оператор распространения описывает неактивную среду, отвечающую только за распространение акустических возмущений, но не имеющую гидродинамических степеней свободы. Такой подход к моделированию звукового излучения струи был реализован в [51], где было предложено новое для метода акустической аналогии разделение акустических и гидродинамических переменных. В этой аналогии оператор распространения для акустического потенциала представляет собой конвективное волновое уравнение, а все вихревые возмущения включены в источник, который выражается через плотность вихревого импульса. В этом случае сдвиговый шум в модели не возникает, и соответствие данным измерений достигается без искусственного исключения сдвиговой компоненты из суммарного звукового излучения с помощью локальной модификации среднего течения.

10. ЗАКЛЮЧЕНИЕ

В работе проведен анализ возможности моделирования звукового излучения турбулентной струи на основе использования акустической аналогии, в которой все линейные по возмущениям члены включены в оператор распространения, а нелинейные члены трактуются как источник. Примерами таких аналогий являются уравнение Лилли [26], акустическая аналогия Голдстейна [15] и др. При таком описании оператор распространения содержит вихревые моды, что приводит к появлению сдвиговой компоненты шума, возникающей из-за накачки вихревых возмущений источниками в правой части.

Показано, что в моделируемом звуковом излучении струи можно выделить две компоненты, определяемые как собственный и сдвиговый шум струи. Собственный шум струи определяется как та часть звукового излучения, на которую среднее течение оказывает влияние через эффекты рефракции звука и конвекции источников, но которая не включает в себя членов, пропорциональных градиенту средней скорости. К сдвиговому шуму отнесена та составляющая звукового излучения, которая пропорциональна градиенту средней скорости в сдвиговом течении. Появление сдвиговой компоненты шума связано с тем, что оператор распространения, описывающий линейные возмущения среднего течения, имеет не только акустическую степень свободы, отвечающую за распространение звуковых волн, но обладает также гидродинамическими (вихревыми) степенями свободы. Возбуждаемые источниками звука вихревые моды генерируют вторичное звуковое излучение, обладающее характеристиками сдвиговой компоненты шума.

Для тестирования модели используются данные измерений азимутальных гармоник звукового излучения струи. Сравнение модели с данными акустических измерений позволило сделать вывод о том, что она способна описать сложную картину направленности азимутальных гармоник при простых предположениях о структуре звукового источника, но лишь в том случае, если в модели учитывается только собственный шум струи. Это означает, что эффект сдвигового шума не отражает реальную физику процесса, а обусловлен особенностями моделирования и, в частности, разделением членов уравнений между оператором распространения и источником в рассматриваемой акустической аналогии.

Рассмотрены возможные причины несоответствия моделей, в которых появляется звуковое излучение со сдвиговой компонентой, реальному процессу генерации шума в турбулентной струе. Показано, что малая модификация среднего течения приводит к существенному изменению сдвиговой компоненты звукового излучения. Это означает, что используемое в модели приближение среднего поля, на фоне которого моделируются источники, является неоднозначным и зависит от локальной структуры поля завихренности на малых масштабах.

Рассмотрены возможные подходы к постановке задачи о звуковом излучении струи, которые позволили бы избежать появление сдвигового шума в модели. Одним из вариантов решения проблемы мог бы быть учет локальной структуры поля завихренности в турбулентной струе, который позволит правильно учитывать условия излучения звука мелкомасштабной турбулентностью. Другой вариант состоит в том, чтобы использовать акустическую аналогию, в которой оператор распространения описывает неактивную среду, т.е. отвечает только за распространение акустических возмущений, но не содержит в себе гидродинамических степеней свободы.

Полученные в работе результаты не только служат основой для моделирования шума струи, но также являются дополнительным вкладом в понимание механизмов излучающей части турбулентности в сдвиговых потоках.

Работа выполнена при поддержке гранта РНФ № 21-71-30016. Экспериментальная часть работы выполнена на базе УНУ “Заглушенная камера с потоком АК-2” ФАУ ЦАГИ, модернизируемой при поддержке Министерства науки и высшего образования Российской федерации по соглашению №075-11-2021-066.