Акустический журнал, 2022, T. 68, № 6, стр. 589-604
Акустические поля и радиационные силы, создаваемые стоячей поверхностной волной в слоистых вязких средах
В. А. Гусев a, b, *, Д. А. Жарков a, b, **
a Московский государственный университет имени М.В. Ломоносова, физический факультет,
ГСП-1
119991 Москва, Ленинские горы 1, стр. 2, Россия
b Институт физики Земли им. О.Ю. Шмидта РАН
123995 Москва, ул. Большая Грузинская 10, стр. 1, Россия
* E-mail: vgusev@bk.ru
** E-mail: denis.Zharkov2014@yandex.ru
Поступила в редакцию 24.06.2022
После доработки 17.07.2022
Принята к публикации 27.07.2022
- EDN: WLMQBM
- DOI: 10.31857/S0320791922060041
Аннотация
Рассчитаны поля, амплитудные и дисперсионные характеристики поверхностной акустической волны в системах: “вязкое жидкое полупространство–твердое полупространство” и “слой вязкой жидкости–упругое полупространство” с учетом сдвиговых компонент в жидкости. Рассчитано результирующее радиационное давление, возникающее в слое вязкой жидкости со стороны стоячей поверхностной волны и действующее на элемент ее объема за счет нелинейности уравнений движения в одномодовом и двухмодовом режимах. Показано, что наличие вязкости приводит к нарушению строгой периодичности и симметричности полей радиационных сил и акустических течений. Сдвиговые компоненты вызывают локализованные в узкой приграничной области, но значительные по величине силы радиационного давления. Возбуждение в системе нескольких волновых мод создает предпосылки для создания сложных пространственных распределений полей радиационных сил. Управляя частотой волны и толщиной слоя, можно добиться либо преобладания поля одной моды, либо сопоставимого вклада нескольких мод. В окрестности волнового резонанса преобладает основная мода.
ВВЕДЕНИЕ
В настоящее время активно развиваются методы управления перемещением различных объектов при помощи акустического поля. Отметим, например, работы, связанные с созданием “акустических ловушек” [1] и управлением ансамблями взвешенных в жидкости частиц [2, 3] и их левитацией [4, 5]. Возможность такого перемещения связана с формированием усредненной ненулевой силы радиационного давления акустического поля [6, 7].
Управление движением взвешенных частиц может применяться для создания искусственных материалов и сред с заранее заданными характеристиками. Среди подобных сред можно выделить метаматериалы, обладающие необычными свойствами, в частности, фотонные и фононные кристаллы. В этом случае требуется формирование упорядоченной пространственной структуры с заранее определенными параметрами. Эффективной методикой создания таких структур является осаждение наночастиц, взвешенных в коллоидном растворе, в процессе диссипативной самосборки [2, 3]. Важным достоинством этой методики является возможность ее расширения за счет приложения внешних полей, например, акустического или электромагнитного. Это позволяет управлять процессом формирования структуры непосредственно при его проведении и гибко менять параметры формируемой структуры. Проведенные ранее экспериментальные [8, 9] и теоретические [10, 11] исследования показали возможность и эффективность методики, основанной на создании стоячей поверхностной акустической волны (ПАВ) в жидком слое на упругой подложке.
Расчет поля ПАВ и радиационных сил, проведенный в [10], основывался на модели идеальной жидкости. Учет такого важного для растворов и взвесей [12, 13] фактора как вязкость был проведен только в приближенной постановке, что не позволило записать точное дисперсионное уравнение и учесть все возникающие эффекты, наиболее существенным среди которых является возникновение сдвиговых компонент поля в вязкой жидкости. В работе [11] получено выражение для дисперсионного уравнения и рассчитаны амплитуды радиационных сил, возникающих в слое вязкой жидкости. Было показано, что учет сдвиговых компонент акустического поля в вязкой жидкости существенно изменяет получаемую пространственную структуру радиационных сил. Кроме того, все расчеты были проведены только в одномодовом режиме. Однако уже при достаточно небольшой толщине слоя могут генерироваться высшие моды. В данной работе представлены расширенные результаты исследования характеристик ПАВ на границе вязкого слоя и упругого полупространства, в частности, анализируются многомодовый режим и особенности формирования акустических течений в данной системе при учете вязкости.
УРАВНЕНИЯ ДЛЯ АКУСТИЧЕСКОГО ПОЛЯ
Вывод уравнений для компонент акустического поля ПАВ в целом стандартен [14] и отличается, главным образом, учетом сдвиговых компонент в вязкой жидкости. Тем не менее, с методической точки зрения целесообразно кратко привести этот вывод.
Акустическое поле в слое вязкой жидкости будем описывать линеаризованной системой уравнений Навье–Стокса, непрерывности и состояния:
(1)
$\begin{gathered} {{{{\rho }}}_{0}}\frac{{\partial {\mathbf{u}}}}{{\partial t}} = - \nabla p{\kern 1pt} '\,\, + {{\eta }}\Delta {\mathbf{u}} + \left( {{{\xi }} + \frac{{{\eta }}}{3}} \right){\text{grad}}~{\text{div}}{\mathbf{u}}, \\ ~~\frac{{\partial {{\rho }}{\kern 1pt} {\text{'}}}}{{\partial t}} + {{{{\rho }}}_{0}}{\text{div}}{\mathbf{u}} = 0,\,\,\,\,~p{\kern 1pt} ' = {{\rho }}{\kern 1pt} {\text{'}}c_{0}^{2}. \\ \end{gathered} $Здесь u – колебательная скорость частиц жидкости, $p{\kern 1pt} '$ – акустическое давление, ${{{{\rho }}}_{0}}$ и ${{\rho }}{\kern 1pt} {\text{'}}$ – равновесная плотность жидкости и ее акустическое приращение, ${{c}_{0}}$ – скорость звука в жидкости, ξ и  – коэффициенты объемной и сдвиговой вязкости соответственно, t – время, Δ – лапласиан.
– коэффициенты объемной и сдвиговой вязкости соответственно, t – время, Δ – лапласиан.
Для расчета поля ПАВ достаточно рассматриваемого линейного приближения. Это связано с тем, что радиационное давление является квадратичной величиной по акустическому полю. Следовательно, учет нелинейных поправок к полю волны даст для радиационного давления члены, уже кубичные по полю. Их учет, вообще говоря, выходит за рамки точности используемой модели. Тем не менее, некоторые выводы, касающиеся нелинейных эффектов, будут приведены ниже.
Введем теперь скалярный φ и векторный A потенциалы колебательной скорости в соответствии с представлением ${\mathbf{u}} = \nabla \varphi + {\text{rot}}{\mathbf{A}}$. Подставляя это выражение в систему (1) и применяя поочередно операции дивергенции и ротора, получим уравнения для потенциалов:
(2)
$~\frac{{{{\partial }^{2}}\varphi }}{{\partial {{t}^{2}}}} - c_{0}^{2}\Delta \varphi = \frac{b}{{{{\rho }_{0}}}}\Delta \frac{{\partial \varphi }}{{\partial t}},\,\,\,\,b = \xi + \frac{4}{3}\eta ,$Уравнение (2) для потенциальной компоненты имеет вид волнового уравнения с затуханием, а для сдвиговой компоненты (3) – уравнения диффузии.
Далее будем рассматривать слоистую структуру, состоящую из упругого полупространства при z ≥ 0 и слоя вязкой жидкости при –h < z < 0 (рис. 1). При этом ось z направлена вертикально вниз, а все границы раздела строго горизонтальны и параллельны оси х. Считаем, что при –∞ < z < –h находится вакуум. В этой системе в горизонтальном направлении могут распространяться ПАВ, локализованные вблизи границы раздела вязкого слоя и упругого полупространства при z = 0. Ограничимся далее рассмотрением двумерной задачи.
С точки зрения практических приложений (формирование упорядоченных структур [2, 3, 8–11]) наибольший интерес представляют периодические поля, создаваемые стоячими ПАВ. Для их расчета удобно сначала найти поле одной бегущей, например, вправо ПАВ. Затем, формируя две бегущие навстречу друг другу ПАВ, можно образовать стоячую ПАВ с периодической пространственной структурой. Необходимо отметить, что при теоретическом анализе бегущие волны рассматриваются на всем бесконечном интервале –∞ < x < ∞. При этом затухающие волны формально будут обладать бесконечной амплитудой в точке возникновения. При физической реализации это означает, что волны создаются двумя излучателями, находящимися на некотором расстоянии справа и слева от центра симметрии.
Решение уравнений (2)–(3) будем искать в виде гармонической бегущей вдоль оси x ПАВ с частотой ω и волновым числом k = ω/c, где c – искомая скорость поверхностной волны. Подставляя в (2) решение вида ${{\varphi }} = B\left( z \right){{e}^{{ - i\left( {{{\omega }}t - kx} \right)}}}$, для функции $B\left( z \right)$, описывающей вертикальную структуру поля в жидком слое, получим:
(4)
$\frac{{{{\partial }^{2}}B}}{{\partial {{z}^{2}}}} + {{r}^{2}}B = 0,~\,\,\,\,~~{{r}^{2}} = \frac{{k_{0}^{2} - {{k}^{2}} + \frac{{i{{\omega }}b}}{{{{{{\rho }}}_{{\text{0}}}}c_{0}^{2}}}{{k}^{2}}}}{{1 - \frac{{i{{\omega }}b}}{{{{{{\rho }}}_{{\text{0}}}}c_{0}^{2}}}}}.$Здесь k0 = ω/c0 – волновое число в жидкости. Знак в уравнении (4) выбран так, чтобы получить решения для ограниченного слоя в виде бегущих волн. Для вязкого полупространства надо знак “+” в уравнении (4) заменить на “–” для получения экспоненциально затухающего на бесконечности решения. Это эквивалентно замене r → r* = ir.
Векторное уравнение (3) для потенциала A в рассматриваемом двумерном случае упрощается и становится скалярным, поскольку при ${{u}_{y}} = 0$ и отсутствии зависимости от координаты y единственной отличной от нуля компонентой векторного потенциала будет ${{A}_{y}} \equiv A$, т.е. ${\mathbf{A}} = \left\{ {0,{\text{A}},0} \right\}$. Отыскивая решение уравнения (3) вида $A = C\left( z \right){{e}^{{ - i\left( {{{\omega }}t - kx} \right)}}}$, для функции $C\left( z \right)$ получим:
(5)
$\frac{{{{\partial }^{2}}C}}{{\partial {{z}^{2}}}} + {{\kappa }^{2}}C = 0,\,\,\,\,{{\kappa }^{2}} = \frac{{i{{\omega }}{{{{\rho }}}_{{\text{0}}}}}}{{{\eta }}} - {{k}^{2}}.$В уравнении (5), как и в уравнении (4), знак “+” выбран так, чтобы в слое получить решения в виде бегущих волн. В случае вязкого полупространства необходимо заменить в уравнении (5) “+” на “–” и κ на κ* = iκ.
В упругом полупространстве поле смещений
также описывается скалярным Φ и векторным ${\mathbf{\Psi }}$ потенциалами, подчиняющимися волновым уравнениям [11]. Ограниченные на бесконечности решения этих уравнений имеют вид:
(6)
$\begin{gathered} \Phi = {{\Phi }_{0}}{{e}^{{ - qz}}}{{e}^{{ - i\left( {\omega t - kx} \right)}}},~\,\,\,\,\Psi = {{\Psi }_{0}}{{e}^{{ - sz}}}{{e}^{{ - i\left( {\omega t - kx} \right)}}},~ \\ q~ = \sqrt {{{k}^{2}} - k_{l}^{2}} ,\,\,\,\,~~s = \sqrt {{{k}^{2}} - k_{t}^{2}} . \\ \end{gathered} $Здесь введены волновые числа ${{k}_{l}} = \frac{{{\omega }}}{{{{c}_{l}}}}$ – для продольных и ${{k}_{t}} = \frac{{{\omega }}}{{{{c}_{t}}}}$ – для поперечных волн.
На границах раздела сред необходимо добавить условия сопряжения акустических полей. На границе вязкий слой–упругое полупространство при z = 0 ставятся четыре условия:
– равенство вертикальных смещений:
(7)
${{\left. W \right|}_{{z = 0}}} = {{\left. { - \frac{{{{u}_{z}}}}{{i{{\omega }}}}} \right|}_{{z = 0}}};$– равенство касательных смещений:
(8)
${{\left. U \right|}_{{z = 0}}} = {{\left. { - \frac{{{{u}_{x}}}}{{i{{\omega }}}}} \right|}_{{z = 0}}};$– равенство нормальных напряжений:
(9)
${{\left. {{{\sigma }_{{zz}}}} \right|}_{{z = 0}}} = - {{\left. {p{\kern 1pt} '} \right|}_{{z = 0}}} + {{\left. {\sigma _{{zz}}^{'}} \right|}_{{z = 0}}};$– равенство касательных напряжений:
(10)
${{\left. {{{\sigma }_{{xz}}}} \right|}_{{z = 0}}} = {{\left. {\sigma _{{xz}}^{'}} \right|}_{{z = 0}}}.$На свободной границе вязкого слоя z = –h ставятся два условия:
– равенство нулю нормального напряжения:
(11)
$ - {{\left. {p{\kern 1pt} '} \right|}_{{z = - h}}} + {{\left. {\sigma _{{zz}}^{'}} \right|}_{{z = - h}}} = 0;$– равенство нулю касательного напряжения:
Здесь σ и σ' – тензор напряжений в упругом полупространстве и тензор вязких напряжений в жидкости соответственно [15].
ПАВ НА ГРАНИЦЕ ВЯЗКОГО ЖИДКОГО И УПРУГОГО ПОЛУПРОСТРАНСТВ
Для того чтобы наглядно разобраться, какой вклад в полное поле вносит учет вязкости, рассмотрим вначале более простую задачу – ПАВ на границе вязкого жидкого и упругого полупространств. Пусть вязкая жидкость заполняет полупространство $z \leqslant 0$. Тогда локализованные около границы раздела сред решения уравнений (4) и (5) для скалярного и векторного потенциалов соответственно имеют вид:
(13)
${{\varphi }} = {{B}_{1}}{{e}^{{r*z}}}{{e}^{{ - i\left( {{{\omega }}t - kx} \right)}}},\,\,\,\,A = {{C}_{1}}{{e}^{{\kappa {\text{*}}z}}}{{e}^{{ - i\left( {{{\omega }}t - kx} \right)}}}.$Подставляя выражения (13) в граничные условия (7)–(10), получаем дисперсионное уравнение, из которого находится скорость c:
(14)
$\left| {\begin{array}{*{20}{c}} { - \frac{{ir}}{{{\omega }}}}&{\frac{k}{{{\omega }}}}&{ - q}&{ik} \\ {\frac{k}{{{\omega }}}}&{\frac{{i\kappa }}{{{\omega }}}}&{ik}&s \\ {{{\eta (}}{{\kappa }^{2}}\, - \,{{k}^{2}})}&{ - 2i{{\eta }}k\kappa }&{ - {{\mu }}({{s}^{2}}\, + \,{{k}^{2}})}&{2i{{\mu }}ks} \\ {2i{{\eta }}kr}&{ - {{\eta (}}{{\kappa }^{2}}\, + \,{{k}^{2}})}&{2i{{\mu }}kq}&{{{\mu }}({{s}^{2}}\, + \,{{k}^{2}})} \end{array}} \right|\, = \,0.$В случае вязкой жидкости дисперсионное уравнение приобретает комплексные коэффициенты. Это означает, что и его решение становится комплексным, т.е. $c = {{c}_{r}} + i{{c}_{i}}$, где мнимая часть интерпретируется как затухание волны. Следует отметить, что истинные значения скорости $c{\kern 1pt} '$ и коэффициента затухания ${{\gamma }}$ находятся как реальная и мнимая части волнового числа
и равны соответственно
Видно, что при $\left| {{{c}_{i}}} \right| \ll \,\,~{{c}_{r}}~$ истинная скорость ПАВ близка к ${{c}_{r}}$, а коэффициент затухания пропорционален ${{c}_{i}}$. Учитывая это, а так же то, что во все дальнейшие выражения входят величины ${{c}_{r}}~\,\,{\text{и}}\,\,~{{c}_{i}}$, будем использовать именно их.
Интересно разобраться, как происходит в дисперсионном уравнении предельный переход от вязкой жидкости к идеальной при η → 0. С физической точки зрения этот переход интересен тем, что меняются граничные условия, в частности, необходимо отбросить условие равенства касательных смещений. В пределе η → 0 не все слагаемые, содержащие η, стремятся к нулю; например, волновое число κ (5), наоборот, стремится к бесконечности. Тогда определитель (14) содержит слагаемые разного порядка относительно волнового числа κ. Обратим внимание, что в определителе (14) второй столбец соответствует сдвиговой компоненте в жидкости. При этом вторая строка соответствует условию равенства касательных смещений, которое отсутствует в случае идеальной жидкости. Распишем определитель (14) по минорам второго столбца:
(15)
$\begin{gathered} \frac{k}{{{\omega }}}\left| {\begin{array}{*{20}{c}} {\frac{k}{{{\omega }}}}&{ik}&s \\ {{{\eta (}}{{\kappa }^{2}} - {{k}^{2}})}&{ - {{\mu }}({{s}^{2}} + {{k}^{2}})}&{2i{{\mu }}ks} \\ {2i{{\eta }}kr}&{2i{{\mu }}kq}&{{{\mu }}({{s}^{2}} + {{k}^{2}})} \end{array}} \right| + \\ + \,\,\frac{{i\kappa }}{{{\omega }}}\left| {\begin{array}{*{20}{c}} { - \frac{{ir}}{{{\omega }}}}&{ - q}&{ik} \\ {{{\eta (}}{{\kappa }^{2}} - {{k}^{2}})}&{ - {{\mu }}({{s}^{2}} + {{k}^{2}})}&{2i{{\mu }}ks} \\ {2i{{\eta }}kr}&{2i{{\mu }}kq}&{{{\mu }}({{s}^{2}} + {{k}^{2}})} \end{array}} \right| \\ - \,\,2i{{\eta }}k\kappa \left| {\begin{array}{*{20}{c}} { - \frac{{ir}}{{{\omega }}}}&{ - q}&{ik} \\ {\frac{k}{{{\omega }}}}&{ik}&s \\ {2i{{\eta }}kr}&{2i{{\mu }}kq}&{2i{{\mu }}kq} \end{array}} \right| - \\ - \,\,{{\eta (}}{{\kappa }^{2}} + {{k}^{2}})\left| {\begin{array}{*{20}{c}} { - \frac{{ir}}{{{\omega }}}}&{ - q}&{ik} \\ {\frac{k}{{{\omega }}}}&{ik}&s \\ {{{\eta (}}{{\kappa }^{2}} - {{k}^{2}})}&{ - {{\mu }}({{s}^{2}} + {{k}^{2}})}&{2i{{\mu }}ks} \end{array}} \right| = 0. \\ \end{gathered} $Легко видеть, что самым старшим членом при η → 0 является второе слагаемое со множителем iκ/ω, причем содержащийся здесь минор как раз является дисперсионным уравнением для случая полупространства идеальной жидкости. Остальные слагаемые в (15) имеют меньший порядок и в пределе η → 0 выпадают. Таким образом, основной вклад при η → 0 вносит элемент определителя, стоящий на пересечении второго столбца и второй строки, которые должны исчезнуть при переходе к идеальной жидкости. Это позволяет получить приближенное выражение для скорости ПАВ при малой вязкости. Для этого представим решение дисперсионного уравнения (14) в виде $c = {{c}_{{00}}} + {{c}_{1}}$, где ${{c}_{{00}}}$ – решение в отсутствие вязкости при η = 0, ${{c}_{1}}~\sim ~\,\,{{\eta }}$ – малая поправка. Для нахождения поправки ${{c}_{1}}$ умножим уравнение (14) на величину $a = \sqrt {{\eta }} $ и соберем слагаемые с одинаковыми степенями $a$: ${{a}^{0}}{\text{de}}{{{\text{t}}}_{0}} + ~\,\,{{a}^{1}}{\text{de}}{{{\text{t}}}_{1}} = 0$, где det0,1 – слагаемые определителя, пропорциональные $a$0 и $a$1 соответственно. Более высокими порядками $a$ пренебрежем. Тогда в представлении (15) третьим слагаемым можно пренебречь. Далее, раскладывая оставшиеся слагаемые в ряд Тейлора вблизи ${{c}_{{00}}}$ и оставляя слагаемые порядка a1, получим:
Так как ${\text{de}}{{{\text{t}}}_{0}}\left( {{{c}_{{00}}}} \right) = 0$ по определению, то поправка к скорости определяется выражением
(16)
${{c}_{1}} = - \frac{{{{a}^{1}}{\text{de}}{{{\text{t}}}_{1}}\left( {{{c}_{{00}}}} \right)}}{{{\text{det}}_{0}^{'}\left( {{{c}_{{00}}}} \right)}}.$На рис. 2 представлено сравнение зависимостей ${{c}_{r}}$ и ${{c}_{i}}$ от частоты, полученных численно на основе точного уравнения (14) и на основе приближенного аналитического выражения (16). Расчеты проводились для двух жидкостей – слабовязкой воды и сильновязкого глицерина. Для воды задавались следующие значения: плотность ${{{{\rho }}}_{0}} = 1000~$ кг/м3, скорость звука с0 = 1500 м/с, коэффициенты вязкости η = 0.0011 Па с, ξ = 0.003 Па с, b = 0.0045 Па с; для глицерина: ${{{{\rho }}}_{0}} = 1260~$ кг/м3, с0 = 1900 м/с, η = 1.1 Па с, ξ = 3 Па с, b = 4.5 Па с. В качестве твердого тела рассматривался материал, близкий к граниту, с параметрами: ${{\rho }} = 2210$ кг/м3сl = 5570 м/с, сt = 3515 м/с. Во всех случаях задавалась частота волны 1 кГц. Видно, что приближенное выражение (16) хорошо описывает изменение комплексной скорости, особенно ее реальной части ${{c}_{r}}$. Для мнимой части ${{c}_{i}}$ есть хорошее совпадение в области низких частот, однако на высоких частотах начинается расхождение, вызванное усилением роли вязкости.
Рис. 2.
Зависимости (а, в) – реальной ${{c}_{r}}$ и (б, г) – мнимой ${{c}_{i}}$ частей скорости c от частоты; (а, б) – вода, (в, г) – глицерин. Точки – численное решение уравнения (14), сплошная линия – приближенное решение (16).

Согласно выражениям (13) акустические поля в жидкости экспоненциально убывают при удалении от границы сред, причем характерный размер области локализации вдоль оси z определяется выражениями 1/Re(r*) и 1/Re(κ*) для скалярного и векторного потенциалов соответственно. На рис. 3 представлены зависимости размера области локализации сдвиговых компонент от частоты в логарифмическом масштабе для воды (синяя кривая) и глицерина (красная кривая). На низких частотах область локализации сдвиговой компоненты увеличивается, причем у глицерина она в несколько раз больше, чем у воды. При частоте 1 кГц волновая толщина fZ/c0 области локализации векторного потенциала для воды составляет 10–4, для глицерина – 0.002, а скалярного потенциала для воды – 12.43, для глицерина – 4.96.
Рис. 3.
Зависимость глубины локализации сдвиговой компоненты от частоты для воды (синяя линия) и глицерина (красная линия) в логарифмическом масштабе; размерный множитель f0 = 1 Гц. Точки – численное решение уравнения (14), сплошная линия – приближенное решение (16).

Как видно из рис. 3, даже для очень вязкой жидкости – глицерина – глубина локализации сдвиговой компоненты оказывается порядка миллиметра. Таким образом, можно ожидать, что вдали от границы раздела роль сдвиговых компонент будет несущественна. Однако в приграничном слое, особенно в случае растворов и взвесей с большой эффективной вязкостью, необходимо учитывать поле сдвиговых компонент.
Сравним теперь амплитуды различных составляющих акустического поля. На рис. 4 представлена зависимость амплитуды векторного потенциала от частоты по отношению к амплитуде сдвиговой компоненты в твердом теле для воды. Она монотонно возрастает с увеличением частоты. Интересно отметить, что на высоких частотах значения амплитуды векторного потенциала в вязкой жидкости превосходят значения амплитуд сдвиговой компоненты в твердом теле на несколько порядков. Согласно проведенным расчетам амплитуда скалярного потенциала еще на порядок больше, чем амплитуда векторного потенциала и также монотонно возрастает с частотой. Интересно также отметить, что амплитуда скалярного потенциала больше для воды, т.е. убывает с ростом вязкости. Амплитуда векторного потенциала, наоборот, больше для глицерина, т.е. возрастает с ростом вязкости. Таким образом, при увеличении вязкости жидкости амплитуда и, соответственно, энергия сдвиговых компонент возрастает.
Рис. 4.
Зависимость от частоты (а) – амплитуды скалярного потенциала B = B1/Ψ0 и (б) – векторного потенциала C = C1/Ψ0 относительно амплитуды векторного потенциала в твердом теле Ψ0 для воды (синяя линия) и глицерина (красная линия). Точки – амплитуды, рассчитанные с использованием численного решения уравнения (14), сплошная линия – приближенного решения (16).

ПАВ НА ГРАНИЦЕ СЛОЯ ВЯЗКОЙ ЖИДКОСТИ И УПРУГОГО ПОЛУПРОСТРАНСТВА
В случае ограниченного по вертикали слоя вязкой жидкости решение уравнений (5) и (6) для бегущей ПАВ задается в виде суммы двух волн:
(17)
$\begin{gathered} {{\varphi }} = \left( {{{B}_{1}}{{e}^{{ - irz}}} + {{B}_{2}}{{e}^{{irz}}}} \right){{e}^{{ - i\left( {{{\omega }}t - kx} \right)}}},~ \\ A = \left( {{{C}_{1}}{{e}^{{ - irz}}} + {{C}_{2}}{{e}^{{irz}}}} \right){{e}^{{ - i\left( {{{\omega }}t - kx} \right)}}}, \\ \end{gathered} $Дисперсионное уравнение и соотношения между амплитудами компонент поля определяются после подстановки решений (17) в граничные условия (7)–(12). Дисперсионное уравнение приводится к виду $\det \Delta \left( k \right) = 0$, матрица $\Delta \left( k \right)$ которого имеет вид [16]:
(18)
$\Delta (k) = \left( {\begin{array}{*{20}{c}} {{{\eta }}({{\kappa }^{2}} - {{k}^{2}}){{e}^{{irh}}}}&{{{\eta }}({{\kappa }^{2}} - {{k}^{2}}){{e}^{{ - irh}}}}&{2{{\eta }}\kappa k{{e}^{{i\kappa h}}}}&{ - 2{{\eta }}\kappa k{{e}^{{i{{\kappa }}h}}}}&0&0 \\ {2{{\eta }}rk{{e}^{{irh}}}}&{ - 2{{\eta }}rk{{e}^{{ - irh}}}}&{{{\eta }}({{\kappa }^{2}} - {{k}^{2}}){{e}^{{i\kappa h}}}}&{{{\eta }}({{\kappa }^{2}} - {{k}^{2}}){{e}^{{ - i\kappa h}}}}&0&0 \\ {\frac{r}{{{\omega }}}}&{ - \frac{r}{{{\omega }}}}&{ - \frac{k}{{{\omega }}}}&{ - \frac{k}{{{\omega }}}}&q&{ - ik} \\ {\frac{k}{{{\omega }}}}&{\frac{k}{{{\omega }}}}&{\frac{\kappa }{{{\omega }}}}&{ - \frac{\kappa }{{{\omega }}}}&{ - ik}&s \\ {{{\eta (}}{{\kappa }^{2}} - {{k}^{2}})}&{{{\eta (}}{{\kappa }^{2}} - {{k}^{2}})}&{2{{\eta }}\kappa k}&{ - 2{{\eta }}\kappa k}&{ - {{\mu }}({{k}^{2}} + {{s}^{2}})}&{2i{{\mu }}ks} \\ {2{{\eta \kappa }}k}&{ - 2{{\eta }}\kappa k}&{{{\eta (}}{{\kappa }^{2}} - {{k}^{2}})}&{{{\eta (}}{{\kappa }^{2}} - {{k}^{2}})}&{2i{{\mu }}kq}&{{{\mu }}({{k}^{2}} + {{s}^{2}})} \end{array}} \right).$Как и в предыдущем случае, решение дисперсионного уравнения с матрицей (18) является комплексным, $c = {{c}_{r}} + i{{c}_{i}}$. На рис. 5 представлены дисперсионные кривые зависимости величины ${{c}_{R}}$ от волновой толщины слоя H = fh/c0, где c0/f = λ0 – длина волны в безграничной жидкости. При расчетах использовались те же параметры, что и на рис. 2–4. На рис. 5 сплошными линиями изображены дисперсионные кривые в отсутствие вязкости, точками – расчеты при учете вязкости. Сопоставление этих зависимостей показывает, что в масштабе рисунка различие практически незаметно. Таким образом, в случае слоя значительное изменение скорости ПАВ происходит при изменении толщины слоя; при этом изменение скорости, обусловленное вязкостью, оказывается малозаметным. В то же время основная часть затухания, как показано в работах [16, 17], связана именно с диссипацией сдвиговых компонент.
Рис. 5.
Зависимость скорости ${{c}_{r}}$ ПАВ в слое от частоты для воды (красные линии) и глицерина (синие линии). Точки – решение с учетом вязкости, сплошная линия – без учета вязкости. Цифры 1–4 обозначают номера мод. Штриховой линией отмечена скорость звука в воде.

Из рис. 5 видно, что существует фундаментальная мода 1, скорость которой при малой толщине стремится к скорости рэлеевской волны на границе упругого полупространства и вакуума, а при большой толщине – к скорости волны Стоунли на границе упругого и жидкого полупространств. Высшие моды 2, 3 и т.д. существуют только в случае жидкого слоя конечной толщины. В частности, в случае воды при толщине слоя H = = 0.07 (h = 0.1 м) существует одна мода ПАВ со скоростью c = 3128 м/с. Для H = 0.3 (h = 0.5 м) существуют две моды со скоростями c1 = 1994.68 м/с и c2 = 3454.13 м/с соответственно. Данные расчетов для воды (толщина слоя H = 0.3 (h = 0.5 м)) и глицерина (толщина слоя H = 0.4 (h = 0.75 м)) приведены в табл. 1.
Таблица 1.
Параметры ПАВ в двухмодовом режиме для слоя воды c волновой толщиной H = 0.3 и слоя глицерина с волновой толщиной H = 0.4. Частота 1 кГц
| Вода, H = 0.3 | Глицерин, H = 0.4 | |||
|---|---|---|---|---|
| первая мода | вторая мода | первая мода | вторая мода | |
| Скорость cr, м/с | 1994.68 | 3454.13 | 2116.70 | 3457.81 |
| Длина волны, м | 2 | 3.45 | 2.2 | 3.46 |
| Затухание (мнимая часть скорости ci, м/с) |
0.000018 | 0.000008 | 0.0062 | 0.0034 |
| Амплитуда скалярного потенциала, отн. Ψ0 |
3051.70 | 2354.39 | 2531.26 | 1819.97 |
| Амплитуда векторного потенциала, отн. Ψ0 |
0.23 | 0.13 | 3.10 | 3.18 |
Далее, используя формулы Крамера, для двухмодового режима были рассчитаны амплитуды скалярного и векторного потенциалов по отношению к амплитуде векторного потенциала ${{{{\Psi }}}_{0}}$ в упругом полупространстве. Данные представлены в табл. 1. Из таблицы видно, что на частоте 1 кГц амплитуда векторного потенциала мала по сравнению с амплитудой скалярного потенциала. Сравнение данных для воды и глицерина показывает, что при увеличении вязкости роль сдвиговой компоненты закономерно растет. Кроме того, при увеличении частоты отношение амплитуд векторного и скалярного потенциалов также заметно возрастает аналогично зависимостям на рис. 4.
Для двухмодового режима оказалось, что амплитуды первой и второй моды сопоставимы друг с другом. Таким образом, в общем случае необходимо учитывать обе моды, а значит, структура поля будет более сложная. Из-за взаимодействия мод строгая периодическая структура нарушится. ПАВ, соответствующие различным модам, имеют разные длины волн. Оказывается, что большую длину волны имеет вторая мода. Это означает, что за крупномасштабную структуру поля отвечает преимущественно вторая мода, тогда как первая мода связана с более мелкомасштабной структурой. Таким образом, можно ожидать, что в многомодовом режиме будет формироваться многомасштабная пространственная структура, причем на крупных масштабах она определяется высшими модами, амплитуды которых могут быть сопоставимы с амплитудой фундаментальной моды.
Проанализируем характер изменения амплитуды ПАВ в зависимости от толщины слоя. На рис. 6 приведена зависимость относительной амплитуды скалярного потенциала от волновой толщины слоя для первой (1) и второй (2) мод. Видно, что при волновой толщине $H \approx 2$, что примерно равно 2.9 м при заданных параметрах задачи, возникает резкий пик амплитуды первой моды. Это связано с тем, что в этой области скорость ПАВ сравнивается со скоростью звука в жидкости, т.е. со значением 1500 м/с, и возникает так называемый волновой резонанс. В этом случае ПАВ и волна в жидкости бегут с близкими скоростями и эффективно обмениваются энергией. В отсутствие вязкости (мода 1, сплошная линия) амплитуда при точном резонансе неограниченно возрастает. При учете вязкости поведение первой моды (мода 1, точки) качественно похоже, но амплитуда при с = с0 достигает конечного максимума, а не стремится к бесконечности. При этом амплитуда второй моды 2 не испытывает такого значительного роста.
Рис. 6.
Зависимость относительной амплитуды скалярного потенциала первых двух мод от толщины слоя (1 – первая мода: точки – с учетом вязкости, сплошная линия – без учета вязкости; 2 – вторая мода с учетом вязкости).

На рис. 6 можно выделить несколько характерных участков: H = 0…0.3 – присутствует только первая мода, H = 0.5…1 – амплитуда первой моды остается практически постоянной, а амплитуда второй моды достигает минимума, H = 1…1.5 – амплитуды мод сопоставимы друг с другом, H = = 1.5…2.5 – волновой резонанс первой моды, ее амплитуда гораздо больше амплитуды второй моды, от H = 2.5 и при большей толщине слоя амплитуда первой моды продолжает преобладать. Подчеркнем, что толщина слоя и частота волны входят в безразмерную волновую толщину слоя в виде сомножителей. Таким образом, регулируя в зависимости от задачи либо толщину слоя, либо частоту волны, можно влиять на пространственный масштаб акустического поля и преобладающую волновую моду. При этом необходимо иметь в виду, что частота фигурирует в дисперсионном уравнении также в качестве независимого параметра в слагаемых, содержащих коэффициент вязкости, так что зависимости скорости от толщины и частоты, вообще говоря, различны.
Рассмотрим теперь пространственную структуру поля стоячей ПАВ, образованной встречными бегущими ПАВ вида (17). Аналитические выражения для амплитуд компонент акустического поля, которые могут быть получены на основе матрицы (18), оказываются слишком громоздкими для воспроизведения и качественного анализа. Возможно только их численное исследование. В то же время согласно рис. 5 изменение скорости волны при учете вязкости оказывается относительно небольшим и для воды составляет доли процента. Поэтому для качественного представления о формирующейся структуре приведем аналитические выражения для колебательной скорости и давления в поле стоячей ПАВ в слое идеальной жидкости [10]:
(19)
$\begin{gathered} {{u}_{x}} = \frac{k}{{{{r}_{0}}}}{{U}_{0}}\sin {{r}_{0}}\left( {z + h} \right)\sin kx\sin {{\omega }}t, \\ {{u}_{z}} = - {{U}_{0}}\cos {{r}_{0}}\left( {z + h} \right)\cos kx\sin {{\omega }}t, \\ p{\kern 1pt} ' = - \frac{{{{{{\rho }}}_{0}}{{\omega }}}}{{{{r}_{0}}}}{{U}_{0}}\sin {{r}_{0}}\left( {z + h} \right)\cos kx\cos {{\omega }}t. \\ \end{gathered} $Здесь U0 – произвольный амплитудный множитель, с точностью до которого решается задача о распространении ПАВ. В случае решения задачи излучения волны этот множитель связан с амплитудой источника. Формулы (19) показывают, что вдоль осей х и z образуются периодические структуры с пространственными частотами $kx$ и ${{r}_{0}}z$, соответственно.
При учете вязкости пространственное распределение вертикальной и горизонтальной компонент колебательной скорости (в относительных единицах) для первой и второй моды, а также для суммы мод представлено на рис. 7. Расчет проводился для слоя воды толщиной H = 0.3. Видно, что графики качественно соответствуют формулам (19). Отдельно для первой и второй моды действительно наблюдаются строгие периодические структуры, но при учете двух мод распределение становится более сложным. На рис. 8 представлено изменение амплитуды колебательной скорости вдоль сечения $kx = 0.5$. Видно, что учет сдвиговых компонент привел к существенному изменению x-компоненты колебательной скорости вблизи границы раздела; изменение амплитуды z-компоненты скорости при этом незначительно.
Рис. 7.
Пространственное распределение (а, в, д) – горизонтальной и (б, г, е) – вертикальной компонент колебательной скорости (относительно амплитуды сдвиговой компоненты колебательной скорости) для (а, б) – первой моды, (в, г) – второй моды и (д, е) – суммы мод.

Рис. 8.
Сечения пространственного распределения колебательной скорости для первой моды (h = 0.1 м) при $kx = 0.5$: (а) – х-компонента, (б) – z-компонента; синяя линия 1 – с учетом вязкости, оранжевая линия 2 – без учета вязкости.

Уже говорилось, что роль нелинейных эффектов несущественна в рамках выбранной точности, тем не менее, полезно вкратце их рассмотреть. Кратко остановимся на нелинейных эффектах. Нелинейность, помимо появления высших гармоник, приводит к взаимодействию волн различного типа; в данном случае представляет интерес взаимодействие потенциальной и сдвиговой компонент. В [18] показано, что систему уравнений гидродинамики с учетом квадратичной нелинейности можно записать в виде
(20)
$\begin{gathered} \frac{{{{\partial }^{2}}p}}{{\partial {{t}^{2}}}} - c_{0}^{2}\Delta p - b\frac{\partial }{{\partial t}}\Delta p = \nabla \left( {p\frac{{\partial {\mathbf{u}}}}{{\partial t}} + \frac{1}{2}\nabla {{{\mathbf{u}}}^{2}}} \right) + \\ + \,\,\left( {\frac{\partial }{{\partial t}} - b\Delta } \right)\left( { - \nabla \left( {p{\mathbf{u}}} \right) + \frac{{{{\gamma }} - 1}}{{{{\rho }}c_{0}^{2}}}\frac{{\partial p}}{{\partial t}}} \right), \\ \end{gathered} $(21)
$~\frac{{\partial {\mathbf{\Omega }}}}{{\partial t}} - \frac{{{\eta }}}{{{\rho }}}\Delta {\mathbf{\Omega }} = - {\text{rot}}\left( {p\frac{{\partial {\mathbf{u}}}}{{\partial t}} + \frac{1}{2}\nabla {{{\mathbf{u}}}^{2}}} \right),~\,\,\,\,~{\mathbf{\Omega }} = \,\,~{\text{rot}}~{\mathbf{u}}.$Подставляя представление ${\mathbf{u}} = \nabla {{\varphi }} + {\text{rot\;}}{\mathbf{A}}$ в правую часть (21), можно показать, что главным членом будет “перекрестное” слагаемое вида ${{\eta rot}}\left( {\frac{{\partial {{\varphi }}}}{{\partial t}}{\text{rot}}{\mathbf{\Omega }}} \right)$, пропорциональное произведению потенциальной и сдвиговой компонент. Порядок малости этого слагаемого ηM2, где M – число Маха. Таким образом, для слабовязких жидкостей и при малых интенсивностях правая часть (21) является величиной третьего порядка малости. Раскрывая подобным образом правую часть (20), получим, что она содержит члены, содержащие квадрат давления, квадрат полной скорости и перекрестные члены. При этом члены, содержащие квадрат давления и квадрат потенциальной компоненты скорости, оказываются в волновом синхронизме с левой частью волнового уравнения (20) и будут эффективно приводить к появлению высших гармоник. В то же время члены, содержащие квадрат сдвиговой компоненты скорости, и перекрестные слагаемые будут распространяться со скоростью, отличной от скорости c0 в (20) и не будут попадать в условия волнового синхронизма. Тем самым, волны, вызванные этими членами в правой части не будут обладать большой амплитудой.
Таким образом, взаимодействие волн различных типов оказывается не очень эффективным и требует достаточно больших амплитуд и вязкости. При малой вязкости эффективными оказываются только нелинейные искажения, связанные с потенциальной частью акустического поля. Точное решение этой нелинейной задачи затруднительно, поскольку требует нахождения скорости волны из дисперсионного уравнения. Поэтому для приближенного описания можно использовать метод последовательных приближений, а можно применить модель модульной нелинейности [19], согласно которой слагаемое с квадратичной нелинейностью заменяется на слагаемое с модульной нелинейностью. Проведенное ранее исследование подобной задачи [20] позволяет заключить, что происходит формирование ПАВ с несимметричным волновым профилем для интервалов положительной и отрицательной полярности. При этом образуются области неоднозначности, в которых необходимо провести разрыв (ударный фронт), и увеличивающие области с плавным профилем малой амплитуды. Таким образом, нелинейность приводит к уменьшению пиковой амплитуды за счет нелинейного затухания, уменьшению интервалов с большой амплитудой и увеличению интервалов с малой амплитудой.
СИЛЫ РАДИАЦИОННОГО ДАВЛЕНИЯ
Существует несколько механизмов возникновения радиационного давления, характерных для различных ситуаций. Наиболее известным, по-видимому, является механизм, связанный с разностью импульсов, действующих с разных сторон на взвешенный в жидкости объект [21, 22]. Однако, в работе [10] показано, что этот механизм оказывается неэффективным в качестве причины возникновения акустических течений в жидкости и движения взвешенных в ней наночастиц. Поэтому в данной работе рассматривается механизм, связанный с нелинейностью уравнений гидродинамики и действующий непосредственно на элемент объема жидкости [7, 23, 24 ]. Наличие нелинейных слагаемых приводит при усреднении по периоду акустической волны к появлению ненулевой силы – радиационного давления. Силы радиационного давления, в свою очередь, вызывают в жидкости акустические течения, которые могут увлекать и наночастицы при их наличии. Собственное движение наночастиц относительно жидкости быстро затухает и они перемещаются вместе с жидкостью [10].
Тензор радиационных напряжений в случае вязкой жидкости имеет вид [24]:
(22)
$\begin{gathered} {\text{П}}_{{ik}}^{{{\text{RAD}}}} = \frac{{{\varepsilon }}}{{{{{{\rho }}}_{0}}c_{0}^{2}}}p{\kern 1pt} {{'}^{2}}{{{{\delta }}}_{{ik}}} + {{{{\rho }}}_{0}}{{u}_{i}}{{u}_{k}} + \hfill \\ + \,\,\frac{{{\eta }}}{{{{{{\rho }}}_{0}}c_{0}^{2}}}\frac{\partial }{{\partial {{x}_{k}}}}p{\kern 1pt} '{{u}_{i}} + \frac{{{{\xi }} + {{{\eta }} \mathord{\left/ {\vphantom {{{\eta }} 3}} \right. \kern-0em} 3}}}{{{{{{\rho }}}_{0}}c_{0}^{2}}}{{{{\delta }}}_{{ik}}}\frac{\partial }{{\partial {{x}_{l}}}}p{\kern 1pt} '{{u}_{l}}. \hfill \\ \end{gathered} $Сила радиационного давления F, действующая на элемент объема жидкости, выражается через тензор $\Pi _{{ik}}^{{{\text{RAD}}}}$:
В выражении (22) угловые скобки означают усреднение по периоду акустической волны, ε – параметр нелинейности жидкости. Формально (22) отличается от аналогичного выражения для идеальной жидкости наличием двух последних слагаемых, пропорциональных коэффициентам вязкости. Но даже простая оценка показывает, что в выражении (22) отношение последних двух слагаемых, например, к первому слагаемому имеет порядок (η/ρc2)f, что для воды составляет ~10–12f. Таким образом, даже на гигагерцовых частотах два последних слагаемых составляют доли процента в общем выражении. Только для такой вязкой жидкости как глицерин на высоких частотах все слагаемые сближаются по порядку величины. В то же время существенно, что наличие вязкости приводит к появлению сдвиговых компонент акустического поля, которые вносят вклад в первые два слагаемых в выражении (22) и, тем самым, значительно влияют на пространственную структуру радиационных сил.
На рис. 9 представлены горизонтальная и вертикальная компоненты радиационной силы (в относительных единицах) с учетом одной (при толщине H = 0.07, рис. 9а, 9б) и двух мод ПАВ (при толщине H = 0.3, рис. 9в, 9г) в случае идеальной жидкости. Видно, что в одномодовом режиме вдоль оси x образуется периодическое распределение радиационной силы. При возбуждении двух мод строгая периодичность нарушается именно из-за взаимодействия мод. Вертикальная структура радиационной силы также существенно изменяется. В одномодовом режиме силы менялись вдоль вертикали преимущественно монотонно, возрастая по направлению к границе раздела, и примерно сохраняли положения экстремумов структуры вдоль горизонтальной оси. В двухмодовом режиме структура вдоль вертикали изменяется более резко и теряет монотонный характер, появляются дополнительные экстремумы пространственной структуры. Положения экстремумов силы вдоль горизонтальной оси оказываются различными на разной глубине. Все это приводит к более сложной структуре возникающих акустических течений.
Рис. 9.
Пространственное распределение радиационной силы (в относительных единицах) без учета вязкости для частоты 1 кГц: (а, б) – одномодовый режим, h = 0.1 м, (в, г) – двухмодовый режим, h = 0.5 м; (а, в) – x-компонента, (б, г) – z-компонента.
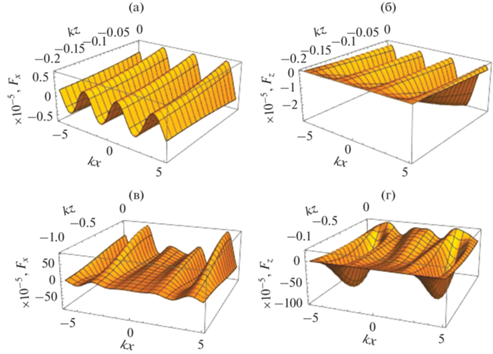
В работе [11] показано, что в одномодовом режиме сдвиговые компоненты приводят к большим значениям x-компоненты радиационной силы, локализованным вблизи границы. В двухмодовом режиме пространственная структура радиационных сил с учетом вязкости представлена на рис. 10. Видно, что в этом случае вблизи границы x-компонента также достигает больших значений. Таким образом, локальные изменения амплитуды колебательной скорости, отмеченные на рис. 8, приводят к радикальному изменению структуры радиационных сил. При этом для z-компоненты эти эффекты выражены гораздо слабее. Можно заметить, что из-за затухания поля ПАВ радиационные силы увеличиваются при удалении от центра структуры, т.е. появляется сила, направленная к середине рассматриваемой системы. Таким образом, можно ожидать, что структура сил и течений в средней части системы будет обладать большей стабильностью и меньшим контрастом по сравнению с периферийными областями. Наличие второй моды еще больше усложняет картину. С одной стороны, вторая мода может помочь формировать поля с более сложным пространственным распределением, а с другой стороны, затрудняет создание строгих периодических структур, например, “простого” синусоидального типа.
Рис. 10.
Пространственное распределение радиационной силы (в относительных единицах) в двухмодовом режиме с учетом вязкости для частоты 1 кГц: (а) – x-компонента, $ - 1 \leqslant kz \leqslant 0$, (б) – x-компонента, $ - 0.00002 \leqslant kz \leqslant 0$, (в) – z-компонента, $ - 1 \leqslant kz \leqslant 0$, (г) – z-компонента, $ - 0.00002 \leqslant kz \leqslant 0$.

При учете нелинейных искажений акустического поля согласно модели модульной нелинейности можно сделать следующие качественные выводы. Нелинейные искажения профиля волны приведут к изменению и, скорее всего, уменьшению действующей радиационной силы, а ее пространственное распределение будет характеризоваться увеличением областей с малыми значениями радиационной силы, где возможно почти равновесное поведение жидкости. С другой стороны, вблизи разрывов во временном профиле радиационные силы будут возрастать, обеспечивая быстрое течение жидкости в этих областях.
АКУСТИЧЕСКИЕ ТЕЧЕНИЯ
Наличие ненулевой усредненной радиационной силы приводит к формированию в жидком слое акустических течений. Их структура при малых гидродинамических числах Рейнольдса рассчитывается на основе системы уравнений в приближении несжимаемой жидкости [18]:
(24)
$ - {{\eta }}\Delta {{{\mathbf{U}}}_{{\text{т}}}} = - \nabla P + {\mathbf{F}},\,\,\,\,{\text{div}}~{{{\mathbf{U}}}_{{\text{т}}}} = 0.$Здесь ${{{\mathbf{U}}}_{{\text{т}}}}$ – скорость акустического течения, P – давление потока. Применяя к этому уравнению операцию rot, получим следующее уравнение для функции тока ${{\psi }}$:
(25)
$\Delta \left( {{{\eta }}\Delta {{\psi }} + V} \right) = 0,\,\,\,\,~{{U}_{{тx}}} = - \frac{{\partial {{\psi }}}}{{\partial z}},~\,\,\,\,{{U}_{{{\text{т}}z}}} = \frac{{\partial {{\psi }}}}{{\partial x}}.$Здесь V – единственная отличная от нуля компонента векторного потенциала ${\mathbf{V}}~$ радиационной силы (${\mathbf{F}} = {\text{rot}}{\mathbf{V}} + \nabla S$). В случае идеальной жидкости сила радиационного давления F оказывалась потенциальной, что значительно упрощало расчеты. В частности, при V = 0 уравнение (25) оказывалось бигармоническим, что позволяло построить его аналитическое решение. При этом акустические течения возникали за счет неоднородных условий на границах жидкого слоя. При учете вязкости радиационная сила содержит как потенциальную, так и вихревую компоненты. В этом случае уравнение (25) решалось путем его разбиения на систему уравнений Пуассона, при этом появлялась дополнительная гармоническая функция ${{\tilde {\psi }}}$:
(26)
$\eta \Delta {{\psi }} = - V + {{\tilde {\psi }}},\,\,\,\,\Delta {{\tilde {\psi }}} = 0,\,\,\,\,{\text{\;}}\Delta V = - {\text{rot\;}}F.$Уравнения (26) должны быть дополнены граничными условиями – условиями отсутствия вертикального потока на границах жидкого слоя и горизонтального потока на границе раздела сред, равенства нулю давления потока на свободной поверхности. Для проведения численных расчетов в ограниченной по горизонтальной оси области добавлялись условия периодичности, обусловленные симметрией задачи. Для замыкания набора граничных условий использовались также результаты решенной задачи для случая отсутствия вязкости [10], применимые при малой вязкости. В частности, при отсутствии вязкости функция тока в геометрии рис. 1 равна нулю в точках с координатами $2kx = {{\pi }}n$, где n – целое число. Наличие малой вязкости не должно изменить период пространственного распределения. Это позволяет сформулировать граничные условия при некоторых x, выбрав конечное число целых периодов поля. Для получения граничных условий для функции продифференцируем первое уравнение (26) по z и используем z-проекцию первого уравнения (24). В итоге получаем следующее уравнение:
(27)
$\frac{{\partial {{\tilde {\psi }}}}}{{\partial z}} = - \frac{{\partial P}}{{\partial x}} + {{F}_{x}} + \frac{{\partial V}}{{\partial z}}.$Теперь воспользуемся тем фактом, что в отсутствие вязкости [10] P = 0 и ∂P/∂x = 0 при $z = - h$. Тогда первое слагаемое в правой части (27) можно считать равным нулю и при наличии вязкости, поскольку распределение давления не связано с вихревыми движениями. Величина ${{F}_{x}} + \frac{{\partial V}}{{\partial z}}$ в (27) представляет собой фактически потенциальную часть радиационной силы при наличии вязкости. Для качественного анализа при малой вязкости эту величину можно приближенно считать равной ее значению в отсутствие вязкости. В итоге получаем следующий набор граничных условий:
На рис. 11 приведены линии тока для акустического течения в слое воды в одномодовом режиме без учета вязкости (рис. 11а) и с учетом вязкости (рис. 11б). На рис. 11в приведены линии тока для глицерина, коэффициент вязкости которого взят для наглядности в 100 раз больше, чем у воды. При построении рис. 11б и 11в заданное значение ${{\gamma }} = 0.05\,\,~{{{\text{м}}}^{{ - 1}}}$ намеренно увеличено относительно расчетного значения для рассматриваемых сред для демонстрации роли затухания; толщина слоя H = 0.07. Видно, что линии тока гуще расположены в окрестностях линий $2kx = {{\pi }}n$. При этом из-за наличия затухания при приближении к точке $x = 0$ площадь контуров уменьшается. Как показано выше, при учете вязкости x-компонента радиационной силы сильно возрастает вблизи границы раздела сред. Это приводит к заметной деформации контуров и изменению густоты линий тока. С увеличением вязкости из-за возрастания роли сдвиговых компонент структура течений теряет симметричность. Таким образом, вязкость жидкости приводит к нарушению строгой периодичности акустических течений в слое.
ЗАКЛЮЧЕНИЕ
В работе рассчитаны с учетом вязкости дисперсионные и амплитудные характеристики поверхностной волны в двух системах: вязкое жидкое полупространство и слой вязкой жидкости, граничащие с твердым полупространством. В последнем случае была учтена вторая волновая мода. Для слоя также были рассчитаны радиационные силы, действующие на элемент объема жидкости и создаваемые ими акустические течения. Показано, что вязкость и вторая мода приводят к значимым изменениям пространственной структуры радиационных сил акустических течений. Как и в одномодовом режиме, дополнительная радиационная сила, обусловленная сдвиговыми компонентами акустического поля в жидкости, сосредоточена в узком слое вблизи границы раздела сред, а вторая мода нарушает строгое периодическое распределение силы.
Применительно к задачам формирования упорядоченных структур при самосборке взвешенных ансамблей наночастиц результаты данной работы позволяют сделать следующие выводы. Для слабовязких сред наподобие воды дисперсионные зависимости скорости волн от частоты и толщины слоя очень близки к зависимостям для идеальной среды. Тем самым, длина волны и период радиационных сил практически не изменяются. Однако в приграничном слое даже для слабовязких жидкостей возникают значительные силы радиационного давления, связанные со сдвиговыми компонентами поля в жидкости. Поскольку именно в этой области происходит формирование упорядоченных структур, учет сдвиговых компонент оказывается необходимым для корректного расчета параметров получаемой структуры. Кроме того, вязкость приводит к нарушению строгой периодичности полей, характерной для случая идеальной жидкости. Генерация высших мод в толстом слое жидкости также приводит к формированию сложного распределения поля радиационных сил. Хотя эти эффекты препятствуют формированию строго периодических структур, тем не менее, они расширяют возможности управления акустическим полем и могут способствовать созданию структур с более сложным рельефом и новыми свойствами. Необходимо также подчеркнуть, что в случае взвесей и растворов с большой концентрацией и, соответственно, большой эффективной вязкостью роль этих эффектов значительно возрастает. Таким образом, именно в задачах формирования упорядоченных структур из ансамблей взвешенных наночастиц вязкость и сдвиговые компоненты поля в жидкости должны быть учтены.
Качественный анализ эффектов нелинейного искажения временных профилей ПАВ показывает, что при увеличении амплитуды должны увеличиваться области с малыми значениями радиационной силы, но в областях разрывов во временном фронте радиационные силы будут значительно возрастать. Таким образом, области сборки наночастиц могут увеличиваться, но при этом эти области будут разделены сильноконтрастными областями, из которых наночастицы будут выноситься радиационными силами.
Работа поддержана грантом РФФИ № 20-02-00493.
Список литературы
Крохмаль А.А., Крохмаль Н.Е., Сапожников О.А. Расчет акустической ловушки для упругого сферического рассеивателя большого волнового размера // Известия Росс. Акад. наук. Сер. физ. 2022. Т. 86. № 2. С. 257–262.
Wixforth A. Acoustically driven planar microfluidics // Superlattices and Microstructures. 2003. V. 33. P. 389–396.
Лебедев-Степанов П.В., Руденко О.В. О затухании звука в жидкости, содержащей взвешенные частицы микро- и нанометровых размеров // Акуст. журн. 2009. Т. 55. № 6. С. 706–711.
Суханов Д.Я., Росляков С.Н., Емельянов Ф.С. Левитация и управление упорядоченной группой частиц и прямолинейных структур в ультразвуковом поле // Акуст. журн. 2020. Т. 66. № 2. С. 154–162.
Li J., Liu C.J., Zhang W.J. Pressure potential and stability analysis in an acoustical noncontact transportation // Acoust. Phys. 2017. V. 63. № 1. P. 125–131.
Sarvazyan A.P., Rudenko O.V., Fatemi M. Acoustic radiation force: A review of four mechanisms for biomedical applications // IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2021. V. 68. № 11. P. 3261–3269. https://doi.org/10.1109/TUFFC.2021.3112505
Жвания И.А., Конопацкая И.И., Миронов М.А., Пятаков П.А. Акустическое течение, возбуждаемое фокусированным ультразвуком // Акуст. журн. 2021. Т. 67. № 3. С. 244–249.
Rudenko O.V., Lebedev-Stepanov P.V., Gusev V.A., Korobov A.I., Korshak B.A., Odina N.I., Izosimova M.Yu., Molchanov S.P., Alfimov M.V. Control of the self-assembly processes in a droplet of a colloidal solution by an acoustic field // Acoust. Phys. 2010. V. 56. № 6. P. 935–941.
Макалкин Д.И., Коршак Б.А., Брысев А.П. Экспериментальное наблюдение структурирования эритроцитов крови в поле стоячих поверхностных акустических волн // Акуст. журн. 2017. Т. 63. № 5. С. 553–559.
Гусев В.А., Руденко О.В. Поля радиационных сил и акустические течения в жидком слое на твердом полупространстве // Акуст. журн. 2019. Т. 65. № 2. С. 166–181.
Гусев В.А., Жарков Д.А. Поля радиационных сил в слое вязкой жидкости // Изв. Росс. Акад. наук. Сер. физ. 2021. Т. 85. № 6. С. 804–810.
Бадмаев Б.Б., Дамдинов Б.Б., Дембелова Т.С. Вязкоупругая релаксация в жидкостях // Известия Росс. Акад. наук. Сер. физ. 2015. Т. 79. № 10. С. 1461–1466.
Макарова Д.Н., Дембелова Т.С., Бадмаев Б.Б. Низкочастотная сдвиговая упругость коллоидной суспензии наночастиц // Акуст. журн. 2020. Т. 66. № 6. С. 610.
Викторов И.А. Звуковые поверхностные волны в твердых телах. М.: Наука, 1981. 288 с.
Красильников В.А., Крылов В.В. Введение в физическую акустику. М.: Наука, 1984. 403 с.
Gusev V.A., Simonova P.A. Effect of shear components of the acoustic field in the viscous liquid on the structure of the Stoncley wave at the interface between the liquid and elastic half-spaces // Physics of Wave Phenomena. 2015. V. 23. № 4. P. 268–272.
Волькенштейн М.М., Левин В.М. Структура волны Стоунли на границе вязкой жидкости и твердого тела // Акуст. журн. 1988. Т. 34. № 4. С. 608–615.
Руденко О.В., Солуян С.И. Теоретические основы нелинейной акустики. М.: Наука, 1975.
Васильева О.А., Руденко О.В. Модульные “солитоны”: взаимное поглощение и аннигиляция в диссипативных средах // Акуст. журн. 2020. Т. 66. № 3. С. 258–264.
Гусев В.А. Трансформация акустических волн в слоистых средах с модульной нелинейностью // Труды Всероссийской акустической конференции. СПб.: ПОЛИТЕХ-ПРЕСС, 2020. С. 101-105.
Горьков Л.П. О силах, действующих на малую частицу в акустическом поле в идеальной жидкости // Докл. Акад. наук СССР. 1961. Т. 140. В. 1. С. 88.
Гольдберг З.А. Давление звука. В книге: Мощные ультразвуковые поля. Т. 2. Под ред. Розенберга Л.Д. М.: Наука, 1968. С. 49.
Гусев В.Э., Руденко О.В. Нестационарные квазиодномерные акустические течения в неограниченных объемах с учетом гидродинамической нелинейности // Акуст. журн. 1979. Т. 25. № 6. С. 875–881.
Руденко О.В. Радиационные силы и акустические течения // В кн. Нелинейные проблемы теории колебаний и теории управления. Вибрационная механика. СПб.: Наука, 2009. С. 402–422.
Дополнительные материалы отсутствуют.
Инструменты
Акустический журнал