Акустический журнал, 2022, T. 68, № 4, стр. 361-372

1. ВВЕДЕНИЕ

Рассматривается задача возбуждения импульсов в многослойном волноводе с компактным постоянным сечением. Поглощения/притока энергии в волноводе не происходит. В качестве наиболее общей приближенной модели волновода рассматривается матричное уравнение Клейна–Гордона. Отметим, что матричное уравнение Клейна–Гордона в литературе иногда называется волноводным методом конечных элементов (Waveguide Finite Element Method [1], waveguide FEM [2]), а также GDSA [3] (Global Discretization, Semi-Analytical formulation). Данное уравнение возникает, например, при дискретизации сечения волновода; продольная координата, как и время, при этом остается непрерывной.

Впервые идея дискретизовать сечение волновода, сохранив при этом непрерывность вдоль волновода и во времени, встречается в работе [4], где показано, что подобная идея может быть использована для расчета дисперсионных диаграмм упругих волноводов произвольного сечения. Более явно матричное уравнение Клейна–Гордона выписано в [5]. В работах [1, 6] уравнение выведено с помощью метода Лагранжа. В работе [3] соответствующее уравнение выводится из модового разложения поля. Кроме того, в [1, 3] получена формула для групповой скорости моды.

Метод матричного уравнения Клейна–Гордона конкурирует с методом групповой импедансной матрицы [7], где дискретизуются как поперечные, так и продольные координаты. Представляет потенциальный интерес построение перехода между этими двумя методами и перенос ряда формул из [7] в контекст матричного импедансного уравнения.

Сформулируем постановку задачи. Пусть направление, в котором волновод бесконечен, совпадает с координатой осью $x$. Пусть ${\mathbf{U}}\left( {t,x} \right)$ – вектор размерности $N \times 1$ ($N~$– целое число, возможно большое). Вектор ${\mathbf{U}}$ описывает состояние сечения волновода. Например, если рассматривается упругий волновод, вектор ${\mathbf{U}}$ может состоять из смещений узлов сетки, аппроксимирующей поперечное сечение волновода. Если волновод жидкий, это могут быть значения акустического потенциала в узлах сетки. Вектор ${\mathbf{U}}$ также может представлять собой амплитуды приближенных нормальных колебаний сечения волновода. Во всех этих случаях матричное уравнение Клейна–Гордона имеет общий вид

где ${{D}_{2}},~{{D}_{1}},~{{D}_{0}},~M$ – некоторые постоянные матрицы размерности $N \times N$, ${\mathbf{F}}$ – постоянный вектор $N \times 1$, описывающий поперечный профиль возмущения.

Мы полагаем, что матрицы, стоящие в (1), действительны и имеют следующие свойства [1]:

где ${{ \cdot }^{T}}$ обозначает транспонирование. Кроме того, мы считаем, что матрицы $M$ и ${{D}_{2}}$ положительно определены, ${{D}_{0}}$ – отрицательно определена. Эти условия необходимы, чтобы потенциальная и кинетическая энергии были неотрицательны. Матрица $M$ отвечает за инерционные свойства волновода (массу), ${{D}_{2}}$ отвечает за продольную жесткость, ${{D}_{0}}$ – за поперечную жесткость, а ${{D}_{1}}$ – за свойства, не сохраняющиеся при симметрии $x \to - x$.

Структура статьи следующая. В разделе 2 обсуждается физический смысл матриц, входящих в (1). В разделах 3 и 4 выводятся несколько представлений поля ${\mathbf{U}}\left( {t,x} \right)$, определяемого уравнением (1). В результате ставится вопрос об эквивалентности этих представлений. Чтобы показать, что полученные представления тождественны в определенных областях, необходимо рассмотреть все (включая комплексные) решения дисперсионного уравнения. В разделе 5 интегральные представления для полей предлагается трактовать как контурные интегралы на комплексном многообразии, представляющем собой дисперсионную диаграмму волновода. В разделе 6 доказываются некоторые полезные свойства дисперсионного уравнения. В разделе 7 показана тождественность различных представлений решения (1).

2. ВЫВОД МАТРИЧНОГО УРАВНЕНИЯ КЛЕЙНА–ГОРДОНА

В качестве пояснения к матричному уравнению Клейна–Гордона покажем, что оно легко выводится из более привычного метода конечных элементов. Чтобы построить конечно-элементную модель волновода, необходимо описать поведение некоторого тонкого среза волновода по продольной координате (пусть этот срез соответствует области $0 \leqslant x \leqslant {{\Delta }}x$), а затем “склеить” бесконечную последовательность таких срезов. Пусть ${{{\mathbf{U}}}^{{\left( 1 \right)}}}$ и ${{{\mathbf{U}}}^{{\left( 2 \right)}}}$ – векторы узловых значений в сечениях $x = 0$ и $x = {{\Delta }}x$, соответственно (см. рис. 1). Будем считать, что других узловых значений для приближенного описания среза не требуется. Пусть элементы вектора ${{{\mathbf{U}}}^{{\left( 1 \right)}}}$ соответствуют элементам ${{{\mathbf{U}}}^{{\left( 2 \right)}}}$ при трансляции $x \to x + \Delta x$. Размерность векторов ${{{\mathbf{U}}}^{{\left( 1 \right)}}}$ и ${{{\mathbf{U}}}^{{\left( 2 \right)}}}$ есть $N \times 1$. Весь срез описывается блочным вектором

Пусть матрицы жесткости и массы для этого слоя записаны в блочной форме:

где все блоки имеют размер $N \times N$.

Перейдем к рассмотрению целого волновода. Пусть состояние волновода описывается векторной функцией ${{{\mathbf{\hat {U}}}}_{m}}\left( t \right)$, где $m$ – номер сечения $x = m{{\Delta }}x$. Пусть в сечении $m = 0$ прикладывается сила с временным профилем $f\left( t \right)$. В этом случае поле в волноводе описывается уравнением:

где ${\mathbf{F}}$ – вектор, описывающий пространственный профиль возмущения в сечении волновода.

Сделаем два упрощения. Во-первых, положим, что матрица массы диагонализована. Из этого следует, что

Во-вторых, будем рассматривать ${{{\mathbf{\hat {U}}}}_{m}}\left( t \right)$ как дискретизацию непрерывной по $x$ функции ${\mathbf{U}}\left( {t,x} \right)$:

Подставляя (5) и (6) в (4), мы получаем уравнение (1), в котором

Поясним роль различных матриц-коэффициентов в уравнении. Рассмотрим сетку, изображенную на рис. 2. Пусть черные точки обозначают массы; они способны двигаться только перпендикулярно плоскости рисунка. Линиями на рисунке показаны натянутые пружины. Пусть натяжение вертикальных пружин есть ${{a}_{1}},$ горизонтальных ${{a}_{2}}$, а диагональных ${{a}_{3}}$. Пусть ${{\Delta }}x = {{\Delta }}y = 1$.

Это простейший волновод из сосредоточенных элементов. Построим его матричное описание. Возьмем элементарный срез, состоящий из двух сечений волновода (чтобы этот срез был периодом системы, узлы разделяются надвое). Матрица массы ${{M}^{d}}$ для такого среза диагональная:

где ${{a}_{0}}$ – масса одного узла. Пусть блоки ${{K}_{{ml}}}$, из которых составлена матрица жесткости, выражены в виде суммы: где $\hat { \cdot }$ означает то, что величины относятся к вертикальным и горизонтальным связям, $\tilde { \cdot }$ означает, что величины относятся к диагональным связям. Соответственно,

Матрицы ${{\hat {K}}_{{ml}}}$ выписаны ниже:

Следовательно, применяя (7)–(9), можно получить

Можно заметить, что с точностью до постоянного множителя ${{\hat {D}}_{0}}$ – это численная аппроксимация оператора $\partial _{y}^{2}$, а ${{\hat {D}}_{2}}$ – это единичная матрица.

Теперь рассмотрим диагональные связи. Соответствующие блоки матрицы жесткости имеют вид:

Отсюда

Как видно из представленных формул, диагональные связи делают матрицу ${{D}_{1}}$ ненулевой. Можно прийти к выводу о том, что вертикальные пружины (поперечная упругость) участвуют в формировании матрицы ${{D}_{0}}$, горизонтальные пружины (продольная упругость) в формировании матрицы ${{D}_{2}}$, а диагональные пружины в формировании всех трех матриц упругости. Очевидно, диагональные пружины нарушают симметрию $x \to - x.$

3. РЕШЕНИЕ МАТРИЧНОГО УРАВНЕНИЯ КЛЕЙНА–ГОРДОНА В ВИДЕ ДВОЙНОГО ИНТЕГРАЛА

Для того чтобы получить решение матричного уравнения Клейна–Гордона (1), необходимо сделать преобразование Фурье по $x$ и преобразование Лапласа по $t$, решить получившееся алгебраическое уравнение относительно образа векторной функции ${\mathbf{U}}\left( {t,x} \right)$ и сделать обратные преобразования Фурье и Лапласа. В результате получается решение в виде двойного интеграла:

где

Произвольное положительное значение ${{\varepsilon }}$ появляется при выполнении преобразования Меллина (обратного преобразования Лапласа). Оно обеспечивает причинность решения.

Применяя формулу для вычисления обратной матрицы, (20) можно переписать так:

где $A\left( {{{\omega }},k} \right)$ – матрица алгебраических дополнений $B$, $D\left( {{{\omega }},k} \right)$ – определитель $B$, или дисперсионная функция волновода:

Заметим, что по построению матрица $A\left( {{{\omega }},k} \right)$ и функция $D\left( {{{\omega }},k} \right)$ – полиномы переменных $\left( {{{\omega }},k} \right).$ Возможно, степень этих полиномов весьма велика.

Для волноводов, описываемых матричным уравнением Клейна–Гордона, верны следующие утверждения. Во-первых, функция

растет как степенная функция ${{\omega }}$ для фиксированного $k$, и как степенная функция от $k$ для фиксированного ${{\omega }}$. Таким образом, рост или убывание подынтегральной функции (20) на бесконечности определяется экспоненциальным множителем. Во-вторых, функции $A$ и $D$ не имеют ни точек ветвления, ни полюсов, а только, возможно, нули.

Вопрос, насколько данные свойства сужают класс волноводов, к которым применимы описываемые методы, остается открытым. Так, например, в [8] написано следующее: “Является общепринятым считать, что для закрытых структур, таких как слой (возможно, с некоторыми бесконечностями), функция $L\left( {s,y} \right)~$ есть мероморфная функция, а для открытых структур, таких как полуплоскость, $L\left( {s,y} \right)$ имеет точки ветвления. Мы не знаем, было ли это утверждение строго доказано где-либо, но нам не известны примеры, которые бы опровергали данное утверждение”. Функция $L\left( {s,y} \right)$ в [8] есть ${{A\left( {{{\omega }},k} \right)} \mathord{\left/ {\vphantom {{A\left( {{{\omega }},k} \right)} {D\left( {{{\omega }},k} \right)}}} \right. \kern-0em} {D\left( {{{\omega }},k} \right)}}$.

Особые точки подынтегрального выражения определяются дисперсионным уравнением:

Эти особые точки являются полюсами (в общем случае первого порядка). Как известно, если ${{\omega }}$ и $k$ являются решениями дисперсионного уравнения (24), в волноводе может свободно распространяться мода вида $W{{e}^{{ - i{{\omega }}t + ikx}}}$, где $W$ – поле в волноводе в сечении $x = 0$ при $t = 0$. В случае дискретизованного сечения волновода $W$ представляет собой вектор. Решения дисперсионного уравнения, такие что ${{\omega }},k \in \mathbb{R}$, соответствуют “обычным” распространяющимся волнам, а решения, такие что ${{\omega }} \in \mathbb{R},$ ${\text{Re}}\left[ k \right] = 0,~$ ${\text{Im}}\left[ k \right] \ne 0$ – затухающим волнам. Далее мы рассматриваем также моды, у которых оба значения ${{\omega }},k~$ комплексные.

Определить положение корней дисперсионного уравнения относительно контура интегрирования в плоскости переменной $k$ помогает следующее утверждение. Пусть матрицы $M$, ${{D}_{2}}$, ${{D}_{1}}$, ${{D}_{0}}$ действительны и подчиняются свойствам (2). Пусть также матрица $M$ положительно определена. Тогда при действительных $k$ уравнение (24), рассматриваемое как уравнение относительно ${{\omega }}$, имеет только действительные корни.

Данное утверждение было доказано в [1]. В дальнейшем мы будем называть его соотношением действительности. Тот факт, что в волноводах без поглощения или притока энергии (при этом в качестве модели волновода не обязательно должно рассматриваться матричное уравнение Клейна–Гордона) действительным $k$ соответствуют действительные решения дисперсионного уравнения ${{\omega }}$, является довольно известным. В ряде статей он приводится как очевидный и не требующий доказательства (например, в [9]). Мы, однако, поясним неформальным образом, почему это утверждение верно.

Введем для действительного $k$ “длину волны” ${{\Lambda }} = {{2{{\pi }}} \mathord{\left/ {\vphantom {{2{{\pi }}} k}} \right. \kern-0em} k}$. “Вырежем” фрагмент волновода $0 \leqslant x \leqslant {{\Lambda }}$ и наложим периодические граничные условия, соединив тем самым концы $x = 0$ и $x = {{\Lambda }}$. В результате, мы получим физически реализуемый резонатор. Если эта система является консервативной, то ее собственные частоты ${{\omega }}$ должны быть действительными. Так как для нормальных волн волновода с длиной волны ${{\Lambda }}$ и волновым числом $k$ решения дисперсионного уравнения (частоты) являются частотами соответствующего резонатора, то они также являются действительными.

В нашем случае соотношение действительности является важным, поскольку гарантирует, что интеграл (22) определен корректно: плоскость интегрирования не пересекает особенности подынтегрального выражения.

4. ПРЕДСТАВЛЕНИЕ РЕШЕНИЯ В ВИДЕ СУММ ОДНОМЕРНЫХ ИНТЕГРАЛОВ

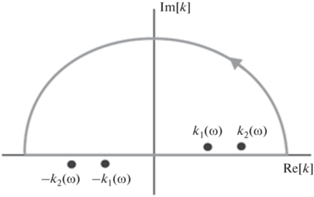
Пусть $~x > 0.$ Для вычисления интеграла (20) можно воспользоваться леммой Жордана и замкнуть контур интегрирования в верхней части комплексной плоскости переменной $k$, как показано на рис. 3. Затем, согласно теореме вычетов, внутренний интеграл может быть представлен (с точностью до коэффициента $2{{\pi }}i$) как сумма вычетов в полюсах, попавших внутрь замкнутого контура.

Зафиксируем значение ${{\omega }} = {{\omega }}{\kern 1pt} {\text{'}} + i{{\varepsilon }}$, ${{\omega }}{\kern 1pt} {\text{'}} \in \mathbb{R}$. Тогда решения ${{k}_{j}}$ дисперсионного уравнения (24) могут быть разложены в ряд Тейлора:

Согласно соотношению действительности, ${{k}_{j}}\left( {{{\omega }}{\kern 1pt} {\text{'}}} \right) \in \mathbb{R}$. Очевидно также, что значение производной ${{\left. {\frac{{d{{k}_{j}}}}{{d{{\omega }}}}} \right|}_{{{{\omega }}{\kern 1pt} {\text{'}}}}}$ является действительным. Следовательно, значения ${{k}_{j}}\left( {{{\omega }}{\kern 1pt} {\text{'}} + i{{\varepsilon }}} \right)$ слегка сдвинуты от действительной оси в комплексную область на величину:

Заметим, что производная в правой части (26) – величина, обратная групповой скорости моды.

Можно показать, что дисперсионная функция $D$, определенная в (23), зависит только от четных степеней $k$ (см. раздел 6). Отсюда следует, что все корни дисперсионного уравнения можно разделить на пары ${{k}_{j}}\left( {{\omega }} \right)$ и $ - {{k}_{j}}\left( {{\omega }} \right)$. Следовательно, половина корней сдвинута в верхнюю полуплоскость, а другая половина – в нижнюю. Будем считать, что значение ${{k}_{j}}({{\omega }})$ имеет положительную мнимую часть.

Таким образом, внутрь замкнутого контура интегрирования попадает только половина корней дисперсионного уравнения (все корни с ${\text{Im}}\left[ k \right] > 0$, см. рис. 3). Взяв вычеты в этих точках, можно получить следующее представление поля в виде суммы интегралов по ${{\omega }}$:

где $N$ – размерность задачи.

При $t > 0$ и произвольном $x$ можно получить еще одно представление поля в волноводе, поменяв порядок интегрирования в (22):

После замыкания контура интегрирования в нижней части комплексной плоскости ${{\omega }}$ (см. рис. 4) внутрь контура попадают все корни ${{{{\omega }}}_{j}}\left( k \right)$ дисперсионного уравнения, так как, согласно соотношению действительности, все корни лежат на действительной оси. С учетом того, что дисперсионная функция (23) зависит только от четных степеней ${{\omega }}$, все корни дисперсионного уравнения можно разделить на пары ${{{{\omega }}}_{j}}\left( k \right)$ и $ - {{{{\omega }}}_{j}}\left( k \right)$. Применяя теорему вычетов, получаем представление поля в виде суммы интегралов по $k$:

Отметим, что если интересоваться полем при $t < 0$, то контур интегрирования внутреннего интеграла в (28) следует замыкать в верхней полуплоскости. Подынтегральная функция в области, которую замыкает такой контур, является аналитичной, следовательно, интеграл равен нулю. Таким образом, решение (28) и в самом деле обладает причинностью.

Отметим также, что вычеты внутреннего интеграла в (28) можно представить в следующей форме:

где ${{{\mathbf{U}}}_{j}}$ – собственный вектор правой обобщенной задачи на собственные значения: где ${{{\mathbf{U}}}_{j}}$ – вектор-столбец, соответствующий собственному значению ${{\omega }}_{j}^{2}$, а вектор ${{{\mathbf{V}}}_{j}}$ – собственный вектор левой обобщенной задачи на собственные значения: где ${{{\mathbf{V}}}_{j}}$ – вектор-строка, соответствующий тому же собственному значению ${{\omega }}_{j}^{2}$. Нетрудно показать, что для действительных k векторы ${{{\mathbf{V}}}_{j}}$ эрмитово сопряжены соответствующим векторам ${{{\mathbf{U}}}_{j}}$. Воспользовавшись (30), выражение (28) можно переписать так:

Это одно из стандартных представлений поля в волноводе в виде ряда по модам. Аналогичное представление можно записать и для (20), но при этом надо вводить более сложную (квадратичную) задачу на собственные значения [7], что выходит за рамки данной статьи.

Таким образом, существует три известных представления поля в волноводе: в виде двойного интеграла (22) или (28), в виде суммы интегралов по ${{\omega }}$ (27), а также в виде суммы интегралов по $k$ (29) (или (33)). Эти представления не эквивалентны. Представление в виде двойного интеграла справедливо для любых $t$ и $x$, оно обладает причинностью. Представление (27) выведено с учетом $x > 0$, оно описывает только волны, распространяющиеся в положительном направлении оси $x$. Представление (29), в свою очередь, справедливо только для $t > 0$. Однако, если рассматривать поле только при $t > 0$ и $x > 0$, то все три представления должны давать один и тот же результат. Следовательно, (27) должно преобразовываться в (29), и обратно. Показать, что (27) и (29) выводятся друг из друга – основная цель данной статьи.

5. ДИСПЕРСИОННАЯ ДИАГРАММА ВОЛНОВОДА КАК КОМПЛЕКСНОЕ МНОГООБРАЗИЕ

Чтобы показать связь между (27) и (29), необходимо изучить строение дисперсионной диаграммы. Как известно, множество точек $\left( {{{\omega }},k} \right)$, удовлетворяющих дисперсионному уравнению (24), образуют дисперсионную диаграмму. Уже в 1952 г. Миндлин [10], изучая волны Лэмба, показал, что не только действительные, но и комплексные решения дисперсионного уравнения могут представлять интерес. Также позднее в работах [9, 11] были отмечены некоторые закономерности в поведении ветвей дисперсионной диаграммы твердотельного волновода для действительных и комплексных $k$. В работах [12–14] также изучалось аналитическое продолжение дисперсионной диаграммы в область комплексных ${{\omega }}$ и $k$.

Рассмотрим дисперсионное уравнение (24) как уравнение относительно комплексных $k$ (считая фиксированным произвольное комплексное ${{\omega }}$). Это уравнение, как уже указывалось, имеет $2N$ решений ${{k}_{j}}\left( {{\omega }} \right)$. Первая из ключевых идей, используемых в настоящей работе, заключается в том, чтобы рассматривать значения ${{k}_{j}}\left( {{\omega }} \right)$ как значения одной многозначной (многолистной) комплекснозначной функции $k\left( {{\omega }} \right).~$ У этой функции есть некоторая риманова поверхность, которая имеет $2N$ листов. Эта поверхность может быть связна или состоять из нескольких компонент. Назовем эту риманову поверхность $R$.

Таким образом, каждое из решений ${{k}_{j}}\left( {{\omega }} \right)$ лежит на своем листе поверхности $R$ многозначной комплексной функции $k\left( {{\omega }} \right)$. Структура подынтегрального выражения в (27) такова, что оно имеет ту же риманову поверхность. Это значит, что в (27) суммируются интегралы не от $N~$ разных функций, а от одной многозначной функции, взятые по $N$ различным контурам, проведенным на ее римановой поверхности. Эти контуры представляют собой $N$ (из $2N$) прообразов прямой ${\text{Im}}\left[ {{\omega }} \right] = {{\varepsilon }}$.

Аналогично, корни ${{{{\omega }}}_{j}}$ дисперсионного уравнения при фиксированном $k$ являются листами римановой поверхности $R{\kern 1pt} '$ многозначной комплексной функции ${{\omega }}\left( k \right)$. Заметим, что формула (29) содержит интегрирование по всем $2N$ листам римановой поверхности $R{\kern 1pt} '$ вдоль прообразов действительной оси k-плоскости. Действительно, $N$ собственных значений ${{\omega }}_{j}^{2}$ порождают $2N$ листов $ \pm {{{{\omega }}}_{j}}$, и нетрудно проверить, что все они участвуют в (29) одинаковым образом.

Согласно теореме Коши, контур интегрирования можно деформировать в областях аналитичности подынтегральной функции. Именно этот инструмент позволит нам показать тождественность (27) и (29) для $t > 0$, $x > 0$. Чтобы деформировать контуры интегрирования на $R$ и $R{\kern 1pt} '$, необходимо изучить строение этих поверхностей.

Очевидно, подынтегральные выражения в (27) и (29), рассматриваемые как функции ${{\omega }}$ и $k$, имеют точки ветвления. Несколько более тонкое рассуждение показывает, что в общем случае они не имеют полюсов.

Вторая математическая идея, используемая в данной работе, заключается в том, что римановы поверхности $R$ и $R{\kern 1pt} '$ связаны друг с другом. А именно, рассмотрим множество $H$ точек $\left( {{{\omega }},k} \right)$ в двумерном комплексном пространстве, удовлетворяющих дисперсионному уравнению (24). Это множество двумерно, т.е. представляет собой поверхность в четырехмерном пространстве. Римановы поверхности $R$ и $R{\kern 1pt} '$ есть в определенном смысле проекции одной и той же поверхности $H$ на координатные плоскости (комплексные прямые) ${{\omega }}$ и $k,~$ соответственно.

На поверхности $H$ можно ввести комплексную структуру, превратив ее в комплексное многообразие. Как известно [15, 16], комплексное многообразие – это поверхность, в окрестности каждой точки которой можно ввести локальную комплексную координату таким образом, чтобы преобразования координат между пересекающимися окрестностями были биголоморфными в области пересечения. Приведем пример таких координат. Везде, кроме прообразов точек ветвления поверхности $R$, вводится локальная координата ${{\omega }}$, а в окрестностях прообразов точек ветвления $R{\kern 1pt} $ вводится локальная координата $k$.

В то время как римановы поверхности $R$ и $R{\kern 1pt} '$ имеют точки ветвления, многообразие $H$ в общем случае не имеет особых точек, т.е. является регулярным везде. Особые точки $R$ и $R{\kern 1pt} '$ появляются как “складки”, возникающие при проектировании $H$ на координаты ${{\omega }}$ и $k$. Разумеется, регулярность многообразия $H$ не делает его топологически простым. Топология у него такая же, как у $R$ и $R{\kern 1pt} '$, т.е. оно может иметь “шейки”, “ручки” и т.д.

Наличие комплексной структуры на дисперсионной диаграмме $H$ позволяет ввести на ней контурное интегрирование, оснащенное теоремой Коши, т.е. с возможностью деформации контуров интегрирования. Интегрирование вводится обычным образом в окрестности каждой точки с помощью локальной комплексной координаты, а затем доказывается независимость интеграла от способа введения локальной координаты. Подынтегральными выражениями являются аналитические дифференциальные 1-формы.

Таким образом, появляется возможность рассматривать (27) и (29) как контурные интегралы непосредственно на дисперсионной диаграмме $H$. Подынтегральными выражениями для аналогов (27) и (29) являются ограничения форм

и на $H$. Сами эти формы различны, но их ограничения на $H$ одинаковы. Действительно, по теореме о неявной функции на $H$ выполняется из которого и следует равенство ограничений форм.

Таким образом, (27) и (29) могут быть переписаны как контурные интегралы на одном и том же комплексном многообразии $H$ от одной и той же формы на $H$. При этом контуры интегрирования для (27) и (29) разные (и даже число контуров различно). Поэтому доказательство эквивалентности представлений (27) и (29) сводится к доказательству возможности деформировать одно семейство контуров в другое.

Мы находим идею записывать волновые поля в виде контурных интегралов на дисперсионной диаграмме очень полезной. В частности, эта идея оказалась продуктивна при описании полей на дискретных периодических сетках [17, 18].

Разумеется, комплексный анализ на многообразиях является достаточно экзотической областью для специалистов по акустике, поэтому, имея в виду все сказанное, мы далее попытаемся построить наше рассуждение в терминах обычных функций одной комплексной переменной и их римановых поверхностей. В частности, тождество

можно трактовать как замену переменной в подынтегральной функции при ${{\omega }} = {{\omega }}\left( k \right)$.

6. СВОЙСТВА ДИСПЕРСИОННОГО УРАВНЕНИЯ

1. Покажем, что дисперсионная функция (23) является полиномом не только от $W = {{{{\omega }}}^{2}}$, но и от $K = {{k}^{2}}$, т.е. не содержит нечетных степеней ${{\omega }}$ и $k$:

Для этого заметим, что

Здесь мы использовали свойства (2). Следовательно, $D$ не может содержать слагаемых, содержащих нечетные степени $k$.

2. В общем случае функция $k\left( {{\omega }} \right)$ является голоморфной в областях с $\frac{{\partial D}}{{\partial k}} \ne 0$. Это следует из теоремы о неявной функции. Оговоримся, что мы не рассматриваем точки, где одновременно выполняются условия $\frac{{\partial D}}{{\partial {{\omega }}}} = 0$, $\frac{{\partial D}}{{\partial k}} = 0$, а также (24), поскольку это накладывает три комплексных ограничения на функции двух комплексных переменных. В общем случае таких точек нет.

Заметим, что точки, в которых $\frac{{\partial D}}{{\partial {{\omega }}}} = 0$, $\frac{{\partial D}}{{\partial k}} = 0$, называются точками Шестопалова [19]. В общем случае они не принадлежат дисперсионной диаграмме, а находятся рядом с ней.

3. В общем случае точки ветвления $R$ имеют второй порядок. Система уравнений

определяет положение точек ветвления $R$. Разложим $D\left( {{{\omega }},k} \right)$ вблизи точки ветвления ${{\omega }_{0}}$ и ветвящегося значения ${{k}_{0}}$ функции $k\left( {{\omega }} \right)$:

Решение дисперсионного уравнения выглядит так:

где

Если $a \ne 0,~\,\,b \ne 0$, то из (38) следует, что точки ветвления поверхности $R$ имеют второй порядок. Аналогичное утверждение верно для $R'$.

4. Все точки ветвления $R$ можно разделить на два типа: частоты отсечки и обменные точки ветвления. Частоты отсечки ${{{{\omega }}}_{{co}}}$ определяются следующей системой уравнений:

Вблизи каждой из таких точек

Из этого соотношения следует, что ${{{{\omega }}}_{{co}}}$ соединяет листы римановой поверхности $R$ с противоположными по знаку значениями (${{k}_{j}}\left( {{\omega }} \right)$ с $ - {{k}_{j}}\left( {{\omega }} \right)$). Кроме того, согласно соотношению действительности, все ${{{{\omega }}}_{{co}}}$ принадлежат действительной оси. Заметим, что контур интегрирования в (27) сдвинут с действительной оси, на которой есть точки ветвления. Поэтому выражение (27) корректно.

Точки ветвления поверхности $R$ второго типа соответствуют $k \ne 0$. Эти точки ветвления лежат не на действительной оси ${{\omega }}$. Существование обменных точек ветвления определяет, в частности, “расталкивание” ветвей дисперсионной диаграммы волноводов (это явление известно как avoiding crossing). Подробнее об этом написано в [13, 14, 20]. Обменные точки ветвления связывают между собой листы, соответствующие различным модам.

5. Аналогично, если мы рассматриваем функцию ${{\omega }}\left( k \right)$, заданную неявно с помощью (24), то риманова поверхность $R{\kern 1pt} {\kern 1pt} '$ этой функции также имеет точки ветвления, положение которых определяется системой уравнений:

Точки ветвления $R{\kern 1pt} {\kern 1pt} '$, аналогично точкам ветвления $R$, также делятся на два типа. “Частоты отсечки” ${{k}_{{co}}}$ определяются соотношением:

Точки ветвления $R'$ второго типа, также как и обменные точки ветвления $R$, лежат в комплексной области k-плоскости и влияют на поведение ветвей дисперсионной диаграммы.

6. Сделаем ряд утверждений о поведении функций $k\left( {{\omega }} \right)$ и ${{\omega }}\left( k \right)$ при $\left| {{\omega }} \right| \to \infty $ и $\left| k \right| \to \infty $ (мы предполагаем, что на $H$ большие $\left| {{\omega }} \right|$ соответствуют большим $\left| k \right|$). При больших значениях $\left| {{\omega }} \right|$ и $\left| k \right|$ дисперсионное уравнение для матричного уравнения Клейна–Гордона приближенно выглядит так:

Введем обозначение:

Тогда (43) преобразуется в

Это характеристическое уравнение для следующей обобщенной задачи на собственные значения:

Так как матрицы ${{D}_{2}}$ и $M$ действительные, симметричные, положительно определенные, то все собственные значения ${{\lambda }}$ задачи (46) являются действительными положительными. Следовательно, при больших значениях $\left| {{\omega }} \right|$ и $\left| k \right|$ для ${{\omega }}\left( k \right)$

или для $k\left( {{\omega }} \right)$

Из последних равенств следует ряд утверждений:

1. Все ветви на бесконечности могут быть разделены на пары мод, распространяющихся в положительном и отрицательном направлении.

2. Если все значения ${{{{\lambda }}}_{j}}$ различны (это общий случай), то бесконечность не является точкой ветвления $R$ ($R{\kern 1pt} {\kern 1pt} '$). Это может быть важным при замыкании контуров на бесконечности в области экспоненциального затухания подынтегрального выражения.

7. ДОКАЗАТЕЛЬСТВО ТОЖДЕСТВЕННОСТИ ПРЕДСТАВЛЕНИЙ ПОЛЯ (27) И (29)

Сформулируем следующий план доказательства тождественности представлений (27) и (29) при $t > 0$, $x > 0$:

1. В представлении (27) сдвигаем контуры интегрирования по $R$ в область больших $\left| {{\omega }} \right|$ и $\left| k \right|$.

2. В представлении (29) сдвигаем контуры интегрирования по $R{\kern 1pt} {\kern 1pt} '$ в область больших $\left| {{\omega }} \right|$ и $\left| k \right|$.

3. Пользуясь (47), показываем, что интегралы вдоль сдвинутых контуров на $R$ и $R{\kern 1pt} {\kern 1pt} '$ равны.

В статье [13] было показано, что в случае двухслойного волновода все контуры интегрирования в представлении поля в виде суммы интегралов по ${{\omega }}$ можно сдвинуть сколь угодно далеко в верхнюю полуплоскость ${{\omega }}$-плоскости так, что значение суммы интегралов при этом не меняется. Это нетривиальное утверждение, поскольку при деформации контуры могут задевать точки ветвления римановой поверхности $R$. Такая деформация может быть невозможна для одного контура, но она оказывается возможна для “пачки” контуров. Контуры при этом перестраиваются определенным образом. На рис. 5 сверху показаны два контура интегрирования, расположенные на двух листах, соединенных общей обменной точкой ветвления (жирная черная точка на рисунке). Проведем разрез так, как показано на рис. 5 черной линией. Согласно теореме Коши, мы можем сдвигать контуры интегрирования в области аналитичности функции, не меняя значение интеграла. Будем смещать оба контура вверх. Контуры при этом будут огибать разрезы, образуя дополнительные петли. В результате появляются пары идущих вдоль разреза, противоположно направленных участков контуров. Интеграл вдоль таких пар в сумме дает ноль. Следовательно, эти участки можно удалить. Таким образом, изначальные контуры интегрирования можно заменить на те, которые изображены на рис. 5 внизу.

Эти же идеи применимы и к (27). Напомним, что интегрирование в представлении (27) происходит только по тем листам, для которых выполняется условие ${\text{Im}}\left[ k \right] > 0$ на прямой ${\text{Im}}\left[ {{\omega }} \right] = {{\varepsilon }}$. Так как все частоты отсечки ${{{{\omega }}}_{{co}}}$ лежат на действительной оси ${{\omega }}$, то при смещении контуров интегрирования в верхнюю полуплоскость необходимо пройти только обменные точки ветвления. Чтобы показать, что все эти точки ветвления можно пройти имеющимися контурами интегрирования, необходимо показать, что эти точки ветвления попарно связывают именно те листы поверхности $R$, по которым идет изначально интегрирование. Заметим, что в процессе непрерывной деформации контуров интегрирования в верхнюю полуплоскость ${{\omega }}$-плоскости знак ${\text{Im}}\left[ k \right]$ не может измениться, что следует из соотношения действительности. Значит, точки ветвления, которые мы проходим, соответствуют также ${\text{Im}}\left[ k \right] > 0$ и соединяют попарно листы $R$, для которых ${\text{Im}}\left[ k \right] > 0$ при ${\text{Im}}\left[ {{\omega }} \right] > 0$, это именно те листы, по которым изначально идет интегрирование в (27). А значит, мы можем сдвинуть все $N$ контуров интегрирования в верхнюю полуплоскость, пройдя все точки ветвления. Деформированные контуры интегрирования обозначены ${{\gamma }}$ на рис. 6а.

Так как интегрирование в (29) происходит вдоль всех листов $R{\kern 1pt} {\kern 1pt} '$, а все точки ветвления (обоих типов) имеют второй порядок, то интегрирование сводится к интегрированию вдоль контуров ${{\gamma }}_{j}^{'}$ (рис. 6б), расположенных на всех $2N$ листах поверхности $R{\kern 1pt} {\kern 1pt} '$.

Рассмотрим поведение экспоненциального множителя в (29) при $\left| k \right| \to \infty $. Применяя (47), получаем

Положим $\sqrt {{{{{\lambda }}}_{j}}} > 0$. Тогда для действительных положительных x, t и $\sqrt {{{{{\lambda }}}_{j}}} $ и k ∈ ${{\gamma }}_{j}^{'}$ все интегралы с экспоненциальным множителем

равны нулю в соответствии с леммой Жордана. Тогда среди $2N$ контуров ${{\gamma }}_{j}^{'}$ остаются только $N$ контуров с экспоненциальным множителем

Рассмотрим отображение $k \to {{\omega }}$ (образованное функцией ${{\omega }}\left( k \right)$) для $k$, движущемуся вдоль некоторого из оставшихся контуров ${{\gamma }}_{j}^{'}$. На этом контуре

Из этой формулы следует, что если контур, вдоль которого изменяется $k$, представляет собой полуокружность на k-плоскости, то соответствующие ${{\omega }}$ также образуют полуокружность в ${{\omega }}$-плоскости (радиус которой в $\sqrt {{{{{\lambda }}}_{j}}} $ раз больше). Очевидно, последние полуокружности можно деформировать в контуры ${{{{\gamma }}}_{j}}$, изображенные на рис. 6а.

Используя равенство для подынтегральных функций, полученное ранее, получаем, что выражения (27) и (29) равны при $x > 0$ и $t > 0$.

8. ЗАКЛЮЧЕНИЕ

Волновод достаточно произвольной природы приближенно описывается матричным уравнение Клейна–Гордона, т.е. считается, что его поперечное сечение дискретизовано. Кроме того, предполагается, что сечение волновода компактно и отсутствует приток/отток энергии.

Выписываются интегральные представления поля в волноводе (27) и (29), а также дисперсионное уравнение (24). Интегральные представления поля интерпретированы как контурные интегралы от многозначных функций по соответствующим римановым поверхностям, а также как контурные интегралы непосредственно по дисперсионной диаграмме волновода. Выведены некоторые свойства дисперсионного уравнения. Показано, что представления (27) и (29) могут быть преобразованы одно в другое путем особой деформации пачки контуров.

Предполагается, что результаты работы могут быть распространены на волноводы с континуальным описанием, но этот вопрос требует дополнительного исследования.

Работа выполнена при поддержке гранта РФФИ 19-29-06048.