Акустический журнал, 2022, T. 68, № 3, стр. 300-311

ВВЕДЕНИЕ

Методы увеличения отношения сигнал/помеха в волноводе основываются на анализе закономерностей формирования звуковых полей сигналов и помех, позволяющих с большей или меньшей эффективностью накапливать в частотно-пространственной области мощность сигнала и подавлять помехи [1–3]. Среди наиболее помехоустойчивых и одновременно робастных – устойчивых к вариации моделей сигналов и помех методов, по нашему мнению, можно выделить голографические алгоритмы [4–6], в рамках которых поставлена и решена задача накопления мощности сигнала вдоль “гребней” – зон интерференционных максимумов (ИМА) в результате применения двумерного преобразования Фурье и траекторного накопления. В [5, 6] показана также возможность одновременной и помехоустойчивой оценки дальности и радиальной компоненты скорости в пассивном режиме. Следует выделить работу [7], в которой также оценивается дальность и применяются близкие принципы накопления мощности сигнала, но для решения задачи применяется преобразование Радона. В результате и экспериментально, и расчетным путем установлено [4–7], что отношение сигнал/помеха при суммировании мощности сигнала вдоль гребней эффективно возрастает, так как кумулятивная энергия накапливается с использованием мощности сигналов в зонах ИМА.

Эти результаты в большей или меньшей степени основываются на том, что при относительном движении приемника и источника или распространении сигналов вдоль апертуры протяженных антенн в частотно-пространственной области поля интенсивности формируется устойчивая веерная структура, в пределах которой чередующиеся зоны максимумов и минимумов подчиняются инвариантным соотношениям [8–12]. Характерным для веерной структуры является ее устойчивость к изменению условий распространения, что и позволило С.Д. Чупрову ввести понятие “интерференционный инвариант” β [8]. Позднее в работах Е.Ф. Орлова, Г.А. Грачева, Л.М. Бреховских [9–12], а также в зарубежных публикациях [13–15] была изучена связь интерференционной частотно-пространственной структуры поля интенсивности с внешними воздействующими факторами – параметрами грунта, глубиной и неоднородностью волновода, внутренними волнами и т.д. Подтверждено, что при ограниченных интервалах Δω и Δr параметр β слабо зависит от частоты и расстояния, и в первом приближении его действительно можно считать постоянным. Но значения инварианта зависят от свойств волновода, в частности, клиновидности [16] и вертикального распределения скорости звука, в зависимости от которого инвариант может иметь значения “1”, “–3”, бесконечность и т.д. [11, 12]. Отметим, что непрерывные (гладкие) зоны ИМА наблюдаются только на небольших расстояниях. При увеличении расстояния и повышении частоты происходит расщепление веерных структур, и формируются сначала зоны "бифуркации”, затем “трифуркации” [17].

В [18, 19] применительно к мелкому морю выполнено дополнительное исследование интерференционной амплитудно-фазовой структуры низкочастотного звукового давления (ЗД). В частности, установлено, что инвариантные характеристики поля наблюдаются не только при частотно-пространственном распределении спектров мощности (интенсивности) сигналов, но и на фазовой плоскости – это позволило ввести понятие фазового инварианта. Но аномальные свойства ни энергетических, ни фазовых инвариантов не исследованы, а методы их описания в рамках дифференциальных уравнений требуют дополнительной проработки. Не выполнено сравнение эффективности накопления мощности сигналов с целью увеличения отношения сигнал/помеха с использованием двух инвариантов. Не вполне ясен вопрос о распределении суммарной мощности сигналов вдоль гребней при переходе от одной частоты к другой. Аналогичную задачу необходимо решать и для линий равных фаз.

Ниже рассматриваются некоторые из поставленных задач. Установлено различие эффективности накопления мощности ЗД в частотно-пространственной области поля интенсивности и на фазовой плоскости. Показано, что накопление мощности при сохранении реализациями постоянной фазы происходит эффективнее, чем при сложении некогерентных сигналов, зарегистрированных вдоль гребней на разных частотах и расстояниях. Отмечается, что, если фазы сигналов не постоянные, когерентность отдельных Фурье-компонент теряется и выполняется видео когерентное суммирование, т.е. на разных частотах суммируются энергии сигналов. Показано, что в отличие от свободного пространства существующие в волноводе аномалии ограничивают интервалы расстояний и диапазоны частот, в пределах которых возможно эффективное накопление энергии как на поле интенсивности, так и на фазовой плоскости. Сформулированы ограничения на интервалы расстояний или диапазоны частот, в пределах которых возможно эффективное накопление энергии.

1. УРАВНЕНИЕ ЛИНИИ РАВНЫХ ФАЗ ДЛЯ ВОЛНОВОДА ПЕКЕРИСА

Известные теоретические построения, описывающие свойства интерференционной структуры в мелком море, основаны на пространственно-частотном анализе поля интенсивности ЗД. Следуя Л.М. Бреховских [11], запишем для волновода Пекериса выражение для звукового давления монопольного излучателя в этом волноводе:

где ω – круговая частота, r – расстояние между источником и приемником, z₀ и z – глубины источника и приемника, t – время, ρ₀ – плотность воды, h – глубина волновода, k = ω/c₀ – волновое число, c₀ – скорость звука в воде, N – количество нормальных волн, ${{p}_{l}} = \sin ({{l\pi {{z}_{0}}} \mathord{\left/ {\vphantom {{l\pi {{z}_{0}}} H}} \right. \kern-0em} H})\sin ({{l\pi z} \mathord{\left/ {\vphantom {{l\pi z} H}} \right. \kern-0em} H})$ – коэффициенты их возбуждения, $H = h + {m \mathord{\left/ {\vphantom {m {k\nu }}} \right. \kern-0em} {k\nu }}$ – эффективная глубина волновода, m = ρ₁/ρ₀, ρ₁ – плотность среды в подстилающем полупространстве, ${{\nu }^{2}}{\kern 1pt} = 1 - {{n}^{2}}$, $n = {{c}_{0}}{\kern 1pt} /{\kern 1pt} {{c}_{1}} < 1$, c₁ – скорость звука в этом полупространстве, ${{\varphi }_{l}}(\omega ,r) = {{k}_{l}}r - \omega t - \pi {\kern 1pt} /{\kern 1pt} 4$ – фаза и ${{k}_{l}} = k\cos (l\pi {\kern 1pt} /{\kern 1pt} kH)$ – волновое число l-й нормальной волны. Полученное Л.М. Бреховских выражение (1) и анализ интерференционной структуры поля интенсивности позволили [8, 9] записать соотношение, описывающее устойчивые интерференционные полосы интенсивности с максимальной амплитудой где β – параметр, названный С.Д. Чупровым “интерференционным инвариантом”. Фактически это соотношение представляет собой дифференциальное уравнение, решения которого существенным образом зависят от значения параметра β. Если параметр β можно считать постоянным, то решение находится в явном виде. А именно, для β > 0 решение уравнения имеет вид $r(\omega ) = a{{\omega }^{\beta }}$, в частном случае при β = 1 графики этих функций являются прямыми линиями. А для β < 0 решениями (2) являются функции $r(\omega ) = {a \mathord{\left/ {\vphantom {a {{{\omega }^{{|\beta |}}}}}} \right. \kern-0em} {{{\omega }^{{|\beta |}}}}}$, в частном случае при β = –1 эти графики являются гиперболами. В выписанных решениях коэффициент a определяется выбранными начальными условиями задачи Коши. Отметим, что уравнение (2) не устанавливает никаких связей параметра β со свойствами волновода.

Использование (1) позволяет по аналогии с (2) записать в пространстве частота–расстояние дифференциальное уравнение, описывающее линии равных фаз поля давления в виде [19]:

где $C = {{{{S}_{1}}} \mathord{\left/ {\vphantom {{{{S}_{1}}} S}} \right. \kern-0em} S}$, $D = {{{{S}_{2}}} \mathord{\left/ {\vphantom {{{{S}_{2}}} S}} \right. \kern-0em} S}$,

В соответствии с изложенными выше рассуждениями, вид решений уравнения (3) существенно зависит от знака параметра ${{\beta }_{\varphi }} = - (1 + {{\pi hC} \mathord{\left/ {\vphantom {{\pi hC} {k{{H}^{2}}}}} \right. \kern-0em} {k{{H}^{2}}}})$. В [19] показано, что в волноводе Пекериса $1 + {{\pi hC} \mathord{\left/ {\vphantom {{\pi hC} {k{{H}^{2}}}}} \right. \kern-0em} {k{{H}^{2}}}} > 0$, т.е. решения уравнения (3) имеют вид $r(\omega ) = {a \mathord{\left/ {\vphantom {a {{{\omega }^{{|\beta |}}}}}} \right. \kern-0em} {{{\omega }^{{|\beta |}}}}}$, и линии равных фаз подобны гиперболам.

2. УРАВНЕНИЕ ЛИНИЙ ГРЕБНЯ

Уравнение линий гребня, т.е. линии максимумов амплитуд давления для волновода Пекериса в пространстве частота–расстояние получим, исходя из того, что амплитуда давления вдоль линии гребня может не оставаться постоянной, но вдоль этого направления она изменяется в наименьшей степени. Будем считать, что в любой точке на линии гребня производная от модуля амплитуды $\left| {P(\omega ,r)} \right|$ по направлению n, касательному к линии гребня в этой точке, принимает минимальное значение при переборе по всем возможным направлениям, которые можно задать с помощью полярного угла α на плоскости (ω, r):

где cos α_ω и cos α_r – направляющие косинусы прямой линии с полярным углом α. Из (1) легко получить следующие значения входящих в (4) частных производных: где ${{A}_{0}}{\kern 1pt} \, = {{{{\rho }_{0}}\sqrt {8\pi } } \mathord{\left/ {\vphantom {{{{\rho }_{0}}\sqrt {8\pi } } h}} \right. \kern-0em} h}$,

Уравнение (4) можно упростить, считая в первом приближении, что минимальное значение производной от модуля амплитуды давления по направлению равно нулю. Приравнивая к нулю полный дифференциал модуля давления $d\left| {P(\omega ,r)} \right| = 0$, получим:

Таким образом, общий вид полученного уравнения линий гребня давления для волновода Пекериса согласуется по структуре с дифференциальным уравнением (2) для линий интерференционных полос интенсивности, полученным в [8–14], но при этом коэффициент уравнения β оказывается не произвольной константой, а определяется через заданные для волновода и нормальных волн исходные параметры.

3. СРАВНЕНИЕ ХАРАКТЕРИСТИК ПОЛЯ ВДОЛЬ ГРЕБНЕЙ И ВДОЛЬ ЛИНИЙ РАВНЫХ ФАЗ. ВЛИЯНИЕ АНОМАЛЬНЫХ ЗОН

Моделирование полей проведено для условий, принятых в [7]: источник монопольный монохроматический, глубина волновода 100 м, скорость звука в воде 1500 м/с, m = 1.7; n = 0.88; глубины приемника 20 м и источника 40 м. Расстояния задаются в интервале 500–2500 м, диапазон частот 350–700 Гц. Результаты расчетов представлены на рис. 1.

Для сравнения результатов расчетов с данными в [7], моделировалась поверхность амплитуд ЗД, контурный и объемный графики которой приведены на рис. 1б и 1в соответственно. Хорошо видно полное соответствие структур линий гребней на контурных графиках поля интенсивности (рис. 1а) и поля амплитуды давления (см. рис. 1б). И это неслучайно, поскольку эти линии, как легко показать, должны иметь одинаковый наклон и расположение. Покажем, например, что эти линии имеют одинаковый наклон: при определении наклона линии гребня интенсивности в [8–12] исходят из соотношения ${{\Delta \omega } \mathord{\left/ {\vphantom {{\Delta \omega } {\Delta r}}} \right. \kern-0em} {\Delta r}} = {{ - ({{\partial I} \mathord{\left/ {\vphantom {{\partial I} {\partial r}}} \right. \kern-0em} {\partial r}})} \mathord{\left/ {\vphantom {{ - ({{\partial I} \mathord{\left/ {\vphantom {{\partial I} {\partial r}}} \right. \kern-0em} {\partial r}})} {({{\partial I} \mathord{\left/ {\vphantom {{\partial I} {\partial \omega }}} \right. \kern-0em} {\partial \omega }})}}} \right. \kern-0em} {({{\partial I} \mathord{\left/ {\vphantom {{\partial I} {\partial \omega }}} \right. \kern-0em} {\partial \omega }})}}$, поэтому

Следовательно, направления линий гребней в поле интенсивности совпадают с направлениями линий гребней в поле звукового давления. Это позволяет рассчитать зависимость фазы ЗД вдоль гребня (в координатах f и r).

Для указанных диапазонов частоты и расстояний были также рассчитаны фазовая поверхность, представляющая собой фрагмент седловой поверхности (гиперболического параболоида). Эта поверхность и ее контурный график приведены на рис. 2.

Очевидны существенные отличия амплитудной и фазовой поверхностей. В частности, амплитудные поверхности на рис. 1 имеют набор поперечных разрезов, на которых они при увеличении частоты претерпевают разрывы – скачки амплитуды давления, вызванные появлением новых нормальных волн. В структуре фазовой поверхности на рис. 2 такие скачки отсутствуют. Однако на фазовой поверхности имеются специфические изломы, связанные с аномалиями – дислокациями фаз [20–22], возникающими в зонах минимумов давления. Таким образом, структура гребней – интерференционных полос максимальной амплитуды интенсивности (или давления) – отличается от структуры фазовой поверхности и линий равных фаз.

В связи с обнаружением этих особенностей, для более детального изучения амплитудной и фазовой структур полей ЗД исследовалась область частот 9–30 Гц и расстояний 200 $ \leqslant r \leqslant $ 2000 м. При этом приемник находился на глубине 100 м, а источник – на глубине 20 м. На рис. 3 приведены полученные объемные изображения и контурные графики амплитудной и фазовой поверхностей звукового давления.

На рис. 3а и 3в видно, что в рассматриваемой частотной области можно выделить четыре зоны, в каждой из которых количество нормальных волн постоянно, а при переходе в соседнюю зону добавляется новая мода. Частоты, на которых появляются новые моды: 10.8, 16.8 и 23.5 Гц. В диапазоне от 9 до 10.8 Гц поле формируется двумя модами, от 10.8 до 16.8 Гц – тремя модами и т.д. В последней из рассматриваемых зон – свыше 23.5 Гц наблюдается четыре нормальные волны. Однако в структуре фазовой поверхности при появлении новых нормальных волн никаких изменений не происходит, что отчетливо видно по рис. 3б и 3г. Но при этом, как отмечено выше, фазовая поверхность имеет свои особенности. На рис. 3а и 3в кружками с номерами 1–5 отмечены зоны минимумов амплитуды давления, которым на рис. 3б и 3г соответствуют аномальные зоны – зоны дислокации [20–22] фазы, помеченные кружками с теми же номерами. Эти дислокации порождают изломы, идущие далее по фазовой поверхности либо параллельно оси расстояний (зоны с номерами 1 и 5), либо под углом к ней (зоны с номерами 2–4). В точках дислокаций и на идущих от них изломах фазовая поверхность имеет скачки значений фазы величиной до π радиан. Величина скачка тем больше, чем глубже минимум амплитуды давления и меньше расстояние до дислокации фазы. Кроме того, на поверхности амплитуд давления имеются зоны минимумов, не связанные с появлением дислокаций фазы и изломов фазовой поверхности. Такие зоны минимумов показаны на рис. 3а и 3в кружками с номерами 6–8. Заметим, что в том случае, когда точка минимума амплитуды давления попадает на границу между зонами с разным количеством нормальных мод (кружки 1, 2, 5), линии разломов фазовой поверхности совпадают с линиями скачков амплитуды давления.

Из приведенных результатов следует, что обнаруженные аномалии как на поверхности, описывающей структуру поля интенсивности, так и на фазовой плоскости, ограничивают стационарные пространственные зоны (участки траекторий) или диапазоны частот, в пределах которых возможно видео когерентное или когерентное накопление мощности сигналов. В свободном однородном пространстве такие ограничения отсутствуют, так как отсутствует дисперсия скорости звука и нет интерференции.

4. СРАВНЕНИЕ ЭНЕРГЕТИЧЕСКОГО И ФАЗОВОГО ИНВАРИАНТОВ

Далее в условиях, принятых выше для первой группы расчетов, определялись фактические линии равных фаз и гребня, а также их теоретические аналоги, являющиеся решением дифференциальных уравнений (3) и (5) соответственно (рис. 4). Кроме того, вычислялись амплитуды и фазы давления вдоль этих линий. Фактические линии гребня и равных фаз определялись путем прямого численного анализа амплитудной и фазовой поверхностей. В качестве начального условия задачи Коши для дифференциальных уравнений выбран один из локальных максимумов на начальной частоте 350 Гц, к которому также были “привязаны” и фактические линии гребня, и фактические линии равных фаз

На рис. 4а и 4б сравниваются решения уравнений (3) и (5) с соответствующими фактическими (численными) линиями для частот 350–385 и 350–700 Гц соответственно. Видно, что знаки наклона линий гребня и равных фаз противоположны, а крутизна наклона кривых возрастает при увеличении частоты. Можно также отметить, что решение дифференциального уравнения (3) (кривая 4) хорошо соответствует фактической линии равных фаз (кривая 3) для достаточно большого диапазона частот 350–700 Гц и соответствующих расстояний. В то же время решение уравнения (5) для линии гребня (кривая 2) соответствует фактической линии гребня (кривая 1) на ограниченном диапазоне частот 350–385 Гц (см. рис. 4а) и отклоняется от нее в диапазоне до 700 Гц. Такое возрастание погрешностей является следствием ограничения, принятого при выводе уравнения (5): количество нормальных волн не должно изменяться, либо эти изменения не оказывают существенного влияния на формируемое поле. Это условие, очевидно, не соблюдается для второго диапазона частот, что приводит к расщеплению веерной структуры поля ЗД и переключению линии зон интерференционных максимумов на вновь образованные гребни. Решения дифференциального уравнения этот эффект не учитывают, поэтому на рис. 4б накапливается отклонение теоретической линии гребня (кривая 2) от фактической (кривая 1). Полученные результаты показывают, что уравнения (3) и (5) могут быть использованы для прогноза ориентации линий равных фаз и гребней в реальных ситуациях, но для уравнения (5) – с ограничениями.

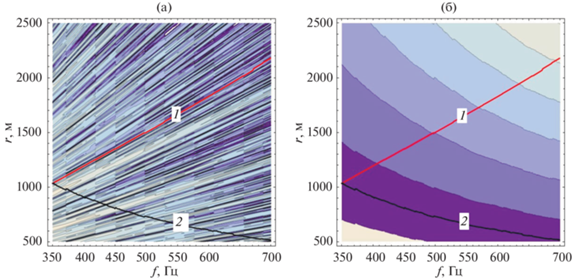
На рис. 5 показаны линии гребня (кривые 1) и равных фаз (кривые 2), совмещенные с контурными графиками амплитуды (рис. 5а) и фазы (рис. 5б) давления. На рис. 5а хорошо видно, что фактическая линия ИМА (кривая 1) из-за расщепления веерной структуры, связанной с появлением новых нормальных волн, может “перескакивать” на соседние гребни с большей амплитудой. А линия равных фаз (кривая 2) пересекает несколько соседних гребней. Видно также (см. рис. 5б), что интегральная фаза ЗД вдоль гребня возрастает пропорционально частоте.

На рис. 6 для различных номеров гребней и для соответствующим образом смещенных линий равных фаз изображены графики амплитуды давления, рассчитанные вдоль фактических линий гребня (рис. 6а) и равных фаз (рис. 6б). Видно, что амплитуды вдоль фактических линий гребней (кривые 1) в среднем убывают. Это совершенно естественно, так как вдоль этой линии при увеличении частоты ω расстояние r также увеличивается, и амплитуда убывает по конкретному закону спадания, зависящему от вертикального распределения скорости звука, глубин волновода, источника и приемника, но с учетом вариации частоты.

На рис. 6а видно, что амплитуды ЗД вдоль линии равных фаз (кривая 2), на которой расстояние $r$ убывает при возрастании частоты ω, на начальном участке (до примерно 550–600 Гц) в основном меньше, чем амплитуды на линии гребня. Затем, по мере убывания амплитуды на линии гребня амплитуда на линии постоянной фазы за счет перемещения в область меньших расстояний и, следовательно, больших амплитуд, становится в среднем больше амплитуды ЗД на линии гребня. Это может оказывать заметное влияние на эффективность накопления энергии сигнала при смещении вдоль гребней и линий равных фаз.

Фаза на фактической линии равных фаз, рис. 6б, как ей и положено, постоянна, что видно по ее параллельности оси абсцисс, а вот на линии гребня (кривые 1) она в соответствии с уравнением (3) линейно возрастает. Этот результат хорошо согласуется с результатами работ [23–25], согласно которым градиенты фазы и групповое время запаздывания вдоль зон интерференционных максимумов (вдоль гребней) определяются стабильными эффективными “фазовой и групповой” скоростями звука в волноводе. Поэтому интегральная фаза увеличивается пропорционально расстоянию, что и наблюдается на рис. 6б (кривые 1).

Как известно [8–12], на плоскости частота–расстояние при ограниченных диапазонах изменений частоты Δω и расстояния Δr, наклон линий гребня β определяется из соотношения $\beta \approx ({{{{r}_{0}}} \mathord{\left/ {\vphantom {{{{r}_{0}}} {{{\omega }_{0}}}}} \right. \kern-0em} {{{\omega }_{0}}}})({{\Delta \omega } \mathord{\left/ {\vphantom {{\Delta \omega } {\Delta r}}} \right. \kern-0em} {\Delta r}})$, где (ω₀, r₀) – выбранная начальная точка. По данным, полученным при расчете изображенной на рис. 4б фактической линии гребня (кривая 1), имеем ω₀ = 350 Гц, ω_K = 700 Гц, Δω = 350 Гц, r₀ = 1034 м, r_K = 2079 м, Δr = 1045 м, где (ω_K, r_k) – конечная точка линии. Получаем известный [8–12] для волновода Пекериса результат: $\beta \approx ({{1034} \mathord{\left/ {\vphantom {{1034} {350}}} \right. \kern-0em} {350}})({{350} \mathord{\left/ {\vphantom {{350} {1045}}} \right. \kern-0em} {1045}}) = 0.99 \approx + 1$. Следовательно, линии гребня на плоскости частота–расстояние действительно описываются уравнением вида $r(\omega ) = a{{\omega }^{\beta }} = {{{{r}_{0}}\omega } \mathord{\left/ {\vphantom {{{{r}_{0}}\omega } {{{\omega }_{0}}}}} \right. \kern-0em} {{{\omega }_{0}}}}$.

Аналогичный расчет можно произвести и для линии равных фаз, но нужно учесть, что в соответствии со сделанными выше выводами это кривая является гиперболоподобной линией, поэтому касательная к линии постоянной фазы совпадает с самой линией только на малых расстояниях. В связи с этим для определения наклона касательной к фактической линии равных фаз выберем данные, использованные для построения графика этой линии на рис. 4а: ω₀ = 350 Гц, ω_K = = 385 Гц, Δω = 35 Гц, r₀ = 1034, r₁ = 936 м, Δr = –98 м. Тогда ${{\beta }_{\phi }} = {{1034} \mathord{\left/ {\vphantom {{1034} {350}}} \right. \kern-0em} {350}} \times {{35} \mathord{\left/ {\vphantom {{35} {( - 98)}}} \right. \kern-0em} {( - 98)}} = - 1.06 \approx - 1$. Отсюда следует, что в волноводе Пекериса линия равных фаз является обычной гиперболой: $r(\omega ) = {a \mathord{\left/ {\vphantom {a \omega }} \right. \kern-0em} \omega }$, где $a = {{{{r}_{0}}} \mathord{\left/ {\vphantom {{{{r}_{0}}} {{{\omega }_{0}}}}} \right. \kern-0em} {{{\omega }_{0}}}}$.

Значения параметров β и β_φ вдоль теоретических линий гребня и равных фаз можно рассчитать одновременно с расчетом самих линий. Эти значения вычислены для двух разных волноводов, графики которых в зависимости от линейной частоты f представлены на рис. 7. Кривые 1 на этом рисунке соответствуют волноводу со следующими характеристиками: источник монопольный, глубина волновода 100 м, скорость звука в воде 1500 м/с, m = 1.7; n = 0.88; глубины приемника 20 м и источника 40 м. Расстояния 500–2500 м, диапазон частот 350–700 Гц. А кривые 2 получены для волновода глубиной h = 200 м, отношение плотностей m = 2.7, отношение скоростей звука n = 0.83. По рисунку хорошо видно, что значения параметров относительно слабо зависят от частоты. Но если значения параметра β колеблются вблизи “+1”, то значения параметра β_φ варьируются вблизи значения “–1”. Как показывают дополнительные расчеты, в определенных пределах значения параметра β_φ слабо зависят и от свойств волновода Пекериса. В связи с этим параметр β_φ также можно считать инвариантом, но фазовым. Заметим, что у фазового инварианта при появлении новых нормальных волн скачки не наблюдаются, но вблизи дислокаций имеются резкие и знакопеременные выбросы, которые хорошо наблюдаются и на рис. 3 и 7.

Из полученных результатов также следует, что для волновода Пекериса (а, возможно, и для других видов волноводов) имеет место соотношение ββ_φ ≈ –1. Так как параметры β и β_φ фактически определяют наклоны линий гребня и наклоны касательных к линиям равных фаз, соотношение ββ_φ ≈ –1 означает, что обсуждаемые линии должны быть приблизительно ортогональны. Стабильность значений β и β_φ далее используется для накопления мощности вдоль линий гребня и линий с постоянной фазой.

5. СРАВНЕНИЕ ЭФФЕКТИВНОСТИ НАКОПЛЕНИЯ МОЩНОСТИ СИГНАЛА

Рассмотрим эффективность накопления мощности сигналов при суммировании спектральных отсчетов вдоль гребней и вдоль линий равных фаз. Накопление мощности сигнала выполним двумя разными способами (рис. 8), но с одинаковым перебором частот на выбранной сетке ${{\omega }_{0}},{{\omega }_{1}},{{\omega }_{2}},...,{{\omega }_{K}}$. При этом для когерентного накопления, т.е. накопления с учетом фазы давления использовалась сумма вида

а для видео когерентного, т.е. накопления без учета фазы

Поскольку речь идет о расчете вдоль некоторой линии r = r(ω), аргумент r в этих суммах однозначно определяется аргументом ω_m. На рис. 8а представлены результаты такого накопления при смещении вдоль фактической линии гребня, соответствующего рис. 4б и рассчитанного для условий, принятых выше для первой группы расчетов. Кривая 1 является графиком накопления мощности сигнала с помощью соотношения (7), а кривая 2 – графиком накопления на основе соотношения (6), т.е. с учетом фазы сигнала. На рисунке видно, что при движении вдоль линии гребня накопление без учета фазы за счет постоянного суммирования максимумов амплитуды оказалось эффективнее, чем накопление с учетом фазы, которая изменяется при вариации ω_m. Причина в том, что при движении вдоль линии гребня фаза Фурье-компонент на разных частотах изменяется. Как следствие, при суммировании сигналов на разных частотах некоторые составляющие увеличивают суммарную мощность, а некоторые – суммируются с противоположным знаком и мощность уменьшается. Это, с одной стороны, делает зависимость от частоты изрезанной (кривая 2), а с другой стороны, суммарная мощность может уменьшаться по сравнению с энергетическим суммированием максимальных уровней сигнала. Таким образом, в общем случае когерентное накопление (6) может оказаться как менее, так и более эффективным, чем энергетическое накопление (7). Это следует из элементарного соображения о том, что сумма квадратов произвольных (с разными знаками) чисел может быть как больше, так и меньше квадрата их суммы.

На рис. 8б представлены результаты накопления мощности при движении вдоль фактической линии равных фаз, которая также показана на рис. 4б. Кривая 3 соответствует накоплению мощности сигнала по соотношению (7), а кривая 4 – накоплению на основе соотношения (6). Видно существенное преимущество когерентного накопления, когда при расчетах учитывается фаза: сумма S₁ на 20–25 дБ превышает сумму S₂. Несложно показать, что этот вывод является общим, поскольку на линии равных фаз для всех выбранных точек сетки ${{\omega }_{0}},{{\omega }_{1}},{{\omega }_{2}},...,{{\omega }_{K}}$ фазы давления одинаковые $\varphi ({{\omega }_{m}},r) = \varphi $. Различие амплитуд $\left| {P({{\omega }_{m}},r)} \right|$ учитывается соотношением

Поскольку квадрат суммы положительных чисел $\left| {P({{\omega }_{m}},r)} \right| > 0$ всегда больше суммы их квадратов, то для линии равных фаз получаем неравенство

т.е. S₁ > S₂ (когерентное накопление мощности эффективней видео когерентного).

И, наконец, примерно совпадающие графики некогерентного накопления на рис. 8в показывают близкую эффективность такого накопления как вдоль линии гребня, так и вдоль линии равных фаз – если сложение выполнять энергетически.

Следует отметить, что в соотношениях (6) и (7) не учитывается помеха, поэтому алгоритм увеличения отношения сигнал/помеха при “движении” вдоль линий равной фазы следует дорабатывать – аналогично алгоритму, разработанному в [6, 7] применительно к суммированию Фурье-компонент вдоль линии гребня. Но если предположить, что помехи являются случайными (гауссовыми), но стационарными, то при суммировании помех по соотношениям (6) и (7), они будут складываться одинаковым способом – некогерентно. Как следствие, увеличение или уменьшение только мощности сигнала будет приводить к увеличению или уменьшению отношения сигнал/помеха. Поэтому соотношения (6) и (7), рассчитанные только по сигналам, дают полное представление о помехоустойчивости двух алгоритмов накопления мощности.

ЗАКЛЮЧЕНИЕ

В многомодовых волноводах интерференционные явления в частотно-пространственной области проявляются при анализе поля интенсивности и на фазовой плоскости. Характеристики двумерных полей, рассчитанных с использованием полученных в статье двух дифференциальных уравнений, существенно различаются, однако их структура в равной мере определяется устойчивыми инвариантными соотношениями. Общеизвестный интерференционный инвариант Чупрова, полученный при анализе поля интенсивности (по нашему мнению – “энергетический” интерференционный инвариант), в мелком море и на низких частотах стремится к “+1”, а фазовый интерференционный инвариант в этих условиях имеет величину, близкую к “–1”. Поверхности гребней и линии равных фаз практически ортогональны и их закономерности отклоняются от “+1” и “–1” только в аномальных зонах, где при увеличении частоты формируются и суммируются новые моды (энергетический инвариант) или образуются зоны с глубокими интерференционными минимумами – дислокациями (фазовый инвариант). Соответственно, для волновода Пекериса имеем ββ_φ ≈ –1. Можно предположить, что аналогичное соотношение имеет место и для других типов волноводов, однако для того, чтобы в этом убедиться, необходимо выполнить дополнительный анализ.

Энергетический и фазовый инварианты отличаются устойчивостью и слабой зависимостью от глубин расположения источника и приемников, частоты звука и условий распространения, но для заданного волновода могут зависеть от вертикального распределения скорости звука. Наблюдается зависимость величины β от сформированных в волноводе групп однотипных мод с разными номерами (водных, вытекающих или захваченных).

Устойчивость инвариантов позволяет построить алгоритмы эффективного обнаружения, основанные на суммировании комплексных спектров сигналов или спектральных плотностей мощности сигналов, соответственно, вдоль линий с постоянной фазой или вдоль гребней. Суммирование Фурье-компонент вдоль линий с постоянной фазой производится когерентно, а потому – в среднем более эффективно. Суммирование спектральных отсчетов интенсивности сигналов вдоль гребней выполняется энергетически – без учета фазы, т.е. видео когерентно. Для увеличения помехоустойчивости можно рекомендовать накапливать мощность сигналов с использованием одновременно двух алгоритмов – при “движении” вдоль гребней и вдоль линий с постоянной фазой.

Интервалы расстояний или диапазоны частот, в пределах которых возможно накопление мощности сигналов, ограничиваются аномальными зонами: а) для гребней – частотами или расстояниями, на которых формируются новые или исчезают ранее сформированные моды; б) для линий с постоянной фазой – зонами с глубокими интерференционными минимумами, т.е. зонами дислокаций – в этих зонах из-за влияния помех оценки фазы могут стать случайными и корреляционная связь сигналов на разных частотах и расстояниях прерывается. Показан принципиально различающийся характер аномалий для линий, описывающих динамику гребней или линий равных фаз.

Формирование при движении источника или приемника особых зон и направлений, имеющих в частотно-пространственной области предсказуемый и стабильный характер, позволяет их использовать для повышения эффективности обнаружения слабых сигналов и оценки их параметров. Особые свойства сигналов, распределенных вдоль гребней зон ИМА, уже используются для увеличения помехоустойчивости и одновременно – определения расстояния до источника и радиальной скорости его движения [5–7]. Накопление мощности сигнала при сложении реализаций вдоль линий с постоянной фазой может оказаться также эффективным, поскольку сигналы, распределенные вдоль этих линий когерентны. Но при “попадании” в зону интерференционного минимума фаза может “теряться” и эффективное накопление реализуется не в полном объеме.

Алгоритмы накопления мощности вдоль линий с постоянной фазой требуют дополнительного исследования.

Работа выполнена при финансовой поддержке программы “Акустика мелкого моря, нелинейная акустическая диагностика, нелинейная динамика волн” (номер гос. регистрации AAAA-A18-118021390174-1), Российского фонда фундаментальных исследований (проект № 19-08-00941) и Министерства науки и высшего образования РФ в рамках государственного задания в сфере научной деятельности № 0852-2020-0015.