Акустический журнал, 2021, T. 67, № 6, стр. 583-594

К теории акустического сканирования повреждений подземных трубопроводов

В. Ш. Шагапов^a, *, Э. В. Галиакбарова^a, b, **, З. Р. Хакимова^a, b, ***

^a Институт механики им. Р.Р. Малютова – обособленное структурное подразделение Федерального государственного бюджетного научного учреждения Уфимского федерального исследовательского центра Российской академии наук (ИМех УФИЦ РАН)
450054 Уфа, Пр. Октября 71, Россия

^b Уфимский государственный нефтяной технический университет
450062 Уфа, ул. Космонавтов 1, Россия

^* E-mail: Shagapov@rambler.ru
^** E-mail: emi.galiakbar@yandex.ru
^*** E-mail: zulfya.hakimova@yandex.ru

Поступила в редакцию 21.04.2021
После доработки 06.07.2021
Принята к публикации 03.08.2021

DOI: 10.31857/S0320791921060113

Полный текст (PDF)

Аннотация

Изучается эволюция импульсного сигнала, инициированного толчком цилиндрического поршня и распространяющегося по неподвижной жидкости, заполняющей трубопровод, который зарыт в грунт и имеет протяженный поврежденный участок. Принятая математическая модель основывается на линеаризованных уравнениях одномерного течения слабосжимаемой жидкости. Пространственная протяженность сканирующего импульсного сигнала полагается значительно меньше длины трубопровода и длины поврежденного участка, но больше диаметра канала. При получении условий отражения на границах поврежденного участка и расчете эволюции сигнала на этом участке принято, что интенсивность утечки жидкости полностью лимитируется проницаемостью грунта. Задача решается численно методом быстрого преобразования Фурье. Для этого получены дисперсионные выражения для фазовой скорости и коэффициента затухания гармонического сигнала на поврежденном участке, коэффициентов отражения и прохождения на границах этого участка. На их основе проведен анализ влияния геометрических параметров канала, проницаемости грунта, реологических свойств жидкости на поведение гармонических волн. Задача об эволюции импульсного сигнала решается в несколько этапов: распространение импульсного сигнала по среде, заполняющей канал; дисперсия сигнала на поврежденном участке с формированием отраженных и прошедших волн возмущения; распространение отраженных и прошедших поврежденный участок импульсных возмущений до модельных датчиков-анализаторов сигналов.

Ключевые слова: импульс, трубопровод, жидкость, фильтрация, грунт

ВВЕДЕНИЕ

Магистральные трубопроводы, являющиеся одними из главных составляющих нашей экономики, используются для транспортировки сырой нефти и нефтепродуктов из районов добычи, производства и хранения до мест потребления, таких как нефтебазы, пункты налива в цистерны промышленных предприятий или нефтеперерабатывающих заводов. Магистральные трубопроводы [1] характеризуются значительной протяженностью (общая протяженность составляет более 250 тыс. км), высокой пропускной способностью, диаметрами труб от 30 до 140 см, толщиной стенок труб, определяемой проектным давлением от 1.2 до 10 МПа. Применяются цельнотянутые или сварные трубы, которые в основном закапывают в грунт на глубину около 0.8 м до верхней образующей трубы, кроме особых случаев, когда глубина прокладки продиктована особыми природно-климатическими условиями. Например, в районах с вечномерзлыми грунтами или при прокладке через болота трубопроводы укладывают на опоры или искусственные насыпи, а на пересечениях крупных рек трубопроводы утяжеляют сплошными бетонными покрытиями и заглубляют ниже дна реки; на пересечениях железных и крупных шоссейных дорог трубопровод проходит в патроне из труб, диаметр которых на 10–20 см больше диаметра магистрального трубопровода.

На магистральных трубопроводах предусмотрены линейные задвижки, которые устанавливают с интервалом в 10–30 км в зависимости от рельефа трассы, и используют для перекрытия участков трубопровода в случае аварии или ремонта. Вдоль трассы также проходит линия связи (телефонная, радиорелейная), имеющая диспетчерское назначение для передачи сигналов телеизмерения и телеуправления. Кроме того, вдоль трассы располагаются станции катодной и дренажной защиты, которые являются дополнением к противокоррозийному изоляционному покрытию трубопровода.

Необходимым элементом магистральных трубопроводов являются также нефтеперекачивающие станции, располагаемые с интервалом 70–150 км, которые оборудованы, в основном, центробежными насосами с электроприводом. Обычно протяженные трубопроводы, длиной более 800 км, разбивают на эксплуатационные участки длиной 100–300 км, для которых предполагаются промежуточные насосные станции с резервуарным парком объема, равного 0.3–1.5 суточной пропускной способности трубопровода.

Проблемами эксплуатация магистральных трубопроводов является своевременное обнаружение местонахождения поврежденных участков, через которые происходят утечки жидкости, загрязняющие окружающую среду.

Мониторинг состояния целостности трубопроводов в настоящее время проводят в основном методом акустической эмиссии, при котором акустический сигнал создается и распространяется по стенке трубы [2–4]. Недостатки этого метода связаны с малой оперативностью определения поврежденного участка, дорогостоящим оборудованием.

Предлагаемый метод акустического сканирования предполагает создание импульсного сигнала конечной длительности в жидкости при остановленном трубопроводе (например, с помощью поршневой системы, приводимой в движение пневматическим или электромеханическим устройством). Анализируя дистанционно с помощью системы контроля, например, затухание импульсного сигнала при распространении по жидкости и дисперсию сигнала на поврежденном участке, приводящего к образованию отраженных и прошедших от его границ сигналов, можно получить информацию о масштабах и степени повреждения данного участка.

Теория акустического сканирования труб обсадных колон нефтяных и газовых скважин представлена в работах [5–8], наземных трубопроводов в [9]. В работе [10] рассмотрено акустическое сканирование подземного трубопровода, заполненного жидкостью (или газом) в длинноволновом приближении, когда длина волны сканирующего импульса превосходит длину поврежденного участка, и участок трубопровода с повреждением принят за отражающую поверхность. В работах [11, 12] показано, что с помощью интеллектуальной системы контроля [13–15] можно “уловить” утечку в трубопроводе на ранних стадиях падения давления по импульсам, отраженным от поврежденного участка.

Настоящая работа является логическим продолжением работ [7–10], в которых предполагалось, что характерная пространственная протяженность сканирующего сигнала значительно превышает участок трубопровода с нарушенной герметичностью или же высоту открытого участка в случае газовых и нефтяных скважин. Такой способ позволяет оценить осредненные параметры характеристик поврежденного участка, а месторасположение этого участка определяется с точностью до длины импульсного сигнала. Переход к более коротким сигналам позволяет точно определить месторасположение и протяженность поврежденного участка. Но, вместе с этим отметим, что короткие сигналы более интенсивно затухают, и может оказаться проблематичным возвращение отраженного сигнала. Поэтому предложенный способ должен предусмотреть запуск систем импульсных сигналов, разнящихся по длительности.

1. ПОСТАНОВКА ЗАДАЧИ И ОСНОВНЫЕ ДОПУЩЕНИЯ

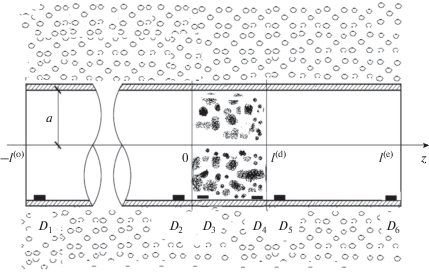
Пусть горизонтальный трубчатый канал (трубопровод) окружен пористой средой и содержит протяженный поврежденный участок, например пораженный коррозией (рис. 1). В исходном состоянии (t < 0) вне канала задано нормальное атмосферное давление p_a, а сам канал заполнен неподвижной жидкостью (уровень фоновых шумов низкий), давление в котором тоже p₀ = p_a. От влияния шумов в значительной степени можно избавиться, переходя к возмущениям более высокой амплитуды.

Рис. 1.

Схема трубы с протяженным поврежденным участком. Датчики-анализаторы сигналов D₁ и D₆ расположены вблизи начала и конца обследуемой трубы; D₂, D₃ и D₄, D₅ – “воображаемые” датчики начала и конца поврежденного участка.

Предполагается, что в начальный период на границе трубопровода создается импульсный сигнал с характерной длительностью Δt, который впоследствии распространяется в жидкости вдоль трубопровода в виде плоской одномерной волны вдоль оси Оz. Причем характерная протяженность импульса λ (λ = С Δt, С – скорость звука) превышает диаметр канала (λ > 2a) [16]. Затухание импульсного сигнала происходит из-за силы вязкого трения жидкости, которая проявляется лишь в тонком пограничном слое, вблизи поверхности стенок канала. Для гармонических волн это означает выполнение следующего неравенства [7]: $a \gg \sqrt {{\nu \mathord{\left/ {\vphantom {\nu \omega }} \right. \kern-0em} \omega }} ,$ где $\nu $ – коэффициент кинематической вязкости жидкости; ω – круговая частота. Кроме того, будем считать, что протяженность сканирующего импульса меньше протяженности поврежденного участка ${{l}^{{(d)}}}$ (λ < ${{l}^{{(d)}}}$).

Для удобства описания и анализа распространения импульсного сигнала по каналу выделим три характерных участка относительно датчика-анализатора сигналов D₁: ближний участок ($ - {{l}^{{(o)}}}$ < < z < 0), дальний участок (${{l}^{{(d)}}}$ < z < ${{l}^{{(e)}}}$) и поврежденный участок (0 < z < ${{l}^{{(d)}}}$). Таким образом, процесс распространения импульсного сигнала в поврежденном канале можно разбить на отдельные этапы: 1) распространение сигнала на участке между границей трубопровода от его границы ($z = - {{l}^{{(o)}}}$) до поврежденного места ($z = 0$), начало координат совпадает с левой границей поврежденного участка; 2) дисперсионные искажения сигнала на поврежденном участке, а также отражение и прохождение на границах ($z = 0$ и $z = $ ${{l}^{{(d)}}}$) этого участка и 3) последующее распространение отраженного сигнала на участке $ - {{l}^{{(o)}}}$ < z < 0, а также распространение прошедшего сигнала на участке ${{l}^{{(d)}}}$ < z < ${{l}^{{(e)}}}$. Границы поврежденного участка ($z = 0$ и $z = $ ${{l}^{{(d)}}}$) примем за отражающие поверхности.

2. УРАВНЕНИЯ НА УЧАСТКАХ БЕЗ ПОВРЕЖДЕНИЯ

Система основных уравнений, описывающая распространение импульсного сигнала по каналу, заполненному жидкостью на этапах 1) и 3), т.е. на ближних $ - {{l}^{{(o)}}}$ < z < 0 и дальних ${{l}^{{(d)}}}$ < z < ${{l}^{{(e)}}}$ участках, и представляющая собой законы сохранения масс и импульса, при указанных допущениях записывается в одномерном приближении [7]:

(1)

$\frac{{\partial p}}{{\partial t}} + {{\rho }_{0}}{{C}^{2}}\frac{{\partial w}}{{\partial z}} = 0,$

где p и w – возмущения давления и скорости; C – скорость звука в жидкости; ${{\rho }_{0}} - $ плотность жидкости в невозмущенном состоянии;

(2)

$\begin{gathered} {{\rho }_{0}}\frac{{\partial w}}{{\partial t}} + \frac{{\partial p}}{{\partial z}} = - \frac{{2\sigma }}{a},\,\,\,\,\sigma = \frac{\mu }{{\sqrt {\pi \nu } }}\int\limits_{ - \infty }^t {\frac{{\left( {{{\partial w} \mathord{\left/ {\vphantom {{\partial w} {\partial \tau }}} \right. \kern-0em} {\partial \tau }}} \right)}}{{\sqrt {t - \tau } }}d\tau } , \\ \nu = \frac{\mu }{{{{\rho }_{0}}}}, \\ \end{gathered} $

где σ – касательное напряжение на поверхности стенки канала, выражение для которого записано согласно [17]; $\mu $ и $\nu $ – динамическая и кинематическая вязкости жидкости.

Из условия существования решения системы (1)–(2) на участках $ - {{l}^{{{\text{(}}o{\text{)}}}}}$ < z < 0 и ${{l}^{{{\text{(}}d{\text{)}}}}}$ < z < ${{l}^{{{\text{(}}e{\text{)}}}}}$ в виде затухающих гармонических волн

(3)

$\begin{gathered} p = {{A}_{p}}\exp \left[ {i\left( {Kz - \omega t} \right)} \right], \\ w = {{A}_{w}}\exp \left[ {i\left( {Kz - \omega t} \right)} \right]\,\,\,\left( {i = \sqrt { - 1} } \right) \\ \end{gathered} $

(где ω > 0 – круговая частота; K = k + iδ – волновой вектор, ${{C}_{{\text{p}}}} = {{{\omega }} \mathord{\left/ {\vphantom {{{\omega }} k}} \right. \kern-0em} k}$ – фазовая скорость, ${{\delta }}$ – коэффициент затухания; A_p и A_w – амплитуды возмущений давления и скорости) следует дисперсионное соотношение в трубчатом канале, заполненном жидкостью [7]

(4)

$K = \pm \frac{\omega }{C}\sqrt {1 + \frac{1}{a}\sqrt {\frac{{2\nu }}{\omega }} \left( {1 + i} \right){\kern 1pt} } .$

Здесь a – радиус канала; величина ${{\delta }^{{(\nu )}}} = \sqrt {{\nu \mathord{\left/ {\vphantom {\nu \omega }} \right. \kern-0em} \omega }} $ выражает [16] характерную глубину проникания поперечных волн в вязкой жидкости. Сохраненные знаки (+) и (–) перед правой частью (4) удобно ассоциировать с волнами, распространяющимися слева в правую сторону и справа в левую сторону, в рамках единого представления (3).

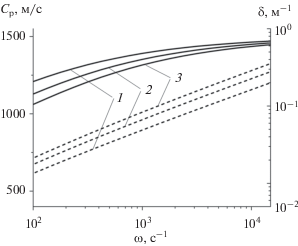
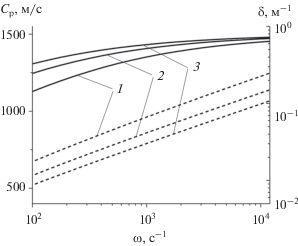
На рис. 2 представлены зависимости фазовой скорости (сплошные линии) и коэффициента затухания (пунктирные линии) от частоты для канала, заполненного различными жидкостями. Для физических параметров нефти, керосина и воды приняты значения:

$\begin{gathered} {{\rho }_{0}} = 890;\,\,820;\,\,{{10}^{3}}{{{\text{кг}}} \mathord{\left/ {\vphantom {{{\text{кг}}} {{{{\text{м}}}^{{\text{3}}}}}}} \right. \kern-0em} {{{{\text{м}}}^{{\text{3}}}}}};\,\,\mu = 20;\,\,1.49; \\ 1 \times {{10}^{{ - 3}}}{\text{Па}}\,{\text{с}};\,\,C = 1.23;1.33;\,\,1.5 \times {{10}^{3}}\,\,{\text{м/с}} \\ \end{gathered} $

соответственно. Анализ дисперсионных кривых показывает, что в диапазоне частот теоретической модели фазовая скорость совпадает со скоростью звука в данных жидкостях; наименьший коэффициент затухания наблюдается у воды, а наибольший – у нефти.

Рис. 2.

Фазовая скорость (сплошная линия) и коэффициент затухания (пунктирная линия) в зависимости от частоты для канала радиуса a = 0.5 м, заполненного жидкостью. Линии 1–3 соответствуют нефти, керосину, воде.

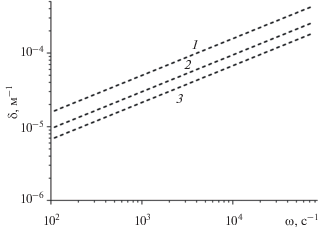
На рис. 3 показано влияние радиуса канала на зависимость коэффициента затухания от частоты. Рассматривается труба, заполненная водой. Из сравнения кривых следует, что уменьшение радиуса канала приводит к увеличению коэффициента затухания. Так, при круговой частоте $\omega = 3 \times {{10}^{3}}\,\,{{{\text{с}}}^{{ - 1}}}$ уменьшение радиуса канала от 0.7 до 0.3 м приводит к росту коэффициента затухания примерно в три раза от 3 × 10^–5 до 10^–4 м^–1.

Рис. 3.

Зависимости коэффициента затухания от частоты в канале, заполненном водой. Линии 1–3 соответствуют каналу радиуса $a$ = 0.3, 0.5, 0.7 м.

3. УРАВНЕНИЯ НА ПОВРЕЖДЕННОМ УЧАСТКЕ

Для описания распространения возмущения по поврежденному участку (0 < z < ${{l}^{{{\text{(}}d{\text{)}}}}}$) примем уравнение импульса (2), а уравнение неразрывности запишем в виде:

(5)

$\frac{1}{{{{C}^{2}}}}\frac{{\partial p}}{{\partial t}} + {{\rho }_{0}}\frac{{\partial w}}{{\partial z}} = - \frac{{2{{\rho }_{0}}u\beta }}{a},$

где $\beta $ – относительная площадь поверхности повреждения; $u$ – скорость фильтрации, являющаяся неизвестной функцией, для определения которой необходимо решать фильтрационную задачу вокруг поврежденного участка.

Будем полагать, что характерная глубина фильтрационных возмущений в грунте при распространении волн в канале от поврежденного участка не превышает радиуса канала. Это допущение несколько занижает учет фильтрационной утечки в окружающий грунт. Данное предположение учитывает специфику задачи обнаружения поврежденного участка короткими сигналами на ранних стадиях возникновения повреждения. Для описания фильтрации жидкости в грунте примем закон Дарси и уравнение нестационарной фильтрации [18] в плоскоодномерном приближении

(6)

$u{\kern 1pt} ' = - \frac{{{{k}_{{{\text{gr}}}}}}}{\mu }\frac{{\partial p{\kern 1pt} '}}{{\partial x}}\,\,\,{\text{(0}} < x < \infty {\text{),}}$

где $u{\kern 1pt} '$ – скорость фильтрации, $p{\kern 1pt} '$ – возмущение давления в грунте;

(7)

$\frac{{\partial p{\kern 1pt} '}}{{\partial t}} = {{\kappa }_{{{\text{gr}}}}}\frac{{{{\partial }^{2}}p{\kern 1pt} '}}{{\partial {{x}^{2}}}}\left( {{{\kappa }_{{{\text{gr}}}}} = \frac{{{{k}_{{{\text{gr}}}}}{{\rho }_{0}}{{C}^{2}}}}{{{{m}_{{{\text{gr}}}}}\mu }}} \right),$

где ${{k}_{{{\text{gr}}}}}$ и ${{m}_{{{\text{gr}}}}}$ – коэффициенты проницаемости и пористости грунта; ${{\kappa }_{{{\text{gr}}}}}$ – коэффициент пьезопроводности грунта; x – координата, отсчитываемая от поверхности стенки канала (0 < x < ∞).

Решение уравнения (7) должно удовлетворять граничным условиям

$p{\kern 1pt} ' = p\,\,\left( {х = 0} \right),\,\,\,p{\kern 1pt} ' = 0\,\,\left( {х = + \infty } \right),$

а скорость фильтрации из трубопровода определяется из уравнения (6) при x = 0:

(8)

$u = - \frac{{{{k}_{{gr}}}}}{\mu }\frac{{\partial p{\kern 1pt} '}}{{\partial x}}\,\,{\text{(}}x = 0{\text{)}}{\text{.}}$

Пусть в исходном состоянии жидкость в трубе и в грунте находится в равновесии. Тогда для скорости и возмущения давления в канале на поврежденном участке и грунте можем записать

(9)

$w = u{\kern 1pt} ' = 0,\,\,\,\,p = p{\kern 1pt} ' = 0\,\,(t = - \infty ).$

Согласно принципу Дюамеля [19] решение уравнения (7), удовлетворяющее условию (9), имеет вид

(10)

$\begin{gathered} p{\kern 1pt} ' = \int\limits_{ - \infty }^t {\frac{{\partial U(x,t - \tau )}}{{\partial t}}} p(\tau )d\tau , \\ U(x,t - \tau ) = \frac{2}{{\sqrt {3\pi } }}\int\limits_{{x \mathord{\left/ {\vphantom {x {\sqrt {4{{\kappa }_{{{\text{gr}}}}}(t - \tau )} }}} \right. \kern-0em} {\sqrt {4{{\kappa }_{{{\text{gr}}}}}(t - \tau )} }}}^\infty {{{e}^{{ - {{\alpha }^{2}}}}}d\alpha } . \\ \end{gathered} $

На основе закона Дарси, используя решение (10), в котором полагаем x = 0, можем получить связь между скоростью $u$ и давлением $p$ в грунте вблизи поврежденного участка

$u = \frac{{{{k}_{{{\text{gr}}}}}}}{{\mu \sqrt {\pi {{\kappa }_{{{\text{gr}}}}}} }}\int\limits_{ - \infty }^t {\frac{{{{\partial p} \mathord{\left/ {\vphantom {{\partial p} {\partial \tau }}} \right. \kern-0em} {\partial \tau }}}}{{\sqrt {t - \tau } }}d\tau } .$

С учетом этого выражения уравнение неразрывности (5) запишется как

(11)

$\frac{1}{{{{C}^{2}}}}\frac{{\partial p}}{{\partial t}} + {{\rho }_{0}}\frac{{\partial w}}{{\partial z}} = - \frac{{2{{\rho }_{0}}\beta }}{a}\frac{{{{k}_{{{\text{gr}}}}}}}{{\mu \sqrt {\pi {{\kappa }_{{{\text{gr}}}}}} }}\int\limits_{ - \infty }^t {\frac{{{{\partial p} \mathord{\left/ {\vphantom {{\partial p} {\partial \tau }}} \right. \kern-0em} {\partial \tau }}}}{{\sqrt {t - \tau } }}d\tau } .$

Уравнения (2) и (11) представляют систему интегро-дифференциальных уравнений для p и w на поврежденном участке (0 < z < ${{l}^{{(d)}}}$). Решение этой системы ищем аналогично решению системы (1)–(2) в виде затухающих гармонических волн вида (3), в которых для волнового вектора введем верхний индекс ^(d). Тогда из системы уравнений (2) и (11) получим

(12)

$\begin{gathered} - \frac{1}{{{{C}^{2}}}}\omega {{A}_{p}} + {{\rho }_{0}}{{K}^{{(d)}}}{{A}_{w}} = \\ = \frac{{2{{\rho }_{0}}\beta }}{a}\frac{{{{k}_{{{\text{gr}}}}}}}{{\mu \sqrt {\pi {{\kappa }_{{{\text{gr}}}}}} }}{{A}_{p}}\frac{{2\omega }}{{\sqrt \omega }}\left( {\frac{1}{2} + \frac{i}{2}} \right)\sqrt {\frac{\pi }{2}} , \\ - {{\rho }_{0}}{{A}_{w}} + {{K}^{{(d)}}}{{A}_{p}} = \frac{2}{a}\frac{\mu }{{\sqrt {\pi \nu } }}{{A}_{w}}\frac{{2\omega }}{{\sqrt \omega }}\left( {\frac{1}{2} + \frac{i}{2}} \right)\sqrt {\frac{\pi }{2}} . \\ \end{gathered} $

Из первого уравнения (12) найдем связь между амплитудами ${{A}_{w}}$ и ${{A}_{p}}$

(13)

${{A}_{p}} = \frac{{{{\rho }_{0}}{{K}^{{(d)}}}}}{{\left( {\frac{1}{{{{C}^{2}}}}\omega + \frac{{2\beta }}{a}\frac{{{{k}_{{{\text{gr}}}}}}}{{\nu \sqrt {\pi {{\kappa }_{{{\text{gr}}}}}} }}\frac{{2\omega }}{{\sqrt \omega }}\left( {\frac{1}{2} + \frac{i}{2}} \right)\sqrt {\frac{\pi }{2}} } \right)}}{{A}_{w}}.$

Далее, подставив A_p во второе уравнение (12), получим дисперсионное уравнение на поврежденном участке

(14)

$\begin{gathered} {{K}^{{(d)}}} = \\ = \pm \frac{\omega }{C}\sqrt {\left( {1 + \frac{1}{a}\sqrt {\frac{{2\nu }}{\omega }} \left( {1 + i} \right)} \right)\left( {1 + \frac{{\beta {{m}_{{{\text{gr}}}}}}}{a}\sqrt {\frac{{2{{\kappa }_{{{\text{gr}}}}}}}{\omega }} \left( {1 + i} \right)} \right)} . \\ \end{gathered} $

Из сравнения дисперсионных соотношений (14) и (4) следует, что распространение импульсного сигнала на поврежденном участке (0 < z < ${{l}^{{(d)}}}$) происходит с более интенсивным затуханием по сравнению с участками $ - {{l}^{{(o)}}}$ < z < 0 и ${{l}^{{(d)}}}$ < z < ${{l}^{{(e)}}}$.

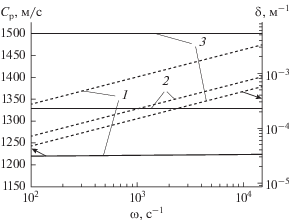
На рис. 4 представлены дисперсионные кривые, построенные по соотношению (14) при различных радиусах трубопровода. Рассматривается заполненная водой поврежденная труба ($\beta $ = 0.7), окруженная проницаемой пористой средой (${{k}_{{{\text{gr}}}}}$ = 10^–11 м², ${{m}_{{{\text{gr}}}}}$ = 0.2). Видно, что с уменьшением радиуса канала отклонение фазовой скорости от скорости звука в сторону ее снижения становится более заметным, также происходит рост коэффициента затухания. Отметим, что при круговой частоте $\omega = 3 \times {{10}^{3}}\,\,{{{\text{с}}}^{{ - 1}}}$ уменьшение радиуса канала от 0.7 до 0.3 м приводит к росту коэффициента затухания примерно в три раза (от 0.06 до 0.2 м^–1). Заметим, что амплитуда сигнала уменьшается в e раз на расстоянии 5 м при прохождении сигнала по поврежденному участку канала радиуса a = 0.3 м, в отличие от распространения сигнала по участку канала такого же радиуса без повреждения, где это расстояние примерно равно 10 км (рис. 3).

Рис. 4.

Фазовая скорость (сплошная линия) и коэффициент затухания (пунктирная линия) в зависимости от частоты на поврежденном участке для различных радиусов канала, заполненного водой. Линии 1–3 соответствуют каналу радиуса $a$ = 0.3, 0.5, 0.7 м.

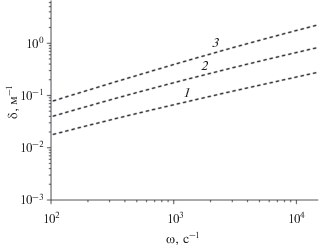
На рис. 5 показано влияние проницаемости грунта на зависимость коэффициента затухания от частоты: линии 1–3 соответствуют значениям ${{k}_{{{\text{gr}}}}}$ = 10^–11; 10^–10; 10^–9 м². Такие проницаемости характерны для глубины заложения подземных трубопроводов при траншейной прокладке 0.8–1.0 м до верхней образующей, где в специально подготовленном ложе используют подсыпку гравия и песка. Характеристики трубы, заполненной водой: $a$ = 0.3 м, $\beta $ = 0.5. Видно, что с увеличением проницаемости грунта происходит более сильное затухание сигнала. Так, при круговой частоте $\omega = 3 \times {{10}^{3}}\,\,{{{\text{с}}}^{{ - 1}}}$ изменение проницаемости грунта в сто раз (от 10^–11 до 10^–9 м²) приводит к росту коэффициента затухания примерно в десять раз (от 0.1 до 1 м^–1).

Рис. 5.

Зависимости коэффициента затухания от частоты на поврежденном участке для канала радиуса $a$ = 3 × 10^–1 м, заполненного водой, построенные для различных значений коэффициента проницаемости грунта. Линии 1–3 соответствуют значениям ${{k}_{{{\text{gr}}}}}$ = = 10^–11, 10^–10, 10^–9 м².

На рис. 6 показано влияние величины повреждения трубы на дисперсионные кривые. Характеристики грунта совпадают с рис. 4. Видно, что с увеличением степени поражения происходит снижение фазовой скорости и более сильное затухание сигнала. Так, при круговой частоте $\omega = 3 \times {{10}^{3}}\,\,{{{\text{с}}}^{{ - 1}}}$ рост величины повреждения трубы от 0.5 до 0.9 приводит к изменениям в значениях фазовых скоростей на 70 м/с (от 1430 до 1360 м/с) и росту коэффициента затухания примерно в два раза (от 0.1 до 0.2 м^–1).

Рис. 6.

Фазовая скорость (сплошная линия) и коэффициент затухания (пунктирная линия) в зависимости от частоты на поврежденном участке для различной степени повреждения канала радиуса $a$ = 0.3 м, заполненного водой. Линии 1–3 соответствуют значениям $\beta $ = 0.5, 0.7, 0.9.

4. УСЛОВИЯ НА ГРАНИЦАХ ПОВРЕЖДЕННОГО УЧАСТКА

На границах поврежденного участка z = 0 и z = ${{l}^{{(d)}}}$ должны быть непрерывны возмущения давления и скорости

(15)

${{p}^{{(1)}}} = {{p}^{{(d)}}},\,\,\,\,{{w}^{{(1)}}} = {{w}^{{(d)}}}\,\,(z = {\text{ }}0),$

(16)

${{p}^{{(2)}}} = {{p}^{{(d)}}},\,\,\,\,{{w}^{{(2)}}} = {{w}^{{(d)}}}\,\,(z = {{l}^{{(d)}}}).$

Здесь и в дальнейшем верхними индексами в скобках j = 1 и 2 снабжены возмущения давления $p$ и скорости $w$, соответственно, на участках $ - {{l}^{{(o)}}}$ < z < 0 и ${{l}^{{(d)}}}$ < z < ${{l}^{{(e)}}}$.

На поврежденном участке будет происходить дальнейшая эволюция импульсного сигнала, включая образование отраженных и прошедших сигналов на границах $z = 0$ и $z = {{l}^{{(d)}}}$ этого участка. Будем полагать, что отраженный от границы и прошедший сигналы представляют сумму плоских гармонических волн [16]. Причем на участке $ - {{l}^{{(o)}}}$ < z < 0 импульсные сигналы представляют сумму волн вида (3) с соответствующими знаками (–) и (+) в дисперсионном уравнении (4), а на поврежденном участке – гармоническую волну с дисперсионным уравнением (14), взятым со знаком (+). Возмущения, соответствующие падающей, отраженной и прошедшей волнам, снабдим верхними значками (О), (R) и (G).

Граничные условия (15) при $z = 0$ выражают условия непрерывности давления и скорости

(17)

$\left\{ \begin{gathered} {{w}^{{\left( O \right)}}} + {{w}^{{\left( R \right)}}} = {{w}^{{\left( G \right)}}}, \hfill \\ {{p}^{{\left( O \right)}}} + {{p}^{{\left( R \right)}}} = {{p}^{{\left( G \right)}}}. \hfill \\ \end{gathered} \right.$

Тогда для падающей, отраженной и прошедшей волн вида (3) при падении на границу $z = 0$ можем записать

(18)

$\begin{gathered} {{p}^{{\left( O \right)}}} = A_{p}^{{\left( O \right)}}{{e}^{{i\left( {Kz - \omega t} \right)}}},\,\,\,\,{{p}^{{\left( R \right)}}} = A_{p}^{{\left( R \right)}}{{e}^{{i\left( {Kz - \omega t} \right)}}}, \\ {{p}^{{\left( G \right)}}} = A_{p}^{{\left( G \right)}}{{e}^{{i\left( {{{K}^{{(d)}}}z - \omega t} \right)}}}. \\ \end{gathered} $

Амплитуда возмущений скоростей с амплитудами давления связаны выражениями вида

(19)

$\begin{gathered} A_{w}^{{\left( O \right)}} = \frac{\omega }{{{{\rho }_{0}}K{{C}^{2}}}}A_{p}^{{\left( O \right)}},\,\,\,\,A_{w}^{{\left( R \right)}} = - \frac{\omega }{{{{\rho }_{0}}K{{C}^{2}}}}A_{p}^{{\left( R \right)}}, \\ A_{w}^{{\left( G \right)}} = \frac{{\omega {{K}^{{(d)}}}}}{{{{\rho }_{0}}K_{{}}^{2}{{C}^{2}}}}A_{p}^{{\left( G \right)}}. \\ \end{gathered} $

На основе условий (17) для решений вида (18) с учетом (19) при $z = 0$ для коэффициентов отражения и прохождения, определенных как ${{N}^{{{\text{(1)}}}}} = {{A_{p}^{{\left( R \right)}}} \mathord{\left/ {\vphantom {{A_{p}^{{\left( R \right)}}} {A_{p}^{{\left( O \right)}}}}} \right. \kern-0em} {A_{p}^{{\left( O \right)}}}},$ ${{M}^{{{\text{(1)}}}}} = {{A_{p}^{{\left( G \right)}}} \mathord{\left/ {\vphantom {{A_{p}^{{\left( G \right)}}} {A_{p}^{{\left( O \right)}}}}} \right. \kern-0em} {A_{p}^{{\left( O \right)}}}}$, получим

(20)

${{M}^{{{\text{(1)}}}}} = \frac{2}{{1 + D}},\,\,\,\,{{N}^{{{\text{(1)}}}}} = {{M}^{{{\text{(1)}}}}} - 1\,\,\left( {D = {{{{K}^{{{\text{(}}d{\text{)}}}}}} \mathord{\left/ {\vphantom {{{{K}^{{{\text{(}}d{\text{)}}}}}} K}} \right. \kern-0em} K}} \right).$

Рассматривая аналогичную задачу на границе $z = {{l}^{{(d)}}}$ для коэффициентов отражения и прохождения на этой границе получим

(21)

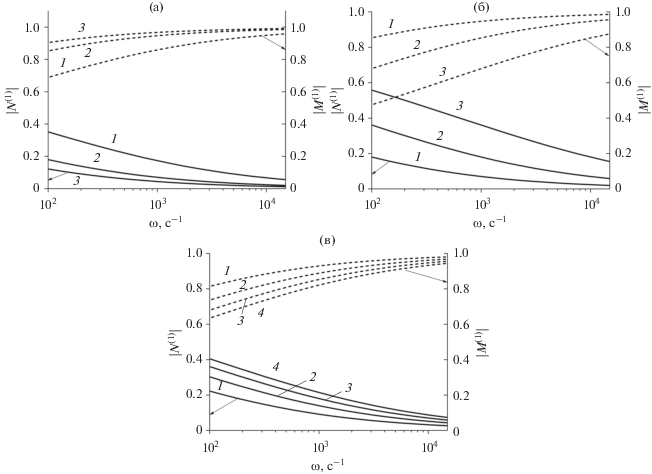
${{M}^{{{\text{(2)}}}}} = \frac{2}{{1 + {1 \mathord{\left/ {\vphantom {1 D}} \right. \kern-0em} D}}},\,\,\,\,{{N}^{{{\text{(2)}}}}} = {{M}^{{{\text{(2)}}}}} - 1.$

На рис. 7 представлены результаты расчетов для модулей коэффициентов отражения ${{N}^{{{\text{(1)}}}}}$ и прохождения ${{M}^{{{\text{(1)}}}}}$ в зависимости от частоты: (а) при различных радиусах канала; (б) при различных проницаемостях грунта; (в) при различных величинах характеристики повреждения $\beta $. Из рис. 7а следует, что в более широких каналах отраженный от границы повреждения сигнал становится более слабым, например, при круговой частоте $\omega = 3 \times {{10}^{3}}\,\,{{{\text{с}}}^{{ - 1}}}$ увеличение радиуса канала в пять раз (от 0.1 до 0.5 м) приводит к снижению модуля коэффициента отражения примерно в пять раз (от 0.15 до 0.03). Из рис. 7б и 7в видно, что с уменьшением относительной площади повреждения, а также проницаемости грунта модуль коэффициента отражения снижается, например, при круговой частоте $\omega = 3 \times {{10}^{3}}\,\,{{{\text{с}}}^{{ - 1}}}$ уменьшение проницаемости грунта в сто раз (от 10^–9 до 10^–11 м²) приводит к падению модуля коэффициента отражения в шесть раз (от 0.3 до 0.05); изменение величины относительной площади повреждения в три раза (от 0.9 до 0.3) – к снижению модуля коэффициента отражения в три раза (от 0.18 до 0.06). Слабое “эхо” сигнала от границ поврежденного участка приводит к требованиям по чувствительности диагностической аппаратуры, а именно к датчикам-анализаторам сигналов.

Рис. 7.

Зависимости коэффициентов отражения (сплошные линии) и прохождения (пунктирные линии) от частоты: (а) – при различных радиусах канала, линии 1–3 соответствуют а = 0.1; 0.3; 0.5 м (${{k}_{{{\text{gr}}}}}$ = 10^–11 м², β = 0.7, ${{m}_{{{\text{gr}}}}}$= 0.2); (б) – при различных проницаемостях грунта, линии 1–3 соответствуют ${{k}_{{{\text{gr}}}}}$ = 10^–11, 10^–10, 10^–9 м² (а = 0.3 м, β = 0.7, ${{m}_{{{\text{gr}}}}}$ = 0.2); (в) – при различных значениях коэффициента β, линии 1–4 соответствуют β = 0.3, 0.5, 0.7, 0.9 (а = 0.3 м, ${{k}_{{{\text{gr}}}}}$ = 10^–10 м², ${{m}_{{{\text{gr}}}}}$ = 0.2).

5. ЧИСЛЕННАЯ РЕАЛИЗАЦИЯ И РЕЗУЛЬТАТЫ РАСЧЕТОВ

Пусть через левую границу трубопровода (z = $ - {{l}^{{(o)}}}$) запускается сигнал $p = {{\tilde {p}}^{{(0)}}}(t)$ с характерной длительностью Δt. При этом полагаем, что пространственная протяженность этого сигнала вдоль канала ${{\lambda }} = С\Delta t$ значительно меньше расстояния ${{l}^{{(o)}}}$ (λ $ \ll $ ${{l}^{{(o)}}}$) и меньше длины поврежденного участка (${{\lambda }^{{(d)}}}$ < ${{C}^{{(d)}}}\Delta t$, ${{C}^{{(d)}}}$ – скорость импульсного сигнала в поврежденном участке (0 < z < ${{l}^{{(d)}}}$)).

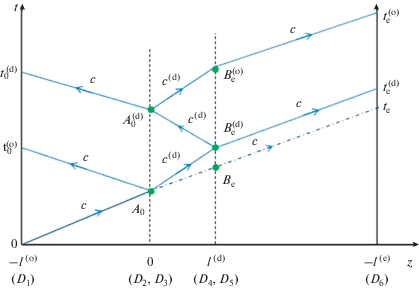
На рис. 8 представлена картина, иллюстрирующая законы распространения импульсного сигнала, запущенного с левой границы трубопровода (z = $ - {{l}^{{(o)}}}$), при наличии поврежденного участка (0 < z < ${{l}^{{(d)}}}$). При $t = {{t_{0}^{{\left( o \right)}}} \mathord{\left/ {\vphantom {{t_{0}^{{\left( o \right)}}} 2}} \right. \kern-0em} 2}$ сигнал доходит до границы поврежденного участка (z = 0). Далее, на этой границе импульсный сигнал распадается на два – на отраженный и проходящий в поврежденную зону сигналы. Будем считать, что скорости звука С и ${{C}^{{(d)}}}$ на неповрежденном и поврежденном участках трубопровода постоянные. Причем, как показывают приведенные выше расчеты, скорость С близка к скорости звука в жидкости, а величина скорости ${{C}^{{(d)}}}$ в поврежденном участке несколько ниже (${{C}^{{(d)}}}$ < С). В момент $t = t_{0}^{{\left( o \right)}}$ отраженный сигнал достигает границы z = $ - {{l}^{{(o)}}}$ (фиксируется датчиком D₁). По значению $t_{0}^{{\left( o \right)}}$ определяется положение левой границы поврежденного участка как ${{l}^{{(o)}}} = C{{t_{0}^{{\left( o \right)}}} \mathord{\left/ {\vphantom {{t_{0}^{{\left( o \right)}}} 2}} \right. \kern-0em} 2}$. Если бы поврежденный участок отсутствовал (${{l}^{{(d)}}} = 0$), то сигнал, запущенный с левой границы трубопровода, достиг бы правой границы трубопровода (z = ${{l}^{{(e)}}}$) за время ${{t}_{e}} = {{\left( {{{l}^{{(o)}}} + {{l}^{{(e)}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{l}^{{(o)}}} + {{l}^{{(e)}}}} \right)} C}} \right. \kern-0em} C}$. Но, поскольку скорость сигнала на поврежденном участке ${{C}^{{{\text{(}}d{\text{)}}}}}$ будет ниже С, то импульсный сигнал достигнет правой границы позже, в момент $t = t_{e}^{{\left( d \right)}}\,\,\left( {t_{e}^{{\left( d \right)}} > {{t}_{e}}} \right)$. При прохождении правой границы поврежденного участка (z = ${{l}^{{(d)}}}$) будет также происходить отражение. Причем, этот отраженный сигнал, переотражаясь на границе z = 0, достигнет левой границы трубопровода в момент $t = t_{0}^{{\left( d \right)}}$. Исходный сигнал, проходящий границу z = ${{l}^{{(d)}}}$ (на рис. 8 – точка $B_{e}^{{\left( o \right)}}$) достигает правой границы трубопровода в момент $t = t_{e}^{{\left( о \right)}}$. На основе схемы, изображенной на рис. 8, с учетом отмеченных замечаний можем записать следующее соотношение

$\frac{{{{l}^{{(d)}}}}}{{{{C}^{{(d)}}}}} - \frac{{{{l}^{{(d)}}}}}{C} = t_{e}^{{\left( d \right)}} - {{t}_{e}},\,\,\,\,\frac{{2{{l}^{{(d)}}}}}{{{{C}^{{(d)}}}}} = t_{0}^{{\left( d \right)}} - t_{0}^{{(o)}}.$

Рис. 8.

Картина эволюции импульсного сигнала в трубопроводе с поврежденным участком в координатной плоскости (z, t).

Разрешая эти уравнения относительно ${{l}^{{(d)}}}$ и ${{C}^{{(d)}}}$, можем получить

(22)

$\begin{gathered} {{l}^{{(d)}}} = C\left( {\frac{{t_{0}^{{(d)}} - t_{0}^{{(o)}} - 2\left( {t_{e}^{{(d)}} - {{t}_{e}}} \right)}}{2}} \right), \\ {{C}^{{(d)}}} = \frac{{2{{l}^{{(d)}}}}}{{t_{0}^{{\left( d \right)}} - t_{0}^{{(o)}}}}. \\ \end{gathered} $

Эти формулы по значениям времен $t_{0}^{{\left( o \right)}}$, $t_{0}^{{\left( d \right)}}$ и $t_{e}^{{\left( d \right)}}$, которые фиксируются по показаниям датчиков D₁ и D₆, позволяют определить месторасположение и протяженность поврежденного участка трубопровода. Далее по совместному анализу этих данных, а также по амплитудно-частотным характеристикам осциллограмм давления, полученным датчиками давления D₁ и D₆, и результатам численных экспериментов, которые описаны ниже, можно получить более полную информацию о состоянии трубопровода. В частности, при известных значениях радиуса трубопровода, фильтрационных характеристик грунта, реологических свойств флюида, а также амплитудно-частотных параметров импульсного сигнала, по номограммам, построенным в виде зависимостей скорости сигнала от параметра β, по скорости сигнала в поврежденном участке, полученной из второй формулы (22) можно определить степень повреждения стенок трубопровода.

Для расчета факторов, искажающих импульсный сигнал при распространении по каналу, будем использовать преобразование Фурье [19] и программу быстрого преобразования для численной реализации [20, 21]. Тогда для сигнала, дошедшего до “воображаемого” датчика D₂, можем записать

(23)

$\begin{gathered} {{p}^{{(О)}}}(0,t) = \\ = - \frac{1}{\pi }\int\limits_0^\infty {\int\limits_{ - \infty }^\infty {{{{\tilde {p}}}^{{({\text{o}})}}}(\tau )\exp (iK(\omega ){{l}^{{{\text{(o)}}}}})\exp \left[ {i\omega (t - \tau )} \right]} } d\omega d\tau . \\ \end{gathered} $

Для импульсных сигналов, отраженного от границы и прошедшего через границу z = 0, имеем

(24)

$\begin{gathered} {{p}^{{(R)}}}(0,t) = \frac{1}{\pi }\int\limits_0^\infty {\int\limits_{ - \infty }^\infty {{{{\tilde {p}}}^{{(0)}}}(\tau ){{N}^{{(1)}}}(\omega )\exp \left[ {i\omega (t - \tau )} \right]} } d\omega d\tau , \\ {{p}^{{(G)}}}(0,t) = \frac{1}{\pi }\int\limits_0^\infty {\int\limits_{ - \infty }^\infty {{{{\tilde {p}}}^{{(0)}}}(\tau ){{M}^{{(1)}}}(\omega )\exp \left[ {i\omega (t - \tau )} \right]} } d\omega d\tau . \\ \end{gathered} $

Для сигнала, возвратившегося к датчику D_1, имеем

(25)

$\begin{gathered} {{{\tilde {p}}}^{{(E)}}}( - {{l}^{{{\text{(o)}}}}},t) = \\ = \frac{1}{\pi }\int\limits_0^\infty {\int\limits_{ - \infty }^\infty {{{p}^{{(R)}}}(0,\tau )\exp (iK(\omega ){{l}^{{(o)}}})\exp \left[ {i\omega (t - \tau )} \right]} } d\omega d\tau . \\ \end{gathered} $

Аналогичные соотношения можно записать для сигнала, дошедшего до “воображаемого” датчика D₄, и сигналов, отраженного от границы и прошедшего через границу z = ${{l}^{{(d)}}}$, а также возвратившегося к датчику D₁:

(26)

$\begin{gathered} {{{\tilde {p}}}^{{(O)}}}({{l}^{{{\text{(}}d{\text{)}}}}},t) = \frac{1}{\pi }\int\limits_0^\infty {\int\limits_{ - \infty }^\infty {{{{\tilde {p}}}^{{(O)}}}(\tau )\exp (i{{K}^{{(d)}}}(\omega ){{l}^{{(d)}}})} } \times \\ \times \exp \left[ {i\omega (t - \tau )} \right]d\omega d\tau \\ \end{gathered} $

(27)

$\begin{gathered} {{p}^{{(R)}}}({{l}^{{(d)}}},t) = \\ = \frac{1}{\pi }\int\limits_0^\infty {\int\limits_{ - \infty }^\infty {{{{\tilde {p}}}^{{(O)}}}({{l}^{{(d)}}},\tau ){{N}^{{(2)}}}(\omega )\exp \left[ {i\omega (t - \tau )} \right]} } d\omega d\tau , \\ {{p}^{{(G)}}}({{l}^{{{\text{(}}d{\text{)}}}}},t) = \\ = \frac{1}{\pi }\int\limits_0^\infty {\int\limits_{ - \infty }^\infty {{{{\tilde {p}}}^{{(O)}}}({{l}^{{{\text{(}}d{\text{)}}}}},\tau ){{M}^{{{\text{(2)}}}}}(\omega )\exp \left[ {i\omega (t - \tau )} \right]} } d\omega d\tau , \\ \end{gathered} $

(28)

$\begin{gathered} {{{\tilde {p}}}^{{(E)}}}( - ({{l}^{{(o)}}} + {{l}^{{(d)}}}),t) = \\ = \frac{1}{\pi }\int\limits_0^\infty {\int\limits_{ - \infty }^\infty {{{p}^{{(R)}}}({{l}^{{(d)}}},\tau )\exp (i{{K}^{{(d)}}}(\omega )({{l}^{{(o)}}} + {{l}^{{(d)}}}))} } \times \\ \times \,\,\exp \left[ {i\omega (t - \tau )} \right]d\omega d\tau . \\ \end{gathered} $

В качестве исходного сигнала возьмем импульс давления колоколообразной формы с амплитудой $\Delta {{p}_{0}}$:

(29)

${{\tilde {p}}^{{(0)}}} = \Delta p\left( t \right) = \Delta {{p}_{0}}\exp \left( { - {{{\left( {\frac{{t - {{t}_{0}}}}{{{{\Delta t} \mathord{\left/ {\vphantom {{\Delta t} 6}} \right. \kern-0em} 6}}}} \right)}}^{2}}} \right),$

где $\Delta t$ – характерная длительность импульса, в момент времени ${{t}_{0}}$ достигается максимальная амплитуда импульса.

Спектральная плотность для импульсного сигнала вида (29) может быть записана [16] в виде

(30)

$\begin{gathered} s\left( {\omega ,{{t}_{0}}} \right) = \frac{{\sqrt \pi \Delta t}}{3}\Delta {{p}_{0}}\exp \left( { - {{{\left( {\frac{{\omega \Delta t}}{{12}}} \right)}}^{2}}} \right)\exp ( - i\omega {{t}_{0}}) = \\ = s\left( {\omega ,0} \right)\exp ( - i\omega {{t}_{0}}). \\ \end{gathered} $

Из (30) следует, что происходит смещение фазовой характеристики спектра сигнала при ${{t}_{0}} \ne 0$ на величину $\omega \,{{t}_{0}}$ по сравнению со спектром сигнала в случае ${{t}_{0}} = 0$.

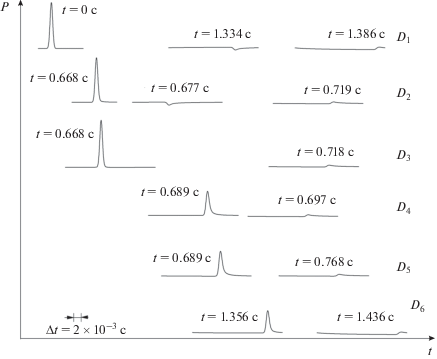
На рис. 9 представлена картина, иллюстрирующая эволюцию импульсного сигнала с характерной временной протяженностью $\Delta t$ = 2 × 10^–3 c для канала радиуса a = 0.3 м общей протяженностью $l \approx 2000$ м и заполненном водой. В качестве момента времени, при котором достигается пиковое значение импульсного сигнала, принято ${{t}_{0}} = {{\Delta t} \mathord{\left/ {\vphantom {{\Delta t} 2}} \right. \kern-0em} 2}$ = ${{10}^{{ - 3}}}$ с. Осциллограммы соответствуют показаниям датчиков D₁, D₂, D₃, D₄, D₅ и D₆. Как уже было отмечено, для рассматриваемой задачи, время $\tilde {t}$ прохождения импульсного сигнала по трубопроводу несоизмеримо больше характерной продолжительности импульсного сигнала $\Delta t$ ($\tilde {t} \gg \Delta t$). Поэтому для большей наглядности и иллюстрации процесса эволюции импульсного сигнала по всему выбранному участку трубопровода введение единого масштаба времени неудобно. В этой связи на рис. 9 указаны времена прихода сигнала к датчикам. Указанный масштаб времени $\Delta t$ относится только к показаниям датчиков. На осциллограмме D₁ первый всплеск представляет собой исходный сканирующий импульс, например, вида (29), который доходит до повреждения (z = 0) несколько ослабленным (на осциллограмме D₂ – первый всплеск) в момент времени $t = $ 0.668 с. На левой границе поврежденного участка происходит формирование отраженного (второй всплеск на осциллограмме D₂) и прошедшего в поврежденную область (первый всплеск на осциллограмме D₃) сигналов за время порядка $\Delta t$. В момент времени $t = $ 1.334 с отраженный сигнал возвращается к датчику D₁ (второй всплеск на осциллограмме). Прошедший границу z = 0 импульс на поврежденном участке затухает, происходит снижение амплитуды более чем в два раза у границы z = ${{l}^{{(d)}}}$ (первый всплеск на осциллограмме D₄), далее отражается от этой границы (второй всплеск на осциллограмме D₄), проходит поврежденный участок (вторые всплески на осциллограмме D₃ и D₂) и в момент времени $t = $1.386 с достигает датчика D₁ (третий всплеск на осциллограмме). На осциллограммах D₅ и D₆ представлены прошедшие через границу z = ${{l}^{{{\text{(d)}}}}}$ импульсы: первые всплески соответствует импульсам, прошедшим первый раз через поврежденный участок, вторые всплески $ - $ переотразившемуся импульсу от границы z = 0 и снова прошедшему поврежденный участок. Переотразившийся импульс в показаниях датчиков D₅ и D₆ (вторые всплески) имеет сильные искажения формы.

Рис. 9.

Расчетные осциллограммы эволюции импульсного сигнала от поврежденного участка (β = 0.7) в канале с водой радиуса $a$ = 0.3 м. Расстояние до и после поврежденного участка ${{l}^{{{\text{(}}o{\text{)}}}}}$ = 1 км и ${{l}^{{(e)}}}$= 1 км, длина поврежденного участка l^(d) = 30 м. Характеристики грунта такие же, как на рис. 4.

В заключение отметим, что анализ расчетных кривых по эволюции импульсного сигнала, представленной на рис. 9, в плане определения его скорости, затухания, а также коэффициентов отражения и прохождения показывает хорошее согласование с расчетными данными по дисперсионным уравнениям, если принять для круговой частоты значение $\omega = {{\omega }_{0}} = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } {\Delta t}}} \right. \kern-0em} {\Delta t}}$ (для представленного примера ${{\omega }_{0}} = \pi \times {{10}^{3}}$).

Исходя из того, что по теоретической модели погрешность нахождения границы начала поврежденного участка определяется с точностью до пространственной протяженности сигнала λ, определяемой длительностью $\Delta t$, то предпочтительнее использовать сигналы с уменьшающейся длительностью.

ЗАКЛЮЧЕНИЕ

На основе принятой технологической схемы и соответствующей математической модели построен алгоритм для численных экспериментов, моделирующих диагностику трубопроводов, зарытых в грунт и имеющих поврежденный участок с нарушением герметичности. Представленная в работе методика, основанная на эволюции импульсного сигнала давления, запущенного с одного конца трубопровода, при последующей регистрации времен достижения проходящих сигналов через весь обследуемый участок датчиками, расположенными вблизи другого конца трубопровода, и отраженных импульсных сигналов датчиками, расположенными вблизи входа трубопровода, позволяют определить месторасположение и протяженность поврежденного участка. Кроме того, совместный анализ амплитудно-частотных характеристик осциллограмм импульсных сигналов, зарегистрированных сигналов датчиками давления с результатами численных экспериментов позволяет оценить степень нарушения герметичности в поврежденном участке.

Исследование выполнено за счет гранта Российского научного фонда № 21-11-00207.

Список литературы

Васильев Г.Г., Коробков Г.Е., Коршак А.А. и др. Трубопроводный транспорт нефти. Под ред. С.М. Вайнштока. М.: Недра, 2002. Т. 1. 406 с.
Ильгамов М.А., Шакирьянов М.М. Взаимодействие вынужденных и параметрических колебаний трубопровода // ПМТФ. 2020. Т. 61. № 6. С. 66–69.
Марапулец Ю.В., Тристанов А.Б., Шевцов Б.М. Анализ структуры сигналов акустической эмиссии звукового диапазона методом разряженной аппроксимации // Акуст. журн. 2014. Т. 60. С. 398–407.
Hase A., Mishina H., Wada M. Correlation between features of acoustic emission signals and mechanical wear mechanisms // Wear. 2012. P. 144–150.
Biot M.A. Propogation of elastic waves in a cylindrical bore containing a fluid // J. Appl. Phys. 1952. V. 23. № 9. P. 497–509.
Shagapov V.Sh., Khlestkina N.M., Lhuillier D. Acoustic waves in channels with porous and permeable walls // Transport in Porous Media. 1999. V. 35. № 3. P. 327–344.
Булатова З.А., Гумерова Г.А., Шагапов В.Ш. Об эволюции волн в каналах, имеющих участки с проницаемыми стенками и окруженных неоднородной пористой средой // Акуст. журн. 2002. Т. 3. С. 23–31.
Nigmatulin R.I., Gubaydullin A.A., Shagapov V.Sh. Numerical investigation of shock and thermal waves in porous saturated medium with phase transitions // Porous Media: Physics, Models, Simulation (World Scientific Publishing). 1999. P. 15–21.
Шагапов В.Ш., Галиакбарова Э.В., Хакимова З.Р. К теории акустического зондирования трубчатых каналов, содержащих участки с нарушением герметичности // ИФЖ. 2018. Т. 91. № 3. С. 709–719.
Шагапов В.Ш., Галиакбарова Э.В., Хусаинов И.Г., Хакимова З.Р. Акустическое сканирование поврежденных трубопроводов, находящихся в грунте // ПМТФ. 2018. Т. 59. № 4. С. 169–178.
Галиакбарова Э.В., Галиакбаров В.Ф. Импульсное сканирование нефтепроводов для обнаружения утечек // Проблемы сбора, подготовки и транспорта нефтепродуктов. 2012. № 3. С. 162–168.
Галиакбарова Э.В. Волновые исследования нефтепродуктопроводов для обнаружения “утечек” // Нефтегазовое дело. 2012. Т. 10. № 2. С. 44–49.
Галиакбаров В.Ф., Гольянов А.А., Коробков Г.Е. Способ определения места утечки жидкости из трубопровода // Пат. 2197679 C2 РФ, F17D5/02, опубл. 27.01.2003. Бюл. № 3.
Плаксин А.И., Шлык Ю.К. Способ диагностики герметичности магистрального трубопровода // Пат. 2565112 РФ, F17D 5/06, опубл. 20.10.2015. Бюл. № 30.
Галиакбаров В.Ф., Галиакбарова Э.В., Ковшов В.Д., Аминев Ф.М., Хакимова З.Р. Система контроля состояния трубопровода // Пат. 2606719 С1 РФ, F17D5/00, опубл. 10.01.2017. Бюл. № 1.
Исакович М.А. Общая акустика. М.: Наука, 1973. 495 с.
Ландау Л.Д., Лифшиц Е.М. Гидродинамика. М.: Наука, 1986. 733 с.
Кочин Н.Е., Кибель И.А., Розе Н.В. Теоретическая гидродинамика. Ч. II. М.: Физматгиз, 1963. 728 с.
Тихонов А.Н., Самарский А.А. Уравнения математической физики. М.: Наука, 1972. 736 с.
Ефимов В.А. Математический анализ (специальные разделы). Ч. I. М.: Высшая школа, 1980. 279 с.
Губайдуллин А.А., Болдырева О.Ю. Компьютерное моделирование волновых процессов в пористых средах // Вестник кибернетики. 2016. № 2(22). С. 103–111.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Акустический журнал

Архивы выпусков Информация о журнале Отправить рукопись в журнал