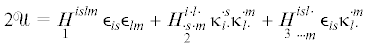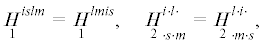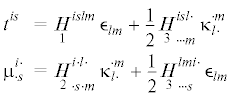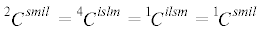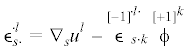Известия РАН. Механика твердого тела, 2023, № 5, стр. 98-110
ТЕНЗОРЫ С ПОСТОЯННЫМИ КОМПОНЕНТАМИ В ОПРЕДЕЛЯЮЩИХ УРАВНЕНИЯХ ГЕМИТРОПНОГО МИКРОПОЛЯРНОГО ТЕЛА
a Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия
* E-mail: radayev@ipmnet.ru
** E-mail: y.radayev@gmail.com
Поступила в редакцию 13.03.2023
После доработки 06.04.2023
Принята к публикации 21.04.2023
- EDN: PHNOCG
- DOI: 10.31857/S057232992370006X
Аннотация
В статье рассматриваются упругие потенциалы и определяющие уравнения механики анизотропных микрополярных тел, кинематика которых может быть задана двумя независимыми векторными полями: контравариантным полем трансляционных перемещений и контравариантным псевдовекторым полем микроповоротов веса +1. Квадратичный потенциал напряжений представлен с помощью трех определяющих тензоров четвертого ранга, два из которых имеют псевдотензорную природу и им можно приписать веса –2 и –1. Такое тело полностью задается 171-м микрополярным упругим модулем. Основное внимание сфокусировано на модели гемитропного (полуизотропного, демитропного) микрополярного упругого тела, характеризующегося девятью определяющими постоянными. Компоненты определяющего псевдотензора веса –1 оказываются чувствительными к преобразованиям зеркального отражения в трехмерном пространстве. Исследована своеобразная алгебраическая структура определяющих тензоров гемитропного тела, точнее, их абсолютных аналогов, получающихся умножением на целые степени псевдоскалярной единицы. Показано, что указанные тензоры всегда могут быть сконструированы из изомеров (изомера) тензора с постоянными компонентами (вообще не чувствительного ни к каким преобразованиям координатной системы) и одного дополнительного тензора четвертого ранга, сконструированного, в свою очередь, из компонент метрического тензора.
1. Предварительные сведения и вводные замечания. В теоретическом плане кинематика микрополярного континуума основана на трех основных результатах, касающихся перемещений абсолютно твердых тел в трехмерном пространстве.
В 1776 г. Эйлером (L. Euler) была установлена знаменитая теорема о перемещении абсолютно твердого тела с одной закрепленной точкой [1, с. 104]: произвольное перемещение абсолютно твердого тела с закрепленной точкой представляет собой конечный поворот относительно оси, проходящей через точку закрепления. В 1830 г. Шалем (M. Chasles) была доказана следующая теорема: самое общее перемещение твердого тела в пространстве складывается из поступательного перемещения, при котором произвольно выбранный полюс перемещается из своего первоначального положения в конечное, и конечного поворота относительно некоторой оси, проходящей через этот полюс11. Наконец винтовая теорема Моцци (G. Mozzi, 1763) – Коши–Шаля (приписываемая в [1, с. 109] Шалю, несмотря на имеющиеся более ранние доказательства, данные Моцци и Коши) гласит: произвольное перемещение абсолютно твердого тела в пространстве может быть осуществлено путем поступательного перемещения вдоль некоторого направления и вращения относительно оси, заданной указанным направлением, т.е. произвольное перемещение абсолютно твердого тела в пространстве реализуется как винтовое, а ось называется винтовой осью.
Из двух теорем Шаля по-существу только первая применялась при формулировках основных положений линейной микрополярной теории упругости, начиная с исторически первой работы [2]. До настоящего времени не предпринималось попыток использовать при математическом моделировании микрополярного континуума винтовую кинематику Шаля, соответствующую его винтовой теореме. Поэтому в конвенциональных микрополярных теориях механики деформируемых сред22 помимо поля трансляционных перемещений приходится оперировать с независимыми от трансляций микроповоротами, которые наиболее просто представляются псевдовекторами (в частности, контравариантыми псевдовекторами веса +1). В свою очередь, алгебра псевдотензоров развивается, исходя из фундаментальных понятий, связанных с перенумерацией координатных направлений, ориентации пространства и псевдоскалярных единиц, степени которых позволяют достаточно просто трансформировать произвольный псевдотензор в абсолютный тензор. Заметим, что необходимые для понимания настоящей работы сведения по теории псевдотензоров излагаются, например, в монографии [4].
Представляемая работа посвящена определяющим тензорам (псевдотензорам) гемитропного микрополярного упругого тела, вводимым в модель с помощью квадратичного потенциала напряжений. Компоненты одного из трех определяющих псевдотензоров оказываются чувствительными к преобразованиям зеркального отражения в трехмерном пространстве и, тем самым, обеспечивается зависимость механического состояния гемитропного тела от ориентации трехмерного пространства. Исследована своеобразная алгебраическая структура определяющих тензоров гемитропного тела, точнее, их абсолютных аналогов, получающихся умножением на целые степени псевдоскалярной единицы. Показано, что указанные тензоры всегда могут быть сконструированы из изомеров (изомера) тензора четвертого ранга с постоянными компонентами (вообще не чувствительного ни к каким преобразованиям координатной системы) и одного дополнительного тензора четвертого ранга, сконструированного, в свою очередь, из компонент метрического тензора.
Несмотря на то, что два из трех определяющих гемитропное тело тензоров на самом деле являются псевдотензорами, изложение удается провести в основном в терминах абсолютных тензоров, опираясь при этом на свойства степеней псевдоскалярных единиц. Такой подход был принят в статье [5], где в более или менее современном стиле реализовано построение модели линейного гемитропного тела, исходя из принципа виртуальных перемещений. Дальнейшее развитие теории было выполнено в работах [6–10]. Внимание к этой модели обусловлено потенциально широким кругом ее приложений к актуальным для всей механики деформируемого твердого тела проблемам.
2. Псевдотензоры и псевдоскаляры, связанные с ориентацией трехмерного пространства. Рассмотрим, прежде всего, основные понятия, относящиеся к представлению об ориентации плоского трехмерного пространства. Ориентировать пространство можно различными способами, разделив их на право- и левоориентированные. В частности, задание ориентации плоского пространства может быть выполнено той или иной схемой нумерации трех линейно независимых прямолинейных осей33. Транспозиция номеров в схеме нумерации будет означать переход от одной ориентации к другой.
Символы перестановок (альтернирующие символы) в трехмерном пространстве определяются согласно
Как известно, символы перестановок являются одновременно ковариатным псевдотензором третьего рангы веса –1 и контравариантным псевдотензором третьего ранга веса +1, т.е. на основании их определения справедливо следующее равенство
Координатные направления в плоском трехмерном пространстве зададим с помощью трех базисных векторов $\mathop \imath \limits_s $ ($s = 1,2,3$), образующих ковариантный базис (локальный, если речь идет о полевых представлениях). Локальный контравариантный базис $\mathop \imath \limits^s $ ($s = 1,2,3$) однозначно определяется следующими соотношениями
Предполагая далее заданными скалярное и векторное произведение двух векторов, введем фундаментальный ориентирующий псевдоскаляр (веса +1):
Ориентации координатных систем в таком случае находятся по знаку первой из псевдоскалярных единиц:
для правоориентированного координатного базиса, для левоориентированного координатного базиса.Введем также целые степени g псевдоскалярных единиц, полагая
Пользуясь псевдоскалярными единицами, определим абсолютные e-тензоры (тензоры перестановок, дискриминантные тензоры) следующими равенствами:
В дальнейшем изложении нам также потребуются еще два спецсимвола, так или иначе связанные с символами перестановок. Однако начать приходится с метрического тензора. Абсолютно инвариантная метрическая дифференциальная форма
порождает метрический тензор ${{g}_{{js}}}$. Квадрат псевдоскалярной единицы оказывается равным детерминанту, составленному из компонент тензора ${{g}_{{js}}}$:Как отмечалось выше, символы перестановок не подчиняются обычным правилам жонглирования индексов. Например, опускать индексы у контравариантного псевдотензора перестановок следует по правилу
(2.2)
$\mathop {{{\epsilon }_{{ijk}}}}\limits^{[ - 1]} = \mathop 1\limits^{[ - 2]} {{g}_{{il}}}{{g}_{{js}}}{{g}_{{kr}}}{{\mathop \epsilon \limits^{[ + 1]} }^{{lsr}}}.$Опираясь на это правило и вводя сначала спецсимволы
Из только что полученного соотношения следует, что
(2.3)
$e_{{i \cdot k}}^{{ \cdot p \cdot }} = \mathop 1\limits^{[ + 1]} \mathop {\epsilon _{{i \cdot k}}^{{ \cdot p \cdot }}}\limits^{[ - 1]} = \mathop 1\limits^{[ - 1]} \mathop {\epsilon _{{i \cdot k}}^{{ \cdot p \cdot }}}\limits^{[ + 1]} $3. Ковариантная теория линейного микрополярного континуума. В этом разделе работы мы будем рассматривать одну абсолютную тензорную формулировку основных уравнений микрополярной теории упругости, в существенных чертах развитую в статье [5].
Введем в пространстве криволинейную координатную сетку и обозначим через xk криволинейные координаты. Для сокращения записи тензорных уравнений будем обозначать через ${{\partial }_{k}}$ оператор частного дифференцирования по переменной xk, а через ${{\nabla }_{k}}$ – оператор ковариантного дифференцирования в метрике ${{g}_{{js}}}$.
Заметим, что ковариантная теория линейного микрополярного континуума [5] на самом деле может быть получена, исходя из ее первичного псевдотензорного аналога, если принять во внимание ковариантное постоянство степеней псевдоскалярных единиц
В статье [5] вектор перемещений предполагался ковариантным, т.е. вводился в теорию компонентами ${{u}_{k}}$. Ковариантное поле перемещений порождает вихрь, вычисляемый согласно
где – ковариантная производная векторного поля ${{u}_{k}}$.Полный микроповорот обычно вводится как псевдовектор, например, как контраваринтный псевдовектор веса ${\text{g}} = + 1$ (см. [12]): $\mathop {{{\phi }^{s}}}\limits^{[ + 1]} $.
Этот вектор затем умножением на вторую псевдоскалярную единицу приводится к абсолютному вектору
Вслед за полным микроповоротом и вихрем поля трансляционных перемещений можно говорить об относительном векторе микроповорота
(3.1)
${{\varphi }^{i}} = {{\phi }^{i}} - {{\omega }^{i}} = {{\phi }^{i}} - \frac{1}{2}{{e}^{{ikl}}}{{\nabla }_{k}}{{u}_{l}}$Этот вектор, наряду с вектором трансляционного премещения, считается в линейных микрополярных теориях малым и используется при контструировании асимметричного тензора деформации.
Асимметричный тензор деформации геометрически линейных микрополярных теорий
складывается из симметричной (определяемой полностью полем перемещений)Его можно также определить через полный вектор микроповорота согласно
или в терминах псевдотензоров – согласно(3.4)
${{\epsilon }_{{ij}}} = {{\nabla }_{i}}{{u}_{j}} - \mathop {{{\epsilon }_{{ijk}}}}\limits^{[ - 1]} \mathop {{{\phi }^{k}}}\limits^{[ + 1]} $Помимо асимметричного тензора деформации, необходим еще тензор изгиба–кручения
который представляет собой пространственный градиент полного вектора микроповорота. Ясно, что первичное определение тензора изгиба–кручения на самом деле имеет псевдотензорную природуОпределим, наконец, следующие присоединенные к тензорам ${{\epsilon }_{{is}}}$ и ${{\kappa }^{{is}}}$ векторы, положив
Уравнения статического равновесия получаются, исходя из принципа виртуальных перемещений [5]
(3.6)
$\begin{gathered} {{\nabla }_{i}}{{t}^{{ik}}} = - {{X}^{k}} \\ {{\nabla }_{i}}\mu _{{ \cdot k}}^{{i \cdot }} - 2{{\tau }_{k}} = - {{Y}_{k}} \\ \end{gathered} $4. Упругий потенциал гемитропного микрополярного тела. В модели упругого микрополярного тела пара ${{\epsilon }_{{ik}}}$, $\kappa _{{i \cdot }}^{{ \cdot s}}$ сопряжена с парой ${{t}^{{ik}}}$, $\mu _{{ \cdot s}}^{{i \cdot }}$ через потенциал напряжений (упругий потенциал) $\mathcal{U}$:
Наиболее общая форма упругого потенциала линейного микрополярного тела $\mathcal{U}$ имеет вид квадратичной формы
где ${{\mathop H\limits_1 }^{{islm}}}$,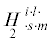 ,
, 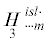 есть определяющие тензоры. Определяющие тензоры имеют в приведенной выше форме (4.1)
совершенно разную структуру индексов. Два из них на самом деле являются псевдотензорами,
но как обычно приводятся к абсолютным тензорам с помощью степеней первой псевдоскалярной
единицы:
есть определяющие тензоры. Определяющие тензоры имеют в приведенной выше форме (4.1)
совершенно разную структуру индексов. Два из них на самом деле являются псевдотензорами,
но как обычно приводятся к абсолютным тензорам с помощью степеней первой псевдоскалярной
единицы:
(4.2)
$\mathop {H_{{ \cdot s \cdot m}}^{{i \cdot l \cdot }}}\limits_2 = \mathop 1\limits^{[ + 2]} \mathop {\mathop {H_{{ \cdot s \cdot m}}^{{i \cdot l \cdot }}}\limits^{[ - 2]} }\limits_2 ,\quad \mathop {H_{{ \cdot \cdot \cdot m}}^{{isl \cdot }}}\limits_3 = \mathop 1\limits^{[ + 1]} \mathop {\mathop {H_{{ \cdot \cdot \cdot m}}^{{isl \cdot }}}\limits^{[ - 1]} }\limits_3 $Нетрудно заметить, что компоненты определяющих тензоров удовлетворяют следующим “условиям симметрии”:
учитывая которые можно показать, что число независимых компонент определяющих тензоров микрополярной теории упругости равно 171.Упругому потенциалу (4.1) соответствуют определяющие уравнения:
которые следует считать пригодными для любого линейно упругого микрополярного тела.В дальнейшем изложении мы будем рассматривать только гемитропные микрополярные среды, т.е. такие среды, определяющие тензоры которых являются гемитропными (полуизотропными, демитропными) и характеризуются неизменностью компонент при любых преобразованиях поворота.
Хорошо известно, что в декартовой системе координат абсолютный полуизотропный тезор четвертого ранга ${{H}_{{islm}}}$ представлется в форме [11, c. 66–70]:
Вводя новые постоянные
полуизотропный тензор четвертого ранга ${{H}_{{islm}}}$ можно также представить в следующем виде:В том случае, когда система координат не будет декартовой, полуизотропное микрополярноре тело характеризуется определяющими тензорами следующей структуры:
Вместо определяющих постоянных
(4.3)
$\begin{gathered} \mathop a\limits_1 = \frac{{2G\nu }}{{1 - 2\nu }},\quad \mathop a\limits_2 = 2G{{L}^{2}}{{c}_{3}},\quad \mathop a\limits_3 = 2GL{{c}_{4}} \\ \mathop b\limits_1 = G(1 + {{c}_{1}}),\quad \mathop b\limits_2 = G{{L}^{2}}(1 + {{c}_{2}}),\quad \mathop b\limits_3 \quad = GL\left( {{{c}_{5}} - \frac{1}{2}{{c}_{6}}} \right) \\ \mathop c\limits_1 = G(1 - {{c}_{1}}),\quad \mathop c\limits_2 = G{{L}^{2}}(1 - {{c}_{2}}),\quad \mathop c\limits_3 \quad = GL\left( {{{c}_{5}} + \frac{1}{2}{{c}_{6}}} \right) \\ \end{gathered} $Здесь $G$ – упругий модуль сдвига, $\nu $ – коэффициент Пуассона, L – характерная микродлина, ${{c}_{k}}$ ($k = \overline {1,6} $) – физически безразмерные микрополярные упругие модули.
5. Абсолютный тензор четвертого ранга с постоянными компонентами в трехмерном пространстве и ряд его изомеров. Абсолютный тензор с постоянными компонентами должен иметь одинаковые ко- и контравалентности, т.е. иметь четную валентность 2r (см., например, [4, с. 171]):
Как известно, для абсолютного тензора с постоянными компонентами справедливо следующее представление
(5.1)
$C_{{{{s}_{1}}{{s}_{2}} \ldots {{s}_{r}}}}^{{{{k}_{1}}{{k}_{2}} \ldots {{k}_{r}}}} = \sum\limits_P {{{c}_{P}}C_{{{{s}_{1}}{{s}_{2}} \ldots {{s}_{r}}}}^{{{{{\{ {{k}_{1}}{{k}_{2}} \ldots {{k}_{r}}\} }}_{P}}}}} $Абсолютный тензор четвертого ранга с постоянными компонентами в трехмерном пространстве на основании данной выше формулы (5.1) следующую общую форму, которую мы приведем, не указывая пустующие позиции для верхних и нижних индексов:
из которой можно вывести ряд изомеров, которые, в свою очередь, также будут тензорами с постоянными компонентами.Изомеры тензора $C_{{il}}^{{sm}}$ в дальнейшем изложении будем обозначать тем же самым корневым символом, снабжая его номером вверху слева. Число возможных изомеров тензора $C_{{il}}^{{sm}}$ оценивается как произведение числа всех возможных перестановок одного ряда символов $s$, $m$, $ \cdot $, $ \cdot $ и числа всех возможных перестановок другого ряда символов $i$, $l$, , $ \cdot $ с учетом того, что перестановка позиций, обозначаемых через $ \cdot $, приводит к одному и тому же изомеру. Таким образом, число возможных изомеров тензора $C_{{il}}^{{sm}}$ оказывается равным
Рассмотрим некоторые из ряда изомеров тензора (2). Определим сначала изомер тензора четвертого ранга с постоянными компонентами, положив
Далее нетрудно проверить, что
Введем изомер
Для него будут выполняться следующие равенства:
и которые позволяют заключить, что изомеры $^{4}{{C}_{{islm}}}$ и $^{1}{{C}_{{islm}}}$ представляют собой совершенно разные тензоры четвертого ранга.Продолжим рассмотрение изомеров тензора четвертого ранга с постоянными компонентами, определив
Легко проверяются следующие равенства, связывающие между собой изомеры $^{4}{{C}^{{ilsm}}}$, $^{1}{{C}^{{ilsm}}}$, $^{2}{{C}^{{ilsm}}}$:
откуда следует вывод о том, что т.е. тензоры $^{2}{{C}^{{smil}}}$ и $^{1}{{C}^{{smil}}}$ равны.Следующим в ряду изомеров выступает тензор
(5.3)
$^{3}C_{{ \cdot i \cdot l}}^{{s \cdot m \cdot }} = a\delta _{i}^{s}\delta _{l}^{m} + c\delta _{i}^{m}\delta _{l}^{s}$Сразу же можно утверждать, что справедливо равенство
и, кроме того, – равенстваПоскольку
то приходим к заключению о равенстве тензоров $^{3}{{C}^{{islm}}}$ и $^{4}{{C}^{{islm}}}$.Таким образом, в цепочке изомеров тензора четвертого ранга с постоянными компонентами
6. Представление определяющих тензоров гемитропного тела с помощью изомера тензора с постоянными компонентами. Основную энергетическую форму гемитропного микрополярного упругого тела можно преобразовать к специальной форме, позволяющей дать оптимальное представление определяющих тензоров в терминах тензоров с постоянными компонентами. С этой целью сначала заметим, что трансляции пространства наиболее естественным образом представляются контравариантным вектором,55 поэтому и вектор перемещений будем считать контравариантным с естественными компонентами ${{u}^{s}}$. Кроме этого полный микроповорот, как продемонстрировано в [12], в одном из вариантов развития микрополярной теории упругости выступает как контравариантный псевдовектор веса ${\text{g}} = + 1$.
С учетом высказанных положений наиболее естественным выглядит следующее определение асимметричного тензора деформации:
или в терминах абсолютных тензоровТензор изгиба–кручения имеет идентичную структуру индексов
Асимметричному тензору деформации $\epsilon _{{i \cdot }}^{{ \cdot k}}$ и тензору изгиба–кручения сопряжены по энергии тензор силовых напряжений $t_{{ \cdot k}}^{{i \cdot }}$ и тензор моментных напряжений $\mu _{{ \cdot k}}^{{i \cdot }}$. Оба тензора также имеют идентичную структуру индексов. Уравнения статического равновесия, очевидно, приобретают следующий вид:
Определяющие тензоры анизотропного микрополярного тела будут иметь однотипную структуру индексов вида: $H_{{ \cdot s \cdot m}}^{{i \cdot l \cdot }}$, поскольку энергетическая форма преобразуется к следующему виду:
(6.1)
$2\mathcal{U} = \mathop H\limits_1 \,_{{ \cdot s \cdot m}}^{{i \cdot l \cdot }}\epsilon _{{i \cdot }}^{{ \cdot s}}\epsilon _{{l \cdot }}^{{ \cdot m}} + \mathop H\limits_2 \,_{{ \cdot s \cdot m}}^{{i \cdot l \cdot }}\kappa _{{i \cdot }}^{{ \cdot s}}\kappa _{{l \cdot }}^{{ \cdot m}} + \mathop H\limits_3 \,_{{ \cdot s \cdot m}}^{{i \cdot l \cdot }}\epsilon _{{i \cdot }}^{{ \cdot s}}\kappa _{{l \cdot }}^{{ \cdot m}}$В случае гемитропного микрополярного упругого тела каждый из трех определяющих тензоров выражается через третий изомер тензора с постоянными компонентами согласно
(6.2)
$\mathop {H_{{ \cdot s \cdot m}}^{{i \cdot l \cdot }}}\limits_\mathfrak{c} = {{\,}^{3}}\mathop {C_{{ \cdot s \cdot m}}^{{i \cdot l \cdot }}\,}\limits_\mathfrak{c} + \mathop b\limits_\mathfrak{c} {{g}_{{sm}}}{{g}^{{il}}}$Таким образом, показано, что каждый из трех определяющих тензоров всегда может быть сконструирован из одного из изомеров тензора с постоянными компонентами (вообще не чувствительного ни к каким преобразованиям координатной системы) и одного дополнительного тензора четвертого ранга, сконструированного, в свою очередь, из компонент метрического тензора (не чувствительного к изометриям трехмерного пространства и даже к его гомотетичным преобразованиям).
Важным представляется также то обстоятельство, что определяющие тензоры (и псевдотензоры (6.2)) в силу (6.2) ковариантно постоянны66. Действительно, тензоры с постоянными компонентами ковариантно постоянны. То же самое относится к метрическому тензору. Определяющие псевдоскаляры
В качестве еще одного примера укажем на ковариантное постоянство характерной микродлины L. Так как
Интересно также отметить, что ковариантное постоянство определяющего псевдоскаляра $\mathop L\limits^{[ - 1]} $, т.е. выполнение условия
сразу же влечет его представимость в формеХарактерная микродлина микрополярной теории упругости $L$ – единственный из модулей, которому может быть приписан вес, и только она получает трактовку как определяющий псевдоскаляр, чувствительный к замене ориентации координатной системы, например, с право- на левоориентированную.
Кроме ковариантного постоянства определяющих тензоров (6.2) выделим присущее им важное свойство нечувствительности компонент при произвольных преобразованиях координат при выполнении условий
В силу (6.2) гемитропное микрополярное тело характеризуется девятью определяющими постоянными. Если считать выполненными приведенные выше условия, то остается всего шесть определяющих постоянных. По смыслу проведенных выше рассуждений такое микрополярное тело следует назвать ультраизотропным. Физически приемлемым такое микрополярное тело будет, очевидно, только в том случае, когда потенциал напряжений суть положительно определенная квадратичная форма от компонент асимметричного тензора деформации и тензора изгиба–кручения.
7. Заключение. В представляемой работе рассмотрены определяющие тензоры (псевдотензоры) четвертого ранга, с которыми приходится иметь дело в атермической механике гемитропного микрополярного упругого тела. Указанные тензоры с различной структурой индексов могут быть введены в модель гемитропного тела с помощью квадратичного потенциала напряжений. Несмотря на первичность псевдотензорного представления энергетического потенциала, изложение удается провести в основном в терминах абсолютных тензоров, опираясь при этом на свойства степеней псевдоскалярных единиц. Компоненты одного из трех определяющих псевдотензоров оказываются чувствительными к преобразованиям зеркального отражения в трехмерном пространстве. Исследована алгебраическая структура определяющих тензоров гемитропного тела. Показано, что последние всегда могут быть сконструированы из изомеров (а в случае идентичности структуры тензорных индексов — одного изомера) тензора четвертого ранга с постоянными компонентами (вообще не чувствительного ни к каким преобразованиям координатной системы) и одного дополнительного тензора четвертого ранга, сконструированного, в свою очередь, из компонент метрического тензора. Тензорам подобной алгебраической структуры могут быть приписаны веса только за счет придания весов определяющим псевдоскалярам. Среди определяющих псевдоскаляров выделяется характерная микродлина – единственная конвенциональная определяющая характеристика микрополярного упругого тела, которая может быть определена как псевдоскаляр нечетного веса, чувствительный к замене ориентации координатной системы с право- на левоориентированную.
Работа выполнена при финансовой поддержке Российского научного фонда (проект № 23-21-00262 “Связанная термомеханика микрополярных полуизотропных сред”).
Список литературы
Парс Л.А. Аналитическая динамика. М.: Наука, 1971. 636 с.
Cosserat E., Cosserat F. Théorie des corps déformables. Paris: Herman et Fils, 1909. 226 p.
Nowacki W. Theory of asymmetric elasticity. Oxford: Pergamon Press, 1986. 383 p.
Гуревич Г.Б. Основы теории алгебраических инвариантов. М., Л.: Гостехтеоретиздат. 1948. 408 с.
Радаев Ю.Н. Правило множителей в ковариантных формулировках микрополярных теорий механики континуума // Вестн. Сам. гос. техн. ун-та. Сер. Физ.-мат. науки. 2018. Т. 22. № 3. С. 504–517. https://doi.org/10.14498/vsgtu1635
Kovalev V.A., Murashkin E.V., Radayev Y.N. On the Neuber theory of micropolar elasticity. A pseudotensor formulation // Вестн. Сам. гос. техн. ун-та. Сер. Физ.-мат. науки. 2020. Т. 24. № 4. С. 752–761. https://doi.org/10.14498/vsgtu1799
Murashkin E.V., Radayev Y.N. An algebraic algorithm of pseudotensors weights eliminating and recovering // Mech. Solids. 2022. V. 57. № 6. P. 1416–1423. https://doi.org/10.3103/s0025654422060085
Murashkin E.V., Radaev Y.N. On theory of oriented tensor elements of area for a micropolar continuum immersed in an external plane space // Mech. Solids. 2022. V. 57. № 2. P. 205–213. https://doi.org/10.3103/s0025654422020108
Мурашкин Е.В., Радаев Ю.Н. К теории гемитропных тензоров четвертого ранга в трехмерных пространствах Евклида // Вестн. Сам. гос. техн. ун-та. Сер. Физ.-мат. науки. 2022. Т. 26. № 3. С. 592–602. https://doi.org/10.14498/vsgtu1941
Мурашкин Е.В., Радаев Ю.Н. О двух основных естественных формах потенциала асимметричных тензоров силовых и моментных напряжений в механике гемитропных тел // Вестн. Чув. гос. пед. универс. им. И.Я. Яковлева. Серия: мех. предельного состояния. 2022. № 3. С. 86–100. https://doi.org/10.37972/chgpu.2022.53.3.010
Jeffreys H. Cartesian tensors. Cambridge: Cambridge University Press, 1969. 93 p.
Radayev Y.N. Two-point rotations in geometry of finite deformations // Theory of Elasticity and Creep. Advanced Structured Materials. V. 185. Springer, 2023. P. 275–283. https://doi.org/10.1007/978-3-031-18564-9_20
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела