Известия РАН. Механика твердого тела, 2023, № 5, стр. 15-26
ОБ ОДНОЙ ДИНАМИЧЕСКИ СОГЛАСОВАННОЙ МОДЕЛИ НОРМАЛЬНЫХ РЕАКЦИЙ В ТОЧКАХ КОНТАКТА МОБИЛЬНОЙ ПЛАТФОРМЫ С ПОВЕРХНОСТЬЮ ПРИ УЧЕТЕ КОНСТРУКЦИИ МЕКАНУМ-КОЛЕС И ПОЛИКОМПОНЕНТНОГО ТРЕНИЯ
Г. Р. Сайпулаев a, *, Б. И. Адамов a, **, А. И. Кобрин a, ***
a Национальный исследовательский университет “МЭИ”
Москва, Россия
* E-mail: saypulaevgr@mail.ru
** E-mail: adamoff.b@yandex.ru
*** E-mail: kobrinai@yandex.ru
Поступила в редакцию 01.09.2022
После доработки 04.10.2022
Принята к публикации 06.10.2022
- EDN: QWTDIZ
- DOI: 10.31857/S0572329922600712
Аннотация
В статье исследуется влияние зависимости нормальных реакций от параметров движения на динамику мобильной платформы при учете конструкции меканум-колес и поликомпонентного трения. Для описания зависимости нормальных реакций от параметров движения используются теоремы об изменении количества движения и момента количества движения, записанные для меканум-платформы. Влияние нормальных реакций на динамику меканум-платформы оценивается по результатам численного моделирования. Модель динамики меканум-платформы учитывает конструкцию меканум-колес и поликомпонентное трение. В качестве модели трения контактирующих роликов с опорной поверхностью рассматривается предложенная В.Ф. Журавлевым модель поликомпонентного трения, учитывающая скольжение и верчение. Даны оценки максимальных отклонений нормальных реакций опор, обусловленных динамикой меканум-платформы, от значений нормальных реакций, рассчитанных для покоящейся мобильной платформы (равные на примере робота KUKA youBot 16.7%). Получены неравенства, ограничивающие максимальные значения управляющих моментов, при выполнении которых не происходит отрыва контактирующих роликов меканум-колес от опорной поверхности. По результатам моделирования показано, что нормальные реакции изменялись на 5–6% от величины нормальной реакции, рассчитанной в случае покоящейся меканум-платформы, что соответствует полученным оценкам. Указанные изменения нормальных реакций могут привести к снижению точности движения меканум-платформы, получаемой при программном управлении.
1. Введение. Исследования мобильных роботов, способных осуществлять всенаправленное движение, являются актуальными из-за широкого применения всенаправленных платформ в области складской логистики, медицины и при работе в труднодоступных местах (стесненные пространства). Способность осуществлять всенаправленное движение появляется за счет оснащения мобильных платформ роликонесущими колесами различных типов: омни-колеса или меканум-колеса [1].
Для управления мобильными платформами с омни- или меканум-колесами необходимо разрабатывать кинематические и динамические модели движения указанных платформ. Для математического описания омни- или меканум-колес широко используется упрощенная модель роликонесущих колес [2], а на динамику мобильных платформ налагаются неголономные связи [3], характеризующие условия непроскальзывания точек контакта роликов с опорной поверхностью.
При этом в недавних исследованиях рассматривается механика всенаправленных платформ с более детальным учетом конструкции роликонесущих колес.
В [4] была описана геометрия и кинематика роликонесущих колес, а для меканум-колес получена зависимость смещения точки контакта вдоль собственной оси колеса от угла поворота колеса.
В [5] построена модель динамики меканум-платформы с учетом конструкции колес (конечного числа и формы роликов) и сухого трения в точках контакта роликов с опорной поверхностью. При этом для замыкания модели трения решена (в рамках статического подхода) статически неопределимая задача нахождения нормальных реакций в точках контакта в случае неподвижной меканум-платформы. Построенная модель динамики была применена для исследования влияния конструкции меканум-колес на динамику мобильной платформы при использовании трения Кулона [5] и модели поликомпонентного трения [6, 7].
В [6, 7] в качестве модели поликомпонентного трения рассматривается связанная модель трения, учитывающая скольжение и верчение контактирующих тел, которая была предложена В.Ф. Журавлевым [8] и проверена в экспериментальных исследованиях [9].
Работы [10, 11] посвящены описанию контактного взаимодействия роликов с опорной поверхностью и исследованию влияния контактных сил на динамику меканум-платформы по результатам экспериментов и компьютерного моделирования.
В рамках данной работы ставится задача определения нормальных реакций с учетом динамической согласованности [12–14] (в рамках динамического подхода) с целью сравнительного анализа динамики меканум-платформы при различных моделях нормальных реакций, полученных при статическом и динамическом подходах.
2. Конструкция меканум-платформы. Объектом исследования является мобильная платформа с двумя парами соосных меканум-колес.
Рассматривается движение меканум-платформы по горизонтальной неподвижной плоскости $xy$. Введем подвижную систему координат $OXYZ$ (рис. 1,a). Начало этой системы координат находится в геометрическом центре $O$ платформы; $OX$ и $OY$ – продольная и поперечная оси платформы; $\psi = \angle (x,X)$ – угол поворота платформы относительно вертикальной оси OZ.
Рис. 1.
Схема мобильной платформы: (a) – платформа, (b) – меканум-колесо, (c) – контактирующий ролик.
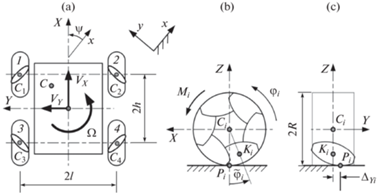
Абсциссы и ординаты центров колес ${{C}_{i}}\;(i = 1,..,4)$ в системе координат $OXYZ$ равны ${{\rho }_{{Xi}}}$ и ${{\rho }_{{Yi}}}$ (${{\rho }_{{X1}}} = {{\rho }_{{X2}}} = h,$ ${{\rho }_{{X3}}} = {{\rho }_{{X4}}} = - h,$ ${{\rho }_{{Y1}}} = {{\rho }_{{Y3}}} = l,$ ${{\rho }_{{Y2}}} = {{\rho }_{{Y4}}} = - l$). Угол между осями роликов i-го колеса и плоскостью ${{C}_{i}}ZX$ обозначим ${{\delta }_{i}}$ (${{\delta }_{2}} = {{\delta }_{3}} = 45^\circ ,$ ${{\delta }_{1}} = {{\delta }_{4}} = - 45^\circ $).
Обозначим ${{K}_{i}}$ центр оси контактирующего ролика, а ${{\tilde {\varphi }}_{i}}$ – угол его поворота вокруг оси i-го колеса (рис. 1,b). Поскольку на каждом колесе расположено по шесть роликов, то $ - 30^\circ \leqslant {{\tilde {\varphi }}_{i}} \leqslant 30^\circ $. При смене контактирующего ролика ${{\tilde {\varphi }}_{i}}$ скачкообразно изменяется на 60°.
Считая, что угол поворота i-го колеса ${{\varphi }_{i}}$ отсчитывается от направления отрицательной полуоси ${{C}_{i}}Z$, угол ${{\tilde {\varphi }}_{i}}$ можно определить с помощью операции взятия остатка от деления mod по формуле ${{\tilde {\varphi }}_{i}} = ({{\varphi }_{i}} + 30^\circ )\bmod (60^\circ ) - 30^\circ $.
Поверхности всех роликов колеса касаются одной цилиндрической поверхности радиуса $R$, поэтому точка контакта ${{P}_{i}}$ ролика с опорной поверхностью смещена относительно центра колеса ${{C}_{i}}$ в направлении оси $OY$ на величину ${{\Delta }_{{Yi}}} = {{R}_{d}}{\text{tan}}{{\delta }_{i}}{\text{tan}}{{\tilde {\varphi }}_{i}}$ [3, 4], где ${{R}_{d}} = \left| {{{C}_{i}}{{K}_{i}}} \right|$ (см. рис. 1,c). Отметим, что в рассматриваемом случае геометрия роликов обеспечивает отсутствие вертикальных вибраций центра колеса при движении по плоскости.
3. Математическая модель меканум-платформы. Исследование влияния модели нормальных реакций будем проводить путем сравнительного анализа динамики нескольких моделей системы. Во всех рассмотренных моделях ролики считаются безынерционными, а в сочленениях тел действуют линейные по скоростям силы трения.
Модель 1. Считается, что ролики колес непрерывно контактируют с опорной поверхностью, а точка контакта находится на центральном поперечном сечении (т.е. ${{\tilde {\varphi }}_{i}} \equiv 0$). В этом случае
(3.1)
$R{{\dot {\varphi }}_{i}} = {{V}_{X}} + \left( {{{V}_{Y}} + {{\rho }_{{Xi}}}\Omega } \right)\tan {{\delta }_{i}} - {{\rho }_{{Yi}}}\Omega ,\quad (i = 1,..,4)$Уравнения динамики для модели 1 построены с учетом неголономных связей (3.1) в работе [3].
Две другие модели описываются уравнениями динамики [5–7]:
(3.2)
${{I}_{R}}\dot {\Omega } + m{{a}_{X}}\left( {{{{\dot {V}}}_{Y}} + \Omega {{V}_{X}}} \right) - m{{a}_{Y}}\left( {{{{\dot {V}}}_{X}} - \Omega {{V}_{Y}}} \right) = \sum\limits_{i = 1}^4 \left[ {M_{{Zi}}^{f} + {{F}_{{Yi}}}{{\rho }_{{Xi}}} - {{F}_{{Xi}}}\left( {{{\rho }_{{Yi}}} + {{\Delta }_{{Yi}}}} \right)} \right]$Модель 2. Описывается уравнениями (3.2) при использовании выражений для нормальных реакций опор, полученных при статическом подходе [5, 6].
Модель 3. Описывается уравнениями (3.2) при использовании выражений для нормальных реакций опор, полученных при динамическом подходе.
Ниже представлен вывод модели нормальных реакций опор из условия динамической согласованности.
4. Модель нормальных реакций. Для определения нормальных реакций из условий динамической согласованности запишем теорему об изменении количества движения системы в проекциях на ось $OZ$ и теорему об изменении момента количества движения системы в проекциях на оси $OX$ и $OY$, а также примем во внимание условие совместности деформаций [5]:
(4.1)
$\begin{gathered} - {{I}_{{wY}}}\Omega \sum\limits_{i = 1}^4 {{{\dot {\varphi }}}_{i}} = - \left( {{{N}_{2}} + {{N}_{4}}} \right)l + \left( {{{N}_{1}} + {{N}_{3}}} \right)l - mg{{a}_{Y}} + \sum\limits_{i = 1}^4 \left( {M_{{Xi}}^{f} + {{F}_{{Yi}}}R} \right) \\ {{I}_{{wY}}}\sum\limits_{i = 1}^4 {{{\ddot {\varphi }}}_{i}} = - \left( {{{N}_{1}} + {{N}_{2}}} \right)h + \left( {{{N}_{3}} + {{N}_{4}}} \right)h + mg{{a}_{X}} + \sum\limits_{i = 1}^4 \left( {M_{{Yi}}^{f} - {{F}_{{Xi}}}R} \right) \\ \end{gathered} $Можно переписать систему уравнений (4.1) в силу уравнений динамики (3.2) для угловых скоростей колес в виде:
(4.2)
$\begin{gathered} {{N}_{1}} + {{N}_{2}} + {{N}_{3}} + {{N}_{4}} = mg + 4{{m}_{w}}g \\ \left( {{{N}_{1}} + {{N}_{3}}} \right)l - \left( {{{N}_{2}} + {{N}_{4}}} \right)l = mg{{a}_{Y}} - {{I}_{{wY}}}\Omega \sum\limits_{i = 1}^4 {{{\dot {\varphi }}}_{i}} - \sum\limits_{i = 1}^4 \left( {M_{{Xi}}^{f} + {{F}_{{Yi}}}R} \right) \\ \left( {{{N}_{3}} + {{N}_{4}}} \right)h - \left( {{{N}_{1}} + {{N}_{2}}} \right)h = - mg{{a}_{X}} + \sum\limits_{i = 1}^4 \left( {{{M}_{i}} - {{\mu }_{w}}{{{\dot {\varphi }}}_{i}}} \right) \\ {{N}_{1}} - {{N}_{2}} - {{N}_{3}} + {{N}_{4}} = 0 \\ \end{gathered} $Учитывая, что в выражения для сил и моментов трения нормальные реакции входят линейно, можно представить силы и моменты трения в виде:
(4.3)
${{F}_{{Xi}}} = {{N}_{i}}{{\tilde {F}}_{{Xi}}},\quad {{F}_{{Yi}}} = {{N}_{i}}{{\tilde {F}}_{{Yi}}},\quad M_{{Zi}}^{f} = {{N}_{i}}\tilde {M}_{{Zi}}^{f},\quad M_{{Xi}}^{f} = {{N}_{i}}\tilde {M}_{{Xi}}^{f},\quad M_{{Yi}}^{f} = {{N}_{i}}\tilde {M}_{{Yi}}^{f}$(4.4)
$\begin{gathered} {{N}_{1}}\left( {l + \tilde {M}_{{X1}}^{f} + {{{\tilde {F}}}_{{Y1}}}R} \right) + {{N}_{3}}\left( {l + \tilde {M}_{{X3}}^{f} + {{{\tilde {F}}}_{{Y3}}}R} \right) + {{N}_{2}}\left( { - l + \tilde {M}_{{X2}}^{f} + {{{\tilde {F}}}_{{Y2}}}R} \right) + \\ \, + {{N}_{4}}\left( { - l + \tilde {M}_{{X4}}^{f} + {{{\tilde {F}}}_{{Y4}}}R} \right) = mg{{a}_{Y}} - {{I}_{{wY}}}\Omega \sum\limits_{i = 1}^4 {{{\dot {\varphi }}}_{i}} \\ \left( {{{N}_{3}} + {{N}_{4}}} \right)h - \left( {{{N}_{1}} + {{N}_{2}}} \right)h = - mg{{a}_{X}} + \sum\limits_{i = 1}^4 \left( {{{M}_{i}} - {{\mu }_{w}}{{{\dot {\varphi }}}_{i}}} \right) \\ \end{gathered} $Решение системы линейных алгебраических уравнений (4.4) имеет вид:
(4.5)
$\begin{gathered} {{N}_{2}} = \frac{{{{m}_{R}}gh\left( {2l + {{W}_{1}} + {{W}_{3}}} \right) - 2h{{b}_{1}} + {{b}_{2}}\left( {2l + {{W}_{1}} - {{W}_{4}}} \right)}}{{2h\left( {4l + {{W}_{1}} + {{W}_{3}} - {{W}_{2}} - {{W}_{4}}} \right)}} \\ {{N}_{3}} = \frac{{{{m}_{R}}gh\left( {2l - {{W}_{2}} - {{W}_{4}}} \right) + 2h{{b}_{1}} - {{b}_{2}}\left( {2l + {{W}_{1}} - {{W}_{4}}} \right)}}{{2h\left( {4l + {{W}_{1}} + {{W}_{3}} - {{W}_{2}} - {{W}_{4}}} \right)}} \\ \end{gathered} $(4.6)
$\begin{gathered} {{W}_{1}} = \tilde {M}_{{X1}}^{f} + {{{\tilde {F}}}_{{Y1}}}R,\quad {{W}_{2}} = \tilde {M}_{{X2}}^{f} + {{{\tilde {F}}}_{{Y2}}}R \\ {{W}_{3}} = \tilde {M}_{{X3}}^{f} + {{{\tilde {F}}}_{{Y3}}}R,\quad {{W}_{4}} = \tilde {M}_{{X4}}^{f} + {{{\tilde {F}}}_{{Y4}}}R \\ {{b}_{1}} = mg{{a}_{Y}} - {{I}_{{wY}}}\Omega \sum\limits_{i = 1}^4 {{{\dot {\varphi }}}_{i}},\quad {{b}_{2}} = mg{{a}_{X}} - \sum\limits_{i = 1}^4 \left( {{{M}_{i}} - {{\mu }_{w}}{{{\dot {\varphi }}}_{i}}} \right) \\ \end{gathered} $Для замыкания уравнений движения в моделях 2 и 3 рассмотрим модель поликомпонентного трения [8], учитывающего скольжение и верчение:
(4.7)
$\begin{gathered} {{F}_{{Xi}}} = - \frac{{f{{N}_{i}}{{V}_{{PiX}}}}}{{\sqrt {V_{{PiX}}^{2} + V_{{PiY}}^{2} + \varepsilon } + \frac{8}{{3\pi }}\chi \left| {{{\omega }_{{riZ}}}} \right|}} \\ {{F}_{{Yi}}} = - \frac{{f{{N}_{i}}{{V}_{{PiY}}}}}{{\sqrt {V_{{PiX}}^{2} + V_{{PiY}}^{2} + \varepsilon } + \frac{8}{{3\pi }}\chi \left| {{{\omega }_{{riZ}}}} \right|}} \\ M_{{Zi}}^{f} = - \frac{{3\pi \chi }}{{16}}f{{N}_{i}}\frac{{\chi {{\omega }_{{riZ}}}}}{{\chi \left| {{{\omega }_{{riZ}}}} \right| + \frac{{15\pi }}{{16}}\sqrt {V_{{PiX}}^{2} + V_{{PiY}}^{2} + \varepsilon } }},\quad M_{{Xi}}^{f} = M_{{Yi}}^{f} = 0 \\ \end{gathered} $При использовании модели трения (4.7) выражения для вспомогательных функций сил и моментов трения имеют вид:
(4.8)
$\begin{gathered} {{{\tilde {F}}}_{{Xi}}} = - \frac{{f{{V}_{{PiX}}}}}{{\sqrt {V_{{PiX}}^{2} + V_{{PiY}}^{2} + \varepsilon } + \frac{8}{{3\pi }}\chi \left| {{{\omega }_{{riZ}}}} \right|}} \\ {{{\tilde {F}}}_{{Yi}}} = - \frac{{f{{V}_{{PiY}}}}}{{\sqrt {V_{{PiX}}^{2} + V_{{PiY}}^{2} + \varepsilon } + \frac{8}{{3\pi }}\chi \left| {{{\omega }_{{riZ}}}} \right|}} \\ \tilde {M}_{{Zi}}^{f} = - \frac{{3\pi \chi }}{{16}}f\frac{{\chi {{\omega }_{{riZ}}}}}{{\chi \left| {{{\omega }_{{riZ}}}} \right| + \frac{{15\pi }}{{16}}\sqrt {V_{{PiX}}^{2} + V_{{PiY}}^{2} + \varepsilon } }},\quad \tilde {M}_{{Xi}}^{f} = \tilde {M}_{{Yi}}^{f} = 0 \\ \end{gathered} $Отметим, что функции компонент трения ограничены неравенствами:
(4.9)
$\left| {{{{\tilde {F}}}_{{Xi}}}} \right| \leqslant f,\quad \left| {{{{\tilde {F}}}_{{Yi}}}} \right| \leqslant f,\quad \sqrt {\tilde {F}_{{Xi}}^{2} + \tilde {F}_{{Yi}}^{2}} \leqslant f,\quad \left| {\tilde {M}_{{Zi}}^{f}} \right| \leqslant \frac{{3\pi \chi }}{{16}}f$Оценим порядки величин, входящих в модель нормальных реакций (4.5) и возникающих из условия динамической согласованности:
(4.11)
$2l\left( {1 - \frac{{fR}}{l}} \right) \leqslant \left( {2l - {{W}_{2}} + {{W}_{3}}} \right) \leqslant 2l\left( {1 + \frac{{fR}}{l}} \right)$Рассмотрев в качестве примера значения параметров для робота KUKA youBot [5]: $f = 0.5$, $R = 0.05$ м, $l = 0.15$ м, получаем, что изменения величин нормальных реакций, связанные с влиянием динамики меканум-платформы, могут оцениваться в $\frac{{fR}}{l} = \frac{{0.5 \cdot 0.05}}{{0.15}} \approx 0.167 = 16.7\% $.
В частности, при движении платформы вдоль ее поперечной оси (${{V}_{X}}\, = \,0,{{V}_{Y}} \ne 0$, Ω = 0) проекция силы трения скольжения на ось $Y$, действующей на контактирующий ролик i-го колеса, будет максимальна по модулю ($\left| {{{{\tilde {F}}}_{{Yi}}}} \right|\, = \,f,\left| {{{W}_{i}}} \right|$ = fR). При этом в рамках неголономной модели боковому движению соответствуют равные по модулю значения управляющих моментов (${{M}_{2}} = {{M}_{3}} = - {{M}_{1}} = - {{M}_{4}}$) и угловых скоростей вращения колес (${{\dot {\varphi }}_{2}} = {{\dot {\varphi }}_{3}} = - {{\dot {\varphi }}_{1}} = - {{\dot {\varphi }}_{4}}$). Тогда выражения нормальных реакций опор (4.5) при поперечном движении мобильной платформы примут вид:
(4.12)
$\begin{gathered} {{N}_{1}} = \frac{{{{m}_{R}}g}}{4}\left( {1 \mp \frac{{fR}}{l}} \right) + \frac{{mg}}{4}\left( {\frac{{{{a}_{Y}}}}{l} + \frac{{{{a}_{X}}}}{h}} \right),\quad {{N}_{2}} = \frac{{{{m}_{R}}g}}{4}\left( {1 \pm \frac{{fR}}{l}} \right) + \frac{{mg}}{4}\left( { - \frac{{{{a}_{Y}}}}{l} + \frac{{{{a}_{X}}}}{h}} \right) \\ {{N}_{3}} = \frac{{{{m}_{R}}g}}{4}\left( {1 \mp \frac{{fR}}{l}} \right) + \frac{{mg}}{4}\left( {\frac{{{{a}_{Y}}}}{l} - \frac{{{{a}_{X}}}}{h}} \right),\quad {{N}_{4}} = \frac{{{{m}_{R}}g}}{4}\left( {1 \pm \frac{{fR}}{l}} \right) + \frac{{mg}}{4}\left( { - \frac{{{{a}_{Y}}}}{l} - \frac{{{{a}_{X}}}}{h}} \right) \\ \end{gathered} $Заметим, что приведенная выше оценка максимальных отклонений (в 16.7%) нормальных реакций от значений, полученных для покоящейся платформы, явно просматривается из формул (4.12) при нулевых смещениях центра масс мобильной платформы (${{a}_{X}} = {{a}_{Y}} = 0$). А в случае смещенного центра масс платформы оценка максимальных отклонений нормальных реакций может изменяться в зависимости от величины смещения центра масс платформы.
Стоит отметить, что при исследовании динамики систем с трением (или односторонними связями) [14, 15] интерес представляют условия безотрывного движения контактирующих тел по опорной поверхности, которые могут быть сформулированы, как положительная определенность нормальных реакций опор (${{N}_{i}} \geqslant 0$). Поэтому ниже получим оценку максимальных управляющих моментов из условий безотрывности движения контактирующих роликов по опорной поверхности.
Для этого рассмотрим движение платформы вдоль ее продольной оси (${{V}_{X}} \ne 0,$ ${{V}_{Y}} = 0,$ $\Omega = 0$). В этом случае проекция силы трения скольжения на ось Y, действующей на контактирующий ролик i-го колеса, будет близка к нулю ($\left| {{{{\tilde {F}}}_{{Yi}}}} \right| = 0,$ $\left| {{{W}_{i}}} \right| = 0$). При этом в рамках неголономной модели продольному движению меканум-платформы соответствуют равные значения управляющих моментов (${{M}_{1}}\, = \,{{M}_{2}}\, = \,{{M}_{3}}\, = \,{{M}_{4}}$ = Mp) и угловых скоростей вращения колес (${{\dot {\varphi }}_{1}} = {{\dot {\varphi }}_{2}} = {{\dot {\varphi }}_{3}} = {{\dot {\varphi }}_{4}} = {{\dot {\varphi }}_{p}}$). Здесь ${{M}_{p}},\;{{\dot {\varphi }}_{p}}$ – значения управляющего момента и угловой скорости вращения колес, которые соответствуют программному движению. Тогда выражения нормальных реакций опор (4.5) при продольном движении мобильной платформы примут вид:
(4.13)
$\begin{gathered} {{N}_{2}} = \frac{{{{m}_{R}}g}}{4} + \frac{{mg}}{4}\left( { - \frac{{{{a}_{Y}}}}{l} + \frac{{{{a}_{X}}}}{h}} \right) - \frac{{{{M}_{p}} - {{\mu }_{w}}{{{\dot {\varphi }}}_{p}}}}{h} \\ {{N}_{3}} = \frac{{{{m}_{R}}g}}{4} + \frac{{mg}}{4}\left( {\frac{{{{a}_{Y}}}}{l} - \frac{{{{a}_{X}}}}{h}} \right) + \frac{{{{M}_{p}} - {{\mu }_{w}}{{{\dot {\varphi }}}_{p}}}}{h} \\ \end{gathered} $По формулам (4.13) можно получить ограничения на величины управляющих моментов, при которых меканум-платформа имеет четыре точки контакта с опорной поверхностью. При этом данные ограничивающие значения минимальны в момент начала движения, когда угловая скорость колес равна нулю (${{\dot {\varphi }}_{p}} = 0$):
(4.14)
$\begin{gathered} \frac{{{{M}_{p}}}}{h} \leqslant \min \left\{ {\frac{{{{m}_{R}}g}}{4} + \frac{{mg}}{4}\left( {\frac{{{{a}_{Y}}}}{l} + \frac{{{{a}_{X}}}}{h}} \right),\frac{{{{m}_{R}}g}}{4} + \frac{{mg}}{4}\left( { - \frac{{{{a}_{Y}}}}{l} + \frac{{{{a}_{X}}}}{h}} \right)} \right\} \\ - \frac{{{{M}_{p}}}}{h} \leqslant \min \left\{ {\frac{{{{m}_{R}}g}}{4} + \frac{{mg}}{4}\left( {\frac{{{{a}_{Y}}}}{l} - \frac{{{{a}_{X}}}}{h}} \right),\frac{{{{m}_{R}}g}}{4} + \frac{{mg}}{4}\left( { - \frac{{{{a}_{Y}}}}{l} - \frac{{{{a}_{X}}}}{h}} \right)} \right\} \\ \end{gathered} $Здесь первое неравенство из (4.14) ограничивает значения управляющих моментов при движении вперед (${{V}_{X}} > 0$), возникающего при ${{M}_{p}} > 0$; а второе неравенство – при движении назад (${{V}_{X}} < 0$), возникающего при ${{M}_{p}} < 0$. В случае совпадения центра масс платформы с ее геометрическим центром (${{a}_{X}} = {{a}_{Y}} = 0$) ограничения модуля управляющих моментов описываются неравенством ${{M}_{p}} \leqslant \frac{{{{m}_{R}}gh}}{4}$. Для параметров робота youBot [5]: ${{m}_{R}} = 35.6$ кг, $h = 0.235$ м, ограничения могут быть оценены, как ${{M}_{p}} = \frac{{35.6 \cdot 9.81 \cdot 0.235}}{4} \approx 20.52$ Нм.
Далее при проведении численного моделирования с целью упрощения модели (4.5) и уменьшения вычислительных затрат можно использовать линеаризованные выражения:
(4.15)
$\begin{gathered} \, - {{b}_{1}}\left( {\frac{{2l - {{W}_{3}} + {{W}_{4}}}}{{8{{l}^{2}}}}} \right) \\ {{N}_{3}} = \frac{{{{m}_{R}}g}}{4}\left( {1 - \frac{{{{W}_{1}} + {{W}_{2}} + {{W}_{3}} + {{W}_{4}}}}{{4l}}} \right) - {{b}_{2}}\left( {\frac{{4l + {{W}_{1}} + {{W}_{2}} - {{W}_{3}} - {{W}_{4}}}}{{16hl}}} \right) + \\ \end{gathered} $Линеаризованные выражения (4.15) для нормальных реакций опор, найденные из условий динамической согласованности, будут использованы в модели 3 при численном моделировании.
Кинематические соотношения для скорости точки ${{P}_{i}}$ и угловой скорости верчения контактирующих роликов имеют вид [3, 5–7]:
(4.16)
$\begin{gathered} {{V}_{{PiX}}} = {{V}_{X}} - {{\rho }_{{Yi}}}\Omega - {{{\dot {\varphi }}}_{i}}R + {{{\dot {\gamma }}}_{i}}\sin {{\delta }_{i}}\left( {{{R}_{d}}\cos {{{\tilde {\varphi }}}_{i}} - R} \right) - {{\Delta }_{{Yi}}}\left( {\Omega - {{{\dot {\gamma }}}_{i}}\sin {{{\tilde {\varphi }}}_{i}}\cos {{\delta }_{i}}} \right) \\ {{V}_{{PiY}}} = {{V}_{Y}} + {{\rho }_{{Xi}}}\Omega + {{{\dot {\gamma }}}_{i}}\cos {{\delta }_{i}}\left( {R\cos {{{\tilde {\varphi }}}_{i}} - {{R}_{d}}} \right) \\ {{\omega }_{{riZ}}} = \Omega - {{{\dot {\gamma }}}_{i}}\sin {{{\tilde {\varphi }}}_{i}}\cos {{\delta }_{i}} \\ \end{gathered} $Модель поликомпонентного трения (4.7) и кинематические выражения (4.16) используются в моделях 2 и 3. При этом в модели 3 для вычисления нормальных реакций по формулам (4.15) используются выражения (4.8).
5. Результаты моделирования. Результаты численного решения уравнений движения для перечисленных моделей представлены на рис. 2. Во всех моделях использовались законы изменения управляющих моментов ${{M}_{i}} = {{M}_{i}}(t)$, при которых в соответствии с моделью 1 платформа совершает поступательное движение ($\psi = 90^\circ $), а ее геометрический центр O равномерно перемещается по окружности.
Рис. 2.
Результаты моделирования: (a) – продольная скорость платформы ${{V}_{X}}$ (м/с), (b) – поперечная скорость платформы ${{V}_{Y}}$ (м/с), (c) – угловая скорость платформы $\Omega $ (рад/с), (d) – угол курса платформы $\psi $ ($ \circ $). (модель 1 – штриховая черная линия; модель 2 – сплошная темно-серая линия; модель 3 – сплошная светло-серая линия).
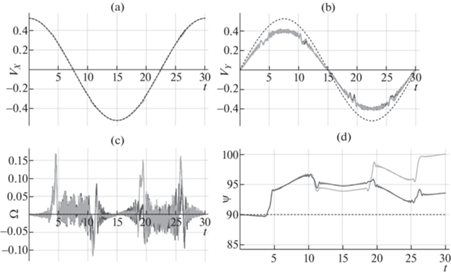
По рис. 2,a видно, что зависимости продольной скорости платформы ${{V}_{X}}$ во всех рассматриваемых моделях динамики достаточно близки. А в зависимостях для поперечной скорости платформы ${{V}_{Y}}$ (см. рис. 2,b) в моделях 2 и 3 учет конструкции меканум-колес приводит к снижению скорости по сравнению с поперечной скоростью, полученной для неголономной модели 1.
Отметим, что влияние изменения нормальных реакций опор при движении меканум-платформы хорошо просматривается по графикам для угловой скорости платформы $\Omega $ и ее угла курса $\psi $ (рис. 2,c и рис. 2,d). Отклонение угла курса от программного значения в модели 3 (при использовании динамического подхода к вычислению нормальных реакций) больше, чем в модели 2 (при использовании статического подхода к вычислению нормальных реакций).
На рис. 3 представлены графики модуля силы трения скольжения и момента трения верчения в зависимости от модуля скорости скольжения ${{P}_{i}}$ и угловой скорости верчения контактирующего ролика.
Рис. 3.
Результаты моделирования для контактирующего ролика 1-го колеса: (a) – зависимость модуля силы трения $F_{1}^{f} = \sqrt {F_{{X1}}^{2} + F_{{Y1}}^{2}} $ (Н) от скорости скольжения ${{V}_{{P1}}} = \sqrt {V_{{P1X}}^{2} + V_{{P1Y}}^{2}} $ (м/с), (b) – зависимость модуля силы трения $F_{1}^{f} = \sqrt {F_{{X1}}^{2} + F_{{Y1}}^{2}} $ (Н) от угловой скорости верчения ${{\omega }_{{r1Z}}}$ (рад/с), (c) – зависимость момента трения верчения $M_{{Z1}}^{f}$ (Нм) от скорости скольжения ${{V}_{{P1}}} = \sqrt {V_{{P1X}}^{2} + V_{{P1Y}}^{2}} $ (м/с), (d) – зависимость момента трения верчения $M_{{Z1}}^{f}$ (Нм) от угловой скорости верчения ${{\omega }_{{r1Z}}}$ (рад/с). (модель 2 – сплошная темно-серая линия; модель 3 – сплошная светло-серая линия).
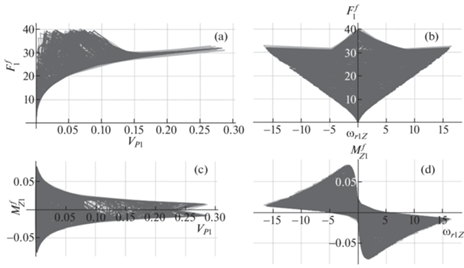
Отметим, что ограничения минимальных значений модуля силы трения скольжения пропорциональны модулю угловой скорости верчения контактирующего ролика. А ограничения максимальных по модулю значений момента трения верчения обратно пропорциональны модулю скорости скольжения центра пятна контакта. По рис. 3 можно наблюдать наличие зон “застоя”, при которых скольжение центра пятна контакта и/или верчение контактирующего ролика отсутствуют.
Рассмотрим, как изменяется величина нормальной реакции опоры, действующая на контактирующие ролики меканум-колес, на примере 1-го колеса. На рис. 4 приведены зависимости нормальной реакции опоры ${{N}_{1}}$ при использовании статического (модель 2) и динамического (модель 3) подходов. Видно, что нормальные реакции опор в модели 3 имеют высокочастотную составляющую, связанную со сменой роликов и возникающую из-за скачкообразных изменений смещения ${{\Delta }_{{Yi}}}$ центра пятна контакта вдоль оси вращения колеса. При рассмотренном движении изменения нормальной реакции опоры 1-го колеса составляли около 5–6% от величины нормальной реакции, вычисленной при статическом подходе.
Рис. 4.
Нормальная реакция опоры ${{N}_{1}}$ (Н), действующая на контактирующий ролик 1-го меканум-колеса: модель 2 (статический подход) – сплошная темно-серая линия; модель 3 (динамический подход) – сплошная светло-серая линия.
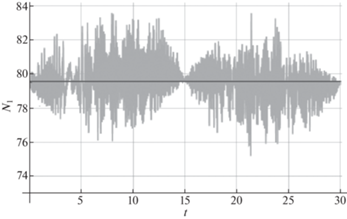
Для демонстрации влияния изменчивость нормальных реакций опор на динамику меканум-платформы были построены траектории движения геометрического центра платформы (см. рис. 5).
Рис. 5.
Траектория движения геометрического центра платформы ${{y}_{O}}({{x}_{O}})$ (в метрах) (модель 1 – штриховая черная линия; модель 2 – сплошная темно-серая линия; модель 3 – сплошная светло-серая линия).
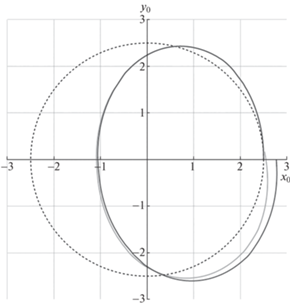
Из рис. 5 видно, что для неголономной модели 1 используемое программное управление приводит к точному исполнению программного движения, а в моделях 2 и 3 учет конструкции меканум-колес приводит к отклонениям от программного движения. При этом отметим, что указанные отклонения от программного движения существенно изменяются при учете изменчивости нормальных реакций опор. Как следствие, изменения нормальных реакций могут существенно повлиять на точность движения меканум-платформы при использовании программного управления.
6. Заключение. В статье представлена математическая модель динамики всенаправленной платформы, учитывающая конструкцию меканум-колес и поликомпонентное контактное трение. При этом одним из основных результатов является построение модели нормальных реакций опор в точках контакта из условий динамической согласованности, которые позволяют учесть изменение нормальных реакций в зависимости от параметров движения меканум-платформы.
Даны оценки максимальных отклонений нормальных реакций опор, обусловленных динамикой меканум-платформы, от значений нормальных реакций, рассчитанных для покоящейся мобильной платформы, на примере робота KUKA youBot равные 16.7%. Получены неравенства, ограничивающие максимальные значения управляющих моментов, при выполнении которых не происходит отрыва контактирующих роликов меканум-колес от опорной поверхности.
По результатам моделирования движения всенаправленной платформы при программном управлении (на примере движения по окружности) показано, что нормальные реакции изменяются на 5–6% от величины нормальной реакции, рассчитанной в случае покоящейся меканум-платформы, что соответствует полученным оценкам. Установлено, что изменения нормальных реакций могут привести к снижению точности движения меканум-платформы, получаемой при программном управлении.
Исследование выполнено за счет гранта Российского научного фонда № 22-21-00831, https://rscf.ru/project/22-2-00831/.
Список литературы
Мартыненко Ю.Г., Формальский А.М. О движении мобильного робота с роликонесущими колесами // Изв. РАН. Теория и системы управления. 2007. № 6. С. 142–149.
Borisov A.V., Kilin A.A., Mamaev I.S. An omni-wheel vehicle on a plane and a sphere // Rus. J. Nonlin. Dyn. 2011. V. 7. № 4. P. 785–801. https://doi.org/10.20537/nd1104004
Adamov B.I. A Study of the Controlled Motion of a Four-wheeled Mecanum Platform // Rus. J. Nonlin. Dyn. 2018. V. 14. № 2. P. 265–290. https://doi.org/10.20537/nd180209
Gfrerrer A. Geometry and kinematics of the Mecanum wheel // Computer Aided Geometric Design. 2008. V. 25. № 9. P. 784–791. https://doi.org/10.1016/j.cagd.2008.07.008
Adamov B.I., Saypulaev G.R. Research on the Dynamics of an Omnidirectional Platform Taking into Account Real Design of Mecanum Wheels (as Exemplified by KUKA youBot) // Rus. J. Nonlin. Dyn. 2020. V. 16. № 2. P. 291–307. https://doi.org/10.20537/nd200205.
Adamov B.I., Saypulaev G.R. A Study of the Dynamics of an Omnidirectional Platform, Taking into Account the Design of Mecanum Wheels and Multicomponent Contact Friction // 2020 International Conference Nonlinearity, Information and Robotics (NIR). IEEE. 2020. https://doi.org/10.1109/nir50484.2020.9290193.
Adamov B.I., Saypulaev G.R. Influence of Dissipative Forces and the Design of Mecanum-Wheels on the Omnidirectional Platform Dynamics // 2021 International Conference “Nonlinearity, Information and Robotics” (NIR). IEEE. 2021. https://doi.org/10.1109/nir52917.2021.9666053.
Zhuravlev V.Ph., Klimov D.M. Global motion of the celt // Mech. Solids. 2008. V. 43. № 3. P. 320–327. https://doi.org/10.3103/s0025654408030023
Kireenkov A.A., Semendyaev S.V., Filatov V.F. Experimental study of coupled twodimensional models of sliding and spinning friction // Mech. Solids. 2010. V. 45. № 6. P. 921–930. https://doi.org/10.3103/s0025654410060142
Bayar G., Ozturk S. Investigation of The Effects of Contact Forces Acting on Rollers of a Mecanum Wheeled Robot // Mechatronics. 2020. V. 72. P. 102467. https://doi.org/10.1016/j.mechatronics.2020.102467
Giurgiu T., Puica C., Pupaza C. et al. Mecanum wheel modeling for studying roller-ground contact issues // U.P.B. Sci. Bull. 2017. V. 79. № 2. P. 147–158.
Zobova A.A. A review of models of distributed dry friction // J. Appl. Math. Mech. 2016. V. 80. № 2. P. 141–148. https://doi.org/10.1016/j.jappmathmech.2016.06.008
Иванов А.П. Об общих принципах механики в системах с трением // Сборник научно-методических статей. Т. 27. М.: МГУ, 2009. С. 69–83.
Иванов А.П. Основы теории систем с трением. М., Ижевск: НИЦ “РХД”, ИКИ. 2011. 304 с.
Розенблат Г.М. Динамические системы с сухим трением. М., Ижевск: НИЦ “РХД”. 2006. 204 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела


