Известия РАН. Механика твердого тела, 2023, № 2, стр. 55-69
ДИНАМИКА ВЕТРОЭНЕРГЕТИЧЕСКОЙ УСТАНОВКИ С ДВУМЯ ПОДВИЖНЫМИ МАССАМИ, ИСПОЛЬЗУЮЩЕЙ ЭФФЕКТ ГАЛОПИРОВАНИЯ
a НИИ механики МГУ
Москва, Россия
* E-mail: seliutski@imec.msu.ru
Поступила в редакцию 22.02.2022
После доработки 26.04.2022
Принята к публикации 26.04.2022
- EDN: DFMZMU
- DOI: 10.31857/S0572329922100117
Аннотация
Рассматривается ветроэнергетическая установка, использующая эффект галопирования, которая включает два упруго соединенных поступательно движущихся тела: одно представляет собой призму квадратного сечения с жестко прикрепленным к ней постоянным магнитом, а другое – материальную точку. Электричество вырабатывается в результате движения магнита в катушке. Анализируется влияние параметров системы на скорость ветра, при которой возникают галопирующие колебания. Показано, что надлежащий выбор параметров позволяет значительно расширить диапазон скоростей ветра, при которых существуют периодические режимы, по сравнению с системой, содержащей одно движущееся тело. Получены аппроксимации для амплитуд и частот предельных циклов, возникающих в системе. Исследована эволюция этих циклов при изменении жесткости пружины между телами. Установлено, что при определенных значениях параметров возможно одновременное существование двух притягивающих периодических решений. Получены условия, при которых мощность, вырабатываемая такой системой, больше, чем мощность, вырабатываемая системой с одной движущейся массой.
1. Введение. Эффект возникновения колебаний плохообтекаемых тел в направлении поперек потока в случае, когда скорость потока превосходит некоторое критическое значение, называют галопированием. Это явление наблюдается для различных конструкций, таких как мосты, высокие конструкции призматической формы и т.д. Вообще говоря, оно обусловлено тем, что при определенных условиях для плохообтекаемых тел аэродинамическое демпфирование оказывается отрицательным. Критерий, определяющий условия возникновения галопирования, впервые был получен Ден Гартогом [1].
Изучению различных аспектов галопирования посвящена обширная литература. Здесь мы сосредоточимся только на работах, в которых рассматривается динамика тел с острыми кромками (таких как прямоугольные призмы). В работах [2, 3] было показано, что квазистатический подход может обеспечить достаточно точное описание данного явления для призмы квадратного сечения. В частности, в работе [3] был объяснен наблюдающийся в экспериментах гистерезис колебаний, существующий в определенном диапазоне скоростей ветра. В работе [4] проведен подробный численный анализ этого гистерезиса для чисел Рейнольдса до 1000. В работе [5] выполнено численное исследование аэродинамических сил, действующих на квадратную призму при числах Рейнольдса порядка 10000. Зависимость характеристик колебаний от удлинения призмы исследована в работе [6].
Существует множество экспериментальных работ, посвященных изучению аэродинамических сил, действующих на прямоугольные и квадратные призмы. Так, в работе [7] определялись характеристики галопирующих колебаний квадратного цилиндра и измерялась боковая (перпендикулярная набегающему потоку) сила, действующая на этот объект, при углах атаки до 18 градусов. В работе [8] исследовалось обтекание квадратной призмы с прикрепленной к ней пластиной и без нее, и измерялись подъемная сила и сила лобового сопротивления во всем диапазоне углов атаки. В [9] описаны эксперименты по исследованию нестационарных аэродинамических сил при галопировании прямоугольной призмы.
Очевидная нежелательность галопирования с точки зрения прочности и износа конструкций привела к появлению целого ряда работ, в которых предлагались различные методы подавления таких колебаний. В частности, в [10] описывается использование пассивного инерционного гасителя для уменьшения амплитуды. В работе [11] проведен подробный анализ бифуркаций Андронова–Хопфа в динамике системы, содержащей плохообтекаемое тело и инерционный гаситель. В [12] анализируется возможность предотвращения галопирования квадратной призмы с помощью “поглотителя энергии”, представляющего собой шар, движущийся по круговой направляющей, прикрепленной к этой призме.
В то же время, галопирующие колебания могут быть использованы для преобразования энергии потока в полезные формы. В последнее время появляется большое количество работ, направленных на разработку и изучение различных колебательных ветроэнергетических установок. Это обусловлено растущей потребностью в использовании возобновляемой энергии. Так, в [13] показано, что галопирующие колебания имеют достаточно хороший потенциал для такого использования. В работе [14] исследована ветроэнергетическая установка на базе галопирования, в которой электричество вырабатывается линейным генератором на постоянном магните. Экспериментальное исследование аналогичного устройства с рабочими элементами в виде квадратной и прямоугольной призмы проведено в [15] и исследовано влияние угла между стороной призмы и направлением потока на характеристики колебаний. В [16] предложена система, состоящая из плохообтекаемого тела и пьезоэлемента. В [17] анализируется ветроэнергетическая установка, использующая галопирование пьезоэлектрической консольно закрепленной балки и исследуется влияние геометрической формы на вырабатываемую мощность. В работе [18] проводится экспериментальное сравнение мощности, вырабатываемой при галопировании призм с разной формой поперечного сечения (прямоугольник, треугольник и т.д.).
Несколько конфигураций галопирующей ветроэнергетической установки с двумя движущимися массами рассмотрены в [19]. Показано, что некоторые конфигурации позволяют добиться увеличения выходной мощности по сравнению с системой, содержащей одну колеблющуюся массу. В [20] рассматривается галопирующая ветроэнергетическая установка с двумя подвижными массами, установленная на подвижном основании.
В данной работе исследуется динамика галопирующей ветроэнергетической установки, содержащей две подвижных массы и линейный генератор. Анализируется влияние параметров системы на область устойчивости равновесия. Проводится численное и аналитическое исследование периодических режимов. Выполняется сравнение выходной мощности такой системы и аналогичной системы с одной подвижной массой.
2. Постановка задачи. Рассмотрим аэроупругую систему, состоящую из тела ${{M}_{1}}$ и ${{M}_{2}}$, которые могут двигаться поступательно вдоль горизонтальной оси $OY$ (см. рис. 1). Тело ${{M}_{1}}$ представляет собой материальную точку, а тело ${{M}_{2}}$ имеет форму квадратной призмы, ось которой перпендикулярна линии движения и вертикальна. Две стороны основания призмы параллельны оси $OY$. Оба тела соединены пружиной. Точка ${{M}_{1}}$, кроме того, прикреплена пружиной к неподвижной точке $O$. К призме жестко прикреплен магнит ${{M}_{3}}$, который может двигаться внутри катушки индуктивности. Эта катушка включена в электрическую цепь, которая также содержит нагрузочное сопротивление ${{R}_{l}}$. При движении призмы магнит движется внутри катушки, и в цепи индуцируется электрический ток (эта схема представляет собой простейший линейный электрогенератор). Тела ${{M}_{1}}$ и ${{M}_{2}}$ находятся в горизонтальном стационарном потоке воздуха. Предполагается, что поток действует только на призму. Скорость потока равна $U$ и перпендикулярна оси $OY$. Такая конфигурация системы отличается от рассмотренных в [19] наличием электрического контура и тем, что аэродинамическое воздействие приложено к первому телу (которое непосредственно связано с неподвижным основанием).
Пусть $OXY$ – неподвижная система координат, ось абсцисс которой направлена вдоль набегающего потока. Чтобы описать динамику нашей электромеханической системы, введем координаты ${{Y}_{1}}$ и ${{Y}_{2}}$ тел ${{M}_{1}}$ и ${{M}_{2}}$, соответственно, и ток $J$ в электрической цепи.
Чтобы смоделировать аэродинамическое воздействие на призму, воспользуемся квазистатическим подходом. В рамках этого подхода аэродинамические силы предполагаются зависящими только от мгновенного состояния движения тела. Он широко используется (например, в [21, 22]), поскольку позволяет эффективно проводить параметрический анализ и во многих случаях обеспечивает достаточно точное описание особенностей поведения тела. Многочисленные исследования (в частности, [3]) показывают, что феномен галопирования достаточно хорошо описывается данной моделью. Аэродинамическую силу, действующую на призму, представим в виде суммы подъемной (или боковой) силы $L$ и силы лобового сопротивления $D$, приложенных в центре призмы, причем сила $D$ направлена вдоль воздушной скорости ${{V}_{a}}$ (т.е. скорости призмы относительно набегающего потока), а сила L – перпендикулярно ей. Эти силы имеют следующую структуру:
(2.1)
$D = \frac{{\rho S}}{2}V_{a}^{2}{{C}_{d}}(\alpha ),\quad L = \frac{{\rho S}}{2}V_{a}^{2}{{C}_{l}}(\alpha )$(2.2)
${{V}_{a}} = \sqrt {V_{2}^{2} + {{U}^{2}}} ,\quad \alpha = \operatorname{arctg} \left( {\frac{{{{V}_{2}}}}{V}} \right),\quad {\text{где}}\quad {{V}_{2}} = \frac{{d{{Y}_{2}}}}{{dt}}$Из (2.1) и (2.2) мы можем найти проекцию ${{F}_{y}}$ результирующей аэродинамической силы на направление движения:
(2.3)
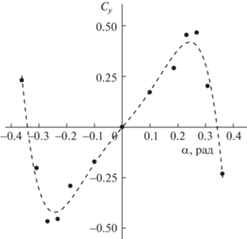
${{F}_{y}} = \frac{{\rho S}}{2}V_{a}^{2}{{C}_{y}}(\alpha ) = \frac{{\rho S}}{2}V_{a}^{2}({{C}_{l}}\cos \alpha - {{C}_{d}}\sin \alpha )$Из соображений симметрии ясно, что ${{C}_{y}}$ в выражении (2.3) представляет собой нечетную функцию $\alpha $. Поэтому в области сравнительно малых $\alpha $ эту функцию можно приближенно представить в виде полинома следующего вида: ${{C}_{y}} = \sum\limits_{i = 1}^n {{{C}_{{y,2i + 1}}}{{\alpha }^{{2i + 1}}}} $. Коэффициенты ${{C}_{{y,2i + 1}}}$ и их количество зависят от формы призмы. Во многих исследованиях (например, [19]) используются кубические полиномы. Однако такое число членов разложения во многих случаях оказывается недостаточным для того, чтобы описать основные особенности поведения ${{C}_{y}}$ даже в диапазоне малых $\alpha $. В частности, рассмотрим экспериментальные данные из работы [8], относящиеся к квадратной призме (без соединенной с ней пластины). Измеренные значения коэффициента ${{C}_{y}}$ представлены на рис. 2 точками. Для того чтобы получить достаточно точную аппроксимацию ${{C}_{y}}$, необходим полином, по крайней мере, 5 степени:
(2.4)
$C_{y}^{{appr}} = {{C}_{{y1}}}\alpha + {{C}_{{y3}}}{{\alpha }^{3}} + {{C}_{{y5}}}{{\alpha }^{5}}$Рис. 2.
Зависимость коэффициента поперечной аэродинамической силы от угла атаки $\alpha $ (рад); точки – экспериментальные данные из [8]; пунктирная линия – аппроксимация (2.4).
Аналогично [14, 23], мы будем использовать следующие формулы для описания ЭДС E, создаваемой в катушке движущимся магнитом, и силы ${{F}_{{em}}}$, действующей на магнит со стороны электромагнитного поля:
При записи уравнения для электрического контура необходимо учитывать наличие у катушки индуктивности ${{L}_{c}}$ и внутреннего сопротивления ${{R}_{c}}$.
Таким образом, уравнения движения рассматриваемой электромеханической системы можно записать следующим образом:
(2.5)
$\begin{gathered} {{m}_{1}}\frac{{{{d}^{2}}{{Y}_{1}}}}{{d{{t}^{2}}}} + {{K}_{1}}{{Y}_{1}} + {{k}_{2}}({{Y}_{1}} - {{Y}_{2}}) + {{H}_{1}}\frac{{d{{Y}_{1}}}}{{dt}} + {{H}_{2}}\left( {\frac{{d{{Y}_{1}}}}{{dt}} - \frac{{d{{Y}_{2}}}}{{dt}}} \right) = 0 \\ {{m}_{2}}\frac{{{{d}^{2}}{{Y}_{2}}}}{{d{{t}^{2}}}} + {{K}_{2}}({{Y}_{2}} - {{Y}_{1}}) + {{H}_{2}}\left( {\frac{{d{{Y}_{2}}}}{{dt}} - \frac{{d{{Y}_{1}}}}{{dt}}} \right) = \frac{{\rho S}}{2}\left( {{{V}^{2}} + {{{\left( {\frac{{d{{Y}_{2}}}}{{dt}}} \right)}}^{2}}} \right){{C}_{y}}\left( \alpha \right) - CJ \\ {{L}_{c}}\frac{{dJ}}{{dt}} = - \left( {{{R}_{l}} + {{R}_{c}}} \right)J + C\frac{{d{{Y}_{2}}}}{{dt}} \\ \end{gathered} $Здесь ${{m}_{1}}$ – масса точки ${{M}_{1}}$, ${{m}_{2}}$ – масса призмы ${{M}_{2}}$ вместе с магнитом ${{M}_{3}}$; ${{K}_{{1,2}}}$ – коэффициенты жесткости пружин; ${{H}_{{1,2}}}$ – коэффициенты демпфирования пружин.
Чтобы уменьшить число параметров, перейдем к безразмерным переменным:
(2.6)
$\begin{gathered} \tau = t\sqrt {\frac{{{{k}_{1}}}}{{{{m}_{1}}}}} ,\quad {{y}_{1}} = \frac{{{{Y}_{1}}}}{b},\quad {{y}_{2}} = \frac{{{{Y}_{2}}}}{b},\quad I = \frac{{J{{R}_{c}}}}{{Cb}}\sqrt {\frac{{{{k}_{1}}}}{{{{m}_{1}}}}} \\ m = \frac{{{{m}_{2}}}}{{{{m}_{1}}}},\quad k = \frac{{{{k}_{2}}}}{{{{k}_{1}}}},\quad {{h}_{{1,2}}} = \frac{{{{H}_{{1,2}}}}}{{\sqrt {{{k}_{1}}{{m}_{1}}} }},\quad V = \frac{U}{b}\sqrt {\frac{{{{m}_{1}}}}{{{{k}_{1}}}}} ,\quad \mu = \frac{{\rho Sb}}{{2{{m}_{1}}}} \\ L = \frac{{{{L}_{c}}}}{{{{R}_{c}}}}\sqrt {\frac{{{{k}_{1}}}}{{{{m}_{1}}}}} ,\quad R = \frac{{{{R}_{l}}}}{{{{R}_{c}}}},\quad \chi = \frac{{{{C}^{2}}}}{{{{R}_{c}}\sqrt {{{k}_{1}}{{m}_{1}}} }} \\ \end{gathered} $Используя (2.6) и обозначая производную по $\tau $ точкой, преобразуем систему (2.5) в следующую систему безразмерных уравнений:
(2.7)
$\begin{gathered} {{{\ddot {y}}}_{1}} + {{y}_{1}} + k({{y}_{1}} - {{y}_{2}}) + {{h}_{1}}{{{\dot {y}}}_{1}} + {{h}_{2}}\left( {{{{\dot {y}}}_{1}} - {{{\dot {y}}}_{2}}} \right) = 0 \\ m{{{\ddot {y}}}_{2}} + k({{y}_{2}} - {{y}_{1}}) + {{h}_{2}}\left( {{{{\dot {y}}}_{2}} - {{{\dot {y}}}_{1}}} \right) = \mu ({{V}^{2}} + \dot {y}_{2}^{2}){{C}_{y}}(\alpha ) - \chi I \\ L\dot {I} = - \left( {R + 1} \right)I + {{{\dot {y}}}_{2}} \\ \end{gathered} $Очевидно, эта система имеет единственное положение равновесия, а именно, тривиальное: ${{y}_{1}} = {{y}_{2}} = I = 0$.
Представляется интересным сопоставить динамику системы (2.7) с поведением системы, содержащей только одно подвижное тело (призму), масса которого равна суммарной массе системы, изображенной на рис. 1.
Безразмерные уравнения движения системы с одной колеблющейся массой, как нетрудно видеть, могут быть представлены в следующем виде с сохранением прежних обозначений:
(2.8)
$\begin{gathered} (m + 1){{{\ddot {y}}}_{2}} + {{y}_{2}} + {{h}_{1}}{{{\dot {y}}}_{2}} = \mu ({{V}^{2}} + \dot {y}_{2}^{2}){{C}_{y}}(\alpha ) - \chi I \\ L\dot {I} = - \left( {R + 1} \right)I + {{{\dot {y}}}_{2}} \\ \end{gathered} $Чтобы сопоставить эффективность отбора энергии потока с помощью систем с одной и двумя подвижными массами, исследуем и сравним области неустойчивости тривиального равновесия этих систем в пространстве параметров и мощность, вырабатываемую этими системами на установившихся колебаниях.
3. Область неустойчивости. Для анализа устойчивости равновесия линеаризуем систему (2.7) в окрестности этой неподвижной точки с учетом соотношений (2.2) и (2.4):
(3.1)
$\begin{gathered} {{{\ddot {y}}}_{1}} + {{y}_{1}} + k({{y}_{1}} - {{y}_{2}}) + {{h}_{1}}{{{\dot {y}}}_{1}} + {{h}_{2}}\left( {{{{\dot {y}}}_{1}} - {{{\dot {y}}}_{2}}} \right) = 0 \\ m{{{\ddot {y}}}_{2}} + k({{y}_{2}} - {{y}_{1}}) + {{h}_{2}}\left( {{{{\dot {y}}}_{2}} - {{{\dot {y}}}_{1}}} \right) = \mu V{{C}_{{y1}}}{{{\dot {y}}}_{2}} - \chi I \\ L\dot {I} = - \left( {R + 1} \right)I + {{{\dot {y}}}_{2}} \\ \end{gathered} $Характеристический полином системы (3.1) можно представить в следующем виде:
(3.2)
$\begin{gathered} \left. {\, + (R + 1)((m + 1){{h}_{2}} + m{{h}_{1}}) + \chi } \right){{\lambda }^{3}} + \\ \, + \left( { - \left( {(k + 1)L + (R + 1)({{h}_{1}} + {{h}_{2}})} \right)V\mu {{C}_{{y1}}} + ({{h}_{1}}k + {{h}_{2}})L + } \right. \\ \end{gathered} $Чтобы проанализировать устойчивость, сделаем некоторые дополнительные предположения. Если тела движутся в воздухе, представляется естественным предположить, что их средняя плотность значительно больше, чем плотность воздуха, т.е. величина $\mu $ мала. Кроме того, предположим, что коэффициенты демпфирования пружин и безразмерный коэффициент электромеханического взаимодействия также малы. Такая ситуация имеет место, в частности, если выбрать параметры, приведенные в работе [14]. Наконец, будем считать, что безразмерный коэффициент индуктивности тоже мал (т.е. характерные времена для процессов, протекающих в электрической цепи, существенно меньше, чем для процессов, протекающих в механической части системы). Иными словами:
(3.3)
$\mu \ll 1,\quad {{h}_{1}}\sim \mu ,\quad {{h}_{2}}\sim \mu ,\quad \chi \sim \mu ,\quad L\sim \mu $Отметим, что в “вырожденном” случае, т.е. при $\mu = {{h}_{1}} = \mu = {{h}_{2}} = \chi = L = 0$, полином (3.2) принимает следующий вид:
С учетом (3.3) мы можем найти корни полинома (3.2) в виде разложения по малому параметру:
(3.4)
$\begin{gathered} {{\lambda }_{1}} = - \frac{{R + 1}}{L} + \frac{\chi }{{m(R + 1)}} + o(\mu ) \\ {{\lambda }_{{2 - 5}}} = \pm i{{\omega }_{{1,2}}} + \frac{{\mu {{C}_{{y1}}}( - \omega _{{1,2}}^{2} + k + 1)}}{{( - 4\omega _{{1,2}}^{2} + 2k + 2)m + 2k}}\left( {V - {{V}_{{c1,2}}}} \right) + o(\mu ) \\ \end{gathered} $(3.5)
${{V}_{{c1,2}}} = \frac{{{{h}_{1}}(k - m\omega _{{1,2}}^{2}) + {{h}_{2}}(1 - m\omega _{{1,2}}^{2} - \omega _{{1,2}}^{2})}}{{\mu {{C}_{{y1}}}( - \omega _{{1,2}}^{2} + k + 1)}} + \frac{\chi }{{\mu {{C}_{{y1}}}(R + 1)}}$Величины ${{\omega }_{{1,2}}}$ представляют собой собственные частоты системы колебаний в отсутствие потока и без сопряжения с электрической частью.
Прямой подстановкой в (3.6) нетрудно показать, что выполняются следующие неравенства:
(3.7)
$\begin{gathered} {{\omega }_{1}} < 1 < {{\omega }_{2}},\quad {{\omega }_{1}} < \sqrt {k + 1} < {{\omega }_{2}},\quad {{\omega }_{1}} < \sqrt {\frac{1}{{m + 1}}} < {{\omega }_{2}} \\ {{\omega }_{1}} < \sqrt {\frac{k}{m}} < {{\omega }_{2}},\quad {{\omega }_{1}} < \sqrt[4]{{\frac{k}{m}}} < {{\omega }_{2}} \\ \end{gathered} $Из (3.4) и (3.7) нетрудно видеть, что вещественная часть корня ${{\lambda }_{1}}$ всегда отрицательна (поскольку величины $L$ и $\chi $ малы), и равновесие становится неустойчивым, когда скорость ветра превышает критическое значение ${{V}_{c}} = \min ({{V}_{{c1}}},{{V}_{{c2}}})$.
Нетрудно показать, что для системы (2.8) в предположениях (3.3) критическая скорость ветра $V_{c}^{s}$ определяется следующим выражением:
Заметим, что из (3.6) следует, что ${{\omega }_{1}} \to {{(m + 1)}^{{ - 1{\text{/}}2}}}\sim 1$ при $k \to \infty $. Соответственно, из (3.5) мы получаем, что имеет место соотношение $V_{c}^{s} = {{\lim }_{{k \to \infty }}}{{V}_{{c1}}}$, как и следовало ожидать.
Вычисление производных от выражений (3.5) по ${{h}_{1}}$, ${{h}_{2}}$ и $\chi $ с учетом неравенств (3.7) показывает, что ${{V}_{{c1}}}$ и ${{V}_{{c2}}}$, монотонно растут с увеличением этих параметров, что представляется вполне естественным.
Чтобы определить влияние жесткости пружины между телами на устойчивость, будем рассматривать величины ${{V}_{{c1,2}}}$ как функции k и вычислим их производные по этому параметру:
(3.9)
$\begin{gathered} \frac{{d{{V}_{{c1}}}}}{{dk}} = - \frac{{4{{m}^{2}}(({{h}_{2}} - (2{{h}_{1}} + {{h}_{2}})k)m + {{h}_{2}}(\Delta - k))}}{{\mu {{C}_{{y1}}}\Delta (m(k + 1) - k + \Delta )}} \\ \frac{{d{{V}_{{c2}}}}}{{dk}} = - \frac{{4{{m}^{2}}(( - {{h}_{2}} + (2{{h}_{1}} + {{h}_{2}})k)m + {{h}_{2}}(\Delta - k))}}{{\mu {{C}_{{y1}}}\Delta ( - m(k + 1) + k + \Delta )}} \\ \end{gathered} $Здесь $\Delta = \sqrt {{{{(m + 1)}}^{2}}{{k}^{2}} + 2mk(m - 1) + {{m}^{2}}} $.
Обе производные (3.9) обращаются в нуль при одном и том же значении k:
(3.10)
${{k}_{c}} = \frac{{m{{h}_{2}}({{h}_{1}} + {{h}_{2}})}}{{{{h}_{1}}(m{{h}_{1}} + m{{h}_{2}} + {{h}_{2}})}}$Заметим, что величина ${{k}_{c}}$ монотонно растет с ростом m. Очевидно, для больших k мы имеем
Учитывая то обстоятельство, что ${{\omega }_{1}}{{\omega }_{2}} = \sqrt {k{\text{/}}m} $, разность значений этих критических скоростей можно представить в следующем виде:
Следовательно, мы можем заключить с учетом (3.7), что если
то ${{V}_{{c1}}} < {{V}_{{c2}}}$ и ${{V}_{c}} = {{V}_{{c1}}}$ для всех k (заметим, что неравенство (3.11) заведомо выполнено в случае $m \geqslant 1$). В этой ситуации критическая скорость ветра ${{V}_{c}}$ имеет единственный минимум на интервале $k \in [0,\infty )$. В то же время,Таким образом, если ${{h}_{2}} > {{h}_{1}}$, то из (3.8) следует, что ${{V}_{c}} > V_{c}^{s}$ при малых k. Если ${{h}_{2}} \leqslant {{h}_{1}}$, то ${{V}_{c}} \leqslant V_{c}^{s}$ при всех k.
Если неравенство (3.11) не выполнено (и, следовательно, $m < 1$ и ${{h}_{2}} < {{h}_{1}}$), то существует такое значение ${{k}_{*}}$ коэффициента жесткости, что ${{V}_{{c1}}} < {{V}_{{c2}}}$ при $k < k_{*}^{{}}$ и ${{V}_{{c1}}} > {{V}_{{c2}}}$ при $k > k_{*}^{{}}$. При этом ${{V}_{{c1}}}{{|}_{{k = 0}}} < V_{c}^{s}$ . Это означает, при нарушении условия (3.11) критическая скорость ветра для системы с двумя массами всегда меньше, чем для соответствующей системы с одной массой.
Если условие (3.11) выполнено и, кроме того, ${{V}_{{c1}}}({{k}_{c}}) < V < {{V}_{{c1}}}(0)$ (где ${{k}_{c}}$ определяется формулой (3.10)), то существует диапазон скоростей ветра, в котором равновесие асимптотически устойчиво при достаточно малых и достаточно больших величинах жесткости и неустойчиво при “промежуточных” значениях k. Этот эффект был отмечен в работе [24] для системы с двумя подвижными массами без электрической цепи. Если $V > \max ({{V}_{{c0}}},V_{c}^{s})$, то равновесие неустойчиво при всех k. В то же время, если условие (3.11) не выполнено, то при некоторых значениях скорости ветра существует интервал положительных значений k, в котором равновесие асимптотически устойчиво. Вне этого интервала (т.е. и при малых, и при больших k) имеет место неустойчивость.
Границы областей устойчивости показаны на рис. 3 на плоскости $(k,V)$ для различных величин $R$, $m$ и ${{h}_{2}}$ при следующих значениях остальных параметров: $\mu = \chi = {{h}_{1}}$ = = L = 0.01. Сплошные линии обозначают границы областей устойчивости, а пунктирные соответствуют значениям критической скорости для системы с одной подвижной массой. На рис. 3,a представлен случай, когда условие (3.11) выполнено, а на рис. 3,b – случай, когда оно не выполняется.
Рис. 3.
Границы области устойчивости на плоскости параметров $V$и k: a) $m = 1$, ${{h}_{2}} = 0.01$; b) $m = 0.5$, ${{h}_{2}} = 0.001$.
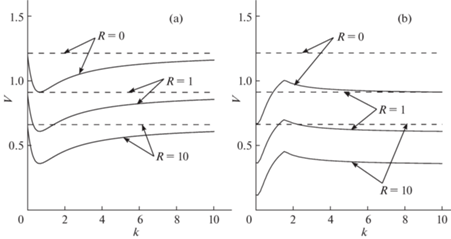
Из результатов расчетов, приведенных на рис. 3, видно, что надлежащим выбором k можно существенно уменьшить скорость, при которой начинается галопирование (и, соответственно, когда становится возможным отбор энергии у потока).
4. Периодические решения. Предположим, что ${{C}_{{y1}}}\sim 1$, ${{C}_{{y3}}}\sim {{\mu }^{{ - 1}}}$ и $\left| {{{C}_{{y5}}}} \right|\sim {{\mu }^{{ - 2}}}$. Для удобства обозначений введем дополнительный малый параметр $\epsilon = \sqrt \mu $. Будем искать периодические решения системы (2.7) следующего вида:
(4.1)
${{y}_{1}} = \epsilon {{y}_{{11}}}\sin \omega \tau ,\quad {{y}_{2}} = \epsilon {{y}_{{21}}}\sin \omega \tau + {{\epsilon }^{3}}{{y}_{{22}}}\cos \omega \tau ,\quad I = {{\epsilon }^{3}}{{I}_{1}}\sin \omega \tau + \epsilon {{I}_{2}}\cos \omega \tau $Подставив (4.1) в (2.7), приравнивая коэффициенты при $\sin \omega \tau $ и $\cos \omega \tau $ и удерживая только члены минимального порядка по $\epsilon $, получим следующие уравнения:
(4.2)
$\frac{5}{{8{{V}^{3}}}}{{C}_{{y5}}}{{\mu }^{2}}{{\omega }^{5}}y_{{21}}^{5} + \frac{3}{{4V}}{{C}_{{y3}}}\mu {{\omega }^{3}}y_{{21}}^{3} + {{C}_{{y1}}}V\omega {{y}_{{21}}} - m{{\omega }^{2}}{{y}_{{22}}} - $Отсюда:
(4.3)
$\begin{gathered} {{y}_{{21}}} = {{y}_{{11}}}\frac{{k + 1 - {{\omega }^{2}}}}{k},\quad {{y}_{{22}}} = {{y}_{{11}}}\omega \frac{{{{h}_{2}}{{\omega }^{2}} + {{h}_{1}}k - {{h}_{2}}}}{{{{k}^{2}}\mu }},\quad {{I}_{2}} = {{y}_{{11}}}\omega \frac{{k + 1 - {{\omega }^{2}}}}{{k(R + 1)}} \\ {{I}_{1}} = {{y}_{{11}}}{{\omega }^{2}}\frac{{Lk(1 + k - {{\omega }^{2}}) + (R + 1){{h}_{2}}(1 - {{\omega }^{2}}) - {{h}_{1}}k(R + 1)}}{{{{k}^{2}}\mu {{{(R + 1)}}^{2}}}} \\ \end{gathered} $Подставив (4.3) в третье уравнение системы (4.2) получим уравнение для частоты предельного цикла:
Это уравнение, как и следовало ожидать при сделанных предположениях относительно параметров, совпадает с уравнением (3.6), так что частоты предельных циклов близки к собственным частотам ${{\omega }_{{1,2}}}$ нашей системы.
Амплитуда колебаний первого тела определяется следующим уравнением:
(4.5)
$\begin{gathered} 5{{\mu }^{2}}{{C}_{{y5}}}\omega _{{1,2}}^{4}{{(k + 1 - \omega _{{1,2}}^{2})}^{4}}y_{{11}}^{4} + 6\mu {{V}^{2}}{{k}^{2}}{{C}_{{y3}}}\omega _{{1,2}}^{2}{{(k + 1 - \omega _{{1,2}}^{2})}^{2}}y_{{11}}^{2} + \\ \; + 8{{V}^{3}}{{k}^{4}}{{C}_{{y1}}}\left( {V - {{V}_{{c1,2}}}} \right) = 0 \\ \end{gathered} $Заметим, что величины ${{C}_{{y1}}}$ и ${{C}_{{y3}}}$ положительны, а ${{C}_{{y5}}}$ – отрицательна.
Формально уравнения (4.4), (4.5) могут иметь до 4 положительных корней, которые отвечают предельным циклам динамической системы (2.7). Вообще говоря, для определения характера устойчивости этих циклов можно воспользоваться методами, основанными на теории Флоке (например, [25]) или на построении систем сравнения (например, [26]). Однако в нашем случае выводы об устойчивости периодических решений можно сделать из некоторых простых соображений.
Пусть выполнено условие (3.11). Тогда равновесие устойчиво при $V < {{V}_{{c1}}}$ и неустойчиво при $V > {{V}_{{c1}}}$ для всех k. При $V = {{V}_{{c1}}}$ имеет место бифуркация Андронова–Хопфа. Рассмотрим случай $\omega = {{\omega }_{1}}$. Нетрудно показать, что при этом уравнение (4.5) имеет два положительных корня, если $V$ меньше ${{V}_{{c1}}}$, но достаточно близко к этой величине. Это означает, что бифуркация является субкритической. Очевидно, один из этих корней (тот, который стремится к нулю при $V \to {{V}_{{c1}}} - 0$), соответствует неустойчивому предельному циклу. Другой корень отвечает притягивающему циклу. Значение V, при котором они сливаются, нетрудно получить из условия обращения в нуль дискриминанта уравнения (4.5) при $\omega = {{\omega }_{1}}$. При $V > {{V}_{{c1}}}$ уравнение (4.5) имеет только один положительный корень, и соответствующий цикл является притягивающим.
Субкритический характер бифуркации можно считать благоприятным с точки зрения выработки энергии, поскольку он позволяет дополнительно увеличить “рабочий” диапазон скоростей ветра.
Пусть теперь $\omega = {{\omega }_{2}}$. Тогда при V, достаточно близких к ${{V}_{{c2}}}$ и не превышающих этого значения, уравнение (4.5) имеет два положительных корня. Меньший из них, который стремится к нулю при $V \to {{V}_{{c2}}} - 0$, отвечает неустойчивому предельному циклу. Когда параметр $V$ проходит значение ${{V}_{{c2}}}$, этот цикл стягивается в начало координат, и знак вещественной части второй пары корней характеристического полинома меняется на положительный. Другой корень уравнения (4.5), который существует и при $V > {{V}_{{c2}}}$, отвечает притягивающему циклу.
Если (3.11) не выполнено, имеет место в целом аналогичная ситуация.
С точки зрения выработки энергии важны, в первую очередь, притягивающие циклы. Предшествующий анализ показывает, что при надлежащем выборе параметров системы такие циклы возникают при скоростях потока, меньших, чем в случае системы с одной подвижной массой.
Другой важной характеристикой ветроэнергетической установки является, разумеется, выходная мощность. Безразмерная мощность, вырабатываемая рассматриваемой системой в электрическом контуре и осредненная на периоде $T$ колебаний, задается следующей формулой:
Вычислим интеграл (4.6) с учетом выражений (4.1) и (4.3) и оставим только члены порядка ${{\epsilon }^{2}}$:
где $\eta = \frac{{\mu y_{{11}}^{2}{{\omega }^{2}}{{{(k + 1 - {{\omega }^{2}})}}^{2}}}}{{{{k}^{2}}}} > 0$.Заметим, что (4.5) можно переписать следующим образом:
(4.8)
$5{{C}_{{y5}}}{{\eta }^{2}} + 6{{V}^{2}}{{C}_{{y3}}}\eta + 8{{V}^{3}}{{C}_{{y1}}}\left( {V - {{V}_{{c1,2}}}} \right) = 0$Нетрудно показать, что для системы с одной подвижной массой величина $\eta $ удовлетворяет уравнению, аналогичному (4.8), где вместо ${{V}_{{c1,2}}}$ стоит $V_{c}^{s}$.
Как нетрудно видеть из (4.8),
(4.9)
$\frac{{d\eta }}{{dk}} = \frac{{8{{V}^{3}}{{C}_{{y1}}}}}{{10{{C}_{{y5}}}\eta + 6{{V}^{2}}{{C}_{{y3}}}}}\frac{{d{{V}_{{c1,2}}}}}{{dk}}$Из двух решений (4.8) притягивающему циклу соответствует большее, поэтому первый сомножитель в (4.9) всегда отрицателен. Соответственно, поскольку ${{V}_{{c1}}}$ имеет минимум при $k = {{k}_{c}}$, то $\eta $ (а значит, и мощность) при этом достигает максимума. Поскольку ${{V}_{{c2}}}$ убывает на интервале $k \in [{{k}_{c}},\infty )$, то мощность на этом промежутке возрастает (конечно, там, где существуют циклы).
Предположим, что условие (3.11) выполнено. Тогда ${{V}_{{c1}}} < {{V}_{{c2}}}$ при всех k и, кроме того, $V_{c}^{s} > {{V}_{{c1}}}$ на интервале $k \in [{{k}_{c}},\infty )$. С учетом этого нетрудно показать, что при таких значениях жесткости мощность на циклах с частотой ${{\omega }_{1}}$ больше, чем в системе с одной подвижной массой, и больше, чем на циклах с частотой ${{\omega }_{2}}$.
Чтобы несколько более подробно исследовать влияние параметров k и $m$ системы на характеристики предельных циклов и на выходную мощность, проведем численное моделирование. Для коэффициентов, описывающих аэродинамическое воздействие и для параметров $\mu $, $L$, $\chi $ и ${{h}_{1}}$ примем значения, указанные в предыдущих пунктах. Предположим также, что коэффициенты демпфирования обеих пружин одинаковы: ${{h}_{2}} = {{h}_{1}}$.
Вначале рассмотрим случай $m = 1$, $R = 1$. Тогда $V_{c}^{s} \approx 0.91$. На рис. 4 представлены амплитуды ${{A}_{{y1}}}$ колебаний точки ${{M}_{1}}$, амплитуды ${{A}_{{y2}}}$ колебаний призмы, частоты колебаний и выходная мощность в зависимости от десятичного логарифма коэффициента жесткости k для нескольких значений V. Сплошные линии обозначают результаты, полученные с помощью соотношений (4.3)–(4.5), а точки – значения, полученные при численном интегрировании системы (2.7) стандартным методом Рунге–Кутты 4 порядка. Черные линии и точки соответствуют притягивающим циклам, а серые – неустойчивым. Мощность показана только для притягивающих решений. Значения мощности, обеспечиваемые системой с одной подвижной массой, $P_{{\max }}^{s}$, показаны пунктиром (разумеется, только для тех скоростей ветра, при которых такая система имеет притягивающее периодическое решение).
Рис. 4.
Характеристики предельных циклов в зависимости от параметров k и $V$: a) амплитуда колебаний точки ${{M}_{1}}$; b) амплитуда колебаний призмы; c) десятичный логарифм частоты; d) мощность.
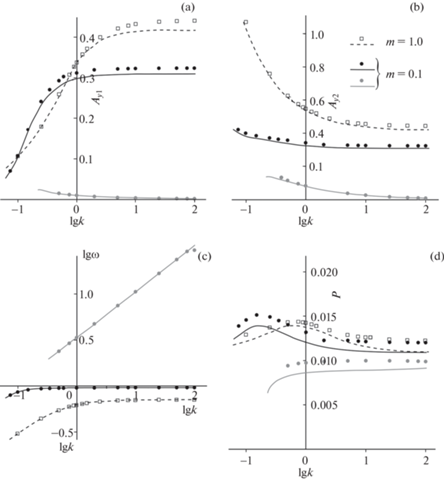
Видно, что аппроксимация достаточно близка к значениям, получаемым прямым интегрированием уравнений движения. Однако точность заметно падает вблизи точек, в которых сливаются устойчивый и неустойчивый периодические режимы. Кроме того, аппроксимация дает несколько заниженные значения амплитуд. С этим связано то обстоятельство, что выходная мощность, даваемая приближенной формулой (4.7), оказывается меньше, чем мощность, полученная непосредственным интегрированием системы (2.7). Для обеспечения большей точности необходим учет членов более высокого порядка.
Тем не менее, аппроксимация отражает основные тенденции в отношении мощности. Для каждого значения $V$ мощность имеет единственный максимум ${{P}_{{\max }}}$ по $k$. Видно, что мощность, вырабатываемая системой с двумя массами, всегда больше, чем $P_{{\max }}^{s}$. В то же время, отношение ${{P}_{{\max }}}{\text{/}}P_{{\max }}^{s}$ уменьшается с ростом $V$: так, при $V = 1$ выигрыш составляет примерно 17%, а при $V = 1.5$ он снижается до примерно 11%.
Отметим, что на рис. 4 представлены только циклы, отвечающие частоте ${{\omega }_{1}}$. Циклы с другой частотой при выбранных значениях параметров существуют только при больших значениях скорости ветра.
Влияние отношения $m$ масс подвижных тел на характеристики притягивающих циклов проиллюстрировано на рис. 5 для случая $V = 1$. Квадратики (кружки) и сплошные (пунктирные) линии обозначают, соответственно, результаты численного интегрирования и расчетов по аппроксимационным формулам при $m = 1$ ($m = 0.1$). В случае $m = 0.1$ видны два семейства притягивающих решений (то, которое отвечает $\omega = {{\omega }_{1}}$, обозначено черным цветом; то, которое отвечает $\omega = {{\omega }_{2}}$ – серым). Следует отметить, что аппроксимации дают заниженное значение k, при котором появляется семейство с $\omega = {{\omega }_{2}}$.
Рис. 5.
Характеристики предельных циклов в зависимости от параметров k и m: a) амплитуда колебаний точки ${{M}_{1}}$; b) амплитуда колебаний призмы; c) десятичный логарифм частоты; d) мощность.
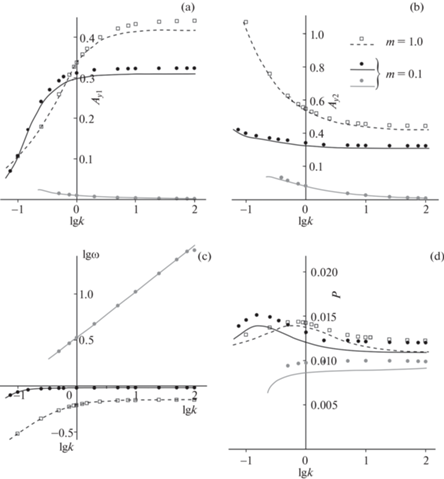
Амплитуды колебаний в решениях семейства $\omega = {{\omega }_{2}}$ достаточно малы и уменьшаются с ростом k. Однако $\omega $ при этом растет, что до некоторой степени компенсирует малость амплитуд в том, что касается мощности. Тем не менее, выходная мощность на этих решениях заметно меньше, чем на решениях семейства с $\omega = {{\omega }_{1}}$. Особенно эта разница заметна при $k$, близких к единице, где она может достигать 40%. Поэтому представляется целесообразным избегать перехода на циклы второго семейства.
Из рис. 5 видно, что уменьшение m приводит к уменьшению амплитуды колебаний призмы. Однако максимальная выходная мощность оказывается даже несколько больше, чем при m = 1, причем этот максимум достигается при меньшем значении k. В будущем представляется целесообразным провести более подробный анализ влияния отношения масс подвижных тел на производительность установки.
6. Заключение. Рассмотрена динамика галопирующей ветроэнергетической установки с двумя подвижными массами. Исследована область устойчивости положения равновесия в зависимости от параметров. Установлено, что при определенных условиях система имеет два притягивающих предельных цикла. Прослежена эволюция этих циклов при изменении различных параметров.
Показано, что рассматриваемая система имеет заметные преимущества по сравнению с системой, содержащей только одну подвижную массу. В частности, при надлежащем выборе параметров она имеет значительно более широкий рабочий диапазон скоростей ветра. Кроме того, ее выходная мощность больше, чем в случае системы с одной подвижной массой, и эта разница особенно заметна при скоростях ветра, близких к критической.
Исследование выполнено при поддержке РНФ (грант № 22-29-00472).
Список литературы
Den Hartog J.P. Transmission line vibration due to sleet // Trans. AIEE. 1932. V. 51. P. 1074–1086.
Parkinson G.V., Brooks N.P.H. On the aeroelastic instability of bluff cylinders // ASME. J. Appl. Mech. 1961. V. 28. № 2. P. 252–258. https://doi.org/10.1115/1.3641663
Parkinson G.V., Smith J.D. The square prism as an aeroelastic non-linear oscillator // Quart. J. Mech. Appl. Math. 1964. V. 17. № 2. P. 225–239. https://doi.org/10.1093/qjmam/17.2.225
Luo S.C., Chew Y.T., Ng Y.T. Hysteresis phenomenon in the galloping oscillation of a square cylinder // J. Fluids Struct. 2003. V. 18. № 1. P. 103–118. https://doi.org/10.1016/S0889-9746(03)00084-7
Oka S., Ishihara T. Numerical study of aerodynamic characteristics of a square prism in a uniform flow // J. Wind Eng. Ind. Aerodyn. 2009. V. 97. P. 548–559. https://doi.org/10.1016/j.jweia.2009.08.006
Люсин В.Д., Рябинин А.Н. О галопировании призм в потоке газа или жидкости // Тр. ЦНИИ им. ак. А.Н. Крылова. 2010. Вып. 53(337). С. 79–84.
Bearman P.W., Gartshore I.S., Maull D.J., Parkinson G.V. Experiments on flow-induced vibration of a square-section cylinder // J. Fluids Struct. 1987. V. 1. № 1. P. 19–34. https://doi.org/10.1016/s0889-9746(87)90158-7
Sarioglu M., Akansu Y.E., Yavuz T. Flow around a rotatable square cylinder-plate body // AIAA J. 2006. Vol. 44. №. 5. P. 1065–1072. https://doi.org/10.2514/1.18069
Gao G.-Z., Zhu L.-D. Nonlinear mathematical model of unsteady galloping force on a rectangular 2:1 cylinder // J. Fluids Struct. 2017. V. 70. P. 47–71. https://doi.org/10.1016/j.jfluidstructs.2017.01.013
Abdel-Rohman M. Design of tuned mass dampers for suppression of galloping in tall prismatic structures // J. Sound Vibr. 1994. V. 171. № 3. P. 289–299. https://doi.org/10.1006/jsvi.1994.1121
Gattulli V., Di Fabio F., Luongo A. Simple and double Hopf bifurcations in aeroelastic oscillators with tuned mass dampers // J. Franklin Inst. 2001. V. 338. P. 187–201. https://doi.org/10.1016/S0016-0032(00)00077-6
Selwanis M.M., Franzini G.R., Beguin C., Gosselin F.P. Wind tunnel demonstration of galloping mitigation with a purely nonlinear energy sink // J. Fluids Struct. 2021. V. 100. P. 103169. https://doi.org/10.1016/j.jfluidstructs.2020.103169
Barrero-Gil A., Alonso G., Sanz-Andres A. Energy harvesting from transverse galloping // J. Sound Vibr. 2010. V. 329. P. 2873–2883. https://doi.org/10.1016/J.JSV.2010.01.028
Dai H.L., Abdelkefi A., Javed U., Wang L. Modeling and performance of electromagnetic energy harvesting from galloping oscillations // Smart Mater. Struct. 2015. V. 24. № 4. P. 045012. https://doi.org/10.1088/0964-1726/24/4/045012
Hemon P., Amandolese X., Andrianne T. Energy Harvesting from Galloping of Prisms: A Wind Tunnel Experiment // J. Fluids & Struct. 2017. V. 70. P. 390–402. https://doi.org/10.1016/j.jfluidstructs.2017.02.006
Javed U., Abdelkefi A., Akhtar I. An improved stability characterization for aeroelastic energy harvesting applications // Comm. Nonlin. Sci. Num. Simul. 2016. V. 36. P. 252–265. https://doi.org/10.1016/j.cnsns.2015.12.001
Wang K.F., Wang B.L., Gao Y., Zhou J.Y. Nonlinear analysis of piezoelectric wind energy harvesters with different geometrical shapes // Arch. Appl. Mech. 2020. V. 90. P. 721–736. https://doi.org/10.1007/s00419-019-01636-8
Zhao D., Hu X., Tan T., Yan Zh., Zhang W. Piezoelectric galloping energy harvesting enhanced by topological equivalent aerodynamic design // Energy Conv. Manag. 2020. V. 222. P. 113260. https://doi.org/10.1016/j.enconman.2020.113260
Vicente-Ludlam D., Barrero-Gil A., Velazquez A. Enhanced mechanical energy extraction from transverse galloping using a dual mass system // J. Sound Vibr. 2015. V. 339. P. 290–303. https://doi.org/10.1016/j.jsv.2014.11.034
Karlicic D., Cajic M., Adhikari S. Dual-mass electromagnetic energy harvesting from galloping oscillations and base excitation // J. Mech. Eng. Sci. 2021. V. 235. № 20. P. 4768–4783. https://doi.org/10.1177/0954406220948910
Dosaev M. Interaction between internal and external friction in rotation of vane with viscous filling // Appl. Math. Mod. 2019. V. 68. P. 21–28. https://doi.org/10.1016/j.apm.2018.11.002
Saettone S., Taskar B., Regener P.B., Steen S., Andersen P. A comparison between fully-unsteady and quasi-steady approach for the prediction of the propeller performance in waves // Appl. Ocean Res. 2020. Vol. 99. P. 102011. https://doi.org/10.1016/j.apor.2019.102011
Abohamer M.K., Awrejcewicz J., Starosta R., Amer T.S., Bek M.A. Influence of the motion of a spring pendulum on energy-harvesting devices // Appl. Sci. 2021. V. 11. P. 8658. https://doi.org/10.3390/app11188658
Selyutskiy Y.D. Potential forces and alternation of stability character in non-conservative systems // Appl. Math. Mod. 2021. Vol. 90. P. 191–199. https://doi.org/10.1016/j.apm.2020.08.070
Lazarus A., Thomas O. A harmonic-based method for computing the stability of periodic solutions of dynamical systems // Comptes Rendus Mecanique. 2021. V. 338. № 9. P. 510–517. https://doi.org/10.1016/j.crme.2010.07.020
Климина Л.А. Метод формирования асинхронных автоколебаний в механической системе с двумя степенями свободы // ПММ. 2021. Т. 85. № 2. С. 152–171. https://doi.org/10.31857/S0032823521020065
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела



