РАДИОХИМИЯ, 2020, том 62, № 1, с. 24-31
УДК 532.77
ПОДХОДЫ К МАТЕМАТИЧЕСКОМУ
МОДЕЛИРОВАНИЮ ПЛОТНОСТИ ВОДНЫХ
АЗОТНОКИСЛЫХ РАСТВОРОВ НА ОСНОВЕ
ПРЕДСТАВЛЕНИЙ О КАЖУЩЕМСЯ МОЛЬНОМ
ОБЪЕМЕ ПРИМЕНИТЕЛЬНО
К ГИДРО-МЕТАЛЛУРГИЧЕСКИМ ПРОЦЕССАМ
ЯДЕРНОГО ТОПЛИВНОГО ЦИКЛА
© 2020 г. Е. А. Пузикова,*, Б. Я. Зильбермана, И. В. Блажеваа,
Е. В. Андрееваа, Н. Д. Голецкийа, А. С. Кудинова
а Радиевый институт им. В. Г. Хлопина, 194021, Санкт-Петербург, 2-й Муринский пр., д. 28
* e-mail: egor_puzikov@mail.ru
Получена 28.08.2019; после доработки 23.09.2019; принята к публикации 23.09.2019
Предложен метод расчета плотности однокомпонентных водных растворов азотной кислоты и нитрат-
ных солей, содержащихся в растворах гидрометаллургических процессов ядерного топливного цикла, с
использованием кажущихся мольных объемов соли и концентрации воды. Метод позволяет рассчитать
плотность растворов азотной кислоты до 17 моль/л (дигидрат HNO3) и солей вплоть до образования на-
сыщенных растворов с погрешностью не выше 0.2%. При этом значения кажущихся мольных объемов
линейно зависят от концентрации воды, а аппроксимированные на бесконечное разбавление значения
кажущихся мольных объемов соответствуют значениям Питцера.
Ключевые слова: вода, азотная кислота, молярные концентрации, плотность, кажущийся мольный объем
DOI: 10.31857/S0033831120010049
В химико-технологических процессах ядерно-
такого подхода являются известные эмпирические
го топливного цикла, как правило, используются
уравнения ρU = 998 + 32.6XH + 318XU, ρPu = 998 +
гидрометаллургические процессы экстракции и
31XH + 349XPu для расчета плотности азотнокис-
выпарки, реализуемые в азотнокислых средах,
лых растворов с умеренной концентрацией ура-
причем растворы имеют сложный солевой состав
нилнитрата или нитрата плутония соответственно
как по целевым компонентам, так и по сопутству-
[1-3] при 25°С. Хорошо известен также подход
ющим элементам или вводимым высаливателям.
[4], основанный на расчете кажущегося мольно-
Для проведения расчетов технологических про-
го объема (AMV - Apparent molar volume) соли в
цессов, включая их математическое моделирова-
растворе в его привязке к моляльной концентра-
ние, а также гидростатических расчетов оборудо-
ции этой соли. Основу таких расчетов составляют
вания необходимо знать плотности этих растворов
справочные данные [5-8] по плотности растворов
с точностью около 1 кг/м3.
известного состава в воде в мас%, пересчитанные
Обычные подходы к расчету плотности рас-
в моляльные или молярные концентрации компо-
творов основаны на составлении эмпирических
нентов. При этом возникают трудности при пе-
корреляционных уравнений, связывающих в яв-
ресчете данных для кристаллогидратов в случаях,
ном виде плотность раствора с концентрацией
когда растворимости даны в граммах на 100 г воды
компонентов, выраженных в моль/л. Примером
без указания, сделан ли пересчет на сухую соль.
24
ПОДХОДЫ К МАТЕМАТИЧЕСКОМУ МОДЕЛИРОВАНИЮ
25
Дополнительно использованы также литератур-
ветствии с правилом Здановского). Во многих слу-
ные данные по плотности растворов лантанидов
чаях данные используются с поправками в виде
и четырехвалентных актинидов [9-12] со ссылкой
коэффициентов активности, например по Питцеру
на них в табл. 1 и 2.
[15]. Однако в последнем случае довольно трудно
Считается, что в этих случаях мольные объемы
предложить метод расчета плотностей многоком-
остаются неизменными в многокомпонентных си-
понентных растворов переменного состава, осо-
стемах, а свойства - аддитивными [13, 14] (в соот-
бенно при высоких концентрациях компонентов. К
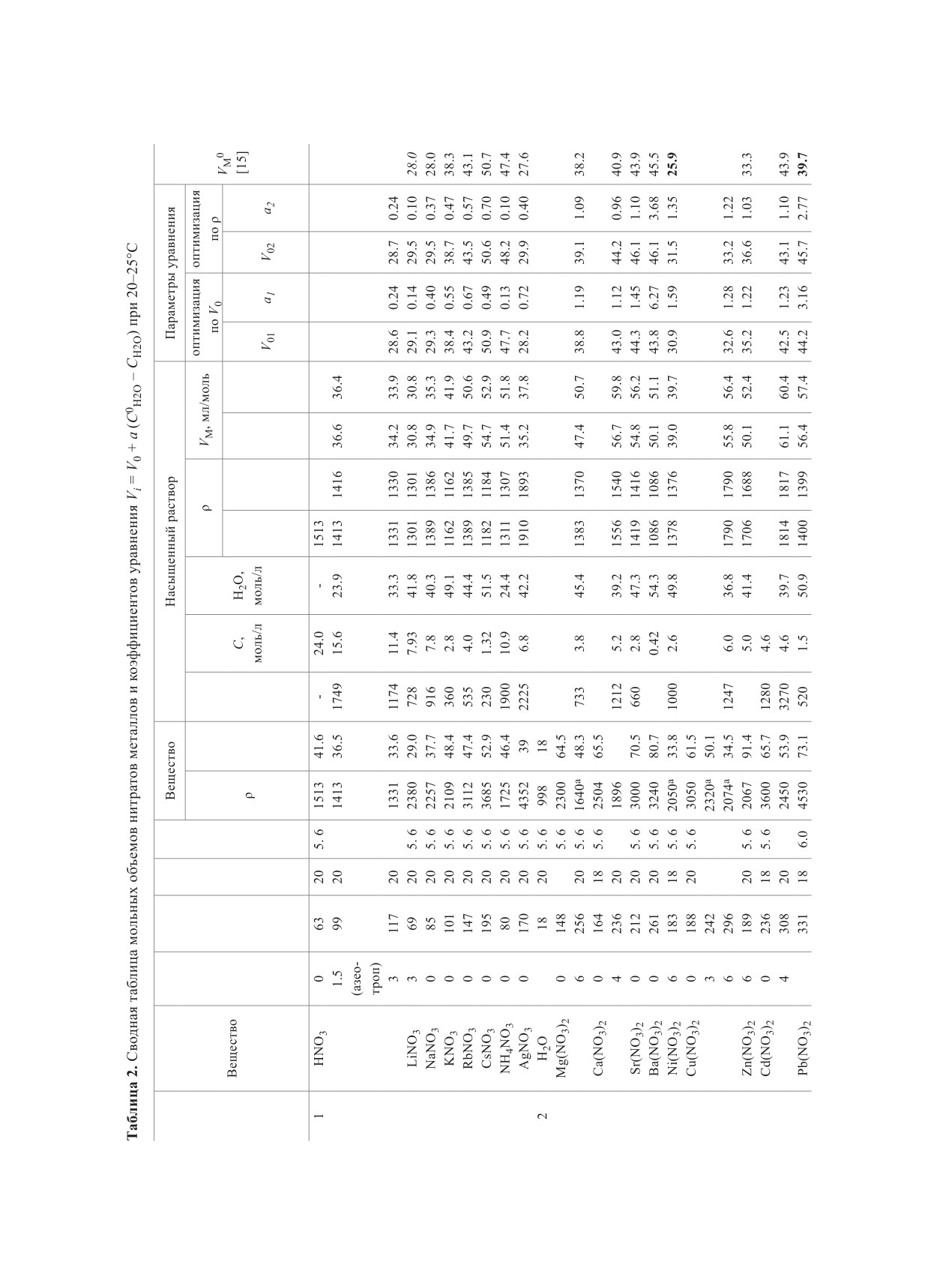
Таблица 1. Примеры расчета плотности растворов (ρ, г/л) и мольного объема (V
, мл/моль) нитратных солей
M
Концентрация
Концентрация соли
Оптимизационный расчет
H2O
Объем
Соль,
По VM
По ρ
ρ, г/л
соли,
ссылка
мас%
г/л
моль/л
г/л
моль/л
мл
VM
ρ
VM
ρ
HNO3
20
1
10.04
0.16
1003.6
993.6
55.2
4.65
29.2
28.8
1003.7
28.9
1003.6
[5, 65, 6]
4
40.8
0.65
1020.1
979.3
54.4
18.9
29.2
29.0
1020.2
29.1
1020.2
6
61.87
0.98
1031.2
969.3
53.9
28.9
29.5
29.2
1031.5
29.2
1031.5
17
186.4
2.96
1096.4
910.0
50.6
88.4
29.9
29.9
1096.2
30.0
1096.1
27
313.2
4.97
1160.0
846.8
47.0
151.7
30.5
30.8
1158.7
30.8
1158.5
36
439.4
6.97
1220.5
781.1
43.4
217.5
31.2
31.6
1217.3
31.7
1217.0
45
575.2
9.13
1278.3
703.1
39.1
295.6
32.4
32.7
1275.6
32.7
1275.3
49
639.0
10.14
1304.0
665.0
36.9
333.8
32.9
33.2
1301.2
33.2
1300.9
53
703.7
11.17
1327.8
624.1
34.7
374.8
33.6
33.7
1325.9
33.8
1325.5
56
756.0
12.00
1346
590.0
32.8
408.9
34.1
34.2
1344.8
34.2
1344.4
60
820.0
13.02
1366.7
546.7
30.4
452.3
34.8
34.7
1366.7
34.8
1366.3
68
955.3
15.16
1404.8
449.5
25.0
549.7
36.3
36.0
1408.1
36.1
1407.6
75
1075.0
17.06
1433.7
358.7
19.9
640.7
37.5
37.2
1439.0
37.3
1438.4
82
1196.0
18.98
1458.9
262.9
14.6
736.6
38.8
38.5
1464.6
38.5
1463.9
86
1266.0
20.10
1471.6
205.6
11.4
794.0
39.5
39.3
1476.6
39.3
1476.0
93
1385.0
21.98
1489.2
104.2
5.8
895.6
40.7
40.6
1492.2
40.6
1491.4
97
1452.0
23.05
1497.4
45.4
2.5
954.5
41.4
41.4
1498.2
41.4
1497.4
100
1513.0
24.02
1512.9
0.0
0.0
1000.0
41.6
42.0
1504.8
42.0
1504.0
LiNO3
20
1
10.0
0.15
1004.1
994.1
55.23
4.18
28.7
29.1
1004.0
29.5
1003.9
[5, 65, 6]
2
20.2
0.29
1010.0
989.8
54.99
8.44
28.8
29.2
1009.9
29.6
1009.8
4
40.9
0.59
1022.0
981.1
54.51
17.14
28.9
29.2
1021.8
29.6
1021.6
6
61.9
0.90
1034.0
969.2
54.01
26.14
29.1
29.3
1033.8
29.6
1033.5
8
83.7
1.21
1046.5
962.8
53.49
35.51
29.2
29.4
1046.3
29.7
1045.9
10
105.9
1.53
1059.0
953.1
52.95
45.21
29.4
29.5
1058.9
29.8
1058.5
12
128.6
1.86
1071.8
943.2
52.40
55.14
29.6
29.5
1071.8
29.8
1071.3
14
151.9
2.20
1084.8
932.9
51.83
65.42
29.7
29.6
1085.0
29.9
1084.4
16
175.7
2.55
1098.1
922.4
51.24
75.96
29.8
29.7
1098.4
29.9
1097.8
18
200.1
2.90
1111.6
911.5
50.64
86.87
29.9
29.8
1112.0
30.0
1111.5
20
225.1
3.26
1125.4
900.3
50.02
98.08
30.0
29.9
1125.9
30.0
1125.4
22
250.7
3.63
1139.5
888.8
49.38
109.6
30.1
30.0
1140.1
30.1
1139.7
26
303.8
4.40
1168.5
864.8
48.04
133.8
30.4
30.2
1169.4
30.2
1169.1
30
359.6
5.21
1198.8
839.2
46.62
159.4
30.6
30.4
1199.8
30.4
1199.7
35
433.7
6.29
1239.2
805.5
44.75
193.1
30.7
30.6
1239.6
30.5
1240.1
40
513.5
7.44
1283.7
770.2
42.79
228.4
30.7
30.9
1281.9
30.7
1283.2
42
546.6
7.93
1301.5
754.9
41.94
243.8
30.8
31.0
1299.3
30.8
1300.9
РАДИОХИМИЯ том 62 № 1 2020
26
ПУЗИКОВ и др.
Таблица 1. (продолжение)
Концентрация
Концентрация соли
Оптимизационный расчет
H2O
Объем
Соль,
По VM
По ρ
ρ, г/л
соли,
ссылка
мас%
г/л
моль/л
г/л
моль/л
мл
VM
ρ
VM
ρ
Al(NO3)3
20
1.0
10.1
0.047
1006.5
996.4
55.36
1.77
37.4
47.0
1006.0
48.2
1006.0
[5, 65, 6]
2.0
20.3
0.10
1014.4
994.1
55.23
4.10
43.0
47.3
1014.0
48.4
1013.9
4.0
41.2
0.19
1030.5
989.3
54.96
8.94
46.2
47.7
1030.2
48.8
1030.0
6.0
62.8
0.29
1046.9
984.1
54.67
14.14
47.9
48.3
1046.8
49.3
1046.5
8.0
85.1
0.40
1063.8
978.7
54.37
19.54
48.9
48.8
1063.8
49.7
1063.5
10.0
108.1
0.51
1081.1
973.0
54.06
25.26
49.8
49.4
1081.3
50.2
1080.9
12.0
131.9
0.62
1098.9
967.0
53.72
31.22
50.4
50.0
1099.2
50.7
1098.7
14.0
156.4
0.73
1117.1
960.7
53.37
37.56
51.2
50.6
1117.5
51.2
1117.1
16.0
181.7
0.85
1135.7
954.0
53.00
44.29
51.9
51.3
1136.3
51.8
1135.8
18.0
207.9
0.98
1154.9
947.0
52.61
51.27
52.5
52.0
1155.5
52.3
1155.1
20.0
234.9
1.10
1174.5
939.6
52.20
58.71
53.2
52.7
1175.1
53.0
1174.8
24.0
291.7
1.37
1215.3
923.6
51.31
74.71
54.6
54.3
1215.6
54.3
1215.7
28.0
352.3
1.65
1258.2
905.9
50.33
92.46
55.9
56.1
1257.9
55.8
1258.4
30.0
384.2
1.80
1280.5
896.4
49.80
102.0
56.6
57.0
1279.7
56.6
1280.5
32.0
417.2
1.96
1303.6
886.4
49.25
112.0
57.2
58.0
1301.9
57.4
1303.2
UO2(NO3)2
25
9.0
96.5
0.24
1077.2
979.5
54.40
16.40
66.9
70.2
1076.4
69.2
1076.7
[66] +
16.5
189.6
0.48
1152.3
962.7
53.50
34.40
71.5
70.7
1152.7
69.8
1153.1
эксперимент
22.8
279.7
0.71
1226.1
946.5
52.60
50.70
71.4
71.2
1226.3
70.4
1226.8
28.3
366.7
0.93
1297.4
930.7
51.70
66.50
71.5
71.6
1297.2
71.0
1297.8
33.0
450.8
1.14
1366.0
915.2
50.80
82.00
71.7
72.0
1365.6
71.5
1366.2
37.1
532.0
1.35
1432.1
900.1
50.00
97.20
72.0
72.5
1431.4
72.1
1431.9
40.8
610.4
1.55
1495.6
885.2
49.20
112.10
72.4
72.9
1494.8
72.6
1495.2
44.1
686.0
1.74
1556.5
870.5
48.40
126.90
72.9
73.3
1555.8
73.2
1555.9
47.0
758.8
1.93
1614.8
856.0
47.60
141.40
73.4
73.7
1614.4
73.7
1614.3
49.6
829.0
2.10
1670.6
841.6
46.80
155.90
74.1
74.1
1670.6
74.2
1670.3
52.0
896.4
2.28
1723.8
827.3
46.00
170.20
74.8
74.5
1724.5
74.7
1723.9
54.2
961.2
2.44
1774.4
813.2
45.20
184.40
75.6
74.8
1776.2
75.3
1775.1
78.0
1923
4.90
2510.0
587.0
32.60
411.00
84.2
81.1
2525.3
83.5
2513.5
тому же такой подход представляется нам некор-
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
ректным, так как неидеальность системы заключе-
При проведении расчетов использовали упо-
на в самом понятии кажущегося мольного объема,
мянутые выше литературные экспериментальные
когда воду считают как бы идеальной и несжимае-
данные, ссылки на которые даны в сводных та-
мой. На необходимость учета концентрации воды
блицах. При наличии противоречий использовали
или, возможно, ее активности при расчете плотно-
более поздние данные, а «кочующая по справочни-
сти высококонцентрированных растворов обраще-
кам» [5-7] плотность тригидрата нитрата магния
но внимание в работах [13, 16].
Mg(NO3)2∙3H2O 1460 г/м3 исправлена на 1640 г/м3
Данная работа является первым этапом в поиске
как явная опечатка, легко выявляемая при сопо-
возможности расчета плотности раствора исходя
ставлении мольных объемов солей в растворах ни-
из кажущегося мольного объема компонентов как
тратов кальция, меди, никеля и цинка.
функции молярной концентрации воды в много-
Концентрационные зависимости плотности
компонентной системе при учтенной температуре.
водных растворов уранилнитрата и нитрата алю-
РАДИОХИМИЯ том 62 № 1 2020
ПОДХОДЫ К МАТЕМАТИЧЕСКОМУ МОДЕЛИРОВАНИЮ
27
РАДИОХИМИЯ том 62 № 1 2020
28
ПУЗИКОВ и др.
миния были проверены экспериментально при
различных температурах классическим методом
с использованием калиброванных пикнометров и
солей, состав которых был проверен весовым ме-
тодом путем аммиачного осаждения и прокалива-
ния осадка.
Расчет мольного объема и плотности соли
в однокомпонентных изотермических водных
растворах. Расчет плотности по предлагаемому
методу базируется на изложенном выше представ-
лении о характерности кажущегося мольного объ-
ема простого соединения известного состава в от-
носительно широком диапазоне составов раство-
ра, но в привязке к молярной концентрации воды
при данной температуре. Это формально описыва-
ется системой уравнений
ρ = mH
+ Σmi = VH
ρH
+ΣCiMi,
(1)
2O
2O
2O
где mH2O - масса воды в 1 литре раствора, mi -
масса i-го компонента в 1 л раствора, Сi - число
молей i-компонента в растворе, Mi - его молярная
масса. Объем воды в растворе может быть рассчи-
тан как
VH
= 1000 - ΣiСiVi,
(2),
2O
где Vi - кажущийся мольный объем i-го компонен-
та в растворе. Таким образом, зная мольные объе-
мы компонентов, можно рассчитать плотность по
уравнению
ρ = (1000 - ΣiСiVi)ρH
+ΣCiMi,
(3)
2O
пользуясь методом итераций.
Некоторую неопределенность вносит аппрок-
симация данных по величине начального мольного
объема соли (V0M) в области сильноразбавленных
растворов, поскольку данные по сравнению плот-
ности растворов и воды в области сильного раз-
бавления неизбежно содержат большую система-
тическую ошибку, в том числе даже при точности
измерений плотности 0.1% (или же 1 г/л), вслед-
ствие отклонения температуры от заявленной бо-
лее 0.2°С. При этом возможны различные подходы
к аппроксимации данных в области разбавленных
растворов [14]. Мы предпочли опираться на значе-
ния плотности при концентрации компонента бо-
лее 0.5 моль/л, а значение V0M определять методом
экстраполяции на молярную концентрацию чи-
стой воды при данной температуре по уравнению
VM = V0M + a(C0H
- CH
),
(4)
2O
2O
где V0M - мольный объем соли в бесконечно раз-
бавленном растворе, CH2O - концентрация воды в
РАДИОХИМИЯ том 62 № 1 2020
ПОДХОДЫ К МАТЕМАТИЧЕСКОМУ МОДЕЛИРОВАНИЮ
29
ɚ
ɛ
¨Th; ƇPb(II); ƑMg; ŶNa; ×U(VI); żLa; ¸Zn;
125
125
¨Th; ƇPb(II); ƑMg; ŶNa; ×U(VI); żLa; ¸Zn;
ŷLi; ƔFe(III); ŸCa; *Ni; +HNO3
ŷLi; ƔFe(III); ŸCa; *Ni; +HNO3
100
100
75
75
50
50
25
25
30
35
40
45
50
55
0
2
4
6
8
10
H22 ɦɨɥɶ ɥ
NO– ɦɨɥɶ ɥ
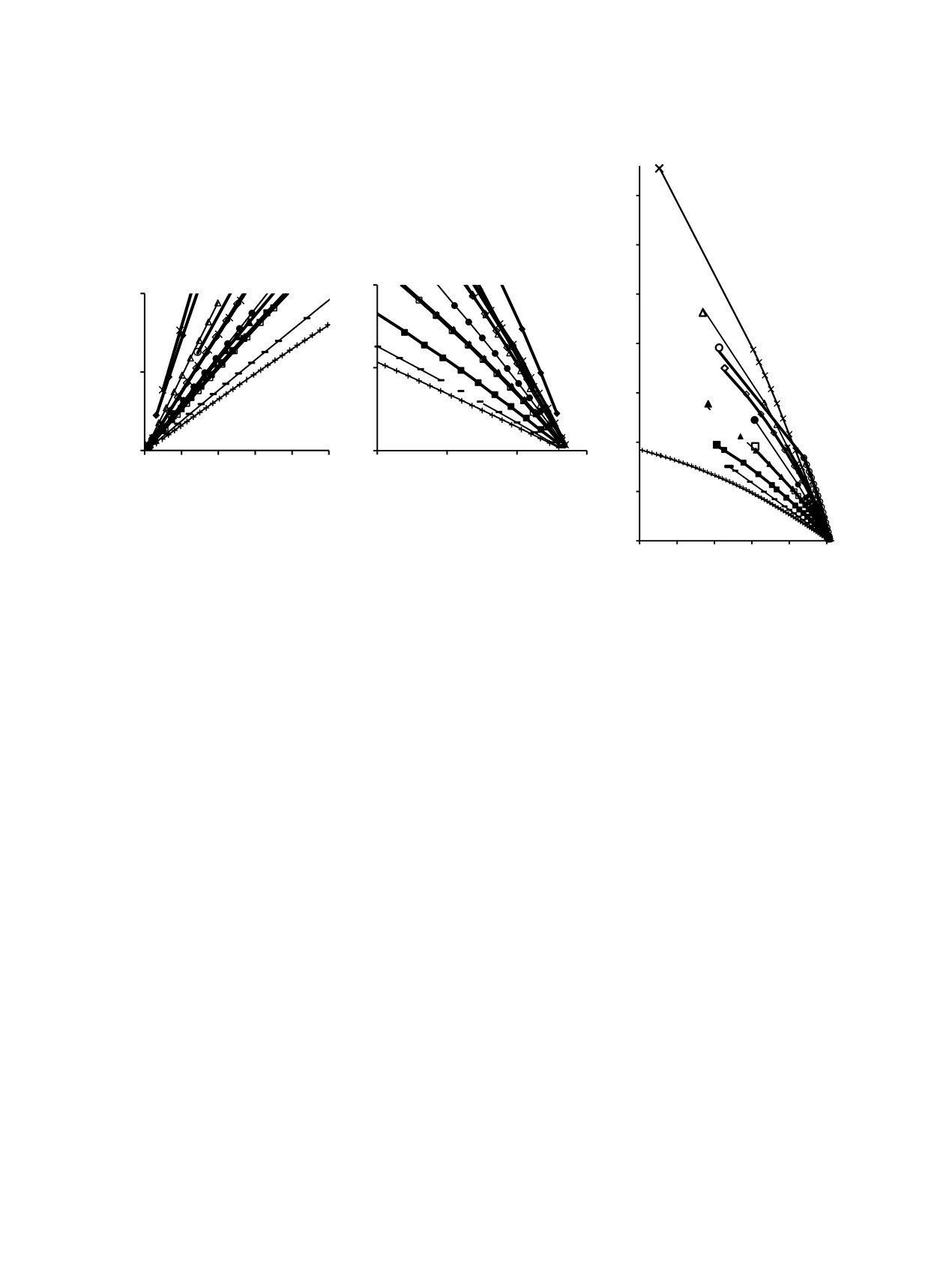
Рис. 1. Зависимости мольного объема от концентрации воды (а) и нитрат-иона соли (б). Линии - расчет, точки - литератур-
ные экспериментальные данные (собственные данные для уранилнитрата). Крупные значки с выделенным контуром - данные
для насыщенных растворов.
растворе при данной температуре, a - коэффици-
Результаты расчета мольного объема и плот-
ент пропорциональности. Значения параметра a
ности соли в однокомпонентных водных рас-
подбирали с помощью оптимизационного пакета
творах нитратов при температуре
20-25°С.
Solver («Поиск решения») в программе MS Excel.
Были проведены расчеты для двухкомпонентных
При этом были рассмотрены два подхода к ли-
систем, а именно водных растворов нитратов ти-
нейной аппроксимации, в которых в качестве кри-
пичных одно-, двух- и трехвалентных элементов
терия оптимизации выбрана либо погрешность
с разной атомной массой (точнее - для элементов,
определения мольного объема соли, либо погреш-
образующих в растворе одно-, двух- или трехза-
ность плотности раствора (табл. 1). С учетом ко-
рядные катионы, при этом шестивалентный уран
нечного прикладного характера задачи (расчет
существует в виде двухзарядного катиона урани-
плотности) более точный результат по всей кривой
ла). Все эти нитраты существуют в твердом состо-
дает оптимизация по плотности, тогда как в обла-
янии в виде сухих солей или кристаллогидратов.
сти низких ее значений ошибка расчета по любому
Из четырехвалентных элементов рассмотрен толь-
из вариантов остается в пределах точности экспе-
ко нитрат тория, поскольку другие такие элементы
риментальных данных (то есть 0.1%). Однако в та-
легко гидролизуются и выпадают в осадок в виде
ком случае появляется небольшая область с посто-
гидроксидов, так что в водном растворе без избыт-
янным значением мольного объема, что, возможно,
ка азотной кислоты они не существуют. Поэтому
реально соответствует понятию «бесконечно раз-
такие нитраты будут рассмотрены позже при ана-
бавленный раствор». Следует также отметить, что
лизе соответствующих трехкомпонентных систем.
предлагаемый результат расчета мольного объема
Образцы расчета на примерах нитратов лития,
простых солей в большинстве случаев достаточно
близок к расчетам Питцера [15]. Причины расхож-
алюминия и уранила даны в табл. 1. Графическое
дения для нитратов никеля и свинца неясны, по-
отображение таких расчетов дано на рис. 1 и 2,
скольку база указана одинаковой [5, 6].
сводные показатели - в табл. 2.
РАДИОХИМИЯ том 62 № 1 2020
30
ПУЗИКОВ и др.
ȡ ɝɥ
ɜ
2400
2200
ɚ
ȡ ɝɥ
ɛ
ȡ ɝɥ
1200
1200
2000
1800
1100
1100
1600
1400
1000
1000
0
1
2
3
4
5
50
52
54
56
NO– ɦɨɥɶ ɥ
H22 ɦɨɥɶ ɥ
1200
1000
30
35
40
45
50
55
¨Th; Ƈ3E ,, ƑMg; ŶNa; ×8 9, żLa; ¸Zn; ŷLi; Ɣ)H ,,, ŸCa; *Ni; +HNO3
H22 ɦɨɥɶ ɥ
Рис. 2. Зависимости плотности от концентрации соли (а) и воды (б, в) в различном масштабе.
Расчеты охватывают область составов от раз-
и 0.168, а в диапазоне 46-18 моль/л H2O (5-
бавленных растворов вплоть до полного насыще-
18 моль/л HNO3) V0 = 27.9 и a = 0.271. Излом на
ния, причем все насыщенные солевые растворы
этих зависимостях ассоциируется с выявленным
содержат не менее половинного количества воды
нами [17] переходом от постоянного коэффициен-
по сравнению с чистой водой. Крайние точки по-
та распределения азотной кислоты между жидко-
мечены на рис. 1 увеличенными обведенными
стью и паром от концентрации азотной кислоты к
значками. Они демонстрируют, что система урав-
его квадратичной зависимости при кипении при
нений (1)-(4) при температуре 20°C справедлива
100 кПа.
во всем диапазоне составов вплоть до насыщен-
Выше 18 моль/л HNO3 (моногидрат азотной
ных растворов (табл. 2).
кислоты) расчетные значения мольного объема и
Несколько хуже результат для азотной кис-
плотности оказываются выше фактических вслед-
лоты, где в области концентраций 7-10 и выше
ствие коренного изменения свойств системы, кото-
15.6 моль/л точность снижается до 0.2%. Следует
рая превращается в раствор воды в азотной кислоте.
отметить, что линия зависимости мольного объема
Линейная зависимость мольного объема соли
нитрата лития от концентрации воды (рис. 1а) пол-
от концентрации воды коррелирует с линейной за-
ностью сливается с таковой для азотной кислоты.
висимостью плотности раствора от концентрации
Более тщательный анализ показывает, что име-
воды лишь на начальном этапе. При приближении
ется две области линейной зависимости кажуще-
к области насыщенных растворов кривые плотно-
гося мольного объема азотной кислоты от концен-
сти для кристаллогидратов (а также для азотной
трации воды (рис. 2б), пересекающиеся при кон-
кислоты) в той или иной мере самопроизвольно
центрации воды около
47 моль/л H2O, что соот-
искривляются при сохранении точности расчета.
ветствует ~ 5 моль/л HNO3.
В табл. 2 для сравнения приведены также ка-
В низкокислотной области коэффициенты
жущиеся мольные объемы сухих солей и таковые
уравнения (4) V0 и a равны соответственно 29.1
в кристаллогидратах. Однако экспериментальные
РАДИОХИМИЯ том 62 № 1 2020
ПОДХОДЫ К МАТЕМАТИЧЕСКОМУ МОДЕЛИРОВАНИЮ
31
данные для обезвоженных кристаллогидратов
СПИСОК ЛИТЕРАТУРЫ
известны лишь для небольшого числа солей (в
1. Reactor Handbook. Fuel Reprocessing / Eds. S. M.
частности, нитраты магния, кальция, алюминия,
Stoller, R. B. Richards. New York: Interscience, 1961.
меди и кадмия). Они приведены для сравнения
2nd ed. Vol. 2. P. 107.
при оценке эффекта гидратации, рассматриваемо-
2. Николотова З.И., Карташова Н.А. Экстракция ней-
го ниже в плане изменения кажущегося мольного
тральными органическими соединениями / Под ред.
объема. При этом коэффициенты концентрацион-
А.М. Розена. М.: Атомиздат, 1976. Т. 1. С. 407.
ных зависимостей к уравнению (4) даны в привяз-
3. Maimoni A. Density and Radiolytic Decomposition
ке к наиболее гидратированной соли, в равновесии
of Plutonium Nitrate Solutions: Report UCRL-52727.
с которой находится насыщенный водный раствор.
Livermore (USA): Lawrence Livermore Laboratory,
1979. P. 20.
Выбор концентрации воды вместо концентра-
4. Hakin A.H., Lui J., Erickson K. et al. // J. Chem.
ции растворенного вещества в качестве аргумента
Thermodyn. 2005. Vol. 37, N 2. P. 153.
функции для расчета мольного объема обусловлен
5. Справочник химика / Под ред. Б. П. Никольского.
не только линеаризацией зависимостей в указан-
М.; Л.: Химия, 1965. 2-е изд. Т. 3. С. 496.
ных координатах, но как основа для расчета плот-
6. International Critical Tables of Numerical Data, Physics,
ности многокомпонентных систем, так как концен-
Chemistry, and Technology. Section 2: Physical and
трация воды в них может быть выбрана в качестве
Chemical Data / Eds C.J. West, C. Hull. New York:
обобщенного параметра для расчета плотности че-
McGraw-Hill, 1933. P. 2.99-2.109.
рез мольные объемы компонентов с последующим
7. Sohnel O., Novotný P. Densities of Aqueous Solutions
проведением итераций.
of Inorganic Substances. Amsterdam: Elsevier, 1985.
335 p.
Данный вопрос нуждается в более глубокой
8. Проценко П.И., Разумовская О.Н., Брыкова Н.А.
проработке. Для этого необходимо провести обра-
Справочник по растворимости нитритных и нитрат-
ботку литературных данных для многокомпонент-
ных солевых систем. Л.: Химия, 1971. 272 с.
ных систем, включая системы с солями компонен-
9. Hu Y.-F., Jin Ch.-W., Ling Sh., Zhang J.-Zh. // J. Chem.
тов, не являющихся делящимися нуклидами и про-
Eng. Data. 2011. Vol. 56, N 3. P. 472.
дуктами их деления, с последующей наработкой
10. Min D.K., Choi B.Il., Ro S.G. et al. // J. Radiat. Protect.
необходимой экспериментальной базы данных.
1986. Vol. 11, N 1. P. 22.
При этом, как указывалось выше, представля-
11. Apelblat A., Azoulay D., Sahar A. // J. Chem. Soc.,
ется ошибочным относить кажущийся мольный
Faraday Trans. 1973. Vol. 69, N 1. P. 1618.
объем вещества в водном растворе к его активно-
12. Charrin N., Moisy Ph., Blanc P. // Radiochim. Acta.
сти, поскольку в этом случае неидеальность систе-
2000. Vol. 88, N 8. P. 445.
мы как бы учитывается дважды, поскольку само
13. Leclaire N., Anno J., Courtois G. et al. // Nucl. Technol.
понятие кажущегося мольного объема учитывает
2003. Vol. 144, N 3. P. 303.
влияние гидратации вещества.
14. Kodejs Z., Pacak P. // Chem. Papers. 1986. Vol. 40,
N 4. P. 523.
В дальнейшем предполагается распространить
15. Krumgalz B.S., Pogorelsky R., Pitzer K.S. // J. Phys.
метод на расчет плотности многокомпонентных
Chem. Ref. Data. 1996. Vol. 25, N 2. P. 663.
растворов.
16. Leclaire N., Anno J., Courtois G. et al. // Proc. 7th Int.
КОНФЛИКТ ИНТЕРЕСОВ
Conf. on Nuclear Critical Safety Tokai-mura: JAERI,
Oct. 20-24, 2003. Vol. I. P. 37.
Авторы заявляют об отсутствии конфликта
17. Зильберман Б.Я., Макарычев-Михайлов М.Н., Ряб-
интересов.
ков Д.В. и др. // Хим. технология. 2009. N 12. C. 755.
РАДИОХИМИЯ том 62 № 1 2020