Радиохимия, 2019, т. 61, N 5, c. 397-403

397

Использование унифицированной модели с разбавлением ТБФ для

описания экстракции азотной кислоты и нитратов шестивалентных

актинидов в многокомпонентных нитратных системах

^а Радиевый институт им. В. Г. Хлопина, 197021, Санкт-Петербург, 2-й Муринский пр., д. 28;

*e-mail: egor_puzikov@mail.ru

Получена 10.01.2019, после доработки 25.03.2019, принята к публикации 26.03.2019

УДК 546.791.6+546.799.3/4 +542.61

На основе литературных и собственных экспериментальных данных предложена унифицированная

модель для описания экстракции An(VI) (An = U, Np, Pu, Am) из растворов HNO₃ в ТБФ различной кон-

центрации. При этом предполагается параллельное протекание нескольких реакций экстракции и несте-

хиометрического физико-химического взаимодействия компонентов. Рассчитанные значения парамет-

ров зависимости концентрационных констант равновесий от общей концентрации ТБФ позволили рас-

ширить диапазон описываемых моделью концентраций экстрагента (от 2.7 до 100%) и снизить погреш-

ность расчета коэффициентов распределения HNO₃ и An(VI). Для описания высаливающего действия

нитратных солей использован параметр кажущейся гидратации катионов этих солей в водной фазе.

Ключевые слова: трибутилфосфат, экстракция, уранилнитрат, плутоний, нептуний, америций, вы-

саливатели, моделирование.

DOI: 10.1134/S003383111905006X

В работе [1] был предложен унифицированный

экстракции моносольвата HNO₃ изменено значение

мультиреакционный подход к описанию равновесий

константы равновесия; при этом введена зависи-

с участием ТБФ любой концентрации при экстрак-

мость константы равновесия от общей концентрации

ции РЗЭ из слабокислых нитратных растворов. Це-

ТБФ через параметр a [1]: lgK = lgK₁₀₀ - alg(C_TBP/

лью данной работы является его распространение на

C₁₀₀), где lgK₁₀₀ - константа экстракции для 100%-

растворы со свободной HNO₃ и шестивалентных

ного ТБФ, lgK - константа экстракции при концен-

актинидов (An) как традиционных участников Пу-

трации ТБФ C_TBP.

рекс-процесса. Описанию экстракции трехвалент-

Вместо экстракции HNO₃ в виде дисольвата по

ных элементов в таких условиях будет посвящено

реакции H

(aq)

+ NO_–(aq) + 2TBP_(s) = HNO₃·(TBP)_2(s)

следующее сообщение.

(индекс aq относится к водной, s - к органической

Ранее с помощью мультиреакционной модели

фазе) было предложено использовать уравнение 1.4

нами была описана экстракция воды, азотной кисло-

(см. таблицу), которое описывает нестехиометриче-

ты и уранилнитрата при концентрации ТБФ 10-65%

скую сольватацию HNO₃ гидратированным ТБФ.

[2-4], однако она оказалась непригодной при более

Кроме того, в функции, описывающей диссоциацию

высоких концентрациях ТБФ, включая 100%-ный

HNO₃ в воде, содержащейся в органической фазе

ТБФ. Поэтому за основу был взят подход с разбавле-

(см. уравнение 1.5, см. таблицу), были откорректи-

нием 100%-ного ТБФ, как и в работах [1, 5].

рованы показатели степеней и значение параметра

Недостающие экспериментальные данные по экс-

FH-H2O. В уравнении реакции присоединения второй

тракции уранилнитрата и других An(VI) взяты из

молекулы HNO₃ к моносольвату HNO₃ (уравне-

ние 1.6) несколько откорректировано значение кон-

работ [6-12].

станты K_2H. Для каждой реакции рассчитан параметр

Экстракция азотной кислоты

а, учитывающий изменение констант при разбавле-

нии ТБФ, а также коэффициент b температурной

Экстракция воды в ТБФ при разбавлении пре-

зависимости константы равновесия lgK(t) = lgK₂₀[1 +

дельными углеводородами была описана ранее в

b(t - 20)/(273 + t)] для реакции 1.6. Константа урав-

работе [2]; параметры уравнений 1.1 и 1.2, приведен-

нения для реакции 1.3 оказалась независящей от

ные в таблице, остались без изменений, но перену-

температуры (коэффициент b равен 0).

мерованы в соответствии с последовательностью

рассмотрения. Описание совместной экстракции

Сопоставление расчетных и экспериментальных

HNO₃ и воды (рис. 1, а-г) потребовало уточнения

данных [13, 14] для экстрагента переменного состава

уравнений 1.3-1.6. Все изменения выделены жир-

и для 100%-ного ТБФ представлено на рис. 1, а, г.

ным шрифтом в сводной таблице. В уравнении 1.3

Из них следует, что усовершенствованная модель

398

Е. А. Пузиков и др.

Унифицированные уравнения модели экстракции HNO₃ и An(VI) в 100%-ный ТБФ^а,б

Номер

Константа (параметр)

Параметр a

Температурная поправка b

уравнения

обозначение

HNO₃

1.1

K_d

0.05

β1,H2O

0.0012

1.2

β_2,H2O

0.11

β_3,H2O

0.2

1.3

K_H

0.085

0.2

1.4

K_2H

0.035

-1.6

1.5

F_H2O-H

0.66

-1.0

1.6

K_2H

0.0018

1.3

3.0

1.7

Значения параметров см. работу [1]

1.8

2.1

K_aqAn(VI)

0.01

2.2

K_An(VI)

6.0

3.8

0.60

-0.52

-0.38

-0.58

-2.8

-0.3

-11.8

2.3

K_An-OH

2.4

F_H-U(VI)

0.218

2.5

F_An-H2O

0.047

1.7

0.2

-1.3

-0.95

-2.5

^а Уравнения: 1.1 - димеризация ТБФ в органической фазе, 2TBP = (TBP)₂; 1.2 - переход воды в органическую фазу (растворение в

ТБФ) по закону Нернста, D_H2O = β_1,H2O[TBP] + β_2,H2O[(TBP)₂] + β_3,H2O(β_2,H2O[(TBP)₂])²; 1.3 - экстракция моносольвата азотной

кислоты, H(aq) + NO–(aq) + TBP(s) = HNO3·TBP(s);

1.4

- взаимодействие HNO₃ с водой в органической фазе, YH2O-TBP =

K_2H[H⁺]^2.5Y_H2O[TBP]^1.5; 1.5 - диссоциация HNO₃ в органической фазе, Y_H2O-H = F_H2O-HY_H2O([HNO₃·TBP]_(s))^0.7; 1.6 - присоединение

второй молекулы HNO₃ к моносольвату HNO₃ с ТБФ, H₃O(aq) + NO–(aq) + HNO3·TBP(s) = (HNO3)2·H2O·TBP(s); 1.7 - пересчет общей

концентрации ТБФ (изменение объема), C^TBP/C_TBP = (C_TBPV_TBP + C_разбV_разб)/(C_TBPV_TBP + C_разбV_разб _.+ Y_H2OV_H2O + Y_HV_H + ∑Y_iV_i); 1.8 -

пересчет концентрации воды с учетом гидратации, X^H2O = (1/M_H2O)(1000ρ - ∑X_iM_i - X_HM_H) - ∑n_iX_i (M_i - молярная масса, г/моль;

X_i - концентрация, моль/л); 2.1 - гидролиз уранилнитрата, UO_2+(aq) + H₂O_(aq) = UO₂OH

(aq)

+ H^(aq); 2.2 - экстракция дисольвата

уранилнитрата с ТБФ, AnO_2+(aq) + 2NO_–(aq) + 2TBP_(s) = AnO₂(NO₃)₂(TBP)_2(s); 2.3 - AnO₂OH^(aq) + NO_–(aq) + TBP_(s) + 2H₂O_(s) =

AnO₂OH(NO₃)(H₂O)₂(TBP)_(s); 2.4 - соэкстракция HNO₃ с уранилнитратом, Y_H-U(VI) = F_H-U(VI)([HNO₃·TBP]_(s)[AnO₂(NO₃)₂(TBP)₂]_(s))^0.3;

2.5 - взаимодействие с водой в органической фазе, Y_An-H2O = F_An-H2O[AnO₂]_(aq)[NO_–]_(aq)Y^H2O.

^б Выделение жирным шрифтом: пояснение см. в тексте.

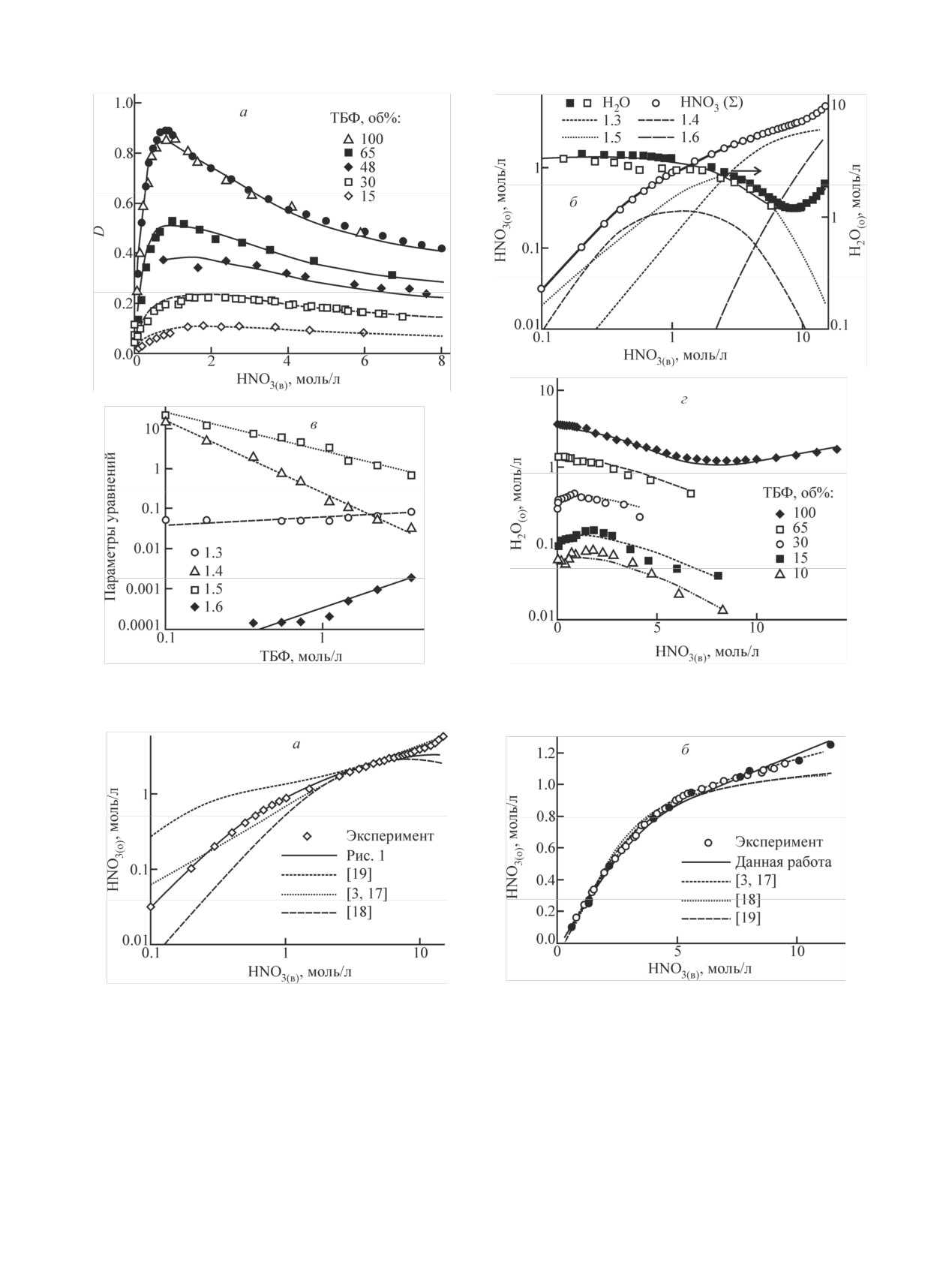
более точно описывает экстракцию HNO₃ и воды

сутствии различных высаливателей представлено на

чистым ТБФ, а также разбавленным ТБФ вплоть до

рис. 3. Из него следует, что экспериментальные [4] и

его объемной концентрации 10% в парафиновом

расчетные данные совпадают вполне удовлетвори-

разбавителе. При более низких концентрациях ТБФ,

тельно в охваченном диапазоне кислотности (до

не имеющих практического значения, точность мо-

8 моль/л). Для учета действия одно- и двухзарядных

дели заметно ухудшается. По-видимому, здесь сле-

катионов высаливателей взяты те же значения коэф-

дует учитывать вклад экстракции компонентов раз-

фициентов гидратации [1], однако для трехзарядных

бавителем [15] по аналогии с работой [16].

катионов (Al³⁺, Fe³⁺) приходится вводить поправку на

зависимость кажущегося коэффициента гидратации

Преимущество представленной выше модели по

от суммарной концентрации протона и катиона выса-

сравнению с предложенными ранее для разбавлен-

ливателя в виде n = (n₀ - n₁X_H + n₂X H)/X_Me1.3, где для

ного ТБФ [17], в том числе на основе модели А. М.

Al³⁺ n₀ = 7, n₁ = 1.8, n₂ = 0.13, а для Fe³⁺ n₀ = 8, n₁ = 2.7,

Розена [18-20], показано на рис. 2. Следует отме-

n₂ = 0.21. Скорее всего, эти поправки связаны с кон-

тить, что модели А. М. Розена для разбавленного и

куренцией с протоном кислоты за координацию во-

неразбавленного ТБФ [18] различаются между со-

ды, а также с возможным гидролизом многозарядных

бой, несмотря на введение коэффициентов активно-

катионов высаливателей, на что было обращено вни-

сти HNO₃ в водной фазе, а ее более ранняя версия

мание в работе [23]. Этот вопрос требует отдельного

[22], модифицированная нами для 30%-ного ТБФ

рассмотрения.

[19], оказывается неприменимой для

100%-ного

ТБФ вследствие отсутствия в ней корректного опи-

В литературе практически отсутствуют данные по

сания экстракции воды в зависимости от концентра-

влиянию высаливателей на экстракцию HNO₃ более

ции ТБФ.

концентрированными растворами ТБФ. Данные ма-

лодоступной работы (см. справочник [24], c. 38) ука-

Экстракция азотной кислоты

зывают на то, что в присутствии нитрата натрия в

в присутствии высаливателей

сериях с постоянной ионной силой значения парамет-

ра а не изменяются (рис. 4).

Сопоставление экспериментальных и расчетных

данных по экстракции HNO₃ 30%-ным ТБФ в при-

При более низких концентрациях ТБФ имеются

Использование унифицированной модели с разбавлением ТБФ

399

Рис. 1. Экстракция HNO3 (а-в) [12] и воды (г) [13] растворами ТБФ в С13 различной концентрации при 20°С. Точки -

эксперимент, линии - расчет по модели (здесь и далее).

Рис. 2. Сопоставление различных моделей экстракции HNO₃ 100%-ным (а) и 30%-ным (б) ТБФ.

данные ([4]; [24], c. 43) по влиянию нитрата алюми-

грешность расчета не превышает 3-4%.

ния на экстракцию HNO₃ (рис. 5). Они показывают

Экстракция уранилнитрата

удовлетворительное совпадение расчетных и экспе-

из нейтральных растворов

риментальных значений коэффициентов распределе-

ния с погрешностью, не превышающей 8-10% при

Сопоставление экспериментальных и расчетных

концентрации HNO₃ менее 1 моль/л. При более вы-

данных по экстракции уранилнитрата из собственных

сокой кислотности и/или концентрации ТБФ по-

растворов трибутилфосфатом при его разбавлении от

400

Е. А. Пузиков и др.

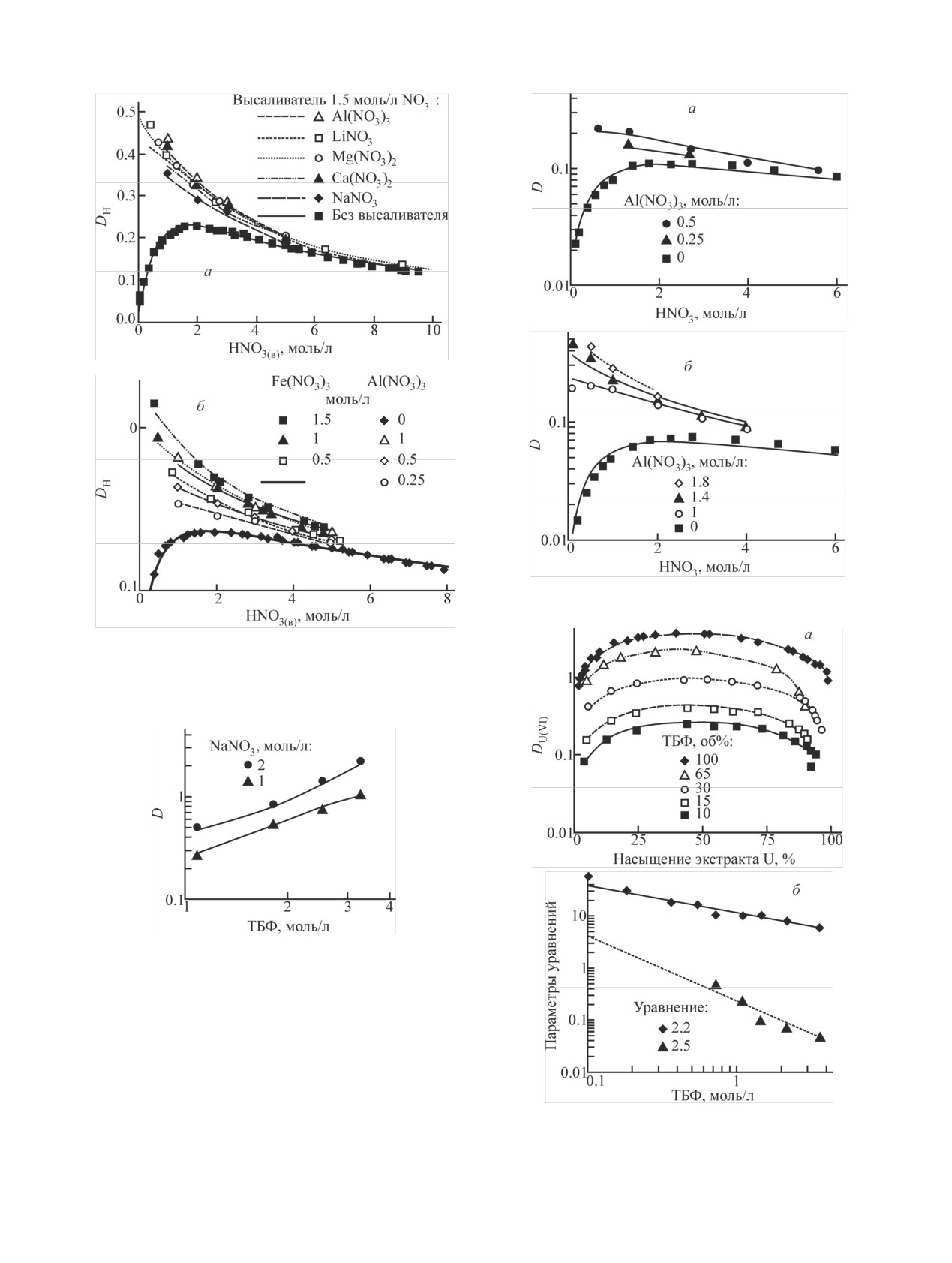
Рис. 5. Экстракция HNO₃ в 15%-ный (а) и 10%-ный (б) ТБФ в

присутствии нитрата алюминия. Температура 20°С.

Рис. 3. Экстракция HNO₃ в 30%-ный ТБФ в присутствии выса-

ливателей: (а) различные высаливатели при постоянной кон-

центрации нитрат-иона, (б) переменная концентрация высали-

вателей с трехзарядными катионами. Температура 20°С.

Рис. 4. Экстракция HNO₃ растворами ТБФ в предельных угле-

водородах различной концентрации в присутствии NaNO₃ при

постоянной ионной силе раствора ~3 моль/л ([24], c. 38). Тем-

пература 20°С.

100 до 10% (рис. 6, а) показывает их хорошее совпа-

дение.

Основной вклад в экстракцию уранилнитрата вно-

сит реакция образования дисольвата по уравнению

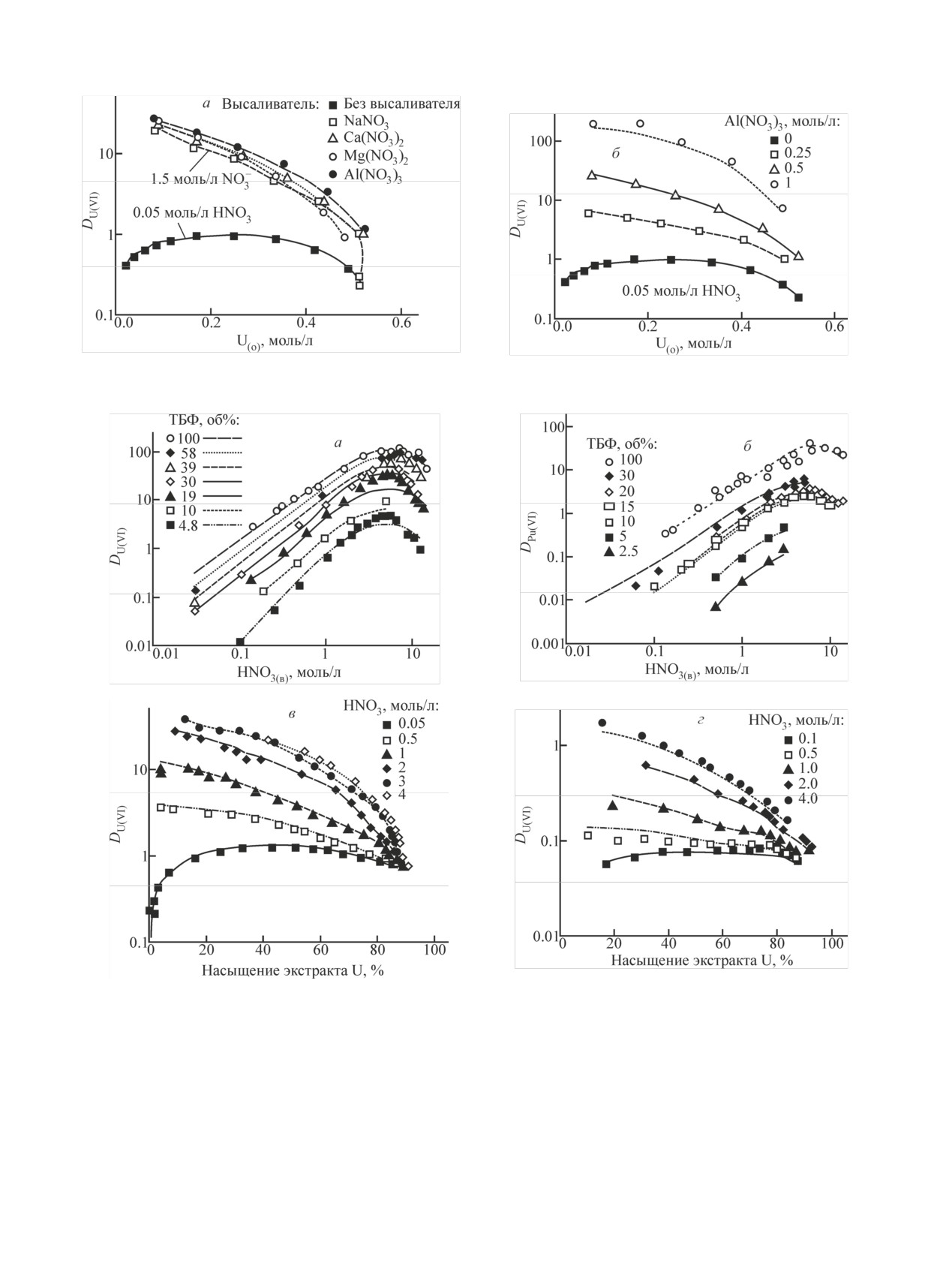
Рис. 6. Экстракция уранилнитрата из собственных растворов

2.2 в таблице (нумерация уравнений в таблице сохра-

трибутилфосфатом при различной его концентрации. а - зави-

нена в соответствии с работой [3]). При высокой кон-

симость D_U от насыщения экстракта, б - зависимость парамет-

центрации ТБФ, а, следовательно, и воды в органиче-

ров уравнений от общей концентрации ТБФ.

Использование унифицированной модели с разбавлением ТБФ

401

Рис. 7. Влияние различных высаливателей при постоянной концентрации нитрат-иона (а) и концентрации нитрата алюминия (б)

на экстракцию уранилнитрата в 30%-ный ТБФ из раствора 0.05 моль/л HNO₃.

Рис. 8. Влияние концентрации HNO₃ (а, б) и насыщения экстракта ураном (в, г) на экстракцию U(VI) (а, в, г) и Pu(VI) (б) в ТБФ

различной концентрации (а - микроконцентрации уранилнитрата, в - 40%-ный ТБФ, г - 2.7%-ный ТБФ). Температура 20°С.

ской фазе некоторый вклад вносит избирательная

гидролиз катиона уранила (реакция

2.1), однако

сольватация уранилнитрата этой водой (уравне-

вклад UO₂OH⁺ в суммарную экстракцию уранилнит-

ние 2.5), которая снижается с понижением концен-

рата расчетами не выявляется, вследствие чего ранее

трации ТБФ (рис. 6, б). При этом оказывается воз-

предложенное уравнение 2.3 [2] следует исключить.

можным рассчитать параметр а для обеих реакций,

В целом точность расчетов по модели по сравне-

что также отражено в таблице.

нию с работой [2] повысилась благодаря введению

При низкой кислотности возможен частичный параметра а.

402

Е. А. Пузиков и др.

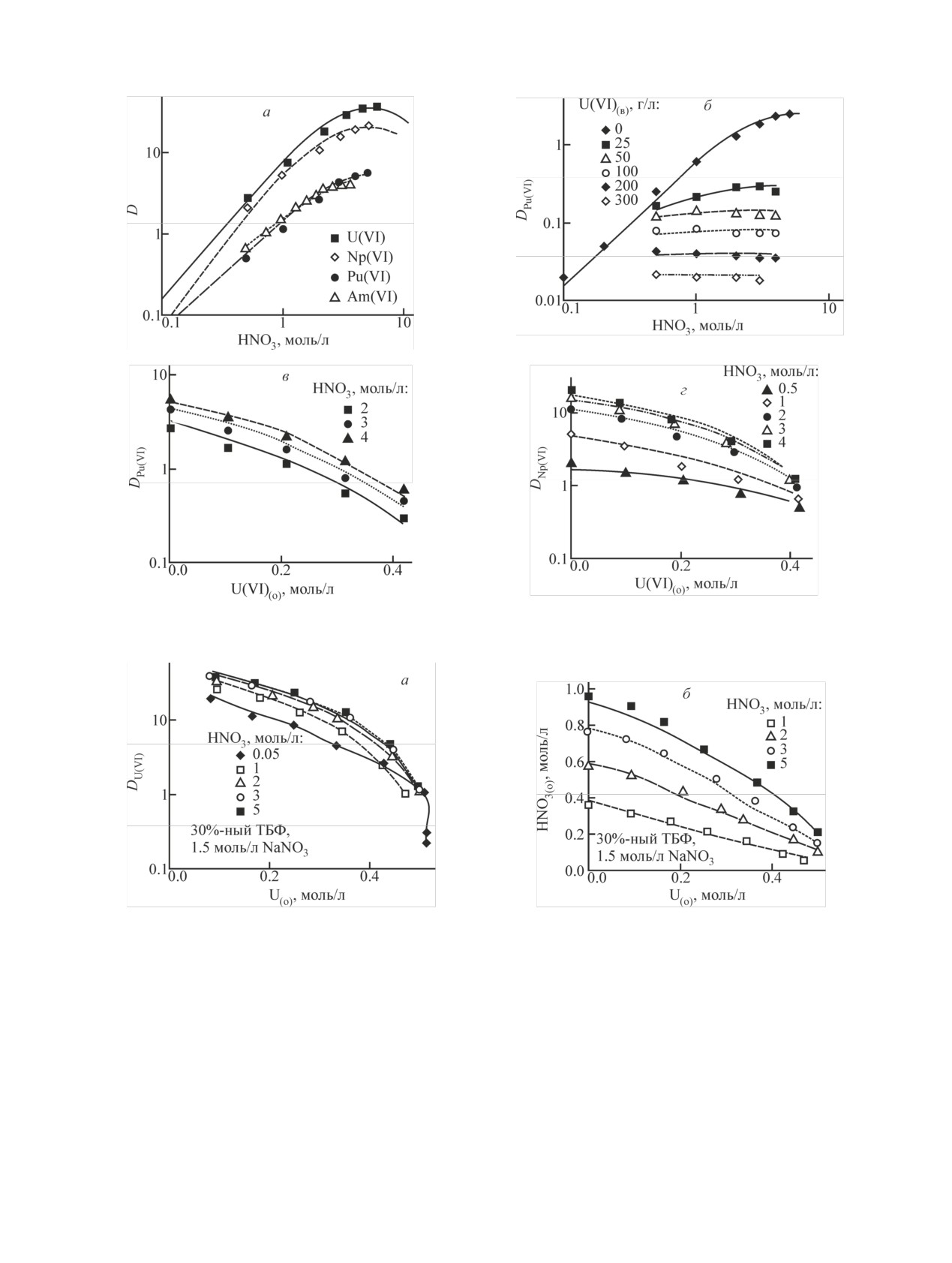
Рис. 9. Влияние HNO₃ (а, б) и уранилнитрата (в, г) на экстракцию An(VI) в 30%-ный ТБФ.

Рис. 10. Экстракция уранилнитрата (а) и HNO₃ (б) в присутствии 1.5 моль/л NaNO₃ в 30%-ный ТБФ. Температура 20°С.

В литературе отсутствуют систематические дан-

Экстракция актинидов(VI) из растворов

ные по экстракции уранилнитрата из нейтральных

азотной кислоты

растворов концентрированными растворами ТБФ.

Данные для 30%-ного ТБФ в условиях подавления

Данные рис. 8 и 9 свидетельствуют о том, что

гидролиза

(0.05 моль/л HNO₃) представлены на

предложенные уравнения реакций (см. таблицу) при

рис. 7. Параметры гидратации катионов высаливате-

использовании приведенных значений параметров а

лей приняты такими же, как и для экстракции кисло-

описывают с приемлемой точностью распределение

ты. Здесь также имеет место хорошее совпадение экс-

шестивалентных U, Np и Pu из растворов HNO₃ (0.1-

периментальных и расчетных данных по предложен-

10 моль/л) в диапазоне концентраций ТБФ от 2.7 до

ной модели.

100%. При этом влияние концентрации HNO₃ на экс-

Использование унифицированной модели с разбавлением ТБФ

403

тракцию макроколичеств уранилнитрата при кон-

[7] Sato T. // J. Inorg. Nucl. Chem. 1958. Vol. 6, N 4. P. 334-

337.

центрациях ТБФ выше 40 об% не могло быть оцене-

[8] Davis W., Mrochek J. // Solvent Extraction Chemistry / Eds

но ввиду отсутствия каких-либо экспериментальных

D. Dyrssen, J.-O. Liljenzin, J. Rydberg. Amsterdam: North-

данных.

Holland, 1967. P. 283-295.

[9] Bernstrom B., Rydberg J. // Acta Chem. Scand. 1957. Vol. 11,

Влияние насыщения органической фазы уранил-

N 7. P. 1173.

нитратом на распределение Np(VI) и Pu(VI) (рис. 9,

[10] Magon L., McKay H. A. C., Wain A. G. // J. Inorg. Nucl.

б-г) описывается без использования дополнитель-

Chem. 1974. Vol. 36, N 12. P. 3849-3851.

[11] Mincher B. J., Martin L. R., Schmitt N. C. // Inorg. Chem.

ных уравнений, что свидетельствует об отсутствии

2008. Vol. 47, N 15. P. 6984-6989.

взаимодействий между сольватами An(VI) и дисоль-

[12] Kamoshida M., Fukasawa T. // J. Nucl. Sci. Technol. 1996.

ватом уранилнитрата.

Vol. 33, N 5. P. 403-408.

[13] Davis W. // Nucl. Sci. Eng. 1962. Vol. 14, N 2. P. 159-168.

Совместная экстракция уранилнитрата и HNO₃ в

[14] Davis W., Mrochek J., Hardy С. J. // J. Inorg. Nucl. Chem.

присутствии высаливателей (рис. 10) описывается с

1966. Vol. 28, N 9. P. 2001-2014.

использованием тех же значений параметров гидра-

[15] Федоров Ю. С., Зильберман Б. Я. // Радиохимия. 1986.

T. 18, N 1. C. 33-37.

тации n, что и при их экстракции из собственных

[16] Наумов А. А., Голецкий Н. Д., Зильберман Б. Я., Мур-

растворов (таблица).

зин А. А. // Радиохимия. 2017. T. 59, N 6. C. 525-533.

[17] Puzikov E. A., Zilberman B. Ya., Fedorov Yu. S. et al. // Sol-

vent Extr. Ion Exch. 2015. Vol. 33, N 4. P. 362-384.

Список литературы

[18] Розен А. М., Решетько Ю. В., Зельвенский М. Я. // Атом.

энергия. 1974. T. 37, N 3. C. 187-193.

[1] Пузиков Е. А., Зильберман Б. Я., Голецкий Н. Д., Куди-

[19] Пузиков Е. А., Зильберман Б. Я., Федоров Ю. С. и др. //

нов А. С. // Радиохимия. 2019. T. 61, N 4. C. 324-333.

Радиохимия. 2004. T. 46, N 2. C. 136-143.

[2] Пузиков Е. А., Зильберман Б. Я., Федоров Ю. С. и др. //

[20] Кудинов А. С., Пузиков Е. А., Блажева И. В. и др. // Радио-

Радиохимия. 2013. T. 55, N 3. C. 236-241.

химия. 2017. T. 59, N 2. C. 127-134.

[3] ПузиковЕ. А., Зильберман Б. Я., Федоров Ю. С. и др. //

[21] Burns P. E., Hanson C. // J. Appl. Chem. 1964. Vol. 14, N 3.

Радиохимия. 2015. T. 57, N 2. C. 119-123.

P. 117-121.

[4] Пузиков Е. А., Блажева И. В., Зильберман Б. Я. и др. //

[22] Николотова З. И., Картащова Н. А. Экстракция ней-

Радиохимия. 2013. T. 55, N 4. C. 302-308.

тральными органическими соединениями / Под ред. А. М.

[5] Marcus Y. Critical Evaluation of Some Equilibrium Constants

Розена. М.: Атомиздат, 1976. Т. 1.

Involving Organophosphorus Extractants: IUPAC Additional

[23] Зильберман Б. Я., Рябков Д. В., Пузиков Е. А. и др. // Ра-

Publication. Part I: Organophosphorus Extractants. London:

диохимия. 2016. T. 58, N 3. C. 206-210.

Butterworth, 1974. P. 29-40.

[24] Николотова З. И. Экстракция нейтральными органиче-

[6] Землянухин В. И., Савоскина Г. П., Пушленков М. Ф. //

скими соединениями. Актиноиды: Справ. М.: Энерго-

Радиохимия. 1964. T. 6, N 6. C. 714-724.

атомиздат, 1987.