324

Радиохимия, 2019, т. 61, N 4, c. 324-333

Описание экстракции нитратов редкоземельных элементов

из слабокислых растворов концентрированными

растворами трибутилфосфата

^а Радиевый институт им. В. Г. Хлопина, 194021, Санкт-Петербург, 2-й Муринский пр., д. 28;

* e-mail: egor_puzikov@mail.ru

Получена 27.08.2018, после доработки 25.03.2019, принята к публикации 26.03.2019

УДК 546.65:542.61

На основе литературных данных разработана математическая модель экстракции нитратов РЗЭ (от

La до Lu, а также Y) в широком диапазоне концентраций в слабокислых ([H⁺] << [РЗЭ]) системах в ТБФ

с учетом его разбавления парафинами, в том числе в присутствии высаливателей. При этом предполага-

ется параллельное протекание нескольких реакций комплексообразования в водной и органической

фазах и нестехиометрического физико-химического взаимодействия компонентов. В модели учитывает-

ся образование трисольвата, тетрасольвата и гидратосольвата РЗЭ, а также соэкстракция цериевых и

иттриевых РЗЭ в виде ионной пары и эффект самовысаливания, обусловленный кажущейся гидратаци-

ей Ln³⁺ в водной фазе. Модель учитывает влияние нитратов аммония, натрия и алюминия в качестве

высаливателей. Описано также влияние температуры на экстракцию РЗЭ этих системах. Погрешность

расчета коэффициентов распределения ≤10%.

Ключевые слова: трибутилфосфат, экстракция, нитраты РЗЭ, высаливатели, моделирование.

DOI: 10.1134/S0033831119040075

Введение

гидрометаллургической переработки руд в присутст-

вии высаливателей с применением растворов ТБФ

В нашей обобщающей работе [1] была предложе-

высокой концентрации вплоть до 100%-ного ТБФ.

на математическая модель экстракции разбавленным

Для адекватного моделирования в области высо-

трибутилфосфатом (ТБФ) воды, азотной кислоты, а

ких концентраций ТБФ нами был изменен подход в

также нитратов шести- и четырехвалентных актини-

том плане, что за базовое состояние был принят

дов с применением мультиреакционного подхода.

100%-ный ТБФ с его разбавлением по аналогии с

Последний заключается в предположении, что ис-

разбавлением азеотропа HNO₃ в работе [3]. Такой

следуемые объекты находятся в различных химиче-

подход тем более логичен, что в перспективе позво-

ских формах в водной и органической фазах, равно-

лит описывать влияние на экстракцию различных по

весие между которыми определяет суммарный коэф-

природе разбавителей как разбавление одного и того

фициент распределения. При этом равновесные кон-

же вещества (ТБФ) в виде расходящихся лучей [4]

центрации компонентов рассчитывают путем совме-

от точки, соответствующей чистому веществу. Это

стного решения уравнений материального баланса с

позволит в перспективе описывать на единой основе

использованием закона действующих масс в концен-

влияние различных разбавителей на экстракцию эле-

трационном виде. В работе [2] была предложена

ментов разбавленным ТБФ, что ранее было сделано

двухуровневая система нумерации уравнений типо-

лишь в рамках модели «прямого счета» А. М. Розена

вых химических реакций, используемых в модели.

[5], созданную в свое время в условиях ограничен-

Модель была ориентирована на описание экстрак-

ных вычислительных ресурсов. Их возросшие воз-

ции компонентов из азотнокислых растворов отра-

можности позволили нам предложить модель экс-

ботавшего ядерного топлива (ОЯТ) с помощью раз-

тракции компонентов ОЯТ и азотной кислоты, бази-

бавленного ТБФ (преимущественно 30%-ного ТБФ в

рующуюся на представлении о множестве парал-

парафиновом разбавителе) и позволяла использовать

лельно протекающих реакций [1], но применительно

ее для сравнительно близких концентраций ТБФ

к разбавленному ТБФ.

(15-40% ТБФ), но не была ориентирована на более

В данной работе описываются эффекты высали-

высокие концентрации экстрагента.

вания и самовысаливания при экстракции РЗЭ из

Упомянутая модель не охватывала экстракцию

слабокислых водных растворов в 100%-ный ТБФ и

трехвалентных актинидов и продуктов деления, по-

при его разбавлении. В дальнейшем предполагается

скольку их экстрагируемость в 30%-ный ТБФ срав-

использовать такой унифицированный мультиреак-

нительно невелика, а основной массив данных по их

ционный подход для описания подобных равнове-

межфазному распределению относится к областям

сий в других системах.

Описание экстракции нитратов редкоземельных элементов

325

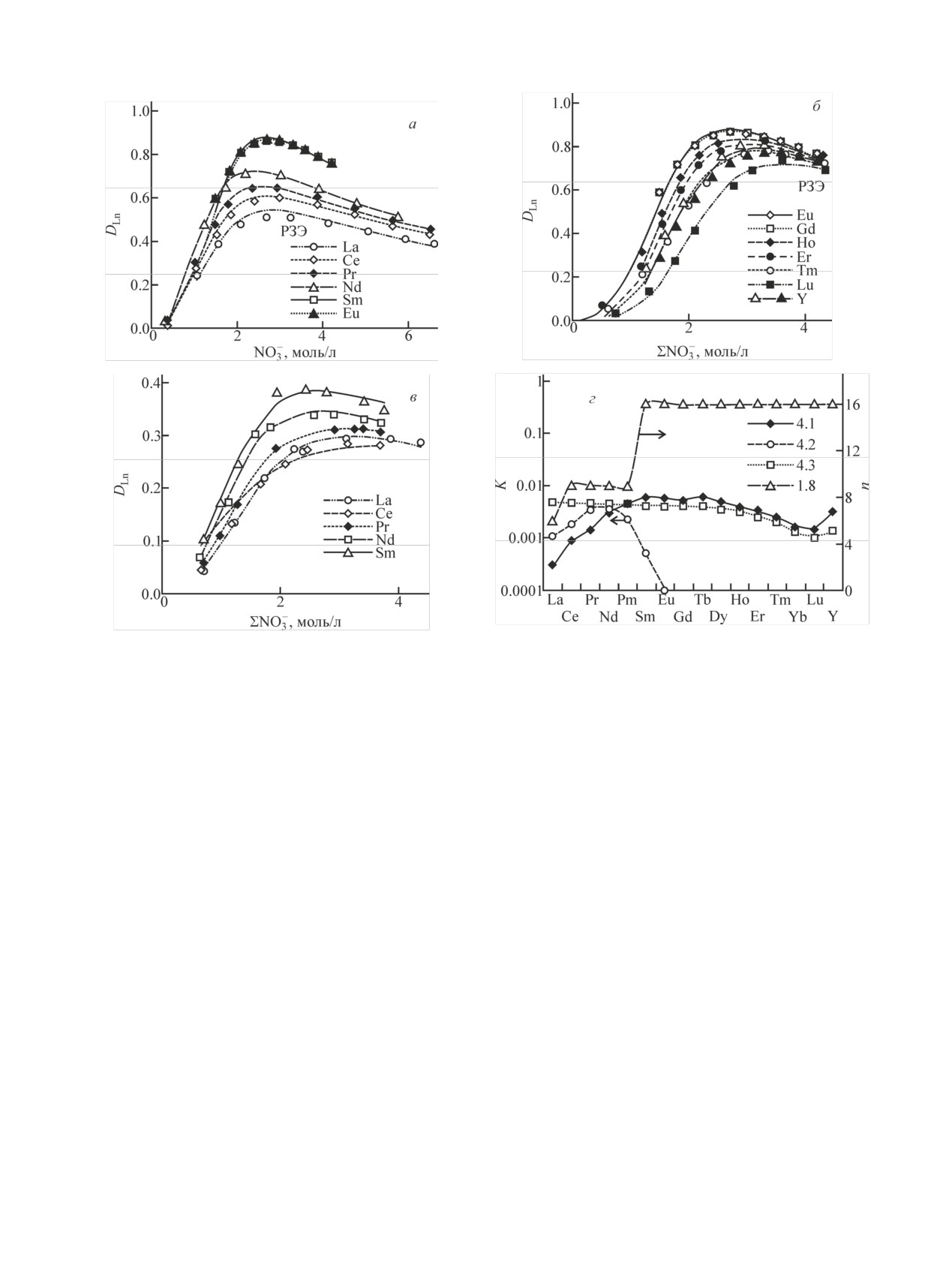
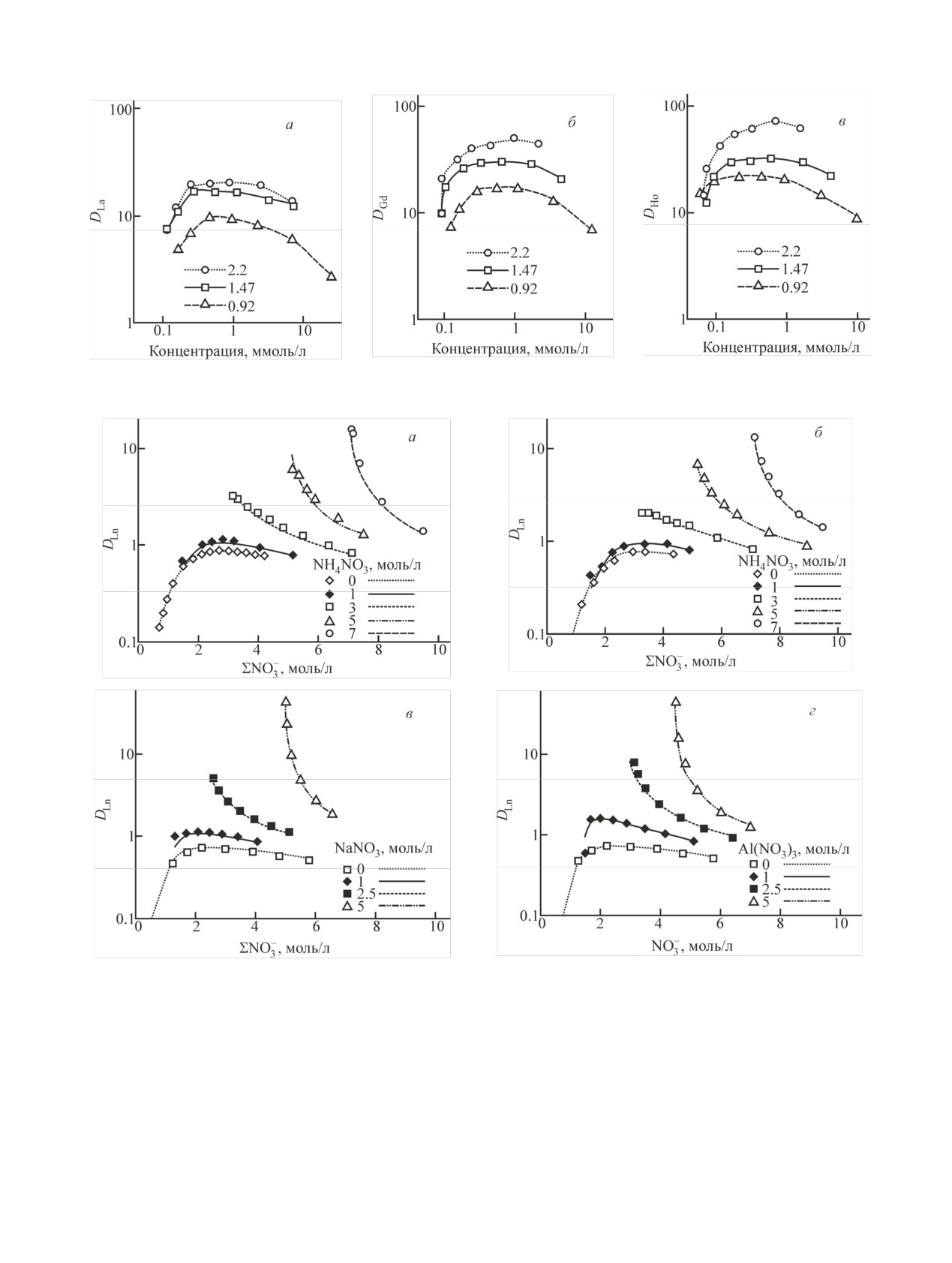
Рис. 1. Изотермы экстракции нитратов цериевых (а, в) и иттриевых (б) РЗЭ в 100%-ный ТБФ (а, б) и в 50%-ный ТБФ с С13 (в), а

также значения параметров уравнений в табл. 1 для каждого элемента (г). Здесь и далее: линии - расчет, точки - эксперименталь-

ные (литературные) данные.

Литературные базы данных приводятся по ходу

ем их нитратов был приближенно принят равным

изложения материала. Учитывая возможный гидро-

60 мл/моль.

лиз катионов РЗЭ в нейтральных растворах, обраба-

Экстракция нитратов индивидуальных РЗЭ

тывали данные в области pH не выше 2, где по лите-

из их слабокислых растворов

ратурным данным гидролиз катионов пренебрежимо

мал.

Основой для разработки модели послужили лите-

ратурные данные [6-8]. На рис. 1 приведены изотер-

Разработка унифицированной модели

мы экстракции нитратов индивидуальных РЗЭ из их

Проведенные оптимизационные расчеты показа-

водных растворов, подкисленных до pH 2, для кото-

ли, что существенной переработки ранее предло-

рых имеется достаточно данных по экстракции рас-

женной модели и метода расчета констант уравне-

творами 50 и 100 об% ТБФ. Для наглядности и со-

ний экстракционного равновесия [1] не потребова-

поставимости изотермы экстракции представлены

лось. Однако оказалось необходимым учесть отно-

как функции от концентрации нитрат-иона в водном

сительное изменение общей концентрации ТБФ

растворе, которая в данном случае представляет со-

(C^TBP/С_TBP) при экстракции, рассчитывая его с ис-

бой утроенную концентрацию РЗЭ. Литературные

пользованием мольных объемов компонентов орга-

экспериментальные данные нанесены на рисунок

нической фазы по уравнению 1.7 из работы [1]

точками, а линиями - результаты расчетов по разра-

C^TBP/C_TBP = (C_TBPV_TBP + C_разбV_разб)/(C_TBPV_TBP + C_разбV_разб +

ботанной модели. При промежуточных и более низ-

ких концентрациях ТБФ достоверные данные отсут-

+ Y_H2OV_H2O + Y_HV_H + Y_LnV_Ln),

ствуют. Наибольший объем информации относится к

где Y - концентрация компонента в органической

европию, который занимает среднее положение в

фазе; V - мольные объемы, мл/моль: ТБФ - 274,

ряду РЗЭ. К сожалению, такие данные, как правило,

парафиновый разбавитель C13 - 228, H₂O - 18,

не охватывают область высококонцентрированных

HNO₃ - 42. В случае экстракции РЗЭ мольный объ-

растворов [>1.5 моль/л Ln(NO₃)₃].

326

Е. А. Пузиков и др.

Таблица 1. Систематизированные уравнения математической модели экстракции трехвалентных РЗЭ в ТБФ и при

его разбавлении парафинами. Параметр а отражает влияние общей концентрации ТБФ, параметр b - влияние темпе-

ратуры на константы равновесий

Значение для РЗЭ

Уравнение^а

Параметр

1.7

V_Ln

~60 мл/моль

1.8

n_{Ln, 1.8}

K_4.1·10³

0.20

0.88

1.5

3.1

4.45

6.0

5.7

5.05

4.0

3.2

2.7

1.6

1.0

2.9

-0.48

4.1

1.7

1.6

1.5

1.4

1.3

1.2

2.2

K_4.2·10³

1.1

2.0

3.5

3.6

2.0

0.5

0.1

-0.57

4.2

2.2

3.5

3.6

3.2

K_4.3·10³

5.0

4.9

4.7

4.6

4.5

4.2

4.0

3.6

3.3

2.5

2.1

1.3

1.0

1.4

-3.3

4.3

3.2

2.3

1.8

1.2

1.1

1.0

0.8

0.7

0.5

0.6

0.5

0.4

1.9

4.4

K_4.4·10⁴

0.8

1.0

1.2

5.3

4.0

3.7

Нет данных

^а Уравнения: 1.7 - C^TBP/C_TBP = (C_TBPV_TBP + C_разбV_разб.)/(C_TBPV_TBP + C_разбV_разб + YH2OVH2O + Y_HV_H + Y_LnV_Ln), 1.8 - X^H

O = (1/MH

O)(1000ρ -

∑X_iM_i - X_HM_H) - ∑n_iX_i (M_i - молярная масса, г/моль; X_i - концентрация, моль/л), 4.1 - Me^3(aq) + 3NO_–(aq) + 3TBP_(s) = Me(NO₃)₃(TBP)_3(s),

4.2 - Me^3(aq) + 3NO_–(aq) + 4TBP_(s) = Me(NO₃)₃ (TBP)_4(s), 4.3 - Me^3(aq) + 3NO_–(aq) + mH₂O·TBP_(s) = Me(NO₃)₃(H₂O·TBP)m(s), 4.4 - Ln^3∑(aq) +

Ln3i(aq) + 6NO_–(aq) + 3TBP_(s) + 1.5H₂O = [Ln_∑(NO₃)₂(TBP)₃(H₂O)_1.5][Ln_i(NO₃)₄]_(s). Индекс (s) указывает на органическую фазу.

При описании экстракции индивидуальных РЗЭ

концентрации ТБФ C_TBP, а параметр a отражает угол

наклона зависимости логарифма константы от лога-

приходится принимать во внимание не только клас-

рифма относительной концентрации ТБФ (рис. 3),

сическое взаимодействие с образованием трисоль-

вата нитрата РЗЭ, описываемое уравнением

4.1

причем значения а совпадали для всех РЗЭ, для ко-

(табл. 1), но и образование тетрасольвата (уравне-

торых имелись соответствующие данные. Это дела-

ние 4.2), роль которого снижается по мере роста

ет модель потенциально пригодной для описания

атомного номера РЗЭ. Возможно, в этом взаимодей-

влияния различных разбавителей через параметр а в

ствии участвует вода. Вклад реакции 4.3 с участием

привязке к константе каждого базового уравнения

воды как растворителя заметен только при низкой

концентрации металла и не превышает 10%. По-

следнее обусловлено низкими коэффициентами рас-

пределения РЗЭ, выходящими за пределы области

достоверных значений. Существенную роль играет

также связывание воды ионами РЗЭ в водной фазе,

ранее введенное нами для высаливателей (урав-

нение 1.8); при этом эффективное число молекул

воды (n), координируемое ионом металла, сущест-

венно выше, чем в кристаллогидрате. Значения

плотности водной фазы (ρ) рассчитывали также с

учетом мольных объемов растворенных компонен-

тов [9]. Значения констант равновесий и параметров

нестехиометрических взаимодействий представле-

ны в сводной табл. 1 и на рис. 1, г, а примеры изме-

нения их вклада для нитратов Ce и Eu с ростом кон-

центрации элементов - на рис. 2. На нем видно, что

для Ce(NO₃)₃ характерна форма тетрасольвата, а

трисольват и гидратосольват существуют по краям

области насыщения, тогда как для Eu(NO₃)₃ во всем

диапазоне преобладает трисольват.

При разбавлении ТБФ за точку отсчета принима-

ются значения констант или параметров равновесия

для 100%-ного ТБФ, а экстракцию при его более

низких молярных концентрациях рассчитывали че-

рез его разбавление по уравнению lgK = lgK₁₀₀ -

alg(C_TBP/C₁₀₀), где lgK100 - константа экстракции

Рис. 2. Вклад различных реакций при экстракции нитратов

для 100%-ного ТБФ (C₁₀₀ = 3.65 моль/л - концентра-

Ce (а) и Eu (б) в 100%-ный ТБФ из их водных растворов раз-

ция чистого ТБФ), lgK - константа экстракции при

личной концентрации.

Описание экстракции нитратов редкоземельных элементов

327

Таблица 2. Составы концентратов РЗЭ

Номер

Высали-

Доля элемента в концентрате, мас%

Ссылка

концентрата

ватель

См. рис. 9, 10 в [11]

8.8

0.85

0.35

[11]

См. рис. 11 в [11]

52.7

1.7

1.0

0.4

0.2

14.4

2.6

18.6

16.4

1.8

21.8

4.6

31.7

7.6

15.4

0.1

[12, 13]

6.66

2.43

9.35

1.82

11.6

2.17

6.32

0.24

0.45

0.35

58.6

10.8

0.72

5.43

0.63

82.5

[18]

NH₄NO₃

0.5

0.3

0.2

равновесия. По смыслу он подобен коэффициенту

активности сольвата металла [10], если принять чис-

тый экстрагент за своего рода стандартное состоя-

ние, несмотря на его пребывание в виде жидкости, с

тем отличием, что эффект смешения сухих экстра-

гента и разбавителя не принимается во внимание,

что значительно упрощает расчеты.

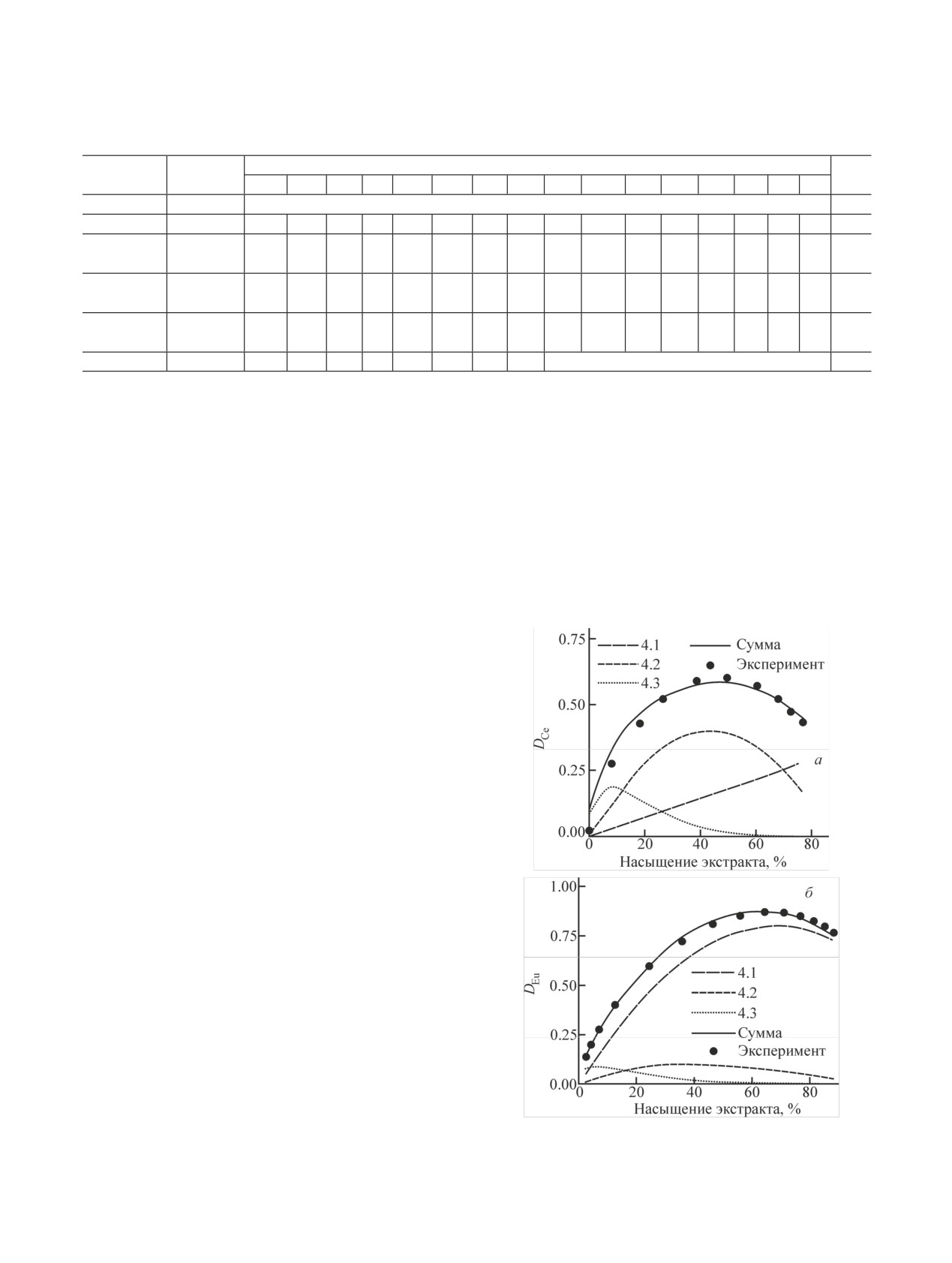
Экстракция нитратов РЗЭ из их концентратов

Более сложным случаем является экстракция

РЗЭ при их совместном присутствии в виде концен-

тратов, составы которых приведены в табл. 2. Име-

ется три группы таких данных [11-13], первая из

которых касается в основном цериевых земель, а

вторые две - иттриевых. Обработка этих данных

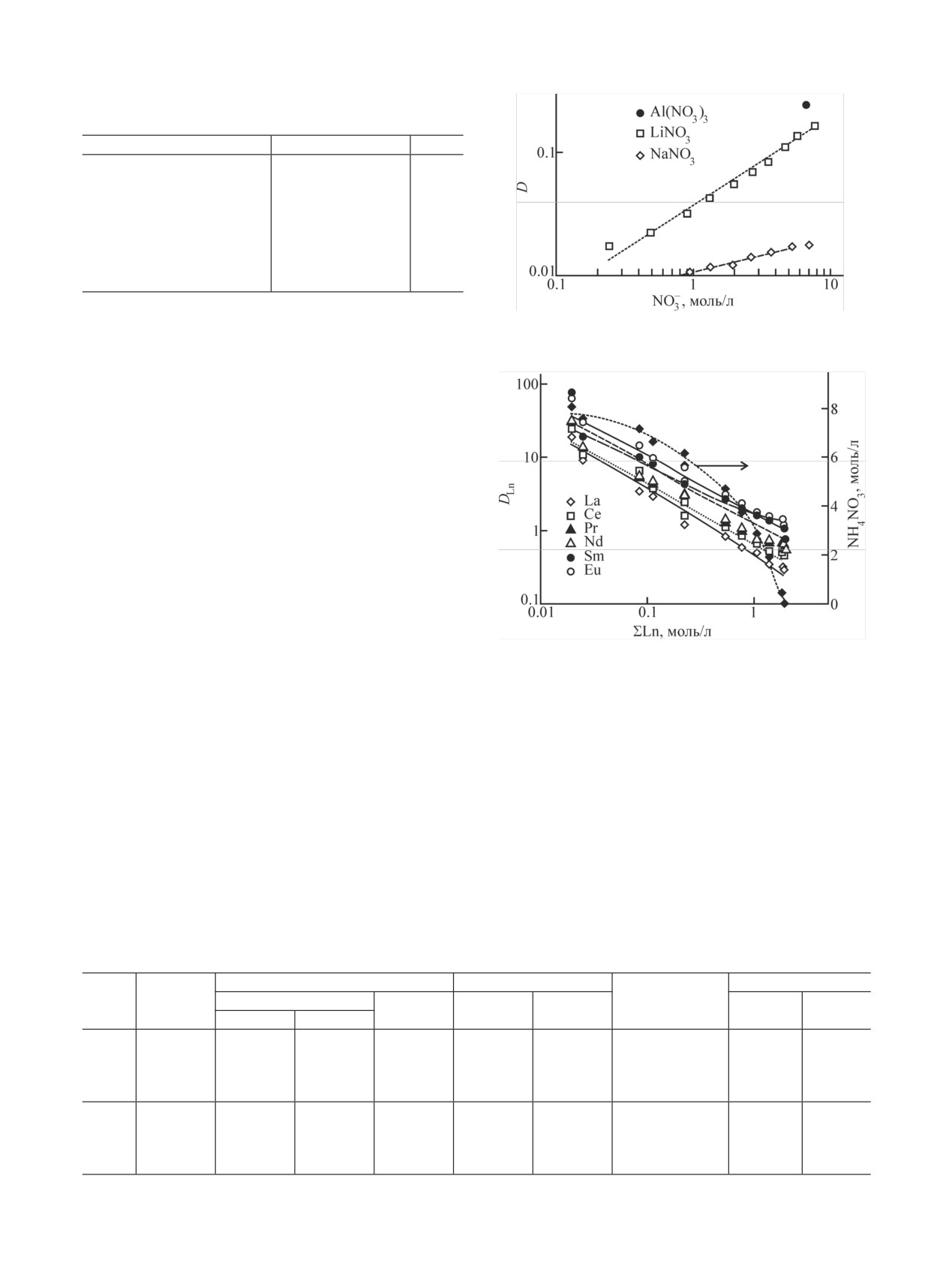
приведена на рис. 4 и 5. Совместное распределение

РЗЭ хорошо описывается приведенными выше

уравнениями и их константами для индивидуаль-

ных РЗЭ при их сопоставимых концентрациях. Од-

нако, когда элементы на стыке цериевой и иттрие-

вой подгрупп оказываются в роли микрокомпонен-

тов [11], а в концентрате лантан и церий составляют

более 50% (табл. 2), извлечение микрокомпонентов

в области концентраций, соответствующей макси-

мальным значениям коэффициента распределения,

оказывается заметно выше прогноза (рис. 4, в), что

указывает, по-видимому, на соэкстракцию РЗЭ се-

редины ряда и иттриевых РЗЭ (Ln(i)) с трисольватом

цериевых РЗЭ (Ln_(Σ)) в виде ионной пары с включе-

нием воды (табл. 1, уравнение 4.4). Этот эффект

Рис. 4. Зависимость коэффициентов распределения РЗЭ церие-

вой подгруппы от их суммарной концентрации в водной фазе

Рис. 3. Зависимость констант уравнений экстракции Eu от

при их экстракции в 100%-ный (а, в) и 70%-ный (б) ТБФ [11] при

концентрации ТБФ.

учете соэкстракции лантанидов (а, б) и без ее учета (в).

328

Е. А. Пузиков и др.

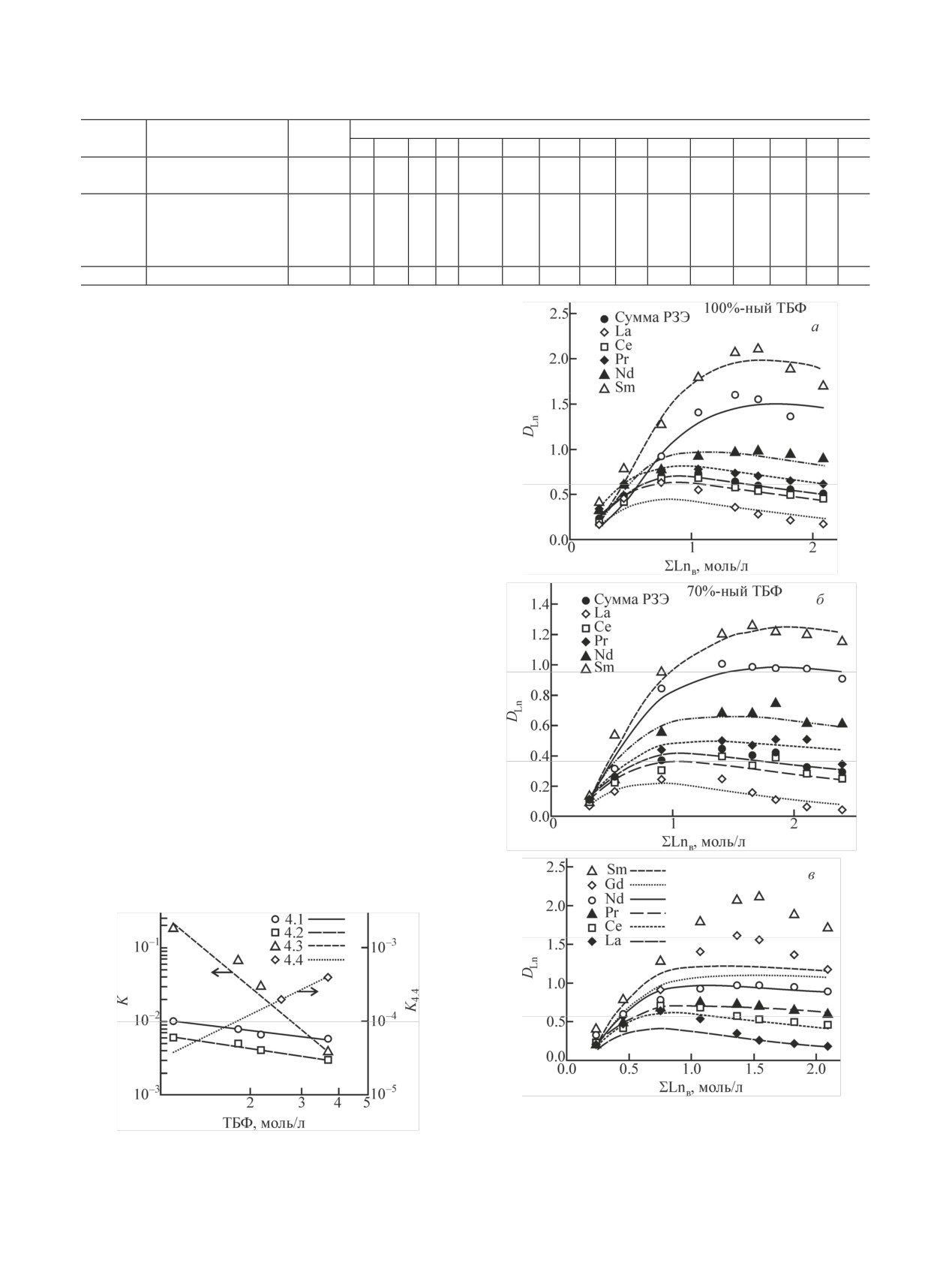
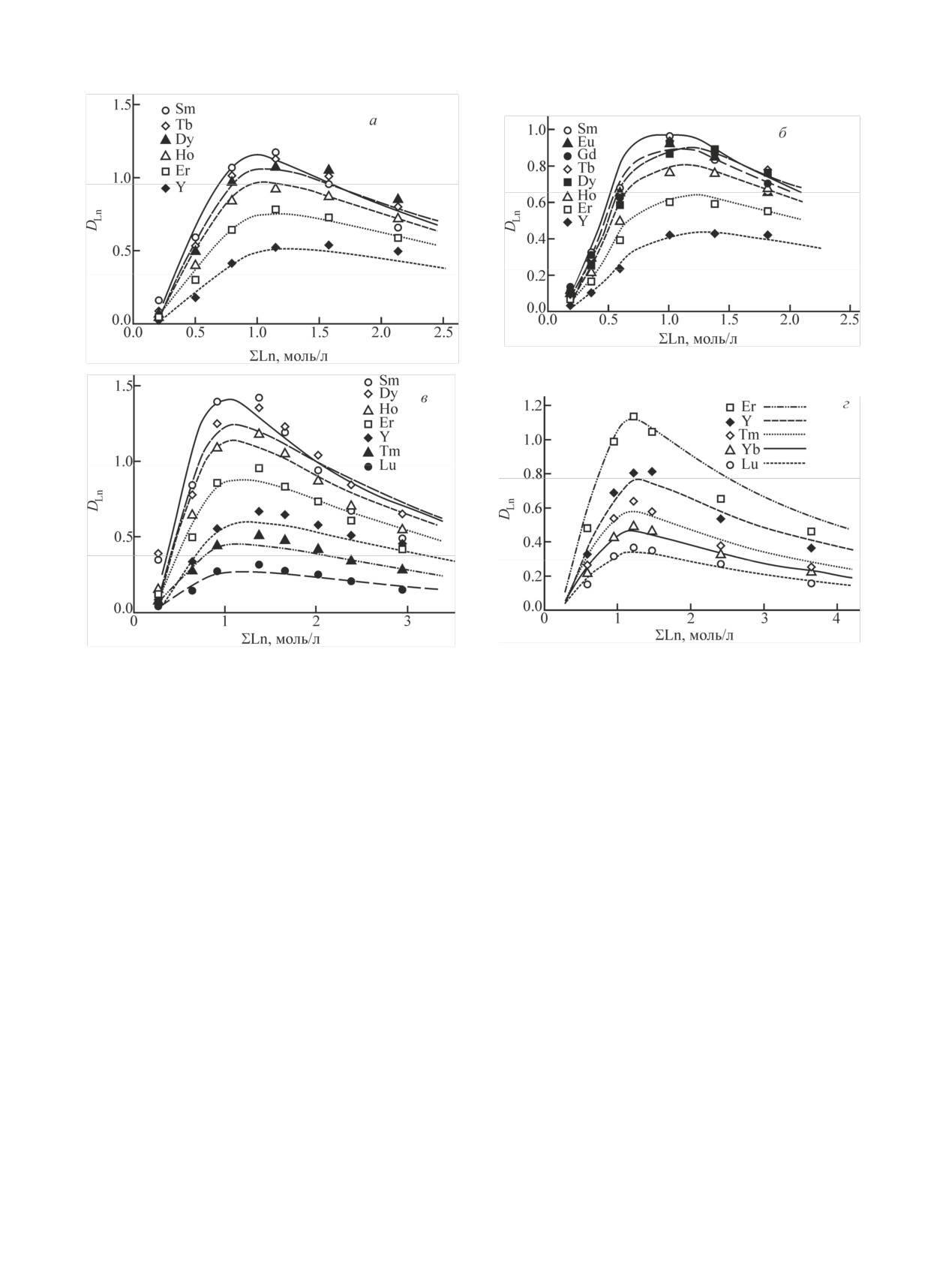
Рис. 5. Зависимость коэффициентов распределения РЗЭ иттриевой подгруппы от их суммарной концентрации в водной фазе [11,

12]. Номер концентрата: а - 1, б - 2, в - 3, г - 4.

требует уточнения с проведением тщательных до-

тов распределения РЗЭ в присутствии высаливате-

полнительных исследований с парами индивидуаль-

лей начинается с 0.002 моль/л Ln, тогда как при бо-

ных веществ для определения констант взаимодей-

лее низких концентрациях при указании микрокон-

ствий каждой пары. Для упрощения модели в дан-

центраций результат становится неопределенным.

ной работе рассчитаны значения K_4.4 для соэкстрак-

Совместное действие неэкстрагируемого нитрата

ции индивидуальных РЗЭ с суммой остальных бо-

высаливателя при наличии самовысаливания макро-

лее легких РЗЭ из водного раствора.

количеств РЗЭ выборочно отражено на рис. 7, а-г

[15-17]. В этих расчетах следует ориентироваться

Экстракция РЗЭ из растворов высаливателей

на суммарную концентрацию нитрат-иона в водной

Влияние высаливателей на экстракцию РЗЭ в

фазе и на способность высаливателей связывать в

ТБФ в чистом виде можно изучать только в области

ней воду, повышая тем самым кажущуюся концен-

их микроконцентраций, не вызывающих самовыса-

трацию экстрагируемого элемента (уравнение 4.6,

ливания. Граница этой области, по данным работы

табл. 1 и 3). Наибольшее влияние оказывает трехза-

[14], при экстракции нитратов лантана, гадолиния и

рядный нитрат алюминия, который связывает более

гольмия в 20-, 40- и 60%-ный ТБФ из раствора

6 молекул воды на 1 моль соли, тогда как одноза-

4 моль/л LiNO₃ приходится на диапазон их концен-

рядные катионы связывают по 1 молекуле воды.

траций 0.005-0.05 моль/л (рис. 6) в соответствии с

Эти выводы не могут быть подтверждены для дру-

общей тенденцией изменения коэффициента рас-

гих концентраций ТБФ, поскольку такие данные

пределения, который проходит через максимум при

практически отсутствуют.

0.0005-0.001 моль/л РЗЭ. Такой характер зависимо-

Особое внимание следует уделить экстракции

сти может быть связан с образованием плохо экст-

РЗЭ при высаливании их нитратом лития, посколь-

рагируемых полиядерных гидроксокомплексов с

ку в этом случае, по-видимому, имеет место кажу-

повышением концентрации РЗЭ. Пока надо принять

щаяся сверхстехиометрическая экстракция РЗЭ

во внимание, что область достоверных коэффициен-

(соотношение ТБФ : Ln в органической фазе оказы-

Описание экстракции нитратов редкоземельных элементов

329

Рис. 6. Влияние малых концентраций La (а), Gd (б) и Ho (в) в водной фазе на их экстракцию в 20-, 40- и 60%-ный ТБФ [14] из

4 моль/л LiNO₃. Цифрами обозначена концентрация ТБФ в органической фазе, моль/л.

Рис. 7. Зависимости коэффициентов распределения макроконцентраций Eu (а, г), Tm (б) и Nd (в) от суммарной концентрация

нитрат-иона при их экстракции 100%-ным ТБФ в присутствии нитратов аммония (а, б), натрия (в) и алюминия (г).

вается меньше 3, табл. 4). Указанный эффект усили-

(TBP)], аналогичной известной комплексной кисло-

вается с уменьшением радиуса иона РЗЭ и со сни-

те H_x[Ln(NO₃)3+x(TBP)_n] [18, 19]. При этом авторы

жением общей концентрации ТБФ. Так, при экс-

работы [11] предполагали, что n = 3, как и в ней-

тракции иттрия в 20%-ный ТБФ из 5.4 моль/л LiNO₃

тральном сольвате. На наш взгляд, n = 1, а значение

с полным насыщением экстракта иттрием отноше-

x зависит от концентрации катиона высаливателя, в

ние ТБФ : Y ≈ 1. Вероятно, такая картина может

частности H⁺ или Li⁺. При этом со снижением кон-

быть обусловлена преобладанием в экстракте ком-

центрации ТБФ достаточно круто падает концен-

плексной соли РЗЭ с литием [11] типа Li[Y(NO₃)₄·

трация экстрагированной воды, что резко снижает

330

Е. А. Пузиков и др.

Таблица 3. Параметры гидратации и экстракции выса-

ливателей на 1 моль/л нитрат-иона в уравнениях 1.8

Вариант уравнения

Высаливатель

n_Me,1.8

1.81

LiNO₃

2.1

1.82

NH₄NO₃

0.8

1.83

NaNO₃

1.0

1.84

Mg(NO₃)₂

1.85

Ca(NO₃)₂

1.5

1.86

Al(NO₃)₃

2.0

1.87

Fe(NO₃)₃

2.1

коэффициент распределения нитрата лития, кото-

Рис. 8. Экстракция высаливателей в 100%-ный ТБФ в отсутст-

рый, вероятно, экстрагируется в виде гидратосоль-

вие РЗЭ.

ватов [20, 21] (рис. 8).

В свою очередь, снижение экстрагируемости

нитрата лития при разбавлении ТБФ способствует

переходу упомянутой выше комплексной соли РЗЭ

и лития в экстракт из концентрированного раствора

высаливателя в водной фазе, где имеет место силь-

ное нитратное комплексообразование [18, 22].

«Сверхстехиометрическая» экстракция значи-

тельно слабее в случае цериевых РЗЭ, где она про-

является только в сильноразбавленном ТБФ, тогда

как в чистом ТБФ и при относительно небольшом

его разбавлении D_Ce заметно ниже расчетного для

аналогичной системы с нитратом алюминия, харак-

теризуемой примерной равным кажущимся коэффи-

циентом гидратации. Известно, что нитратное ком-

плексообразование у цериевых РЗЭ является более

Рис. 9. Зависимости коэффициентов распределения РЗЭ це-

слабым в сравнении с иттриевыми РЗЭ, и поэтому

риевой и переходной подгрупп в 100%-ный ТБФ от их сум-

марной концентрации в равновесной водной фазе в присутст-

сдвиг в сторону экстракции комплексного аниона

вии снижающегося количества нитрата аммония [23].

является для них менее выраженным [19]. К сожале-

нию, количественно эти эффекты не могут быть

описаны моделью в настоящее время ввиду ограни-

трата в 100%-ный ТБФ (табл. 2). Высаливателем

ченности экспериментальных данных.

являлся нитрат аммония, причем его концентрация

понижалась с ростом суммарной молярной концен-

Экстракция нитратов РЗЭ из их концентратов

трации РЗЭ. Результат обработки этих данных с ис-

в присутствии высаливателей

пользованием вышеуказанных уравнений вполне

В работе [23] приводится математическое описа-

удовлетворителен, что отражено на рис. 9. Данные

ние экспериментальных данных, полученных одним

для более сильных высаливателей [11] носят отры-

из авторов в дипломной работе, которая посвящена

вочный характер и не могут быть однозначно ин-

экстракции цериевых РЗЭ из соликамского концен-

терпретированы.

Таблица 4. Сопоставление расчетных и экспериментальных данных при экстракции нитратов Y и Ce(III) (M) в ТБФ

(разбавитель - бензол) на фоне 5.4 моль/л LiNO₃

C_TBP

Эксперимент

Расчет

Максимальная

TBP/M_(о)

общая,

C_M в фазе, моль/л

С_M(o),

концентрация

экспери-

расчет

моль/л

(в)

(о)

моль/л

[M(NO₃)₃(TBP)₃]

мент

3.65

1.19

1.31

1.10

1.17

0.98

1.17

2.68

3.01

2.56

1.19

0.85

0.92

0.81

0.68

0.82

2.89

3.03

1.83

1.17

0.87

0.74

0.57

0.49

0.58

2.02

3.07

0.73

1.22

0.65

0.54

0.22

0.18

0.23

1.07

3.15

3.65

0.88

0.72

0.81

1.05

1.19

1.17

4.90

3.34

2.56

0.88

0.56

0.64

0.72

0.82

4.37

3.40

1.83

0.88

0.48

0.55

0.51

0.58

3.65

3.47

0.91

0.87

0.35

0.40

0.24

0.28

0.29

2.51

3.66

Описание экстракции нитратов редкоземельных элементов

331

Рис. 11. Изотермы экстракции нитрата неодима при различной

температуре (а) [17] и влияние температуры на константы рав-

новесий реакций 4.1-4.3 (б) при экстракции в 100%-ный ТБФ в

присутствии нитратов натрия или алюминия. На а через запя-

тую указаны концентрация NaNO₃ (моль/л) и температура (°С).

молярная концентрация ТБФ, однако емкость экст-

рагента по лантану остается неизменной вследствие

снижения роли экстракции в форме тетрасольвата

(уравнение 4.2) при возрастании роли трисольвата

(уравнение 4.1) (рис. 10, б).

В присутствии высаливателей (нитраты натрия и

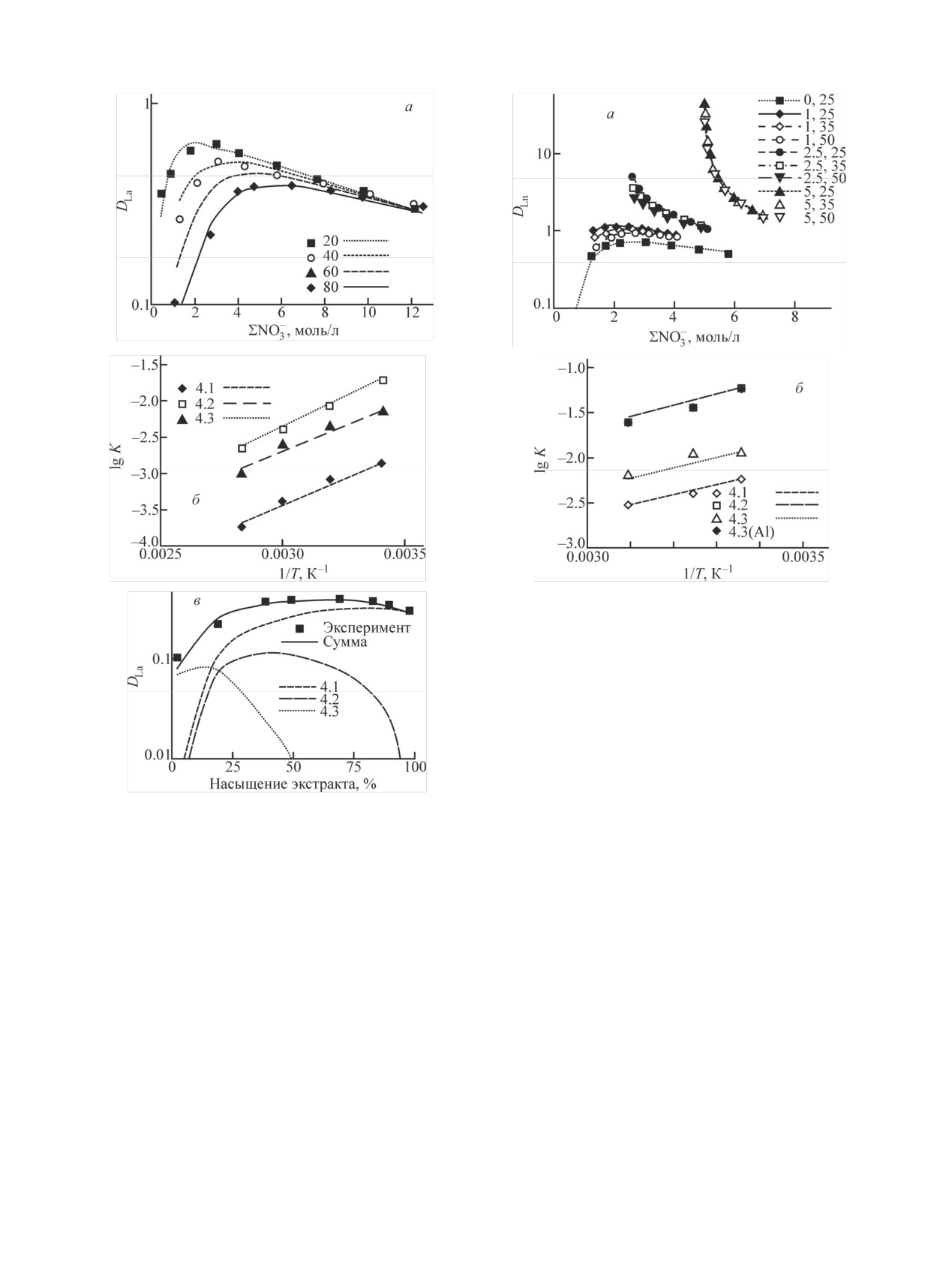
Рис. 10. Изотермы экстракции нитрата лантана при различной

алюминия) [16, 17] характер температурных зависи-

температуре (а) [24], влияние температуры на константы рав-

новесий реакций 4.1-4.3 (б) при экстракции в 100%-ный ТБФ,

мостей при экстракции цериевых РЗЭ не изменяется

а также расчетное распределение экстрагированных форм от

(рис. 11).

насыщения экстракта (в) при 80°С.

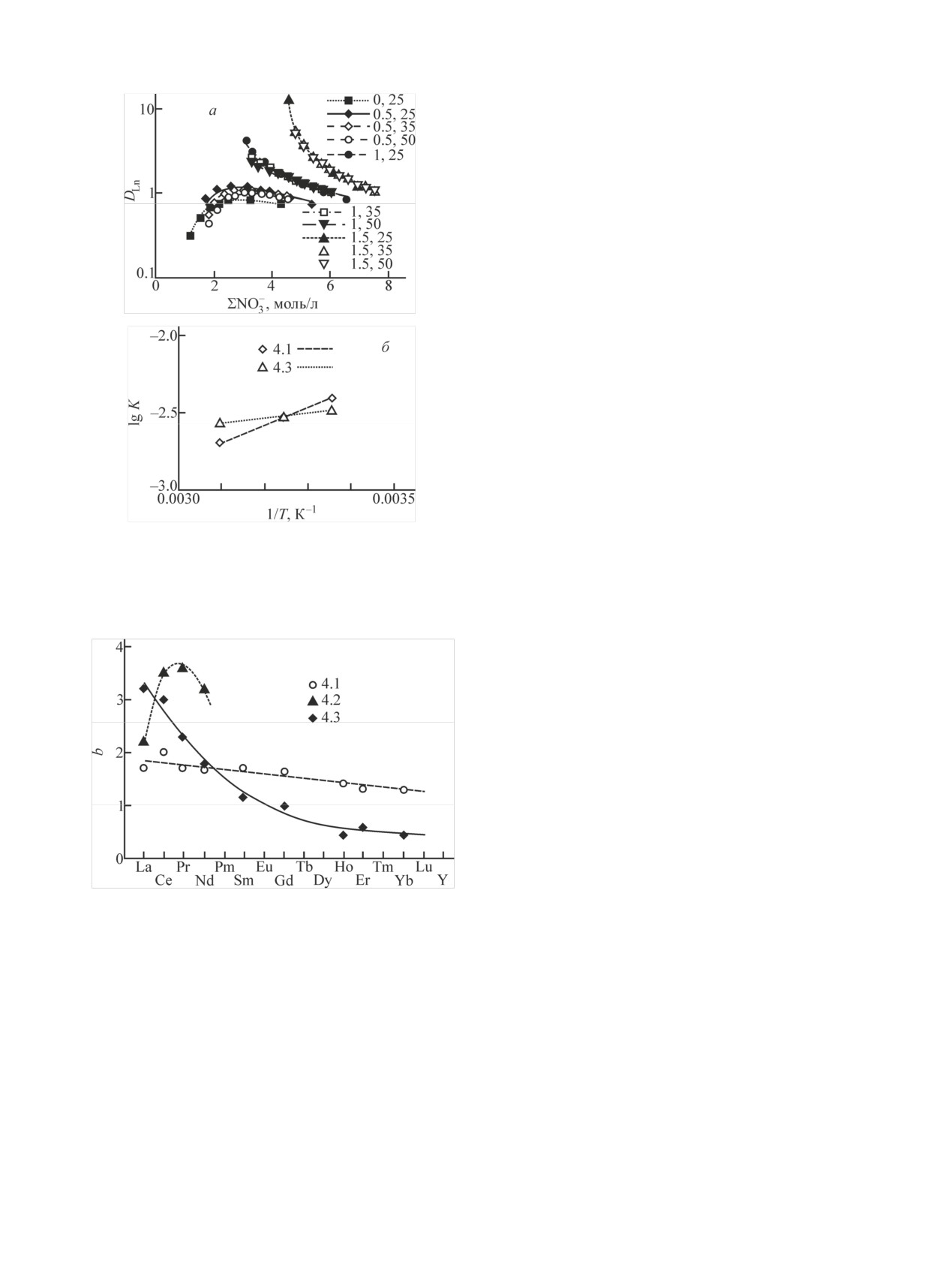
Для иттриевых РЗЭ прямые экспериментальные

данные приведены для гольмия (рис. 12). Однако

Влияние температуры на экстракцию РЗЭ

для остальных они могут быть восстановлены с ис-

из слабокислых растворов

пользованием так называемых термодинамических

Из данных, приведенных на рис. 10 [24], следует,

констант образования трисольвата РЗЭ при разных

что экстрагируемость лантана в ТБФ заметно падает

температурах, приведенных в работах [16, 17].

с ростом температуры, причем эффект снижается с

Обработка всех данных показывает (рис. 13), что

ростом концентрации элемента (рис. 10, а). Темпе-

значения коэффициента b для констант уравнения

ратурные зависимости логарифмов констант урав-

4.1 линейно снижаются от значения 1.9 до 1.3. Урав-

нений 4.1-4.3 (рис. 10, б) удовлетворительно описы-

нение 4.2, как указывалось выше, вырождается для

ваются уравнением [2]

иттриевых РЗЭ. Для цериевых РЗЭ значения коэф-

фициентов b для уравнения 4.2 лежат в интервале

lg K(t) = lg K₂₀[1 + b(t - 20)/(273 + t)].

2.2-3.5, проходя через максимум. Для констант

При этом с ростом температуры медленно снижа-

уравнения 4.3 это значение нелинейно падает с

ется плотность органической фазы и соответственно атомным номером РЗЭ в интервале 3.2-0.5 (рис. 13).

332

Е. А. Пузиков и др.

протекании большого числа равновесных взаимо-

действий одного компонента в водной и органиче-

ской фазах, причем эти взаимодействия связаны

уравнениями материального баланса по каждому

компоненту системы. В данной работе это описание

ограничено слабокислыми растворами нитратов

чистых РЗЭ и их смесей, а также присутствием

нейтральных нитратных солей в качестве высалива-

телей.

Показано, что экстракция макроконцентраций

РЗЭ (выше 0.005 моль/л) в слабокислой среде при

любой концентрации ТБФ описывается системой из

трех уравнений параллельно протекающих экстрак-

ционных взаимодействий с образованием трисольва-

та, тетрасольвата и гидратосольвата (уравнения 4.1,

4.2 и 4.3 соответственно) при учете кажущейся гид-

ратации РЗЭ и высаливателей в водной фазе с помо-

щью параметра уравнения 1.8. Уравнения примени-

мы в присутствии различных высаливателей (в част-

ности, нитратов аммония, натрия, кальция и алюми-

ния), за исключением нитрата лития, где возможно

образование солевых форм ацидокомплексов

(ионных пар) в обеих фазах. Преобладающим взаи-

Рис. 12. Изотермы экстракции нитрата гольмия при различной

модействием, характерным для всех РЗЭ, является

температуре (а) [16], а также влияние температуры на констан-

образование трисольвата и гидратосольвата, тогда

ты равновесий уравнений 4.1 и 4.3 (б) при экстракции в 100%-

ный ТБФ в присутствии нитрата алюминия. На а через запятую

как образование тетрасольвата заметно проявляется

указаны концентрация Al(NO₃)₃ (моль/л) и температура (°С).

лишь у первых РЗЭ цериевой подгруппы.

Одновременно с ростом номера элемента возрас-

тает склонность к экстракции в виде анионного ком-

плекса, что проявляется в случае соэкстракции ит-

триевых РЗЭ с превосходящим количеством церие-

вых РЗЭ (уравнение 4.4) и соэкстракции РЗЭ в раз-

личной мере с нитратом лития. Этот эффект подле-

жит прямой экспериментальной проверке с отдель-

ными парами РЗЭ. Вместе с тем, эффект экстракции

РЗЭ в виде анионного комплекса не доходит до их

димеризации в экстракте или соэкстракции с други-

ми нейтральными высаливателями.

Разбавление ТБФ парафинами (в принципе, лю-

бым разбавителем) описывается показателем а зави-

Рис. 13. Изменение температурного коэффициента b для урав-

симости логарифма константы реакции от логариф-

нений 4.1-4.3 по ряду РЗЭ.

ма относительной концентрации ТБФ.

Температурная зависимость констант равновесия

Для реакции 4.4 (соэкстракция иттриевых и церие-

описывается обычным уравнением для каждой реак-

вых РЗЭ) отсутствует база данных при различных

ции и каждого элемента с помощью параметра b,

температурах. Итоговые результаты отражены в

значение которого для базовой реакции 4.1 (образо-

сводной табл. 1.

вание трисольвата РЗЭ) медленно снижается по ряду

РЗЭ. Для уравнения 4.2 кривая ограничивается фак-

Заключение

тически четырьмя элементами (La-Nd) и характери-

На примере РЗЭ предложена и применена к ши-

зуется наличием максимума (как и для самой кон-

рокому массиву экспериментальных данных унифи-

станты), но далее вырождается сама реакция 4.2.

цированная математическая модель экстракции в

Применительно к уравнению 4.3 соответствующая

ТБФ и растворы, полученные его разбавлением. Мо-

кривая имеет монотонно падающий характер, обу-

дель базируется на представлениях о параллельном

словленный, по-видимому, относительным ростом

Описание экстракции нитратов редкоземельных элементов

333

роли экстракции РЗЭ в виде гидратосольвата с повы-

[5] Кудинов А. С., Пузиков Е. А., Блажева И. В. и др. // Радио-

химия. 2017. T. 59, N 2. C. 127-134.

шением температуры.

[6] Пяртман А. К., Копырин А. А. // Радиохимия. 1997. T. 39,

Зависимости коэффициентов распределения всех

N 2. C. 149-154.

РЗЭ от концентрации нитрат-иона (рис. 1) имеют

[7] Кудрова А. В. Фазовые равновесия в системах нитраты

редкоземельных металлов(III)-вода-три-н-бутилфосфат-

максимум при 2-3 моль/л NO_–, однако взаимное рас-

разбавители (экстрагенты) различных классов: Дис

положение и вид этих зависимостей для последова-

к.х.н. СПб.: СПбГТИ(ТУ), 2004. 211 с.

тельного ряда РЗЭ заметно отличаются от привыч-

[8] Bednarczyk L., Siekierski S. // Solvent Extr. Ion Exch. 1989.

ного вида таковых при экстракции микроконцентра-

Vol. 7, N 2. P. 273-287.

[9] Dash D., Kumar Sh., Mallika C., Mudali U. K. // J. Solution

ций РЗЭ из растворов HNO₃. Последние имеют мак-

Chem. 2015. Vol. 44, N 9. P. 1812-1832.

симум и минимум для РЗЭ цериевой группы, тогда

[10] Пушленков М. Ф., Шувалов О. Н. // Радиохимия. 1963.

как для РЗЭ иттриевой группы экстремумы сглажи-

T. 5, N 5. C. 536-543.

ваются и зависимость превращается в монотонно

[11] Корпусов Г. В., Ескевич И. В., Патрушева Е. Н. и др. //

возрастающую. При этом кривые для почти всех

Экстракция. Теория. Применение. Аппаратура / Под ред.

А. П. Зефирова. М., 1962. Вып. II. С. 117-140.

цериевых РЗЭ (начиная с празеодима) и для все ит-

[12] Пяртман А. К., Копырин А. А., Кескинов В. А., Солоду-

триевых РЗЭ пересекаются примерно в той же об-

хин С. С. // Радиохимия. 1992. T. 34, N 6. C. 39-47.

ласти 2-3 моль/л NO_–.

[13] Пяртман А. К., Копырин А. А., Кескинов В. А., Солоду-

хин С. С. // Радиохимия. 1992. T. 34, N 6. C. 48-55.

Суммарная погрешность расчета коэффициентов

[14] Прояев В. В., Копырин А. А., Бурцев И. В. и др. // Радиохи-

распределения ≤10%.

мия. 1987. T. 29, N 6. C. 763-767.

[15] Пяртман А. К., Копырин А. А., Солодухин С. С. и др. Деп.

Описание экстракции микроконцентраций РЗЭ и

ВИНИТИ N 1116-В91. 1990. 46 с.

ряда трансурановых элементов, заметно экстраги-

[16] Пяртман А. К., Копырин А. А., Шувалов А. Н. Математи-

руемых трибутилфосфатом, в том числе в присутст-

ческое и термодинамическое описание фазовых равнове-

вии HNO₃

и ее смешанных растворов с солевыми

сий в экстракционных системах, содержащих нитраты

высаливателями, будет дано в следующем сообще-

редкоземельных металлов(III) и иттрия(III), нитрат алю-

миния(III) и три-н.-бутилфосфат: Учеб. пособие. СПб.:

нии.

СПбГТИ, 2001. 36 с.

В дальнейшем планируется опробовать данный

[17] Пяртман А. К., Копырин А. А., Кескинов В. А., Шувалов А. Н.

подход к моделированию для описания экстракции

Деп. ВИНИТИ N 3611-В98. 1998. 36 с.

[18] Шека З. А., Крисс Е. Е., Сенявская Э. И. // Редкоземель-

других компонентов растворов отработавшего ядер-

ные элементы / Под ред. Д. И. Рябчикова. М.: Наука,

ного топлива и ряда других редких металлов, а так-

1963. С. 240-245.

же ряда веществ, вовлекаемых в технологические

[19] Михлин Е. Б., Корпусов Г. В. // ЖНХ. 1967. T. 12, N 6.

процессы их извлечения и разделения.

C. 1633-1637.

[20] McKay H. A. C., Healy T. V. // Progress in Nuclear Energy.

Ser. III: Process Chemistry. London: Pergamon, 1958. Vol. 2.

Список литературы

P. 546-556.

[21] Тебелев А. Г., Мелкая Р. Ф. // Радиохимия. 1976. T. 18,

[1] Puzikov E. A., Zilberman B. Ya., Fedorov Yu. S. et al. // Sol-

N 6. C. 864-869.

vent Extr. Ion Exch. 2015. Vol. 33, N 4. P. 362-384.

[22] Шмидт О. В., Зильберман Б. Я., Фёдоров Ю. С. и др. //

[2] ПузиковЕ. А., Зильберман Б. Я., Федоров Ю. С. и др. //

Радиохимия. 2002. T. 44, N 5. C. 428-433.

Радиохимия. 2015. T. 57, N 2. C. 119-123.

[23] Родыгина Л. С., Афонин М. А. // Тез. докл. V научно-

[3] Зильберман Б. Я., Рябков Д. В., Пузиков Е. А. и др. // Ра-

технической конф. «Неделя науки-2015» (25-27 марта

диохимия. 2016. T. 58, N 3. C. 206-210.

2015 г.) СПб.: СПбГТИ(ТУ), 2015. c. 185.

[4] Федоров Ю. С., Зильберман Б. Я., Поверкова Л. Я. // Ра-

[24] Михлин Е. Б., Михайличенко А. И., Вдовина Л. В. // Радио-

диохимия. 2000. T. 42, N 5. C. 417-422.

химия. 1981. T. 23, N 3. C. 347-353.