Письма в ЖЭТФ, том 117, вып. 11, с. 808 - 813

О возможности изготовления PT -симметричных оптических

димеров без поглощающего свет материала

А. А. Дмитриев⁺¹⁾, К. В. Барышникова⁺, М. В. Рыбин^+∗

⁺Физико-технический мегафакультет, университет ИТМО, 197101 С.-Петербург, Россия

^∗Физико-технический институт им. Иоффе РАН, 194021 С.-Петербург, Россия

Поступила в редакцию 30 марта 2023 г.

После переработки 17 апреля 2023 г.

Принята к публикации 28 апреля 2023 г.

Рассмотрен подход к созданию оптического димера частиц, работающих в спектральной области

вблизи дипольного резонанса, обладающего свойствами симметрии четность-время. Предполагается,

что обе частицы состоят из активной среды с одним и тем же показателем преломления и коэффици-

ентом экстинкции. Мы предлагаем ввести контраст усиления-потери путем изменения радиационных

потерь частиц за счет вариации их формы. Чтобы проиллюстрировать данный подход, мы рассмот-

рели димер, состоящий из заполненного и полого бесконечных цилиндров. Продемонстрировано, что

увеличение диаметра полости приводит к более сильному радиационному затуханию. После, мы нашли

параметры димера с исключительной точкой на вещественной частоте, в котором при увеличении кон-

траста усиление-потери появляются две вещественные собственные частоты.

DOI: 10.31857/S1234567823110022, EDN: dinfsx

За последнее десятилетие было проведено множе-

точках, необходимо использовать резонансные час-

ство исследований в области неэрмитовой фотоники

тицы, размер которых меньше или сравним с длиной

[1-4]. Связанная с неэрмитовостью системы контрин-

волны. В этом случае применение пространственно-

туитивная физика, которая проявляется, например,

структурированной накачки ограничено дифракци-

в вещественности спектра гамильтониана в системах

онным пределом, а для изготовления метаматериала,

с симметрией четность-время (PT ), и в вырождении

элементарная ячейка которого состоит из активной

(т.е. недиагонализуемости) гамильтониана в исклю-

среды и материала с поглощением, необходим слож-

чительных точках (EP), приводит к множеству опти-

ный технологический процесс.

ческих эффектов, таких как одномодовая лазерная

генерация в системе из двух резонаторов [5], одно-

направленная передача света без отражения [6, 7],

нарушение взаимности [8] и расщепление собствен-

ных частот по корневому закону при снятии вырож-

дения [9].

Данные эффекты были успешно продемонстриро-

ваны в системах, размеры которых значительно пре-

вышают длину волны, такие как связанные волно-

воды, связанные кольцевые и дисковые резонаторы

и плоские слоистые структуры. Неэрмитовость вво-

Рис. 1. (Цветной онлайн) Эскиз исследуемой системы -

дится в эти системы как потери и усиление - за счет

димера полого цилиндра и заполненного цилиндра

поглощения в среде и вынужденного излучения при

наличии накачки соответственно [10], - или же пу-

В данной работе рассматривается идея подбора

тем пространственно структурированной оптической

формы резонаторов, изготовленных из активной сре-

накачки активной среды [11]. Для создания неэрми-

ды, таким образом, чтобы ввести в систему контраст

товых метаповерхностей с уникальными свойствами,

усиление-потери за счет отличия в коэффициентах

основанными на PT -симметрии и исключительных

радиационного затухания, что позволит создать ме-

таповерхность с PT -симметрией из одной только ак-

¹⁾e-mail: alexey.dmitriev@metalab.ifmo.ru

тивной среды, работающей при равномерной накач-

808

Письма в ЖЭТФ том 117 вып. 11 - 12

2023

О возможности изготовления PT -симметричных оптических димеров...

809

ке. Чтобы продемонстрировать применение данного

значением основного уравнения системы вместо час-

подхода, мы рассмотрели простейшую систему, пред-

тоты.

ставляющую собой димер, изображенный на рис. 1,

Вторая сложность связана с наличием радиаци-

состоящий из бесконечного цилиндра из диэлектри-

онных потерь, что делает потери и связь нераздели-

ческой усиливающей среды и бесконечного же поло-

мыми. В волноводных структурах, таких как резо-

го цилиндра из того же материала. Исследован слу-

наторы на модах шепчущей галереи, потери на из-

чай ТЕ-поляризации, в которой вектор магнитного

лучение обычно незначительны, при этом основным

поля ориентирован вдоль осей цилиндра. Показано,

каналом потерь обычно является рассеяние либо по-

что радиационные потери усиливаются при наличии

глощение, что позволяет исследовать систему свя-

полости, что обеспечивает возможность достижения

занных резонаторов при помощи двухуровневой мо-

контраста усиление-потери в димере из одного ма-

дели. Напротив, когда размер резонаторов сравним с

териала. Также была найдена геометрия димера, со-

длиной волны, радиационные потери и связь между

стоящего из цилиндра и полого цилиндра, реализую-

резонаторами остаются неразделимы [13].

щего режим исключительной точки (EP), и исследо-

Несмотря на эти сложности, двухуровневая мо-

ваны его собственные частоты и спектры рассеяния

дель может быть выведена для данной системы при

вблизи EP.

помощи подхода, основанного на теории многократ-

Фотоника в системах с PT симметрией и исклю-

ного рассеяния для связанных фотонных резонато-

чительными точками традиционно изучается в рам-

ров, работающих на дипольном резонансе Ми, одна-

ках хорошо известных из квантовой электродинами-

ко эффективный гамильтониан H оказывается за-

ки в резонаторе (КЭД-р) неэрмитовых двухуровне-

висимым от собственного значения [13]

вых моделей путем сопоставления “уровней” локали-

[

(

)]

ω-ω_c

iΓ_cH⁽¹⁾

зованным возбуждениям в резонаторах или волно-

ωI - H =

(_˜

)

(1)

iΓ_hH⁽¹⁾

ω-ω_h

водах [12]. Системы, размеры которых значительно

превышают длину волны, были всесторонне изуче-

Здесь ω - комплексная собственная частота диме-

ны и хорошо описываются этими моделями. Однако,

ра, ω_c,h - полюса рассеяния каждого рассеивателя

несмотря на простоту двухуровневой модели, стро-

димера (цилиндра и полого цилиндра) по отдель-

гое рассмотрение лежащей в ее основе задачи о рас-

ности, Γ_c,h - соответствующие силы осцилляторов,

пространении электромагнитных волн часто оказы-

H⁽¹⁾⁰(x) - функция Ханкеля первого рода, описыва-

вается довольно сложным. Причина этой сложности

ющая дипольное поле в двумерном пространстве, c -

заключается в том, что, в отличие от КЭД-р, где свя-

скорость света, а d - расстояние между центрами ци-

заны разные типы частиц (например, возбужденные

линдров.

электрон и фотон являются “уровнями”, а связь осу-

Для описания электромагнитных волн вокруг ци-

ществляется посредством межуровневых квантовых

линдров мы используем базис мультиполей, постро-

переходов), в системах связанных оптических резо-

енных на функциях Бесселя и Ханкеля. В этом слу-

наторов, и “уровни”, и связь - это по существу одно

чае рассеяние на цилиндре описывается коэффици-

и то же возбуждение, а именно, электромагнитное

ентами Лоренца-Ми. Для бесконечных цилиндров

поле. Из этого следуют два утверждения, каждое из

радиуса R_c коэффициент рассеяния Лоренца-Ми мо-

которых соответствует усложнению задачи.

жет быть выражен как

Первое из них заключается в том, что обмен энер-

гией между резонаторами осуществляется электро-

T^(c)21

a_c =

(2)

магнитными волнами, в которые входят запазды-

T^(c)

вающие потенциалы. Связь между резонаторами, в

где

свою очередь, также подвержена эффектам запаз-

дывания. В фотонике эффективный двухуровневый

T^(c)11 = H^(1)l(x)J^′l(ñx) - ñH^(1)′l(x)J_l(ñx),

гамильтониан определяется как оператор эволюции

T^(c)12 = H^(1)l(x)H^(1)′l(ñx) - ñH^(1)′l(x)H^(1)l(ñx),

системы во времени, и в данном случае он становит-

ся зависимым от своего же собственного значения,

T^(c)21 = ñJ^′l(x)J_l(ñx) - J_l(x)J^′l(ñx),

т.е. от частоты. Однако в случае, когда резонаторы

T^(c)22 = ñH^(1)l(ñx)J^′l(x) - H^(1)′l(ñx)J_l(x),

большие по сравнению с длиной волны, их можно

рассматривать как некое подобие волноводов, а в них

ñ = n + iκ - показатель преломления цилиндра, l -

благодаря трансляционной симметрии можно ввести

азимутальное число, которое в случае диполей равно

волновой вектор, который и становится собственным

нулю, и x = ωR_c/c.

Письма в ЖЭТФ том 117 вып. 11 - 12

2023

810

А. А. Дмитриев, К. В. Барышникова, М. В. Рыбин

Полюсы рассеяния - это точки, в которых знаме-

натель двумерного коэффициента дипольного рассе-

яния Лоренца-Ми равен нулю, т.е. T^(c)11(ω = ω_c) = 0.

Решая это уравнение относительно ω_c, получаем по-

казатель преломления ñ_c цилиндра, имеющего полюс

рассеяния на частоте ω_c = ω_c - iγ_c. После этого ко-

эффициент Лоренца-Ми можно аппроксимировать

вблизи полюса рассеяния выражением

-iΓ_c

a_c ≃

Γ_c = lim i(ω - ω_c)a_c,

(3)

ω-ω_c

ω→ωc

где Γ_c - сила осциллятора.

Далее рассмотрим полый цилиндр, который мож-

но исследовать как частицу ядро-оболочка. Приме-

няя граничные условия на границах раздела, мож-

но получить следующую формулу для коэффициен-

та рассеяния Лоренца-Ми полого цилиндра с оболо-

чечным показателем преломления ñ, внешним ради-

усом R_c и внутренним радиусом R_h

(c)

T₂

T^(h)11 + T^(c)22T^(h)21

a_h =

(4)

T^(c)11T^(h)11 + T^(c)12T^(h)

где

T^(h)11 = ñH^(1)l(ñξ)J^′l(ξ) - H^(1)′l(ñξ)J_l(ξ),

T^(h)12 = ñH^(1)l(ñξ)H^(1)′l(ξ) - H^(1)′l(ñξ)H^(1)l(ξ),

T^(h)21 = J^′l(ñξ)J_l(ξ) - ñJ_l(ñξ)J^′l(ξ),

T^(h)22 = J^′l(ñξ)H^(1)l(ξ) - ñJ_l(ñξ)H^(1)′l(ξ),

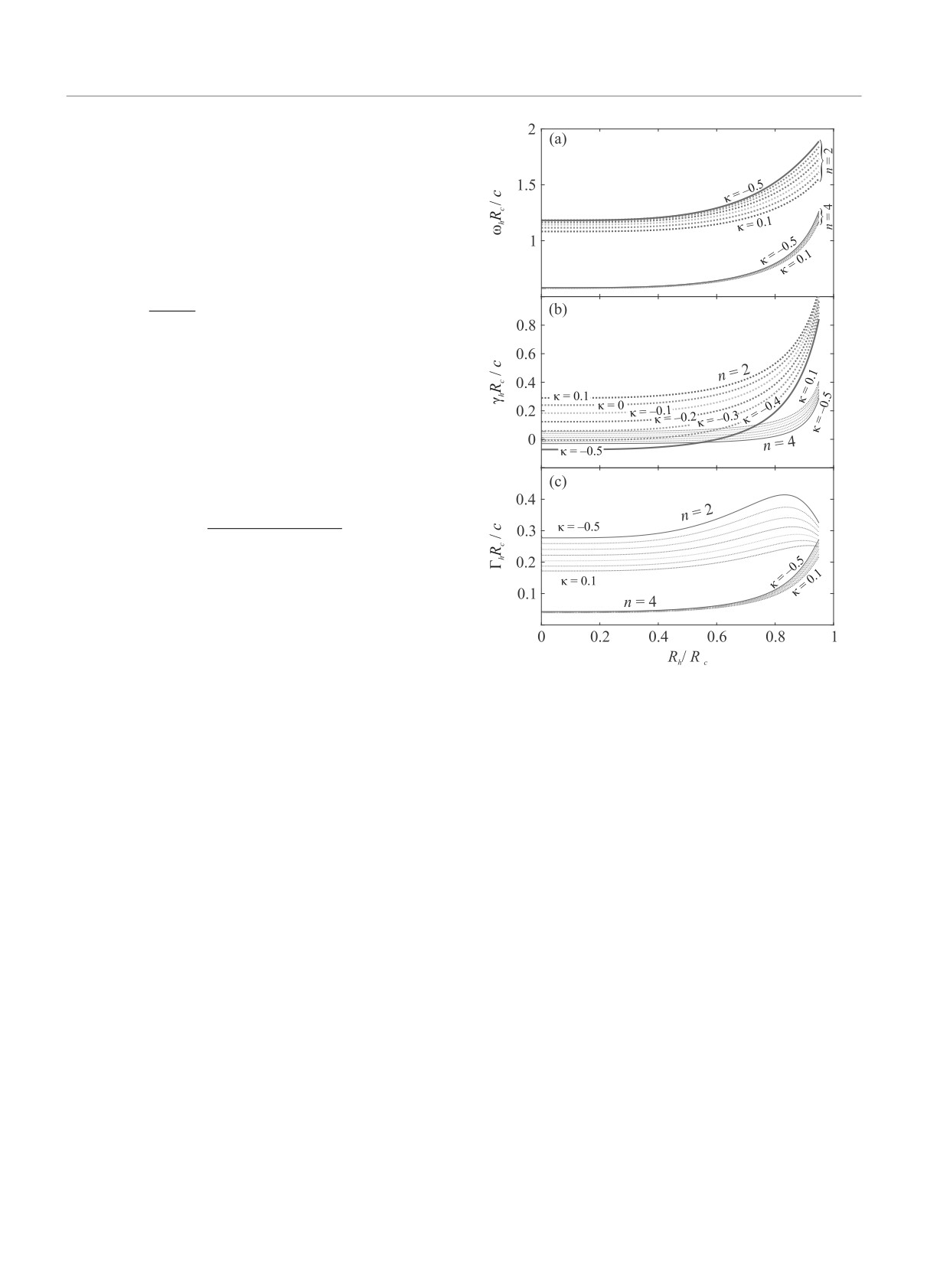
Рис. 2. (Цветной онлайн) Зависимости дипольного по-

люса рассеяния бесконечного полого цилиндра из ди-

и ξ = ωR_h/c.

электрика с комплексным показателем преломления

Чтобы найти полюс рассеяния, вновь приравняем

ñ = n + iκ от радиуса полости (R_h), по отношению

знаменатель коэффициента рассеяния к нулю:



к внешнему радиусу (Rc): резонансная частота (a), ко-

[

]

эффициент затухания резонансного состояния (b) и си-



T^(c)11T^(h)11 + T^(c)12T^(h)21



= 0.

(5)

ла осциллятора (c). Рассматривается ТЕ-поляризация,



ω=ω_h

показатели преломления n = 2 и n = 4, коэффициенты

Решая это уравнение относительно ω_h, можно най-

экстинкции κ = -0.5, -0.4, . . . , +0.1

ти показатель преломления оболочки ñ и радиус по-

лости R_h, которые соответствуют полому цилиндру,

имеющему полюс рассеяния на частоте ω_h = ω_h -iγ_h.

усиливающие среды (κ < 0, показаны сплошной и

В этом случае коэффициент рассеяния a_h можно ап-

штриховыми линиями), среды без потерь и усиле-

проксимировать вблизи полюса таким же образом,

ния (κ = 0, показано пунктиром) и поглощающие

как в формуле (3).

среды (κ > 0, показано штрихпунктиром). Во всех

Исследуем зависимость радиационных потерь от

трех случаях коэффициент затухания увеличивается

радиуса полости. На рисунке 2a, b показаны зависи-

при уменьшении объема среды, таким образом мож-

мости собственной частоты ω_h и коэффициента зату-

но утверждать, что это увеличение связано с радиа-

хания собственных состояний γ_h полых цилиндров с

ционными потерями.

различными показателями преломления от диамет-

Увеличение радиационных потерь сопровождает-

ра полости, а на рис. 2c приведены соответствующие

ся сдвигом частоты, как видно из рис. 2a. Посколь-

силы осцилляторов Γ_h. Видно, что потери увеличи-

ку нашей целью является ввести контраст усиления-

ваются с увеличением диаметра полости. Чтобы раз-

потери без сдвига частоты, к полому цилиндру сле-

личить увеличение радиационных потерь и уменьше-

дует применить масштабное преобразование, чтобы

ние объема усиливающей среды, были рассмотрены

компенсировать частотный сдвиг.

Письма в ЖЭТФ том 117 вып. 11 - 12

2023

О возможности изготовления PT -симметричных оптических димеров...

811

Теперь проанализируем собственные частоты ди-

в исключительной точке, введем симметричную от-

мера, состоящего из цилиндра и полого цилиндра.

стройку δω = δω - iδγ по частоте в полюсы рассе-

Гамильтониан зависит от своих собственных значе-

яния, определенные по формуле (8): ω_c = (1.19 +

ний, из-за чего уравнение на собственную частоту не

+0.0642i)c/R_c+δω/2 и ω_h = (1.19-0.161i)c/R_c-δω/2.

является квадратичным. Поэтому для определения

Будем искать собственные частоты ω_± = ω_± - iγ_±

собственных частот димеров необходимо найти нули

гамильтониана, как зависимость комплексной рас-

функции f(ω), определенной следующим образом:

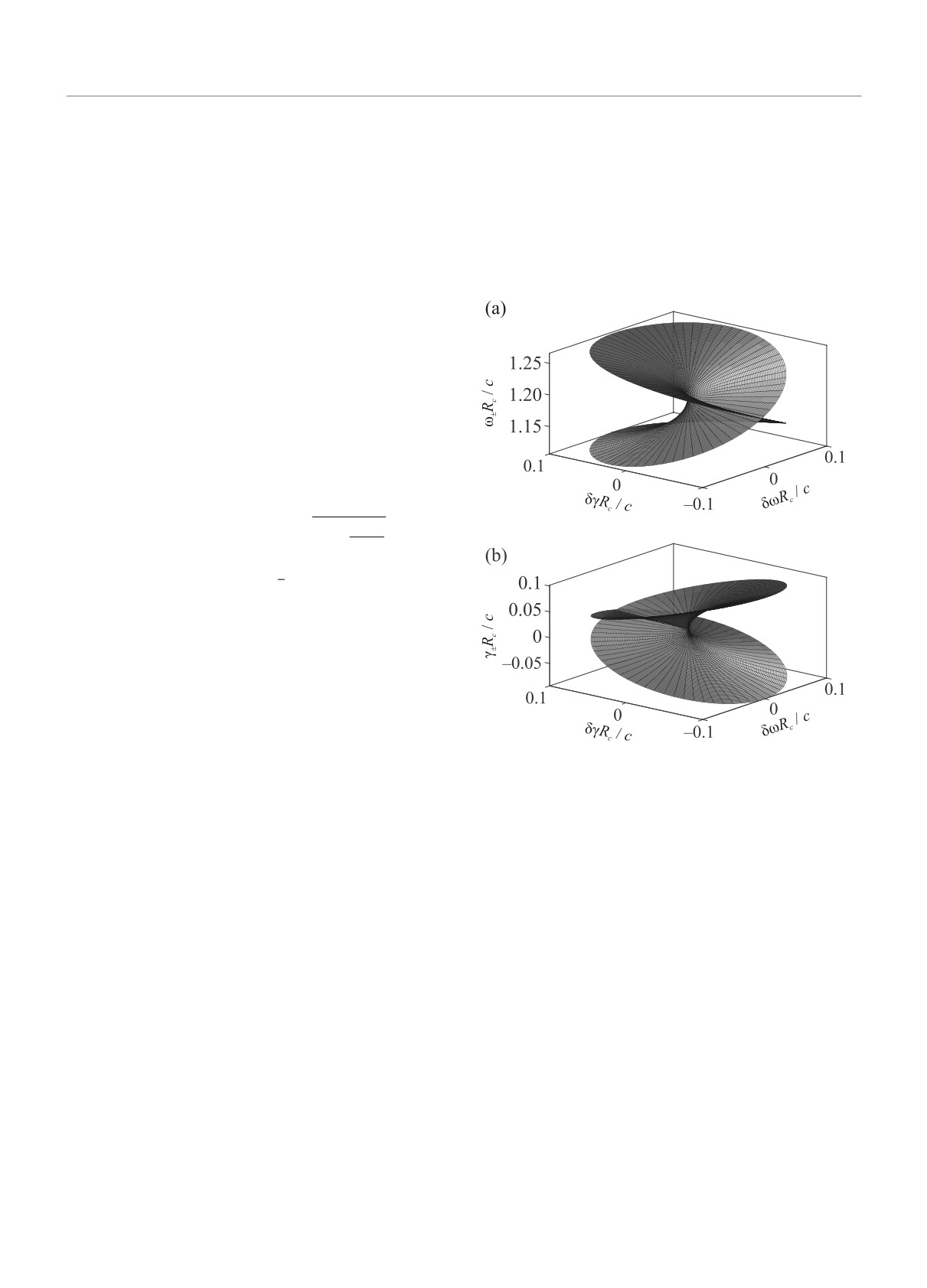
стройки δω. Полученные листы собственных частот,

показанные на рис. 3, демонстрируют топологию, по-

f(ω) = det(ωI - H ).

(6)

Наша задача - найти исключительную точку, т.е.

точку, в которой сливаются две или более собствен-

ных частот. Используя разложение Тейлора, нетруд-

но показать, что такая точка ω_EP удовлетворяет сле-

дующим условиям:

{

f(ω_EP) = 0,

(7)

f^′(ω_EP) = 0.

Решая эту систему уравнений относительно полюсов

рассеяния ω_c,h, приходим к следующему выражению

[

√

]

ω_c,h = ω_EP - AΓ_cΓ_h τ ± τ² +

(8)

Γ_cΓ_h

где A = H⁽¹⁾⁰(ω_EPd/c) и τ =^dc H⁽¹⁾¹(ω_EPd/c). Исполь-

зуя формулу (8), можно найти полюса рассеяния час-

тиц, которые, находясь на расстоянии d, образуют

димер, находящийся в режиме исключительной точ-

ки, т.е. имеющий только одну собственную моду на

частоте ω_EP, вместо пары собственных мод на раз-

личных частотах.

Пользуясь формулой (8), найдем полюсы рассея-

ния димера, который, как ожидается, будет иметь

исключительную точку на частоте ω = 1.186c/R_c

Рис. 3. (Цветной онлайн) Собственные частоты диме-

(что соответствует длине волны в вакууме 530 нм

ра, состоящего из полого и заполненного цилиндров,

и радиусу цилиндра R_c

= 100 нм). Также, выбе-

как зависимость комплексной отстройки δω - iδγ от

рем и зафиксируем расстояние между центрами рав-

исключительной точки: частота собственной моды (a),

ным d = 4.65R_c, таким образом, чтобы получить чи-

коэффициент затухания собственной моды (b)

сто мнимую разность между полюсами рассеяния,

необходимую для режима PT -симметрии. Форму-

добную римановой поверхности функции комплекс-

ла (8) в этом случае дает следующие полюса рас-

ного квадратного корня, что является характерным

сеяния: ω_c = (1.19 + 0.0642i)c/R_c, что соответствует

признаком исключительной точки [1, 3, 4]. Отме-

ñ = 1.99 - 0.488i и ω_h = (1.19 - 0.161i)c/R_c. Чтобы

тим также, что при изменении только контраста

приравнять частоты ω_c и ω_h, применим к полому ци-

усиление-потери (δω = 0) наблюдается поведение

линдру масштабное преобразование, таким образом,

по типу PT симметрии. Когда контраст усиление-

чтобы его внешний радиус стал равен R_s = 1.286R_c,

потери уменьшается по сравнению с его значением

где R_c - радиус цилиндра без отверстия. Радиус по-

в исключительной точке, димер имеет две чисто ве-

лости, соответствующий полюсу рассеяния в точке

щественные собственные частоты. Увеличение кон-

ω_h, равен R_h = 0.8R_s. Силы осцилляторов цилин-

траста усиление-потери, в свою очередь, приводит к

дров в этом случае оказываются равны Γ_c = 0.28 и

поведению, подобному разрушению PT симметрии,

Γ_h = 0.317.

с возникновением затухающей (γ_± < 0) и усилива-

Данные значения были подставлены в эффек-

ющейся (γ_± > 0) мод на одной и той же частоте

тивный гамильтониан в уравнении (1). Затем, что-

(ω_± = ω_EP). Заметим, однако, что сам димер не под-

бы проверить, действительно ли система оказалась

чиняется PT симметрии в строгом смысле этого сло-

Письма в ЖЭТФ том 117 вып. 11 - 12

2023

812

А. А. Дмитриев, К. В. Барышникова, М. В. Рыбин

ва: из-за отличающейся геометрии рассеивателей (за-

полненный и полый цилиндр), композиция преобра-

зований четности и инверсии времени дает систему,

отличную от изначально рассматриваемого димера.

Наконец, рассмотрим спектры рассеяния на ди-

мере из активной среды с показателем преломления

n = 1.99 и коэффициентом экстинкции κ = -0.488,

состоящем из цилиндра радиусом R_c и полого цилин-

дра с внешним радиусом R_s = 1.286R_c. Для получе-

ния спектров рассеяния мы используем описанную

в литературе теорию многократного рассеяния [13-

24], рассматривая только дипольный вклад. Возбуж-

дение представляет собой плоскую волну с направле-

нием падения, перпендикулярным плоскости, прохо-

дящей через оси цилиндров. Так как димер состоит

из активной среды и находится в режиме излучения,

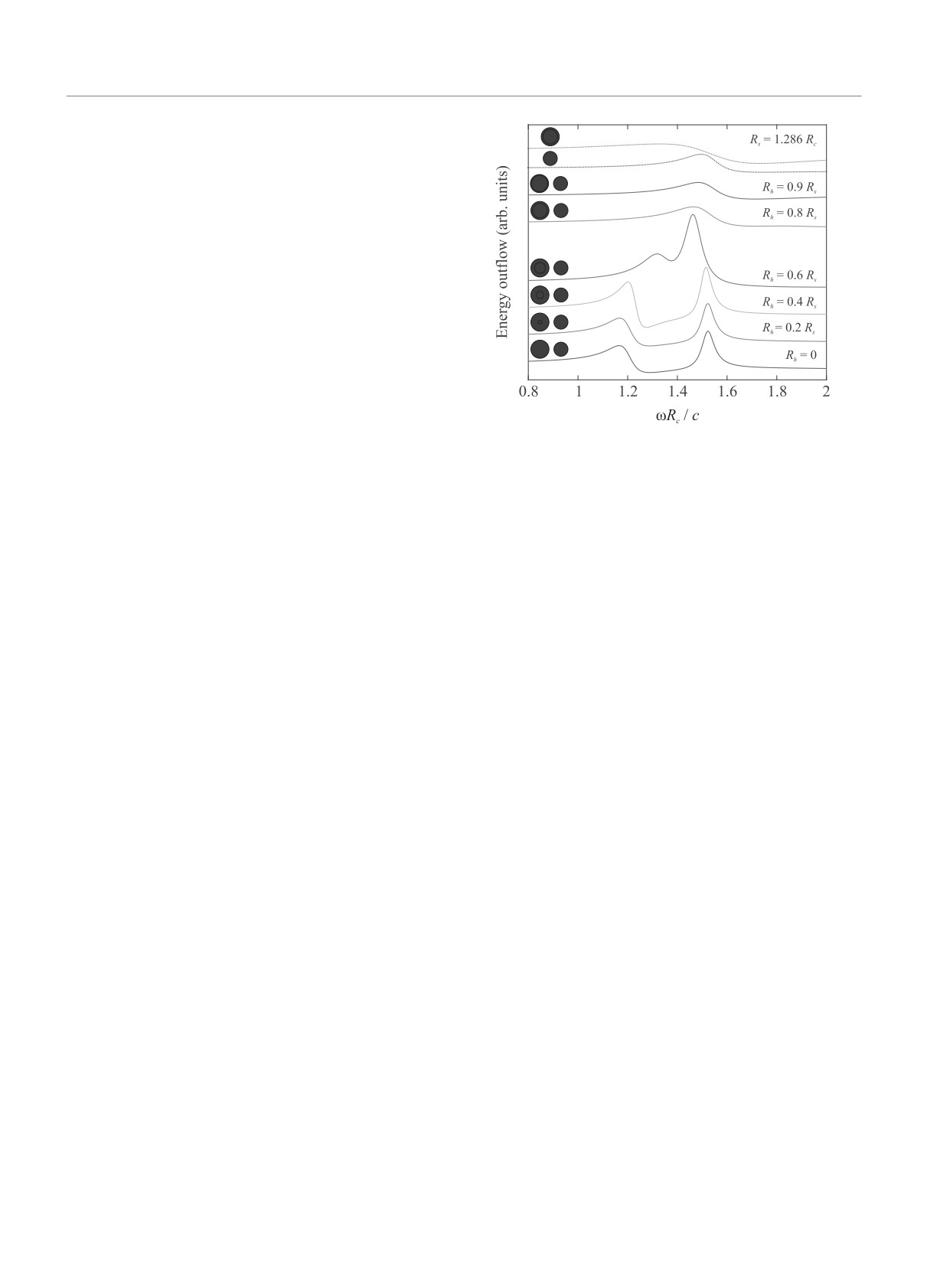
Рис. 4. (Цветной онлайн) Спектры вытекающей энер-

мы рассматриваем вытекающую из димера энергию,

гии димера полого (радиус Rs) и заполненного (радиус

которую определяем как сечение экстинкции, взятое

Rc) цилиндров из активной среды с показателем пре-

со знаком минус. Спектры показаны на рис.4 в за-

ломления ñ = 1.99- 0.488i при освещении плоской вол-

висимости от радиуса отверстия. Уменьшение раз-

ной, в зависимости от радиуса полости (R_h). ТЕ поля-

мера отверстия приводит к уменьшению контраста

ризация

усиление-потери в совокупности с небольшим сдви-

гом собственной частоты. Как результат, моды свя-

заны сильнее, чем в исключительной точке, что обу-

частоте. Мы проанализировали спектры рассеяния

славливает наличия расщепления по частоте. Уве-

на димерах сплошного цилиндра и полого цилин-

личение радиуса полости соответствует увеличению

дра с различным диаметром полости и показали,

контраста усиление-потери, что приводит к разру-

что уменьшение контраста усиление-потери за счет

шению PT симметрии. В этом режиме собственные

уменьшения диаметра полости приводит к расщеп-

моды существуют отдельно в цилиндре, мода в ко-

лению резонанса в спектрах.

тором оказывается излучательной, и в полом цилин-

Полученные результаты могут быть полезны для

дре, в котором локализуется затухающая мода на той

проектирования метаповерхностей, работающих в

же частоте.

режимах, близких к PT симметрии и к исключи-

Заключение. Мы рассмотрели бесконечные ди-

тельной точке. Мы признаем, что столь большое зна-

электрические цилиндры с полостью и продемон-

чение отрицательной мнимой части показателя пре-

стрировали, что радиационное затухание растет с

ломления - κ = -0.5, - необходимой для того, чтобы

увеличением диаметра полости. Эта зависимость

наш димер демонстрировал поведение по типу PT

позволила нам получить контраст усиление-потери

симметрии, не может быть достигнуто в активных

между полым цилиндром и цилиндром без отвер-

средах оптического диапазона, где значения поряд-

стия из того же материала. В дипольном приближе-

ка κ ∼ 10^-2 на данный момент являются порогом.

нии нами были получены уравнения для геометри-

Столь большое усиление требуется для компенсации

ческих параметров димера, состоящего из цилиндра

значительного радиационного затухания дипольных

и полого цилиндра, имеющего исключительную точ-

резонансов. Вместе с тем, если радиационное зату-

ку на заданной частоте. Выбрав чисто вещественную

хание не скомпенсировано, то средние потери будут

частоту исключительной точки и расстояние, соот-

значительно больше контраста потерь, что приведет

ветствующее чисто мнимой разности между полю-

к невозможности пронаблюдать эффекты PT сим-

сами рассеяния сплошного и полого цилиндра, мы

метрии. Таким образом, переход к геометрическим

смогли найти параметры димера с поведением, по-

резонансам более высокого порядка, таким как квад-

добным PT симметрии. При уменьшении контраста

рупольные или октопольные состояния, для которых

усиление-потери данный димер имеет две чисто ве-

характерна более высокая добротность, представля-

щественные собственные частоты, а увеличение кон-

ется способом решить эту проблему. В частности,

траста усиление-потери приводит к появлению за-

подходящей активной средой могут быть галогенид-

тухающей и усиливающейся мод на одной и той же

ные перовскиты, так как на этой платформе экспери-

Письма в ЖЭТФ том 117 вып. 11 - 12

2023

О возможности изготовления PT -симметричных оптических димеров...

813

ментально продемонстрирована компенсация радиа-

K. J. H. Peters and S. R. K. Rodriguez, Phys. Rev. Lett.

ционных потерь усилением в квадрупольных и окто-

129, 013901 (2022).

Özdemir,F.Lei,F.Monifi,M.Gianfreda,

польных состояниях, приводящим к одночастичной

10.

B. Peng, S. K.

генерации [25].

G. L. Long, S. Fan, F. Nori, C. M. Bender, and L. Yang,

Бесконечные цилиндры были рассмотрены из-

Nat. Phys. 10, 394 (2014).

за простоты анализа. Для изготовления реальных

11.

H. Hodaei, A. U. Hassan, S. Wittek, H. Garcia-

структур необходимы частицы конечного размера,

Gracia, R. El-Ganainy, D. N. Christodoulides, and

в роли которых могут выступать и конечные ци-

M. Khajavikhan, Nature 548, 187 (2017).

линдры. Для реализации в терагерцовом диапазоне

12.

A. F. Kockum, A. Miranowicz, S. D. Liberato,

S. Savasta, and F. Nori, Nat. Rev. Phys.

могут быть использованы пустотелые волноводы,

(2019).

технология изготовления которых с диаметрами от

13.

A. A. Dmitriev and M. V. Rybin, Phys. Rev. A 99,

10 мкм является хорошо отработанной [26]. В опти-

063837 (2019).

ческом же диапазоне при помощи электронной ли-

14.

A. Egel, L. Pattelli, G. Mazzamuto, D. S. Wiersma, and

тографии могут быть изготовлены цилиндры с ра-

U. Lemmer, Journal of Quantitative Spectroscopy and

диусом от 100 нм с отверстием внутри. Высота та-

Radiative Transfer 199, 103 (2017).

ких цилиндров может превышать радиус в несколько

15.

D. Felbacq, G. Tayeb, and D. Maystre, J. Opt. Soc. Am.

раз [27]. Однако в этом случае из-за взаимодействия

A 11, 2526 (1994).

мод Ми цилиндра с модами Фабри-Перо происхо-

16.

K. M. Leung and Y. Qiu, Phys. Rev. B 48, 7767 (1993).

дит сдвиг резонансной частоты относительно пред-

17.

P. Lloyd and P. Smith, Adv. Phys. 21, 69 (1972).

сказанного теорией Ми значения (около 10 % в слу-

18.

P. Markoš and V. Kuzmiak, Phys. Rev. A 94, 033845

чае высоты цилиндра, равной трем радиусам [28]),

(2016).

который необходимо учитывать отдельно.

19.

P. Markoš, Opt. Commun. 361, 65 (2016).

Авторский коллектив благодарит за финансо-

вую поддержку Российский научный фонд (грант

20.

E. E. Maslova, M. F. Limonov, and M. V. Rybin, Opt.

Lett. 43, 5516 (2018).

#21-79-10190).

21.

A. Moroz, J. Phys. Condens. Matter 6, 171 (1994).

22.

N. A. Nicorovici, R.C. McPhedran, and L. C. Botten,

1. R. El-Ganainy, K. G. Makris, M. Khajavikhan,

Phys. Rev. E 52, 1135 (1995).

Z. H. Musslimani, S. Rotter, and D. N. Christodoulides,

23.

G. Tayeb and S. Enoch, J. Opt. Soc. Am. A 21, 1417

Nat. Phys. 14, 11 (2018).

(2004).

2. L. Feng, R. El-Ganainy, and L. Ge, Nature Photon. 11,

24.

X. Wang, X.-G. Zhang, Q. Yu, and B. Harmon, Phys.

752 (2017).

Rev. B 47, 4161 (1993).

3. M.-A. Miri and A. Alù, Science 363, eaar7709 (2019).

25.

E. Tiguntseva, K. Koshelev, A. Furasova, P. Tonkaev,

S. K.

Özdemir, S. Rotter, F. Nori, and L. Yang, Nat.

V. Mikhailovskii, E. V. Ushakova, D.G. Baranov,

Mater. 18, 783 (2019).

T. Shegai, A. A. Zakhidov, Y. Kivshar, and

5. L. Feng, Z. J. Wong, R.-M. Ma, Y. Wang, and X. Zhang,

S. V. Makarov, ACS Nano 14, 8149 (2020).

Science 346, 972 (2014).

26.

F. Yu, W. J. Wadsworth, and J. C. Knight, Opt. Express

6. Z. Lin, H. Ramezani, T. Eichelkraut, T. Kottos, H. Cao,

20, 11153 (2012).

D. N. Christodoulides, Phys. Rev. Lett. 106, 213901

27.

Z.-B. Fan, H.-Y. Qiu, H.-L. Zhang, X.-N. Pang,

(2011).

L.-D. Zhou, L. Liu, H. Ren, Q.-H. Wang, and

7. L. Feng, X. Zhu, S. Yang, H. Zhu, P. Zhang, X. Yin,

J.-W. Dong, Light Sci. Appl. 8, 67 (2019).

Y. Wang, X. Zhang, Opt. Express 22, 1760 (2013).

28.

M. V. Rybin, K. B. Samusev, P. V. Kapitanova,

8. L. Feng, M. Ayache, J. Huang, Y.-L. Xu, M.-H. Lu,

D. S. Filonov, P. A. Belov, Y.S. Kivshar, and

Y.-F. Chen, Y. Fainman, and A. Scherer, Science 333,

729 (2011).

M. F. Limonov, Phys. Rev. B 95, 165119 (2017).

Письма в ЖЭТФ том 117 вып. 11 - 12

2023