Письма в ЖЭТФ, том 116, вып. 2, с. 116 - 122

Максимум в спектре терагерцового фотоотклика квантового

точечного контакта

Д.М.Казанцев^+∗, В.Л.Альперович^+∗1), В.А.Ткаченко^+∗×, З.Д.Квон^+∗

⁺Институт физики полупроводников им. А. В. Ржанова Сибирского отделения РАН, 630090 Новосибирск, Россия

^∗Новосибирский государственный университет, 630090 Новосибирск, Россия

^×Новосибирский государственный технический университет, 630073 Новосибирск, Россия

Поступила в редакцию 8 июня 2022 г.

После переработки 8 июня 2022 г.

Принята к публикации 12 июня 2022 г.

Эффект исчезновения гигантской терагерцовой фотопроводимости квантового точечного контак-

та при увеличении энергии фотонов, обнаруженный экспериментально (M. Otteneder et al., Phys. Rev.

Appl. 10, 014015 (2018)) и изученный численным моделированием фотонно-стимулированного транс-

порта (О. А. Ткаченко и др., Письма в ЖЭТФ 108, 396 (2018)), объяснен необходимостью выполнения

закона сохранения импульса при поглощении фотонов туннелирующими электронами и на основе рас-

чета по теории возмущений.

DOI: 10.31857/S1234567822140087, EDN: izlsqs

Физические явления в наноструктурах, обу-

гии кванта ℏω₀

= 6.74 мэВ, хотя и согласуется с

словленные влиянием высокочастотных элек-

результатами численного решения нестационарного

тромагнитных полей на квантовый транспорт

уравнения Шредингера [7, 16], не получило ясно-

электронов, рассматривались в большом числе

го физического объяснения. Другая (отличная от

работ

[1-11]. В первую очередь теоретически

ФСТ) картина формирования гигантского фотоот-

и экспериментально исследовалось резонансное

клика КТК, основанная на эффекте модуляции вы-

фотонно-стимулированное туннелирование в сверх-

соты туннельного барьера электромагнитным полем,

проводящих и полупроводниковых структурах

была развита в недавней работе [18] для объясне-

с атомно-резкими потенциальными барьерами

ния сильной сверхлинейной зависимости величины

[1-6]. Создание квантового точечного контакта

фотопроводимости от интенсивности терагерцового

(КТК) - латеральной наноструктуры, состоящей

излучения в глубоком туннельном режиме. Одна-

из короткого, управляемого затвором сужения в

ко в рамках картины, построенной в [18], вопрос о

высокоподвижном двумерном электронном газе

причине исчезновения фотопроводимости при уве-

(ДЭГ) [12-14], открыло путь к изучению фотонно-

личении частоты излучения также оставался откры-

стимулированного прохождения электронов че-

тым. В данной работе предлагается объяснение эф-

рез плавный потенциальный барьер, однако до

фекта исчезновения фотопроводимости КТК при вы-

недавнего времени эти исследования были только

соких частотах, основанное на необходимости со-

теоретическими [7-9].

хранения квазиимпульса при оптических переходах

В работах [15-17] был впервые обнаружен и

и обоснованное расчетом спектров ФСТ по теории

исследован эффект гигантской фотопроводимости

возмущений.

арсенид-галлиевого КТК при облучении терагерцо-

На качественном уровне объяснение максимума

вым излучением с энергией кванта ℏω₀ = 2.85 мэВ,

ФСТ при энергии квантов, близкой к разности меж-

близкой к разности между энергией Ферми и верши-

ду вершиной барьера и уровнем Ферми, состоит в

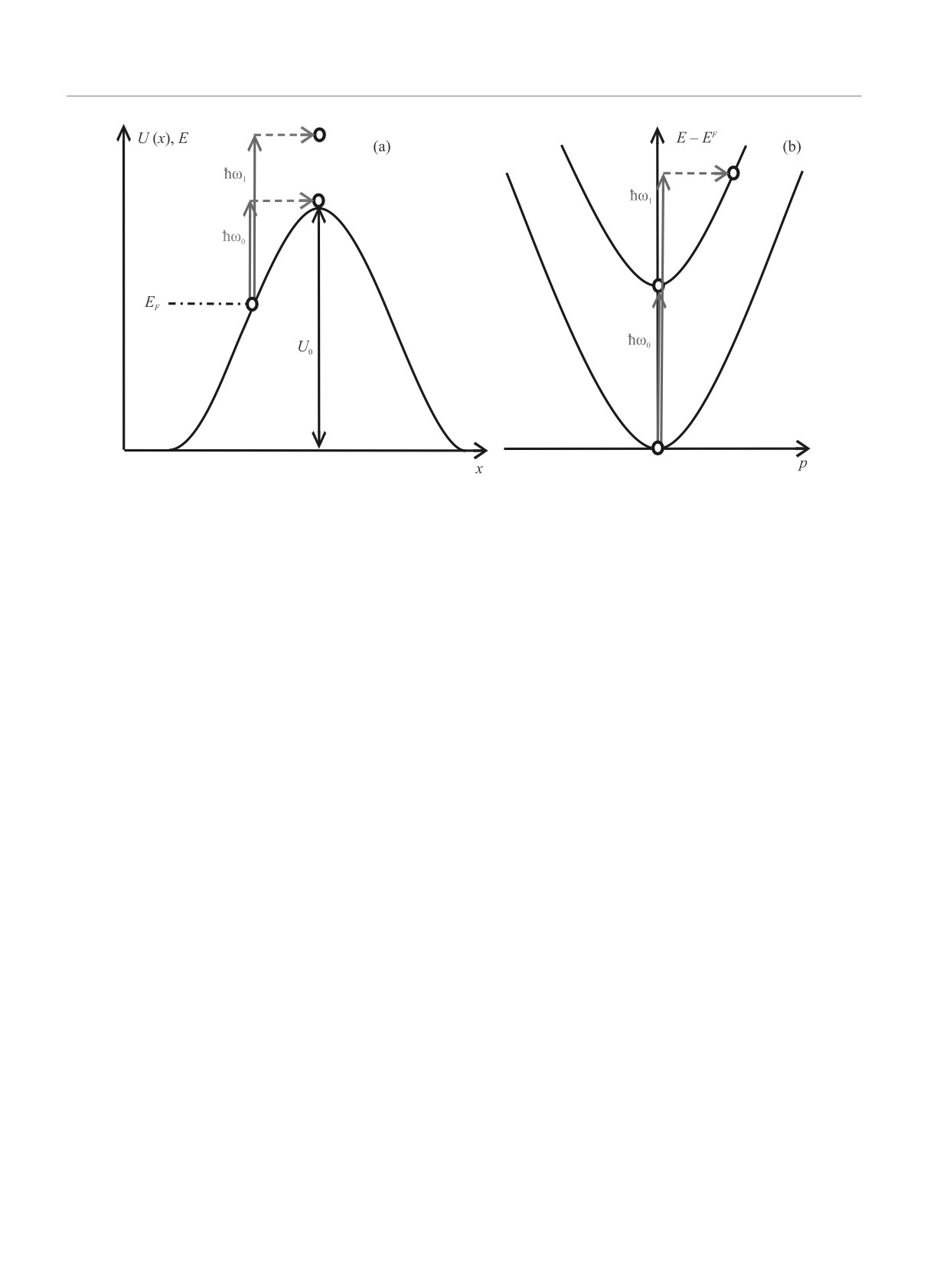
ной потенциального барьера ℏω₀ = U₀ - E_F (рис. 1a).

следующем. В присутствии электромагнитной вол-

Эффект был объяснен фотонно-стимулированным

ны с частотой ω, закон сохранения энергии позволяет

транспортом (ФСТ) электронов, обусловленным по-

электрону переходить в состояния Флоке с энергия-

глощением фотонов [15-17]. Однако обнаруженное

ми E₀±n·ℏω, где E₀ - начальная энергия, n = 1, 2, . . .

в [15] исчезновение фотоотклика для большей энер-

- число поглощенных (+) или испущенных (-) кван-

тов излучения. Для выполнения закона сохранения

¹⁾e-mail: alper@isp.nsc.ru

импульса, поглощение фотонов должно происходить

116

Письма в ЖЭТФ том 116 вып. 1 - 2

2022

Максимум в спектре терагерцового фотоотклика квантового точечного контакта

117

Рис. 1. (Цветной онлайн) Иллюстрация ФСТ через плавный потенциальный барьер на диаграммах энергия-координата

(a) и энергия-квазиимпульс (b) при поглощении электронами фотонов с энергией ℏω0 = U0 - EF , соответствующей

переходу к вершине барьера, и для большей энергии фотонов ℏω1 > ℏω0. На рисунке 1b нижняя и верхняя параболы

соответствуют законам дисперсии электронов вблизи точки остановки и вблизи вершины барьера, соответственно;

рассеяние по импульсу показано горизонтальной штриховой стрелкой

с одновременным рассеянием по импульсу: на фо-

требует одновременного рассеяния по импульсу, по-

нонах или примесях в объеме кристалла, либо при

этому вероятность такого перехода мала в силу ма-

взаимодействии с наноструктурами. Для нанострук-

лости вероятности приобретения большого импуль-

тур с квантовыми уровнями или квазиуровнями, ко-

са при прохождении плавного барьера. В результате

торые существуют и в отсутствие облучения, резо-

при ℏω > ℏω₀ вероятность ФСТ уменьшается при

нансы ФСТ проявляются, как правило, в виде фо-

увеличении ℏω благодаря уменьшению вероятности

тонных реплик резонансов в туннельном транспорте

поглощения фотонов. При ℏω < ℏω₀, когда конеч-

электронов.

ная энергия электрона меньше высоты барьера, ФСТ

В КТК с одиночным плавным барьером, в ко-

увеличивается при увеличении энергии фотонов из-

тором нет резких скачков потенциала, уровней или

за увеличения вероятности туннелирования электро-

квазиуровней, в отсутствие излучения нет и резо-

нов через барьер. В результате величина ФСТ дости-

нансов в энергетической зависимости коэффициента

гает максимума при ℏω ≈ ℏω₀. Аналогичная картина

прохождения D(E); как следствие, фотонные репли-

формирования спектральных максимумов справед-

ки наблюдаться не могут. Тем не менее, в фотооткли-

лива и для многофотонных переходов с n > 1.

ке такого КТК может наблюдаться спектральный ре-

Следует отметить, что в предложенной каче-

зонанс при переходе электронов к вершине барьера.

ственной картине формирования спектра ФСТ, “ре-

Причина резонанса проиллюстрирована на диаграм-

зонансный” оптический переход является прямым

ме энергия-квазиимпульс (рис. 1b), где показаны за-

(вертикальным) в k-пространстве (рис. 1b), но непря-

коны дисперсии электронов вблизи точки остановки

мым в обычном, x-пространстве. Другими словами,

и вблизи вершины барьера, а также оптические пе-

в процессе перехода электрон сдвигается из точки

реходы с энергиями фотонов ℏω₀ и ℏω₁. Видно, что

остановки к вершине барьера (рис.1a). На самом де-

для “резонансной” энергии фотонов ℏω₀ = U₀ - E_F

ле, стационарные электронные состояния делокали-

оптический переход со дна нижней на дно верхней

зованы как в обычном, так и в импульсном простран-

параболы является вертикальным и не требует до-

стве, поэтому простая картина оптических перехо-

полнительного рассеяния по импульсу, поэтому ве-

дов между состояниями с хорошо определенными за-

роятность такого перехода велика. Напротив, при

конами дисперсии справедлива, по-видимому, толь-

ℏω1 > ℏω0, переход в состояние с большой кине-

ко для достаточно плавных потенциальных барье-

тической энергией электрона над вершиной барьера

ров, когда неопределенность импульса сравнитель-

Письма в ЖЭТФ том 116 вып. 1 - 2

2022

118

Д.М.Казанцев, В.Л.Альперович, В.А.Ткаченко, З.Д.Квон

но мала. Из соотношения неопределенностей мож-

но оценить квазиимпульс Δp, приобретаемый элек-

троном при прохождении через КТК, и полушири-

ну спектрального максимума ΔE ∼ (Δp)²/2m^∗, где

m^∗ - эффективная масса электрона. Взяв неопреде-

ленность координаты равной полуширине потенци-

ального барьера на уровне Ферми Δx ≈ 30 нм, по-

лучаем ΔE ≈ 0.5 мэВ, что согласуется по порядку

величины с результатами численного расчета [17].

Несмотря на простоту и наглядность предло-

женного объяснения “резонансного” спектрального

максимума, вопрос о том, в какой степени это

объяснение применимо к реальной картине форми-

рования спектра фотоотклика КТК, остается откры-

тым. Действительно, с одной стороны, согласно это-

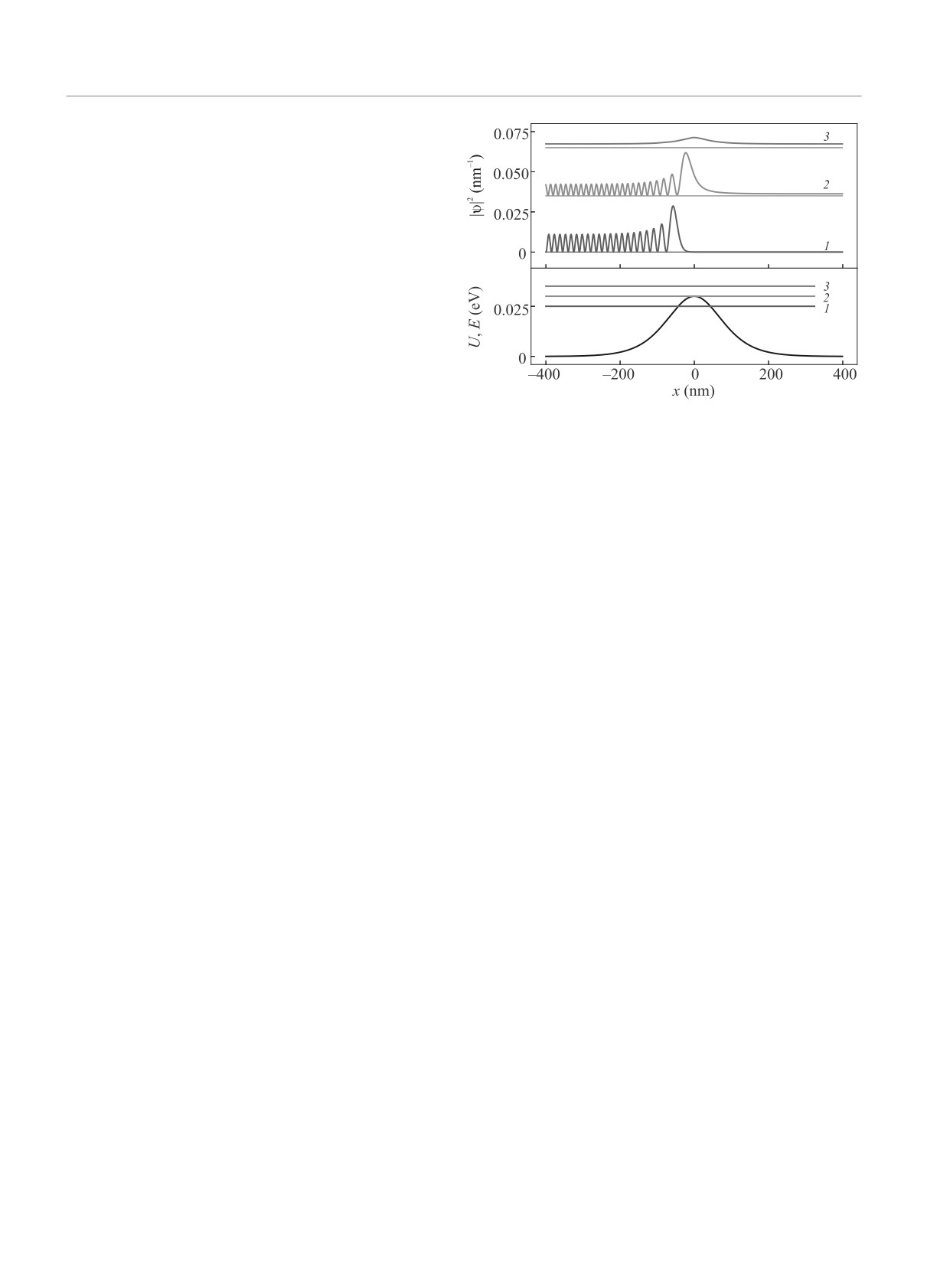
Рис. 2. (Цветной онлайн) Верхняя часть рисунка: квад-

му объяснению, благодаря приблизительному равен-

раты модуля волновых функций |ψ(x)|² в координат-

ству волновых векторов начального и конечного со-

ном представлении для энергий налетающих электро-

стояний в пространственных областях вблизи то-

нов ниже вершины барьера E = 25 мэВ (1), вровень с

чек остановки, эти области должны давать основной

вершиной E = 30 мэВ (2) и выше вершины E = 35 мэВ

вклад в матричный элемент перехода. С другой сто-

(3). Графики |ψ(x)|² для различных энергий сдвину-

роны, и начальное, и конечное состояния электро-

ты по вертикали для удобства восприятия. Нижняя

часть рисунка: потенциальный барьер Эккарта высо-

на принадлежат непрерывному спектру и являются

делокализованными, поэтому значительный вклад в

той U0 = 30 мэВ и шириной d = 100 нм. Горизонталь-

ные линии показывают соответствующие энергии на-

матричный элемент перехода может вносить широ-

летающих электронов

кая область вдали от точек остановки. Однако этот

вклад ослаблен различием квазиклассических волно-

вых векторов; в частности, на большом расстоянии

электронов 10¹² с^-1. В верхней части рис. 2 показаны

от потенциального барьера оптические переходы во-

графики квадрата модуля волновых функций |ψ(x)|²

обще невозможны, поскольку, как известно, свобод-

в координатном представлении для трех различных

ный электрон не может поглотить фотон.

энергий электронов. В нижней части рисунка, по-

Для того чтобы выяснить, какая область про-

казан потенциальный барьер U(x), а энергии элек-

странства вносит основной вклад в спектральный

тронов обозначены горизонтальными линиями. Вид-

максимум фотоотклика КТК и проанализировать

но, что для низкой энергии налетающего электрона

вклад различных факторов в формирование этого

E = 25мэВ (на 5мэВ ниже вершины барьера), слева

максимума, мы рассчитали спектр ФСТ как произ-

от барьера образуется стоячая волна благодаря прак-

ведение вероятности оптического перехода W на ве-

тически полному отражению. Для энергии электро-

роятность прохождения электрона D через потенци-

на, равной высоте барьера E = 30 мэВ, коэффициен-

альный барьер в конечном состоянии. Следует отме-

ты отражения и прохождения приблизительно равны

тить, что идея использования такого произведения

0.5, поэтому справа от барьера имеется заметная ам-

для объяснения спектрального максимума фотоот-

плитуда прошедшей волны, а слева величина |ψ(x)|²

клика КТК была ранее предложена, хотя и не реали-

не достигает нуля (составляет около 3 % от макси-

зована, в работе [7]. Мы рассчитали вероятность оп-

мума). Наконец, для энергии E = 35 мэВ (на 5 мэВ

тического перехода из начального состояния с энер-

выше вершины барьера) наблюдается практически

гией Ферми E_i = E_F в конечное состояние с энергией

полное прохождение D ≈ 0.99999, амплитуда осцил-

E_f = E_F + ℏω в рамках теории возмущений первого

ляций |ψ(x)|², связанная с надбарьерным отражени-

порядка, с использованием золотого правила Ферми

ем, составляет менее 1 %, а максимум |ψ(x)|² связан с

W = 2π/ℏ · |〈ψ_f|H^′|ψ_i〉|²δ(E_f - E_i - ℏω). Волновые

квазиклассическим торможением, т.е. с уменьшени-

функции начального ψ_i и конечного ψ_f состояний

ем скорости электрона при движении над вершиной

были взяты из решения задачи о прохождении элек-

барьера.

трона через плавный потенциальный барьер Эккар-

Гамильтониан H^′ взаимодействия между элек-

та с характерной шириной d: U(x) = U₀/cosh²(x/d)

троном и электромагнитным излучением был взят

[19]. Волновые функции были нормированы на поток

из [20], а коэффициент прохождения электронов в

Письма в ЖЭТФ том 116 вып. 1 - 2

2022

Максимум в спектре терагерцового фотоотклика квантового точечного контакта

119

конечном состоянии D(E_F + ℏω₀) - из [19]. Расчет

переходов W ; в результате, формируется

“резо-

проводился для интенсивности терагерцового излу-

нансный” пик при ℏω

≈ ℏω₀. Эти соображения

чения, независящей от ℏω и равной 200 мВт/см².

соответствуют качественному объяснению пика в

Использовалась одномерная плотность состояний

спектре фотоотклика КТК.

√

ρ(E) =

2m/πℏ

E для кинетической энергии элек-

Сравнение спектров для различных величин L

тронов E = E_F + ℏω, находящихся вдали от барьера.

показывает, что основной вклад в резонансный пик

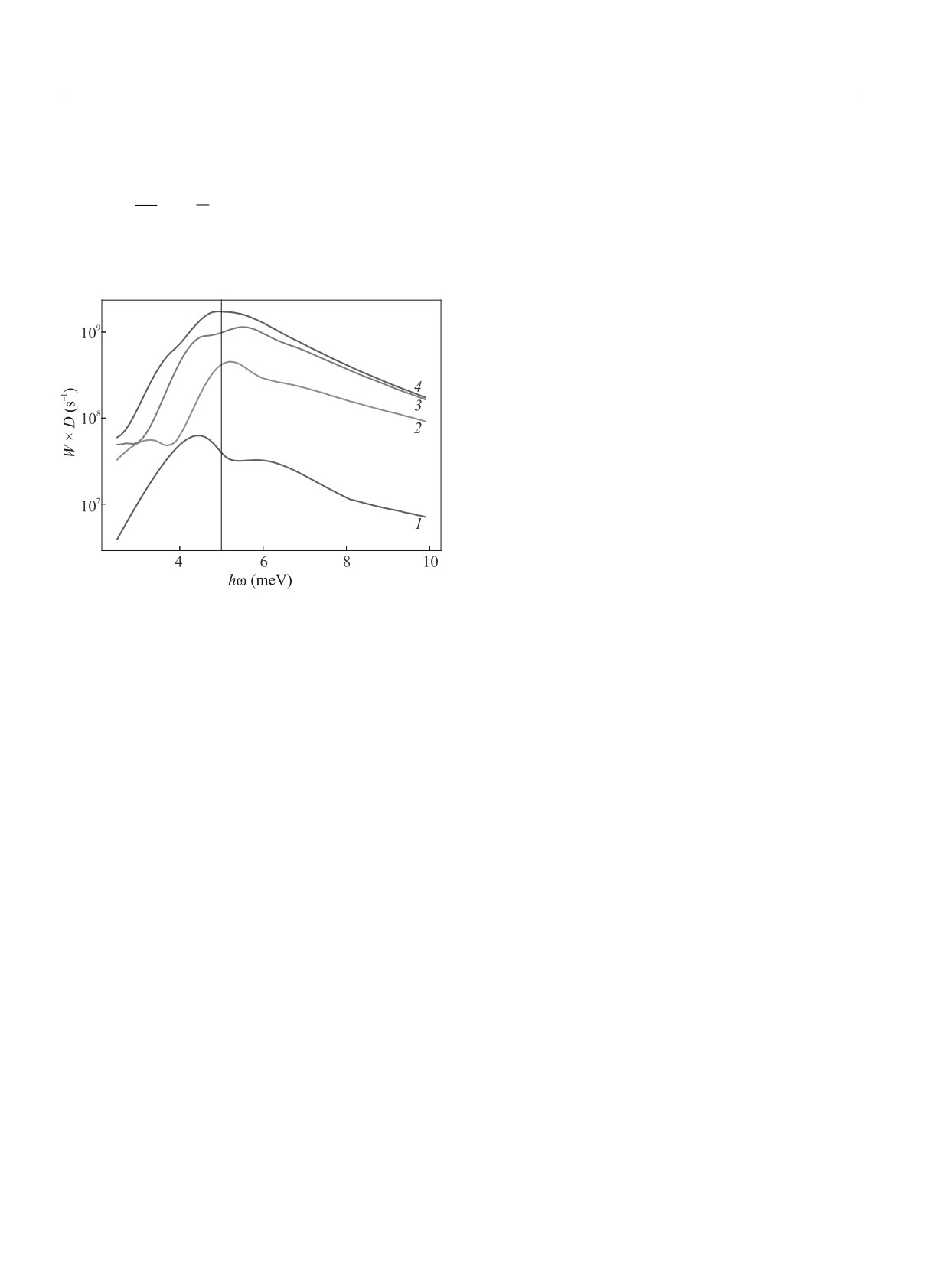
На рисунке 3 показаны спектры величины

ФСТ вносит интегрирование по области L ≤ 3d; в

ФСТ ≈ W × D, рассчитанные для КТК с шириной

этой области потенциальный барьер модифицирует

волновые функции электронов таким образом, что

оптические переходы становятся возможными. Вид-

но, что уменьшение ширины области интегрирова-

ния до L = d ведет к значительному уменьшению

амплитуды пика, в то время как для L > 3d, ам-

плитуда и форма пика насыщаются при дальнейшем

увеличении L. Следует отметить, что для выбран-

ных параметров барьера и энергии электронов, точка

остановки лежит в пределах L ∼ d. Этот факт огра-

ничивает применимость предложенного выше каче-

ственного объяснения, основанного на предположе-

нии, что основной вклад в оптические переходы дают

области вблизи точек остановки. На самом деле, су-

щественный вклад в матричный элемент дает более

широкая область потенциального барьера, включаю-

щая его “подножие”.

Рис. 3. (Цветной онлайн) Спектры фотоотклика, рас-

Отметим, что сравнительно слабые дополнитель-

считанные для КТК с шириной барьера d = 100 нм,

ные “плечи” и экстремумы, которые проявляются на

высотой U0

= 30 мэВ, энергией Ферми электронов

фоне основного пика для малых областей интегри-

EF = 25 мэВ. Матричный элемент оптического перехо-

рования L, являются “боковыми лепестками”, возни-

да рассчитывался интегрированием по пространствен-

кающими из-за конечной величины окна интегриро-

ной области |x| < L, с различной величиной L по от-

вания. Другой артефакт состоял в похожих на шум

ношению к характерной ширине барьера d: 1 - L = d;

колебаниях, которые проявлялись в расчетных спек-

2 - 2d; 3 - 3d; 4 - 4d. “Резонансная” энергия фотонов

трах ФСТ из-за вариаций фазы подынтегрального

ℏω0 = U0 - EF = 5 мэВ показана вертикальной линией

выражения матричного элемента на границах обла-

и высотой потенциального барьера d = 100 нм и

сти интегрирования при изменении ℏω; эти колеба-

U₀ = 30 мэВ, фиксированной энергии E_F = 25 мэВ

ния подавлялись усреднением по фазе.

и различных значений L - полуширины области

На рисунке 4 показаны спектры ФСТ, рассчитан-

пространства от -L до +L вокруг центра барье-

ные при фиксированной высоте потенциального ба-

ра, по которой проводилось интегрирование при

рьера U₀ и различных положениях уровня Ферми

вычислении матричного элемента оптического пере-

E_F . Видно, что для всех значений E_F , спектральное

хода. Спектральная область ограничена энергиями

положение основного пика соответствует оптическим

квантов ℏω > (U₀ - E_F )/2, поскольку для меньших

переходам с уровня Ферми к вершине потенциально-

энергий квантов существенный вклад в ФСТ вно-

го барьера, в соответствии с результатами численных

сят многофотонные процессы [16, 17], которые не

расчетов [17] и с качественным объяснением пика в

учитывались в данном расчете. Видно, что во всех

ФСТ, предложенным в данной работе (рис. 1). С уве-

спектрах основной пик центрирован приблизительно

личением E_F , пик уширяется и становится менее вы-

вблизи энергии фотонов ℏω₀ ≈ U₀ - E_F

= 5мэВ,

раженным. Этот факт согласуется с приведенными

соответствующей оптическим переходам с уровня

выше соображениями, основанными на соотношении

Ферми к вершине барьера. При ℏω

< ℏω₀, рост

неопределенностей. Видно также, что наклон высо-

ФСТ при увеличении энергии фотонов обусловлен

коэнергетического крыла пика слабо зависит от по-

увеличением коэффициента прохождения D; при

ложения уровня Ферми.

ℏω

> ℏω₀, D насыщается, а уменьшение ФСТ

Для дальнейшего прояснения вопроса о механиз-

обусловлено уменьшением вероятности оптических

ме формирования максимума, мы рассчитали спектр

Письма в ЖЭТФ том 116 вып. 1 - 2

2022

120

Д.М.Казанцев, В.Л.Альперович, В.А.Ткаченко, З.Д.Квон

Рис. 5. (Цветной онлайн) Квадраты модуля волновых

функции |ψ(k)|² в импульсном представлении для энер-

гий налетающих электронов ниже E

= 25 мэВ (1),

вровень E

= 30 мэВ (2) и выше вершины барьера

E = 35мэВ (3). Для удобства восприятия, части вол-

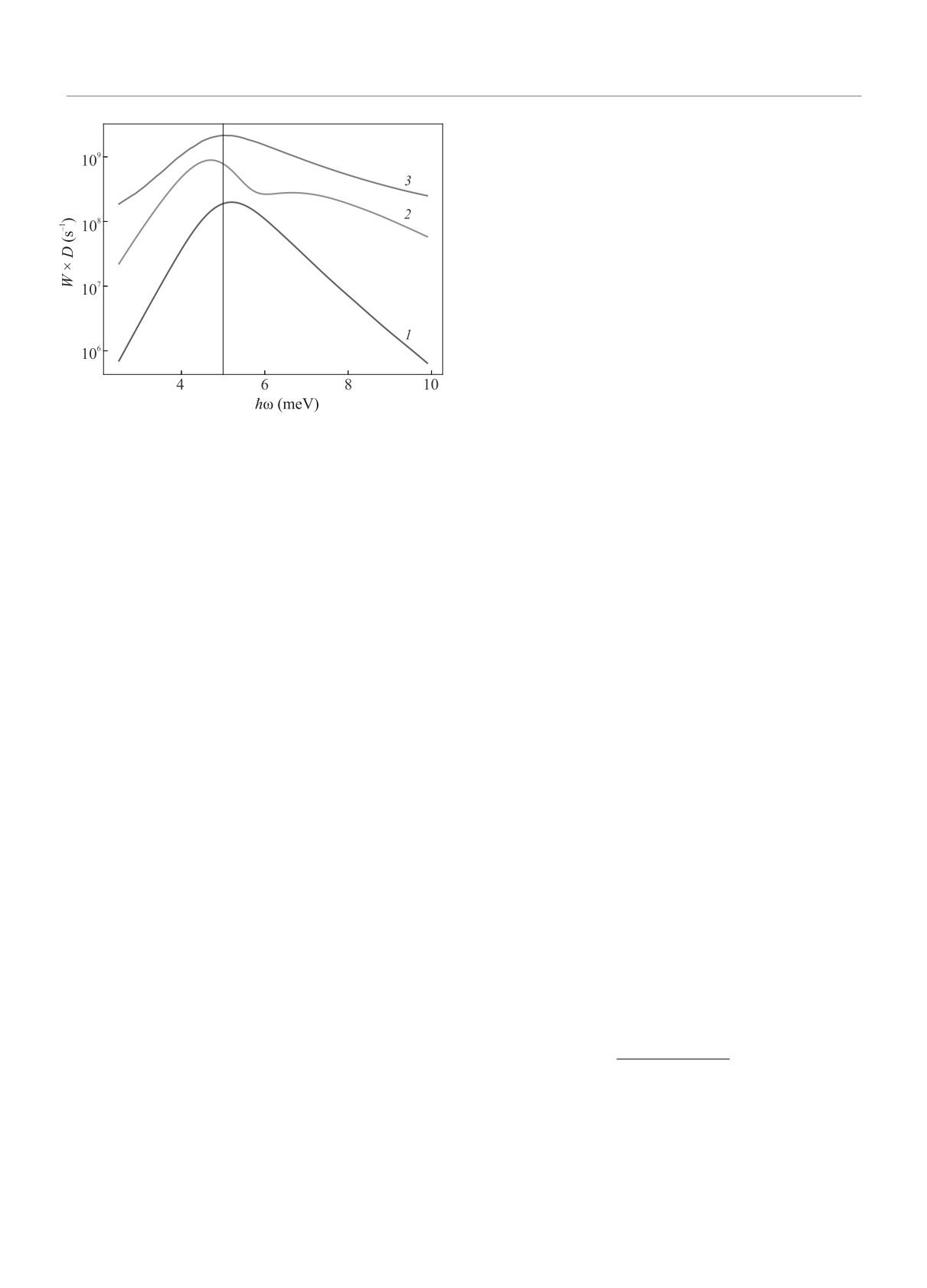
Рис. 4. (Цветной онлайн) Спектры ФСТ, рассчитан-

новых функций между дельта-образными пиками, со-

ные для КТК с шириной потенциального барьера d =

ответствующими налетающим и отраженным электро-

100 нм, высотой U0 = 30 мэВ и различных положений

нам, увеличены в 10 раз, а графики для различных

уровня Ферми: 1 - EF = 23 мэВ; 2 - 25 мэВ; 3 - 27 мэВ.

энергий сдвинуты по вертикали

Для каждого спектра стрелкой показана соответству-

ющая “резонансная” энергия фотонов ℏω0 = U0 - EF

при больших импульсах представляют собой, веро-

ятно, “боковые лепестки” (“гиббсовские осцилляции”)

ФСТ через волновые функции электронов в импульс-

величины |ψ(k)|², возникающие в Фурье-образе бла-

ном представлении. Квадраты модуля этих функций

годаря локализации волновой функции электрона в

|ψ(k)|² для различных энергий налетающих электро-

области барьера (рис.2).

нов показаны на рис. 5. Видно, что для энергии элек-

трона на 5 мэВ ниже высоты барьера, |ψ(k)|² состо-

Импульсное представление величины

|ψ(k)|²

ит из двух дельта-образных пиков, соответствующих

(рис. 5) позволяет дать дополнительное обоснование

импульсам налетающего (правый пик) и отраженно-

роли закона сохранения импульса в эффекте исчез-

го (левый пик) электрона, а также слабой симмет-

новения фотопроводимости при больших энергиях

ричной монотонной “подкладки” между пиками, от-

фотонов. Действительно, в исходном состоянии

ражающей процесс торможения налетающего и уско-

(нижняя кривая на рис. 5) средний импульс равен

рения отраженного электрона на левом склоне по-

нулю, а в конечном состоянии выше вершины барье-

тенциального барьера. Для энергии, равной высоте

ра E > U₀ импульс отличен от нуля и соответствует

барьера, коэффициент прохождения D ∼ 0.5; соот-

практически полному прохождению электрона. Как

ветственно, левый дельта-пик существенно меньше

следствие, в силу закона сохранения импульса,

правого. При этом волновая функция |ψ(k)|² между

вероятность оптического перехода между этими

дельта-пиками становится асимметричной: домини-

состояниями мала и падает с увеличением энергии

рует область положительных импульсов, в которой

фотонов.

наблюдаются дополнительные, сравнительно широ-

На рисунке 6 показаны спектры ФСТ, рассчитан-

кие пики. Для энергии на 5 мэВ выше высоты ба-

ные для КТК с шириной и высотой потенциально-

рьера, левый дельта-пик не наблюдается, поскольку

го барьера d = 100 нм и U0 = 30 мэВ, для фик-

отраженная волна практически отсутствует, а допол-

сированной энергии E_F = 25 мэВ и для различных

нительные пики сдвигаются в сторону больших по-

значений K - полуширины области k-пространства

ложительных импульсов. Положение наиболее выра-

от -K до +K, по которой проводилось интегриро-

женного пика, лежащего ближе к k = 0, соответ-

вание при вычислении матричного элемента оптиче-

ствует импульсу электронов, пролетающих в обла-

ского перехода. Видно, что аналогично расчету мат-

сти вблизи вершины барьера. Дополнительные пики

ричного элемента по координатным волновым функ-

Письма в ЖЭТФ том 116 вып. 1 - 2

2022

Максимум в спектре терагерцового фотоотклика квантового точечного контакта

121

использованы для объяснения не только спектров

ФСТ КТК, но и для качественной интерпретации

спектров фотоионизации других физических объек-

тов и, в частности, атома водорода. Сечение фото-

ионизации атома водорода падает с ростом энергии

фотонов во всех известных моделях, включая бор-

новское приближение и модель Зоммерфельда, учи-

тывающую кулоновское взаимодействие электрона с

ионом [21]. На это падение полезно посмотреть с точ-

ки зрения закона сохранения импульса при оптиче-

ском переходе из связанного состояния в непрерыв-

ный спектр. Действительно, в связанном состоянии у

электрона нет определенного импульса, но есть рас-

пределение по импульсам, ширина которого порядка

ℏ/a_B, где a_B - боровский радиус. Можно сказать,

Рис. 6. (Цветной онлайн) Спектры фотоотклика, рас-

что фотон “выхватывает” электрон из этого распре-

считанные для КТК с шириной барьера d = 100 нм, вы-

деления и переводит в непрерывный спектр. Пре-

сотой U0 = 30 мэВ, энергией Ферми электронов EF =

небрегая малым импульсом фотона, на диаграмме

= 25 мэВ. Матричный элемент оптического перехода

энергия-импульс оптический переход можно считать

рассчитывался интегрированием по областям импуль-

вертикальным. Вероятность найти электрон с опре-

сов |k| < K, с различной величиной K (по отношению к

деленным импульсом в связанном состоянии падает

волновому вектору электронов до (k1) и после (k2) оп-

при увеличении импульса. Как следствие, с ростом

тического перехода): 1 - K = 0.25k1; 2 - 0.5k1; 3 - 1.1k2.

энергии фотонов сечение фотоионизации уменьшает-

“Резонансная” энергия фотонов ℏω0 = U0 - EF = 5 мэВ

ся. Характерная ширина хвоста спектра фотоиони-

показана вертикальной линией

зации соответствует импульсу ионизованного элек-

трона k ∼ ℏ/a_B, в согласии с приведенным каче-

циям (рис. 3), основной пик во всех спектрах цен-

ственным объяснением. Аналогичные соображения

трирован приблизительно вблизи энергии фотонов

справедливы для объяснения спектра фотоиониза-

ℏω₀ = U₀ - E_F = 5 мэВ, соответствующей оптиче-

ции мелких водородоподобных примесных центров в

ским переходам с уровня Ферми к вершине барьера.

Сравнение спектров на рис. 6 для различных вели-

полупроводниках.

Таким образом, соображения о сохранении квази-

чин K показывает, что значительный вклад в резо-

нансный пик ФСТ вносит интегрирование по всей об-

импульса при поглощении фотонов дают качествен-

ное объяснение немонотонной (“резонансной”) зави-

ласти между дельта-пиками, соответствующими па-

дающей и прошедшей волне, а не только области

симости фотоотклика КТК с максимумом вблизи

энергии фотонов ℏω₀ = U₀ - E_F , наблюдавшейся в

вблизи точек остановки, где квазиклассический им-

эксперименте [15], а также полученной численным

пульс близок к нулю. Это согласуется со сделанным

из рис. 3 выводом о том, что значительный вклад

расчетом [17]. В рамках предложенной картины оце-

нена ширина спектральных максимумов и качествен-

в матричный элемент оптического перехода вносит

“подножие” барьера, а не только области вблизи то-

но объяснена эволюция формы спектров при измене-

нии положения уровня Ферми. Проведенный расчет

чек остановки, как предполагалось в простом ка-

чественном объяснении происхождения резонансно-

спектра ФСТ по теории возмущений качественно со-

гласуется с предложенным объяснением, однако на-

го пика в спектре ФСТ, проиллюстрированном на

рис. 1. Тем не менее, мы полагаем, что это объяснение

кладывает на него количественные ограничения.

Работа выполнена при поддержке Министерства

правильно указывает на главную причину экспери-

ментально наблюдавшегося падения величины ФСТ

науки и высшего образования РФ (Государственное

задание для ИФП СО РАН).

при превышении энергии фотонов над резонансным

значением. Эта причина состоит в падении матрич-

ного элемента оптического перехода при большом

1. A. H. Dayem and R. J. Martin, Phys. Rev. Lett. 8, 246

различии импульсов начального и конечного состо-

(1962).

яний электрона.

2. P. K. Tien and J. P. Gordon, Phys. Rev. 129, 647 (1963).

Соображения о сохранении импульса при оптиче-

3. M. Büttiker and R. Landauer, Phys. Rev. Lett. 49, 1739

ских переходах имеют общий характер и могут быть

(1982).

Письма в ЖЭТФ том 116 вып. 1 - 2

2022

122

Д.М.Казанцев, В.Л.Альперович, В.А.Ткаченко, З.Д.Квон

4. D. D. Coon and H. C. Liu, J. Appl. Phys. 58, 2230

D. A. Ritchie, and G. A.C. Jones, J. Phys. C: Solid State

(1985).

Phys. 21, L209 (1988).

5. M. Grifoni and P. Hünggi, Phys. Rep. 304, 229 (1998).

14. M. Büttiker, Phys. Rev. B. 41, 7906 (1990).

6. G. Platero and R. Aguado, Phys. Rep. 395, 1 (2004).

15. M. Otteneder, Z. D. Kvon, O. A. Tkachenko,

7. J.-Y. Ge and J. Z. H. Zhang, J. Chem. Phys. 105, 8628

V. A. Tkachenko, A. S. Jaroshevich, E. E. Rodyakina,

(1996).

A. V. Latyshev, and S.D. Ganichev, Phys. Rev. Appl.

10, 014015 (2018).

8. K. Yakubo, S. Feng, and Q. Hu, Phys. Rev. B 54, 7987

(1996).

16. О. А. Ткаченко, В. А. Ткаченко, Д. Г. Бакшеев,

З. Д. Квон, Письма в ЖЭТФ 108, 422 (2018).

9. O. A. Tkachenko, V. A. Tkachenko, D. G. Baksheyev,

and H. Nejoh, Proc. 5th Int. Symp. Foundations of

17. В. А. Ткаченко, З. Д. Квон, О. А. Ткаченко,

Quantum Mechanics in the Light of New Technology

A. C. Ярошевич, E. E. Родякина, Д.Г. Бакшеев,

(ISQM-Tokyo’95), Japan, August 21-24, 1995, ed. by

А. В. Латышев, Письма в ЖЭТФ 113, 328 (2021).

K. Fujikawa and Y. A. Ono, Elsevier/North Holland,

18. M. Otteneder, M. Hild, Z. D. Kvon, E. E. Rodyakina,

N.Y. (1996), p. 207.

M. M. Glazov, and S. D. Ganichev, Phys. Rev. B 104,

10. S. Morina, O. V. Kibis, A. A. Pervishko, and

205304 (2021).

I. A. Shelykh, Phys. Rev. B 91, 155312 (2015).

19. Л. Д. Ландау, Е. М. Лифшиц, Квантовая механи-

11. V. M. Kovalev, W.-K. Tse, M. V. Fistul, and

ка: нерелятивистская теория, 3-е изд., Наука, М.

I. G. Savenko, New J. Phys. 20, 083007 (2018).

(1974), т. 3, c. 105.

12. B. J. van Wees, H. van Houten, C. W. J. Beenakker,

20. А. И. Ансельм, Введение в теорию полупроводников,

J. G. Williamson, L. P. Kouwenhoven, D. van der Marel,

Наука, М. (1978), c. 407.

and C. T. Foxon, Phys. Rev. Lett. 60, 848 (1988).

21. В. А. Астапенко, Взаимодействие излучения с ато-

13. D. Wharam, T. J. Thornton, R. Newbury, M. Pepper,

мами и наночастицами, Издательский дом “Интел-

H. Ahmed, J. E. F. Frost, D.G. Hasko, D.C. Peacock,

лект”, Долгопрудный (2010), 496 с.

Письма в ЖЭТФ том 116 вып. 1 - 2

2022