Письма в ЖЭТФ, том 115, вып. 9, с. 562 - 570

Фокусировка атомного пучка для эффективной загрузки

атомного чипа

А. Е. Афанасьев⁺¹⁾, Д. В. Быкова^+∗, П. И. Скакуненко^+×◦, В. И. Балыкин⁺

⁺Институт спектроскопии РАН, 108840 Троицк, Москва, Россия

^∗Национальный исследовательский университет “Высшая школа экономики”, 101000 Москва, Россия

^×Московский физико-технический институт (НИУ), 141701 Долгопрудный, Россия

^◦Сколковский институт науки и технологий, 143026 Москва, Россия

Поступила в редакцию 23 марта 2022 г.

После переработки 28 марта 2022 г.

Принята к публикации 28 марта 2022 г.

Рассмотрен метод увеличения скорости загрузки атомов в U-образную магнито-оптическую ловуш-

ку (МОЛ) атомов вблизи атомного чипа. Подход основан на фокусировке низкоскоростного атомного

пучка в область локализации атомов на атомном чипе. Рассмотрен режим фокусировки с избыточным

демпфированием. В этом случае фокусное расстояние не зависит от начальной поперечной скорости

атомов. Показано, что за счет фокусировки атомного пучка возможно увеличение скорости загрузки в

160 раз в области локализации с диаметром 250 мкм.

DOI: 10.31857/S1234567822090038, EDN: dwplcz

Введение. Локализованные атомы лежат в ос-

Определяющими параметрами квантовых сенсо-

нове многих прецизионных экспериментов в обла-

ров, влияющими на их точность и удобство использо-

сти атомной интерферометрии. Развитие данного на-

вания, являются: количество охлажденных атомов,

правления уже привело к созданию нового поколе-

их температура, геометрические размеры атомного

ния сенсоров - квантовых сенсоров, основанных на

ансамбля и время проведения измерений. Современ-

измерении влияния физических полей на квантовые

ные квантовые сенсоры работают в периодическом

степени свободы атомов. Квантовые сенсоры превос-

режиме, что определяется периодическим режимом

ходят по точности существующие классические сен-

создания ансамбля холодных атомов: охлаждением

соры. К наиболее развитым квантовым сенсорам от-

тепловых атомов, их локализацией, дополнительной

носятся сенсоры, основанные на использовании атом-

стадией охлаждения в атомной ловушке, оптической

ной интерферометрии для измерения инерциальных

накачкой на определенный магнитный подуровень и

сил [1, 2]. К таким сенсорам относятся гравиметры

взаимодействием приготовленного атомного ансам-

[2, 3], градиометры [4, 5] и гироскопы [6]. Точность

бля с заданной последовательностью лазерных (в

современных атомных гравиметров и градиометров

случае гравиметра и градиометра) или микроволно-

уже превосходит точность многих классических ана-

вых (в случае атомных часов) импульсов. Суммарное

логов [7], а их практическое применение демонстри-

время измерения зависит от времени работы на каж-

рует высокую степень надежности [8-12].

дом из этапов экспериментальной последовательно-

Другой тип квантовых сенсоров на основе атом-

сти. Критическим параметром здесь выступает ско-

ной интерферометрии - это атомные часы и стан-

рость охлаждения тепловых атомов и формирова-

дарты частоты [13, 14]. Использование локализован-

ния первичного ансамбля холодных атомов, локали-

ных атомов позволяет создавать компактные систе-

зованного в магнито-оптической ловушке. Этот этап

мы, которые могут быть использованы на борту лета-

является наиболее долгим по времени и определяет

тельных аппаратов. Продемонстрированная стабиль-

частоту получения данных, измеренных квантовым

ность таких часов [15] позволяет говорить о том, что

сенсором. Как правило, уменьшение времени охла-

они могут повысить точность существующих борто-

ждения атомов в магнито-оптической ловушке ведет

вых систем за счет использования холодных атомов.

к уменьшению общего количества атомов, что, в ко-

нечном счете, ведет к увеличению шумов измеряемо-

го квантовым сенсором сигнала.

¹⁾e-mail: afanasiev@isan.troitsk.ru

562

Письма в ЖЭТФ том 115 вып. 9 - 10

2022

Фокусировка атомного пучка для эффективной загрузки атомного чипа

563

В последнее время наблюдается тенденция к

справедливо при пренебрежении третьим слагае-

построению квантовых сенсоров с использованием

мым в уравнении (1). Как видно из выражения

атомных чипов. Данный подход позволяет повы-

(2), для увеличения количества локализованных в

сить степень контроля при приготовлении первич-

МОЛ атомов (вне зависимости от рассматриваемо-

ного атомного ансамбля, используемого для изме-

го приближения) необходимо либо увеличивать эф-

рений физических полей. В случае создания атом-

фективность загрузки, либо уменьшать потери, свя-

ных часов технология атомного чипа позволит со-

занные со столкновениями локализованных атомов

здать компактные часы с точностью, превосходящей

с остаточным газом в камере. В последнем случае

существующие компактные часы. Такие часы могут

это достигается увеличением эффективности откач-

быть установлены на борту летательных аппаратов.

ки вакуумной системы. В настоящее время рабо-

Недавно нами был продемонстрирован однослойный

чее давление остаточных газов в камере при созда-

атомный чип [16], который может выступать в ка-

нии квантовых сенсоров составляет значение поряд-

честве стартовой платформы для создания прецизи-

ка 10^-10 Торр. Такой ультравысокий вакуум необхо-

онных квантовых сенсоров. Основным достоинством

дим и для возможности работы с атомами в состоя-

продемонстрированного подхода является возмож-

нии Бозе-Эйнштейновского конденсата. Дальнейшее

ность непрерывного охлаждения атомов в магнито-

улучшение вакуума является сложной и дорогостоя-

оптической ловушке с использованием только токов,

щей задачей и делает проблематичным создание мо-

протекающих по микропроводам атомного чипа в

бильных квантовых сенсоров.

присутствии внешнего однородного магнитного по-

Другим способом увеличения количества локали-

ля. Однако количество атомов, которые могут быть

зованных атомов в МОЛ является увеличение скоро-

локализованы вблизи продемонстрированного чипа,

сти загрузки R. В классических трехмерных МОЛ, в

ограничено отклонениями магнитного поля в обла-

которых магнитное поле формируется двумя макро-

сти локализации от идеального квадрупольного по-

скопическими катушками в анти-гельмгольцевской

ля в магнито-оптической ловушке [17-19]. Настоя-

конфигурации, данный параметр пропорционален

щая работа посвящена исследованию возможности

размеру лазерных лучей [21, 22]. Это является след-

использования фокусировки атомного пучка в об-

ствием того факта, что квадрупольное поле макро-

ласть локализации с целью увеличения количества

скопических катушек МОЛ позволяет эффективно

локализованных атомов.

производить охлаждение в любой точке лазерного

2. Загрузка атомов в магнито-оптическую

луча. Фактически область захвата атомов в этом слу-

ловушку. Изменение количества атомов в магнито-

чае определяется именно размерами лазерных лучей.

оптической ловушке (МОЛ) подчиняется следующе-

В случае использования атомного чипа ситуация

му выражению [20]:

иная. Аналогом МОЛ вблизи атомного чипа являет-

ся U-образная ловушка (рис. 1). Основой такой ло-

=R-

-β_cN²,

(1)

вушки является магнитное поле, создаваемое током,

протекающим по U-образному микропроводу, в сово-

где N - количество атомов в магнито-оптической ло-

купности с внешним однородным магнитным полем

вушке, R - скорость загрузки атомов, τ - время жиз-

[23]. Поскольку геометрия атомного чипа ограничи-

ни атомов в МОЛ, β_c - коэффициент, характеризую-

вает доступ лазерного поля в области локализации

щий потери ловушки при двухчастичных столкно-

атомов, используется иная конфигурация лазерно-

вениях атомов внутри ловушки. Первое слагаемое

го поля: зеркальный МОЛ. В зеркальной МОЛ один

описывает скорость загрузки атомов в МОЛ, вто-

из охлаждающих лучей распространяется вдоль по-

рое - описывает потери атомов и, как правило, опре-

верхности атомного чипа, а второй отражается от

деляется столкновением атомов с остаточным газом

нее под углом 45^◦. Такая конфигурация лазерных

в вакуумной камере. Последний член отвечает за по-

полей эквивалентна конфигурации, используемой в

тери вследствие двухчастичных столкновений, кото-

классической МОЛ, и можно было бы ожидать, что

рые также ограничивают максимальную плотность в

скорость загрузки атомов в U-образную МОЛ будет

МОЛ на уровне n ∼ 10¹⁰ ат/см³. Максимальное ко-

определяться так же размерами лазерных лучей, од-

личество атомов, которое может быть локализовано,

нако это не так. Основной проблемой загрузки U-

определяется следующим выражением [20]:

образной МОЛ является отклонение распределения

(

)

N =

(1 + 4β_cRτ²)^1/2 - 1

≈ Rτ.

(2)

магнитного поля от квадрупольного поля, которое

2β_cτ

реализуется при использовании двух катушек в анти-

Выражение (2) для количества атомов в МОЛ

гельмгольцевской конфигурации [17]. Для создания

Письма в ЖЭТФ том 115 вып. 9 - 10

2022

2^∗

564

А. Е. Афанасьев, Д. В. Быкова, П. И. Скакуненко, В. И. Балыкин

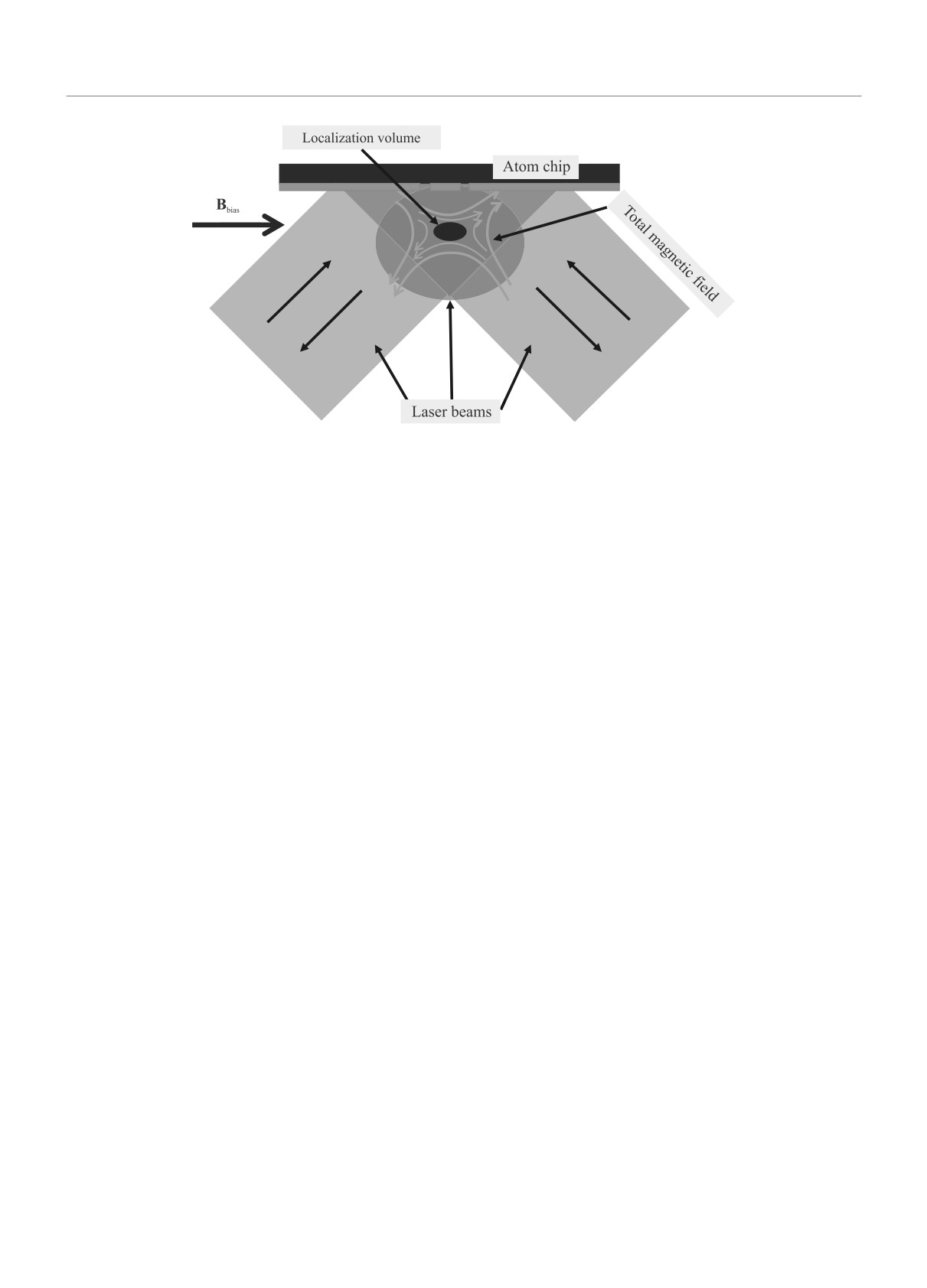
Рис. 1. (Цветной онлайн) Схема U-образной МОЛ с использованием атомного чипа. Объем локализации определяется

областью, в которой отклонение поля от идеального квадрупольного поля не слишком велико

U-образной МОЛ на атомном чипе необходимо ис-

фективной загрузки потенциала U-образной МОЛ

пользовать тонкие провода, и в этом случае распре-

можно использовать промежуточную МОЛ, сформи-

деление магнитного поля отличается от квадруполь-

рованную магнитными катушками в конфигурации

ного поля. Отклонение магнитного поля от квадру-

зеркальной МОЛ [26]. Однако такой подход требу-

польного поля ограничивает объем охлаждения ато-

ет размещения магнитных катушек в малом объеме,

мов. В этом случае скорость охлаждения определя-

что не всегда возможно с технической точки зрения.

ется не геометрическим размером лазерных лучей, а

Иной подход заключается в использовании для

размером области магнитного поля, в котором реа-

загрузки атомов предварительно охлажденных ато-

лизуется режим охлаждения атомов.

мов. Действительно, эффективность загрузки зави-

Существует несколько подходов к решению за-

сит не только от объема, в котором реализованы оп-

дачи эффективной загрузки атомов в U-образную

тимальные условия для охлаждения и локализации,

МОЛ. Наиболее распространенным является увели-

но и от фазовой плотности атомов при скоростях, ко-

чение ширины центральной части U-образного про-

торые могут быть локализованы в U-образной МОЛ.

вода [17-19]. Такой подход использовали ряд науч-

Отклонение магнитного поля от идеального ограни-

ных групп [24], в работах которых для первичного

чивает максимально возможную скорость атомов, с

охлаждения атомов вблизи атомного чипа использу-

которой они могут быть охлаждены и локализованы.

ются широкие макропровода для создания магнит-

Использование предварительного охлаждения поз-

ного поля чипа. Такие макропровода располагаются

воляет повысить число атомов с малыми скоростя-

под основным атомным чипом и выполняют несколь-

ми, что обеспечивает их эффективную загрузку U-

ко задач. Во-первых, они позволяют проводить боль-

образной МОЛ.

шие токи без существенного нагрева макропрово-

Возможным вариантом использования предвари-

да. Это, в свою очередь, позволяет увеличить вре-

тельного охлаждения является загрузка атомов из

мя необходимое для охлаждения атомов. Во-вторых,

предохлажденного атомного пучка. Такой подход

потенциал такой ловушки более приближен к требу-

широко используется не только для загрузки атом-

емому потенциалу в квадрупольном магнитном поле.

ных чипов [24], но и для загрузки классических

Альтернативным вариантом увеличения ширины

трехмерных МОЛ [27]. Предварительное охлаждение

микропровода является предложение по использо-

атомного пучка может быть реализовано с использо-

ванию нескольких микропроводов с разными пара-

ванием Зеемановского охладителя как, например, в

метрами и направлениями токов [25]. В таком под-

работе [27]. Однако такой подход не всегда является

ходе появляется дополнительная возможность опти-

удобным. Другим подходом является использование

мизации распределения магнитного поля в области

источников атомов, формирующих холодные пучки,

локализации атомов. Однако, такая конфигурация

такие как 2D-МОЛ [28], 2D + МОЛ [29] и низкоско-

сложна с технической точки зрения. Также для эф-

ростной интенсивный источник атомов (LVIS) [30].

Письма в ЖЭТФ том 115 вып. 9 - 10

2022

Фокусировка атомного пучка для эффективной загрузки атомного чипа

565

Такие источники позволяют создавать интенсивные

ном направлении от их поперечной скорости, по-

пучки холодных атомов и широко используются для

скольку при насыщении атомного перехода атом в

загрузки атомных чипов [24].

поле 2D-МОЛ можно рассматривать как осциллятор

Одной из особенностей таких систем является

с избыточным демпфированием.

формирование атомного пучка с малой продольной

Для оценки применимости данного подхода к за-

скоростью [29]. Недостатком такого подхода являет-

даче увеличения скорости загрузки МОЛ, сформи-

ся то, что за счет наличия остаточной поперечной

рованной вблизи атомного чипа, рассмотрим взаимо-

скорости и большого времени пролета от LVIS до

действие атома с лазерным полем в присутствии гра-

атомного чипа, в силу малой продольной скорости,

диента магнитного поля. В силу симметрии данная

диаметр атомного пучка в области чипа увеличи-

задача может быть рассмотрена на примере одномер-

вается и может составлять несколько миллиметров.

ной магнито-оптической ловушки (рис. 2). Атомный

Данное обстоятельство не существенно, если первич-

пучок формируется из низкоскоростного источника

ное охлаждение и локализация вблизи атомного чипа

атомов (LVIS) и распространяется вдоль оси Z. Ла-

реализуются с использованием зеркальной МОЛ или

зерное поле сформировано двумя лазерными луча-

U-образной МОЛ, сформированной широкими мак-

ми с круговыми σ⁺-σ^- поляризациями, распростра-

ропроводами. В этих случаях пространственный раз-

няющимися друг на встречу другу вдоль оси X, и

мер области эффективного захвата МОЛ будет срав-

имеет отстройку по частоте относительно резонан-

ним с размером атомного пучка. В случае же, ко-

са покоящегося атома - δ. Основное состояние ато-

гда речь идет о непосредственной загрузке атомного

ма обладает полным моментом F_g = 0, а возбуж-

чипа без использования дополнительных магнитных

денное F_e = 1, полуширина резонансной линии по-

катушек и макропроводов, как, например, в работе

глощения атома - γ (рис. 3). Градиент магнитного

[16], возникает необходимость уменьшения попереч-

поля формируется проводниками с током, располо-

ных скоростей низкоскоростного пучка.

женными вдоль оси Z. В этом случае формирует-

3. Фокусировка атомного пучка. Контроль

ся квадрупольное поле с градиентом вдоль оси X:

поперечной скорости атомного пучка может быть

g = dB/dx. Длина области взаимодействия атома с

произведен тремя способами. Первый способ осно-

лазерным излучением в магнитном поле - L, кото-

ван на создании двумерной оптической патоки на пу-

рая в реальном эксперименте ограничена размера-

ти распространения атомного пучка [31]. Такой спо-

ми лазерного луча. Длина области взаимодействия

соб позволяет произвести коллимацию атомного пуч-

определяет время взаимодействия t_int = L/v_z для

ка и повысить фазовую плотность атомов. Это, в

каждого из атомов, обладающих скоростью v_z вдоль

свою очередь, позволяет получить высокую фазовую

оси Z. На атом с координатой x в зоне взаимодей-

плотность атомов в области их локализации. Другой

ствия действует сила светового давления [36], состо-

способ основан на двумерном сжатии атомного пучка

ящая из двух составляющих: F (Δm_F

= -1), дей-

с использованием двумерной магнито-оптической ло-

ствующая на переходе {F_g = 0, m_F = 0} → {F_e =

вушки [32]. Такие способы контроля поперечной ско-

1, m_F = -1} и F(Δm_F = 1), действующая на пере-

рости атомного пучка активно используются для со-

ходе {F_g = 0, m_F = 0} → {F_e = 1, m_F = 1}. Данные

здания высокоинтенсивных холодных атомных пуч-

силы направлены в противоположные стороны, по-

ков [33]. Двумерное сжатие атомного пучка может

скольку образованы взаимодействием атома с проти-

решить проблему повышения плотности холодных

воположно направленными лазерными лучами. Сум-

атомов в области локализации атомов на атомном

марная сила имеет вид:

чипе. Минусом такого подхода является необходи-

мость использования высоких градиентов магнитно-

F = F(Δm_F = -1) - F(Δm_F = 1) = ℏkγG ×

го поля.





Третьим подходом является использование фоку-





сировки атомного пучка с использованием двумер-

×

(

)₂ -

(

)₂,

ной магнито-оптической ловушки, который может

δ-kx-αgx

δ+kx+αgx

1+G+

быть реализован при меньших градиентах магнит-

ного поля [34, 35]. Этот метод является двумерным

где α - величина сдвига резонансной линии поглоще-

аналогом трехмерного импульсного сжатия магнито-

ния в следствии эффекта Зеемана в магнитном поле

оптической ловушки, рассмотренного в [34]. Основ-

B_x = gx (α = 2π×1.4 МГц/Гс). Как показано в рабо-

ной особенностью такого подхода является независи-

те [34], в рассмотренном приближении точка фоку-

мость точки фокусировки атомов пучка в продоль-

сировки не зависит от поперечной скорости атома.

Письма в ЖЭТФ том 115 вып. 9 - 10

2022

566

А. Е. Афанасьев, Д. В. Быкова, П. И. Скакуненко, В. И. Балыкин

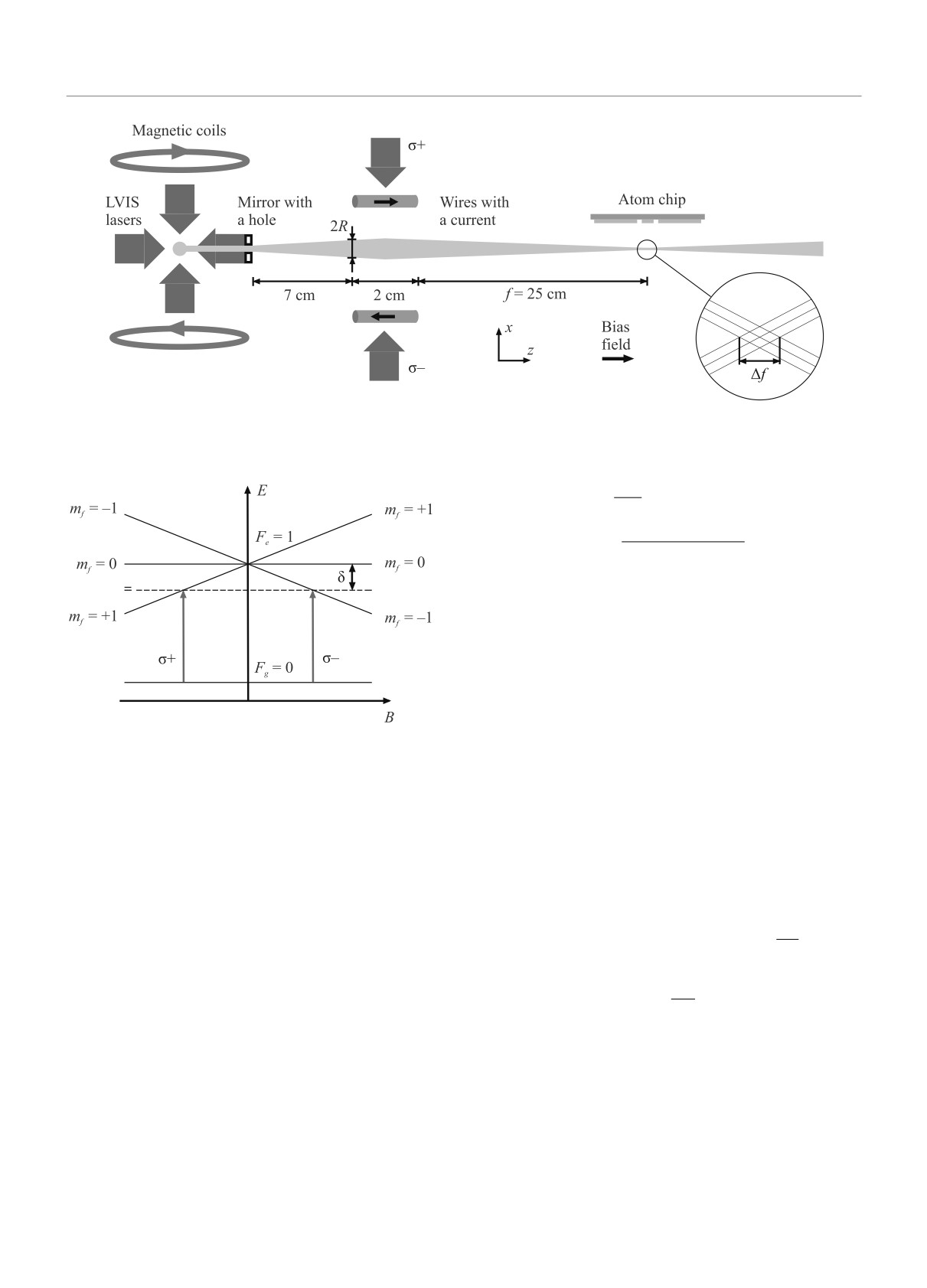
Рис. 2. (Цветной онлайн) Принципиальная схема фокусировки атомного пучка, сформированного из низкоскоростного

атомного источника, в область локализации атомного чипа

αgx

v_x =

(e^βt - 1) + v^0xe^βt,

(3)

4ℏk²γ³Gδ

β =

m((1 + G)γ² + δ²

где m - масса атома, v^0x - начальная поперечная ско-

рость атома. Видно, что при отрицательных отстрой-

ках параметр β < 0 и, в этом случае, атом полу-

чает дополнительный импульс, направленный к оси

Z. Можно определить фокусное расстояние атомной

линзы f как расстояние от зоны двумерной МОЛ до

точки пересечения атомом оси Z.

Из выражения (3) видно, что при выполнении

условия t_int = L/v_z > |1/β| поперечная скорость ато-

Рис. 3. (Цветной онлайн) Энергетическая схема уров-

мов после взаимодействия с 2D-МОЛ не будет зави-

ней атома в линейном изменяющимся вдоль оси X маг-

сеть от начальной поперечной скорости. В таком ре-

нитном поле. Атом обладает полным моментом Fg = 0

жиме атомы взаимодействуют с лазерным полем как

в основном состоянии и Fe = 1 в возбужденном и на-

ходится в лазерном поле, сформированном двумя ла-

осциллятор с избыточным демпфированием. Именно

зерными лучами с круговыми σ⁺-σ^- поляризациями,

это определяет независимость фокусного расстояния

распространяющимися друг на встречу другу и имею-

от поперечной скорости атома. Помимо этого, в этом

щим отстройку по частоте относительно резонанса по-

случае можно пренебречь экспоненциальным членом

коящегося атома - δ

в выражении (3) (при отрицательной отстройке час-

тоты лазерного излучения) и поперечная скорость

При условии δ ≫ αgx + k ˙x (что выполняется при

будет определяться выражением: v_x = -^αgxk , что да-

малых поперечных скоростях атомного пучка, кото-

ет фокусное расстояние:

рые могут быть достигнуты в LVIS) выражение в

kv_z

скобках может быть разложено в ряд. Нас интересует

f =

(4)

αg

значение поперечной скорости атома v_x при пролете

через зону взаимодействия с лазерным излучением.

Из выражения (4) видно, что фокусное рассто-

Его можно определить из второго закона Ньютона

яние зависит от продольной скорости атома и ато-

F = dp/dt, где изменение импульса dp определяет-

мы разных скоростных групп будут фокусировать-

ся временем взаимодействия атома лазерным излу-

ся на разных расстояниях от линзы. Это аналогично

чением t_int. Отсюда, предполагая, что за время вза-

хроматической аберрации обычной линзы. Данный

имодействия с лазерным излучением не происходит

эффект может быть использован для монохромати-

изменение координаты атома вдоль оси X, имеем:

зации атомного пучка [35]. С точки зрения увеличе-

Письма в ЖЭТФ том 115 вып. 9 - 10

2022

Фокусировка атомного пучка для эффективной загрузки атомного чипа

567

ния эффективности загрузки атомного чипа, данный

где d - диаметр атомного пучка на входе в 2D-МОЛ.

эффект носит негативный характер, поскольку огра-

В рассматриваемом случае длина области фокуси-

ничивает возможности сбора всех скоростных групп

ровки Δf связана с фокусным расстоянием f выра-

атомов в области локализации в U-МОЛ.

жением Δf = fΔv_z/v_z, получаем:

Определим размеры области локализации атомов

Δv_z/v_z

Δv_z

в продольном направлении Δf в зависимости от ве-

d_min =

d≈

(6)

2(1 + Δv_z /v_z)

2v_z

личины Δv_z в скоростном распределении атомов в

пучке. Данный размер будет определяться следую-

Из выражения (6) можно оценить требуемый ми-

щим выражением:

нимальный диаметр области локализации d_min

≈

≈ 310 мкм, что меньше оценочного диаметра эффек-

Δf =

Δv_z .

(5)

тивного захвата в работе [16].

αg

На рисунке 4 представлены расчеты траекторий

атомов для случая одномерной фокусировки атом-

Отметим, что в таком режиме фокусное расстоя-

ного пучка с начальным диаметром d₀

= 1мм.

ние и размер области фокусировки не зависят от ин-

В расчетах длина взаимодействия атомов с 2D-МОЛ

тенсивности лазерного излучения. Характерные ско-

принималась равной L = 2 см. Такая геометрия фо-

рости, которые достигнуты в LVIS для атомов руби-

кусировки может быть реализована с использова-

дия [30] следующие: v_z = 14 м/с; Δv_z = 2.7 м/с. В

нием стандартных высоковакуумных элементов. Па-

этом случае для атомов с наиболее вероятной скоро-

раметр насыщения атомного перехода был выбран

стью v_z = 14 м/с фокусное расстояние будет равно

равным G = 10, величина отстройки δ

= -2Γ.

25 см при градиенте магнитного поля порядка g =

В этом случае, при выбранных параметрах, β

= 0.51 Гс/см. При таких параметрах размер области

= -10⁴ c^-1. Принятые выше условия при выводе

фокусировки будет составлять значение Δf = 4.8 см.

выражения (4) удовлетворены для всех скоростей

4. Фокусировка атомного пучка в область

v_z < βL = 200 м/с.

локализации U-МОЛ. Количество атомов в U-

Как уже было сказано ранее, при средней про-

МОЛ будет определяться выражением (2). При этом,

дольной скорости v_z = 14 м/с и v_x = 0.22 м/с раз-

как уже отмечалось выше, скорость загрузки атомов

мер атомного пучка на входе в 2D-МОЛ составляет

R будет определяться не размерами лазерных лучей,

значение d = 3.2 мм. Расчеты проводились для раз-

а размерами области магнитного поля, в котором по-

ных продольных (v_z = 12.7 м/с, v_z = 14 м/с, v_z =

тенциал имеет близкую к квадратичной зависимость

= 15.4 м/с) и поперечных (v_x = 0.22 м/с, v_x = 0 м/с,

от координат. Оценки показывают, что размер такой

v_x = -0.22 м/с) скоростей атомов (рис.4). Из встав-

области для атомного чипа, который был использо-

ки, на которой увеличена область фокусировки, вид-

ван в работе [16], составляет значение порядка 1 мм в

но, что атомы разных продольных скоростных групп

диаметре. Это значит, что поперечные размеры атом-

фокусируются на разных расстояниях, т.е. у линзы

ного пучка должны быть не более 1 мм.

существует хроматическая аберрация. Важно отме-

Рассмотрим атомный пучок, сформированный

тить, что условие δ ≫ αgx+k x, сделанное при выводе

LVIS и имеющий диаметр 1 мм и угловую расходи-

выражения (3), справедливо при v_x < 2.5 м/с.

мость пучка порядка 30 мрад (характерная для LVIS)

Рассмотрим функцию распределения атомов в

[30]. В этом случае при средней продольной скоро-

продольном направлении по оси распространения

сти vz = 14 м/с значение поперечной скорости бу-

атомного пучка и в поперечном в точке фокуса для

дет v_x = 0.22 м/с. Это означает, что на расстоянии

наиболее вероятной скорости атомов (f₀ = 25 см).

l = 7см диаметр атомного пучка будет составлять

Количество атомов N(z) на расстоянии z от 2D-МОЛ

значение d = 3.2 мм. При таком большом размере

будет определяться линейной функцией плотности

атомного пучка часть атомов пучка не захватывает-

∫

ся ловушкой атомного чипа и скорость загрузки ато-

F_z(z) такой, что F_z(z)dz = 1:

мов будет низкой. Для увеличения скорости загруз-

ки необходимо использовать фокусировку атомного

dN_z(z) = N₀F_z(z)dz,

пучка.

где N₀ - количество атомов, прошедших через LVIS.

Легко показать, что минимальный размер обла-

Функция F_z (z), рассчитанная методом Монте-Карло,

сти локализации d_min определяется следующим вы-

представлена на рис. 5a. Ширина данной функции

ражением:

Δf/2

показывает продольные размеры фокусировки с уче-

d_min =

том максвелловского распределения атомов по про-

f + Δf

Письма в ЖЭТФ том 115 вып. 9 - 10

2022

568

А. Е. Афанасьев, Д. В. Быкова, П. И. Скакуненко, В. И. Балыкин

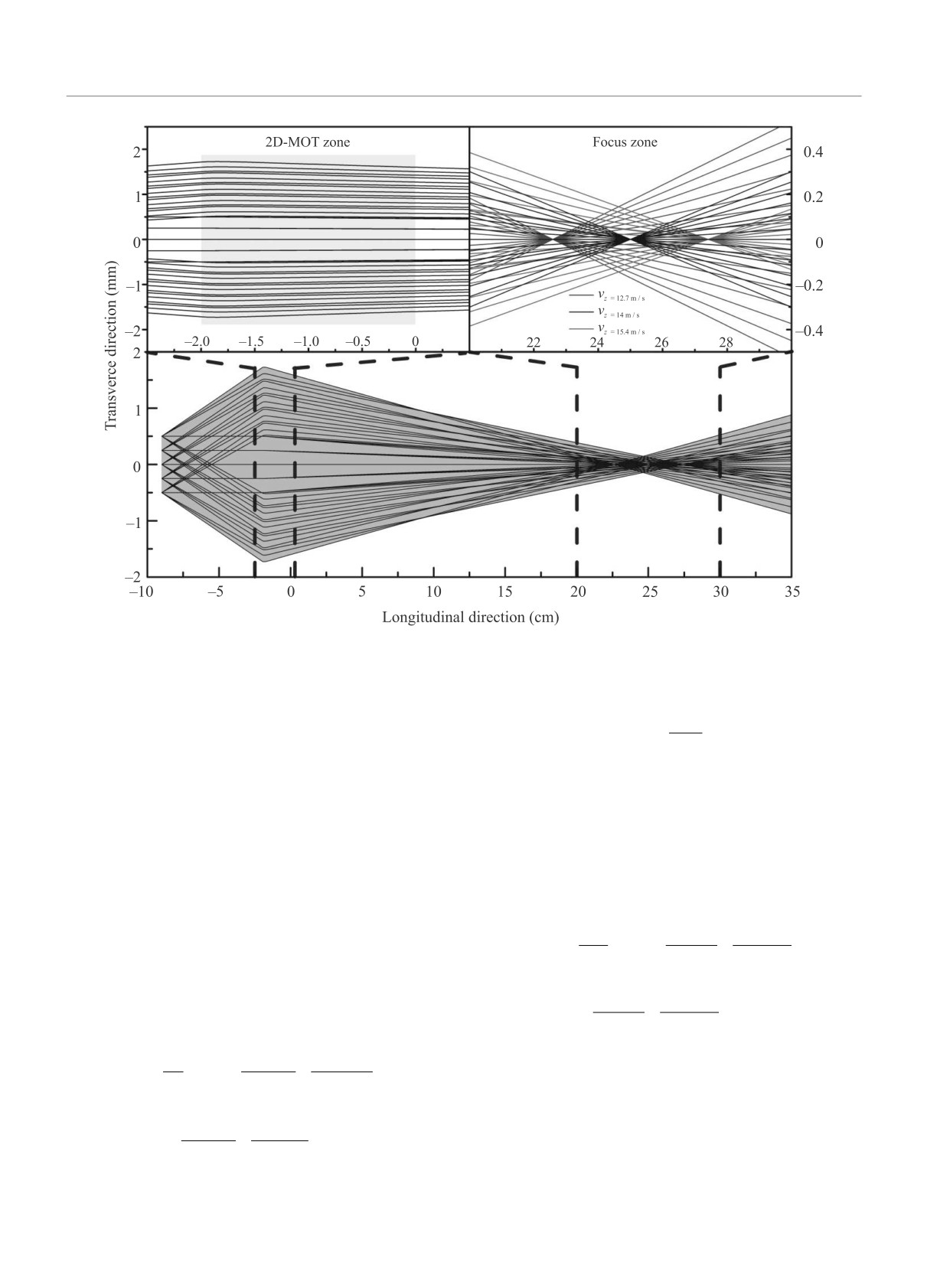
Рис. 4. (Цветной онлайн) Фокусировка атомного пучка. Траектории атомов рассчитаны для разных продольных

(vz

= 12.7 м/с, vz = 14 м/с, vz = 15.4 м/с) и поперечных (vx = 0.22 м/с, vx = 0 м/с, vx = -0.22 м/с) скоростей

атомов

f₀αg

дольным скоростям. Ширина данного распределения

v₀ =

совпадает с рассчитанным по формуле (5).

где v₀ - скорость, соответствующая скоростной груп-

В поперечном направлении можно ввести анало-

пе атомов, которые фокусируются в продольной точ-

гичную функцию распределения F_x(x) такой, что

∫

ке рассмотрения поперечного распределения (в при-

F_x(x)dx = 1:

веденном примере f₀ = 25 см).

-∞

Аналогичное распределение можно получить и в

dN_x(x) = N₀F_x(x)dx.

двумерном случае:

Результаты расчета F_x(x) для одномерного слу-

dN(r, ϕ) = N₀F (r, ϕ)drdϕ,

чая представлены на рис. 5b серой кривой. Видно,

что в поперечном направлении область фокусировки

(∫R

(

)

r^′v₀

r^′2v₀

обладает резко выраженным максимумом. Порядка

F (r, ϕ) =

dr^′ +

πR

(r^′ - r) (r^′ - r)²

90 % всех атомов содержится в области с размерами

200 мкм. Выпишем здесь без вывода аналитическое

∫

(

)

выражение для F_x(x), которое представлено пунк-

r^′v₀

r^′2v₀

+ f

dr^′

, r > 0.

(8)

тирной линией на рис. 5b:

(r^′ + r) (r^′ + r)²

-R

(∫R

(

)

x^′v₀

Порядка 90 % всех атомов содержится в области

F_x(x) =

dx^′ -

(x^′ - x) (x^′ - x)²

с диаметром 250 мкм. В рассматриваемом приближе-

нии увеличение локальной плотности атомов, а сле-

∫0

(

)

довательно и потока, будет равно отношению площа-

x^′v₀

x^′v0

, x > 0,

(7)

дей. Это позволяет говорить о более чем 16-ти крат-

(x^′ + x) (x + x)²

ном увеличении потока атомов в эффективной зоне

-R

Письма в ЖЭТФ том 115 вып. 9 - 10

2022

Фокусировка атомного пучка для эффективной загрузки атомного чипа

569

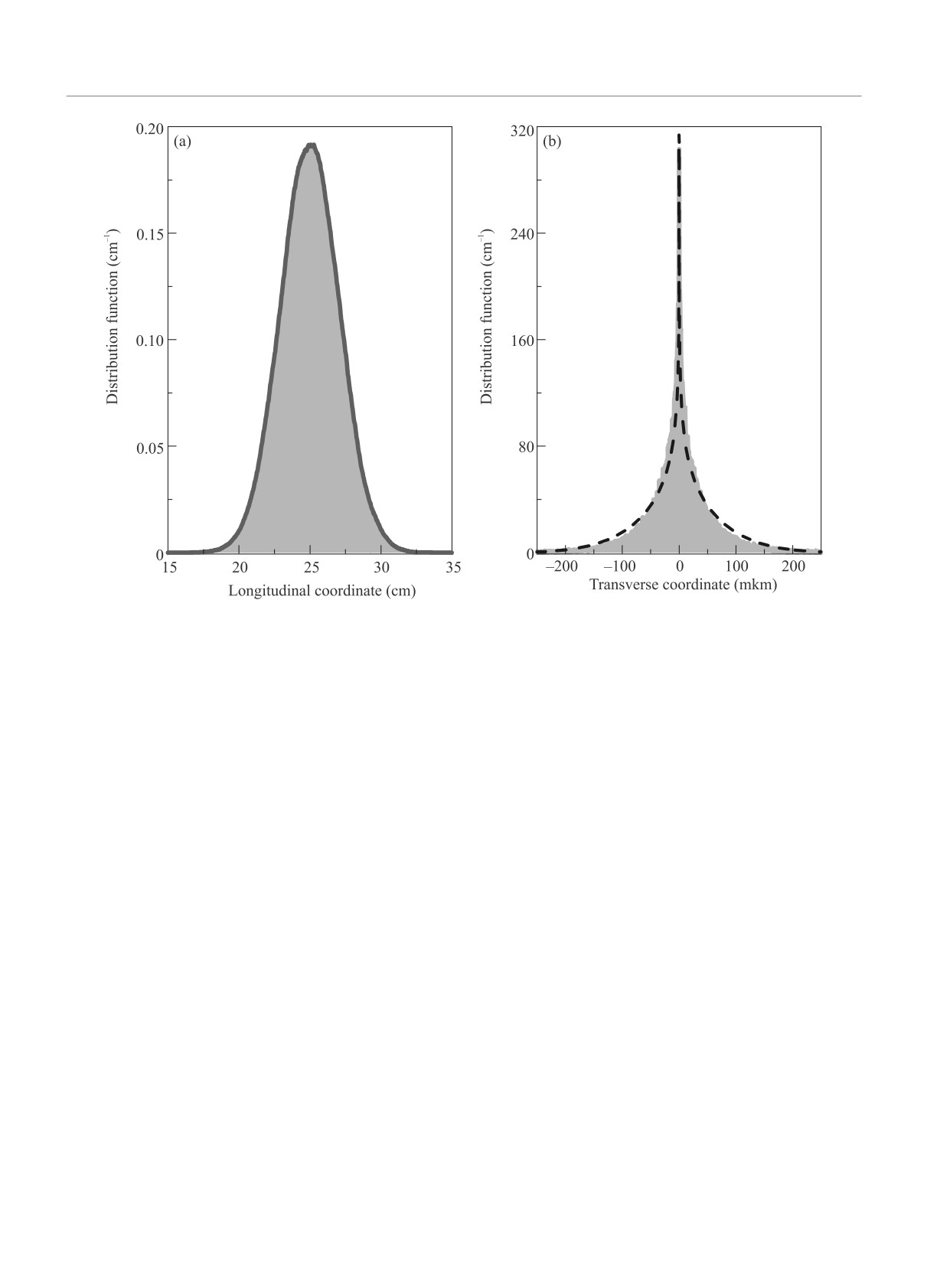
Рис. 5. (Цветной онлайн) Функции распределения атомов в области фокуса атомной линзы в продольном (a) и попереч-

ном (при z = 25 см) направлениях (b). Пунктиром представлена аналитическая кривая, рассчитанная в соответствии

с выражением (7)

локализации атомного чипа по отношению к потоку

импульса атомов при взаимодействии с 2D-МОЛ.

атомов в LVIS и порядка 160-ти кратного увеличения

Учет диффузии может быть проведен относительно

по отношению ко входной апертуре 2D-МОЛ.

легко при малых параметрах насыщения атомного

5. Заключение. В работе рассмотрен подход

перехода. В этом случае существует аналитическое

по увеличению скорости загрузки атомов в U-МОЛ

выражение для тензора, определяющего коэффици-

атомного чипа. В основе рассмотренного подхо-

ент диффузии импульса [37]. Однако при таких пара-

да лежит фокусировка атомного пучка двумерной

метрах не будет реализован режим осциллятора с из-

магнито-оптической ловушкой, расположенной на

быточным демпфированием. Для полного описания

пути распространения атомов от LVIS к атомному

процесса диффузии импульса в описанном в насто-

чипу. Подход на основе фокусировки атомов имеет

ящей статье случае необходимо численное решение

ряд преимуществ по сравнению с подходом на основе

уравнения Фоккера-Планка.

коллимации атомного пучка. Фокусировка позволяет

Поскольку работа атомного чипа является по

сжать атомный пучок в области локализации до раз-

своему характеру периодичной (цикл, состоящий

меров, при которых магнитное поле имеет еще квад-

из загрузки атомов в ловушку и последующего

рупольный характер и способно локализовать атомы.

измерения), то увеличение скорости загрузки поз-

Ранее экспериментально было продемонстрировано

воляет произвести увеличение частоты рабочего

[35], что с использованием такого подхода возможна

цикла загрузки атомов и, как результат, повы-

фокусировка в область порядка 270 мкм, что являет-

шения точности квантовых сенсоров на основе

ся достаточным для увеличения скорости загрузки

холодных атомов. Помимо этого, развитие атом-

атомных чипов, обладающих малой областью лока-

ных чипов может быть востребовано и для ряда

лизации [16].

других экспериментов, например, исследования

Рассчитанная в настоящей работе область фоку-

спектральных свойств холодных атомов [38], иссле-

сировки порядка 250 мкм не учитывает диффузию дования холодной плазмы [39], а также расширит

Письма в ЖЭТФ том 115 вып. 9 - 10

2022

570

А. Е. Афанасьев, Д. В. Быкова, П. И. Скакуненко, В. И. Балыкин

возможности по созданию компактных атомных

19.

V. Singh, V. B. Tiwari, and S. R. Mishra, Laser Phys.

часов [40].

Lett. 17, 035501 (2020).

Исследование выполнено за счет гранта

20.

S. A. Hopkins, PhD thesis The Open University, Milton

Российского научного фонда # 21-12-00323 и гранта

Keynes, England (1996).

Российского фонда фундаментальных исследований

21.

C. Monroe, W. Swann, H. Robinson, and C. Wieman,

#19-29-11004.

Phys. Rev. Lett. 65(13), 1571 (1990).

22.

A. M. Steane, M. Chowdhury, and C. J. Foot, J. Opt.

Soc. Am. B 9(12), 2142 (1992).

R. Geiger, A. Landragin, S. Merlet, and F. Pereira Dos

Santos, AVS Quantum Sci. 2(2), 024702 (2020).

23.

J. Reichel, Appl. Phys. B 74(6), 469 (2002).

G. M. Tino, Quantum Sci. Technol. 6, 024014 (2021).

24.

J. Rudolph, W. Herr, C. Grzeschik, T. Sternke,

A. Grote, M. Popp, D. Becker, H. Müntinga, H. Ahlers,

V. Ménoret, P. Vermeulen, N. Le Moigne, S. Bonvalot,

A. Peters, C. Lämmerzahl, K. Sengstock, N. Gaaloul,

P. Bouyer, A. Landragin, and B. Desruelle, Sci. Rep.

8(1), 12300 (2018).

W. Ertmer, and E. M. Rasel, New J. Phys. 17(6), 065001

(2015).

D. K. Mao, X. B. Deng, H. Q. Luo, Y. Y. Xu, M. K. Zhou,

X.C. Duan, and Z. K. Hu, Rev. Sci. Instrum. 92(5),

25.

S. Jollenbeck, J. Mahnke, R. Randoll, W. Ertmer,

053202 (2021).

J. Arlt, and C. Klempt, Phys. Rev. A 83, 043406 (2011).

C. Janvier, V. Ménoret, B. Desruelle, S. Merlet,

26.

J. Reichel, W. Hänsel, and T. W. Hänsch, Phys. Rev.

A. Landragin, and F. Pereira dos Santos, Phys. Rev.

Lett. 83(17), 3398 (1999).

A 105, 022801 (2022).

27.

A. Golovizin, D. Tregubov, D. Mishin, D. Provorchenko,

C. L. Garrido Alzar, AVS Quantum Sci. 1(1), 014702

and N. Kolachevsky, Opt. Express 29, 36734 (2021).

(2019).

28.

S. Weyers, E. Aucouturier, C. Valentin, and N. Dimarcq,

P. Gillot, O. Francis, A. Landragin, F. Pereira Dos

Opt. Commun. 143(1-3), 30 (1997).

Santos, and S. Merlet, Metrologia 51, L15 (2014).

29.

K. Dieckmann, R. J. C. Spreeuw, M. Weidemüller, and

Y. Bidel, N. Zahzam, C. Blanchard, A. Bonnin,

J. T. M. Walraven, Phys. Rev. A 58(5), 3891 (1998).

M. Cadoret, A. Bresson, D. Rouxel, and

30.

Z. T. Lu, K. L. Corwin, M. J. Renn, M. H. Anderson,

M. F. Lequentrec-Lalancette, Nat. Commun.

E. A. Cornell, and C. E. Wieman, Phys. Rev. Lett.

627 (2018).

77(16), 3331 (1996).

Y. Bidel, N. Zahzam, A. Bresson, C. Blanchard,

31.

V. I. Balykin, V.S. Letokhov, V. G. Minogin,

M. Cadoret, A. V. Olesen, and R. Forsberg, J. Geod.

Yu. V. Rozhdestvensky, and A. I. Sidorov, J. Opt.

94, 20 (2020).

Soc. Am. B 2(11), 1776 (1985).

10.

A.-K. Cooke, C. Champollion, and N. Le Moigne,

32.

J. Nellessen, J. Werner, and W. Ertmer, Opt. Commun.

Geosci. Instrum. Method. Data Syst. 10, 65 (2021).

78(3-4), 300 (1990).

11.

L. Antoni-Micollier, D. Carbone, V. Ménoret, J. Lautier-

33.

J. M. Kwolek, C. T. Fancher, M. Bashkansky, and

Gaud, T. King, F. Greco, A. Messina, D. Contrafatto,

A. T. Black, Phys. Rev. Appl. 13(4), 044057 (2020).

and B. Desruelle, Earth and Space Science Open

34.

V. I. Balykin, JETP Lett. 66, 349 (1997).

Archive, 10.1002/essoar.10510251.1 (2022).

35.

P. N. Melentiev, P. A. Borisov, S. N. Rudnev,

12.

B. Stray, A. Lamb, A. Kaushik et al. (Collaboration),

A. E. Afanasiev, and V. I. Balykin, JETP Lett.

Nature 602, 590 (2022).

83(1), 14 (2006).

13.

P. Rosenbusch, Appl. Phys. B 95(2), 227 (2009).

36.

V. I. Balykin, V.G. Minogin, and V. S. Letokhov, Rep.

14.

P. Böhi, M. Riedel, J. Hoffrogge, J. Reichel,

Prog. Phys. 63, 1429 (2000).

T. W. Hänsch, and P. Treutlein, Nature Phys. 5, 592

37.

S. Chang and V. Minogin, Phys. Rep. 365(2), 65 (2002).

(2009).

38.

A. E. Afanasiev, A. M. Mashko, A.A. Meysterson, and

15.

R. Szmuk, V. Dugrain, W. Maineult, J. Reichel, and

P. Rosenbusch, Phys. Rev. A 92, 012106 (2015).

V. I. Balykin, JETP Lett. 111, 608 (2020).

16.

A.E. Afanasiev, A. S. Kalmykov, R.V. Kirtaev,

39.

B. B. Zelener, E. V. Vilshanskaya, S. A. Saakyan,

A.A. Kortel, P. I. Skakunenko, D.V. Negrov, and

V. A. Sautenkov, B. V. Zelener, and V. E. Fortov, JETP

V.I. Balykin, Opt. Laser Technol. 148, 107698 (2022).

Lett. 113, 82 (2021).

17.

S. Wildermuth, P. Krüger, C. Becker, M. Brajdic,

40.

K. S. Kudeyarov, A.A. Golovizin, A.S. Borisenko,

S. Haupt, A. Kasper, R. Folman, and J. Schmiedmayer,

N. O. Zhadnov, I. V. Zalivako, D. S. Kryuchkov,

Phys. Rev. A 69(3), 030901 (2004).

E. O.

Chiglintsev,

G. A.

Vishnyakova,

18.

V. Singh, V.B. Tiwari, K. A. P. Singh, and S.R. Mishra,

K. Yu. Khabarova, and N.N. Kolachevsky, JETP

J. Mod. Optic. 65(21), 2332 (2018).

Lett. 114, 243 (2021).

Письма в ЖЭТФ том 115 вып. 9 - 10

2022