Письма в ЖЭТФ, том 115, вып. 7, с. 424 - 430
© 2022 г. 10 апреля
Режим сильной связи и осцилляции Раби в GaAs/AlGaAs
гетероструктурах как следствие конденсации электронно-дырочных
пар при комнатной температуре
П.П.Васильев1)
Физический институт им. П. Н. Лебедева РАН, 119991 Москва, Россия
Поступила в редакцию 22 февраля 2022 г.
После переработки 9 марта 2022 г.
Принята к публикации 9 марта 2022 г.
Приведены результаты экспериментов по исследованию когерентных осцилляций оптического поля
в диапазоне ТГц, наблюдавшихся в GaAs/AlGaAs объемных гетероструктурах при генерации импульсов
сверхизлучения. Обнаружены оптические спектры в виде дублетов, характерных для осцилляций Раби
с расщеплением в диапазоне 1.3-4.4 мэВ на длине волны 860-890 нм и соответствующие когерентные ко-
лебания поля во временной области. Эффект возникал только в режиме сильной связи оптического поля
с электронно-дырочной системой. Продемонстрировано, что режим сильной связи в условиях экспери-
мента возможен только при условии конденсации электронно-дырочных пар в фазовом пространстве.
Результаты экспериментов являются еще одним убедительным доказательством конденсации электронов
и дырок в объемном GaAs при комнатной температуре, обсуждавшейся в наших работах ранее.
DOI: 10.31857/S1234567822070047, EDN: fkvuxh
Исследование резонансного взаимодействия
проницаемость среды, а V
- объем, занимаемый
электромагнитного поля с квантовыми система-
оптической модой в среде. Очевидно, что для уве-
ми различной природы является важной частью
личения параметра связи разумно использовать
современной квантовой оптики и квантовых ин-
микрорезонаторы различного типа с малой величи-
формационных технологий [1]. Одним из основных
ной V . Экспериментально и теоретически показано,
фундаментальных эффектов такого взаимодействия
что увеличение числа N взаимодействующих с по-
являются осцилляции Раби, представляющих собой
лем излучателей приводит к росту параметра связи
√
периодический обмен энергией между полем и
по формуле g(N) = g0
N [6, 9, 10]. Необходимым
квантовой средой. В последние годы осцилляции
условием возникновения осцилляций Раби является
Раби интенсивно исследовались в широком спектре
выполнение соотношения
квантовых систем, включая ульрахолодные газы,
квантовые точки, отдельные спины, сверхпроводя-
2g > (κ + γ)/2,
(1)
щие кубиты, экситонные поляритоны в микроре-
где κ - величина, обратная времени жизни фотонов
зонаторах, и др. [2-5]. Возникновение осцилляций
в резонаторе, а γ - скорость спонтанной рекомбина-
Раби характерно не только для взаимодействия
ции [1]. Это соотношение демонстрирует преимуще-
поля с одиночными квантовыми излучателями, но
ства использования высокодобротных резонаторов с
также наблюдалось в экспериментах с ансамблями
малой величиной κ [5, 11-13].
осцилляторов, включая режимы коллективного
Квантовые точки и экситоны-поляритоны в кван-
спонтанного распада (сверхизлучения) [6].
товых ямах, помещенные в микрорезонаторы, яв-
В настоящее время общепризнано, что для
ляются основными полупроводниковыми объектами
возникновения осцилляций Раби необходим ре-
для исследований в области резонаторной кванто-
жим сильной связи между электромагнитным
вой электродинамики [14-16]. В таких устройствах
полем и квантовым излучателем [1, 7, 8]. Количе-
при определенных условиях возможно наблюдение
ственной величиной этой связи является параметр
√
Бозе конденсации экситон-поляритонов при криоген-
g0
= µ
ℏω/2εV , где µ есть матричный элемент
ных температурах [17]. Однако широко распростра-
перехода, ℏω - энергия кванта, ε - диэлектрическая
ненные лазерные гетероструктуры с типичными дли-
нами резонаторов 100-500 микрон никогда ранее не
1)e-mail: peter@lebedev.ru
рассматривались в качестве кандидатов для исследо-
424
Письма в ЖЭТФ том 115 вып. 7 - 8
2022
Режим сильной связи и осцилляции Раби в GaAs/AlGaAs гетероструктурах. . .
425
ваний режимов сильной связи и наблюдения осцил-
ляций Раби. Действительно, при характерных значе-
ниях параметров µ, ε и V величина g0/2π ∼ 108 Гц
или 0.4 мкэВ, что на несколько порядков меньше ти-
пичных значении (κ + γ) [18], делает невозможным
наблюдение этих эффектов в таких структурах.
Однако, как было указано выше, эффективным
методом увеличения связи поля со средой являет-
ся увеличение числа излучателей, взаимодействую-
щих с одной и той же модой поля. В наших преды-
дущих работах [19-22] был экспериментально обна-
ружен факт возникновения сверхизлучающего фа-
зового перехода в лазерных гетероструктурах при
комнатной температуре. При этом оказалось, что,
электронно-дырочный ансамбль обладает дальним
порядком [23], когерентность сверхизлучения пре-
восходит когерентность лазерного излучения, на-
блюдавшегося в этих же образцах, а распростране-
ние импульсов в среде имеет сверхсветовую приро-
ду [23, 24]. Кроме того, сверхизлучение имеет супер-
пуассоновую статистику, а функции Вигнера излу-
чения имеют обширные области отрицательных зна-
чений, что говорит о квантовой природе импульсов
сверхизлучения [25]. В данной работе эксперимен-
тально продемонстрировано, что конденсация элек-
тронов и дырок на дно зон, происходящая при по-
средничестве резонансных фотонов поля при свер-
хизлучающем квантовом переходе, позволяет осуще-
ствить режим сильной связи поля и среды и наблю-
Рис. 1. (Цветной онлайн) Фотографии (вид сверху)
дать осцилляции Раби.
двух гетероструктур с длиной 350 (вверху) и 100 (вни-
В экспериментах использовались модифици-
зу) микрон. Горизонтальная линия соответствует ак-
рованные лазерные гетероструктуры на основе
тивной области шириной 5-6 микрон. Стрелками пока-
GaAs/AlGaAs. Активная область состояла из соб-
заны направления генерируемого излучения
ственного GaAs толщиной
0.2 микрона. Длина
образцов варьировалась от 100 до 450 микрон, шири-
на излучающей области была в пределах 6-7 микрон.
щего фазового перехода [21]. При малых токах на-
Коэффициент отражения от граней образцов равен
качки и отсутствии запирающего напряжения все
0.32. Вдоль оси резонатора формировались три
образцы генерировали стандартное лазерное излуче-
области с целью реализации режима сверхизлуче-
ние, спектр которого состоял из одной или несколь-
ния [20, 22]. Фото двух образцов представлено на
ких продольных мод резонатора. В режиме сверхиз-
рис. 1. Две области, прилегающие к граням струк-
лучения образцы излучали фемтосекундные импуль-
туры, накачивались импульсами тока с амплитудой,
сы с энергией в диапазоне 10-30 пДж, и в определен-
в несколько раз превосходящей порог лазерной
ных диапазонах накачки оптический спектр состоял
генерации.
из дублетов.
Для предотвращения возникновения лазерного
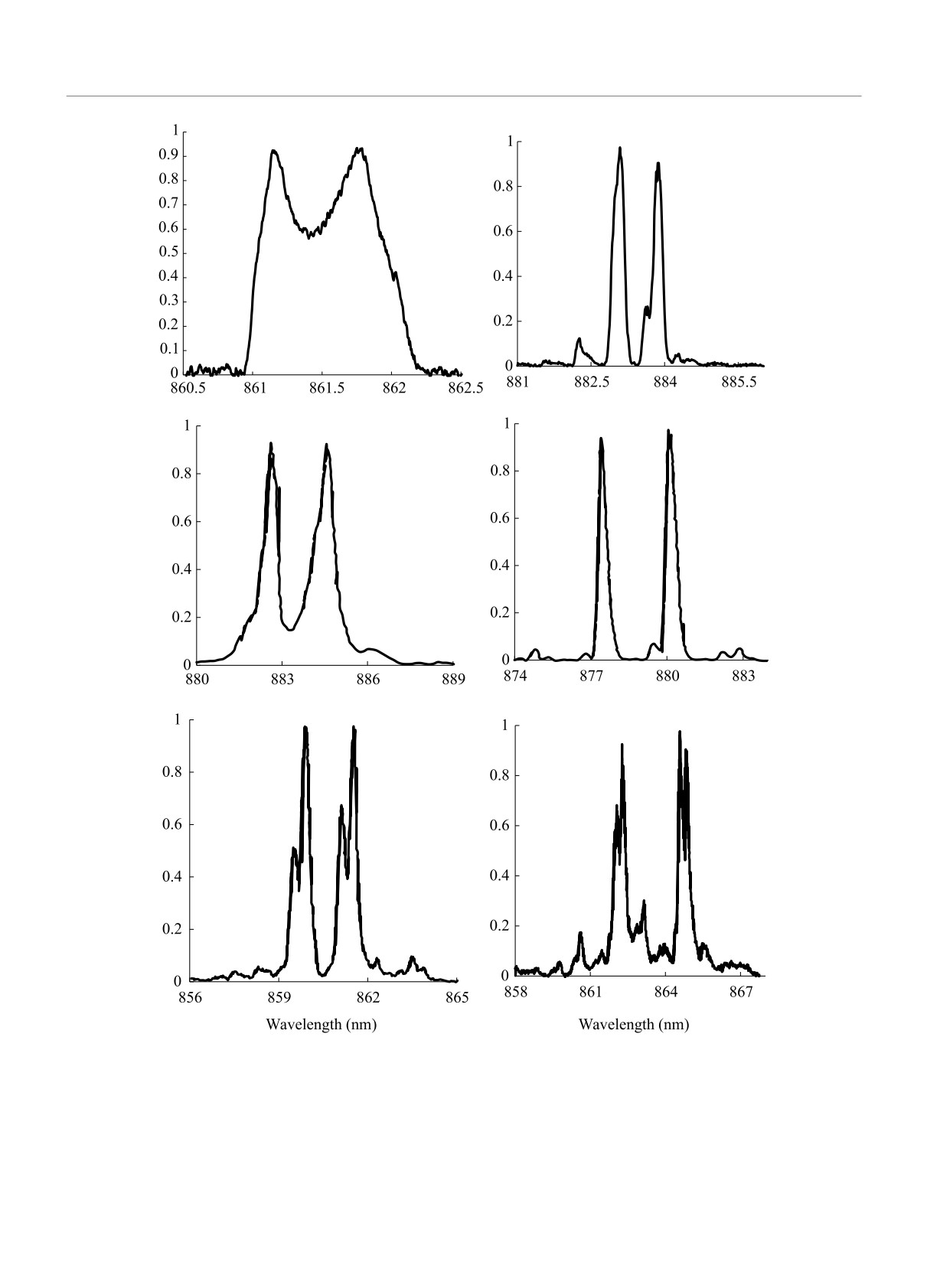
На рисунке 2 представлены типичные дублетные
излучения на центральную часть образцов подава-
спектры сверхизлучения, генерируемого разными об-
лось постоянное запирающее напряжение в диапа-
разцами. Все спектры смещены в длинноволновую
зоне - (1-10)В. Это позволяло получать концентра-
область на более, чем 10 нм по сравнению с со-
ции электронно-дырочных пар более 6 × 1018 см-3,
ответствующими лазерными спектрами. Спектраль-
достичь выполнения критерия квантового вырожде-
ное расщепление между компонентами составляло от
ния [26] и наступления режима нестационарной кон-
0.49 до 2.61 нм в зависимости от параметров струк-
денсации в фазовом пространстве и сверхизлучаю-
тур и параметров накачки.
2
Письма в ЖЭТФ том 115 вып. 7 - 8
2022
426
П.П.Васильев
Рис. 2. Оптические спектры 6 образцов в режиме сверхизлучения
Одновременно с измерениями в спектральной об-
гармоники в сканирующем интерферометре Май-
ласти регистрировались автокорреляционные функ-
кельсона. Эта методика позволяет с фемтосекунд-
ции интенсивности излучения при генерации второй
ной точностью измерить когерентность и параметры
Письма в ЖЭТФ том 115 вып. 7 - 8
2022
Режим сильной связи и осцилляции Раби в GaAs/AlGaAs гетероструктурах. . .
427
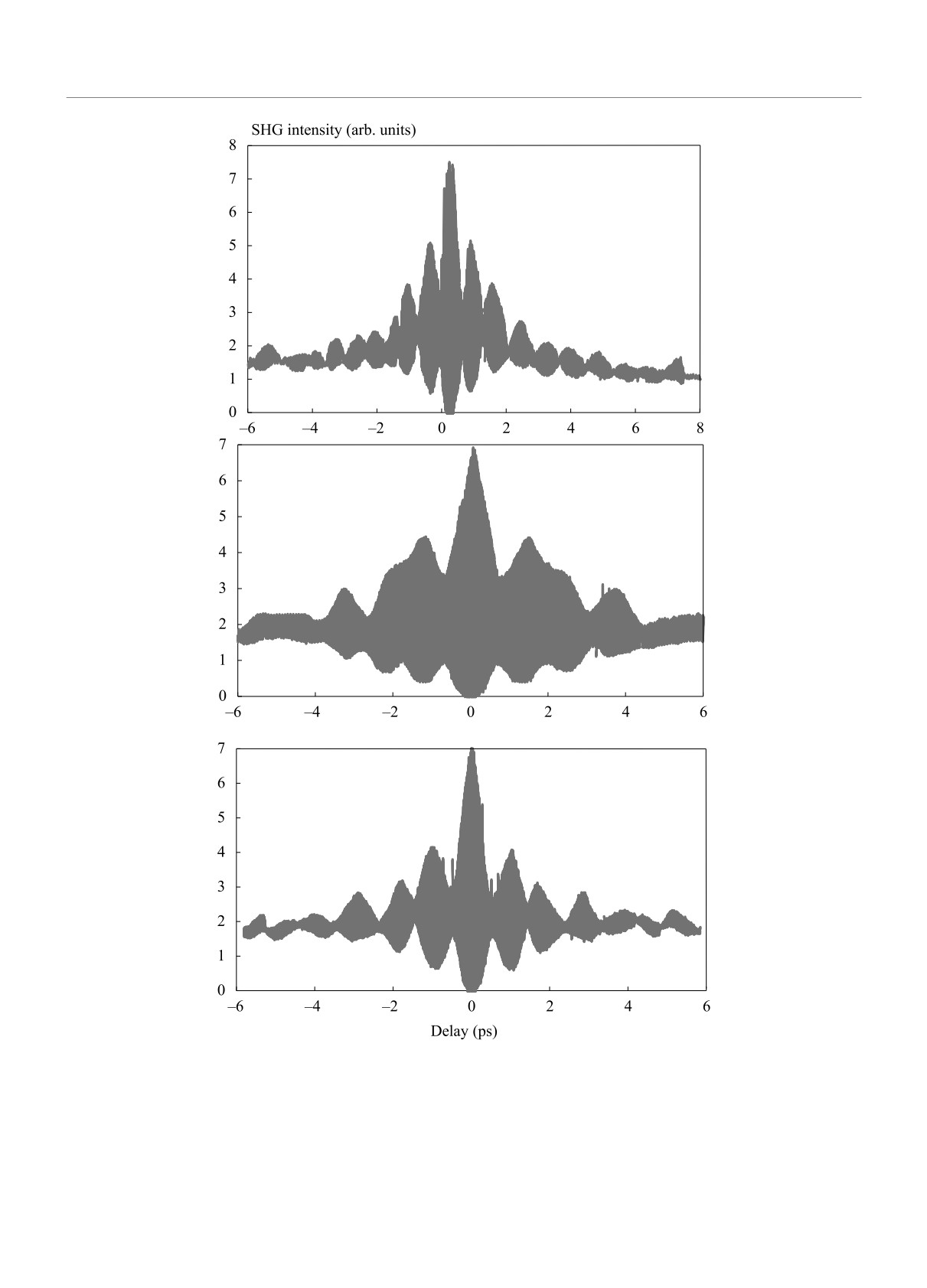
Рис. 3. Автокорреляционные функции 2-го порядка сверхизлучения для образцов S03 при двух значениях запирающего
напряжения (вверху) и H16 (внизу)
осцилляций оптического поля [18]. На рисунке 3 по-
тенсивности, снятые с разрешением по интерферен-
казаны типичные автокорреляционные функции ин-
ционным полосам в сканирующем интерферометре
Письма в ЖЭТФ том 115 вып. 7 - 8
2022
2∗
428
П.П.Васильев
Майкельсона, для двух образцов с длиной резонато-
ра 100 микрон. Время двукратного обхода света в ре-
зонаторе составляло 3.1-3.2 пс. На рисунке 3 хорошо
видны осцилляции поля с частотой около 1 ТГц. Рас-
стояние между компонентами спектральных дубле-
тов и частота осцилляций поля зависели от парамет-
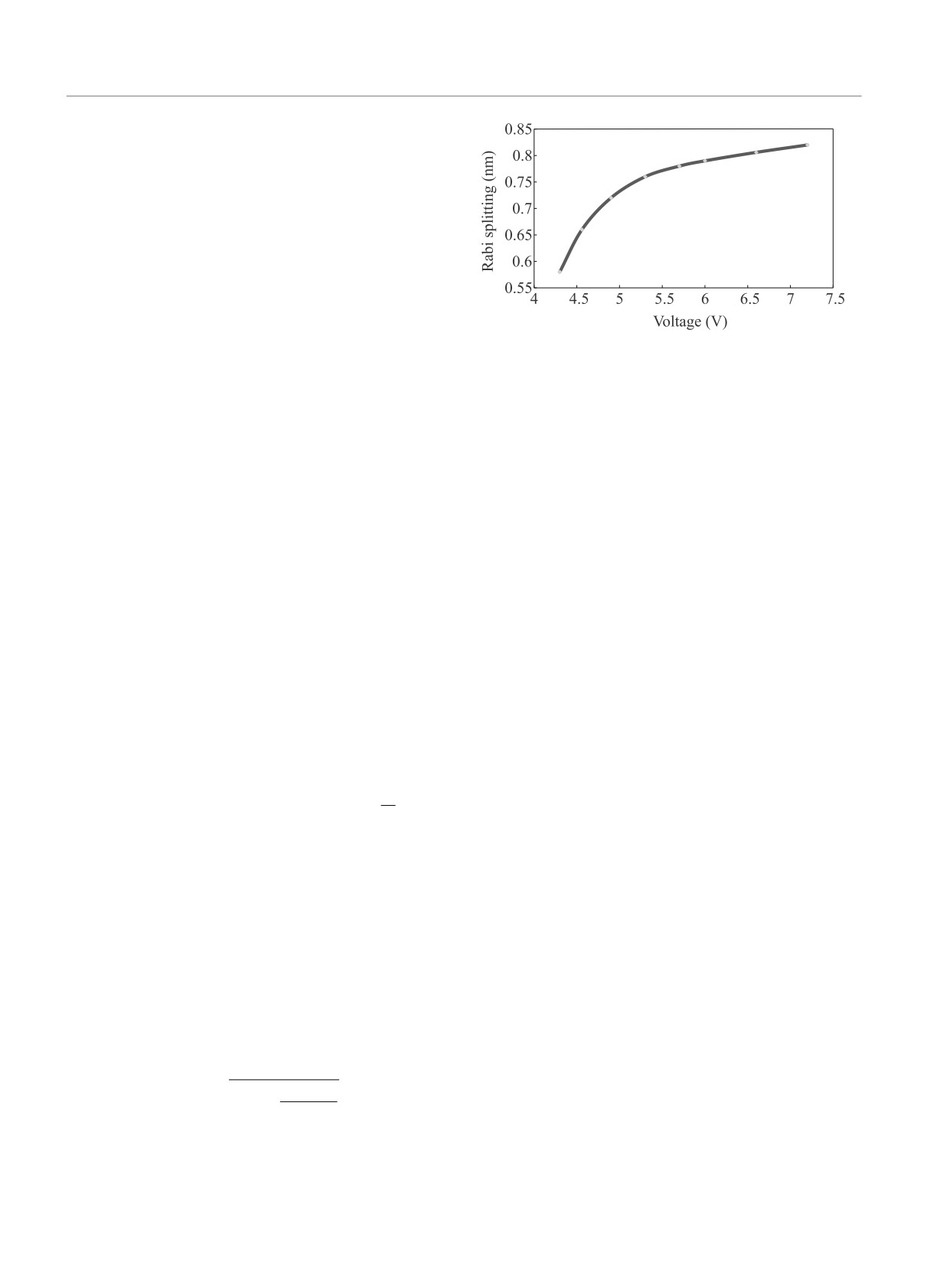
ров накачки. Рисунок 4 иллюстрирует измеренное
спектральное расщепление для одного из образцов
как функцию величины запирающего напряжения.
В таблице 1 приведены параметры 6 образцов
и соответствующие данные измерений. Эксперимен-
тальные данные, представленные на рис. 2-4 и в
Рис. 4. (Цветной онлайн) Расщепление между
табл. 1, можно объяснить в рамках режима сильной
компонентами дублета как функция зпирающего
связи и осцилляций Раби. Действительно, в обычном
напряжения
лазерном режиме в используемых гетероструктурах
наблюдение осцилляций Раби невозможно из-за сла-
проводников, где большую роль могут играть мно-
бой связи электронно-дырочной системы с электро-
гочастичные взаимодействия [30]. Однако ,эта фор-
магнитным полем в резонаторе. Типичная ширина
мула дает качественно правильную оценку часто-
лазерной моды в нашем случае составляет не более
ты Раби и в нашем случае. Действительно, чис-
0.2 нм. Из-за принципа Паули электроны и дырки
ло электронно-дырочных пар, исходя из измерений
сильно “размазаны” по энергии. Поэтому, только ма-
энергии импульсов сверхизлучения, можно оценить
лая часть всех носителей заряда, инжектированных
величиной N = 5.8 × 107-1.2 × 108. Для дипольного
в активную область, взаимодействует с лазерной мо-
момента межзонного перехода µ в GaAs различные
дой. Эту часть легко оценить, зная плотность состо-
публикации дают значения в диапазоне 20-29 Дебай
яний в зонах, пороговую плотность лазерного излу-
[31]. Для значений параметров κ и V , приведенных
чения, длину волны излучения и ширину лазерной
в табл. 1, формула (2) дает величины частоты Ра-
моды. Эта оценка дает значение для величины N при
би Ω/2π = (0.6-1.7)ТГц, что хорошо соответствует
лазерном излучении в диапазоне 103-104, что явно
экспериментальным данным.
недостаточно для выполнения критерия (1). Одна-
Стоит обратить внимание еще на одну важную
ко в процессе сверхизлучающего фазового перехода
деталь. На двух нижних спектрах на рис. 2 отчетливо
происходит нестационарная конденсация электронов
видна тонкая структура дублетов, состоящая из двух
и дырок на дно зон. Этот процесс подробно описан
субгармоник. Появление тонкой структуры можно
нами ранее [21, 27, 28]. В результате конденсации чис-
объяснить взаимодействием квантовых излучателей
ло излучателей, взаимодействующих с полем, быст-
друг с другом. Действительно, как продемонстриро-
√
ро растет, и параметр связи g(N) = g0
N увели-
вано в [8,32,33], учет этого взаимодействия приводит
чивается на много порядков. Когда число N стано-
к более сложной структуре спектра, по сравнению
вится настолько велико, что выполняется критерий
с дублетным спектром, описываемым формулой (2).
(1), то наступает режим сильной связи и, наблю-
Из-за взаимодействия диполей друг с другом воз-
дение осцилляций Раби становится возможным. Ра-
никают субгармоники, и спектр становится ассимет-
нее нами было выяснено, что с ростом запирающего
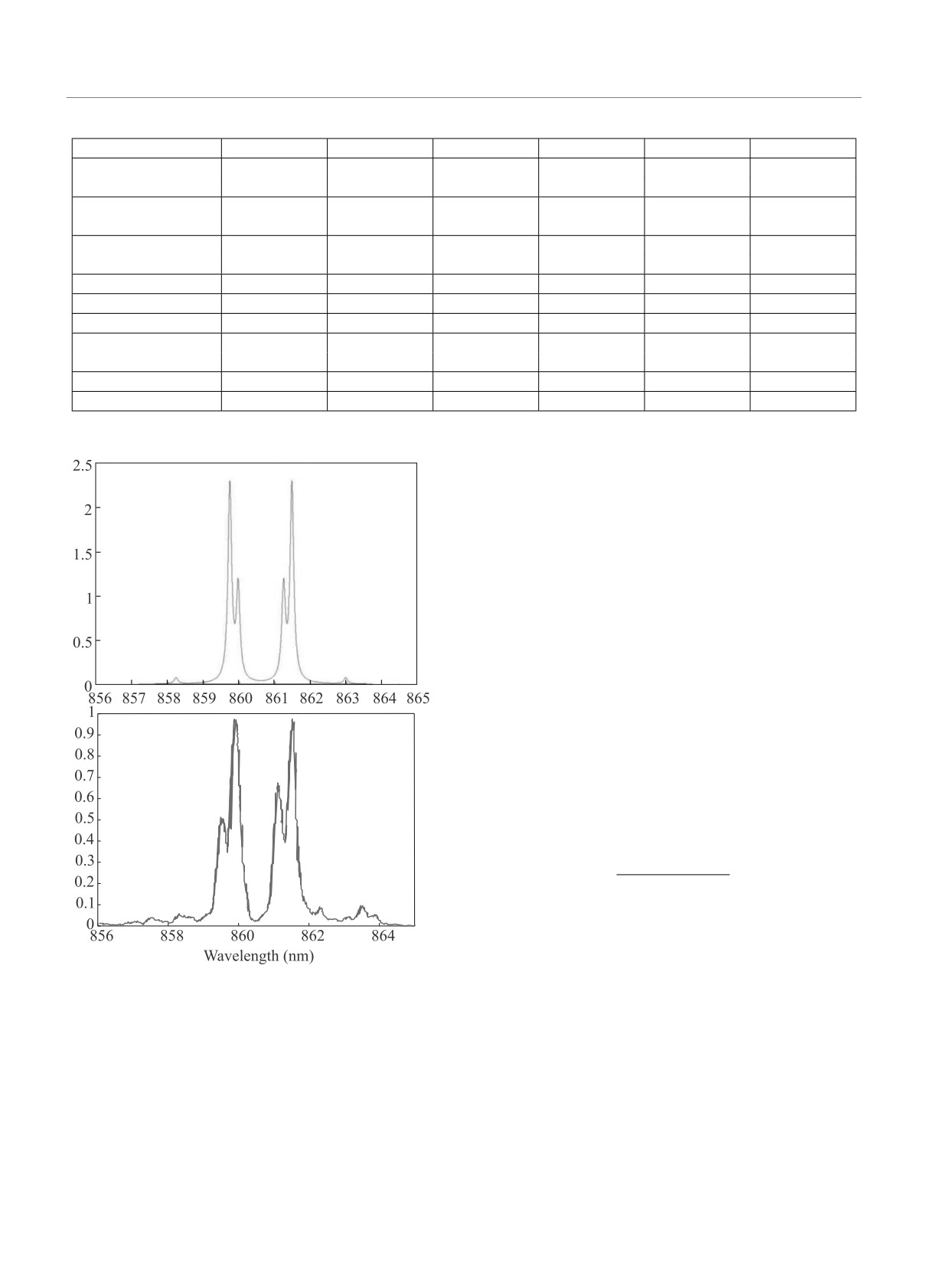
ричным. Автор воспользовался формулой (5.14) из
напряжения увеличивается количество электронно-
работы [8] и формулой (10) из работы [32] и вычис-
дырочных пар, сконденсированных на дно зон и
лил спектр осцилляций Раби для параметров образ-
участвующих в сверхизлучении [29]. Этот факт объ-
ца Н11 из табл. 1. Сравнение рассчетного спектра и
ясняет наблюдаемое увеличение спектрального рас-
экспериментального представлено на рис. 5.
щепления с напряжением,представленным на рис.4.
Формы спектров качественно похожи, хотя и от-
Измеренные величины частоты Раби Ω в табл.1
личаются зеркальным расположением субгармоник.
достаточно хорошо описываются формулой [1]
Другой причиной возникновения тонкой структуры
√
спектра осцилляций Раби может быть неоднородное
2
(κ - γ)
Ω=2
g20N -
(2)
пространственное заполнение резонатора когерент-
4
ным электронно-дырочным состоянием и его разде-
Строго говоря, это выражение имеет ограниченную
ление на две симметричные части. Этот вопрос тре-
применимость в случае сильно возбужденных полу-
бует дополнительного исследования.
Письма в ЖЭТФ том 115 вып. 7 - 8
2022
Режим сильной связи и осцилляции Раби в GaAs/AlGaAs гетероструктурах. . .
429
Таблица 1. Экспериментальные результаты
Образец
H11
S03
H16
C13
D07
B08
Длина волны
861
856
864
885
879
881
излучения (нм)
Длина резонатора
100
100
100
150
150
350
(микрон)
Межмодовое
0.81
0.84
0.83
0.68
0.67
0.26
расстояние (нм)
Q
1.35 × 104
1.35 × 104
1.35 × 104
1.98 × 104
1.97 × 104
4.63 × 104
V (см-3)
1.2 × 10-10
1.2 × 10-10
1.2 × 10-10
1.8 × 10-10
1.8 × 10-10
4.2 × 10-10
k/2pi (TГц)
0.74
0.74
0.74
0.50
0.50
0.21
Спектральное
1.79
2.72
2.52
0.84
2.49
2.37
расщепление (нм)
Ω/2π (TГц)
0.72
1.09
1.01
0.32
0.97
0.91
Ω (мэВ)
2.91
4.41
4.09
1.29
3.92
3.65
лучения. Продемонстрировано, что в отличие от ла-
зерного режима в этих структурах, когда суще-
ствует режим слабой связи, в случае сверхизлуче-
ния наблюдается режим сильной связи поля с полу-
проводниковой средой. Показано, что режим силь-
ной связи в условиях эксперимента возможен только
при условии конденсации достаточно большого чис-
ла электронно-дырочных пар в фазовом простран-
стве. Обнаружены осцилляции Раби со спектраль-
ным расщеплением в диапазоне 1.3-4.4 мэВ на длине
волны 860-890 нм и соответствующие когерентные
колебания поля во временной области с частотами
до 1.1 ТГц. Результаты экспериментов являются еще
одним убедительным доказательством конденсации
электронов и дырок в объемном GaAs при комнат-
ной температуре, обсуждавшейся в наших работах
ранее.
В заключение автор выражает благодарность
Х. Кан и Х. Ота за создание образцов гетерострук-
тур и Р.Пенти за поддержку.
1. G. S. Agarwal, Quantum Optics, Cambridge University
Press, Cambridge (2012).
2. Y. Ota, D. Takamiya, R. Ohta, H. Takagi, N. Kumagai,
S. Iwamoto, and Y. Arakawa, Appl. Phys. Lett. 112,
093101 (2018).
Рис. 5. (Цветной онлайн) Вычисленный с учетом меж-
3. W. Guerin, T. S. do Espirito Santo, P. Weiss, A. Cipris,
дипольного взаимодействия (вверху) и эксперимен-
J. Schachenmayer, R. Kaiser, and R. Bachelard, Phys.
тальный (внизу) спектр осцилляций Раби
Rev. Letts. 123, 243401 (2019).
4. F. Yoshihara, Y. Nakamura, F. Yan, S. Gustavsson,
J. Bylander, W. D. Oliver, and J.-S. Tsai, Phys. Rev.
Таким образом, в данной работе были исследо-
B 89, 020503 (2014).
ваны дублетные спектры и соответствующие коге-
5. G. Khitrova, H. M. Gibbs, M. Kira, S. W. Koch, and
рентные осцилляции оптического поля, генерируе-
A. Scherer, Nat. Phys. 2, 81 (2006).
мые объемными полупроводниковыми гетерострук-
6. Y. Kaluzny, P. Goy, M. Gross, J. M. Raimond, and
турами на основе GaAs/AlGaAs в режиме сверхиз-
S. Haroche, Phys. Rev. Lett. 51, 1175 (1983).
Письма в ЖЭТФ том 115 вып. 7 - 8
2022
430
П.П.Васильев
7. D. S. Dovzhenko, S. V. Ryabchuk, Yu. P. Rakovich, and
19. П. П. Васильев, Х. Кан, Х. Ота, Т. Хирума, ЖЭТФ
I. R. Nabiev, Nanoscale 10, 3589 (2018).
120, 1486 (2001).
8. A. F. Kockum, A. Miranowicz, S. De Liberato,
20. P. P. Vasil’ev, H. Kan, H. Ohta, and T. Hiruma, JETP
S. Savasta, and F. Nori, Nat. Rev. Phys. 1, 19 (2019).
96, 310 (2003).
9. G. S. Agarwal, J. Opt. Soc. Am. B 2, 480 (1985).
21. P. P. Vasil’ev, Phys. Stat. Sol. (b) 241, 1251 (2004).
10. S. Rudin and T. L. Reineckle, Phys. Rev. B 59, 10227
22. П. П. Васильев, Письма в ЖЭТФ 82, 129 (2005).
(1999).
23. P. P. Vasil’ev, V. Olle, R. V. Penty, and I. H. White, EPL
11. C. Weisbuch, M. Nishioka, A. Ishikawa, and Y. Arakawa,
104, 40003 (2013).
Phys. Rev. Lett. 69, 3314 (1992).
24. P. P. Vasil’ev, R. V. Penty, and I. H. White, Light Sci.
12. A. A. Anappara, S. De Liberato, and A. Tredicucci,
Appl. 5, e16086 (2016).
Phys. Rev. B 79, 201303(R) (2009).
25. P. P. Vasil’ev and R. V. Penty, New J. Phys. 22, 083046
13. С. С. Демирчян, И. Ю. Честнов, С. М. Аракелян,
(2020).
А.П. Алоджанц, А.В. Кавокин, Письма в ЖЭТФ
26. P. P. Vasil’ev and R. V. Penty, EPL 133, 37004 (2021).
103, 56 (2016).
27. P. P. Vasil’ev and I. V. Smetanin, Phys. Rev. B 74,
14. H. Kamada, H. Gotoh, J. Temmyo, T. Takagahara, and
125206 (2006).
H. Ando, Phys. Rev. Lett. 87, 246401 (2001).
28. П. П. Васильев, Письма в ЖЭТФ 115, 35 (2022).
15. S. V. Poltavtsev, M. Reichelt, I. A. Akimov,
29. P. P. Vasil’ev, Rep. Prog. Phys. 72, 076501 (2009).
G. Karczewski, M. Wiater, T. Wojtowicz,
30. M. Kira and S. W. Koch, Semiconductor Quantum
D. R. Yakovlev, T. Meier, and M. Bayer, Phys.
Optics, Cambridge University Press, Cambridge (2012).
Rev. B 96, 075306 (2017).
31. A. Schülzgen, R. Binder, M. E. Donovan, M. Lindberg,
16. J. Cao, S. De Liberato, and A. V. Kavokin, New J. Phys.
K. Wundke, H.M. Gibbs, G. Khitrova, and
23, 113015 (2021).
N. Peyghambarian, Phys. Rev. Lett. 82, 2346 (1999).
17. H. Deng, H. Haug, and Y. Yamamoto, Rev. Mod. Phys.
32. A. Joshi and S. V. Lawande, J. Mod. Opt. 40, 1035
82, 1489 (2010).
(1993).
18. P. Vasil’ev, Ultrafast Diode Lasers: Fundamentals and
33. G. S. Agarwal, R. K. Bullough, and N. Nayak, Opt.
Applications, Artech House, Norwood (1995).
Commun. 85, 202 (1991).
Письма в ЖЭТФ том 115 вып. 7 - 8
2022