ВВЕДЕНИЕ
Исследования механизма горения октогена (НМХ) ведутся уже более пятидесяти лет [1–14]. При этом механизм горения рассматривался в качестве устойчивого одномерного режима как в конденсированной (к), так и в газовой фазах волны горения. Хотя в ряде работ отмечался (особенно при низких давлениях – атмосферных и субатмосферных) нестабильный характер горения октогена [2]. По форме пламени неустойчивый режим наблюдался в диапазоне давлений 1.8–3 атм [6]. Периодические колебания температуры в зоне пламени (пульсации температуры ±200 K) имели место при давлениях <1 атм, а устойчивое горение наблюдалось при давлениях >2 атм [7, 9, 11]. На временнóй развертке профилей концентраций вeществ регистрировались периодические пульсации, связанные с нестабильным горением – с изменением скорости горения октогена [12], колебаниями как скорости оттока продуктов сгорания, так и их светимости [8]. Отмечался сильный разброс значений скорости горения, полученных на малых базах измерения, и температур поверхности горения до ±35% [1, 13].
Цель настоящей работы – не только обосновать очаговый механизм горения октогена (по крайней мере при давлениях 0.5–60 атм), возникающего благодаря зафиксированным очагам [15–17] и локальным скоростям горения [18], но и показать закономерную для поперечных волн связь разброса значений локальных скоростей и температур поверхности, значительно превышающего возможные ошибки измерения.
ЭКСПЕРИМЕНТ
В нашей работе [15] на рис. 1 представлены результаты исследования механизма горения октогена при давлениях 0.5–50 атм. Показано, что нормальная средняя скорость горения описывается законом U = 0.36р0.81, где [U] = мм/c, [р] = атм. Эта зависимость описывает наши данные с точностью ±3%, а данные работ [1, 2, 4–7, 9, 11–14] – с точностью до ±15%. Вместе с тем в работе [15] показано, что октоген горит в очаговом режиме; определен размер очагов.
Рис. 1.
Зависимость размеров очагов от скорости горения. Темные точки – максимальные размеры очагов – Lmax; светлые – размеры очагов Lav, зафиксированные на тех же поверхностях горения и отличающиеся от максимальных; 1 – среднеквадратичная зависимость U для максимальных размеров очагов (1); 2 – среднеквадратичная зависимость U по всем размерам очагов.
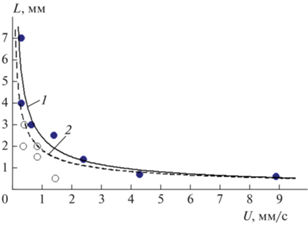
Представленные на рис. 1 зависимости характерных размеров очагов от скорости горения при ее изменении в диапазоне 0.3–10 мм/с (при давлениях 0.5–60 атм) имеют вид
Заметим, что зависимость (1) хорошо описывает максимальные размеры очагов, которые точнее отражают характерные размеры очагов, поскольку момент гашения был случайным и на погашенной поверхности горения очаги могли находиться в различных стадиях развития.Поскольку фронт горения очага – это фронт поперечной волны, очаговый режим горения характеризуется наличием локальных скоростей горения (Un) на фронте. Величину Un можно получить из анализа температурного распределения в конденсированной фазе, что было сделано в нашей работе [18].
На рис. 2 приведены значения локальных скоростей Un, полученные из анализа зависимостей T(t) – изменения температуры во времени в к-фазе. На отдельных временны́х отрезках зависимостей, соответствующих большим временам релаксации теплового слоя, выбирали прямолинейные отрезки. Эти температурные распределения считали “михельсоновскими” и по крутизне профилей оценивали локальные скорости горения по формуле
Рис. 2.
Разброс значений локальных скоростей Un относительно средней нормальной скорости горения U0 при давлениях от 0.5 до 50 атм и начальной температуре T00 = 20 °С: ○ – U0 – настоящая работа; ∆ – Un – настоящая работа; ◊ – Un из [1]; ◻ – Un из [13]; 1 – U00/e; 2 – ${{{{U}_{{00}}}} \mathord{\left/ {\vphantom {{{{U}_{{00}}}} {\sqrt е }}} \right. \kern-0em} {\sqrt е }};$ 3 – U00 = 0.36р0.81, где [U] = мм/с, [p] = атм; 4 – U(p) при Т0 = 152 °С [13]; 5 – U(p) при Т0 = 150 °С; 6 – U(p) при Т0 = 300 °С.
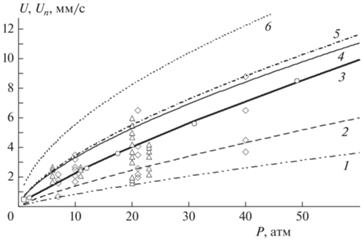
На рис. 2 представлены следующие зависимости: кривая 1 показывает критические значения скоростей, U/e, ниже которых горение прерывается из-за предельной кривизны поверхности горения; кривая 2 отвечает скоростям ${U \mathord{\left/ {\vphantom {U {\sqrt е }}} \right. \kern-0em} {\sqrt е }}$ – критическим значениям, ниже которых невозможно горение из-за потери устойчивости режима, согласно нестационарной теории горения Зельдовича–Новожилова [19–23]; кривая 3 – зависимость средней нормальной скорости от давления: U00 = 0.36р0.81, где [U] = мм/с, [p] = атм: кривые 1–3 получены для значений давления в диапазоне от 0.5 до 60 атм и при начальной температуре T00 = = 20 °С. Кривая 4 – зависимость U(p) при Т0 = 152 °С [13]. Данные для построения кривых 5 и 6 получены по зависимости U = U0 + α(T – T0), которая удовлетворительно описывает табличные данные из работ [1, 9, 13] в диапазоне начальных температур 0–150 °С и дает возможность провести экстраполяцию до 300 °С. Заметим, что коэффициент температуропроводности α зависит от давления согласно табл. 1.
Таблица 1.
Зависимость коэффициента температуропроводности α от давления
| р, атм | α, мм/с |
|---|---|
| 1 | 0.003 |
| 5 | 0.005 |
| 10 | 0.008 |
| 20 | 0.011 |
| 40 | 0.013 |
| 50 | 0.014 |
Как видно из рис. 2, зависимости 1 и 6 полностью ограничивают область разброса значений локальных скоростей. Заметим, что в работе [13] отмечается: “Как видно из рис. 5 (от автора: на рис. 5 приведены зависимости U(T0) для давлений 0.1 и 0.5 МПа), разброс значений скорости горения НМХ достигает 35%, что значительно превышает обычную ошибку измерения 5%… С повышением давления различия в скоростях заметно уменьшаются”.
Значительный разброс значений локальных скоростей горения объясняется механизмом очагового горения, осуществляемого поперечными волнами. Так, начальная температура T0 перед верхними участками профиля поперечной волны, распространяющейся по “негорящей “ поверхности образца, в том числе за счет кривизны фронта горения [24], может составлять ~100–300 °С, что, согласно [1, 9, 13, 14], даст увеличение скорости горения (см. зависимости 4, 5 и 6 на рис. 2). Минимальные значения Un могут быть связаны с кривизной нижней части профиля волны, что на пределе приводит к уменьшению скорости U в е раз [19]. Заметим также, что в зависимости от геометрической формы образца и уровня теплопотерь критическая скорость горения может быть меньше адиабатической скорости Uad в $\sqrt е $ раз [20], в е раз [21, 22], и даже в е2 раз [23]. Так что полученный разброс значений Un, значительно превышающий ошибку измерений, является естественным и представляет собой набор скоростей на фронте поперечных волн.
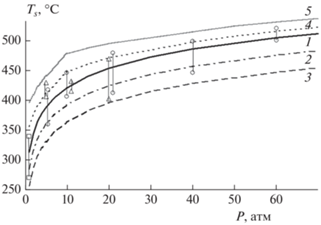
Наряду с широким разбросом значений Un анализ температурных профилей показывает и разброс температур поверхности Ts, определенных по излому профиля при выходе термопары из к-фазы в газовую фазу. Рисунок 3 демонстрирует этот разброс значений температуры поверхности в зависимости от локальной скорости. Аналогичный разброс значений отмечается и в работе [13]: “Несмотря на то, что в интервале 0.1–0.5 МПа перегиб на профиле виден достаточно четко, разброс данных, тем не менее, довольно значителен (до 40 К)”.
Рис. 3.
Разброс значений температуры поверхности Ts при скоростях горения U в диапазоне давлений 1–60 атм [1]: ○ – разброс значений Ts (максимальное и минимальное значения соединены вертикальным отрезком прямой) при заданных значениях U и Т0 = = 20°С; ∆ – то же, но при Т0 = 100 °С; 1 – осредненные значения Ts (U) при Т0 = 20 °С; 2 – осредненные значения Ts(U) при Т0 = 100 °С.
Покажем, что значительный разброс температур поверхности горения – результат широкого набора локальных скоростей горения на фронте поперечной волны. Рассмотрим “однозначную” зависимость скорости горения от температуры поверхности, теоретически представленную и экспериментально подтвержденную на примере исследований пороха марки Н в работе [25]. Зависимости Ts(U), полученные в работах [1, 9, 13, 14, 26], представлены на рис. 4. Здесь зависимости 1–4 получены методом наименьших квадратов с использованием значений U (мм/с), Ts (°С) и p (атм) из таблиц, представленных в работе [1]:
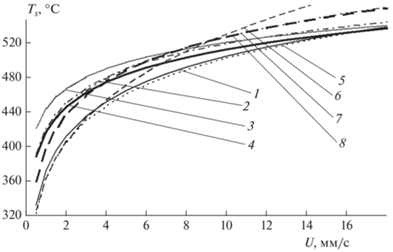
Рис. 4.
Зависимость температуры поверхности от скорости горения октогена: 1 – Ts(U) при Т0 = 20 °С [1]; 2 – Ts(U) при Т0 = 100 °С [1]; 3 – Ts (U) при Т0 = –170 °С [1]; 4 – Ts(U) при Т0 = –170, 20 и 100 °С –зависимость, построенная по совокупности данных для зависимостей 1–3; 5 – Ts(U) при Т0 = –170, 20 и 100 °С [9]; 6 – Ts(U) при Т0 = –170, 20 и 100 °С [14, 27 ] ; 7 – Ts(U) [13]; 8 – Ts(U) – зависимость, построенная по совокупности данных зависимостей 4–7.
1 – Ts = 372 + 57.6lnU при Т0 = 20 °С (R = 0.99, SD = 6.4);
2 – Ts = 421 + 42.6lnU при Т0 = 100 °С (R = 0.995, SD = 6.0);
3 – Ts = 444 + 33.2lnU при Т0 = –170 °С (R = 0.977, SD = 10);
4 – Ts,av = 417 + 41.4lnU, по совокупности данных при Т0 = –170, 20 и 100 °С;
5 – Ts = 364 + 60lnU, по совокупности данных при Т0 = –170, 20 и 100 °С (R = 0.99, SD = 8.45) [9];
6 – Ts = [7050/(11.08 – lnU)] – 273 при Т0 = –170, 20 и 100 °С, получена путем преобразования зависимости m = 1.1 ∙ 104exp(–28 000/2RTs), где [m] = = г/см2 · с, [Ts] = K, ρ = 1.7 г/см3 для 1< р < 100 атм и Ts < 773 К [14, 26];
7 – lnp = –14092/Ts + 21.72, применялась с использованием U = 0.36р0.81 [13];
8 – Ts,av = 398 + 56lnU (R = 0.955, SD = 18.4, N = = 26) – зависимость, построенная по совокупности данных зависимостей 4–7. Как видно из рис. 4, зависимость 8 описывает все имеющиеся данные в диапазоне начальных температур от –170 до 100 °С c точностью ±10%.
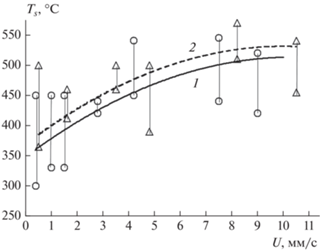
Так как при определении локальных скоростей Un из профиля температур не представляется возможным найти температуру поверхности Ts, соответствующую конкретному значению Un, в соответствии с однозначной зависимостью определим области разброса значений Ts, отвечающие областям разброса значений Un (рис. 5). Кривая 1 на рис. 5 построена с учетом однозначной зависимости Ts от U (зависимость 2, см. выше) при T0 = = 20 °С для заданных значений p; кривые 2 и 3 – зависимости Ts(р), полученные для заданных значений p и минимально возможных значений скоростей ${U \mathord{\left/ {\vphantom {U {\sqrt е }}} \right. \kern-0em} {\sqrt е }}$ и U/e; кривые 4 и 5 построены путем пересчета зависимости Ts(UТ) при Т01 = 150 °С и Т02 = 300 С, где UT = U0 + α(T0i – T0).
Полученный в настоящей работе и работах [1, 13] разброс значений Ts снизу ограничен кривой, которая соответствует уменьшению в е раз средней скорости при данном давлении и может иметь место при критической кривизне нижней части профиля поперечной волны (очага). Разброс максимальных значений Тs “укладывается” ниже кривой, описывающей расчетные значеия Тs для U(p) при начальной температуре T0 = 300 °С. Более точная оценка затруднена, так как с одной стороны, известно, что локальная скорость на поверхности образца, в верхней точке фронта, может быть в 2–3 раза больше средней по образцу, но “начальная” температура перед ней неизвестна. С другой стороны известно, что на поверхности образца имеется расплавленный слой октогена, а он плавится при 300 °С, но данных о скорости горения при таких температурах нет.
ЗАКЛЮЧЕНИЕ
Экспериментальными исследованиями механизма горения октогена показано, что при давлениях 0.5–60 атм отсутствует плоский одномерный фронт горения, а горение осуществляется за счет очагов. Оценен их размер и предложена зависимость характерного размера очага от средней скорости горения: L = 2.34U–0.65, где L – в мм, а U – в мм/с [15]. Из анализа изменения температуры во времени при прохождении термопары к-фазы были оценены локальные скорости на фронте очага. Показано, что нижняя граница области наблюдения локальных скоростей Un есть U/e, а верхняя – значение скорости горения при начальной температуре несколько ниже 300 °С ([18] и настоящая работа). Показано, что широкий разброс значений Un, значительно превышающий возможную ошибку измерений, определяет и широкий разброс температур поверхности, который отмечался нами и в работах [1, 13]. На основе анализа данных работ [1, 9, 13, 26] получена однозначная зависимость температуры поверхности от скорости горения в виде Ts = 398 + + 56 ln U, где Ts – в °C, а U – в мм/с, и рассчитаны границы разброса значений Ts, отвечающие вышеуказанным границам Un. Получено, что расчетные границы согласуются с имеющимся разбросом значений Ts. Таким образом, показано, что полученные параметры волны горения объясняются очаговым режимом горения октогена.
Настоящая работа была выполнена в рамках Программы фундаментальны научных исследований РФ “Процессы горения и взрыва” (регистрационный № 122040500073-4).