ЖЭТФ, 2023, том 163, вып. 4, стр. 480-487

РАСТЕКАНИЕ ТОКА В ТОНКИХ ФОЛЬГАХ ИЛИ ПЛОСКИХ

ТОКОВЫХ СЛОЯХ

С. Ф. Гаранин, Е. М. Кравец^*

Всероссийский научно-исследовательский институт экспериментальной физики,

607188 Саров, Нижегородская обл., Россия

Поступила в редакцию 17 октября 2022 г.,

после переработки 17 октября 2022 г.

Принята к публикации 31 октября 2022 г.

Для рассмотрения эволюции распределения токов в неоднородных тонких проводящих слоях или фольгах

используется интегро-дифференциальное уравнение, с помощью которого трехмерная задача для магнит-

ного поля сводится к двумерной, а для распределения токов по ширине неоднородных проводящих слоев

или фольг это уравнение позволяет свести двумерную задачу для магнитного поля к одномерной. Для

однородных проводящих слоев с постоянной проводимостью пространственный масштаб распределения

тока, сосредоточенного вначале в ограниченной области, растет пропорционально времени со скоростью

u = c²/4πσΔ, где σ — проводимость материала слоя, Δ — его толщина. В качестве приложения к за-

дачам переброса тока с помощью электровзрывных размыкателей рассмотрено распределение тока по

ширине фольги для периодической системы плоских фольг типа «змеек». Показано, что в этой системе

вначале в фольге устанавливается распределение тока, соответствующее идеальной проводимости фоль-

ги. Затем за времена порядка s/u (2s — ширина фольги) происходит релаксация распределения тока в

фольге к равномерному. Оценки показывают, что если фольги используются в качестве размыкателей,

то токи по фольгам в процессе переброса тока в нагрузку должны успевать распределяться равномерно

по их ширине, поэтому поправки на неоднородность распределения тока в размыкателях должны быть

невелики.

DOI: 10.31857/S0044451023040041

филаментации (устойчивость токовых слоев отно-

EDN: LNLHHG

сительно стратификации изучалась в работе [4]).

На стадии роста сопротивления при джоулевом теп-

1. ВВЕДЕНИЕ

ловыделении условие устойчивости проводника от-

носительно филаментации должно выполняться, и

Во многих системах с тонкими фольгами, в част-

ности в фольговых размыкателях тока [1-3], широ-

предположение об однородности фольги может быть

оправданным.

ко применяющихся для обострения импульсов тока,

важным вопросом является вопрос о распределении

Довольно часто в технике применяются фольги

конечной ширины или же наборы плоских фольг ти-

тока по ширине фольги. Обычно для описания рабо-

ты этих систем предполагают, что ток распределен

па «змеек», которые в последнее время изучаются

равномерно по ширине. Это предположение, одна-

как возможные быстрые размыкатели [3] в мощных

источниках тока. В этом случае возникают вопро-

ко, может быть не всегда оправданным даже для

однородных фольг, если учесть зависимость сопро-

сы: как будет распределяться ток по ширине таких

фольг и насколько правильно описывать их сопро-

тивления фольги от джоулева тепловыделения. В

этом случае, если в местах повышенного джоулева

тивление, как сопротивление фольги с однородным

распределением тока?

тепловыделения будет уменьшаться сопротивление,

что возможно при переходе проводника в плазму,

Вопросы растекания тока в тонких токовых сло-

то ток может перебрасываться в области больше-

ях изучались в целом ряде работ [5-9]. В этих ра-

ботах показано, что при анализе процессов растека-

го разогрева. Таким образом, на этой стадии воз-

можна неустойчивость токового слоя относительно

ния появляется физическая величина u = c²/4πσΔ

(σ — проводимость фольги, Δ — ее толщина, а вели-

^* E-mail: EMKravets@vniief.ru

чина σΔ является поверхностной проводимостью) с

480

ЖЭТФ, том 163, вып. 4, 2023

Растекание тока в тонких фольгах. . .

размерностью скорости, которая характеризует про-

из которого видно, что поскольку при y = 0 век-

цесс выравнивания токов по ширине фольги. Вооб-

тор r лежит в плоскости xz, вектор B перпендику-

ще говоря, даже в предположении зависимости ве-

лярен этой плоскости. Можно показать, что фурье-

личин в фольге только от координаты вдоль шири-

компоненты величин B(r) и j(r),

∫

ны фольги магнитные поля будут иметь двумерный

B (r) =

B_ke^i(k·r) dk,

характер и будут также зависеть от координаты,

2π

перпендикулярной фольге. Тем не менее в работе [9]

∫

показано, что задачу о растекании тока по ширине

j (r) =

j_ke^i(k·r) dk,

2π

фольги можно свести к одномерному интегро-диф-

связаны соотношениями

ференциальному уравнению для плотности тока.

В настоящей работе мы выведем интегро-

2πi

B_k = -

[j_k × k] ,

дифференциальное уравнение для плотности тока в

общем двумерном случае, проанализируем свойства

его решений для замкнутой системы токов (вихри

j_k =

[k × B_k] .

2πk

токов на поверхности), а также применим одно-

Обращая интегральный оператор в формуле (1)

мерное интегро-дифференциальное уравнение

[9]

с помощью преобразования Фурье, можно выразить

для расчета распределения и выравнивания тока

плотность тока через магнитное поле на поверхно-

по ширине фольги в системах плоских фольг типа

сти:

∫ [

]

«змеек» или конечных по ширине плоских токовых

слоях.

j (r) = -

× B(r^′) dr^′.

(2)

4π²

R³

Динамика магнитного поля определяется уравнени-

2. РАСТЕКАНИЕ ТОКА В ДВУМЕРНОМ

ем Максвелла

СЛУЧАЕ

∂B

= -c rot₂E

(3)

∂t

(индекс «2» у ротора означает, что дифференциро-

вание происходит только по координатам x и z), в

котором для нахождения электрического поля сле-

дует использовать закон Ома для поверхностного

тока:

j = σΔE.

(4)

Подставляя E из (4) в (3) и выражая плотность тока

через магнитное поле с помощью (2), получим

∂B

4π

rot₂(uj) =

Рис. 1. Геометрия задачи

∂t

(

∫ [

]

)

rot2 u(r)

× B(r^′) dr^′

(5)

Рассмотрим плоский и бесконечно тонкий токо-

R³

вый слой, ось y направим перпендикулярно его плос-

кости (рис. 1). Плотность тока j в нем будем считать

При u = const уравнение (5) можно переписать в

зависящей от x и z. Интегро-дифференциальное

виде

уравнение, описывающее динамику магнитного по-

∫

∂B(r)

(R)

ля на поверхности слоя с постоянной проводимо-

B(r^′)div2

dr^′ =

∂t

R³

стью, выведено в работе [8]. Мы получим интегро-

∫

B (r^′)

дифференциальное уравнение, описывающее дина-

dr^′ =

Δ₂

dr^′

R³

|r - r^′|

мику растекания тока в двумерной задаче (плоском

токовом слое), когда все величины зависят от x и z.

(индекс «2» здесь, по аналогии с (3), означает, что

Найдем магнитное поле на поверхности, т. е. при

дифференцирование происходит только по двум ко-

y = 0. По закону Био-Савара ток и создаваемое им

ординатам, а Δ₂ — двумерный лапласиан), и оно

магнитное поле связаны соотношением

совпадет с выведенным в работе [8].

∫

[j (r^′) × r - r^′]

Получим теперь уравнение для плотности то-

B(r) =

dr^′,

(1)

|r - r^′|

ка. Продифференцируем (2) по времени и исполь-

481

С. Ф. Гаранин, Е. М. Кравец

ЖЭТФ, том 163, вып. 4, 2023

зуем (5):

получаем закон сохранения магнитного момента для

∫ [

]

системы замкнутых токов на проводящей плоско-

∂ j(r)

∂B(r^′)

dr^′ =

сти:

∂t

4π²

R³

∂t

∫ [

]

= 0.

(8)

× rot^′2 (u (r^′)j(r^′)) dr^′ ≡

R³

∫ [

]

≡

R× rot^′2 E (r^′) dr^′

(6)

3. РАСТЕКАНИЕ ТОКА В

ОСЕСИММЕТРИЧНОЙ СИСТЕМЕ

(введены обозначения

R=R/R3, E= uj = c²E/4π,

Любая ограниченная замкнутая конфигурация

а rot^′2 означает дифференцирование по r^′). Интегри-

плоских токов (токовый вихрь) со временем по ме-

руя (6) по частям, учитывая, что ротор от всего вы-

ре растекания будет становиться осесимметричной,

ражения сводится к интегралу по удаленному кон-

с центром, совпадающим с первоначальной локали-

туру, переводя дифференцирование на

R и меняя

зацией этого вихря. В этом случае для больших вре-

дифференцирование с r^′ на r, получим

мен имеем j (r) = j (r) e_ϕ, и уравнение (7), определя-

∫ [

]

∂ j(r)

ющее динамику растекания тока, можно переписать

R× rot^′2E(r^′) dr^′ =

∂t

в виде

[

]

∫

↓

∫

∞

∫

rot^′2

R × E(r^′) dr^′ =

∂j

1 ∂

u (r^′) j (r^′) ×

∂t

π∂r

∫

[

]

rot₂

R× E(r′) dr^′ =

r^′ - r cosϕ

r^′ dϕdr^′ =

(∫ [

]

)

(

)_3/2

r² + r^′2 - 2rr^′ cosϕ

rot₂

× u(r^′)j(r^′) dr^′

(7)

R³

∫

∞

∫

∂

u (rw) j (rw) ×

(стрелка означает, что rot^′2 действует только на век-

π∂r

тор

R).

w - cosϕ

Рассмотрим динамику магнитного момента M,

dϕ w dw,

образуемого вихревыми токами j(r),

(w² + 1 - 2w cos ϕ)^3/2

∫

[r × j] dr.

где w = r^′/r. Интеграл по углу ϕ дает

∫

∞

Производная по времени от M, согласно (7), будет

∂j

∂

u(rw) j(rw) D(w) dw,

(9)

определяться выражением

∂t

∂r

∫ [

[

]]

r×

R× rot^′2 E(r^′) dr^′ dr.

2πc

где

(

)

Раскрывая двойное векторное произведение, полу-

( 2√w

( 2√w ))

D(w) =

чаем

π w+1

w+1

w-1

w+1

∫

rot^′2 E(r^′)(r · R)dr^′ dr.

Здесь K(w) и E(w) — полные эллиптические инте-

2πc

гралы первого и второго рода соответственно. Функ-

Проводя интегрирование по частям по dr^′ и считая,

цию D(w) после некоторых преобразований можно

что на бесконечности электрическое поле достаточ-

переписать в виде

но быстро стремится к нулю (критерий для этого

⎧

будет получен в следующем разделе), можно полу-

⎨

E(w)

K(w) +

w < 1,

чить

(-)1

D(w) =

∫

π⎩

dM_i

∂

w > 1.

ε_ikl

E_l (r^′)

dr^′ dr,

w² - 1

2πc

∂x_k′ R

где ε_ikl — единичный антисимметричный псевдотен-

Важным свойством функции D(w) является то, что

зор. Перенося дифференцирование с r^′ на r и учи-

∫

∞

тывая, что

∫

D(w)

∂

dw = 0.

dr = 0,

w²

∂x_k

482

ЖЭТФ, том 163, вып. 4, 2023

Растекание тока в тонких фольгах. . .

dr/dt ∝ u ∝ r^α; одновременно при α > 1 оценка

интеграла (9) для больших r приводит к расходимо-

сти). Таким образом, следует считать, что при α > 1

магнитный момент не сохраняется. Тогда плотность

тока будет экспоненциально затухать в зависимости

от времени, а на больших r, поскольку электриче-

ское поле ведет себя, как 1/r², плотность тока будет

j ∝ 1/r^2+α.

3.1. Автомодельное решение

Рассмотрим случай постоянной проводимости

слоя, u

= const. Поскольку в этом случае для

больших времен характерные расстояния меняют-

ся как r ∝ ut, а магнитный момент M сохраняется,

Рис. 2. Графики функций D(w) (1) и D(w)/w² (2)

M = const, для больших t следует искать решение в

виде

c M

Пользуясь этим свойством, можно показать, что

j =

j(ξ),

π (ut)³

уравнение (9), в соответствии с (8), удовлетворяет

закону сохранения полного магнитного момента

где ξ = r/ut — безразмерная автомодельная пере-

менная, а

j(ξ) — безразмерная автомодельная плот-

∫

∞

∫

∞

∂ 1

∂j

ность тока. Из (9) получаем уравнение для

j(ξ):

j(r) r²dr =

r²dr = 0.

∂tc

∂t

∫

∞

∂

˜(ξw) D(w) dw = 0.

ξj′(ξ) + 3j(ξ) +

∂ξ

Графики функций D(w) и D(w)/w² представле-

ны на рис. 2. Величина D(w) ≃ -w² при малых w и

Мы нашли точное аналитическое решение это-

D(w) ≃ 2/w при больших w.

го уравнения. Решением этого уравнения для плот-

Зная j(r), из закона Био - Савара (1) в нашем

ности тока

j(ξ), нормированной на автомодельный

осесимметричном случае можно найти магнитное

магнитный момент,

поле на плоскости, B_z(r) ≡ B(r):

∞

∫

∞

∫

j(ξ)ξ² dξ = 1,

B(r) =

j(rw) D(w) dw.

является функция

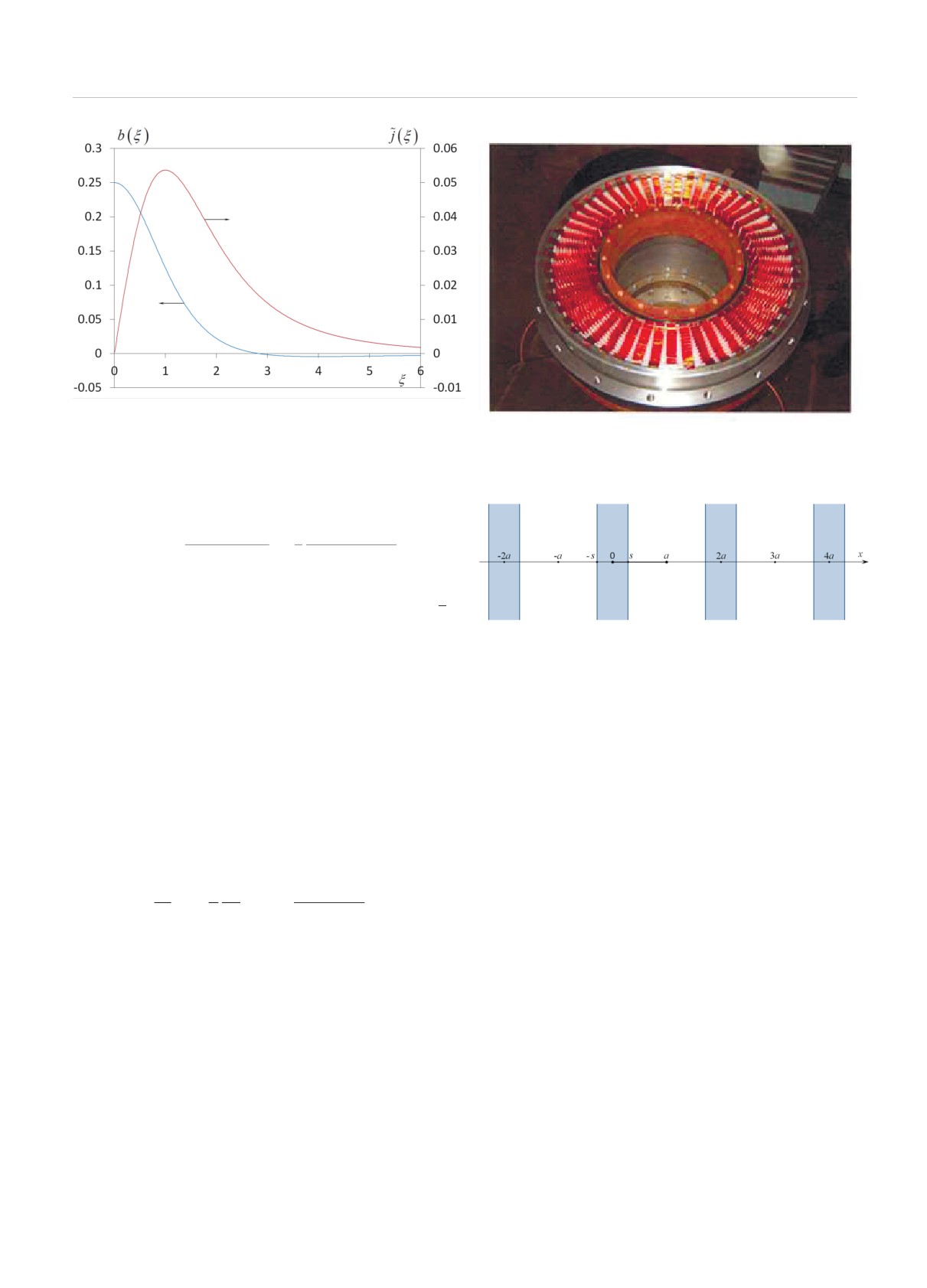
Рассмотрим, как ведет себя j(r) на больших рас-

d β

3β²

стояниях r ≫ 1. Большие r в интеграле (9) соответ-

j(ξ) = -

ствуют малым w. Но D(w) ∝ w² при малых w, а

dξ 2 (1 + βξ²)^3/2

2(1 + βξ²)^5/2

значит, интеграл в (9) пропорционален 1/r³ и, сле-

при β = 1/4, т. е.

довательно, ∂j/∂t ∝ 1/r⁴ и, можно думать, что на

больших расстояниях j ∝ 1/r⁴.

j(ξ) =

Для того чтобы выполнялся закон сохранения

32 (1 + ξ²/4)^5/2

магнитного момента, электрическое поле на боль-

Эта величина представлена на рис. 3. Плотность то-

ших расстояниях должно убывать быстрее, чем 1/r²

ка линейно растет при малых ξ, достигает максиму-

(изменения магнитного момента приводят к такой

ма при ξ = 1 и убывает как 1/ξ⁴ на больших ξ.

зависимости от r для вектор-потенциала, а следова-

Магнитное поле на поверхности в автомодель-

тельно, и электрического поля). Поскольку, соглас-

ных переменных определяется формулой

но закону Ома, электрическое поле E ∝ uj, для со-

хранения магнитного момента, казалось бы, необхо-

B(r) =

b(ξ).

(ut)³

димо, чтобы на больших расстояниях u росло мед-

леннее, чем r². Однако фактически, если на боль-

Безразмерная величина магнитного поля

ших расстояниях u ∝ r^α, то при α > 1 ток и маг-

∫

∞

нитный момент могут за конечное время перебра-

b(ξ) =

j(ξw) D(w) dw,

сываться на бесконечность (это следует из оценки

483

С. Ф. Гаранин, Е. М. Кравец

ЖЭТФ, том 163, вып. 4, 2023

Рис. 3. Автомодельная плотность тока

j(ξ) и магнитное

поле b (ξ) токового вихря

Рис. 4. Электровзрывной размыкатель тока типа «змеек»

для обострения тока в ВМГ

соответствующая току

j(ξ), равна

1 - βξ²/2

1 - ξ²/8

b(ξ) = β

(1 + βξ²)^5/2

4 (1 + ξ²/4)^5/2

и также показана на рис. 3. Магнитное поле макси-

√

мально при ξ = 0, меняет направление при ξ = 2

а на больших расстояниях ведет себя как 1/ξ³.

Рис. 5. Система периодических плоских фольг

Мы будем решать задачу для распределения то-

4. СИСТЕМА ПЛОСКИХ ФОЛЬГ.

ков в плоских токовых слоях, в том числе и для си-

ОДНОМЕРНОЕ РАССМОТРЕНИЕ

стем плоских фольг типа «змеек» (рис. 4). Предпо-

ложим, что имеется бесконечная периодическая си-

4.1. Постановка задачи

стема плоских фольг шириной 2s, находящихся на

В одномерном случае, когда все величины зави-

расстояниях 2(a - s) друг от друга (рис. 5). Период

сят только от x, а j(r) = j(x) e_z , уравнение (7) сво-

системы по координате x равен 2a. В частном случае

дится к полученному нами ранее [9] уравнению

a → ∞ система превращается в уединенную фольгу,

а малые расстояния между фольгами 2(a - s) будут

∫

∞

соответствовать почти сплошной фольге.

∂j

2 ∂

u(x^′) j(x^′)

dx^′

(10)

Будем считать, что полный ток по системе посто-

∂t

π∂x

x-x^′

янен в каждом из полупериодов, проводимость в об-

−∞

ласти между фольгами мала и, соответственно, ско-

Это уравнение может использоваться для расче-

рость u_v очень велика, u_v ≫ u. Мы хотим промоде-

тов распределения токов в плоских токовых слоях, в

лировать ситуацию, когда в начальный момент вре-

том числе и для систем плоских фольг типа «змеек».

мени ток быстро распределяется по ширине фоль-

Интересно отметить, что из дивергентного характе-

ги так, как если бы она вначале была практически

ра уравнения (10) следует, что для локализованного

сверхпроводящей, а затем уже более медленно (со

распределения тока и неограниченного по простран-

скоростью u) стремится распределиться равномер-

ству распределения ненулевой проводимости (т. е. не

но по ширине фольги. Для такого моделирования

обращающейся в бесконечность скорости u) полный

задачу можно поставить так: вначале ток j вообще

∫_∞

ток по системе

j dx сохраняется. Таким обра-

равномерно распределен по системе. В этом случае

-∞

зом, это уравнение особенно удобно использовать в

в начальный момент времени нормальная компонен-

задачах с поддерживаемым в системе током.

та магнитного поля B_y везде, в том числе и на по-

484

ЖЭТФ, том 163, вып. 4, 2023

Растекание тока в тонких фольгах. . .

верхности фольги, равна нулю. Затем ток быстро, со

ных расчетах интегро-дифференциального уравне-

скоростью u_v ≫ u, перераспределится, но на поверх-

ния растекания тока (11) в начальный момент вре-

ности фольги нормальная компонента B_y останется

мени t = 0 задавалось равномерное распределение

равной нулю, поскольку по фольге ток распределя-

тока по координате x. Для удобства нормировки мы

ется более медленно, со скоростью u. Таким обра-

задавали плотность тока таким образом, чтобы пол-

зом, в данной задаче мы сможем узнать, как распре-

ный ток по отрезку (0, a) был равен единице:

деляется ток по почти сверхпроводящей фольге (на

∫

малых временах) и как будет перераспределяться и

j (x, 0) dx = 1,

выравниваться ток по фольге на больших временах.

Такой прием для описания динамики распределения

тока по фольге является в некоторой степени искус-

т. е. чтобы плотность тока в начальный момент вре-

ственным, однако он позволяет, оставаясь в рамках

мени была равна

одномерной задачи, описать динамику распределе-

ния токов по фольге, начиная с малых времен и до

j(x, 0) = 1/a.

полного выравнивания тока.

В частности, мы сможем получить ответ на во-

В нашей задаче между фольгами располагался

прос о том, как будет меняться от времени эф-

вакуум или диэлектрик, поэтому величина u_v в ва-

фективное сопротивление фольги и насколько точ-

кууме задавалась значительно большей, чем внутри

но предположение о том, что ток по фольге рас-

фольги, u_v(s < x < a) = 10⁴.

пределяется равномерно. Эффективное сопротивле-

ние фольги в рассматриваемой системе определяет-

ся электрическим полем в центре фольги, поскольку

4.3. Результаты расчетов

именно это электрическое поле соответствует уходу

Плотность тока j(x, t) в фольге, полученная в

магнитного потока из системы и, соответственно, пе-

расчете с a = 2 на различные моменты времени,

редаче магнитного потока в нагрузку.

представлена на рис. 6.

На рис. 6 видно, что ток j(x, t) в фольге при

4.2. Расчетная методика

малых временах распределяется так же, как и в

сверхпроводящей фольге, и имеет особенность ви-

√

С учетом периодичности рассматриваемой зада-

да 1/

1 - x/s (стандартную для задач с решением

чи перепишем выражение (10) в виде

уравнением Лапласа в плоском случае вблизи гра-

ницы отрезка [10]) вблизи границы фольги x = s,

∫

∂j (x,t)

2 ∂

dξ

т. е. концентрируется вблизи границы, а затем стре-

(u (x + ξ) j (x + ξ, t) -

∂t

π∂x

мится к равномерному распределению по ширине

фольги. К моменту времени t = 1 распределение

тока уже близко к равномерному.

- u (x - ξ)j (x - ξ,t))×

(

( (

)

(

)))

× 1-

-ψ

(11)

где ξ = x^′ - x, ψ — пси-функция Эйлера. Таким

образом, от интегрирования по бесконечной прямой

в (10) мы перешли к интегрированию по конечному

отрезку (0, a) в (11).

Перейдем к безразмерным переменным, взяв за

единицу измерения длины полуширину фольги s, за

единицу измерения скорости — скорость u; в этом

случае время будет измеряться в единицах s/u.

В соответствии с вышесказанным для моделиро-

вания с первоначальным распределением магнитно-

го поля, которое в начальный момент не должно

Рис. 6. Плотность тока в фольге в расчете с a = 2 на

иметь нормальной компоненты на фольге, в числен-

различные моменты времени

485

С. Ф. Гаранин, Е. М. Кравец

ЖЭТФ, том 163, вып. 4, 2023

чению 2/π ≈ 0.6366 для изолированной фольги.

При уменьшении расстояния между фольгами ве-

личина f(a) медленно увеличивается. Например,

f (2) = 0.708. По мере сближения фольг функция

f (a) линейно стремится к единице.

4.4. Некоторые оценки для системы типа

«змеек»

Для системы типа «змеек», применяемой в рабо-

те [3], внутренний радиус серпантина R₁ = 15.5 см,

период 2a = 1.87 см, ширина фольги 2s = 1.6 см,

зазоры между фольгами 2(a - s) = 0.27 см. Тогда

(a - s)/a = 0.144 и соответствующее уменьшение

Рис. 7. Зависимость от времени отношения плотности то-

эффективного сопротивления (см. рис. 8) f = 0.877.

ка при x = 0 к среднему значению тока в фольге jave(t)

Для внешнего радиуса серпантина R₂ = 22.8 см име-

для различных расстояний между фольгами

ем зазоры 2(a - s) = 1.16 см и (a - s)/a = 0.42,

f = 0.734. Система фольг удалена от генератора и

нагрузки на расстояние d, большее 10 см, так что

условие для рассмотрения системы фольг как от-

дельного узла, d ≫ s, выполняется. Оценим время

выравнивания тока и необходимость учета неравно-

мерности его распределения для работы фольгового

размыкателя.

Выравнивание тока, согласно рис. 7, происходит

за безразмерное время 0.13-0.14 (для которого раз-

ница между величиной j(0, t)/j_ave(t) и единицей

уменьшается в 2 раза), и оно не сильно зависит от

величины (a - s)/a.

Для медной фольги [3] в начальном состоянии

Рис. 8. Величина f(a) для различных значений (a - s)/a

величина u

= c²/4πσΔ

= 8.92 · 10⁴ см/с. Если

= 1.6 см, то безразмерному времени 1 соот-

На рис. 7 показана зависимость от времени отно-

ветствует размерное время s/u = 9 · 10^-6 с, зна-

шения плотности тока при x = 0 к среднему зна-

чит, характерное время выравнивания тока порядка

чению тока в фольге j_ave (t). В момент начала сче-

10^-6 с. Само по себе время выравнивания оказыва-

та, согласно постановке задачи, эта величина равна

ется сравнимым и даже большим времени переброса

единице, однако очень быстро достигает минимума.

тока в этом размыкателе и, казалось бы, могло по-

На рис. 7 данные начальные участки не показаны,

требовать введения поправок f ≈ 0.88, f ≈ 0.73 к

поскольку при увеличении u_v эти временные интер-

эффективному сопротивлению. Однако фактически

валы уменьшаются. В дальнейшем с течением вре-

сопротивление фольг в размыкателе за счет нагрева

мени величина j(0, t)/j_ave (t) возрастает и стремится

при протекании тока растет значительно (скорость

к единице по мере выравнивания тока.

u может возрастать на два порядка). Поэтому токи

На рис. 8 представлена величина f(a), равная

по ширине фольги практически выравниваются и,

значению при t = 0 функции, полученной экстра-

соответственно, нет необходимости вводить поправ-

поляцией до t = 0 зависимости j(0, t)/j_ave(t), у ко-

ки на неоднородность распределения тока по ши-

торой отброшены значения при малых t, т. е. по су-

рине фольги.

ществу отношение тока в центре фольги к среднему

току по фольге для сверхпроводящих фольг. По оси

5. ЗАКЛЮЧЕНИЕ

абсцисс отложена величина (a - s)/a, равная доле

вакуумной области в полупериоде a.

Эволюцию двумерного распределения токов в

Для самого большого полупериода a, для ко-

неоднородных тонких проводящих слоях или фоль-

торого проводились расчеты (a

= 100), значе-

гах можно описывать с помощью интегро-диф-

ние f(a) равно 0.637, что очень близко к зна-

ференциального уравнения, что позволяет свести

486

ЖЭТФ, том 163, вып. 4, 2023

Растекание тока в тонких фольгах. . .

трехмерную задачу для магнитного поля к двумер-

в процессе переброса тока в нагрузку должны успе-

ной, а для распределения токов по ширине неодно-

вать распределяться равномерно по их ширине. По-

родных проводящих фольг двумерная задача для

этому поправки на неоднородность распределения

магнитного поля сводится к одномерной. Показано,

тока в размыкателях должны быть невелики.

что в двумерном случае для замкнутой системы то-

Однако для плоских токовых слоев рассмотрен-

ков сохраняется магнитный момент этой системы.

ные в работе распределения тока и их эволюция мо-

Замкнутая система токов при больших временах

гут играть важную роль, в том числе в развитии

становится азимутально симметричной. Для этого

тиринг-неустойчивости этих слоев.

случая получены интегро-дифференциальное урав-

нение и его автомодельное решение, для которого

сохраняется магнитный момент, а пространствен-

ЛИТЕРАТУРА

ные масштабы растут линейно со временем.

1. В. А. Бурцев, Н. В. Калинин, А. В. Лучинский,

Рассмотрена задача о распределении токов для

Электрический взрыв проводников и его при-

систем плоских фольг типа «змеек». Для описания

менение в электрофизических установках,

эволюции распределения токов при фиксированном

Энергоиздат, Москва (1990).

полном токе через систему следует считать, что в

начальный момент плотность тока является посто-

2. A. M. Buyko, J. Appl. Mech. Tech. Phys.

56,

114

янной по всей системе, включая промежутки между

(2015).

фольгами, а затем происходит быстрая релаксация

3. А. А. Базанов, Е. И. Бочков, С. Г. Гаранин и др.,

этого распределения со скоростью u_v ≫ u. В резуль-

ДАН 489, 355 (2018).

тате в фольге быстро устанавливается распределе-

ние тока, соответствующее идеальной проводимости

4. S. F. Garanin and S. D. Kuznetsov, J. Appl. Phys.

фольги. Затем за времена s/u происходит релакса-

123, 133301 (2018).

ция распределения тока в фольге к равномерному.

5. Е. Б. Татаринова, К. В. Чукбар, ЖЭТФ 92, 809

Проведены расчеты распределения тока по

(1987).

фольге для разных значений a/s. Показано, что на

стадии быстрого включения тока эффективное со-

6. М. И. Дьяконов, А. С. Фурман, ЖЭТФ 92, 1012

противление фольги не очень значительно отлича-

(1987).

ется от сопротивления, вычисленного в предположе-

7. В. В. Смирнов, К. В.Чукбар, Физика плазмы 25,

нии равнораспределения тока. Наибольшее разли-

610 (1999).

чие имеет место для далеко разнесенных фольг. На

стадии релаксации распределения тока к равномер-

8. К. В. Чукбар, Лекции по явлениям переноса в

ному величина j(0, t)/j_ave(t) стремится к единице,

плазме, ИД «Интеллект», Долгопрудный (2008).

причем характерное время этого выравнивания со-

9. S. F. Garanin, E. M. Kravets, and V. Yu. Dolinskiy,

ставляет (0.13-0.14)s/u и слабо зависит от значений

IEEE Trans. Plasma Sci. 48, 4279 (2020).

зазоров между фольгами.

Оценки показывают, что если фольги использу-

10. С. Ф. Гаранин, С. Д. Кузнецов, УФН

190,

1109

ются в качестве размыкателей, то токи по фольгам

(2020).

487