ЖЭТФ, 2022, том 162, вып. 5 (11), стр. 796-805

ДИНАМИКА ВЗАИМОДЕЙСТВИЯ ДВУХ ОБЛАКОВ

СОЛИТОННЫХ ГАЗОВ

А. М. Камчатновa*, Д. В. Шайкинb**

^a Институт спектроскопии Российской академии наук

108840, Москва, Троицк, Россия

^b Московский физико-технический институт

141701, Долгопрудный, Московская обл., Россия

Поступила в редакцию 06 июня 2022 г.,

после переработки 06 июня 2022 г.

Принята к публикации 24 июня 2022 г.

На основе связи кинетического уравнения, описывающего взаимодействие двух солитонных облаков в

теории уравнения Кортевега-де Фриза, с уравнениями динамики для газа Чаплыгина показано, что

фундаментальным свойством нелинейной динамики солитонных газов является существование волн,

распространяющихся без изменения формы. Приведены решения нескольких типичных задач динамики

солитонных газов и указаны характерные черты такой динамики, позволяющие дать оценку эффектов

взаимодействия солитонных газов.

DOI: 10.31857/S0044451022110207

солитонное решение имеет вид

EDN: BHFAX

κ²

u(x, t) =

(2)

2 ch²[κ(x - κ²t - x₀)/2]

1. ВВЕДЕНИЕ

т.e. скорость солитона s = κ² пропорциональна его

амплитуде a = κ²/2. Если в начальный момент вре-

Как известно, солитоны получили свое название

мени волновое возбуждение может быть представ-

[1] по аналогии с названиями элементарных частиц

лено с хорошей точностью в виде двух удаленных

(электрон, протон и т.п.) в силу их упругого взаимо-

друг от друга солитонных импульсов (2), причем

действия друг с другом для важного класса нели-

более быстрый солитон с параметром κ = κ₂ имеет

нейных волновых уравнений. А именно, две уеди-

начальную координату x₀₂ левее координаты x₀₁ бо-

ненные волны, находящиеся до их «столкновения»

лее медленного солитона с параметром κ₁ (κ₁ < κ₂),

вдали друг от друга, пройдя через стадию взаи-

то их первоначальные траектории x = κ²¹t + x₀₁,

модействия, возвращаются к своей первоначальной

x = κ²²t+x₀₂ приобретут после столкновения сдвиги

форме без образования каких-либо дополнительных

волн. Тем не менее акт их взаимодействия не прохо-

x = κ²¹t + x₀₁ + Δx₁, x = κ²²t + x₀₂ + Δx₂,

дит совсем бесследно и в результате него траектории

где

солитонов приобретают дополнительные сдвиги по

сравнению с их первоначальными траекториями [2].

κ₂ + κ₁

Δx₁ = -

Δx₂ =

(3)

Например, в случае уравнения Кортевега-де Фри-

κ₁

κ₂ - κ₁

κ₂

κ₂ - κ₁

за (КдФ), являющегося универсальным волновым

Таким образом, быстрый солитон с большой ампли-

уравнением для описания волн с учетом малых эф-

тудой сдвигается вперед, а медленный и низкий —

фектов нелинейности и дисперсии, которое мы за-

назад, причем по абсолютной величине сдвиг низко-

пишем в стандартных безразмерных переменных,

го больше, чем сдвиг высокого. Замечательно, что

для важного класса интегрируемых уравнений мо-

u_t + 6uu_x + u_xxx = 0,

(1)

гут быть получены решения с любым числом соли-

тонов. При этом в результате одновременного столк-

^* E-mail: kamch@isan.troitsk.ru

^** E-mail: shaykin.dv@phystech.edu

новения трех или большего их числа суммарный

796

ЖЭТФ, том 162, вып. 5 (11), 2022

Взаимодействие двух солитонных газов

сдвиг каждого солитона равен сумме сдвигов вида

например, [12-14]), что требует создания ясной кар-

(3) для парных столкновений (см., например, [3,4]),

тины динамики солитонных газов. В данной статье

т.е. множественные столкновения солитонов одно-

мы представим несколько примеров такой типичной

временно в одной области пространства не отлича-

динамики, которые позволяют понять некоторые су-

ются в этом смысле от последовательных простран-

щественные свойства газовой динамики солитонов,

ственно разделенных парных столкновений солито-

отличающие ее от динамики обычных газов.

нов друг с другом.

Представим теперь, что в нашей волновой си-

стеме возбуждено очень большое число солитонов,

2. КИНЕТИЧЕСКОЕ УРАВНЕНИЕ ДЛЯ ГАЗА

каждый из которых характеризуется своим пара-

СОЛИТОНОВ

метром κ. Тогда можно говорить о газе солито-

нов и использовать для его описания представ-

ления газовой кинетики. Если обозначить через

Сначала приведем для полноты краткий вы-

f (κ, x, t)dxdκ число солитонов с координатами в ин-

вод кинетического уравнения для солитонного газа

тервале (x, x+dx), которые имеют параметр κ в ин-

КдФ, следуя методу работы [7]. Прежде всего заме-

тервале (κ, κ+dκ) в момент времени t, то эволюция

тим, что в силу интегрируемости уравнения КдФ,

такого газа характеризуется зависимостью функции

открытой в работе [15], эволюция волны u(x, t) про-

распределения f(κ, x, t) по координате и параметру

исходит таким образом, что спектр задачи на соб-

ственные значения для ассоциированного с урав-

κ от времени. Задача найти кинетические уравнения

для такой эволюции была поставлена Захаровым в

нением КдФ стационарного уравнения Шрёдингера

работе [5] и решена им для разреженного газа соли-

ψ_xx = -(u(x, t)+λ)ψ не зависит от времени t и каж-

тонов, когда их столкновения друг с другом в сред-

дому солитону отвечает некоторое значение λ < 0

нем мало изменяют скорости s = κ². Позже Эль, ис-

дискретного спектра. Более удобный параметр κ, ис-

следуя специальный предел модуляционных уравне-

пользованный в записи солитонного решения в ви-

√

ний Уизема для бесконечнофазного решения урав-

де (2), связан с λ соотношением κ =

-λ. Следо-

нения КдФ, получил в работе [6] обобщение кине-

вательно, при эволюции волны согласно уравнению

тического уравнения Захарова на плотный солитон-

КдФ как спектр, так и набор значений κ при дви-

жении солитонов, сопровождаемом их столкновени-

ный газ. Более простой вывод этого уравнения на ос-

нове самосогласованного определения средней ско-

ями, не изменяется. Если бы солитоны при их столк-

рости солитона, движущегося сквозь газ, был дан

новениях не претерпевали сдвигов (3), то их скоро-

в работе [7] и там же было получено простейшее

сти выражались бы формулой s = κ² для всех соли-

решение этих уравнений, описывающее столкнове-

тонов с параметром κ. Однако столкновения моди-

ние двух облаков солитонных газов, в каждом из

фицируют эту скорость. При каждом столкновении

которых параметры κ близки друг к другу. Фор-

солитона с более медленными солитонами, имеющи-

мальные решения для любого числа таких обла-

ми параметр η < κ, «пробный» κ-солитон продвига-

ков изучались в работах [8, 9]. В настоящее вре-

ется вперед на дополнительное расстояние

мя теория кинетических уравнений для солитонов

стала частью активно развивающейся так называе-

κ+η

мой «обобщенной гидродинамики», которая находит

κ-η

приложения к различным интегрируемым моделям

систем многих взаимодействующих частиц (см., на-

и число таких столкновений в единицу времени рав-

пример, обзоры [10, 11] и имеющиеся там ссылки).

но относительной скорости s(κ) - s(η), умноженной

Однако, несмотря на такой значительный формаль-

на плотность η-солитонов. Следовательно, благода-

ный прогресс, физическое понимание поведения со-

ря таким столкновениям κ-солитон приобретает до-

литонных газов представляется недостаточным, так

бавку к скорости

как до сих пор имеется лишь очень небольшое чис-

∫κ

ло решенных задач, дающих представление о харак-

κ+η

терных чертах динамики взаимодействующих соли-

[s(κ) - s(η)]f(η)dη.

(4)

κ-η

тонных газов. В то же время в настоящее время на-

чались экспериментальные исследования динамики

солитонных газов в различных физических систе-

Аналогичным образом каждый солитон с парамет-

мах, включая волны на воде и холодные атомы (см.,

ром η > κ, обгоняющий «пробный» κ-солитон, сме-

797

А. М. Камчатнов, Д. В. Шайкин

ЖЭТФ, том 162, вып. 5 (11), 2022

щает его за единицу времени назад на расстояние

3. ДВУХПОТОКОВЫЕ ТЕЧЕНИЯ

СОЛИТОННЫХ ГАЗОВ

∫∞

η+κ

[s(η) - s(κ))]f(η)dη =

Чтобы получить представление о динамике со-

η-κ

литонных газов согласно кинетическому уравнению

∫∞



κ+η

(5), (6), предположим, что функция распределения



s(κ) - s(η)]f(η)dη,

[

имеет два очень узких пика вблизи значений κ₁ и

^κ-η

κ₂, т.е. ее можно представить в виде

получаемое умножением сдвига -2κ lnη+κη-κ при еди-

f (κ, x, t) = f₁(x, t)δ(κ - κ₁) + f₂(x, t)δ(κ - κ₂).

(8)

ничном столкновении на число таких столкновений

[s(η) - s(κ))]f(η) и интегрированием по значениям

Это означает, что мы рассматриваем динамику вза-

η > κ. Прибавляя эти добавки к немодифицирован-

имодействующих газов на временах, когда столкно-

ному значению скорости κ², получаем самосогласо-

вениями солитонов одного сорта с очень близкими

ванное уравнение

скоростями можно пренебречь и учитывать только

∫

∞



столкновения между солитонами разных сортов. То-

κ+η



гда подстановка функции распределения (8) в (6) и

s(κ) = κ² +

s(κ) - s(η)]f(η)dη.

(5)

[

^κ-η

(7) дает законы сохранения

Таким образом, функция распределения солитонов

∂f₁

∂(s₁f₁)

∂f₂

∂(s₂f₂)

= 0,

(9)

с параметром κ переносится вдоль оси x со скоро-

∂t

∂x

∂t

∂x

стью s(κ), определяемой интегральным уравнени-

где скорости s₁, s₂ удовлетворяют уравнениям

ем (5), и условие сохранения спектра при эволюции

волны согласно уравнению КдФ записывается в ви-

s₁ = κ²¹+α₁f₂(s₁-s₂), s₂ = κ²²+α₂f₁(s₂-s₁), (10)

де закона сохранения:

и мы ввели для удобства обозначения

∂f(κ,x,t)

∂[s(κ)f(κ, x, t)]



= 0.

(6)

κ1 +



κ1 + κ₂

∂t

∂x



α₁ =

α₂ =

(11)



,



.

κ₁

κ₁ - κ₂

κ₂

κ₁ - κ₂

Это уравнение, дополненное интегральным уравне-

нием (5), называется кинетическим уравнением для

Уравнения (10) позволяют выразить перенормиро-

газа солитонов КдФ, и оно было другим способом

ванные скорости через плотности солитонных газов:

получено в работе Эля [6]. Отметим, что учет лишь

парных столкновений в уравнении (5) в плотном

κ²¹(1 - α₂f₁) - κ²²α₁f₂

s₁ =

солитонном газе оправдывается упомянутым выше

1-α₁f₂ -α₂f₁

(12)

сложением сдвигов при кратных столкновениях со-

κ²²(1 - α₁f₂) - κ²α2f1

s₂ =

литонов.

1-α₁f₂ -α₂f₁

Если газ солитонов разреженный, т.е.

∫

Если же выразить из (10) плотности f1,2 через ско-

f (κ)dκ

≪ κ₀, где κ₀ — характерное значение

рости s1,2,

параметра κ в распределении f(κ), то поправочный

член в формуле (5) мал и в него можно подставить

s₂ - κ²²

κ²¹ - s₁

немодифицированное значение s(κ) ≈ κ²:

f₁ =

f₂ =

(13)

α₂(s₂ - s₁)

α₁(s₂ - s₁)

∫

∞



κ+η



и подставить эти выражения в (9), то эта система

s(κ) = κ² +

κ² - η²)f(η)dη.

(7)

⁽

^κ-η

приводится к замечательно простому диагонально-

му виду:

Это выражение определяет функцию s(κ) замкну-

∂s₁

∂s₂

той формулой в отличие от интегрального уравне-

+s₂

= 0,

+s₁

= 0,

(14)

ния (5) для плотного газа солитонов. Система (6),

∂t

∂x

∂t

∂x

(7) была получена Захаровым в работе [5] вместе со

где перенормированные скорости s₁, s₂ являются

сформулированным здесь подходом к кинетике га-

римановыми инвариантами этой системы уравнений

за солитонов. Ясно, что такого рода кинетические

гидродинамического типа.

уравнения могут быть получены и для других пол-

Формально уравнения (14) похожи на уравнения

ностью интегрируемых уравнений с изоспектраль-

газовой динамики в римановой форме, но физиче-

ной эволюцией нелинейных волн.

ские свойства солитонного газа весьма отличны от

798

ЖЭТФ, том 162, вып. 5 (11), 2022

Взаимодействие двух солитонных газов

свойств обычного газа. Прежде всего заметим, что,

простой волной и выражаться формулой Пуассона

хотя скорости солитонов перенормируются в обла-

(см. [16])

сти перекрытия солитонных облаков, такое измене-

ρ = ρ₀[x - (c + u)t],

(17)

ние скорости нельзя интерпретировать как ускоре-

ρ₀(x) — профиль плотности в такой волне, распро-

ние солитонов под действием давления: после вы-

страняющейся со скоростью c + u. При этом связь

хода из области перекрытия их скорости восстанав-

между ρ и u выражается условием постоянства ри-

ливают свои первоначальные значения. Далее, га-

манова инварианта:

зы свободно протекают сквозь друг друга с пере-

∫

нормированными скоростями, не испытывая ника-

u - cdρ/ρ = r_- = const.

ких диссипативных процессов. При этом динамиче-

ские уравнения (9) имеют форму законов сохране-

Для существования волны со стационарным про-

ния и, как и в теории вязких ударных волн, допус-

филем необходимо, чтобы выполнялось условие

кают разрывные решения. Наконец, в нашем случае

c + u = const. Подставляя сюда соотношения

можно считать, что солитонные газы имеют нуле-

√

∫

вую температуру, так что переход через разрыв не

dp dρ

связан с увеличением энтропии, т.е. теорема Жуге-

+ const,

dρ

dρ ρ

Цемплена (см., например, [16]) неприменима и раз-

рыв может иметь любой знак. Из этого же следу-

получаем после дифференцирования по ρ уравнение

ет, что существование таких формально разрывных

для допускающих стационарную волну уравнений

течений не связано с опрокидыванием солитонно-

состояния газа p = p(ρ):

го импульса и последующим формированием узко-

го переходного слоя, связывающего два течения с

d²p

2 dp

= 0.

разными параметрами, как это происходит в теории

dρ²

ρ dρ

вязких ударных волн. Прояснить этот вопрос помо-

Это уравнение легко решается и дает как раз ука-

гает связь уравнений (14) с теорией газа Чаплыги-

занную выше зависимость (15). Приняв для просто-

на. В работе [17] Чаплыгин указал, что уравнение

ты B = 1, мы тогда имеем c² = dp/dρ = 1/ρ², c = 1/ρ

состояния газа

и римановы инварианты (см. [16]) оказываются рав-

p=A-

(15)

ными

∫

(p — давление газа, ρ — его плотность, A, B — по-

cdρ

s₁ = u +

=u-

стоянные параметры) может служить удобным при-

∫

(18)

ближением на отдельных участках адиабаты Пуасс-

cdρ

s₂ = u -

=u+

сона, когда формулы теории значительно упроща-

ются. (Обратим внимание, что им также была отме-

где u и ρ подчиняются уравнениям Эйлера для газа

чена связь уравнений газовой динамики для этого

Чаплыгина

случая с теорией минимальных поверхностей). Мы,

однако, подойдем к теории газа Чаплыгина с другой

ρ_x

ρ_t + (ρu)_x = 0,

u_t + uu_x +

(19)

стороны.

ρ³

Еще на первоначальном этапе создания теории

и выражаются через римановы инварианты как

ударных волн в работах Стокса и Кельвина обсуж-

дался вопрос, допускают ли уравнения газовой ди-

ρ=

(s₂ + s₁).

(20)

s₂ - s₁

намики

Если переписать уравнения (19) через римановы ин-

ρ_t + (ρu)_x = 0, u_t + uu_x +

ρ_x = 0

(16)

варианты (18), то простые вычисления приводят к

уравнениям для динамики газа Чаплыгина в диаго-

(c² = dp/dρ, c — скорость звука) решения в виде ста-

нальной римановой форме, совпадающей с уравне-

ционарной распространяющейся волны. При такой

ниями (14), описывающими динамику двух взаимо-

постановке вопроса ясно, что в стационарном реше-

действующих солитонных газов.

нии как плотность ρ, так и скорость течения u явля-

Если теперь мы будем искать решение уравне-

ются функциями только координаты, ξ = x-V t, т.е.

ний (19) в виде бегущей с постоянной скоростью V

они связаны друг с другом однозначной зависимо-

волны ρ = ρ(ξ), u = u(ξ), ξ = x - V t, то легко най-

стью. Следовательно, такое решение должно быть

дем, что эти уравнения удовлетворяются при любой

799

А. М. Камчатнов, Д. В. Шайкин

ЖЭТФ, том 162, вып. 5 (11), 2022

функции ρ(ξ), если скорость течения газа Чаплыги-

f1c + f2c

на выражается через ρ(ξ) формулой

f₂₀

u(ξ) = V +

(21)

f2c

ρ(ξ)

f₁₀

В этом случае инварианты Римана равны

s₁ = V,

s₂ = V +

(22)

ρ(ξ)

Очевидно, что эти формулы дают решение уравне-

c^-t

c⁺t

ний (14) в виде простой волны: если положить, на-

пример, s₁ = V = const, то второе уравнение пре-

Рис. 1. Зависимость плотностей солитонных газов от коор-

вращается в s2,t + V s2,x = 0 с общим решением

динаты при их взаимопроникновении после столкновения

s₂ = F(x - V t), что совпадает с (22), если записать

солитонных облаков с постоянными начальными плотно-

функцию F(ξ) в виде F(ξ) = V + 2/ρ(ξ). В частно-

стями и скоростями.

сти, функция F (ξ) может включать в себя разрыв,

распространяющийся без изменения формы в обла-

сти перекрытия двух газов.

Связь между уравнениями для газа Чаплыгина и

причем мы считаем, что κ₂ > κ₁, так что более быст-

кинетическим уравнением, описывающим динамику

рое облако солитонов с плотностью f₂₀ в момент

двух взаимодействующих солитонных облаков, поз-

времени t = 0 настигает в точке x = 0 более мед-

воляет строить поучительные примеры решений ки-

ленное облако с плотностью f₁₀ и начинается про-

нетического уравнения.

цесс их взаимопроникновения. Как обычно в слу-

чае начального разрыва, решение должно зависеть

только от автомодельной переменной ζ = x/t. По-

4. СТОЛКНОВЕНИЕ ДВУХ СОЛИТОННЫХ

этому начальный разрыв ведет к образованию плато

ГАЗОВ

между двумя простыми волнами, каждая из кото-

рых представляет собой разрыв с постоянным зна-

Уравнения (14) имеют очевидное вырожденное

чением одного из римановых инвариантов — суще-

решение, в котором s₁ и s₂ являются постоянны-

ствование таких решений обусловлено указанными

ми, не зависящими ни от x, ни от t. Несмотря на

выше свойствами газа Чаплыгина. В целом же ре-

тривиальность этого решения, оно имеет ясное фи-

шение представляет собой последовательность трех

зическое содержание: оно может служить «плато»,

течений с постоянными плотностями, которые раз-

соединяющим два указанных выше решения в ви-

деляются разрывами:

де простых волн. В частности, при столкновении

двух проникающих друг в друга газов с постоянны-

⎧

ми плотностями f₁, f₂ и, значит, значениями рима-

⎨

f₂₀,

x < c^-t,

новых инвариантов s₁, s₂, образуется область двух-

f (x, t) =

f1c + f2c, c^-t < x < c⁺t,

(24)

потокового течения, в которой скорости солитонов

⎩

f₁₀,

x > c⁺t.

одного сорта перенормируются вследствие их взаи-

модействия с солитонами другого сорта. Таким об-

разом, задача о столкновении двух газов заключает-

Из рис. 1 ясно, что передний край плато движется

ся в нахождении плотностей и скоростей солитонов

с перенормированной скоростью s2c быстрого газа,

в области их «перемешивания», а также скоростей

а задний край плато — с перенормированной ско-

краев этой области. Хотя эта задача уже обсужда-

ростью s1c медленного газа, так как на этих кра-

лась в работах [7,18], мы кратко остановимся на ней,

ях плотности соответствующих газов обращаются

так как соответствующие результаты будут исполь-

скачком в нуль:

зованы в дальнейшем. Предположим, что в началь-

ный момент времени в распределениях плотностей

c^- = s1c,

c⁺ = s2c.

(25)

двух сортов солитонов имеется разрыв:

f₂(x, 0) = f₂₀, f₁(x, 0) = 0,

x < 0,

В двухпотоковой области плато c^-t < x < c⁺t скоро-

(23)

f₂(x, 0) = 0,

f₁(x, 0) = f₁₀, x > 0,

сти солитонов перенормированы их взаимодействи-

800

ЖЭТФ, том 162, вып. 5 (11), 2022

Взаимодействие двух солитонных газов

ем и согласно (12) мы имеем

(а)

f₁,f₂

κ²¹(1 - α₂f1c) - κ²²α₁f2c

0.10

s1c =

1-α₁f2c -α₂f1c

(26)

0.08

κ²²(1 - α₁f2c) - κ²α2f1c

s2c =

0.06

1-α₁f2c -α₂f1c

0.04

Медленный газ втекает через правый разрыв

f₁

0.02

в область плато и приравнивание выражений

для его потока по разные стороны от разры-

-4

-2

ва в системе отсчета, где он покоится, дает

f1c(s1c - c⁺) = f₁₀(κ²¹ - c⁺). Через левый разрыв в

область плато втекает быстрый газ и аналогичный

(б)

s₁, s₂

подсчет дает f₂₀(κ²² - c^-) = f2с(s2c - c^-). С уче-

3.5

том (25) и (26) полученные равенства приводят к

3.0

уравнениям

2.5

2.0

s2c - κ²¹

1.5

f1c = f₁₀

= f₁₀(1 - α₁f2c),

s2c - s1c

1.0

(27)

κ²

-s1c

0.5

s₁

f2c = f₂₀

= f₂₀(1 - α₂f1c),

s2c - s1c

-4

-2

откуда находим выражения

f₁₀(1 - α₁f₂₀)

f1c =

Рис. 2. Распределения плотностей солитонных газов (а)

1-α₁α₂f₁₀f₂₀

(28)

и их перенормированных скоростей (б) в зависимости

f₂₀(1 - α₂f₁₀)

от координаты для профиля волны, задаваемого форму-

f2c =

1-α₁α₂f₁₀f₂₀

лой (36). Параметры солитонных газов равны κ1 = 1,

κ2 = 1.8, f10 = 0.05, f20 = 0.1. Скорость волны, совпада-

для плотностей солитонных газов в двухпотоковой

ющая со скоростью течения медленных солитонов, равна

области плато. Ясно, что полученные формулы име-

V = s1 = 0.174, а скорость течения газа быстрых солито-

ют смысл лишь при выполнении неравенства

нов на бесконечности равна s20 = 3.469, что больше, чем

неперенормированная скорость κ²² = 3.24.

α₁f1c + α₂f2c < 1,

(29)

когда перенормированные скорости (26) положи-

волны. Пусть плотности солитонных газов на беско-

тельны, т.е. плотности солитонных газов не могут

нечности стремятся к постоянным значениям:

быть слишком большими. Фактически еще более

сильные ограничения на плотность солитонов нала-

f₁ → f₁₀,

f₂ → f₂₀

при

x → ±∞.

(30)

гает условие, что вариация флуктуирующего вол-

нового поля u² - u² в солитонном газе должна быть

Тогда постоянное значение риманова инварианта s₁

положительной (см. [19]). Полученные соотношения

равно скорости волны солитонного газа (см. (26))

хорошо согласуются с результатами численного ре-

шения уравнения КдФ с начальными данными в ви-

κ²¹(1 - α₂f₁₀) - κ²²α₁f₂₀

де большого числа солитонов двух разных типов, на-

V =s₁ =

(31)

1-α₁f₂₀ -α₂f₁₀

ходящихся по разные стороны от начала координат

(см. [18]).

совпадающей с перенормированной скоростью мед-

ленного газа, а формулы (13) дают выражения для

плотностей солитонных газов:

5. ТЕЧЕНИЕ ДВУХ СОЛИТОННЫХ ГАЗОВ В

[

]

ВИДЕ ПРОСТОЙ ВОЛНЫ

f₁(ξ) =

(V - κ²²)ρ(ξ) ,

α₂

(32)

Формулы (22) дают более общую форму решения

f₂(ξ) =

(κ²¹ - V )ρ(ξ).

для течения двух солитонных газов в виде простой

2α₁

801

А. М. Камчатнов, Д. В. Шайкин

ЖЭТФ, том 162, вып. 5 (11), 2022

Легко видеть, что они связаны соотношением

Поскольку s₁ = s₂, приходим к уравнению

∂²t

1-α₁f₂ -α₂f₁ =

(κ²² - κ²¹)ρ,

(33)

= 0,

(38)

∂s₁∂s

из которого следует, в частности, формула

общее решение которого запишем через две произ-

вольные функции, которые удобно обозначить как

2(1 - α₁f₂₀ - α₂f₁₀)

F^′′(s₁) и G^′′(s₂), в виде

ρ₀ =

(34)

κ²² - κ²

t(s₁, s₂) = F^′′(s₁) + G^′′(s₂).

(39)

Распределения плотности (32) содержат произволь-

ную функцию ρ(ξ) и через нее же выражается рас-

Из уравнений (37) легко находим

пределение перенормированной скорости быстрого

x(s₁, s₂) = s₁F^′′(s₁)+s₂G^′′(s₂)-F^′(s₁)-G^′(s₂). (40)

солитонного газа согласно второй формуле (22). На

бесконечности s₂ стремится к значению (см. (26))

Это решение можно преобразовать к форме

κ²²(1 - α₁f₂₀) - κ²¹α₂f₁₀

s₂₀ =

(35)

x - s₁t = (s₂ - s₁)G^′′(s₂) - F^′(s₁) - G^′(s₂),

1-α₁f₂₀ -α₂f₁₀

(41)

x - s₂t = -(s₂ - s₁)F^′′(s₁) - F^′(s₁) - G^′(s₂),

Полученное решение имеет физический смысл при

в которой оно было получено другим способом в ра-

таких значениях параметров κ₁, κ₂, f₁₀, f₂₀, что и

боте [20].

распределения плотностей f₁, f₂ солитонных газов,

Приведем для полноты другие представления об-

и их перенормированные скорости s₁, s₂ повсюду по-

щего решения, которые могут оказаться более удоб-

ложительны.

ными при решении конкретных задач. Если обра-

Найденное нами течение двух солитонных газов

титься к методу годографа в форме Царева [21], то

проиллюстрировано на рис. 2 для функции ρ(ξ),

общее решение можно записать в форме

равной

ρ(ξ) = ρ₀ +

(36)

∂W

x-s₂t=

x-s₁t=

∂W,

(42)

ch ξ

∂s₁

∂s₂

В этом случае профиль плотности f₁ медленного га-

где функция W = W (s₁, s₂) должна удовлетворять

за движется вместе с этой компонентой со скоро-

уравнению Эйлера-Пуассона:

стью V = s₁. Быстрый же газ течет сквозь медлен-

)

ный с локальной скоростью s₂, которая уменьшает-

∂²W

⁽∂W

∂W

= 0.

(43)

ся в области «ямы» в распределении f₁, вследствие

∂s₁∂s₂

s₁ - s₂

∂s₁

∂s₂

чего плотность f₂ в этой области увеличивается.

Легко убедиться, что решения уравнения (43) вы-

ражаются через две произвольные функции F (s₁) и

6. ОБЩЕЕ РЕШЕНИЕ ДЛЯ ТЕЧЕНИЯ ДВУХ

G(s₂) следующим образом:

СОЛИТОННЫХ ГАЗОВ

W (s₁, s₂) = (s₁-s₂)[F^′(s₁)-G^′(s₂)]-2[F (s₁)+G(s₂)].

Известный из газовой динамики метод годогра-

(44)

фа (см., например, [16]) позволяет легко получить

Подстановка (44) в (42) дает решение в форме (41).

общее решение уравнений (14), когда обе скоро-

Функции F (s₁) и G(s₂) должны находиться из на-

сти s₁ и s₂ изменяются в пространстве и со време-

чальных условий задачи.

нем. Делая стандартное преобразование годографа

Как было показано Риманом (см., например,

t = t(s₁,s₂), x = x(s₁,s₂), мы приводим эти уравне-

[22]), вместо использования этого общего решения,

ния к виду

выраженного через произвольные функции, часто

бывает удобно использовать метод, выражающий

∂x

∂t

∂x

∂t

решение задачи непосредственно через начальные

-s₁

= 0,

-s₂

= 0.

(37)

∂s₁

∂s₂

условия с помощью так называемой функции Ри-

мана. В нашем случае функция Римана может быть

Исключение x дает

получена из общей формулы для динамики полит-

(

)

∂²t

∂²x

∂

∂t

s₂

∂²t

ропного газа при показателе адиабаты γ = -1. Вхо-

∂s₁∂s₂

s₁ ∂s₁∂s₂

s₁ ∂s₁

s₂ ∂s₂

s₁ ∂s₁∂s₂

дящая в это выражение гипергеометрическая функ-

802

ЖЭТФ, том 162, вып. 5 (11), 2022

Взаимодействие двух солитонных газов

ция сводится к F (-1, 2; 1; z) = 1 - 2z и функция Ри-

f₂,κ2

мана для уравнений (14) принимает особенно про-

f₂₀, s₂

стой вид:

f₁, κ

f₁₀, s₁

(r₁ + r₂)(s₁ + s₂) - 2(r₁r₂ - s₁s₂)

R(r₁, r₂; s₁, s₂) =

(r₁ - r₂)²

(45)

где (r₁, r₂) — текущие координаты на плоскости го-

−₂

+κ²¹t

−₂

+s₂t

+s₁t

+κ²²t

дографа, а (s₁, s₂) — координаты точки P , в которой

ищется значение функции W = W (P ) = W (s₁, s₂).

Мы не будем приводить здесь весьма громоздкие об-

Рис. 3. Зависимость плотностей облаков двух солитон-

щие формулы, которые мало что добавляют к пони-

ных газов от координаты при эволюции начального слоя

манию динамики взаимодействующих солитонных

из двух таких газов до момента их разделения. Жирной

газов, а обратимся вместо этого к решению одной

штриховой линией изображен график плотности медлен-

ного газа, а сплошной линией — график плотности быст-

из типичных задач газовой динамики — задаче о

рого газа.

расширении слоя газа. Решение может быть легко

получено в элементарной форме и его отличие от

решений этой же задачи для других физических си-

имеется смесь двух солитонных газов с параметрами

стем хорошо демонстрирует существенное различие

κ₁, κ₂ (κ₁ < κ₂) и плотностями f₁₀ и f₂₀, то эволю-

между обычной газовой динамикой и динамикой со-

ция этих газов будет более сложной: в процессе раз-

литонных газов.

деления этих газов на два облака, движущихся со

скоростями κ²¹ и κ²², возникнет двухпотоковое плато.

Нашей целью является описание процесса простран-

7. РАСШИРЕНИЕ СЛОЯ ИЗ СМЕСИ ДВУХ

ственного разделения солитонных облаков, а также

СОЛИТОННЫХ ГАЗОВ

определение их параметров после разделения.

Одной из типичных задач, в которой возника-

Ясно, что в возникшем в процессе разделения

ет область общего решения, является задача о рас-

плато газы будут двигаться с перенормированны-

ширении газового слоя. Она была рассмотрена в

ми скоростями s₁, s₂, сохраняя начальные плотности

[23] для классического одноатомного газа, в [24] для

f₁₀, f₂₀. Впереди этого слоя из смеси газов возник-

бозе-эйнштейновского конденсата, в [25] для двух-

нет слой быстрого газа с плотностью f₂, а позади —

температурной плазмы и в [26-28] для ультрареля-

слой медленного газа с плотностью f₁. Левый край

тивистского газа. Во всех этих случаях от краев слоя

области перекрытия движется со скоростью s₂, а ее

вглубь него распространялись волны разрежения и

правый край — со скоростью s₁. Следовательно, об-

после их столкновения в центре образовывалась об-

ласть перекрытия существует в течение времени

ласть общего решения, граничащая по краям с вол-

нами разрежения. Однако в случае солитонного га-

T =

(46)

s₂ - s₁

за решения в виде волн разрежения отсутствуют, а

и при t > T газы разделяются. Из рис. 3 легко уви-

вместо них возникают разрывные решения, между

деть, что длины облаков медленного и быстрого га-

которыми образуется плато с постоянными значе-

зов в момент разделения соответственно равны

ниями римановых инвариантов. Построенное таким

способом решение позволяет сделать некоторые за-

s₂ - κ²¹

l₁ = l

ключения общего характера об эволюции перекры-

s₂ - s₁

(47)

вающихся облаков солитонных газов.

κ²

-s₁

l₂ = l

s₂ - s₁

Если допустить, что в начальный момент време-

причем обе они меньше первоначальной длины l, так

ни единственный солитонный газ с параметром κ₁

имеет распределение плотности в виде столика со

как s₁ < κ²¹ и s₂ > κ²². Из сохранения числа солито-

значением f₁₀ при -l/2 ≤ x ≤ l/2, то его движение

нов в каждой компоненте находим амплитуды:

в последующие моменты времени очевидно: это рас-

s₂ - s₁

f₁ = f₁₀

пределение будет переноситься вдоль оси x со ско-

s₂ - κ²

(48)

ростью κ²¹ без изменения формы. Однако если в на-

s₂ - s₁

f₂ = f₂₀

чальный момент времени в области -l/2 ≤ x ≤ l/2

κ²² - s₂

803

А. М. Камчатнов, Д. В. Шайкин

ЖЭТФ, том 162, вып. 5 (11), 2022

В момент разделения облаков центры тяжести об-

лака медленных солитонов и облака быстрых соли-

0.8

тонов находятся соответственно в точках

l s₁ +κ²¹

0.6

x₁(T) =

2s₂ -s₁

(49)

l s₂ +κ²

0.4

x₂(T) =

².

2s₂ -s₁

0.2

Если бы солитоны не взаимодействовали друг с дру-

гом, то эти облака двигались бы с неперенормиро-

ванными скоростями и находились бы в этот момент

в точках

0.5

1.5

2.5

κ²¹l

x₁₀(T) =

s₂ - s₁

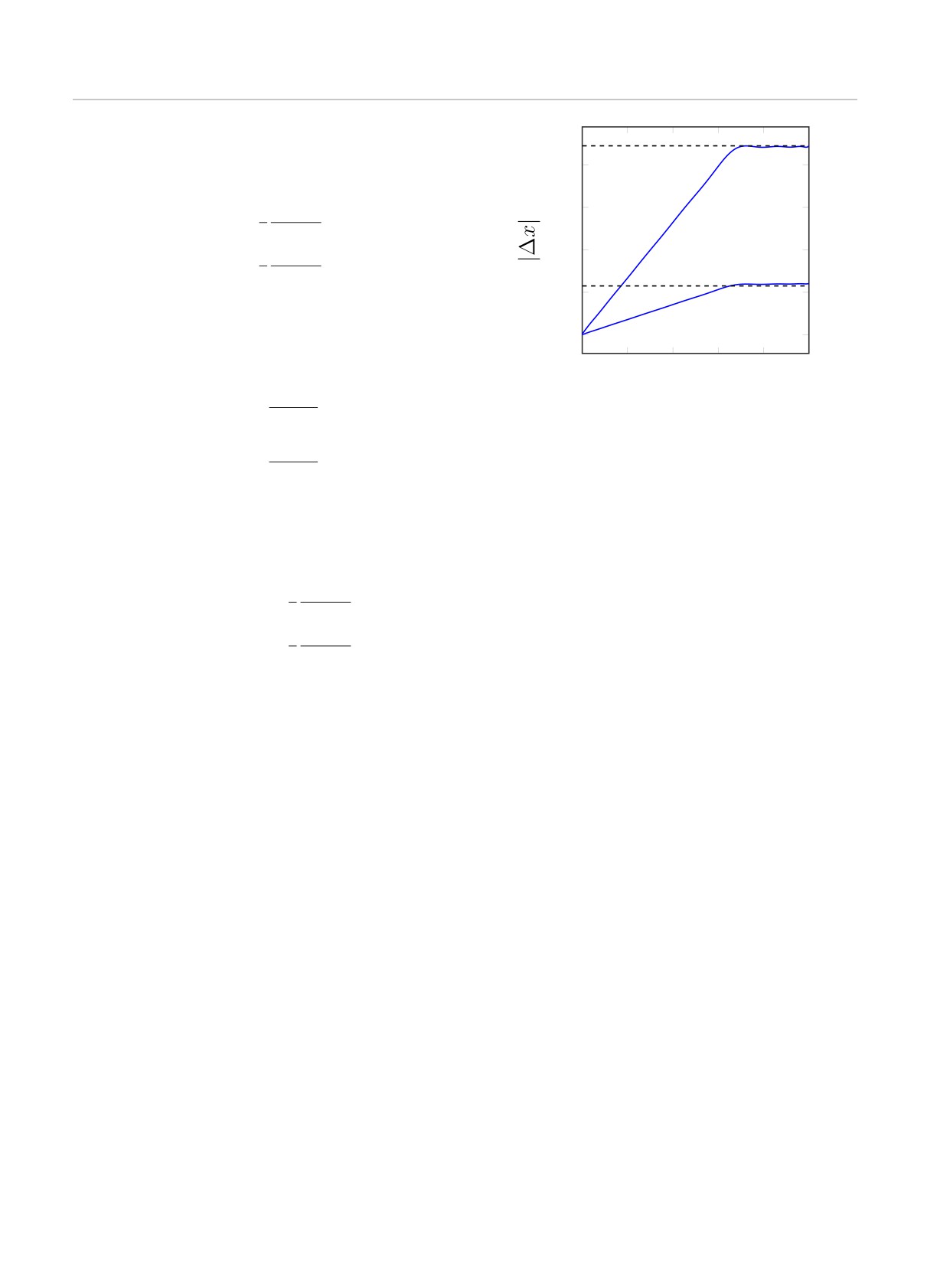
Рис. 4. Сдвиги центров тяжести облаков от их положе-

κ²²l

ний в отсутствие взаимодействия, полученные численным

x₂₀(T) =

s₂ - s₁

решением уравнений для газа Чаплыгина при начальных

значениях параметров f10 = 0.05, f20 = 0.1, κ1 = 1.3,

т.е. из-за взаимодействия они сдвигаются соответ-

κ2 = 2.5, l = 10. В момент T = 1.6 разделения они прини-

ственно на расстояния

мают теоретические значения, даваемые формулами (50).

8. ЗАКЛЮЧЕНИЕ

l s₁ -κ²¹

Δx₁ = x₁(T ) - x₁₀(T ) =

< 0,

2s₂ -s₁

(50)

l s₂ -κ²

В настоящей работе показано, что фундамен-

Δx₂ = x₂(T ) - x₂₀(T ) =

² > 0.

2s₂ -s₁

тальным свойством динамики двух взаимодейству-

ющих солитонных газов является существование

простых волн, распространяющихся без изменения

Таким образом, вследствие взаимодействия облака

формы. В частности, такие простые волны могут

сужаются, плотности солитонов в обоих увеличива-

иметь разрывы, так что в задачах типа «разруше-

ются и медленное облако сдвигается назад, а быст-

ния плотины» вместо волн разрежения динамики

рое — вперед. Переход к этим значениям сдвигов

обычных газов возникают простые волны с разрыва-

иллюстрируется на рис. 4, полученном согласно чис-

ми, соединяемые вместо общего решения, в котором

ленному решению уравнений для газа Чаплыгина. В

в обычной теории изменяются оба римановых инва-

начальный момент времени центры тяжести обоих

рианта, областью плато с постоянными римановыми

газов находились в начале координат и по мере раз-

инвариантами. Это свойство динамики солитонных

деления облаков центр тяжести быстрого газа опе-

газов резко контрастирует со свойствами газовой ди-

режал движение, которое он совершал бы со сво-

намики обычных газов. В то же время на основе

ей неперенормированной скоростью, а центр тяже-

указанной картины могут быть построены простые

сти медленного газа отставал от аналогичного дви-

аналитические решения типичных задач, подтвер-

жения со своей неперенормированной скоростью.

ждаемые точными численными решениями кинети-

После момента разделения центры тяжести обоих

ческого уравнения, приведенного к эквивалентной

газов продолжают движение со своими неперенор-

форме уравнений для динамики газа Чаплыгина. Из

мированными скоростям, приобретая дополнитель-

построенных решений следует интуитивно понятная

ные сдвиги вследствие взаимодействия с солитона-

картина поведения облаков солитонных газов: в ре-

ми другого сорта. Хорошее согласие предсказывае-

зультате взаимодействия облако быстрых солитонов

мых теорией значений сдвигов (50) с численным ре-

сдвигается вперед, а облако медленных солитонов

шением показывает, что наша картина формирова-

сдвигается назад, причем оба облака сужаются, а

ния из начальных разрывов простых волн с разры-

плотность солитонов в них возрастает. Полученные

вами соответствует реальной динамике взаимодей-

формулы позволяют дать оценку этих эффектов в

ствующих солитонных облаков согласно кинетиче-

ведущихся в настоящее время экспериментальных

скому уравнению.

804

ЖЭТФ, том 162, вып. 5 (11), 2022

Взаимодействие двух солитонных газов

исследованиях солитонных газов в волнах на воде,

13.

P. Suret, A. Tikan, F. Bonnefoy, F. Copie,

нелинейной оптике и физике холодных атомов (см.,

G. Ducrozet, A. Gelash, G. Prabhudesai,

например, [12-14]).

G. Michel, A. Cazaubiel, E. Falcon, G. El,

and S. Randoux, Phys. Rev. Lett. 125, 264101

Благодарности. Выражаем благодарность

(2020).

Г. А. Элю за полезное обсуждение.

14.

I. Bouchoule and J. Dubail, J. Stat. Mech. 2022,

Финансирование. Работа выполнена при фи-

014003 (2022).

нансовой поддержке Российского фонда фундамен-

тальных исследований (грант № 20-01-00063).

15.

S. C. Gardner, J. M. Greene, M. D. Kruskal, and

R. M. Miura, Phys. Rev. Lett. 19, 1095 (1967).

16.

Л. Д. Ландау, Е. М. Лифшиц, Гидродинамика,

ЛИТЕРАТУРА

Физматлит, Москва (2001).

N. J. Zabusky and M. D. Kruskal, Phys. Rev. Lett.

17.

С. А. Чаплыгин, О газовых струях, Унив. тип.,

15, 240 (1965).

Моксва (1902); С. А. Чаплыгин, Собрание со-

P. D. Lax, Comm. Pure Appl. Math. 21, 467

чинений, т. II, ОГИЗ-ГИТТЛ, Москва (1948),

(1968).

с. 19-137.

В. Е. Захаров, С. В. Манаков, С. П. Новиков,

18.

F. Carbone, D. Dutykh, and G. A. El, Europhys.

Л. П. Питаевский, Теория солитонов. Метод

Lett. 113, 30003 (2016).

обратной задачи, Наука, Москва (1980).

19.

G. A. El, Chaos 26, 023105 (2016).

А. Ньюэлл, Солитоны в математике и физике,

20.

М. В. Павлов, ТМФ 73, 316 (1987).

Мир, Москва (1989).

21.

С. П. Царев, Изв. АН СССР, сер. матем. 54,

В. Е. Захаров, ЖЭТФ 60, 993 (1971).

1048 (1990).

G. A. El, Phys. Lett. A, 311, 374 (2003).

22.

А. Зоммерфельд, Дифференциальные уравнения

G. A. El and A. M. Kamchatnov, Phys. Rev. Lett.,

в частных производных физики, Изд-во иностр.

95, 204101 (2005).

лит., Москва (1950).

G. A. El, A. M. Kamchatnov, M. V. Pavlov, and

23.

В. Г. Носов, А. М. Камчатнов, ЖЭТФ 70, 768

S. A. Zykov, J. Nonlinear Sci., 21, 151 (2011).

(1976).

E. V. Ferapontov and M. V. Pavlov, J. Nonlinear

24.

S. K. Ivanov and A. M. Kamchatnov, Phys. Rev.

Sci., 32, 26 (2022).

A 99, 013609 (2019).

10.

B. Doyon, Lecture notes on Generalised

25.

S. K. Ivanov and A. M. Kamchatnov, Phys. Fluids

Hydrodynamics, SciPost Phys. Lect. Notes

32, 126115 (2020).

18 (2020).

26.

Л. Д. Ландау, Изв. АН СССР, сер. физ. 17, 51

11.

G. A. El, J. Stat. Mech. 2021 114001 (2021).

(1953).

12.

I. Redor, E. Barthélemy, H. Michallet, M. Onorato,

27.

И. М. Халатников, ЖЭТФ, 27, 529 (1954).

and N. Mordant, Phys. Rev. Lett. 122, 214502

(2019).

28.

А. М. Камчатнов, ЖЭТФ 156, 689 (2019).

805

ЖЭТФ, вып. 5 (11)