ЖЭТФ, 2022, том 162, вып. 5 (11), стр. 750-766

ГРАНИЧНЫЕ УСЛОВИЯ, РАСПРЕДЕЛЕНИЕ ФАЗ И СКРЫТАЯ

СИММЕТРИЯ В ОДНОМЕРНОЙ ЛОКАЛИЗАЦИИИ

И. М. Суслов^*

Институт физических проблем им. П. Л. Капицы Российской академии наук

119334, Москва, Россия

Поступила в редакцию 04 июня 2022 г.,

после переработки 04 июня 2022 г.

Принята к публикации 20 июня 2022 г.

Рассматриваются одномерные неупорядоченные системы со случайным потенциалом малой амплитуды

и короткодействующими корреляциями для энергий вблизи края зоны идеального кристалла. Получено

уравнение эволюции для совместной функции распределения P (ρ, ψ) ландауэровского сопротивления ρ

и фазовой переменной ψ = θ - ϕ (θ и ϕ — фазы, входящие в трансфер-матрицу) при изменении длины

системы L. В пределе больших L уравнение допускает разделение переменных, что обеспечивает су-

ществование стационарного распределения P (ψ), определяющего коэффициенты в уравнении эволюции

для P(ρ). Предельное распределение P(ρ) при L → ∞ является логномальным и не зависит от гранич-

ных условий. Оно определяется “внутренним” распределением фазы ψ, форма которого изучена во всей

области энергий, включая запрещенную зону. Приближение случайных фаз справедливо в глубине раз-

решенной зоны, но сильно нарушается при других энергиях. Фаза ψ оказывается “плохой” переменной,

а “правильной” переменной является ω = -ctg ψ/2. Форма стационарного распределения P(ω) опре-

деляется внутренними свойствами системы и не зависит от граничных условий. Изменение граничных

условий приводят к масштабному преобразованию ω → sω и трансляциям ω → ω + ω0 и ψ → ψ + ψ0, что

определяет “внешнее” распределение фаз, входящее в уравнения эволюции. Независимость предельного

распределения P(ρ) от внешнего распределения P(ψ) позволяет говорить о скрытой симметрии, харак-

тер которой выявляется ниже.

DOI: 10.31857/S0044451022110165

где t и r — амплитуды прохождения и отражения и

EDN: LAXMNI

ρ = |r/t|² — безразмерное сопротивление по Ландау-

эру [2]. При последовательном расположении рас-

сеивателей их трансфер-матрицы перемножаются.

1. ВВЕДЕНИЕ

Для слабого рассеивателя матрица T близка к еди-

ничной, что позволяет выводить дифференциаль-

При исследовании одномерных неупорядо-

ные уравнения эволюции для ее параметров и в

ченных систем удобно использование трансфер-

частности — для ландауровского сопротивления ρ.

матрицы T , которая связывает амплитуды волн

В приближении случайных фаз (когда распреде-

слева (Ae^ikx + Be^-ikx) и справа (Ce^ikx + De^-ikx) от

ления ϕ и θ считаются однородными) такое уравне-

рассеивателя,

ние для распределения P (ρ) имеет вид (параметр D

(

)

(

)

— порядка обратной длины пробега) [3]- [8]

(1)

[

]

∂P(ρ)

∂

∂P(ρ)

ρ(1+ρ)

(3)

∂L

∂ρ

и при наличии инвариантности относительно обра-

щения времени допускает параметризацию [1]:

и описывает эволюцию начального распределения

(

)

P₀(ρ) = δ(ρ) на нулевой длине L к логнормально-

iθ

1/t -r/t

(√ρ+1 eiϕ√ρ e

му распределению при больших L.

T =

(2)

−r^∗/t^∗ 1/t^∗

√ρ+1 e^-iϕ

Согласно [9], распределение фаз ϕ и θ перестает

быть однородным при введении полунепроницаемых

^* E-mail: suslov@kapitza.ras.ru

границ, отделяющих систему от присоединенных к

750

ЖЭТФ, том 162, вып. 5 (11), 2022

Граничные условия, распределение фаз и. ..

ней идеальных контактов, даже если оно было од-

нородным в исходной системе; в последнем случае

возникает более общее уравнение

[

]

∂P(ρ)

∂

∂P(ρ)

-γ(1+2ρ)P(ρ) + ρ(1+ρ)

∂L

∂ρ

(4)

которое в приближении случайных фаз сводится

к (3). Последнее приближение хорошо работает в

глубине разрешенной зоны для “естественных” иде-

альных контактов (изготовленных из того же ма-

териала, что изучаемая система, но без примесей),

что обычно и предполагается в теоретических рабо-

тах (см. ссылки в [10-12]); ситуация внутри запре-

щенной зоны идеального кристалла рассматривает-

ся сравнительно редко [13-15] и лишь на уровне вол-

новых функций. Для исследования эволюции P(ρ)

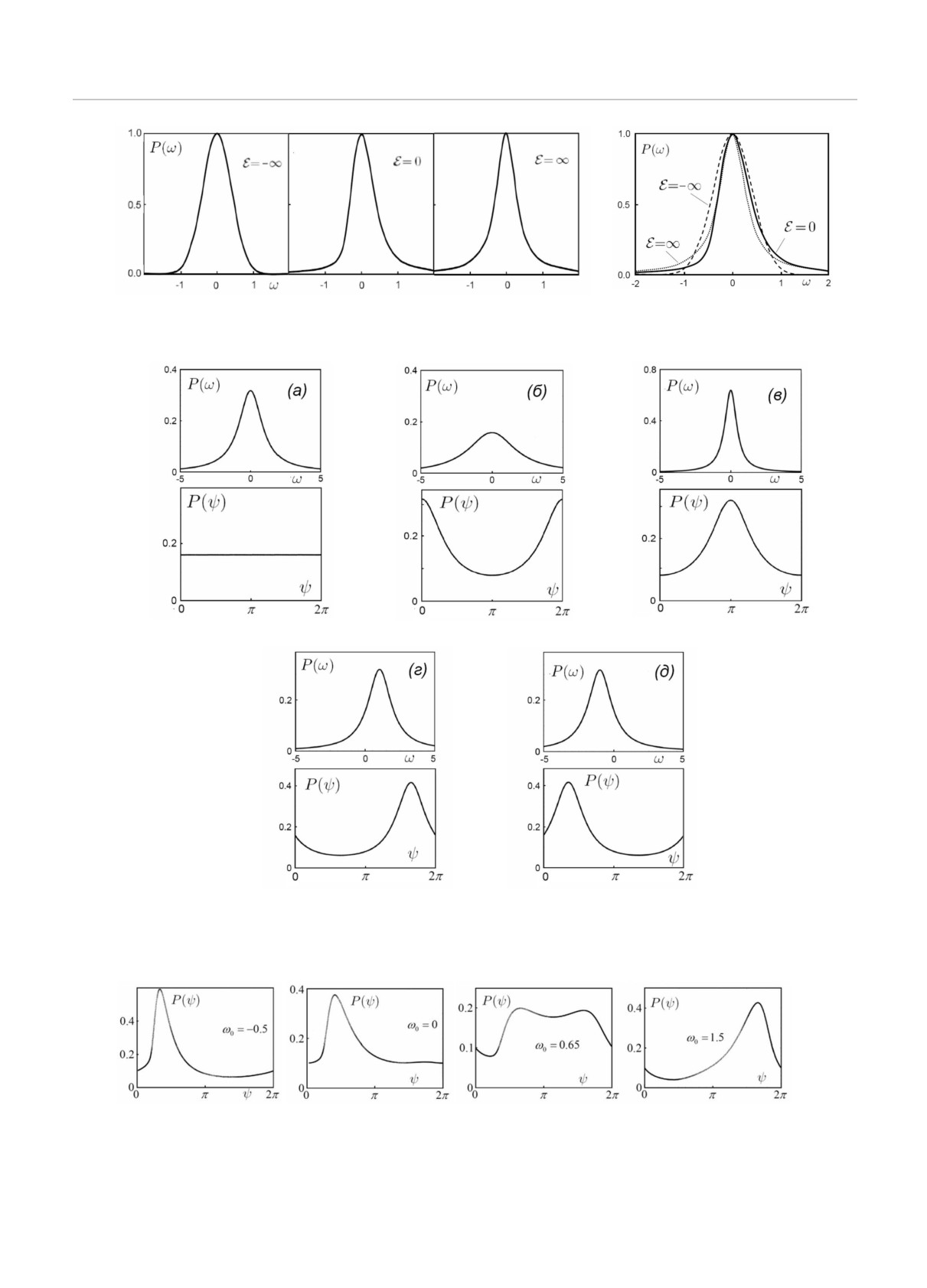
Рис. 1. Зависимость параметра γ в уравнении (4) от при-

при произвольном положении уровня Ферми (вклю-

веденной энергии

E = E/W4/3. Параметр γ мал в глубине

чая запрещенную зону) требуется введение “чуже-

разрешенной зоны в соответствии с приближением случай-

родных” контактов из хорошего металла¹⁾, что авто-

ных фаз.

матически усложняет граничные условия. Это при-

водит к еще более общему уравнению [16]

[

∂P(ρ)

∂

-γ₁(1+2ρ)P(ρ) -

∂L

∂ρ

]

√

∂P(ρ)

-2γ₂

ρ(1+ρ)P (ρ) + ρ(1+ρ)

(5)

∂ρ

коэффициенты которого в пределе больших L опре-

деляются стационарным распределением фаз (см.

ниже (34)). Для больших L типичные значения ρ

велики и уравнение (5) сводится к (4) с γ = γ₁ +γ₂.

На рис. 1 показана зависимость параметра γ от

E = E/W4/3, где E — энергия Ферми, отсчитанная

Рис.

2. Зависимость параметров

= v/W2/3 и

от нижнего края исходной зоны, и W — амплиту-

D = D/W2/3 от приведенной энергии

E = E/W4/3. Ра-

да случайного потенциала (все энергии измеряются

венство v = D, справедливое в приближении случайных

в единицах интеграла перекрытия для одномерной

фаз, реализуется лишь в глубине разрешенной зоны.

модели Андерсона, см. ниже (13)). Параметр γ бли-

зок к нулю в глубине разрешенной зоны в соответ-

{

}

ствии с приближением случайных фаз, но наруше-

[ln ρ - vL]²

ние последнего во всем энергетическом интервале

P (ρ) =

√

exp

(6)

4πDL

4DL

представляет собой совсем не малый эффект. Такое

нарушение происходит по внутренним причинам и

где v = (2γ +1)D, определяется внутренними свой-

введение полупрозрачных границ не является для

ствами изучаемой системы (рис. 2) и не зависит от

этого необходимым. Более того, предельное (логнор-

граничных условий.

мальное) распределение P (ρ) в области больших L

Зависимость γ от

E (рис. 1) однозначно свиде-

тельствует о нарушении приближения случайных

фаз, но получена в [16] на основе анализа момен-

¹⁾ Нетрудно понять, что для энергий внутри запрещенной

тов распределения (см. ниже), при котором вопрос

зоны идеального кристалла “естественные” идеальные кон-

о распределении фаз полностью обходится. Прояс-

такты оказываются непроводящими, тогда как в изучаемой

нение вопроса о распределении фаз необходимо для

неупорядоченной системе имеются флуктуационные состоя-

ния.

логической завершенности теории одномерной лока-

751

И. М. Суслов

ЖЭТФ, том 162, вып. 5 (11), 2022

√

лизации и является целью настоящей работы. Это

√ρe^-iθ = χ² T^′ ,

1+ρe^-iϕ =χ²T^′,

(8)

неразрывно связано с исследованием роли гранич-

где T^′ = T₁₁-T₁₂+T₂₁-T₂₂ и T_ij — элементы матрицы

ных условий и требует разрешения кажущихся про-

T. При больших χ имеем ρ ∼ χ⁴, так что 1+ρ ≈ ρ и

тиворечий.

Действительно, в работах [9, 16] высказаны два

ϕ = ±π/2, θ = ±π/2 при χ → ∞.

(9)

утверждения, которые выглядят трудно совмести-

мыми. С одной стороны, изменение граничных усло-

Таким образом, при больших χ фазы ϕ и θ лока-

вий существенно влияет на распределение фаз, ко-

лизуются вблизи значений ±π/2, независимо от их

торое в общем случае меняет параметры уравне-

распределения в исходной системе.

ний эволюции (3-5) и даже их структуру. С дру-

С физической точки зрения ситуация выглядит

гой стороны, эти изменения не влияют на форму

следующим образом (рис. 3). В глубине достаточ-

предельного распределения (6) в области больших

но длинной неупорядоченной системы реализуется

L. Справедливость этих утверждений означает, что

некоторое “внутреннее” распределение фаз, не зави-

в системе имеется скрытая симметрия, т.е. инва-

сящее от граничных условий. При рассмотрении си-

риантность физических параметров относительно

стемы со стороны идеальных контактов наблюдает-

некоторого класса преобразований. С теоретической

ся “внешнее” распределение фаз, определяемое гра-

точки зрения, выявление скрытой симметрии пред-

ничными условиями; именно такие фазы входят в

ставляет безусловный интерес, указывая на возмож-

трансфер-матрицу. Влияние границ раздела суще-

ность существенных упрощений. Практически же,

ственно на масштабе порядка длины локализации ξ,

без выяснения характера указанной инвариантности

что определяет переходную область, в которой внут-

невозможно отделить реальные физические эффек-

реннее распределение фаз постепенно трансформи-

ты от фиктивных. Выявление этой инвариантности

руется к внешнему. В пределе больших L распре-

оказывается очень нетривиальным и требует вывода

деление P (ρ) определяется внутренним распределе-

уравнений эволюции в наиболее общем виде.

нием фаз, что обеспечивает его независимость от

Поясним происхождение двух упомянутых

граничных условий. Однако, в уравнения эволюции

утверждений. При изменении граничных условий

входит именно внешнее распределение фаз²⁾, и нуж-

трансфер-матрица T преобразуется в

T = T_lTT_r,

но понять, почему это не влияет на предельное рас-

где T_l и T_r

— краевые матрицы, связывающие

пределение P (ρ). Второй вопрос, связанный с пер-

амплитуды волн слева и справа от границы разде-

вым, состоит в следующем: каким образом можно

ла. Таким образом, изменение граничных условий

найти внутреннее распределение фаз, если оно не

приводит к линейному преобразованию элементов

входит в уравнения?

трансфер-матрицы. Линейное преобразование не

Обсудим характер упомянутой инвариантности.

меняет показателей экспоненциального роста для

Изменение матрицы T с длиной системы L опреде-

вторых и четвертых моментов, которые находятся

ляется соотношением

по известной матрице T и определяются внут-

ренними свойствами системы. Знание этих двух

TL+ΔL = T_L TΔL ,

(10)

показателей позволяет установить “коэффициент

диффузии” D и “скорость дрейфа” v в предельном

где матрица TΔL близка к единичной, что позволяет

распределении (6) (рис. 2), которые таким образом

выводить дифференциальные уравнения эволюции.

не зависят от граничных условий [16]; после этого

Для перехода к другим граничным условиям умно-

нетрудно получить поведение параметра γ (рис. 1).

жим (10) слева и справа на краевые матрицы T_l и

Влияние граничных условий на распределение

T_r, вводя произведение T_rT-1r = 1 между двумя со-

фаз легко продемонстрировать путем введения то-

множителями:

чечных рассеивателей на границах системы, когда

T_l TL+ΔLT_r = T_lT_LT_r · T-1rTΔLT_r .

(11)

(

)

1-iχ

-iχ

T =T_lTT_r,

T_l = T_r =

(7)

Тогда для матрицы

T_L = T_lT_LT_r справедливо соот-

iχ

1+iχ

ношение, аналогичное (10),

Принимая для

T параметризацию (2), получим в

²⁾ Это вполне естественно, так как при малых L внутрен-

главном приближении при больших χ

нее распределение фаз вообще не проявляется, и граничные

√

условия существенно влияют на распределение P (ρ), как это

1+ρe^iϕ = -χ2 T′ ,

√ρ e^iθ = -χ² T^′ ,

подробно обсуждалось в [16].

752

ЖЭТФ, том 162, вып. 5 (11), 2022

Граничные условия, распределение фаз и. ..

Описание рассеивателя внутри запрещен-

ной зоны осуществляется с помощью псевдо-

трансфер-матрицы t, связывающей решения слева

(Ae^κx + Be^-κx) и справа (Ce^κx + De^-κx) от рас-

сеивателя. Матрица t(n) для последовательности

рассеивателей с амплитудами V₀, V₁, V₂,. . ., V_n, на-

ходящихся в точках 0, L₁, L₁+L₂, . . . , L₁+L₂+. . .+L_n,

Рис. 3. Внешнее и внутренне распределение фаз

имеет вид

t(n) = tϵ0 tδ1 tϵ1 tδ2 tϵ2 . . . tδn tϵn ,

(14)

где

(

)

1+ϵ_n

ϵn

V_n

tϵn =

ϵn =

(15)

-ϵ

1-ϵ_n

2κa₀

(

)

e-δn

tδn =

δ_n = κL_n

e^δ

Рис. 4. Модель для учета размытия границ раздела

и a₀ — межатомное расстояние. Переход к истинной

трансфер-матрице T(n) = T_l t(n) T_r осуществляет-

ся с помощью краевых матриц, описывающих при-

соединение к системе идеальных контактов. Вводя

TL+ΔL =

T_L T′ΔL ,

(12)

произведение T_rT_l = 1 между каждыми двумя мно-

где матрица T′ΔL = T-1rTΔLT_r по-прежнему близка

жителями в (14), имеем³⁾

к единичной. Переход от TΔL к T′ΔL изменяет фор-

T(n) = Tϵ0 Tδ1 Tϵ1 Tδ2 Tϵ2 . . . Tδn Tϵn ,

(16)

му уравнений эволюции, определяемую параметра-

ми α, β, γ, Δ, ϵ² (см. разд. 2, 3), а переход от T_L

где

T_L меняет стационарное распределение фаз, опре-

Tϵn = T_l tϵn T_r ,

Tδn = T_l tδn T_r .

(17)

деляющее коэффициенты в уравнении (5) для P (ρ).

В модели Андерсона рассеиватели находятся на

Эти два фактора должны компенсировать друг дру-

каждом узле решетки, поэтому все δ_n одинаковы,

га, чтобы предельное распределение P (ρ) остава-

лось инвариантным. Однако, уравнения эволюции

δn = κa0. Примеры краевых матриц даны ниже,

и в наиболее общем случае приводят к следующей

не обладают никакой очевидной инвариантностью,

и ее выявление требует серьезных усилий. Разреше-

структуре матриц Tϵn и T_δ

(

)

ние этих трудностей непосредственно связано с ре-

1-iϵ_n ϵ_ne^iγ

шением вопроса о внутреннем распределении фаз.

Tϵn =

ϵ_n = Kϵ_n ,

(18)

ϵ_ne^-iγ

1+iϵ_n

(

)

( √

)

iβ

A B

1+Δ²e^iα

Δe

2. ПОСЛЕДОВАТЕЛЬНОСТЬ ТОЧЕЧНЫХ

T_δ =

√

РАССЕИВАТЕЛЕЙ

B^∗ A^∗

Δe^-iβ

1+Δ²e^-iα

является трансфер-матрицей общего

Матрица T_δ

Как ясно из опыта работы [16], анализ удобно

вида, тогда как для Tϵn достаточно указанной фор-

проводить для энергий внутри запрещенной зоны

мы. В дальнейшем считаем, как обычно, что все V_n

идеального кристала, а описание разрешенной зо-

статистически независимы, 〈V_n〉 = 0, 〈V2n〉 = W².

ны получать как аналитическое продолжение. Для

Тогда уравнения эволюции будут определяться па-

определенности рассматриваем одномерную модель

раметрами α, β, γ, Δ и величиной

модель Андерсона

ϵ² = 〈ϵ2n〉 = constW² .

(19)

Ψn+1 + Ψn-1 + V_nΨ_n = EΨ_n

(13)

³⁾ Условие Tr Tl

= 1 может быть принято без ограниче-

ния общности. Если это не так, то полагаем T_l = T^′lT^′′l, где

вблизи края исходной зоны, где она соответствует

Tr T^′′l = 1, и используем матрицу T^′′l в качестве Tl. При этом

дискретизации обычного уравнения Шредингера (E

роль матрицы T^′l сводится к изменению начальных условий

— энергия, отсчитанная от центра зоны).

в уравнениях эволюции, тогда как их структура не меняется.

753

И. М. Суслов

ЖЭТФ, том 162, вып. 5 (11), 2022

Внутри разрешенной зоны для

“естественных”

Теперь возьмем произведение второго уравнения

идеальных контактов последовательность точечных

(22) с комплексно сопряженным первым

рассеивателей описывается не произведением (14),

√

[

]

а произведением (16), где

ρ(1+ ρ) e

^ψ = (1+2ρ)

Δe^iβ +ϵe^iγ +iϵ²e^iγ

(

)

√

[(

)

]

1 - iϵ_n

-iϵ_n

V_n

ρ(1+ρ)

e-2iα+2iϵ-ϵ²

e^iψ + ϵ² e2iγ-iψ

(28)

Tϵn =

ϵ_n =

iϵ_n

1 + iϵ_n

2ka₀

Исключая ρ с помощью уравнения (25), получим

(

)

связь

ψ иψ

e-iδn

Tδn =

δ_n =

kL_n ,

(20)

ψ = ψ + 2(ϵ-α) + (R²/2-1)ϵ²sin2(ψ-γ)-

eiδn

[

]

-R

Δsin(ψ-β) + ϵ sin(ψ-γ) + ϵ² cos(ψ-γ)

и k — фермиевский импульс в изучаемой системе,

что соответствует замене κ → ik в предыдущих со-

(29)

отношениях. Такая замена соответствует гладкому

где

1+2ρ

переходу от энергии E = -κ² в запрещенной зоне

√

(30)

ρ(1+ρ)

к E =

k² в разрешенной. При изменении гранич-

ных условий возникают матрицы

Tϵn = TlTϵnTr и

Используя (25), (29) и следуя схеме работ [9,16,17],

Tδn = T_lTδn T_r, имеющие структуру (18).

получим уравнение эволюции для P (ρ, ψ)

{

∂P

[

]

= ϵ²

1-2cos2 (ψ-γ)

(1+2ρ)P -

3. УРАВНЕНИЯ ЭВОЛЮЦИИ

∂L

[

]√

Воспользуемся рекуррентным соотношением

−2

Δcos (ψ-β) + ϵ² sin (ψ-γ)

ρ(1+ρ)P +

T(n+1) = T(n)T_δT_ϵ ,

(21)

+2ϵ²cos²(ψ-γ)ρ(1+ρ)P^′ρ+

}_′

[

]√

где матрицы T(n) и T_ϵ статистически независимы, а

+2ϵ²cos(ψ-γ)

2-Rsin(ψ-γ)

ρ(1+ρ)P^′

T_δ постоянна. Принимая для T(n) параметризацию

{

[

]

(2) и обозначая параметры матрицы T(n+1) как ρ,

ϕ,

+ ϵ2 cos(ψ-γ)

2 sin(ψ-γ)-R

P+

^θ, имеем

[

]

√

2α+RΔsin(ψ-β)

P+

1+ρe

^ϕ =

1+ρe^iϕ(A + ϵC) +

√ρ e^iθ(B^∗ + ϵD^∗) ,

}_′

(22)

[

]₂

√

ϵ²

2-Rsin(ψ-γ)

P^′

(31)

ρe^iθ =

1+ρe^iϕ(B+ϵD) +

√ρ e^iθ(A^∗ + ϵC^∗) ,

где мы положили

Правая часть является суммой полных производ-

ных, что обеспечивает сохранение вероятности.

C =Be^-iγ-iA

D =Ae^iγ+iB.

(23)

Связь распределений ρ и ψ определяется величиной

R, которая стремится к 2 в пределе больших L,

В дальнейшем рассматриваем предел

когда типичные значения ρ велики. Тогда решение

уравнения (31) факторизуется, P (ρ, ψ) = P (ρ)P (ψ),

δ → 0, ϵ → 0, δ/ϵ² = const

(24)

хотя ситуация несколько необычна для разделе-

и сохраняем члены первого порядка по δ и второго

ния переменных (см. Приложение 1); уравнение

по ϵ. Возводя по модулю в квадрат одно из уравне-

эволюции для P (ψ) отщепляется

ний (22), получим

∂P(ψ)

{[

√

2α+2Δsin(ψ-β) - 2ϵ² cos(ψ-γ)+

ρ=ρ+K

ρ(1+ρ) + ϵ²(1+2ρ) ,

(25)

∂L

]

где

+ϵ² sin2(ψ-γ)

P (ψ)+

}_′

[

]

K = 2Δcos(ψ-β) + 2ϵcos(ψ-γ) - 2ϵ2 sin(ψ-γ) (26)

+ 2ϵ²

1-sin(ψ-γ)

² P^′ψ(ψ)

(32)

и дает условие для стационарного распределения

и введена комбинированная фаза

фазы ψ

[

]₂

ψ=θ-ϕ.

(27)

ϵ²

1-sin(ψ-γ)

P^′ψ-

754

ЖЭТФ, том 162, вып. 5 (11), 2022

Граничные условия, распределение фаз и. ..

[

]

-ϵ²

1-sin(ψ-γ)

cos(ψ-γ)P+

v = 2Δ〈sinψ〉 + 2ϵ²〈1-cosψ〉 - 2ϵ²〈sin2 ψ〉,

[

]

α+Δsin(ψ-β)

P =C₀,

(33)

а уравнение для стационарного распределения P(ψ)

принимает вид

где константа C₀ определяется из нормировки.⁴⁾

Усреднение по ψ приводит к уравнению (5) с па-

ϵ² (1-cosψ)² P^′ψ + ϵ² sinψ(1-cosψ)P+

раметрами

+ (α-Δ cos ψ ) P = C₀ .

(39)

D = 2ϵ²

cos² (ψ-γ)

Замена переменных в уравнении (39)

γ₁D = ϵ²

1-2cos2 (ψ-γ)

(34)

ω = -ctgψ/2

(40)

γ₂D = Δ

cos(ψ-β)

-ϵ²

sin(ψ-γ)

учетом

перенормировки

вероятности

откуда для “скорости дрейфа” в (6) получим

P → P(1+ω²)/2, следующей из P(ψ)dψ = P(ω)dω,

приводит его к простой форме

v = 2Δ

cos(ψ-β)

P^′ω + P(b + aω²) = C₀ ,

(41)

+2ϵ²

sin² (ψ-γ) - sin(ψ-γ)

(35)

Входящие в (34, 35) средние определяются стацио-

где

α-Δ

α+Δ

нарным распределением P (ψ).

(42)

2ϵ²

или

α = ϵ²(b + a),

Δ = ϵ²(b - a).

(43)

4. ЗАВИСИМОСТЬ ОТ СВОЙСТВ

ИДЕАЛЬНЫХ КОНТАКТОВ

Уравнение (41) интегрируется в квадратурах, но эта

квадратура практически бесполезна. Более эффек-

Пусть фермиевский импульс k в идеальных кон-

тивным оказывается исследование трансформаци-

тактах отличен от фермиевского импульса

k в изу-

онных свойств. Если P_a,b(ω) — решение уравнения

чаемой системе, а граница раздела является резкой.

(41), то справедливо соотношение

Тогда краевые матрицы в запрещенной зоне могут

быть выбраны в виде

P_a,b(ω) = s-1P_as3_,bs(ω/s).

(44)

(

)

(

)

∗

r r^∗

Оно устанавливается с помощью замены ω = sω и

T_l =

T_r =

(36)

l^∗ l

r^∗ r

приведения уравнения к прежнему виду путем пе-

реопределения параметров ã = as³,

b₌ bs, так что

(

)

(

κ⁾

P_a,b(ω) совпадает с P˜a,˜b(ω) с точностью до коэф-

фициента, который устанавливается из нормировки.

Заметим, что

приводя к результатам (18) для матриц Tϵn и T_δ с

параметрами

α² - Δ²

δ²

)

ab =

(45)

⁽k

κ² - k²

4ϵ⁴

α=-

δ=

a₀ ,

и масштабное преобразование a → as³, b → bs при-

)₂

водит к перенормировке ϵ → ϵ, где

⁽κ

W²

β =

γ=-

ϵ² = ϵ²

(37)

4k²a²

ϵ=ϵs-1 =ϵ

s-1 .

(46)

)

⁽k

κ² + k

Δ=

δ=

a₀ ,

Подставляя (37) в (42), получим исходные значения

параметров a и b

которые являются регулярными функциями энер-

k δ

κ δ

гии E = -κ² и аналитически продолжаются в раз-

a=-

(47)

решенную зону. Тогда для параметров D и v имеем

κ 2ϵ²

k 2ϵ²

после чего соотношения (43) позволяют установить

D = 2ϵ²〈sin2 ψ〉,

(38)

перенормировку α → α, Δ →

Δ в результате мас-

штабного преобразования

⁴⁾ Уравнения

(31, 32) аналогичны уравнениям

(10.27),

(10.28) в книге [10], выведенным в рамках другого форма-

(

)

(

)

лизма, так что связь входящих в них величин с параметрами

Δ=

α=

s-1 -

s δ,

s-1 +

s δ.

трансфер-матрицы не очевидна. То же относится к уравне-

ниям (39, 40) в работе [18].

(48)

755

И. М. Суслов

ЖЭТФ, том 162, вып. 5 (11), 2022

Соотношения (46) и (48) показывают, что преобра-

что после подстановки физических значений (51) да-

зование всех параметров α, Δ, ϵ², входящих в урав-

ет

нения эволюции, сводится к замене

k δ

κ² - κ

κ₁ δ

a=-

, b=

, c=

(54)

κ 2ϵ²

κk

2ϵ²

κ ϵ²

→

(49)

Решение уравнения (52) удовлетворяет соотноше-

эквивалентной изменению фермиевского импуль-

нию

са в идеальных контактах. И наоборот, изменение

P_a,b,c(ω) = s-1P_as3_,bs,cs2 (ω/s),

(55)

свойств идеальных контактов приводит к масштаб-

и, как нетрудно проверить, масштабное преобразо-

ному преобразованию распределения P (ω).

вание P(ω) по-прежнему соответствует изменению

фермиевского импульса k в идеальных контактах.

Нетрудно видеть, что сдвиг ω → ω - ω₀ пере-

5. ВЛИЯНИЕ δ-ОБРАЗНОГО ПОТЕНЦИАЛА

менной ω позволяет привести уравнение (52) к виду

НА ГРАНИЦЕ

(41), что дает соотношение

Если на границе раздела между изучаемой

системой и идеальными проводами имеется δ-

P_a,b,c(ω) = P˜a,˜b,0(ω+ω₀),

(56)

образный потенциал, то краевые матрицы

(36)

преобразуются к виду

κ₁

k δ

κ δ

ω₀ = -

ã=a=-

^b=

κ 2ϵ²

k 2ϵ²

(

)

l∗1

ik+κ-κ₁

ik+κ+κ₁

где значения параметров ã и

b соответствуют ситу-

T_l =

, l₁ =

l^∗ l₁

2ik

ации κ₁ = 0. Таким образом, появление δ-образного

(50)

потенциала на границе приводит к трансляции рас-

(

)

∗

пределения P (ω) на величину ω₀, пропорциональ-

r r

ik+κ-κ₂

ik+κ+κ₂

T_r =

, r₁ =

ную амплитуде δ-образного потенциала.

r∗1 r1

2κ

где κ₁ и κ₂ определяют скачки логарифмической

производной волновой фуекции на левой и правой

6. РАЗМЫТИЕ ГРАНИЦЫ РАЗДЕЛА

границах раздела. Условие T_rT_l = 1 справедливо

Если рассматриваются энергии внутри запре-

при κ₂ = -κ₁, что можно принять без ограниче-

щенной зоны, то изучаемая система при отсутствии

ния общности (см. примечание 3). Тогда матрица

примесей сводится к потенциальному барьеру. Раз-

Tϵn остается неизменной, а матрица T_δ принимает

мытие границ раздела можно моделировать, вводя

вид (18) с параметрами

прослойки металла с фермиевским импульсом k₁ и

k² - κ² + κ²¹

толщинами d₁ и d₂

на границах системы (рис. 4).

α=-

δ,

2κk

Краевые матрицы T_l и T_r для такой модели приведе-

ны в Приложении 2. Условие T_rT_l = 1 выполняется,

κ₁

Δcosβ = -

δ,

(51)

если d₁ и d₂ подчинить ограничениям

k² + κ² - κ²¹

k₁(d₁+d₂) = 2πm , k(d₁+d₂) = 2πn ,

(57)

Δsinβ =

δ,

2κk

является

где m и n — целые числа. Матрица T_δ

которые, как и раньше (ввиду δ = κa₀), регулярны

трансфер-матрицей общего вида, и ее вычисление

по энергии E = -κ². Таким образом, по-прежнему

не представляет интереса. Для матрицы Tϵn полу-

имеем γ = -π/2, тогда как параметр β становится

чается выражение (18) с параметрами

отличным от π/2. Замена (40) приводит уравнение

(33) к виду

κR

⁽sinα⁾

kα

K =

γ = arcsin

(58)

k₁

P^′ω + P(b + cω + aω²) = C₀ ,

(52)

где

с параметрами

R = P+Qcosα, α = k₁(d₂ - d₁),

α-Δsinβ

α+Δsinβ

Δcosβ

k²¹+k2

k²¹-k²

, b=

, c=-

(53)

P =

(59)

2ϵ²

ϵ²

2kk₁

756

ЖЭТФ, том 162, вып. 5 (11), 2022

Граничные условия, распределение фаз и. ..

Значение γ, отличное от -π/2, получается при

T₂₂T⁺²² - T₂₁T⁺²¹ = 1 ,

(61)

d₁ = d₂. Поскольку параметр γ входит как в вы-

T₁₁T⁺²¹ - T₁₂T⁺²² = 0 ,

ражения (34, 35) для D и v, так и в уравнение (33)

для стационарного распределения P (ψ), то сдвигом

которые следуют из условия сохранения потока.

ψ → ψ + ψ₀ его можно привести к значению -π/2,

Потребуем, чтобы матрицы T_δ и T_ϵ, входящие в

что приводит лишь к переопределению параметра

(16,17) были истинными трансфер-матрицами. То-

β. После этого замена переменных (40) приводит к

гда (см. Приложение 3) допустимые краевые мат-

уравнению (52) предыдущего раздела.

рицы образуют трехпараметрическое семейство

Если фермиевский импульс k₁ выбран пропор-

(

)

циональным k, то параметры P и Q являются по-

|r₁|eiα1

|r₂|eiα2

T_l =

(62)

стоянными, и масштабное преобразование P(ω) по-

±i|r1|e-iα1±i|r₂|e-iα2

прежнему приводит к перенормировке (49) ферми-

евского импульса k. В общем случае пропорцио-

1=2|r₁r₂|sin(α₂-α₁),

нальность k₁

∝ k не имеет места, но изменение

где верхний знак выбирается при sin(α₂ -α₁) > 0,

свойств идеальных контактов по-прежнему приво-

дит к масштабному преобразованию P (ω), однако

а нижний — в противоположном случае. Тогда для

с более сложной связью импульса k и масштабного

матриц T_δ и T_ϵ получим выражения (18) с парамет-

фактора s.

рами

α = -2δ|r₁||r₂|cos(α₂-α₁),

β=α₁+α₂,

7. ОБЩИЙ ПОДХОД К КРАЕВЫМ

МАТРИЦАМ

|r₂| cos(α₂ -α₁)

γ = 2α₁ - 2arcsin

Обсудим общий подход к исследованию роли гра-

ничных условий, не связанный с модельными пред-

Δ = 2δ|r₁||r₂|,

(63)

положениями. Для этого нужно выяснить степень

K = r² = |r₁|²+|r₂|²- 2|r₁||r₂|cos(α₂-α₁).

произвола, допустимого в краевых матрицах

Как указывалось в разд.2, условие T_rT_l = 1 мо-

Аналогичный анализ в разрешенной зоне при-

жет быть принято без ограничения общности. Со-

водит к физически очевидному результату

—

гласно (16,17), для нас актуальны выражения, со-

краевые матрицы являются истинными трансфер-

держащие одинаковое число матриц T_r и T_l, а сле-

матрицами общего вида

довательно общие множители можно свободно из-

(

)

влекать из одной матрицы и переносить в другую.

|r₁|eiα1

|r₂|eiα2

T_l =

(64)

Поэтому без ограничения общности матрицы T_r и T_l

|r₂|e-iα2

|r₁|e-iα1

можно выбрать в виде

(

)

(

)

|r₁|² - |r₂|² = 1.

a b

d -b

T_l =

T_r =

(60)

Для матриц T_δ и T_ϵ получаются выражения (18) с

c d

−c a

параметрами

ad - bc = 1,

(

)

α = -δ

|r₁|² + |r₂|²

принимая единичное значение для детерминантов.

Роль краевых матриц наиболее существенна в за-

β = π/2 + α₁+α2 ,

прещенной зоне — с их помощью псевдо-трансфер-

|r₂| cos(α₁ -α₂)

матрица t превращается в истинную трансфер-

γ =-

+ 2α₁ - 2arcsin

матрицу T = T_l t T_r. Условие того, что матрица T

является истинной трансфер-матрицей, выражается

Δ = 2δ|r₁||r₂|,

(65)

соотношениями для матричных элементов T_ij [19]⁵⁾

K = r² = |r₁|²+|r₂|²- 2|r₁||r₂|cos(α₂-α₁).

T₁₁T⁺¹¹ - T₁₂T⁺¹² = 1 ,

Как ясно из предыдущих разделов, весь трехпара-

метрический произвол краевых матриц может быть

⁵⁾ Мы приводим эти соотношения в виде, пригодном для

реализован физически, а уравнения эволюции, при-

описания квазиодномерных систем, когда элементы T_ij явля-

ются матрицами.

веденные в разд.3, являются наиболее общими.

757

ЖЭТФ, вып. 5 (11)

И. М. Суслов

ЖЭТФ, том 162, вып. 5 (11), 2022

8. РАСПРЕДЕЛЕНИЕ P (ω)

в разрешенной зоне возникают осцилляции распре-

деления P (ρ, ψ), связанные с тем, что матрица T при

Как ясно из предыдущего, наиболее общие ре-

отсутствии примесей является трансфер-матрицей

зультаты для параметров уравнения эволюции (5) и

потенциального барьера, который становится про-

предельного распределения (6) даются соотношени-

зрачным, если на его ширине укладывается полуце-

ями (34, 35), где усреднение по ψ производится по

лое число волн де Бройля (аналогично просветле-

стационарному распределению P (ψ), определяемо-

нию в оптике) [16]. При нарушении условия |a| = |b|

му уравнением (33). Сдвиг ψ → ψ + ψ₀ позволяет

в запрещенной зоне распределение P(ρ, ψ) локали-

привести параметр γ к значению -π/2, после чего

зуется вблизи значения ψ, отличного от π/2, что

замена переменных ω = -ctgψ/2 приводит к уравне-

приводит к его медленной релаксации к последне-

нию (52). Далее трансляция ω → ω + ω₀ переводит

му значению.

(52) в уравнение (41), которое масштабным преоб-

Вблизи края исходной зоны уравнение (41) удоб-

разованием ω → sω может быть приведено к одной

но приводить к канонической форме с a = -1. Его

из канонических форм — либо с |a| = |b|, либо с

решение при b = 0 соответствует “критической” об-

a = -1, зависящих от одного параметра; этот одно-

ласти для размытого перехода Андерсона [16] и мо-

параметрический произвол ассоциируется с зависи-

жет быть представлено в виде (см. Приложение 4)

мостью от приведенной энергии

E. Таким образом,

форма распределения P(ω) с ω = -ctg ψ/2 опреде-

∫∞

ляется внутренними свойствами системы, тогда как

P (ω) = A₀ dte^-tt-1/3

(70)

ω³ + 3t

изменение граничных условий переводит его в рас-

пределение P (ω), где переменная

где A₀ определяется из нормировки. При больших ω

ψ+ψ₀

имеем P (ω) ∼ ω-2, что является общим свойством

ω = ω₀ - sctg

(66)

(см. Приложение 4) и соответствует конечным зна-

связана с ω дробно-линейным преобразованием

чениям P (ψ) на границах интервала (0, 2π).

Если масштабным преобразованием и трансля-

Aω + B

ω=

(67)

цией обеспечить максимум P (ω) при ω = 0 с единич-

Cω+D

ным значением в нем, то распределения (68-70) раз-

Согласно [16], ситуация |a|=|b| является выделен-

личаются не очень сильно (рис. 5), свидетельствуя

ной тем, что в глубине разрешенной и запрещенной

о слабой зависимости P(ω) от приведенной энергии

зон параметры уравнения (5) остаются постоянны-

ми до очень малых масштабов⁶⁾ длины L. Случай

a=b, реализуемый в разрешенной зоне соответству-

ет “естественным” идеальным контактам (разд.1).

9. ВНЕШНЕЕ РАСПРЕДЕЛЕНИЕ ФАЗ

При -a=-b ≫ 1 (в глубине разрешенной зоны) в

Если распределение P (ω) известно, то его изме-

уравнении (41) можно опустить член P^′ω и получить

нение при вариации граничных условий сводится к

масштабному преобразованию и трансляциям. При

P (ω) =

(68)

π 1+ω²

этом изменение внешнего распределения P (ψ) на ка-

что соответствует P (ψ) = const, т.е. приближению

чественном уровне является легко предсказуемыми

случайных фаз. При -a = b ≫ 1 (в глубине запре-

и иллюстрируются на рис. 6. Распределение P (ψ)

щенной зоны) константой C₀ в (41) можно прене-

является однородным (рис. 6,а), если P (ω) имеет

бречь вблизи максимума распределения, и полагая

вид (68) и соответствует приближению случайных

ω = -1 + ω, получим P^′ω ≈ -2|a|ωP, что дает гаус-

фаз. Уширение распределения P(ω) приводит к ло-

совское распределение

кализациии P (ψ) вблизи краев интервала (0, 2π), а

√

сужение — к локализации P (ψ) в середине интерва-

|a|

{

}

ла (0, 2π) (рис. 6,в). Сдвиг P (ω) вправо или влево

P (ω) =

exp

-|a|ω²

(69)

приводит к появлению максимума в правой или ле-

локализованное вблизи ω =-1; оно соответствует

вой части интервала (0, 2π) (рис. 6,г,д). Если пара-

гауссовскому распределению P (ψ), локализованно-

метр γ отличен от -π/2, то происходит трансляция

му вблизи π/2 [16]. При нарушении условия |a| = |b|

по ψ и представленные зависимости справедливы не

в интервале (0, 2π), а в интервале (ψ₀, 2π + ψ₀

⁶⁾ Для достаточно больших L они всегда постоянны, так

как определяются стационарным распределением P (ψ).

758

И. М. Суслов

ЖЭТФ, том 162, вып. 5 (11), 2022

Если распределение P (ω) принимается не в виде

(68), а в гауссовской форме (69), то рис. 6 качествен-

но сохраняется, но P (ψ) не будет постоянным на

рис. 6,а. Асимметрия функции P (ω) при E = 0, соот-

ветствующей критическому распределению (рис. 5),

приводит к новому качественному моменту — при ее

трансляциях ω → ω +ω₀ в некотором интервале зна-

чений ω₀ возникает двухгорбое распределение P (ψ)

(рис. 7).

10. ВНУТРЕННЕЕ РАСПРЕДЕЛЕНИЕ ФАЗ

Вернемся к случаю β = π/2, γ = -π/2, рассмот-

Рис. 9. Параметры a и b для внутреннего распределения

ренному в разд.4, и сделаем замену ω = -ctg ψ/2

фаз как функции приведенной энергии

в полном уравнении эволюции (31). Если типичные

значения ρ достаточно велики, то уравнение эволю-

Последний член в (72) имеет тот же вид, что в (71),

ции для P (ρ, ω) принимает вид

тогда как остальные члены не являются инвариант-

{

∂P

4ω²

2ω

ными. Согласно (5), параметр D определяется коэф-

= ϵ²(

)₂ ρ²P^ρ - Δ

ρP +

фициентом при ρ²P^′ρ и уравнения (71, 72) приводят

2∂L

1+ω²

к двум выражениям

}_′

{

}_′

(

)

+ϵ²

ρP + . . .

+ϵ²

P^′ω +

b + aω²

4ω²

1+ω²

D = 2ϵ²

(73)

(

)₂

1+ω²

(71)

a,b

Делая замену ω = sω и переобозначая параметры

ã = as³,

b = bs, ϵ² = ϵ²s-2, имеем

4s²ω²

D=2ϵ²s²

(

)₂

(74)

{

1+s²ω²

ã,b

∂P

4s² ω²

2sω

ϵ²s²

(

)₂ ρ²P^ρ -

ρP +

2∂L

1+s²ω²

которые эквивалентны в силу соотношения (44). Ес-

1+s²ω²

ли (74) принято в качестве определения коэффици-

}_′

{

}_′

(

)

ента диффузии D, то его инвариантность относи-

+ϵ²s²

ρP + . . .

+ϵ²

P′˜ω +

^b+ãω2 P

тельно изменения граничных условий выполняется

1+s²ω²

автоматически. Однако, замена a, b, ϵ на ã,^b, ϵв (71)

(72)

приводит к аналогичным заменам в (73), что вместе

с (74) дает соотношение

4ω²

4s²ω²

(

)₂

=s²

(

)₂

(75)

1+ω²

1+s²ω²

ã,b

которое не выполняется при произвольных s, но

справедливо лишь при некотором “правильном” вы-

боре масштабного фактора. Нетрудно понять, что

этот “правильный” выбор соответствует “внутренне-

му” распределению фаз. Аналогичные соображения

можно привести в отношении параметра v в распре-

делении (6), который определяется коэффициентом

при ρP .

Пусть начальные значения a₀, b₀ параметров a и

b выбраны из условия |a₀| = |b₀|, которое является

“естественным” вдали от края исходной зоны. Если

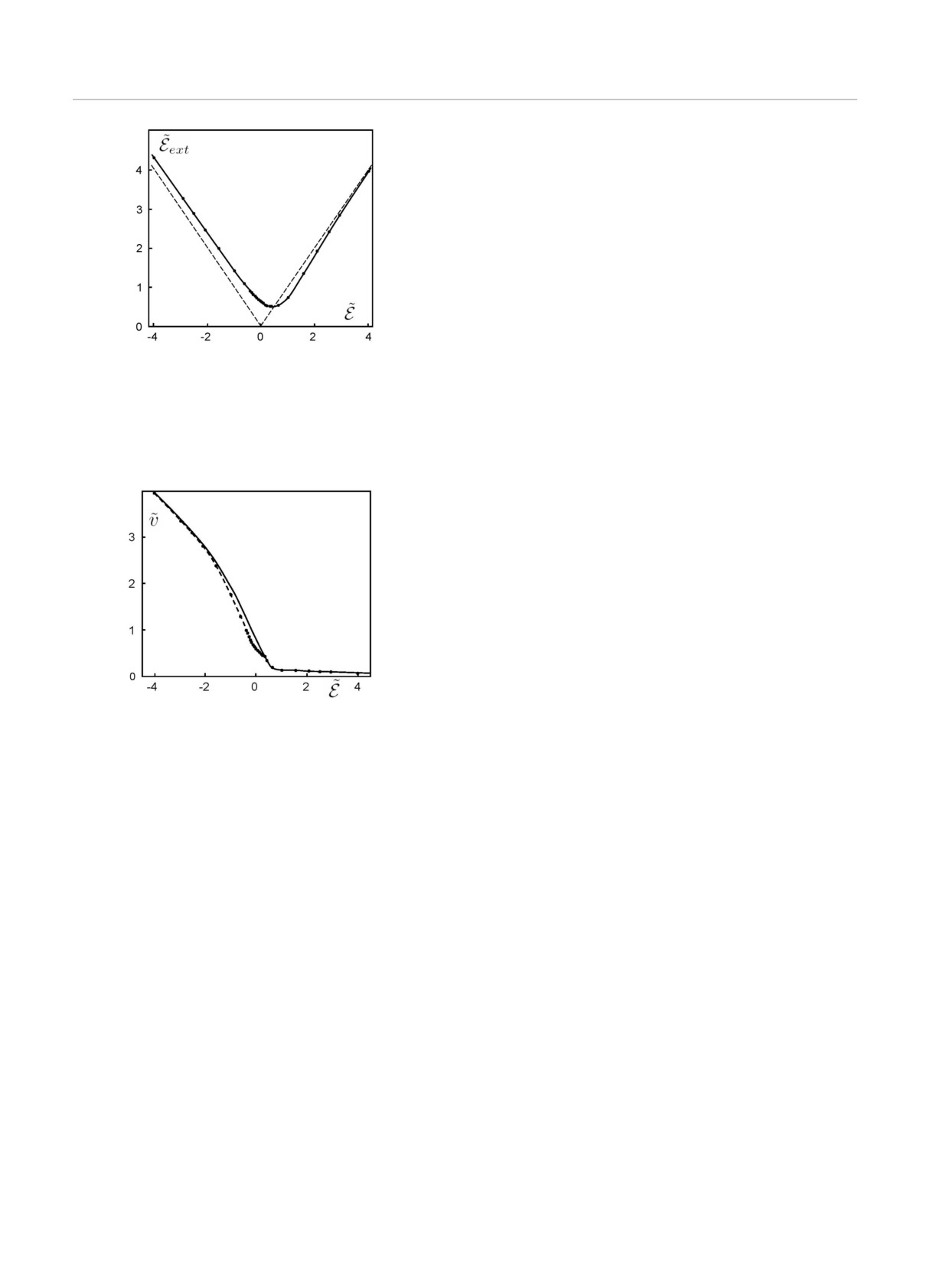
Рис. 8. Зависимость масштабного фактора s и трансляци-

P (ω) — решение уравнения (41) с параметрами a₀,

онного сдвига ω0 от приведенной энергии

b₀, то замена ω → s(ω+ω₀) при надлежащем выборе

760

ЖЭТФ, том 162, вып. 5 (11), 2022

Граничные условия, распределение фаз и. ..

ного потенциала. Этот вывод подтверждается тем,

что при

E <

E₀ трансляционный сдвиг ω₀ уходит в

комплексную плоскость, что имеет простой физиче-

ский смысл. При

E =

E₀ имеем

E_ext =

E₀ (рис. 10)

и сдвинутый край зоны оказывается ниже уровня

Ферми в идеальных контактах при

E >

E₀ и выше

при

E <

E₀. В последнем случае внутренние свой-

ства системы описываются не истинной, а псевдо-

трансфер-матрицей, и распределение P (ψ) стано-

вится комплексным. Детальное изучение последне-

го не очень интересно, поэтому при

E <

E₀ в ка-

честве “внутреннего” распределения P (ψ) мы при-

водим внешнее распределение, наиболее близкое к

Рис. 10. Зависимость энергии Ферми

Eext в идеальных

внутреннему — практически оно близко к модулю

контактах от энергии Ферми в изучаемой системе

E для

комплексного распределения P (ψ). Последнее сле-

внутреннего распределения фаз. Пунктиром показана за-

дует из того, что сдвиг параметра ω₀ в комплексную

висимость

Eext =

плоскость сравнительно мал и допускает аналити-

ческое исследование (см. Приложение 5): это иллю-

стрируется рисунком 11, показывающем наилучшую

подгонку параметра v (при точном воспроизведении

D), возможную при действительных ω₀.

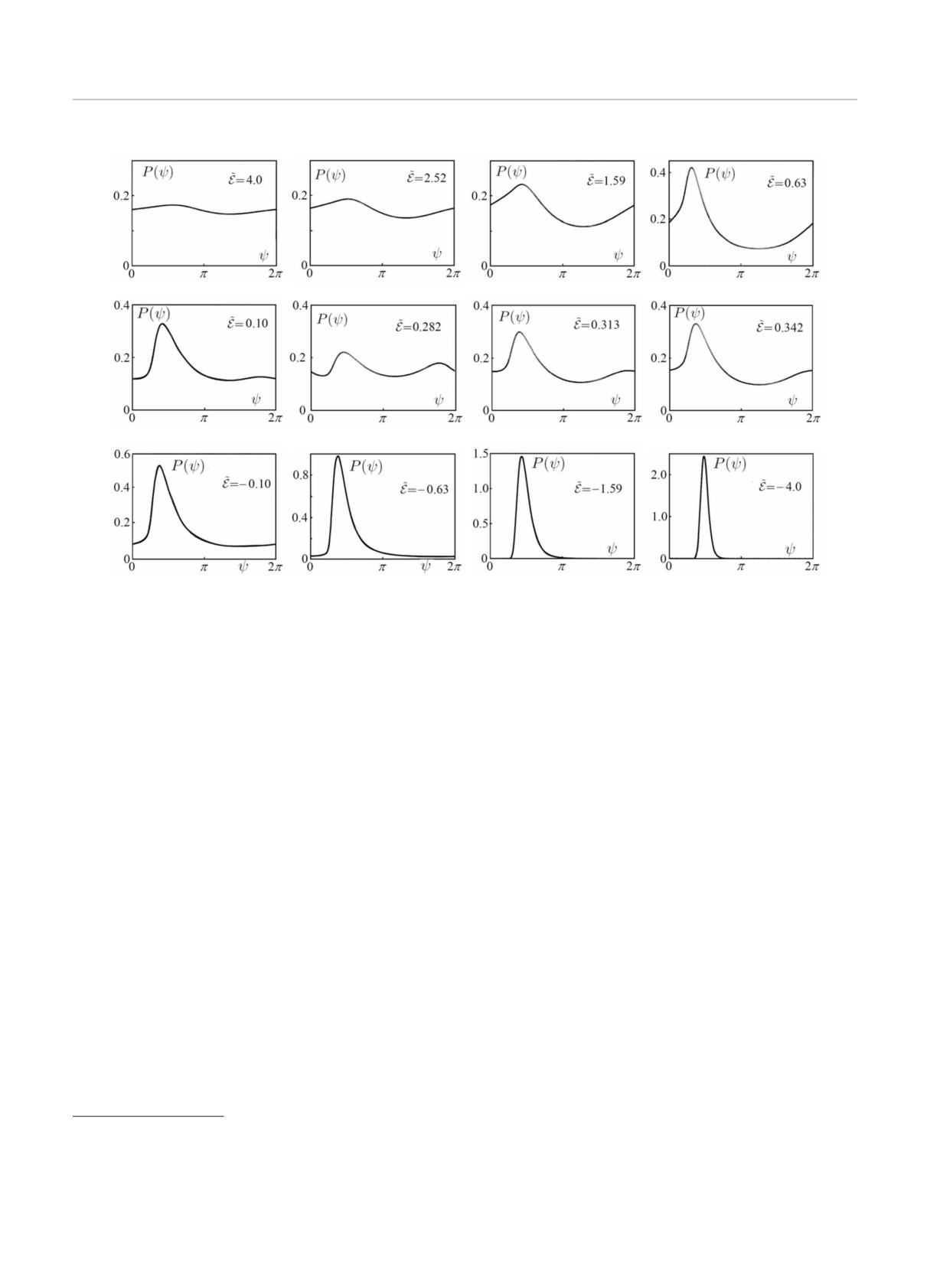
Эволюция внутреннего распределения P (ψ) (с

указанной оговоркой) при изменении энергии

E по-

казана на рис. 12. Первый ряд рисунков соответ-

ствует изменению

E от больших положительных

значений до значения

E = 0.63, соответствующего

правому минимуму ω₀ на рис. 8; при этом распре-

деление P (ω) близко к лоренцевской форме (68), а

изменение P (ψ) связано в основном с трансляцией

P (ω) в левую сторону (рис. 6,д). Нижний ряд ри-

сунков 12 соответствует изменению

E от больших

Рис. 11. Наилучшая подгонка параметра v при действи-

отрицательных значений до значения

E = -0.10, со-

тельных значениях трансляционного сдвига ω0

ответствующего левому минимуму ω₀ на рис. 8; при

этом распределение P (ψ) локализовано вблизи π/2

s и ω₀ позволяет обеспечить правильные значения

и постепенно уширяется при росте

E, эволюциони-

параметров D и v, следующие из анализа момен-

руя от гауссовской формы (69) к критической форме

тов. Полученное распределение P(ω) после возвра-

(70).

щения к переменной ψ будет определять внутреннее

Средний ряд рисунков 12 соответствует измене-

распределение фаз. Поведение s и ω₀ как функции

нию

E между двумя минимумами ω₀ на рис. 8; фор-

приведенной энергии

E показано на рис. 8. Масштаб-

ма P (ω) близка к критической, а изменения P (ψ)

ный фактор s расходится при

E → 0, в результате

в основном определяются трансляционным сдвигом

чего преобразованные параметры a = a₀s³ и b = b₀s

ω₀ и соответствуют рис. 7. Заметим, что четвертый

уже не связаны соотношением |a| = |b| (рис. 9), ко-

и девятый графики на рис. 12 близки друг к другу,

торое выполняется лишь при больших

E |, т. е. в глу-

так как форма P (ω) близка к критической, а транс-

бине разрешенной и запрещенной зон. Физический

ляции по ω примерно одинаковы.

смысл этого обстоятельства более ясен на рис. 10,

Обсудим механизм реализации внутреннего рас-

показывающем зависимость энергии Ферми

E_ext в

пределения фаз. Как обсуждалось в [16,20,21], рас-

идеальных контактах от энергии Ферми

E в изуча-

пределение ландауэровских сопротивлений P (ρ) ис-

емой системе. Минимум

E_ext достигается при зна-

пытывает осцилляции апериодического характера,

чении

E =

E₀ = 0.28, которое нужно интерпрети-

связанные с тем, что форма распределения P (ρ) су-

ровать как перенормированную границу разрешен-

щественно зависит от нескольких первых моментов,

ной зоны, сдвинутую за счет флуктуаций случай-

тогда как моменты 〈ρⁿ〉 являются осциллирующи-

761

И. М. Суслов

ЖЭТФ, том 162, вып. 5 (11), 2022

Рис. 12. Эволюция внутреннего распределения фаз при изменении приведенной энергии

ми функциями L; при этом n-й момент определя-

го распределения P (ψ), определяющего коэффици-

ется суперпозицией n дискретных гармоник. Отно-

енты в уравнении эволюции (5) для P (ρ).

сительная амплитуда осцилляций экспоненциально

убывает на масштабе L ∼ ξ и при больших L они

несущественны. Аналогичная ситуация имеет место

В результате проведенного анализа мы приходим

для полного распределения P (ρ, ω);⁷⁾ при этом ос-

к очень простой картине. Фаза ψ оказывается “пло-

цилляциям подвержены как среднее значение ω, так

хой” переменной, а “правильной” переменной явля-

и ширина его распределения. Поэтому как трансля-

ется ω = -ctg ψ/2. Форма стационарного распреде-

ционный сдвиг ω₀, так и масштабный фактор s су-

ления P (ω) определяется внутренними свойствами

щественно осциллируют на масштабах L ∼ ξ, стре-

системы и не зависит от граничных условий. Изме-

мясь при больших L к “правильным” значениям, ко-

нение граничных условий приводят к трем эффек-

торые и определяют внутреннее распределение фаз.

там: (а) масштабному преобразованию ω → sω, в ос-

новном связанному с изменением свойств идеальных

контактов; (б) трансляции ω → ω + ω₀, в основном

11. ЗАКЛЮЧЕНИЕ

определяемой наличием δ-образного потенциала на

границах системы; (в) трансляциии ψ → ψ + ψ₀,

В настоящей работе мы вывели уравнение эволю-

определяемой размытием границ раздела. Гранич-

ции для совместного распределения P (ρ, ψ) ландау-

ные условия существенно влияют на “внешнее” рас-

эровского сопротивления ρ и фазовой переменной ψ.

пределение фаз, которое входит в уравнения эво-

При больших L оно допускает разделение перемен-

люции, но не влияют на предельное распределение

ных, что обеспечивает существование стационарно-

P (ρ) в области больших L, что позволяет говорить

о существовании скрытой симметрии в уравнениях

⁷⁾ Распределение P (ρ) определяется четными моментами

эволюции. Предельное распределение P (ρ) является

от элементов T_ij трансфер-матрицы T . При анализе P (ρ, ω)

нужно рассматривать и нечетные моменты.

логнормальным, что может быть установлено при

762

ЖЭТФ, том 162, вып. 5 (11), 2022

Граничные условия, распределение фаз и. ..

самых общих условиях⁸⁾. Предельное распределе-

и интегрируя по ρ получим F (ψ) ≡ 0, т.к. левая

ние P (ρ) определяется “внутренним” распределени-

часть обращается в нуль, а интеграл от P (ρ) равен

ем P(ψ), которое получается из стационарного рас-

единице в силу нормировки. В результате правая

пределения P (ω) при подходящем выборе масштаб-

и левая части уравнения (A.3) обращаются в нуль

ного фактора s и трансляционных сдвигов ω₀ и ψ₀.

независимо друг от друга, и уравнение для P (ψ)

Обсуждаемая проблематика не ограничена одно-

отщепляется. При этом средние от тригонометриче-

мерными системами — аналогичные трудности воз-

ских функций ψ, входящие в (34), (35), определяют-

никают при анализе ляпуновских экспонент в рам-

ся стационарным распределением P (ψ), удовлетво-

ках обобщенной версии [17] уравнения Дорохова-

рящим уравнению (33).

Мелло-Перейра-Кумара [28, 29]. Минимальная ля-

пуновская экспонента определяет критические свой-

ПРИЛОЖЕНИЕ 2. КРАЕВЫЕ МАТРИЦЫ

ства для перехода Андерсона (на этом основан из-

ДЛЯ РАЗМЫТОЙ ГРАНИЦЫ РАЗДЕЛА

вестный численный алгоритм, см. ссылки в [17]),

и указанная скрытая симметрия может быть суще-

Краевые матрицы для модели, представленной

ственной при исследовании последнего.

на рис. 4, могут быть выбраны в виде

(

) (

)

eikd1

e-ik1d¹

ПРИЛОЖЕНИЕ 1. О РАЗДЕЛЕНИИ

T_l =

T_a

T_c

e-ikd1

eik1d¹

ПЕРЕМЕННЫХ В УРАВНЕНИИ (31)

(A.5)

(

) (

)

Для разделения переменных в задаче на соб-

e-ik1d²

eikd2

T_r = T_c

T_ã

ственные значения

eik1d²

e-ikd2

где

L P(ρ,ψ) = λP(ρ,ψ)

(A.1)

(

)

a₁

a₂

k+k₁

k-k₁

оператор

L должен представляться в виде суммы

T_a =

a₁ =

a₂ =

a₂

a₁

двух операторов

L_ρ +

M_ψ, зависящих только от ρ и

ψ соответственно. Условия для разделения перемен-

(

)

c c^∗

ik₁ + κ

ных в уравнении (31) оказываются более слабыми.

T_c =

(A.6)

c^∗ c

2ik₁

В пределе больших L, когда типичные значения ρ

(

)

достаточно велики, можно положить R = 2, после

ã₁

ã₂

k₁ + k

k₁ - k

чего уравнение (31) имеет структуру

T_ã =

ã₁ =

ã₂ =

ã₂

ã₁

2k₁

{

}_′

{

}_′

∂P

(

)

L_ρ,ψP

M_ψP

(A.2)

c∗

κ + ik₁

∂L

T_c =

c∗

2κ

Подставляя P = P (ρ)P (ψ) и разделив на P (ρ), име-

Сравнение с [16] показывает, что T_a и T_ã — это кра-

ем

{

}_′

∂P(ψ)

евые матрицы для границы раздела двух металлов,

M_ψP(ψ)

(A.3)

∂L

а T_c и T_c — краевые матрицы для границы раздела

{

}_′

металл-диэлектрик.

P (ψ) ∂P (ρ)

L_ρ,ψP

Сотавляя произведение T_lT_r, заметим, что соот-

P (ρ)

∂L

P (ρ)

ношения T_cT_c = 1 и T_aT_ã = 1 приводят к существен-

Левая часть не зависит от ρ и есть некоторая функ-

ным упрощениям и при условии (57) произведение

ция F (ψ). Тогда

сводится к единичной матрице.

Для вычисления T_ϵ запишем

{

}_′

∂P(ρ)

(

)

(

)

P (ψ)

L_ρ,ψP

= F(ψ)P(ρ)

(A.4)

∂L

T_ϵ =

+ ϵT_l

T_r

(A.7)

-1

⁸⁾ Более точно, мы рассматривали случайный потенци-

ал малой амплитуды с короткодействующими корреляциями

и воспользуемся тем, что

для энергий вблизи края исходной зоны. Если энергия срав-

(

)

(

)

нима с шириной зоны, то возникают эффекты соизмеримости

фермиевского импульса

k с постоянной решетки a₀ [22, 23],

T_c

T_c =

что может приводить к усложнению ситуации [24, 25].

-1

ik₁

-1

763

И. М. Суслов

ЖЭТФ, том 162, вып. 5 (11), 2022

(

) (

)(

)

e-ik1d¹

e-ik1d²

eiα+iβ+iγ+iδ = -1 ,

1 = -2|a||b|cos(β+γ). (A.13)

eik1d¹

-1

eik1d²

Вычисляя матрицу T_ϵ

(

)

iα

(

)

(A.8)

1 - ϵ(a-b)(c-d)

ϵ(a-b)²

T_ϵ =

−e^-iα

-1

-ϵ(c-d)²

1 + ϵ(a-b)(c-d)

(

)

(A.14)

e^iα

T_a

T_ã =

и требуя, чтобы она была истинной трансфер-

-e^-iα

-1

матрицей, получим

(

)

P + Qcosα

Q + P cosα + isinα

(a-b)(c-d) + (a^∗ -b^∗)(c^∗ -d^∗) = 0 ,

-Q - P cosα + i sinα

-P - Q cosα

(a-b)² + (c^∗ -d^∗)² = 0 ,

(A.15)

после чего соотношение P² = Q² + 1 позволяет при-

вести T_ϵ к виду (18).

Полагая

(a -b) = reiθ/2 , (c-d) = r₁eiϕ/2 ,

(A.16)

ПРИЛОЖЕНИЕ 3. СТЕПЕНЬ ПРОИЗВОЛА

ДЛЯ КРАЕВЫХ МАТРИЦ

получим r = r₁, ϕ = π - θ + 2πn, так что

(

)

Принимая краевые матрицы T_l и T_r в виде (60),

1 - iϵr²(-1)ⁿ

ϵr²e^iθ

T_ϵ =

(A.17)

потребуем, чтобы матрица T_δ = T_l t_δ T_r была истин-

ϵr²e^-iθ

1 + iϵr²(-1)ⁿ

ной трансфер-матрицей, удовлетворяющей соотно-

шениям (61); последние достаточно наложить при

где n — целое. Замечая, что

малых δ, что приводит к условиям

r² = |a-b|² = |a|²+|b|²- 2|a||b| cos(α-β),

ad + bc + a^∗d^∗ + b^∗c^∗ = 0, ab + c^∗d^∗ = 0 . (A.9)

r² = |c-d|² = |a|²+|b|²- 2|a||b| cos(γ-δ), (A.18)

Первое из них вместе с условием на детерминант

(60) приводит к более простым соотношениям

имеем (α - β) = ±(γ - δ) + 2πk. При верхнем знаке

получим противоречие , так как β+γ = π/2 + πk и

2Re ad = 1 ,

2Re bc = -1 .

(A.10)

левая часть первого соотношения (A.12) обращается

в нуль. При нижнем знаке имеем γ = π/2 - α + πk,

Полагая

δ = π/2 - β + πk^′, где k и k^′ выбираются четными

a = |a|e^iα, b = |b|e^iβ, c = |c|e^iγ, d = |d|e^iδ ,

при sin(β-α) > 0 и нечетными в обратном случае. В

(A.11)

результате для матрицы T_l приходим к представле-

получим полный набор условий

нию (62) с трехпараметрическим произволом. При

четных k, k^′ имеем четное n в выражении (A.17)

2|b||c| cos (β+γ) = -1 ,

для T_ϵ, в результате чего оно сводится к (18) с пара-

метрами K и γ, определенными в (63). При нечет-

2|a||d| cos (α+δ) = 1 ,

ных k, k^′ имеем нечетное n в (A.17), и приведение

|a||b| = |c||d| ,

(A.12)

к форме (18) производится путем несущественного

изменения знака ϵ.

eiα+iβ+iγ+iδ = -1 ,

|a||d| sin (α+δ) - |b||c| sin (β+γ) = 0 .

ПРИЛОЖЕНИЕ 4. РАСПРЕДЕЛЕНИЕ P (ω)

Нетрудно видеть, что sin(α+δ)

= sin(β+γ),

ПРИ E = 0

cos(α+δ) = - cos(β+γ); тогда из последнего соот-

ношения в (A.11) имеем |a||d| = |b||c|, что вместе

Дифференцируя (41) и предполагая при ω → ∞

с третьим соотношением дает |a| = |c|, |b| = |d|. В

степенную асимптотику P(ω)

∼ ω^-α, получим

результате, условие того, что T_δ является истинной

α = 2. Вычисляя поправки к асимптотике в виде ря-

трансфер-матрицей, определяет 4-параметрический

да по обратным степеням ω,

произвол для матрицы T_l

(

)

∑

iβ

P (ω) = ω-2 A_nω^-n ,

(A.19)

|a|e^iα

|b|e

T_l =

n=0

iδ

|a|e^iγ

|b|e

764

ЖЭТФ, том 162, вып. 5 (11), 2022

Граничные условия, распределение фаз и. ..

имеем рекурренцию

что в пределах точности согласуется с результатами

из анализа моментов [16]; здесь ω — отклонение от

A₀ = 1 , A₁ = 0 , A₂ = -b/a ,

максимума и учтено, что при |a| = |b| параметр ϵ

сводится к ϵ.

aAn+1 = -bAn-1 + nAn-2 , n ≥ 2 .

(A.20)

Чтобы воспризвести D и v с более высокой точ-

Для критического распределения (E

= 0) имеем

ностью, производем масштабное преобразование и

b = 0, и коэффициенты ряда находятся в явном виде

трансляцию распределения (A.22) с -a = b; тогда

(

)_k

для s = 1 - s, ω₀ = s + ω₀ и s, ω₀ ≪ 1 получим

∑

Γ(k + 2/3)

P (ω) =

(A.21)

(

)

ω²

Γ(2/3)

aω³

k=0

D=2ϵ²

1 + 2s- ϵ²/δ

(A.25)

(

)

(

)

Расходящийся ряд можно просуммировать по Боре-

v = 2δ - ϵ² +

s² - ω²⁰

δ-ϵ²

2ω₀ + 2s+ 9ϵ²/(4δ)

лю [26], записывая гамма-функцию Γ(k+2/3) в виде

представляющего ее интеграла и суммируя возника-

где учтены сдвиг максимума распределения и сла-

ющую геометрическую прогрессию. Полагая a=-1

бое отклонение от гауссовской формы. Сопоставляя

и вводя нормировочный множитель, получим (70).

с результатами из анализа моментов [16]

Выражения (A.19), (A.20) полезны при числен-

15 ϵ²

27 ϵ²

ном интегрировании уравнения (41) при произволь-

D=2ϵ² -

v = 2δ - ϵ² +

(A.26)

ных b. При |ω| > 5 функция P (ω) хорошо аппрок-

симируется рядом (A.19), понимаемом в асимпто-

и учитывая, что δ/ϵ² = 4

E|3/2, получим

тическом смысле и суммируемом до минимального

√

члена.Такую аппроксимацию можно использовать в

-19 ± i

215

s=1+

ω₀ =

(A.27)

качестве начального условия при больших положи-

E|3/2

тельных ω и интегрировать в сторону уменьшения

ω.⁹⁾ При использовании стандартных программ с

что объясняет поведение кривых в левой части

контролем точности [27] решение автоматически вы-

рис. 8. Трансляционный сдвиг ω₀ оказывается ком-

ходит на правильную асимптотику при ω → -∞.

плексным; для гауссовского распределения легко

проверить, что при |ω₀| ≪ 1 пренебрежение мнимой

частью ω₀ соответствует переходу к модулю ком-

ПРИЛОЖЕНИЕ 5. ПОВЕДЕНИЕ s И ω0 В

плексного распределения P (ω).

ЗАПРЕЩЕННОЙ ЗОНЕ

В глубине запрещенной зоны константа C₀ в (41)

ЛИТЕРАТУРА

экспоненциально мала и распределение P (ω) можно

принять в виде

1. P. W. Anderson, D. J. Thouless, E. Abrahams, D.

{

}

P (ω) = const exp

-bω - aω³/3

(A.22)

S. Fisher, Phys. Rev. B 22, 3519 (1980).

При -a = b ≫ 1 распределение имеет максимум при

2. R. Landauer, IBM J. Res. Dev. 1, 223 (1957); Phil.

ω = -1, в окрестности которого оно сводится к гаус-

Mag. 21, 863 (1970).

совой форме (69). Вычисление средних в (38) дает

3. В. И. Мельников, ФТТ 23, 782 (1981).

B A

2ω

ω²

〈sin ψ〉 =

≈

=1-

4. A. A. Abrikosov, Sol. St. Comm. 37, 997 (1981).

1+ω²

4|a|

5. N. Kumar, Phys. Rev. B 31, 5513 (1985).

4ω²

sin² ψ

≈

1-ω²

≈1,

(1 + ω²)²

6. B. Shapiro, Phys. Rev. B 34, 4394 (1986).

^Aω² -1

〈cos ψ〉 =

≈ 〈-ω〉 ≈ 0 ,

(A.23)

7. P. Mello, Phys. Rev. B 35, 1082 (1987).

1+ω²

так что для параметров D и v имеем

8. B. Shapiro, Phil. Mag. 56, 1031 (1987).

D = 2ϵ2 , v = 2δ - ϵ2 ,

(A.24)

9. И. М. Суслов, ЖЭТФ 151, 897 (2017).

⁹⁾ При интегрировании в сторону увеличения ω возникают неустойчивости, связанные с наличием растущей экспоненты,

являющейся решением (41) при C₀ = 0.

765

И. М. Суслов

ЖЭТФ, том 162, вып. 5 (11), 2022

10. И. М. Лифшиц, С. А. Гредескул, Л. А. Пас-

20. V. V. Brazhkin, I. M. Suslov, J. Phys.: Cond. Matt.

тур, Введение в теорию неупорядоченных си-

32 (35), 35LT02 (2020).

стем, Москва, Наука, 1982.

21. И. М. Суслов, ЖЭТФ 158, 911 (2020).

11. C. W. J. Beenakker, Rev. Mod. Phys. 69, 731

(1997).

22. M. Kappus, F. Wegner, Z. Phys. B 45, 15 (1981).

12. X. Chang, X. Ma, M. Yepez, A. Z. Genack, P. A.

23. V. E. Kravtsov, V. I. Yudson, Ann. Phys. (NY)

Mello, Phys. Rev. B 96, 180203 (2017).

326, 1672 (2011).

13. L. I. Deych, D. Zaslavsky, A. A. Lisyansky, Phys.

24. H. Schomerus and M. Titov, Phys.Rev. B 67,

Rev. Lett. 81, 5390 (1998).

100201(R) (2003).

14. L. I. Deych, A. A. Lisyansky, B. L Altshuler, Phys.

25. L. I. Deych, M. V. Erementchouk, A. A. Lisyansky,

Rev. Lett. 84, 2678 (2000); Phys. Rev. B 64,

B. L. Altshuler, Phys.Rev.Lett. 91, 096601 (2003).

224202 (2001).

26. И. Харди, Расходящиеся ряды, Москва, ИИЛ,

15. L. I. Deych, M. V. Erementchouk, A. A. Lisyansky,

1951.

Phys. Rev. Lett. 90, 126601 (2001).

27. W. H. Press, B. P. Flannery, S. A. Teukolsky,

16. И. М. Суслов, ЖЭТФ 156, 950 (2019).

W. T. Wetterling, Numerical Recipes in Fortran,

Cambridge University Press, 1992.

17. И. М. Суслов, ЖЭТФ 154, 152 (2018).

18. В. Л. Березинский, Л. П. Горьков, ЖЭТФ 77,

28. О. Н. Дорохов, Письма в ЖЭТФ 36, 259 (1982).

2498 (1979).

29. P. A. Mello, P. Pereyra, N. Kumar, Ann. Phys.

19. P. Markos, Acta Physica Slovaka 56, 561 (2006).

(N.Y.) 181, 290 (1988).

766