ЖЭТФ, 2022, том 162, вып. 5 (11), стр. 743-749

ПРОСТРАНСТВЕННОЕ РАСПРЕДЕЛЕНИЕ ВАКАНСИЙ,

ОБРАЗОВАННЫХ КАСКАДОМ ВЫБИТЫХ АТОМОВ

В ТВЕРДОМ ТЕЛЕ

Е. В. Метелкин^*, М. В. Лебедева^a

^a Российский химико-технологический университет им. Д. И. Менделеева,

124047, Москва, Россия

Поступила в редакцию 25 мая 2022 г.,

после переработки 25 мая 2022 г.

Принята к публикации 26 мая 2022 г.

На основе решения кинетического уравнения Больцмана получено выражение, описывающее простран-

ственное распределение вакансий, образованных каскадом атомных столкновений в твердом теле. Это

выражение представлено в простом безразмерном виде, зависящем от единственного безразмерного па-

раметра ε0 = E0/εd (E0 — энергия первично выбитых атомов, εd — энергия связи атомов в узлах

решетки). При решении кинетического уравнения предполагалось, что твердое тело состоит из одина-

ковых атомов, рассеяние движущихся атомов является упругим и сферически-симметричным в системе

центра инерции, а сечение взаимодействия является постоянной величиной.

DOI: 10.31857/S0044451022110153

зываемый каскад атомных столкновений. При раз-

EDN: LABWVD

витии каскада столкновений в твердом теле обра-

зуется целый комплекс дефектов (вакансии и меж-

узельные атомы, кластеры и т. д.), определяющих

1. ВВЕДЕНИЕ

степень повреждения материала и его дальнейшие

физические свойства [1-5]. В связи с этим исследо-

Элементы конструкций ядерных реакторов

вание процессов, протекающих в каскаде атомных

и термоядерных установок работают в условиях

столкновений, представляет большой интерес.

продолжительного радиационного облучения. Это

Описание развития каскадов в твердом теле и со-

приводит к изменению их физических, упругих

провождающих его процессов представляет собой

и прочностных характеристик. Повреждаемость

достаточно сложную задачу. В связи с этим для

материалов нейтронным облучением во многом

ее решения в подавляющем большинстве случаев

определяет ресурс эксплуатации ядерных устано-

используется компьютерное моделирование [2, 6-8].

вок. Понимание физических основ протекающих

Аналитические решения соответствующей задачи

процессов необходимо для получения радиационно-

на основе линейного уравнения Больцмана суще-

стойких конструкционных материалов, удовлетво-

ствуют в исключительных случаях. Тем не менее

ряющих потребности ядерной техники.

они также представляют значительный интерес, по-

Облучение твердых тел быстрыми нейтронами

скольку дают наглядное представление о протекаю-

приводит к тому, что атомы кристаллической ре-

щем процессе и его особенностях и могут быть ис-

шетки, получившие от налетающей частицы энер-

пользованы для тестирования достаточно сложных

гию, большую некоторой пороговой величины (ε_d),

численных расчетов.

вылетают из своих равновесных положений. В даль-

нейшем обмен энергии между движущимися атома-

Исследованию развития каскадов атомных

ми и атомами, находящимися в узлах кристалличе-

столкновений в твердом теле на основе аналитиче-

ской решетки, приводит к появлению новых поколе-

ского решения кинетического уравнения Больцмана

ний выбитых атомов. В результате возникает так на-

было посвящено достаточно большое количество

работ

[9-22]. В

[9, 10] с помощью построенной

^* E-mail: sitech47@mail.ru

модельной индикатрисы рассеяния было получе-

743

Е. В. Метелкин, М. В. Лебедева

ЖЭТФ, том 162, вып. 5 (11), 2022

но стационарное энергетическое распределение

получено выражение, описывающее пространствен-

каскада движущихся атомов для произвольно-

ное распределение вакансий, образующихся при рас-

го потенциала межатомного взаимодействия.

пространении каскада движущихся атомов в твер-

В работах [11-13] анализировалась возможность

дом теле. Это выражение представлено в простом

образования субкаскадов — ряда неперекрываю-

безразмерном виде, зависящем от единственного

щихся между собой областей в процессе развития

безразмерного параметра ε₀ = E₀/ε_d (E₀ — энергия

каскада атомных столкновений. В работе [14] была

первично выбитых атомов (ПВА)). При решении ки-

разработана теоретическая модель для исследова-

нетического уравнения предполагалось, что твердое

ния образования каскадов и субкаскадов атомных

тело состоит из одинаковых атомов, рассеяние дви-

столкновений в облучаемых твердых телах, осно-

жущихся атомов является упругим и сферически-

ванная на использовании расширенного толкования

симметричным в системе центра инерции, а сечение

понятия первично выбитый атом (ПВА). В [14] был

взаимодействия является постоянной величиной.

сформулирован критерий для определения поро-

говой энергии образования субкаскадов в твердом

2. ПОСТАНОВКА ЗАДАЧИ

теле и получены формулы для определения сред-

них размеров и их числа в зависимости от энергии

Рассмотрим распространение каскада выбитых

ПВА. На основе результатов, представленных в [14],

атомов в твердом теле, состоящем из одинако-

в работе [15] были проведены численные расче-

вых атомов. Кинетическое уравнение Больцмана,

ты для конкретных материалов, согласующиеся

описывающее этот процесс, при использовании P₁

с экспериментальными данными.

и диффузионно-транспортного приближений имеет

В работе [16] была рассчитана функция распре-

следующий вид [22, 23]:

деления по энергиям, описывающая стационарное

энергетическое распределение каскада движущихся

1 ∂Φ(E, r, t)

Δ_rΦ(r, E, t)+Σ(E)Φ(E, r, t) =

атомов при степенном потенциале взаимодействия

∂t

3Σ_tr

(U ∼ 1/rⁿ[17]) с учетом энергии связи атомов в уз-

∫

лах решетки.

= dE^′P (E^′ → E)Σ(E^′)Φ(E^′, r, t) +

В работах [18-20] было получено точное реше-

ние кинетического уравнения Больцмана при усло-

∫

вии, что материал состоит из одинаковых ато-

+ dE^′ P (E^′ → E^′ - E - ε_d)Σ(E^′)Φ(E^′, r, t) +

мов, рассеяние движущихся атомов является упру-

гим и сферически-симметричным в системе центра

E+ε_d

инерции, а энергии связи атомов в узлах решетки

+ N₀δ(E - E₀)δ(r)δ(t),

(1)

не учитывалась (ε_d = 0). В [18, 19] было получе-

где f(E, r, t) dE dr — число атомов с энергией E в ин-

но решение, описывающее нестационарное энерге-

тервале dE в момент времени t в объеме dr около

тическое распределение каскада движущихся ато-

точки r;

мов. В [18] предполагалось, что сечение рассея-

Φ(E, r, t) = vf(E, r, t)

ния является постоянной величиной (Σ = const),

а в [19] оно полагалось обратно пропорциональ-

— поток движущихся атомов; v — их скорость;

ным скорости (Σ

= Σ₀/v; Σ₀

= const). В ра-

боте [20] с использованием P1 и диффузионно-

P (E^′ → E) = Σ(E^′ → E)/Σ(E^′)

транспортного приближений было получено неста-

— индикатриса рассеяния (вероятность того, что

ционарное пространственно-энергетическое распре-

движущийся атом с энергией E^′ в результате рассея-

деление каскада выбитых атомов (при Σ = const).

ния перейдет в единичный интервал энергий вблизи

При тех же условиях в работах [21, 22] было

значения E); Σ(E^′ → E) и Σ(E^′) — дифференциаль-

получено решение модельного уравнения Больцма-

ное и полное макроскопические сечения рассеяния

на с учетом энергии связи атомов в узлах решет-

атомов;

ки (ε_d = 0). В [21] сечение рассеяния полагалось

Σ_tr(E) = (1 - μ_l)Σ(E)

обратно пропорциональным скорости (Σ = Σ₀/v;

Σ₀ = const), а в [22] оно считалось постоянной ве-

— транспортное сечение; μ_l — средний косинус угла

личиной (Σ = const).

рассеяния частицы в лабораторной системе коорди-

В настоящей работе на основе решения модель-

нат; Δ_r — оператор Лапласа; δ(x) — дельта-функция

ного кинетического уравнения Больцмана (см. [22])

Дирака; E₀ — начальная энергия первично выбитых

744

ЖЭТФ, том 162, вып. 5 (11), 2022

Пространственное распределение вакансий, образованных каскадом...

атомов (ПВА); N₀ — их полное число; ε_d — энергия

в нуль. Сами законы сохранения (2), (3) подробно

связи атомов в узлах решетки. Источник ПВА счи-

обсуждаются в [22].

тается изотропным, точечным, импульсным и моно-

Следуя работе [22], упростим уравнение (1), по-

хроматическим.

требовав, чтобы из упрощенного уравнения вытека-

Первый интеграл, стоящий в правой части кине-

ли те же законы сохранения, что и из уравнения (1)

тического уравнения (1), описывает переход в ре-

(см. (2)-(7)). В таком случае для упрощенного урав-

зультате рассеяния движущегося атома с энерги-

нения при E ≥ ε_d получим следующее выражение:

ей E^′ в состояние с энергией E. Второй интеграл

описывает образование выбитого атома с энерги-

1 ∂Φ(E, r, t)

ей E, когда движущийся атом перешел в состояние

Δ_rΦ(r, E, t) +

∂t

3Σ_tr

с энергией (E^′ - E - ε_d). Точное решение уравне-

[

]

Δ₀(E)

ния (1), как отмечалось выше, было получено в ра-

+ Σ(E)

+ p(E) Φ(E, r, t) =

боте [20] для упругого, сферически-симметричного

Δ(E)

рассеяния в системе центра масс без учета энергии

∫

]

^[Δ₀(E^′

)

связи атомов в узлах решетки (ε_d = 0).

= dE^′ P (E^′ → E)Σ(E^′)

+p(E^′) Φ(E^′,r,t)+

Δ(E^′)

Из уравнения (1) вытекают следующие законы

сохранения полного числа частиц и энергии [22]:

∫

+ dE^′ P (E^′ → E^′ - E)Σ(E^′)p(E^′)Φ(E^′, r, t) +

∫

= dE p(E)Σ(E) dr Φ(E, r, t),

(2)

+ N₀δ(E - E₀)δ(r)δ(t).

(8)

ε_d

∫

dE(t)

= - dE Δ₀(E)Σ(E) drΦ(E,r,t),

(3)

3. РЕШЕНИЕ КИНЕТИЧЕСКОГО

УРАВНЕНИЯ

где

∫E0

∫

N (t) = dE dr f(E, r, t),

Далее будем считать, что рассеяние движущих-

ся атомов на покоящихся является сферически-

(4)

симметричным в системе центра инерции и описыва-

∫E0

∫

ется индикатрисой рассеяния, имеющей следующий

E(t) = dE E dr f(E, r, t),

вид [23]:

∫

P (E^′ → E) =

Θ(E^′ - E),

(9)

p(E) =

P (E → E^′) dE^′,

(5)

E^′

где Θ(z) — единичная функция Хевисайда. В таком

а функция Δ₀(E) определяется следующими выра-

случае при E ≥ ε_d уравнение (8) принимает следу-

жениями:

ющий вид (см. (5)-(7), (9)):

∫E

Δ₀(E) = Δ(E) = dE^′ (E - E^′)P(E → E^′)

(6)

∂Ψ(E, r, t)

vΣ

∂t

[

)₂]

при E ≤ ε_d и

ε_d

⁽ε_d

Δ_rΨ(r, E, t) + 1+

Ψ(E, r, t) =

3ΣΣ_tr

∫E

∫

)₂]

dE^′ [

⁽ε_d

Δ₀ = p(E)ε_d +

dE^′ (E - E^′)P (E → E^′)

(7)

Ψ(E^′, r, t) +

E^′

E-ε_d

+ N₀δ(E - E₀)δ(r)δ(t),

(10)

при E ≥ ε_d. Величина p(E) представляет собой ве-

роятность, что движущийся атом с энергией E пе-

редает атому решетки энергию, большую ε_d. Оче-

где Ψ(r, E, t) = Σ(E)Φ(r, E, t) — плотность соударе-

видно, что при E ≤ ε_d величина p(E) обращается

ний и μ_l = 2/3 [23].

745

Е. В. Метелкин, М. В. Лебедева

ЖЭТФ, том 162, вып. 5 (11), 2022

Применяя к уравнению (10) преобразование Ла-

теле. Найдем образ Фурье от пространственно-

пласа по времени и преобразование Фурье по про-

энергетического распределения полной плотности

странственным координатам:

соударений, которые испытал каскад движущихся

атомов при своем развитии (при E ≥ ε_d):

∫∞

Ψ(E, k, s) = dt exp(-st) ×

Ψ₀(E, k) =

∫

∞

∫∫∞

∫

∫∫∞

∫

= dt

dx dy dz exp(-ikr)Ψ₀(r, E, t).

(16)

dx dy dz exp(-ikr)Ψ(r, E, t),

(11)

-∞

−∞

Учитывая (11), найдем (см. (15))

получим

Ψ₀(E, k) =

Ψ₀(E, k, s = 0) =

)₂]

[ s

k²

ε_d

⁽ε_d

[

+1+

Ψ(E, k, s) =

( ε_d )2^]

vΣ

3ΣΣ_tr

N₀ 2 -

E₀

∫E0

[

)₂]

k²

ε_d

( ε_d )2^]2 ^×

dE^′ [

⁽ε

Ψ(E^′, k, s) +

E₀ 1 +

E^′

3ΣΣ_tr

E₀

⎧

⎫

[

⎪

( ε_d )2^]

⎪

⎨∫

dE^′ 2 -

⎬

+ N₀δ(E - E₀).

(12)

E^′

× exp

(17)

[

)₂]

⎪

ε_d

⁽ε_d

⎪

Выделим в решении уравнения (12) нерассеянное

⎩E E^′ 1 +

⎭

3ΣΣ_tr

E^′

излучение:

Вернувшись к уравнению (12), можно заметить,

Ψ(E, k, s) =

Ψ₀(E, k, s) +

что выражение (17) представляет собой образ Фурье

N₀δ(E - E₀)

от пространственно-энергетического распределения

[

(13)

k²

ε_d

⁽ε_d)2].

плотности соударений каскада движущихся атомов,

vΣ

3ΣΣ_tr

образующегося от точечного стационарного источ-

ника.

Подставив (13) в (12) и положив Σ = const, получим

Вычисление оригинала по формуле (17) связа-

уравнение для определения функции

Ψ₀(E, k, s):

но с определенными математическими трудностями.

В связи с этим функцию Ψ₀(E, r) будем искать в сле-

Ψ₀(E, k, s) =

дующем виде:

[

]

⁽ε_d)2^]

Ψ₀(E, r) = A(E)exp

-α(E)r²

(18)

2vΣ

[

k²

ε_d

⁽ε_d)2]×

Параметры A(E) и α(E) найдем из условия, чтобы

E 1+

пространственные моменты от функции (18),

vΣ

3ΣΣ_tr

∫

× Ψ₀(E, k, s),

(14)

Ψ₀(E) = drΨ₀(E, r),

(19)

решение которого легко найти (см. [21, 22]):

∫

r²(E)

dr r²Ψ₀(E, r),

(20)

Ψ₀(E)

Ψ₀(E,k,s)=

[

)₂]

совпадали с аналогичными величинами, полученны-

⁽ε

N₀ 2-

ми из выражения (17). Используя (18), найдем

E₀

[

k²

ε_d

( ε_d )2^]2

E₀ 1+

A(E) =

²Ψ₀(E),

v₀Σ

3ΣΣ_tr

E₀

2π〈r²(E)〉

⎧

⎫

(21)

[

⎪

ε_d

( ε_d )2^]

⎪

∫

α²(E) =

⎨

dE^′ 2-

⎬

r²(E)

2v^′Σ

E^′

×exp

[

)₂]

(15)

⎪

k²

ε_d

⁽ε_d

⎪

⎭

Пространственные моменты (19), (20) можно опре-

⎩E E^′ 1+

v^′Σ

3ΣΣ_tr

E^′

делить с помощью выражения (17) по формулам

Функция (15) представляет собой образ Лапласа-

Ψ₀(E) =

Ψ₀(E, k = 0),

Фурье от нестационарного пространственно-

{[

]}

Δ_k Ψ₀(E, k)

(22)

энергетического распределения плотности соуда-

r²(E)

рений каскада движущихся атомов в твердом

Ψ₀(E, k)

k=0

746

ЖЭТФ, том 162, вып. 5 (11), 2022

Пространственное распределение вакансий, образованных каскадом...

где Δ_k — оператор Лапласа в k-пространстве. Про-

Используя выражение (25), эту величину можно

ведя вычисления по формулам (22), получим выра-

представить в следующем безразмерном виде:

жения для пространственных моментов в следую-

∫

ε0

щем безразмерном виде:

)3/2

(

1 (

1⁾

n^′v(ρ) = n_v(r)

=ε₀

dϵ 1-

Ψ^′(ε)×

ΣΣ_tr

E₀

Ψ^′(ε) = Ψ₀(E)

[

]3/2

[

]

N₀

3ρ²

)3/2

exp -

(27)

(2ε²⁰ - 1)

⁽ε²⁰ +ε₀ -1

= εε₀

2π

ρ²(ε)

(ε²⁰

+ ε₀ - 1)²

ε² + ε - 1

)]3/(2^√5)

[( 2ε₀ + 1 +^√5)( 2ε + 1 -√5

√

(23)

4. АНАЛИЗ ПОЛУЧЕННОГО РЕШЕНИЯ

2ε₀ + 1 -

2ε + 1 +

Проанализируем полученные результаты.

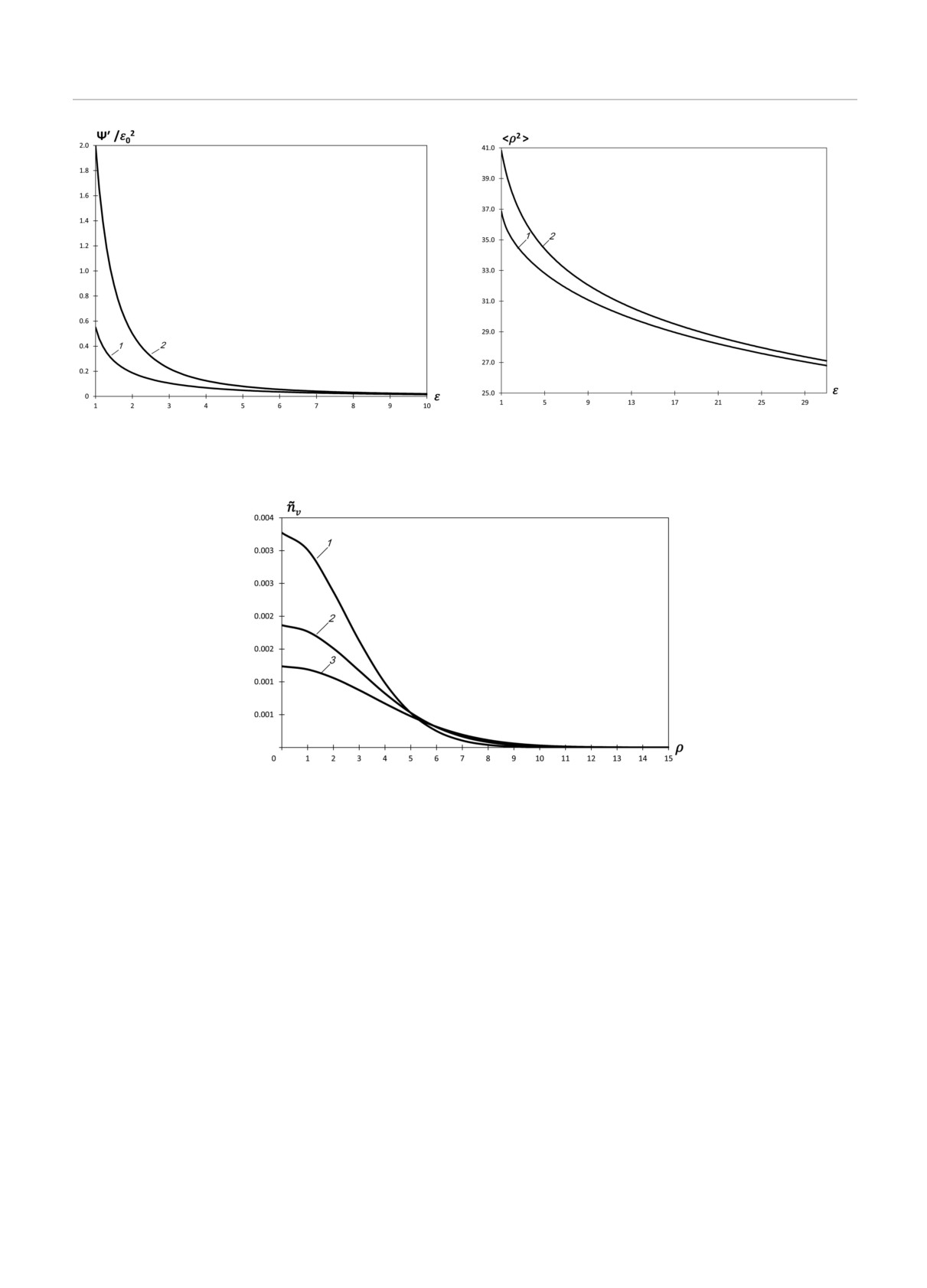
На рис. 1 приведен график функции Ψ^′(ε), по-

〈ρ²(ε)〉 = ΣΣ_tr

r²(E)

строенный по формуле (23) (см. кривую 1 ). Кроме

)

4ε²⁰

⁽ε²⁰ +ε₀ -1

того, что она является нормирующем множите-

+ 2ln

(ε²⁰ + ε₀ - 1)

ε² + ε - 1

лем в выражении (25), эта функция представляет

)

6( 4ε0 - 3

4ε - 3

самостоятельный интерес. Она описывает энерге-

ε²⁰ + ε₀ - 1

ε² + ε - 1

тическое распределение каскада выбитых атомов,

)]

распространяющихся от однородно распределенного

[( 2ε₀ + 1 -√5)(2ε + 1 +√5

√

(24)

в пространстве стационарного моноэнергетического

2ε₀ + 1 +

2ε + 1 -

источника ПВА (см. (12) при s = 0 и k = 0).

где ε = E/ε_d и ε₀ = E₀/ε_d.

Кривой 2 на этом рисунке представлен график

С учетом сказанного выше окончательное вы-

той же функции при ε_d = 0:

ражение для пространственно-энергетического рас-

[

]

пределения полной плотности столкновений каскада

Ψ^′(ε)_ε

= 2ε²⁰/ε².

(28)

d=0

движущихся атомов, испущенных импульсным ис-

Видно, что учет энергии связи приводит к более

точником (см. (10), (16)), можно представить в сле-

медленному росту функции при ε → 1, что обу-

дующем безразмерном виде (см. (18), (21)):

словлено учетом потерь энергии на выбивание ато-

)3/2

мов из узлов решетки. Расчеты, представленные

E₀ (

Ψ′0(ε, ρ) = Ψ₀(E, r)

на рис. 1, проводились при ε₀ = 10⁴.

N₀

ΣΣ_tr

[

]

3/2

[

]

На рис. 2 кривой 1 представлен график зависи-

3ρ²

= Ψ^′(ε)

exp -

= ,

(25)

мости от энергии среднего квадрата длины замедле-

2π

ρ²(ε)

ния, построенный по формуле (24). Кривой 2 здесь

представлена та же зависимость при ε_d = 0:

где ρ = r√ΣΣtr, а функции Ψ′(ε) и

ρ²(ε)

опреде-

[

]

ляются выражениями (23), (24).

〈ρ²(ε)〉

= 4 + 4ln(ε₀/ε).

(29)

εd=0

Выражение (25) можно трактовать и несколько

иначе. Положив в уравнении (12) s = 0, получим,

Видно, что учет энергии связи приводит к мень-

что оно описывает пространственно-энергетическое

шим значениям величины

ρ²(ε)

при энергиях ε,

распределение плотности столкновений каскада

близких к единице. Здесь так же полагалось, что

движущихся атомов, испускаемых стационарным

ε₀ = 10⁴.

точечным моноэнергетическим источником (в этом

Проинтегрировав функцию (27) по всему про-

случае N₀ — число ПВА, испускаемых в единицу

странству, мы, очевидно, получим выражение для

времени).

каскадной функции (см. в [22] формулы (29)-(31)):

Пространственное распределение плотности ва-

∫

∞

∫

ε0

кансий, образовавшихся при распространении кас-

(

1⁾

када движущихся атомов от импульсного источни-

4π dρ ρ²n^′

(ρ) = ε₀

dϵ 1-

Ψ^′(ε)=ν(ε₀).

(30)

ка, очевидно имеет следующий вид:

∫E0

В таком случае функция ñ_v(ρ) = n^′v(ρ)/ν(ε₀) пред-

n_v(r) = dE p(E)Ψ₀(E, r).

(26)

ставляет собой относительное распределение в про-

странстве плотности вакансий. Графики простран-

ε_d

747

Е. В. Метелкин, М. В. Лебедева

ЖЭТФ, том 162, вып. 5 (11), 2022

Рис.

1. Зависимость функции Ψ^′(ε) от энергии при Рис. 2. Зависимость среднего квадрата длины замедления

ε0 = 10⁴ (кривая 1 — εd = 0, кривая 2 — εd = 0)

от энергии ε0 = 10⁴ (кривая 1 — εd = 0, кривая 2 — εd = 0)

Рис. 3. Пространственное распределение относительной плотности вакансий при ε0 = 10³ (кривая 1); ε0 = 10⁴ (кривая 2);

ε0 = 10⁵ (кривая 3)

ственного распределения этой функции при различ-

инерции, а сечение рассеяния считается постоян-

ных значениях ε₀ представлены на рис. 3. Из приве-

ным.

денных результатов следует, что с увеличением на-

На основе решения модельного кинетического

чальной энергии ПВА образование вакансий интен-

уравнения Больцмана проанализировано образова-

сивнее происходит на больших расстояниях от ис-

ние вакансий в каскаде движущихся атомов от им-

точника, что обусловлено соответствующим ростом

пульсного, точечного, моноэнергетического источ-

среднего квадрата длины замедления.

ников ПВА. Для пространственного распределения

вакансий, образовавшихся при развитии каскада,

получено простое безразмерное выражение (27), за-

5. ВЫВОДЫ

висящее от единственного безразмерного парамет-

ра ε₀.

В работе рассматривается развитие каскада вы-

Показано, что с ростом этого параметра про-

битых атомов в твердом теле, состоящем из одинако-

исходит перемещение относительного числа об-

вых атомов. Рассеяние атомов предполагается упру-

разующихся вакансий на большие расстояния от

гим и сферически-симметричным в системе центра

748

ЖЭТФ, том 162, вып. 5 (11), 2022

Пространственное распределение вакансий, образованных каскадом...

источника (см. рис. 3). Это обстоятельство обуслов-

11.

Y. Sato, S. Kojimo, T. Yoshiie, et al., J. Nucl. Mater.,

лено ростом величины среднего квадрата длины за-

179-181, 901 (1991).

медления с увеличением ε₀ (см. (24), (29)).

12.

Y. Sato, T. Yoshiie, and M. Kiritani, J. Nucl. Mater.,

Полученное в работе решение кинетического

191-194, 1101 (1992).

уравнения также позволяет получить выражения

для функции распределения движущихся атомов

13.

Е. В. Метелкин, А. И. Рязанов, Атомная энергия

от стационарного, моноэнергетического равномерно

83, 183 (1997).

распределенного по пространству (см. (23)) и точеч-

14.

Е. В. Метелкин, А. И. Рязанов, Е. В. Семенов,

ного (см. (24)) источников.

ЖЭТФ 134, 469 (2008).

15.

A. I. Ryazanov, E. V. Metelkin, E. V. Semenov, J.

ЛИТЕРАТУРА

Nucl. Mater. 386-388, 132 (2009).

1. К. Лейман, Взаимодействие излучения с твер-

16.

A. A. Aleksandrov, V. A. Akatev, E. V. Metelkin,

E. J. Barycheva, Herald of the Bauman Moscow State

дым телом и образование элементарных дефек-

тов, Атомиздат, Москва (1979).

Technical University, Series Natural Sciences, n. 1, 27

(2019).

2. С. Вас Гэри, Основы радиационного материало-

ведения. Металлы и сплавы, Техносфера, Москва

17.

J. Lindhard, V. Nielsen, and M. Scharff, Mat. Fys.

(2014).

Medd. Dan. Vid. Selsk. 36, 1 (1968).

3. И. А. Портных, А. В. Козлов, ФММ 119, 636

18.

A. A. Aleksandrov, V. A. Akatev, E. V. Metelkin,

(2018).

E. J. Barycheva, Herald of the Bauman Moscow State

Technical University, Series Natural Sciences, n. 6, 40

4. Л. С. Васильев, С. Л. Ломаев, ФММ 120, 771

(2019).

19.

Е. В. Метелкин, А. Н. Манвелов, А. Я. Пономарев

5. А. Р. Исинбаев, И. А. Портных, А. В. Козлов,

и др., ФММ 120, 892 (2019).

ФММ 121, 99 (2020).

20.

Е. В. Метелкин, В. А. Акатьев, В. И. Шмырев

6. K. Nordlund, A. E. Sand, F. Granberg et al., J. Nucl.

и др., ЖЭТФ 156, 387 (2019).

Mater. 512, 450 (2018).

21.

Е. В. Метелкин, М. В. Лебедева, ФММ 122, 446

7. K. Nordlund, J. Nucl. Mater. 520, 273 (2019).

(2021).

8. K. Arakawa, Z. Bergstrom, B. D. Wirth et al., J. Nucl.

22.

Е. В. Метелкин, М. В. Лебедева, ЖЭТФ 160, 167

Mater. 554, 153113 (2021).

(2021).

9. А. И. Рязанов, Е. В. Метелкин, Препринт ИАЭ-

23.

А. И. Исаков, М. В. Казарновский, Ю. А. Медве-

3223 (1979).

дев и др., Нестационарное замедление нейтронов.

10. A. I. Ryazanov, and E. V. Metelkin, Rad. Effects 52,

Основные закономерности и некоторые приложе-

15 (1980).

ния, Наука, Москва (1984).

749