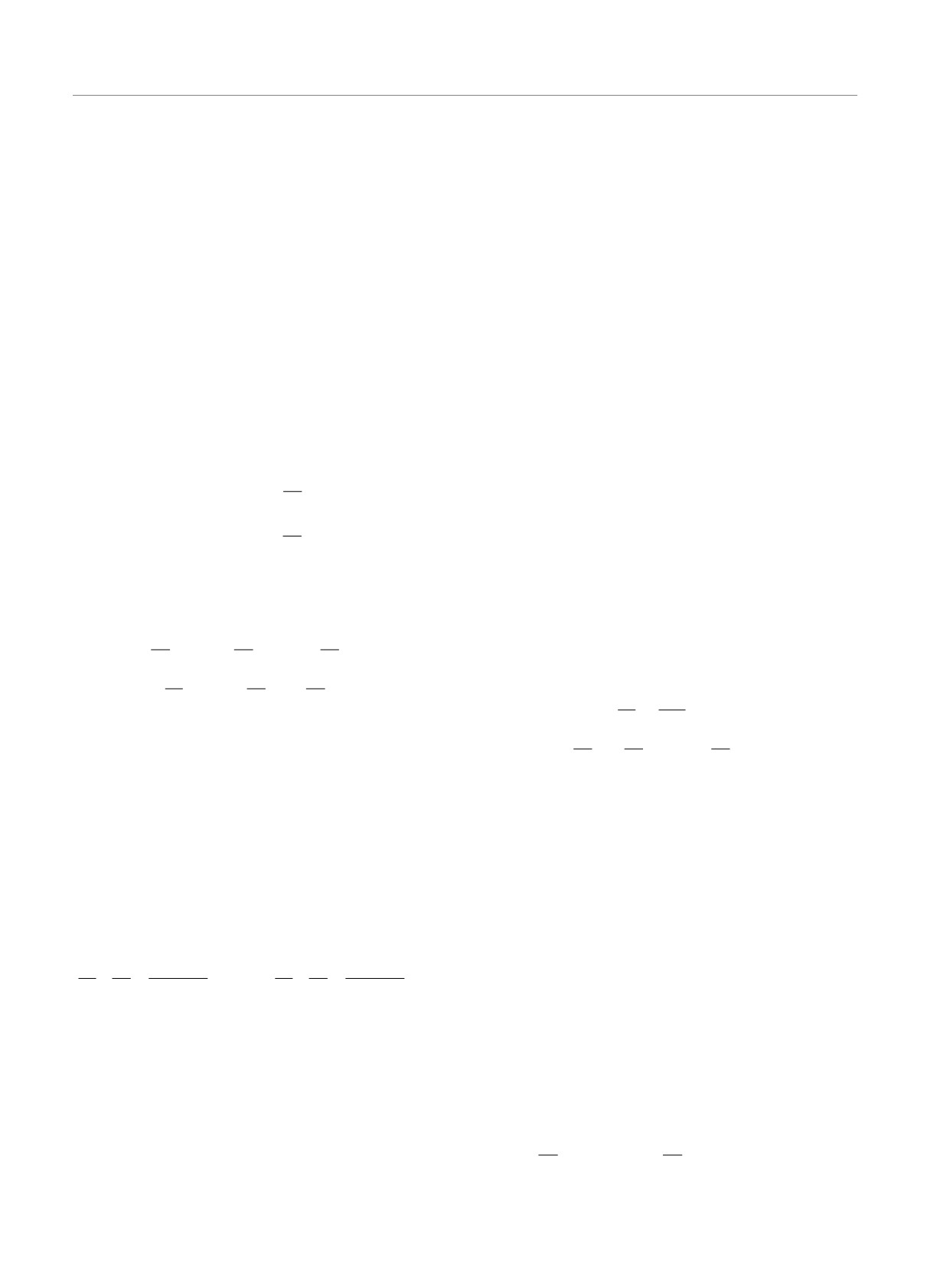ЖЭТФ, 2022, том 161, вып. 6, стр. 897-908

ОСОБЕННОСТИ ДИНАМИКИ САМОВОЗДЕЙСТВИЯ

ВОЛНОВЫХ ПАКЕТОВ С ИСХОДНО НОРМАЛЬНОЙ

ДИСПЕРСИЕЙ ГРУППОВОЙ СКОРОСТИ

В НЕЛИНЕЙНЫХ РЕШЕТКАХ

Л. А. Смирновa,b*, В. А. Миронов^a, А. Г. Литвак^a

^a Институт прикладной физики Российской академии наук

603950, Нижний Новгород, Россия

^b Институт информационных технологий, математики и механики,

Нижегородский государственный университет им. Н. И. Лобачевского

603950, Нижний Новгород, Россия

Поступила в редакцию 16 января 2022 г.,

после переработки 27 января 2022 г.

Принята к публикации 22 февраля 2022 г.

Исследованы особенности процессов самовоздействия волновых полей в рамках дискретного нелинейно-

го уравнения Шредингера. Аналитически и численно показано, что динамика волновых пакетов с исходно

нормальной дисперсией групповой скорости в системах, описываемых данным модельным уравнением,

может существенным образом отличаться от эволюции аналогичных распределений в сплошной среде.

Детально проанализировано поведение волновых полей с изначально гладкими (по сравнению с пери-

одом рассматриваемых решеток) амплитудным профилем и фазовым фронтом и изучен механизм их

разрушения в цепочках эквидистантно расположенных элементов. Предложена модификация бездиспер-

сионного приближения, с использованием которой удается теоретически описать эффекты, приводящие

к развитию мелкомасштабных неустойчивостей на фоне плавной огибающей и к ее последующим су-

щественным деформациям (вплоть до распада). Представлены оценки критических параметров, при

превышении которых следует ожидать указанных (нехарактерных для континуальных сред) процессов.

DOI: 10.31857/S004445102206013X

щего успешно описать процессы самовоздействия в

EDN: DVESCO

сплошных средах и вместе со своими разнообразны-

ми обобщениями представляющего один из наибо-

1. ВВЕДЕНИЕ

лее важных классов модельных уравнений в част-

ных производных, в пространственно-структуриро-

В настоящее время нелинейные решеточные мо-

ванной ситуации эволюция полей оказывается на-

дели находят широкое применение при теоретиче-

много сложнее и естественно ожидать эффектов, ко-

ском исследовании физических явлений в различ-

торые отсутствуют в континуальной задаче. В част-

ных по своей природе дискретных системах и при

ности, на данное обстоятельство указывает разли-

интерпретации экспериментально полученных дан-

чие в дисперсионных свойствах и особенности, свя-

ных

[1-6]. При изучении распространения волно-

занные с периодичностью выражающих их законов

вых полей в наборах, состоящих из большого чис-

в дискретном случае и спецификой отдельно взятой

ла связанных между собой эквидистантно располо-

зоны Бриллюэна, в которой присутствуют одновре-

женных элементов, активно используется дискрет-

менно области как с нормальной, так и с аномальной

ное нелинейное уравнение Шредингера (ДНУШ)

дисперсией групповой скорости.

[1-6]. Несмотря на то, что оно является непо-

средственным аналогом непрерывного нелинейно-

Детальный анализ динамики волновых пакетов в

го уравнения Шредингера (НУШ) [6-8], позволяю-

решетках в основном опирается на результаты чис-

ленного моделирования. Как показывают такого ро-

^* E-mail: smirnov_lev@appl.sci-nnov.ru

да расчеты (например, см. работы [9-14]), для плав-

897

Л. А. Смирнов, В. А. Миронов, А. Г. Литвак

ЖЭТФ, том 161, вып. 6, 2022

ных (по сравнению с периодом рассматриваемой ре-

В данной работе рассматриваются особенности

шетки) начальных распределений поля их дальней-

динамики и процесса самовоздействия волновых па-

шее поведение может рассматриваться в контину-

кетов с нормальной дисперсией групповой скорости,

альном пределе лишь на ограниченных трассах или

когда не удается сделать столь определенного про-

в течение конечных временных интервалов. Приме-

гноза о возможных сценариях распространения по-

нимость непрерывной аппроксимации для дискрет-

ля, как в случае аномальной дисперсии. В первую

ных уравнений оправдана только до тех пор, пока

очередь связано это с тем, что в обсуждаемых усло-

характерные пространственные масштабы локали-

виях среда фактически становится дефокусирую-

зации неоднородностей не становятся того же по-

щей, вследствие чего использование пробных функ-

рядка, что и расстояния между соседними структур-

ций в виде гауссиана с линейной и квадратичной

ными элементами обсуждаемой системы. Это приво-

коррекциями фазового фронта при вариационном

дит к тому, что даже в одномерной цепочке возни-

подходе не представляется до конца оправданным.

кает целый ряд эволюционных сценариев, которые

Кроме того, на первый взгляд, есть основания пола-

не встречаются в сплошной среде [9-14]. Например,

гать, что можно ограничиться вообще только конти-

в работах [9-12] изучалось распространение исходно

нуальным пределом, в рамках которого все протека-

широких квазиоптических пучков, инжектируемых

ющие процессы описываются с помощью НУШ, по-

в решетку эквидистантно расположенных светово-

скольку на начальных этапах исходно плавные рас-

дов, и было показано, что их самофокусировка при

пределения будут еще больше расплываться. Одна-

превышении критической мощности заканчивается

ко, как показывают численные расчеты, существу-

локализацией большей части электромагнитного из-

ют критические значения параметров таких распре-

лучения в одном из волноводов. Кроме того, подоб-

делений, при превышении которых на фоне рас-

ный процесс самоканалирования приводит к откло-

ширяющегося гладкого профиля поля развивается

нению трассы распространения максимума интен-

неустойчивость, приводящая к его разрушению. По-

сивности от прямой линии [9, 11, 12, 15].

добные динамические режимы, на которые отчасти

обращалось внимание в работах [16-18,21], заведомо

отсутствуют в аналогичных непрерывных моделях.

Похожие эффекты обсуждались также и в при-

Основная цель представленной статьи заключа-

ложении к динамике набора взаимодействующих

ется в объяснении механизмов возникновения дан-

между собой облаков бозе-эйнштейновского конден-

ных сценариев поведения волнового поля в рам-

сата, каждое из которых сосредоточено вблизи одно-

ках ДНУШ. При этом для определенности поста-

го из соответствующих минимумов внешнего пери-

новка задачи формулируется применительно к рас-

одического потенциала, созданного оптической ло-

пространению оптического излучения в дискретной

вушкой [16-21]. Подчеркнем, что выводы, сделан-

системе, состоящей из большого числа связанных

ные в большинстве из указанных выше статей, спра-

между собой световодов, хотя результаты проведен-

ведливы, только когда волновые пакеты находятся

ного анализа несложно перенести и на другие слу-

в области аномальной дисперсии. Стоит отметить,

чаи, где речь идет об эволюции нелинейных воз-

что во всех перечисленных здесь случаях, несмот-

буждений в цепочках эквидистантно расположен-

ря на разную физическую природу объектов, ис-

ных элементов, для которых могут быть использо-

следование проводилось в рамках ДНУШ, для ко-

ваны соответствующие модельные уравнения.

торого развито существенно меньше аналитических

Прежде чем переходить к изложению основно-

методов построения точных и приближенных реше-

го материала, сделаем еще ряд важных замечаний.

ний по сравнению с НУШ. Оказалось, что для дис-

Во-первых, нетривиальные режимы эволюции ди-

кретных моделей весьма полезным и конструктив-

намических систем нередко удается успешно клас-

ным может быть использование вариационного под-

сифицировать, изучая устойчивость стационарных

хода, основанного на априорных представлениях о

состояний и автомодельных решений исследуемой

форме изучаемых нелинейных возбуждений конеч-

задачи [1, 6-8, 22, 23]. В большинстве случаев это

ной амплитуды и позволяющего качественно, а по-

можно сделать посредством процедуры линеари-

рой и количественно адекватно описать в безабер-

зации исходных уравнений, описывающих то, как

рационном приближении ключевые аспекты эволю-

протекают интересующие нас процессы (например,

ции и самоканалирования локализованных образо-

распространение электромагнитного излучения в

ваний в пространственно-структурированных сре-

пространственно-структурированных средах, взаи-

дах [10-14, 16].

модействие когерентных волн материи и формиро-

898

ЖЭТФ, том 161, вып. 6, 2022

Особенности динамики самовоздействия волновых пакетов. ..

вание интерференционных картин в гидро- и газо-

ются и при столкновении волн рефракции, взаимо-

динамике). Анализ поведения малых возмущений на

действие которых изучалось в статьях [36-43, 49].

заданном фоне достаточно часто позволяет оценить

В данной работе представлены численные и ана-

типичные времена перехода от одного нелинейного

литические аргументы в пользу того, что учет дис-

режима к другому, присущие масштабы возникаю-

кретности среды в надпороговых условиях приво-

щих неоднородностей, а также пороговые величи-

дит в ходе эволюции к формированию локально

ны для основных характеристик волнового поля и

неустойчивых распределений волнового поля. От-

бифуркационные значения управляющих парамет-

метим, что подобные процессы, по всей видимости,

ров рассматриваемой системы, при которых начи-

могут также наблюдаться при распространении ла-

нают развиваться те или иные неустойчивости. В

зерного излучения в волокнах, в которых проявля-

итоге такого рода подход в целом помогает прогно-

ются линейные дисперсионные эффекты высокого

зировать возможные сценарии эволюции нелиней-

порядка [48, 50-53]. Ниже описана постановка зада-

ных возбуждений и объяснить ключевые моменты

чи, которая для определенности выполнена в тер-

в динамике их развития, наблюдаемые на различ-

минах распространения электромагнитного излуче-

ных этапах непосредственно в эксперименте или при

ния в наборе эквидистантно расположенных свето-

численном моделировании. Особенностью интересу-

водов, и приведены основные приближения, позво-

ющей нас здесь ситуации является то, что ее можно

ляющие использовать ДНУШ в качестве базовой

интерпретировать как «жесткий» режим возникно-

модели. Затем проведено обобщение метода нели-

вения неустойчивости, когда распространение оги-

нейной геометрической оптики на случай дискрет-

бающей волнового поля довольно долго оказывается

ной среды. Оно состоит в более корректном учете

плавным (практически равновесным), перед тем как

изменения фазы волнового поля по сравнению с тем,

перейти к существенно нелинейному неравновесно-

как это обычно делается при использовании квази-

му варианту своего поведения.

классического подхода для построения приближен-

Во-вторых, в рамках НУШ с дефокусирующей

ных решений НУШ [24-33,36-53]. Полученная в ре-

нелинейностью, для которого хорошо известно, что

зультате совокупность бездисперсионных соотноше-

однородный фон конечной амплитуды устойчив,

ний, как и в случае сплошной среды, имеет схожий

численно, аналитически, а также эксперименталь-

вид с системами квазилинейных уравнений, часто

но подробно изучалась задача о разлете локализо-

встречающихся в газодинамике [22-33,36-49]. Одна-

ванных распределений поля, заданных как на пье-

ко в рассматриваемой нами ситуации данная сово-

дестале [24-33], так и на спадающих до нуля на

купность уравнений в частных производных не яв-

бесконечности (т.е., можно сказать, расплывающих-

ляется строго гиперболической. С учетом указанно-

ся в «вакуум») [24, 25, 34-45]. В частности, было

го обстоятельства удается показать, что при выпол-

наглядно показано, что для исходно широких сиг-

нении надпороговых условий в процессе плавного

налов дисперсионными эффектами можно прене-

расплывания локализованных распределений поля в

бречь [24-33, 36-45] и, кроме того, для ряда ситу-

периферийной области тип системы квазилинейных

аций свести описание динамики поля к уравнению

уравнений меняется на эллиптический, что свиде-

простой волны (уравнению Хопфа) [24, 25, 46-48],

тельствует о потенциальной возможности развития

скорость распространения которой зависит от ин-

неустойчивости гладкого профиля огибающей вол-

тенсивности в отдельно взятой точке. Следователь-

нового пучка.

но, в ходе расширения изначально гладких огибаю-

щих волновых пакетов следует ожидать укручения

профиля [24-33, 36-48]. Такого рода процесс спосо-

2. ОПИСАНИЕ РАСПРОСТРАНЕНИЯ

бен быть причиной возникновения мелкомасштаб-

ВОЛНОВОГО ПОЛЯ В ПРОСТРАНСТВЕН-

НО-СТРУКТУРИРОВАННЫХ

ных возмущений, на формирование и эволюцию ко-

СРЕДАХ

торых уже оказывает принципиальное влияние кон-

куренция нелинейности и дисперсии

[24-33, 36-48].

Однако детальные исследования, выполненные на

2.1. Базовая модель в виде цепочки

основе НУШ, в том числе с помощью прямого

дискретных уравнений. Формулировка

его моделирования, достоверно демонстрируют, что

основной проблемы

при указанных условиях появляющиеся на плавном

фоне неоднородности не приводят к его разрушению

Рассмотрим распространение одномерных ква-

[24-33,36-49]. Похожие процессы также не наблюда-

зиоптических волновых пучков, инжектируемых в

899

Л. А. Смирнов, В. А. Миронов, А. Г. Литвак

ЖЭТФ, том 161, вып. 6, 2022

пространственно-неоднородную среду, состоящую

сопоставление имеет смысл при рассмотрении дина-

из набора эквидистантно расположенных одно-

мики исходно широких волновых пакетов.

модовых световодов. Анализ проведем на базе

Проведем более детальный, чем это обычно дела-

стандартной теоретической модели

[1-5, 9-14], в

ется, анализ процессов в ДНУШ и получим полез-

рамках которой предполагается, что фундамен-

ные для понимания результатов численных расче-

тальные направляемые моды ориентированных

тов аналитические соотношения. Для этого, во-пер-

параллельно оси z оптических волноводов слабо

вых, выделим у комплексного поля ψ_n(z) амплитуду

связаны между собой. Огибающие поля каждой из

и фазу, т.е. представим ψ_n(z) в виде

таких мод медленно эволюционируют вдоль z и

ψ_n(z) = φ_n(z)exp(-iθ_n(z)),

(3)

характеризуются своими комплексными амплиту-

дами. Изменение этих индивидуальных амплитуд в

где φ_n(z) и θ_n(z) являются действительными функ-

зависимости от координаты z описывается системой

циями. Затем, подставив (3) в (1) и приравняв по от-

уравнений, учитывающих как собственную нели-

дельности к нулю действительную и мнимую части

полученного соотношения, в итоге придем к следу-

нейность структурных элементов рассматриваемой

решетки, так и взаимодействие с ближайшими

ющей системе дискретных уравнений:

соседями, возникающее из-за перекрытия направ-

∂φ_n

+ φn+1 sinvn+1 - φn-1 sinv_n = 0,

(4)

ляемых ими мод. При отсутствии потерь в среде из

∂z

неограниченного числа тонких световодов с дефо-

∂θ_n

φn+1

φn-1

cosvn+1 -

cosv_n + φ2n = 0.

(5)

кусирующей керровской нелинейностью приходим

∂z

φ_n

к бесконечной упорядоченной последовательно-

Здесь для удобства дальнейшего рассмотрения

сти соотношений, которая называется ДНУШ и

введено обозначение для разности фаз v_n(z)

имеет в нормированных переменных следующий

= θ_n(z) - θn-1(z) волновых функций ψ_n(z) и

вид [1-5, 9-14]:

ψn-1(z) в соседних элементах рассматриваемой

∂ψ_n

цепочки. Несложно заметить, что именно v_n(z),

- ψn-1 - ψn+1 + |ψ_n|2 ψ_n = 0.

(1)

а не θ_n(z) играет роль истинной динамической

∂z

переменной, так как ДНУШ (1), а вслед за ним

Здесь функция ψ_n (z) определяет комплексную амп-

и соотношения (4), (5) инвариантны относительно

литуду моды n-го волновода. ДНУШ (1) является

преобразования θ_n(z) → θ_n(z)+const, т. е. все равен-

одной из наиболее простых и универсальных дис-

ства остаются неизменными при сдвиге фазы θ_n(z)

кретных моделей и при этом (не только качествен-

на произвольную постоянную величину. Поэтому

но, но и количественно) адекватно описывает фи-

для теоретического рассмотрения динамических

зическую ситуацию, когда пучок непрерывного из-

процессов в решетках локально связанных элемен-

лучения падает на решетку с большим числом на-

тов совместно с (4) зачастую стоит использовать

правляющих элементов, в каждом их которых мож-

уравнение для v_n(z), которое непосредственно

но пренебречь дисперсионными и дифракционными

следует из (5):

эффектами [1-5].

Формально дискретному уравнению (1) можно

∂v_n

φn+1

φ_n

cosvn+1 +

cosv_n -

поставить в соответствие континуальное НУШ

∂z

φ_n

φn-1

∂ψ

∂²ψ

φn-1

φn-2

+ 2i sinκ

- cosκ

+ |ψ|² ψ = 0.

(2)

−

cosv_n+

cosvn-1+φ2n-φ2n-1 = 0.

(6)

∂z

∂x

∂x²

φ_n

n-1

Для этого обычно вводят непрерывную координа-

Таким образом, при описании эволюции волнового

ту x, ассоциированную с индексом n, и затем де-

поля в дискретной среде далее будем отталкиваться

лают замену ψ_n (z) на ψ (x, z), считая функцию

от упорядоченной последовательности пар соотно-

ψ (x, z) плавной по x на масштабах, сравнимых с

шений (4), (6).

периодом рассматриваемой одномерной решетки, а

В данной работе нас прежде всего интересуют

также предварительно выделив в фазе компонен-

особенности процесса самовоздействия пучков, из-

ты ψ_n(z) комплексного вектора составляющую ви-

начально плавных на масштабах, сравнимых с пери-

да 2 cos κ z - κ n, которая может достаточно резко

одом решетки. При этом основное внимание уделе-

изменяться по величине при переходе от одного эле-

но ситуации, когда согласно представлениям, кото-

мента цепочки к соседнему, когда характерное зна-

рые основаны на хорошо известных результатах, по-

чение волнового числа κ лежит вне малой окрест-

лученных в рамках НУШ, исходно широкие волно-

ности центра зоны Бриллюэна. Отметим, что такое

вые пакеты будут расплываться, а все возникающие

900

ЖЭТФ, том 161, вып. 6, 2022

Особенности динамики самовоздействия волновых пакетов. ..

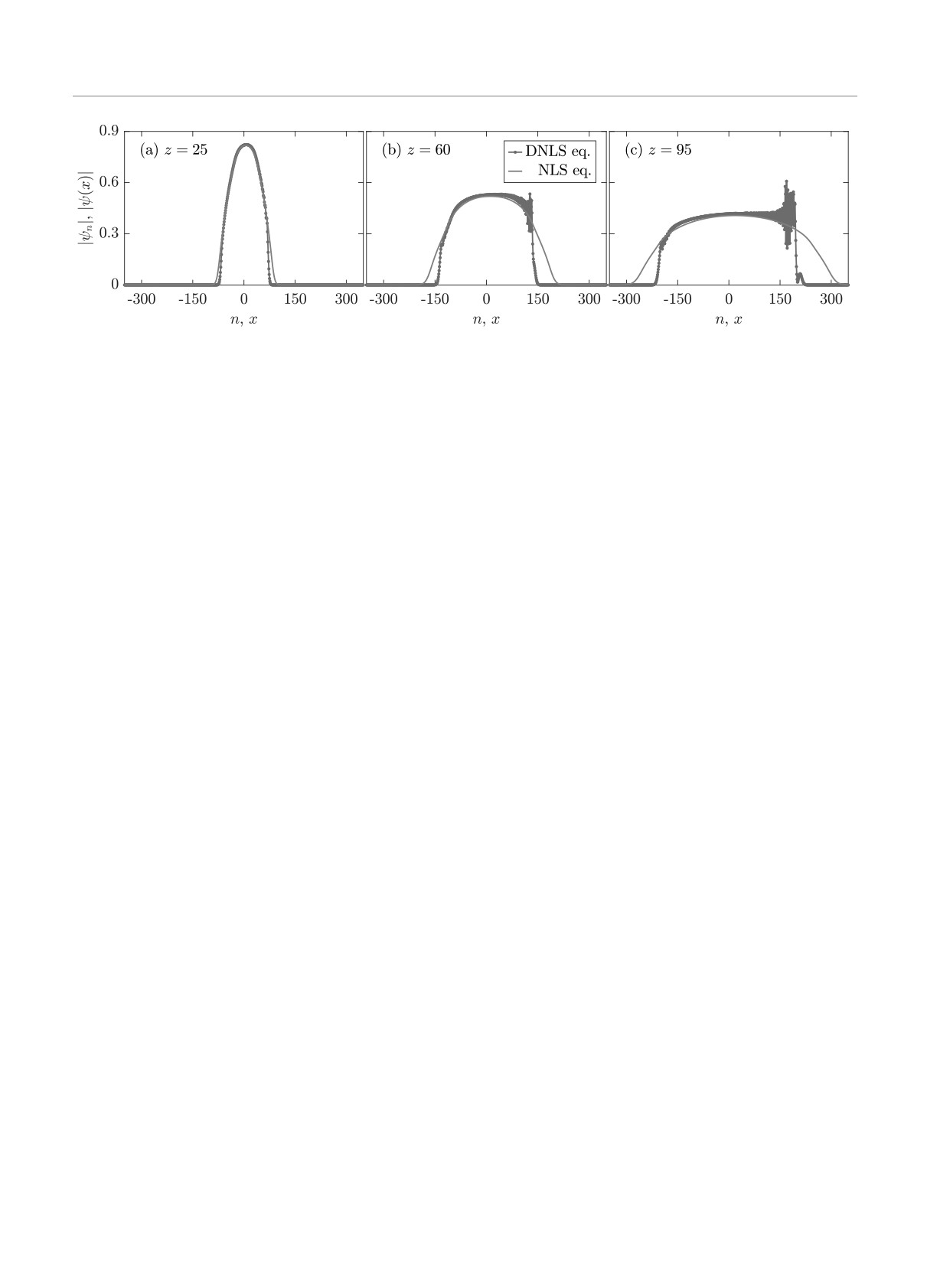
Рис. 1. (В цвете онлайн) Рассчитанные с помощью прямого численного моделирования в рамках ДНУШ (1) и НУШ (2)

соответственно распределения амплитуды |ψn(z)| волнового поля в узлах эквидистантной решетки световодов (точки,

соединенные между собой линиями синего цвета) и профили аналогичной характеристики |ψ(x, z)| в континуальной за-

даче (сплошные линии красного цвета) для пучков, заданных при z = 0 в форме ψn(0) = ψ(x = n, 0) exp(-iγn) и

[

]

ψ(x, 0) = a exp

-(x/σ)2m

с параметрами γ = 0.1, a = 1.125, σ = 15 и m = 3. На начальном этапе своего распро-

странения (a) такие пучки в дискретном и континуальном случаях ведут себя схожим образом (не только качественно,

но и количественно с допустимой степенью точности). Однако в процессе дальнейшей эволюции различия постепенно

становятся намного более существенными (b). На периферии локализованного амплитудного распределения начинает-

ся резкий рост мелкомасштабных возмущений, который в конечном итоге приводит к разрушению плавного профиля

волнового поля (c)

(например, из-за возможных эффектов укручения

используемой нами для изучения распространения

фронта и его опрокидывания) неоднородности не

излучения в системе эквидистантно расположенных

должны сильно нарастать [24-48]. Однако, как пока-

нелинейных одномодовых световодов и записанной

зывают численные расчеты (рис. 1), проведенные на

в терминах счетного набора комплексных амплитуд,

базе ДНУШ (1), динамика распределения поля в ре-

характеризующих поле в каждом из структурных

шетке нередко существенно отличается от того, что

элементов обсуждаемой цепочки, к уравнениям в

предсказывают вычисления, выполненные в непре-

частных производных для гладких функций, непре-

рывном пределе. Несмотря на достаточно хорошее

рывно распределенных в поперечном к оси z направ-

совпадение на начальном этапе (рис. 1a), начиная

лении и совпадающих в узлах решетки со значени-

с некоторого момента, в целом ряде случаев раз-

ями истинных динамических переменных.

личия становятся значительными (рис. 1b). Распро-

Прежде чем привести последовательное описа-

страняющийся в цепочке пучок сильно искажается,

ние основных идей развитого теоретического подхо-

чаще всего перестает быть симметричным относи-

да, заранее обратим внимание на довольно неожи-

тельно своего центра, мелкомасштабные возмуще-

данный и относительно нетривиальный факт. Ока-

ния на периферии демонстрируют резкий рост, что

зывается достаточным ограничиться бездисперсион-

в конечном итоге приводит к разрушению плавного

ным приближением, когда учитываются только про-

профиля, из которого выделяются локализованные

изводные первого порядка (производные же второго

образования довольно большой амплитуды (рис. 1c).

порядка и выше отбрасываются), а специфика дис-

Отмеченный процесс носит взрывной характер и не

кретности в первую очередь проявляется в модифи-

укладывается в рамки стандартного континуально-

кации уравнения непрерывности и соотношения для

го рассмотрения задачи, что указывает на разви-

градиента фазы, которая позволяет их применять

тие неустойчивости, обусловленной дискретностью

в любой части зоны Бриллюэна и отслеживает эф-

системы.

фективный тип нелинейности.

Мы предприняли попытку объяснить причины

2.2. Бездисперсионный предел для

возникновения подобного процесса и выявить основ-

дискретной модели

ной физический механизм, вызывающий такое де-

структивное поведение. Согласно изложенному ни-

В качестве отправной точки для дальнейшего

же анализу, для этого достаточно сделать чуть бо-

анализа нами была выбрана полученная выше сис-

лее корректный переход от математической модели,

тема разностных уравнений (4), (6). Для того чтобы

901

Л. А. Смирнов, В. А. Миронов, А. Г. Литвак

ЖЭТФ, том 161, вып. 6, 2022

перейти к ее аналогу в непрерывном пределе, пред-

как именно в такие уравнения трансформируются

положим, что значения φ_n(z) и v_n(z) слабо изменя-

равенства (7), (8) при условии, что в процессе рас-

ются при уменьшении или увеличении индекса n на

пространения излучения отклонения v(x, z) гради-

несколько единиц ñ, т. е. при смещении вдоль цепоч-

ента фазы от исходно заданного значения v₀ оказы-

ки на конечное число ячеек. Такое предположение

ваются малыми, т. е. |v(x, z)| ≪ π в ситуации, когда

справедливо при плавном на масштабах неоднород-

v(x, z) = v₀ + v(x, z), где v₀ = const. Следовательно,

ности среды распределениях величин φ_n(z) и v_n(z).

в системе (7), (8) выполнен более корректный учет

В этом случае можно перейти от дискретного на-

особенностей изменений фазового фронта и его ло-

бора пар φ_n(z) и v_n(z) к двум непрерывным функ-

кальных перестроек в дискретном случае.

циям φ(x, z) и v(x, z), зависящим не только от пе-

ременной z, но и от координаты по оси x, направ-

ленной вдоль одномерной решетки эквидистантно

3. ЭВОЛЮЦИЯ

расположенных элементов. Если выразить φ_n±ñ(z)

ПРОСТРАНСТВЕННО-НЕОДНОРОДНЫХ

и v_n±ñ(z) соответственно через φ(x, z) и v(x, z), огра-

РАСПРЕДЕЛЕНИЙ ВОЛНОВОГО ПОЛЯ И

РАЗВИТИЕ НА ИХ ФОНЕ ХАРАКТЕРНОЙ

ничившись лишь двумя основными членами в фор-

ДЛЯ ДИСКРЕТНОЙ СИСТЕМЫ

мальном разложении в ряд Тейлора вблизи точки

НЕУСТОЙЧИВОСТИ

x = n,

(

)

∂

3.1. Ключевые отличия бездисперсионного

φ_n±ñ(z) ≈

1±ñ

φ(x, z),

∂x

предела для дискретной модели от

(

)

континуального аналога

∂

v_n±ñ(z) ≈

1±ñ

v(x, z),

∂x

Для удобства дальнейшего рассмотрения введем

то несложно получить для φ(x, z) и v(x, z) замк-

обозначения

нутую систему квазилинейных уравнений в частных

ρ(x, z) = φ²(x, z), u(x, z) = 2 sin v(x, z),

(9)

производных первого порядка:

∂φ

∂v

+ 2sinv

+ φcosv

= 0,

(7)

которые позволяют переписать соотношения (7), (8)

∂z

∂x

в виде

∂v

∂φ

+ 2sinv

+ 2φ

= 0.

(8)

∂z

∂x

∂ρ

∂uρ

= 0,

(10)

При выводе данных соотношений считалось, что

∂z

∂x

∕

применение дифференциального оператора ∂

∂x к

∂u

∂ρ

+ 2cosv

= 0,

(11)

функциям φ(x, z) и v(x, z) повышает порядок ма-

∂z

∂x

лости тех комбинаций, в которых они возникают,

наиболее близком по своей структуре к уравнениям

что позволяет не принимать во внимание целый ряд

одномерной газодинамики [22, 23]. Если поставить

слагаемых, содержащих произведения первых про-

величинам ρ(x, z) и u(x, z) в соответствие плотность

изводных от φ(x, z) и v(x, z) по x или более высокие

и поле скоростей, то несложно заметить, что пер-

производные и не оказывающих существенного вли-

вое равенство системы (10), (11) фактически играет

яния при анализе указанных выше эффектов. От-

роль уравнения непрерывности, а второе является

метим также тот факт, что совокупность уравнений

аналогом уравнения Эйлера. Основное различие за-

(7), (8) может быть представлена в неканонической

ключается в специфическом для рассматриваемой

гамильтоновой форме

нами задачи множителе 2 cos v, стоящем перед по-

∂ρ

∂

⁽∂H(ρ, v)⁾

∂v

∂

⁽∂H(ρ, v)⁾

следним слагаемым в левой части равенства (11).

= 0,

∂z

∂x

∂v

∂z

∂x

∂ρ

Согласно принятой классификации набора ква-

∕

зилинейных уравнений, совокупность соотношений

с гамильтонианом H(ρ, v)

= ρ²

2 - 2ρcosv, где

(10), (11) может быть либо эллиптического, либо

ρ = φ². Фактически, систему (7), (8) можно интерп-

гиперболического типа [22, 23]. Для определения,

ретировать как бездисперсионный предел дискрет-

к какому типу относится интересующая нас систе-

ной модели (4), (6). Здесь прослеживается полная

ма (10), (11), поступим следующим образом. Ис-

аналогия с приближением нелинейной геометричес-

пользуя выражения

кой оптики для сплошной среды (см., например, ра-

боту [54]), в которой эволюция огибающей волно-

∂χ

вого поля описывается континуальным НУШ, так

= -ρ(x, z),

= u(x, z)ρ(x, z),

(12)

∂x

∂z

902

ЖЭТФ, том 161, вып. 6, 2022

Особенности динамики самовоздействия волновых пакетов. ..

введем формально функцию χ(x, z), удовлетворяю-

(таким образом, вторые производные от χ(x, z) по x

щую тождественно уравнению непрерывности (10).

и z относительновелики). Подставим в (13) суперпо-

Затем, продифференцировав по z второе из опреде-

зицию χ(x, z) = χ(x, z)+ χ(x, z) и линеаризуем полу-

ляющих χ(x, z) равенств (12), после несложных пре-

ченное выражение относительно χ(x, z), принимая

образований с учетом (10), (11) получим соотноше-

во внимание выбранный нами вид поправок χ(x, z)

ние, связывающее между собой частные производ-

к исходному решению χ(x, z) и связанным с ним ре-

ные второго порядка от χ(x, z) по z и x, линейное

шений ρ(x, z) и v(x, z). В итоге придем к следующе-

по ним и записанное в канонической форме [23]

му уравнению для χ(x, z):

∂²χ

∂² χ

A(ρ, v)

+ 2B(ρ, v)

+ C(ρ, v)

= 0,

(16)

+ 2B

= 0,

(13)

∂z²

∂z∂x

∂x²

∂z²

∂z∂x

∂x²

в котором коэффициенты A(ρ, v), B(ρ, v) и C(ρ, v)

где коэффициенты A, B и C в свою очередь зави-

рассчитываются с применением невозмущенных

сят от ρ(x, z) и v(x, z) (т. е. могут быть представле-

распределений поля

ρ(x, z) и

v(x, z). В частнос-

ны только через производные первого порядка от

ти, из (16) непосредственно вытекает, что в тех

χ(x, z) по z и x):

областях, где выполняется неравенство

A = 1, B = 2sinv, C = 2ρcosv + 4sin2 v.

(14)

B²(ρ, v) - A(ρ, v)C(ρ, v) = 2ρcos v > 0,

Исходя из общих представлений в случае, когда вы-

малоамплитудные возбуждения, обусловливающие

полняется неравенство B² - AC = 2ρ cos v > 0, урав-

наличие поправок χ(x, z), ρ(x, z) и v(x, z), по мере

нение (13) (а вместе с ним и система (10), (11), как

проникновения излучения в пространственно-струк-

и ее эквивалент (7), (8)) относится к гиперболичес-

турированную среду нарастать не будут, а их рас-

кому типу, а в противоположной ситуации, когда

пространение на заданном фоне χ(x, z), ρ(x, z) и

B² - AC = 2ρ cosv < 0, соответствующие соотно-

v(x, z) происходят вдоль соответствующих характе-

шения принадлежат к эллиптическому классу. От-

ристик (15). В этом несложно убедиться, воспользо-

метим, что в первом из указанных двух вариантов

вавшись стандартным методом перехода от волно-

уравнения

вой к геометрической акустике [23,54], т. е. предста-

√

вив χ(x, z) в виде

B±

B² - AC

√

= 2sinv ±

2ρ cosv

(15)

[

]

χ(x, z) = Re α(x, z)e-iβ(x,z)

определяют в плоскости xz два семейства характе-

и построив на базе (16) уравнение для эйконала

ристик x_±(z) (для заданных ρ(x, z), v(x, z), а вместе

β(x, z). С другой стороны, из (16) также наглядно

с ними для χ(x, z)) [22, 23].

видно, что в той части пространства, где

Если для системы квазилинейных уравнений (7),

(8) известно решение ρ(x, z), v(x, z), которому отве-

B²(ρ, v) - A(ρ, v)C(ρ, v) = 2ρcos v < 0,

чает своя функция χ(x, z), удовлетворяющая (12) и

(13), то можно рассмотреть задачу об устойчивос-

должен наблюдаться экспоненциальный рост рас-

ти данного решения относительно малых возмуще-

сматриваемого класса возмущений.

ний ρ(x, z), v(x, z) в рамках соотношения (13). При

В итоге эквивалентные друг другу системы ква-

этом предположим, что для возникающих в силу

зилинейных уравнений (10), (11) и (7), (8), опи-

тех или иных физических причин поправок χ(x, z) к

сывающие эволюцию исходно широких волновых

сформировавшемуся профилю χ(x, z) выполняются

пучков в дискретных цепочках в бездисперсион-

несколько требований, которые можно интерпрети-

ном приближении, являются гиперболическими, ес-

ровать при B² -AC > 0 как условия геометрической

ли cos v(x, z)

> 0, и эллиптическими там, где

акустики [23]. Будем считать, что подобные откло-

cosv(x, z) < 0. Из приведенных выше аргументов

нения, описываемые χ(x, z), а также ρ(x, z) и v(x, z),

можно сделать вывод, что в пространственно-струк-

на начальном этапе слабо отражаются на характер-

турированных средах характерное поведение поля

ной динамике волнового поля (т.е. функция χ(x, z) и

в различных локализованных областях может су-

ее первые производные малы), однако сами возму-

щественным образом различаться и определяется

щения являются достаточно мелкомасштабными и

прежде всего знаком величины cos v(x, z) в отдельно

претерпевают довольно сильные изменения на срав-

выделенной и рассматриваемой окрестности, охва-

нительно небольших пространственных интервалах

тывающей конечное число структурных элементов

903

Л. А. Смирнов, В. А. Миронов, А. Г. Литвак

ЖЭТФ, том 161, вып. 6, 2022

решетки. В данном обстоятельстве состоит прин-

значительная часть которого сосредоточена в огра-

ципиальное отличие дискретной задачи от конти-

ниченной области, при его проникновении в прост-

нуальной, в которой класс системы квазилинейных

ранственно-структурированную среду и как следу-

уравнений, полученной из НУШ (2) аналогичным

ет интерпретировать наблюдаемые эффекты. Ниже

путем, состоящим по сути в пренебрежении дис-

продемонстрировано, что для указанной ситуации

персионными эффектами высшего порядка, одно-

удается построить автомодельное решение, а затем

значно определяется типом нелинейности. Так, для

использовать его совместно с развитым нами подхо-

дефокусирующих сред в динамике плавных непре-

дом, что позволяет найти критическое значение па-

рывных распределений амплитуды и фазы во всем

раметра ρ₀, при котором качественная картина рас-

пространстве проявляются только черты, присущие

пространения волнового поля меняется кардиналь-

гиперболическим моделям (распространение вдоль

но.

характеристик, возникновение участков с резкими

По аналогии с одномерной газодинамикой [23],

градиентами вследствие процессов опрокидывания),

где подобные автомодельные движения, возника-

тогда как для фокусирующей нелинейности в силу

ющие, в частности, в цилиндрической трубе при

эллиптичности структуры базовых уравнений одну

равномерном перемещении поршня, играют важную

из основных ролей играет развитие модуляционной

роль, в случае рассматриваемой дискретной систе-

неустойчивости.

мы анализ эволюции распределения поля изначаль-

В дискретных системах, как показывают наши

но ступенчатой формы является одной из отправ-

рассуждения, возможно возникновение ситуации,

ных точек для общего понимания специфики и вы-

когда одновременно на разных участках наблюда-

деления ключевых отличительных черт поведения

ются разноплановые варианты поведения. В одних

локализованных образований.

областях эволюция поля будет протекать по сцена-

Будем искать решение совокупности уравнений

риям, характерным исключительно для дефокуси-

(10), (11) в виде

рующего (гиперболического) случая, а в других об-

ρ(x, z) = ρ(ξ), v(x, z) = v(ξ), u(x, z) = sin v(ξ),

ластях пойдет усиление мелкомасштабных возмуще-

где все перечисленные величины зависят только от

ний на фоне гладкого профиля с последующим рез-

∕

ким ростом интенсивности поля и его локализаци-

безразмерной автомодельной переменной ξ = x

[23, 43, 55, 56]. Другими словами, предположим, что

ей в ограниченных пространственных областях, как

форма каждой отдельно взятой интересующей нас

при самофокусировке (свойственной эллиптической

функции при различных конечных значениях z > 0

ситуации).

подобна самой себе и отличается лишь своим мас-

штабом вдоль оси x, увеличивающимся пропорцио-

3.2. Распространение пучка со ступенчатым

нально z. В результате придем к следующей сово-

профилем интенсивности. Автомодельные

купности обыкновенных дифференциальных урав-

решения в рамках бездисперсионного

нений:

приближения для дискретной модели

dρ

(u - ξ)

+ρ

= 0,

(18)

dξ

В этом разделе рассмотрим модельную

dρ

задачу о распаде полуограниченного пучка

2 cosv

+ (u - ξ)

= 0.

(19)

[22-25, 36-43, 55, 56] с исходно линейным фазо-

dξ

∕

вым фронтом, для которого v(x, 0) = γ (|γ| < π

2),

Для того чтобы найти нетривиальные решения дан-

а профиль интенсивности ρ(x, z)

= φ²(x, z) в

ной системы, во-первых, исключим (например) из

сечении z

= 0 задан в виде кусочно-постоянной

(18) производные, выразив и подставив их из (19).

(ступенчатой) функции действительного аргумен-

Эта процедура эквивалентна приравниванию к ну-

та x:

лю определителя системы (18), (19). В итоге на-

{

ρ₀, x ≤ 0,

ходим, что в бездисперсионном приближении для

ρ(x, 0) =

(17)

решений, имеющих автомодельную форму, должно

0, x > 0.

выполняться соотношение

Такая постановка начальных условий для рассмат-

∕

√

ξ=x

z=u±

2ρ cosv,

(20)

риваемой проблемы дает возможность аналитичес-

ки описать особенности протекающих процессов и

которое, в частности, лишний раз подчеркивает, что

получить наглядное представление о том, что мо-

волны такого типа существуют только в области ги-

жет происходить с плавной огибающей излучения,

перболичности квазилинейных уравнений (18), (19),

904

ЖЭТФ, том 161, вып. 6, 2022

Особенности динамики самовоздействия волновых пакетов. ..

т. е. при cos v(x, z) > 0. Прежде чем переходить к

привести к разрушению пучка. Принимая во вни-

дальнейшему изложению результатов данного раз-

мание данные обстоятельства и соотношение (21),

дела, обратим внимание, что в ситуации, когда

справедливое для автомодельного решения, неслож-

∕

v(x, 0) = γ, где -π

2 < γ ≤ 0, а распределение

но показать, что гиперболичность системы (7), (8)

ρ(x, 0) в плоскости z = 0 достаточно хорошо ап-

сохраняется в процессе эволюции волнового пучка

проксимируется выражением (17), при z > 0 есте-

лишь при начальных интенсивностях ρ₀, не превы-

ственно ограничить возможные значения v(x, z) ин-

шающих критическое значение

∕

тервалом γ ≤ v(x, z) < π

2, а в (20) выбрать знак

(

∕

)

(

∕

«-». Оправданность таких предположений обосно-

ρ0cr = 2 E

2, 2

-E

2, 2))2.

(22)

вывается в первую очередь физическими соображе-

ниями и интуитивными представлениями, согласно

В итоге естественно ожидать, что в ситуациях, ког-

которым граница резкого перехода между областью,

да ρ₀ > ρ0cr, дискретность среды принципиальным

занятой полем конечной амплитуды

√ρ₀, и «вакуу-

образом сказывается на динамике световых пучков

мом» (той частью пространства, где внутри струк-

в одномерной решетке волноводов и приводит к раз-

турных элементов решетки излучение практически

рушению плавных распределений поля. Этот вывод

подтверждается сравнением данных прямого чис-

отсутствует) должна постепенно размываться преж-

де всего за счет возникновения знакоопределенных

ленного моделирования эволюции поля в рамках

ДНУШ (1) и НУШ (2), исходный профиль которого

градиентов фазы, что в гидродинамической терми-

нологии отвечает процессу разлета «газа», а распро-

был задан в форме соответственно

странение малых возмущений по однородному фону

ψ_n(0) = ψ(x = n, 0)e^-iγn и

с ρ(x, z) = ρ₀ и v(x, z) = γ от места исходного разры-

]

√ [

(23)

ва происходит со скоростью

√ρ₀, являющейся ана-

ψ(x, 0) =

ρ₀ 1 - th (x/σ) ,

логом «скорости звука» [55, 56].

которая является часто используемой непрерывной

Подставив ξ

= u -

^√2ρ cos v в (18) и проин-

аппроксимацией кусочно-постоянной функции.

тегрировав полученное дифференциальное уравне-

На рис. 2 представлен случай, когда величина

ние с учетом граничных условий ρ(-∞, z) = ρ₀ и

интенсивности ρ₀ ниже критического значения (22).

v(-∞, z) = γ, найдем следующее соотношение:

Видно, что результаты расчетов для дискретной

∫

и континуальной задач практически совпадают не

√

√ρ₀ -√ρ =

√

cosw dw =

только качественно, но и количественно. Однако в

ситуации, показанной на рис. 3 и отвечающей выбо-

√ (

(

∕

)

(

∕

))

ру ρ₀ > ρ0cr, заметны существенные различия, объ-

2 E

2, 2

-E

2, 2

(21)

яснить которые можно развитием неустойчивости.

В процессе эволюции в периферийной части волно-

которое совместно с задействованным при его вы-

вого пучка возникает область, в которой поведение

воде выражением для ξ дает полное аналитическое

поля определяется эллиптической системой квази-

решение интересующей нас задачи об эволюции по-

линейных уравнений и малые возмущения нараста-

луограниченного пучка с кусочно-постоянным про-

ют экспоненциально, распространяясь к зону гипер-

филем интенсивности в рамках бездисперсионного

боличности (см. рис. 3b, c).

приближения для ДНУШ. Отметим, что в (21) ис-

(

∕

)

пользуется стандартное обозначение E

2, 2

для

неполного эллиптического интеграла второго рода.

4. ЗАКЛЮЧЕНИЕ

Согласно проведенному нами в предыдущем раз-

деле анализу, до тех пор пока в каждой точке про-

В заключение отметим, что сделанный выше вы-

странства выполняется неравенство cosv(x, z) > 0,

вод не зависит от сосредоточенной в пучке мощно-

совокупность квазилинейных уравнений (7), (8) (как

сти. Следовательно, для любых широких распреде-

и эквивалентная ей форма записи (10), (11)) являет-

лений произвольной амплитуды с исходно плоским

ся всюду гиперболической. Следовательно, неодно-

(v_n(0) = 0) или слегка наклонным (v_n(0) = γ, где

∕

родное распределение волнового поля при распро-

|γ| < π

2) фазовым фронтом начальная стадия эво-

странении не подвержено неустойчивости. Однако

люции достаточно хорошо описывается системой ги-

если возникают области, где cosv(x, z) < 0, то ма-

перболических квазилинейных уравнений и практи-

лые возмущения на этих участках будут экспонен-

чески не отличается от того, что происходит с та-

циально нарастать, что в конечном итоге должно

кими же волновыми полями в непрерывной зада-

905

ЖЭТФ, вып. 6

Л. А. Смирнов, В. А. Миронов, А. Г. Литвак

ЖЭТФ, том 161, вып. 6, 2022

Рис. 2. (В цвете онлайн) То же, что на рис. 1, для пучков, заданных при z = 0 в форме (23). Представленные резуль-

таты отвечают параметрам γ = -0.25, σ = 1.33 и

√ρ0 = 0.85√ρ0_cr , где ρ0_cr ≈ 0.493 — рассчитанное по формуле (22)

критическое значение интенсивности для данной ситуации. Результаты расчетов практически совпадают для всех пред-

ставленных сечений z = 50 (a), z = 400 (b) и z = 750 (c). Отличия между ними можно считать несущественными, так

как на сплошные кривые красного цвета фактически накладываются точки, соединенные между собой линиями синего

цвета

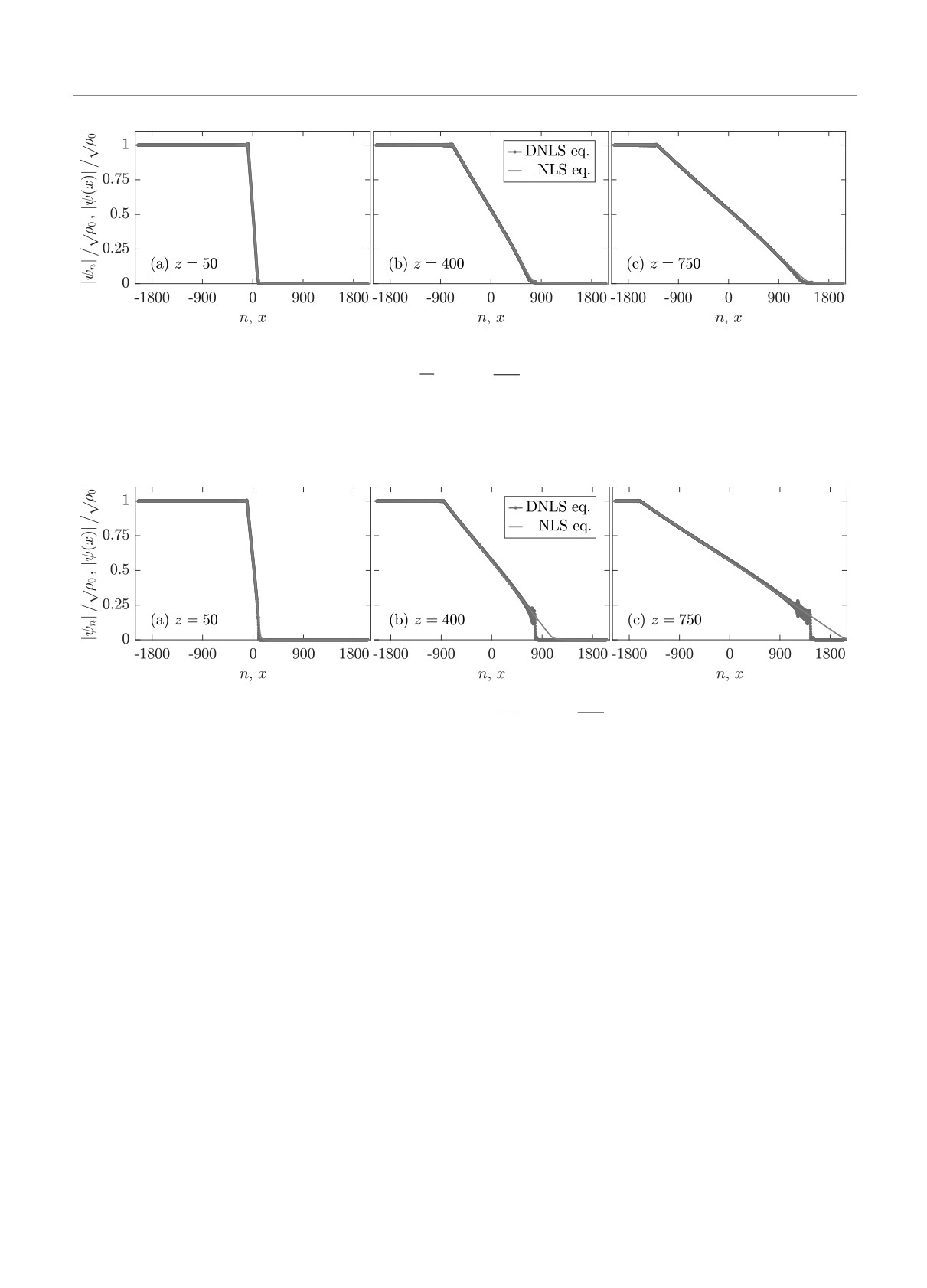
Рис. 3. (В цвете онлайн) То же, что и на рис. 2, только для

√ρ0 = 1.15√ρ0_cr. В этой ситуации пороговое значение

ρ0_cr ≈ 0.493 превышено, что, согласно развитым нами теоретическим представлениям, должно приводить к разрушению

профиля пучка в дискретном случае. Видно, что данный процесс начинается с нарастания возмущений на периферии

плавного профиля поля, которое вызвано развитием неустойчивости на его фоне. В расчетах, выполненных в рамках

НУШ (2), подобного эффекта не наблюдается

че при описании их динамики в рамках дефокуси-

ческие параметры начальных распределений поля,

рующего НУШ. Другими словами, нелинейные эф-

для которых следует ожидать развития неустойчи-

фекты в первую очередь приводят к расплыванию

вости, приводящей впоследствии к их разрушению.

огибающей пучка, на фоне которого происходит ло-

Численное моделирование эволюции системы в

кальное укручение поперечного профиля и образо-

рамках ДНУШ подтверждает сделанные выводы

вание резкого перепада аналогично тому, как про-

относительно динамики поля в дефокусирующем

текают подобные процессы в газодинамике. Одна-

режиме. В работе приведены примеры различ-

ко последующие этапы распространения в контину-

ных вариантов эволюции неоднородных профилей

альной и дискретной моделях могут как совпадать,

интенсивности электромагнитных пучков, инжек-

так и существенным образом различаться в зави-

тируемых в одномерную решетку эквидистантно

симости от того, выполняется ли для разности фаз

расположенных световодов. При этом наглядно

v_n(z) = θ_n(z)-θn-1(z) комплексной волновой функ-

продемонстрировано, что существуют сценарии,

ции ψ_n(z) = φ_n(z) exp[-iθ_n(z)] в соседних элемен-

которые отсутствуют в аналогичных ситуаци-

тах решетки условие cos v_n(z) > 0 по-прежнему во

ях в сплошной (неструктурированной) среде и

всем пространстве или же возникают области, где

характеризуются ростом малых возмущений и

cosv_n(z) < 0. Как показывает проведенный нами

возникновением изрезанностей на периферии плав-

анализ, данное условие позволяет находить крити-

ных распределений поля. В конечном счете этот

906

ЖЭТФ, том 161, вып. 6, 2022

Особенности динамики самовоздействия волновых пакетов. ..

процесс распространяется на центральную часть

12.

A. A. Balakin, A. G. Litvak, V. A. Mironov, and

волнового пучка. При дальнейшем увеличении

S. A. Skobelev, Quant. Electr. 48, 720 (2018).

амплитуды поля интенсивность мелкомасштабной

13.

A. A. Balakin, A. G. Litvak, V. A. Mironov, and

неустойчивости увеличивается. Это означает, что

S. A. Skobelev, Laser Phys. 28, 045401 (2018).

волновые поля с амплитудой, превышающей крити-

ческое значение, теряют когерентность в процессе

14.

A. A. Balakin, A. G. Litvak, V. Mironov et al., Laser

распространения в дефокусирующей среде. Есте-

Phys. 28, 105401 (2018).

ственно ожидать нарушения плавной структуры

15.

O. Bang and P. D. Miller, Opt. Lett. 21, 1105 (1996).

поля и при распространении его в активной среде.

Такого рода нарушение когерентности наступает

16.

A. Trombettoni and A. Smerzi, Phys. Rev. Lett. 86,

катастрофическим образом.

2353 (2001).

17.

A. Smerzi, A. Trombettoni, P. G. Kevrekidis, and

Финансирование. Работа выполнена в Науч-

A. R. Bishop, Phys. Rev. Lett. 89, 170402 (2002).

ном центре мирового уровня «Центр фотоники»

при финансовой поддержке Министерства на-

18.

T. Anker, M. Albiez, R. Gati et al., Phys. Rev. Lett.

уки и высшего образования РФ (соглашение

94, 020403 (2005).

№075-15-2020-906).

19.

R. Franzosi, R. Livi, G.-L. Oppo, and A. Politi,

Nonlinearity 24, R89 (2011).

ЛИТЕРАТУРА

20.

H. Hennig and R. Fleischmann, Phys. Rev. A 87,

033605 (2013).

P. G. Kevrekidis, The Discrete Nonlinear Schrödinger

Equation: Mathematical Analysis, Numerical Compu-

21.

H. Hennig, T. Neff, and R. Fleischmann, Phys. Rev.

tations and Physical Perspectives, Springer Science &

E 93, 032219 (2016).

Business Media (2009).

22.

Дж. Уизем, Линейные и нелинейные волны, Мир,

C. Denz, S. Flach, Yu S. Kivshar et al., Nonlinearities

Москва (1977).

in Periodic Structures and Metamaterials, Springer

23.

Л. Д. Ландау, Е. М. Лифшиц, Гидродинамика,

(2010).

Физматлит, Москва (2001).

F. Lederer, G. I. Stegeman, D. N. Christodoulides et

24.

S. Trillo and M. Conforti, in Handbook of Optical Fi-

al., Phys. Rep. 463, 1 (2008).

bers, ed. by G.-D. Peng, Springer Singapore (2019),

Yu. V. Kartashov, B. A. Malomed, and L. Torner,

pp. 373-419.

Rev. Mod. Phys. 83, 247 (2011).

25.

А. М. Камчатнов, УФН 191, 52 (2021).

I. L. Garanovich, S. Longhi, A. A. Sukhorukov, and

26.

А. М. Камчатнов, ЖЭТФ 154, 1016 (2018).

Yu. S. Kivshar, Phys. Rep. 518, 1 (2012).

27.

A. M. Kamchatnov, Phys. Rev. E 99, 012203 (2019).

Э. Скотт, Нелинейная наука: рождение и разви-

тие когерентных структур, Физматлит, Москва

28.

M. Isoard, A. M. Kamchatnov, and N. Pavloff, Phys.

(2007).

Rev. A 99, 053819 (2019).

Э. Инфельд, Дж. Роуландс, Нелинейные волны,

29.

M. Isoard, A. M. Kamchatnov, and N. Pavloff, Euro-

солитоны и хаос, Физматлит, Москва (2005).

phys. Lett. 129, 64003 (2020).

J. Yang, Nonlinear Waves in Integrable and Noninte-

30.

S. Ivanov and A. Kamchatnov, Phys. Fluids 31,

grable Systems, SIAM (2010).

057102 (2019).

A. B. Aceves, C. De Angelis, T. Peschel et al., Phys.

31.

S. K. Ivanov and A. M. Kamchatnov, Phys. Fluids

Rev. E 53, 1172 (1996).

32, 126115 (2020).

10.

A. A. Balakin, A. G. Litvak, V. A. Mironov, and

32.

S. K. Ivanov, J.-E. Suchorski, A. M. Kamchatnov et

S. A. Skobelev, Phys. Rev. A 94, 063806 (2016).

al., Phys. Rev. E 102, 032215 (2020).

11.

А. Г. Литвак, В. А. Миронов, С. А. Скобелев,

33.

G. Xu, A. Mussot, A. Kudlinski et al., Opt. Lett. 41,

Л. А. Смирнов, ЖЭТФ 153, 28 (2018).

2656 (2016).

907