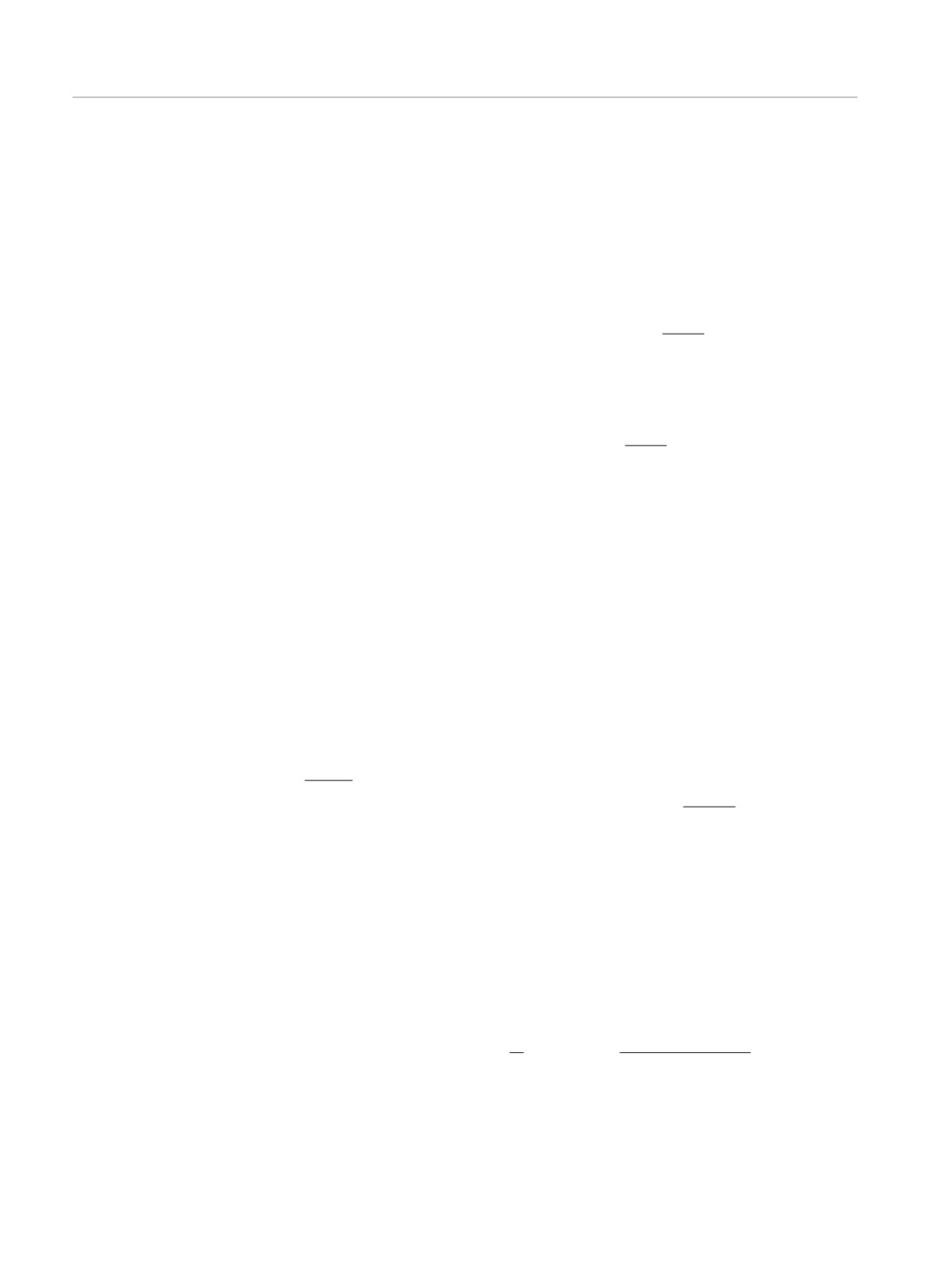ЖЭТФ, 2021, том 160, вып. 4 (10), стр. 498-507

ПРОЦЕССЫ ВТОРОГО ПОРЯДКА В ИЗЛУЧЕНИИ АНСАМБЛЯ

КВАНТОВЫХ ОСЦИЛЛЯТОРОВ

А. М. Башаровa,b*, А. И. Трубилкоc**

^a Национальный исследовательский центр «Курчатовский институт»

123182, Москва, Россия

^b Московский физико-технический институт (технический университет)

141701, Долгопрудный, Московская обл., Россия

^c Санкт-Петербургский университет ГПС МЧС России

196105, Санкт-Петербург, Россия

Поступила в редакцию 16 июня 2021 г.,

после переработки 16 июня 2021 г.

Принята к публикации 21 июня 2021 г.

Показано, что в локальном подходе к открытым осцилляторным системам, в случае наличия у ансамбля

одинаковых квантовых осцилляторов общего бозонного термостата, коллективное излучение ансамбля

осцилляторов демонстрирует признаки невинеровской динамики. Интенсивность излучения достаточно

большого числа Nc осцилляторов ансамбля уменьшается с ростом Nc и периодически оказывается полно-

стью подавленной процессами второго порядка по константе связи осцилляторов с общим термостатным

полем.

DOI: 10.31857/S0044451021100060

торную модель квантовой частицы [3] или предел

слабого возбуждения квантовой частицы, в кото-

ром атомный осциллятор математически описыва-

ется так же, как и квантовый осциллятор.

1. ВВЕДЕНИЕ

Эти основные квантовые объекты участвуют в

Под квантовым осциллятором мы понимаем од-

сходных процессах — рассматривают когерентные

номодовое электромагнитное поле в высокодоброт-

процессы, процессы возбуждения и релаксации, кол-

ном (микро)резонаторе и/или его описание, при-

лективные процессы в ансамблях, процессы запу-

чем о самом таком микрорезонаторе говорим как

тывания квантовых состояний. Все указанные про-

о квантовом осцилляторе. Например, можно гово-

цессы, в зависимости от типа осцилляторов, име-

рить об эффективном квантовом осцилляторе резо-

ют свои четкие отличия и особенности, определя-

натора с движущимся зеркалом [1]. Излучение и на-

емые алгеброй операторов, описывающих осцилля-

качка квантового осциллятора есть взаимодействие

торы. Есть различия и в реализации ансамбля ос-

электромагнитного поля (микро)резонатора с ваку-

цилляторов того или иного типа. Если атомные ос-

умным электромагнитным полем и/или с когерент-

цилляторы — просто примесные квантовые части-

ным полем на границе микрорезонатора или на зер-

цы, частицы в газообразном состоянии, то предста-

кале. С общетеоретической точки зрения, одномодо-

вить реализацию ансамбля квантовых осцилляторов

вый микрорезонатор и N-уровневая квантовая ча-

аналогично ансамблю одинаковых квантовых час-

стица являются двумя основными объектами кван-

тиц несколько сложнее. Ансамбль одинаковых ато-

товой оптики, о которых и говорят соответствен-

мов (квантовых частиц) взаимодействует с общим

но как о квантовом осцилляторе и атомном осцил-

электромагнитным полем. Чтобы такое реализовать

ляторе [2]. Часто вообще рассматривают осцилля-

в виде ансамбля квантовых осцилляторов и считать

их взаимодействующими с одним и тем же вакуум-

^* E-mail: basharov@gmail.com

ным электромагнитным полем и/или когерентным

^** E-mail: trubilko.andrey@gmail.com

полем, необходимо рассматривать различные искус-

498

ЖЭТФ, том 160, вып. 4 (10), 2021

Процессы второго порядка в излучении ансамбля...

ственные среды, например, пучок световодов, со-

нако не всегда это разделение можно просто и на-

единенных с одним общим световодом; направлен-

глядно провести.

ные ответвители; квантовые точки в диэлектриче-

Обычно антивращающие слагаемые просто отб-

ской среде и иные искусственные объекты. Взаи-

расывают, говоря о приближении вращающейся вол-

модействие ансамбля осцилляторов с единым воз-

ны. При этом выделенный квантовый осциллятор и

буждением можно также реализовать в резонато-

представляет собой открытую систему, которая на

рах с общим движущимся зеркалом и рассматри-

границе (зеркале в случае резонатора) взаимодей-

вать различные оптомеханические системы. Изуче-

ствует с окружением. Рассматривая осциллятор как

ние ансамбля одинаковых квантовых осцилляторов

открытую систему, важно считать все константы

востребовано в задачах построения многокубитного

взаимодействия осциллятора малыми. Еще в работе

квантового процессора.

[17] было обнаружено, что именно в приближении

вращающейся волны получаются корректные кине-

В настоящее время ведутся интенсивные иссле-

тические уравнения для описания распада кванто-

дования различных систем квантовых осцилляторов

вого осциллятора. Однако до сих пор открыт вопрос

[4-12]. Мы не будем в дальнейшем говорить о кон-

о корректном учете антивращающих слагаемых в

кретной реализации ансамбля одинаковых кванто-

кинетическом уравнении для квантового гармониче-

вых осцилляторов, а обсудим эффекты, родствен-

ского осциллятора. Решение этого вопроса позволит

ные обнаруженным авторами эффектам в случае

также записывать кинетические уравнения, учиты-

ансамбля атомных осцилляторов. Речь, в первую

вающие антивращающие слагаемые, и для ангармо-

очередь, пойдет об эффекте, аналогичном эффек-

нического осциллятора, и для других осциллятор-

ту стабилизации возбужденных состояний локали-

ных моделей [4-12, 18-20].

зованного атомного ансамбля одинаковых атомов по

Подчеркнем, что с математической точки зре-

отношению к коллективному распаду. С точки зре-

ния, квантовые осцилляторы, взаимодействующие

ния математического описания подобных эффектов,

между собой и/или с окружением, описываются

в статье выводится релаксационный оператор, вхо-

квадратичным гамильтонианом по бозонным опера-

дящий в стандартное кинетическое уравнение, по-

торам (в случае бозонного окружения), который мо-

лучаемое в марковском приближении. При этом мы

жет быть диагонализован в рамках глобального под-

не обсуждаем случай ангармонизма у квантового ос-

хода к открытым системам [21, 22], например, при

циллятора (с точки зрения математического описа-

помощи преобразования Боголюбова. В результате

ния коллективного распада, здесь релаксационный

можно получить весьма общие, но громоздкие фор-

оператор неизменен), и все рассматриваемые кван-

мулы, и проблемой будет являться их анализ, так

товые осцилляторы считаются гармоническими.

что для рассматриваемого в данной статье случая

Заметим, что задачи о взаимодействии квантово-

результатов, следующих из глобального подхода, по-

го осциллятора с широкополосным вакуумным элек-

ка нет. Однако требование малости констант взаи-

тромагнитным полем, иначе релаксация или распад

модействия позволяет в анализе осцилляторных си-

возбужденных состояний осциллятора, всегда рас-

стем прибегнуть к локальному подходу, который

сматривают в приближении вращающейся волны,

проще и нагляднее глобального подхода подчерки-

отбрасывая антивращающие слагаемые. Самое про-

вает общность локального подхода к анализу раз-

стое представление о вращающих и антивращающих

личных по природе квантовых открытых систем и

слагаемых дает алгебраическая теория возмущений

позволяет увидеть новые именно физические зако-

[13-15]. В представлении взаимодействия оператор

номерности, которые, быть может, и содержатся в

взаимодействия открытой системы с окружением

общих формулах глобального подхода, но о которых

и/или с элементами самой открытой системы всегда

на данный момент пока ничего не известно.

содержит два типа слагаемых. Одни из них явля-

ются медленно меняющимися функциями по срав-

Когда мы говорим об общности локального под-

нению с величинами типа exp(±iΩt), где Ω — харак-

хода к теории открытых квантовых систем, мы име-

терная частота открытой системы. Такие слагаемые

ем в виду следующее. Оптические открытые кванто-

удобно называть вращающими слагаемыми (геомет-

вые системы обладают такой принципиальной осо-

рическую интерпретацию см. в [16]). Другие слага-

бенностью, что оператор их взаимодействия с окру-

емые называют антивращающими слагаемыми. Та-

жением всегда содержит вращающие и антивраща-

кое разделение слагаемых в операторе взаимодейст-

ющие слагаемые. В работах [13-15] развита алгеб-

вия сохранится и в представлении Шредингера, од-

раическая теория возмущений применительно к за-

499

А. М. Башаров, А. И. Трубилко

ЖЭТФ, том 160, вып. 4 (10), 2021

дачам учета антивращающих слагаемых, а в рабо-

dρ^S (t)

[

]

ρ^S(t), H^S

= -^Γρ^S (t),

тах [23-29] показано, как алгебраическая теория воз-

ℏ

[

]

мущений сочетается с техникой квантовых стохасти-

^Γρ^S (t) = -

ρ^S(t), H^L-S

ческих дифференциальных уравнений для получе-

ℏ

)

⁽1

ния эффективного гамильтониана задачи и кинети-

+χ

L₊L_-ρ^S(t)+

ρ^S(t)L₊L_--L_-ρ^S

(t)L₊

(1)

ческого уравнения. Более того, в работах [24,27] до-

казана необходимость использования эффективного

Различия релаксационных операторов определяют-

гамильтониана (вместо полного гамильтониана) от-

ся алгеброй операторов Линдблада L_±, входящих

крытой системы и ее окружения в оптических зада-

в уравнение (1). В винеровском [24] описании ди-

чах для возможности описания окружения откры-

намики ансамбля под операторами L_± следует по-

той системы белым шумом. Однако в случае локаль-

нимать коллективные повышающий и понижающий

ного подхода авторам до сих пор не известен способ

операторы R_± всей системы, отвечающие комму-

корректного учета антивращающих слагаемых в ре-

тационным соотношениям операторов углового мо-

лаксации осцилляторных моделей открытых кван-

мента. Динамика излучения коллектива осциллято-

товых систем. Авторы продемонстрировали нагляд-

ров описывается коллективными операторами рож-

ность и эффективность локального подхода на осно-

дения и уничтожения. Оператор H^L-S определяет

ве алгебраической теории возмущений в выделении

сдвиги энергии уровней открытой системы, обуслов-

интерференционных слагаемых в задачах о возбуж-

ленные релаксационными переходами. В подавля-

дении и распаде изолированных (нерезонансно свя-

ющем большинстве работ оператор H^L-S кладется

занных с другими) осцилляторов [25, 26, 28, 29], ко-

равным нулю, поскольку авторы не выходят за рам-

торые еще не выделены из общих решений глобаль-

ки винеровской динамики. Эффективный гамильто-

ного подхода.

ниан открытой системы H^S введен для учета других

В ряде работ рассматривалось коллективное из-

возможных взаимодействий. Однако надо помнить,

лучение ансамбля квантовых осцилляторов в при-

что любые новые взаимодействия, как правило, по-

ближении вращающейся волны. Для сравнения со

рождают и новые интерференционные каналы ре-

случаем атомных осцилляторов напомним известное

лаксации [24], и весь вопрос состоит только в том,

обстоятельство в модели Дике — отсутствие посто-

насколько они значимы для данной задачи.

янного дипольного момента как всей атомной систе-

Мы показали, что коллективное излучение ан-

мы, так и каждого излучателя. Импульс коллектив-

самбля квантовых осцилляторов, рассматриваемых

ного излучения возникает с задержкой во времени.

как открытая система, может быть полностью по-

Возможный всплеск и импульс коллективного излу-

давлено в модельном случае, когда все осцилляторы

чения осцилляторов, которые ассоциированы в рам-

взаимодействуют с общим вакуумным электромаг-

ках классической электродинамики излучателями,

нитным полем, а число самих осцилляторов в ан-

следует ожидать только в моменты времени, отвеча-

самбле достаточно велико. Подавление возникает в

ющие образованию системы сфазированных осцил-

результате учета антивращающих слагаемых, кото-

ляторов. Такое оказывается возможным, только в

рые проявляются в алгебраической теории возмуще-

изначально пусть даже слабых, но нелинейных си-

ний в виде слагаемых эффективного гамильтониа-

стемах [30,31]. Для случая системы линейных кван-

на, квадратичных по параметру связи осциллятора

товых осцилляторов увеличение интенсивности ока-

с общим квантованным электромагнитным вакуум-

зывается возможным только при условии изначаль-

ным полем. В уравнении (1) это отражается в появ-

но сфазированных осцилляторов, при этом макси-

лении у операторов L_± невинеровского множителя,

мум интенсивности сверхизлучательного импульса

осциллирующего с изменением числа осцилляторов.

наблюдается только в начальный момент времени

Кроме того, коллективные релаксационные перехо-

излучения и никакой задержки импульса не возни-

ды определяют специфический частотный сдвиг ос-

кает. Динамика как ансамбля атомов модели Дике,

цилляторов H^L-S = 0, величина которого сосчита-

так и ансамбля квантовых осцилляторов описывает-

на.

ся единым квантовомеханическим уравнением для

матрицы плотности ρ^S системы, называемой откры-

2. ПОСТАНОВКА ЗАДАЧИ И

той, с релаксационным оператором

^Γρ^S (t) одного и

ЭФФЕКТИВНЫЙ ГАМИЛЬТОНИАН

того же вида (ρ^S(t) — матрица плотности открытой

системы в представлении взаимодействия, на что

Пусть имеется ансамбль независимых друг от

указывает явное написание аргумента времени):

друга одинаковых квантовых осцилляторов часто-

500

ЖЭТФ, том 160, вып. 4 (10), 2021

Процессы второго порядка в излучении ансамбля...

ты Ω_c в количестве N_c. Эти осцилляторы взаимодей-

няет, только уравнение Шредингера для преобразо-

ствуют с общим вакуумным квантованным электро-

ванного вектора состояний |Ψ(t)〉 определяется пре-

магнитным полем нулевой плотности фотонов, так

образованным гамильтонианом

^H(t):

что вся система описывается уравнением Шредин-

d|Ψ(t)〉

гера с гамильтонианом H:

iℏ

= H(t)|Ψ(t)〉,

(3)

d|Ψ〉

H(t)=

T (t)V (t

T^†(t) - i

T (t)

T^†(t),

iℏ

= H|Ψ〉,

∫

∑

где V (t) — оператор взаимодействия в представле-

H = ℏΩ_cc^†ic_i + ℏωb^†ωb_ωdω +

(2)

нии взаимодействия.

i=1

∫

Алгебраическая теория возмущений строится на

∑

+γ_c

(c_i + c^†i)(b_ω + b^†ω) dω.

разложении генератора унитарного преобразования

S(t) и генератора сдвига системы во времени

^H(t)

в ряд по константе связи γ_c. При этом использу-

Здесь |Ψ〉 — вектор состояний ансамбля осцилля-

ются формула Бейкера - Кемпбелла - Хаусдорфа и

торов и окружающего поля, c^†i и c_i — операторы

условие отсутствия быстро меняющихся во времени

рождения и уничтожения квантов i-го осциллятора

[

]

слагаемых по сравнению с exp(±iΩ_ct). Это процеду-

с коммутационными соотношениями

c_i, c^†j

= δ_i,j,

[

]

ра неоднократно проделывалась в работах авторов

c_i, c_j

= 0, b^†ω и b_ω — операторы рождения и уни-

[1, 24-29] поэтому приводим результаты:

чтожения квантов вакуумного квантованного элект-

∫

ромагнитного поля с коммутационными соотноше-

∑

c_jb_ω exp[i(ω + Ω_c)t] dω

[

]

S⁽¹⁾(t) = γc

ниями

b_ω, b^†ω′

= δ(ω - ω^′), γ_c — константа связи

iℏ(ω + Ω_c)

квантового осциллятора с вакуумным полем.

ω∈(-Ωc)

∫

С точки зрения терминологии квантовой теории

∑

c^†jb_ω exp[-i(ω - Ω_c)t] dω

+γ_c

(4)

открытых систем, ансамбль независимых друг от

iℏ(ω - Ω_c)

друга одинаковых квантовых осцилляторов пред-

ω∈(Ωc)

ставляет собой открытую систему, если константы

∑

∫ (

H (1)

связи γ_c малы, а общее вакуумное квантованное

(t) = γ_c

c_jb^†ω exp[-i(Ω_c-ω)t] +

электромагнитное поле является окружением от-

ω∈(Ωc)

)

крытой системы. Уравнение Шредингера и гамиль-

+ c^†jbω exp[i(Ω_c - ω)t] dω,

тониан (2) записаны в представлении Шрединге-

ра, однако в дальнейшем при выводе кинетического

∫

∑

dω

H (2)(t)=-γ2

c^†cj

уравнения удобно преобразования проводить в пред-

ℏ(ω + Ω_c)

ставлении Дирака [24].

j=1

ω∈(-Ωc)

(5)

⎛

Наша задача — вывести кинетическое уравнение

∫

для ансамбля осцилляторов. Его вид в марковском

⎜

b^†ωb_ω′ exp[i(ω - ω^′)t] dω dω^′

-γ2cN_c

⎝

приближении — общий вид Линдблада (1) кинети-

2ℏ(ω + Ω_c)

ω,ω^′∈(Ωc)

ческого уравнения открытых систем. В локальном

⎞

подходе для вывода кинетического уравнения необ-

∫

b^†ω′ bω exp[i(ω^′ - ω)t] dω^′dω⎟

ходимо сначала получить эффективный гамильто-

⎠.

2ℏ(ω + Ω_c)

ниан задачи, не содержащий в представлении взаи-

ω,ω^′∈(Ωc)

модействия быстро меняющихся во времени слагае-

Здесь через (Ω_c) обозначена частотная область спек-

мых, иначе приближение белого шума для вакуум-

тра частот окружения открытой системы вблизи

ного поля окажется некорректным [17]. Самый прос-

центральной частоты ω = Ω_c. Для частот ω из этой

той и универсальный способ получения эффектив-

области экспоненты exp[±i(ω - Ω_c)t] являются мед-

ного гамильтониана — алгебраическая теория воз-

ленно меняющими функциями времени по сравне-

мущений, основанная на унитарном преобразовании

нию с exp (±iΩ_ct). Ширина области (Ω_c) определя-

вектора состояния |Ψ〉 и гамильтониана H:

ется скоростью затухания фотонов в микрорезона-

|Ψ(t)〉 =

T (t)|Ψ(t)〉,

T (t) = eiS(t), S^†(t) = S(t).

торе в случае, когда открытая система состоит из

одного квантового осциллятора. Мы распространи-

С точки зрения описания открытой системы и ее

ли область суммирования по частотам непрерывно-

окружения, унитарное преобразование ничего не ме-

го спектра окружения, положив b_-ω = b^†ω, ω > 0, но

501

А. М. Башаров, А. И. Трубилко

ЖЭТФ, том 160, вып. 4 (10), 2021

при этом исключили из области интегрирования би-

нитного поля. Вакуумное поле, как обычно, дель-

линейных по операторам b^†ω, b_ω′ слагаемых все дру-

та-коррелированное поле, т. е.

гие области, согласно общему анализу [24].

〈Ξ₀|b_ω|Ξ₀〉 = 〈Ξ₀|b^†ω|Ξ₀〉 = 〈Ξ₀|b^†ωb_ω′ |Ξ₀〉 = 0,

Выписанные слагаемые представляют собой пер-

(7)

вый и второй порядки разложения генераторов по

〈Ξ₀|b_ωb^†ω′ |Ξ0〉 = δωω′ ,

константе связи. Эффективный гамильтониан с точ-

и с нулевой плотностью квантов.

ностью до первого порядка по константе связи есть

При условиях (7), независимости константы свя-

H (1)(t),

зи γ_c от частот (в (2) мы ее сразу вынесли за знак

H^eff (t) =

интеграла) и дополнительном предположении о сле-

дующем виде слагаемого (5) эффективного гамиль-

и именно он используется в теориях взаимодействия

тониана:

вакуумного электромагнитного поля с квантовы-

ми осцилляторами. Алгебраическая теория возму-

H (2)(t)=-γ2

N_c ×

щений накладывает жесткие ограничения на фор-

∫

мально введенное приближение вращающейся вол-

b^†ωb_ω′ exp[i(ω - ω^′)t] dω dω^′

(8)

ны, состоящие в требовании суммирования по часто-

2ℏΩ_c

там в формуле (4) только по области (Ω_c). Выход за

ω,ω^′∈(Ωc)

рамки таких ограничений приводит в ряде задач к

уравнение Шредингера (3) с

^H(t) = H^eff (t) стано-

«парадоксам» типа нарушения второго начала тер-

вится математически неопределенным [33, 34]. Его

модинамики [32].

принято доопределять, вводя стохастические ин-

Эффективный гамильтониан с точностью до вто-

тегралы Ито в формальном решении уравнения

рого порядка по константе связи есть

Шредингера, выраженном через оператор эволюции

U (t, t₀) и T -экспоненту:

H (1)(t)+ H(2)(t).

H^eff (t) =

(6)

(

)∫ t

(

)₂

В представленном виде эффективный гамильтони-

U (t, t₀) = I +

H^eff (t^′)dt^′ +

ан с точностью до второго порядка алгебраической

ℏ

теории возмущений ранее не рассматривался. В за-

∫

t^′

дачах, в которых фигурируют две константы взаи-

модействия, например, «изолированный» микроре-

H^eff (t^′)H^eff (t^′′)dt^′dt^′′ + . . . =

зонатор, нерезонансно связанный с микрорезонато-

⎛

⎞

ром, мода которого затухает вследствие потерь на

∫

←

зеркалах, слагаемые второго порядка алгебраиче-

=T exp⎝-

H^eff (t^′)dt^′⎠,

ℏ

ской теории возмущений описывали интерференци-

онный канал релаксации и накачки «изолированно-

го» осциллятора [28, 29]. Учет слагаемого (6) и его

|Ψ(t)〉 = U(t, t₀)|Ψ₀〉.

роль в динамике ансамбля одинаковых квантовых

В условиях (7) и (8) естественно ввести следу-

осцилляторов обсудим ниже.

ющие операторы квантовых уничтожающего B(t),

рождающего B⁺(t) и считывающего Λ(t) процессов

[35-37]:

3. КИНЕТИЧЕСКОЕ УРАВНЕНИЕ ДЛЯ

АНСАМБЛЯ ОДИНАКОВЫХ КВАНТОВЫХ

∫t

ОСЦИЛЛЯТОРОВ

dB(t) = B(t + dt) - B(t), B(t) = b(t^′) dt^′,

Пусть преобразованный вектор состояния ан-

(9)

∫∞

самбля одинаковых квантовых осцилляторов и его

b(t) =

√

dω exp [-i(ω - Ω_c)t] b_ω,

окружения в начальный момент времени фактори-

2π

-∞

зован:

|Ψ0〉 = |Φ₀〉 ⊗ |Ξ₀〉.

∫

Здесь |Φ₀〉 — начальный вектор состояния ансамбля

Λ(t) = dt^′b^†(t^′)b(t^′),

(10)

квантовых осцилляторов, |Ξ₀〉 — начальный вектор

состояния вакуумного квантованного электромаг-

dΛ(t) = Λ(t + dt) - Λ(t).

502

ЖЭТФ, том 160, вып. 4 (10), 2021

Процессы второго порядка в излучении ансамбля...

Физическое обоснование замен пределов интегриро-

Из разложения экспоненты (13) в ряд с уче-

вания см. в [33,34,37]. Под дифференциалом пони-

том всех членов разложения и алгебры (11) сле-

мается дифференциал в смысле Ито [33-37]. В вы-

дует более привычный вид стохастического диффе-

ражениях (9), (10) и ниже считаем время и частоты

ренциального уравнения для оператора эволюции,

безразмерными, пока не будет оговорено о возврате

используя который стандартным образом [24], нахо-

к размерному времени.

дим искомое кинетическое уравнение. Кинетическое

Дифференциалы (9) и (10) удовлетворяют сле-

уравнение, как и все в марковском приближении,

дующей алгебре Хадсона - Партасарати:

имеет вид (1) с операторами

∑

dΛ(t) dΛ(t) = dΛ(t), dB(t) dB⁺(t) = dt,

2πγ2c sinY_Λ - Y_Λ

H^L-S =

c^†

c_k,

ℏ²Ω_c

Y²

dΛ(t) dB⁺(t) = dB⁺(t), dB(t) dΛ(t) = dB(t),

j=1

k=1

dΛ(t) dB(t) = dΛ(t) dt = dB⁺(t) dΛ(t) =

(11)

∑

L_- =

c_j,

= dB⁺(t) dB(t) = dB⁺(t) dt = dB(t) dt =

Y_Λ

(16)

j=1

= dt dt = 0.

∑

1 - cosY_Λ

L₊L_- = 2

c^†

c_k,

При этом средние от дифференциалов Ито введен-

Y²

j=1

k=1

ных случайных процессов — нулевые:

Y e_Λ = exp(-iY_Λ) - 1, χ = 1.

(

)

(

)

Tr_env ρS+env

dB(t)

= Tr_env ρS+envdB⁺(t)

Подчеркнем, что с операторами и величинами (16)

(

)

кинетическое уравнение рассматривается как урав-

= Tr_env ρS+envdΛ(t)

= 0.

(12)

нение в безразмерных величинах.

Кинетическое уравнение (1) с операторами и

След берется по состоянию вакуумного электромаг-

величинами, определяемыми соотношениями (16),

нитного поля, ρS+env(t) = |Ψ(t)〉〈Ψ(t)| — преобразо-

описывает динамику ансамбля одинаковых, не за-

ванная матрица плотности системы квантовых ос-

висящих друг от друга квантовых осцилляторов,

цилляторов и окружения. Получение уравнения для

взаимодействующих с общим вакуумным широкопо-

ρS+env(t) и (путем указанной выше процедуры взя-

лосным электромагнитным полем с нулевой плотно-

тия следа) для ρ^S (t) — следующие этапы подхода

стью фотонов. В отличие от традиционных исследо-

к теории открытых квантовых систем на основе ал-

ваний, операторы (16) кинетического уравнения (1)

гебраической теории возмущений (унитарного пре-

получены с точностью до второго порядка по конс-

образования) и техники квантовых стохастических

танте связи γ_c. Оператор H^L-S и множители

дифференциальных уравнений.

Ye_Λ

sinY_Λ - Y_Λ

1 - cosY_Λ

Для нахождения кинетических уравнений запи-

Y_Λ, YeΛ,

(17)

Y_Λ

Y^2Λ

Y²

сываем стохастическое дифференциальное уравне-

ние для оператора эволюции. Используем следую-

входящие в соотношения (16), отличают получен-

щее представление:

ное кинетическое уравнение от традиционных урав-

нений. Мы говорим, что уравнение (1) с операто-

dU(t, t₀) = [exp(-iH^eff (t) dt) - 1]U(t, t₀),

(13)

рами (16) относится к уравнениям невинеровско-

го типа, поскольку учет второго порядка алгебра-

в котором эффективный гамильтониан в базовых

ической теории возмущений вводит в рассмотрение

квантовых процессах приобретает вид

квантовый считывающий процесс Λ(t). Множители

(17) называем невинеровскими множителями, а ди-

H^eff-S(t)dt = Y⁺dB(t)+Y dB⁺(t)+Y_ΛdΛ(t).

(14)

намику ансамбля квантовых осцилляторов, описы-

ваемую при помощи уравнения (1) и соотношений

В уравнениях (13) и (14) все величины безразмер-

(16), — невинеровской динамикой.

ные. Введены операторы

В отсутствие считывающего процесса YΛ ≡ 0

√

∑

невинеровские операторные множители равны

γ_c

2π

πγ2cN_c

Y =

c_j, Y_Λ = -

(15)

Ye_Λ

sinY_Λ - Y_Λ

ℏ

c j=1

Y e_Λ = 0,

= -i,

= 0,

Y_Λ

Время измеряется в единицах Ω-1c, частота — в еди-

1 - cosY_Λ

ницах Ω_c.

Y^2Λ

503

А. М. Башаров, А. И. Трубилко

ЖЭТФ, том 160, вып. 4 (10), 2021

что обеспечивает описание процессов в ансамбле

малого числа N_c осцилляторов в ансамбле наблюда-

одинаковых квантовых осцилляторов только с точ-

ется (должна наблюдаться) линейная зависимость

ностью до первого порядка по константе связи.

частот осциллятора от числа осцилляторов в ансам-

Заметим, что в классическом случае считываю-

бле. Если представить новое приближение эффек-

щий процесс представляет собой пуассоновский про-

тивной частоты осциллятора как

цесс. В квантовом случае винеровский W(t) и пуас-

соновский P (t) процессы взаимосвязаны и определя-

Ω^′′c = Ω_c + ΔΩ_c + ΔΩ_R,

(19)

ются рождающим, уничтожающим и считывающим

то

процессами по формулам

(

)

π²γ4c

W (t) = B(t)+B⁺(t), P (t) = Λ(t)+i B⁺(t)-B(t) .

ΔΩ_R ≈

N_c,

(20)

3ℏ⁴Ω

Говоря о невинеровской динамике, мы подчеркива-

хотя корректнее говорить о сдвиге частоты коллек-

ем, что не только винеровский процесс, но и пуассо-

тивного состояния или о коллективной энергии

новский процесс определяют такую динамику.

∑

π²γ4c

^L-S =

N_c

c^†

c_k.

(21)

3ℏ³Ω

4. КОЛЛЕКТИВНАЯ НЕВИНЕРОВСКАЯ

j=1

k=1

ДИНАМИКА ОСЦИЛЛЯТОРОВ

Видим, что направление коллективного сдвига про-

Проанализируем полученный эффективный га-

тивоположно лэмбовскому сдвигу ΔΩ_c.

мильтониан (6) со слагаемыми первого (4) и второго

В данной статье, применяя локальный подход

(5) порядков малости по константе связи и невине-

к теории открытых квантовых систем, мы пресле-

ровское кинетическое уравнение (1), определяемое

довали цель найти в ансамбле одинаковых кванто-

операторами (16). Одним из важнейших его отли-

вых осцилляторов аналоги новым эффектам, кото-

чий от традиционного уравнения является непосред-

рые ранее были обнаружены в коллективной атом-

ственное появление дополнительных к частоте Ω_c

ной динамике [24]. Помимо релаксационного сдви-

рассматриваемых квантовых осцилляторов двух ча-

га энергии коллективного состояния рассмотрим те-

стотных сдвигов. Один из них для ансамбля осцил-

перь проявление коллективной динамики осцилля-

ляторов из малого числа осцилляторов определя-

торов в явлении сверхизлучения ансамбля. Зависи-

ет новую эффективную частоту осциллятора Ω^′c =

мость интенсивности I(t) импульса сверхизлучения

= Ω_c + ΔΩ_c, где

такой системы от времени определяется следующим

∫

размерным выражением:

dω

ΔΩ_c = -γ2c

(18)

ω+Ω_c

d〈C^†C〉

ω∈(-Ωc)

I(t) = -ℏΩ_c

(22)

Это — аналог лэмбовского сдвига энергии уровней

где динамика среднего от оператора числа возбуж-

для атомов. В случае осцилляторов сдвиг проис-

дений коллектива осцилляторов

ходит в длинноволновую область. Для корректнос-

ти выражения необходимо учесть исходную зависи-

∑

мость параметра связи γ_c от частоты и внести ее под

〈C^†C〉 =

〈c^†jc_j 〉,

знак интеграла.

j=1

Но помимо аналога лэмбовского сдвига есть и

следует уравнению, полученному усреднением на-

коллективный сдвиг энергии уровней осцилляторов,

званного оператора, и, согласно уравнению (1), име-

зависящий от числа осцилляторов в ансамбле. По-

ем

скольку этот сдвиг определяется слагаемым H^L-S

в релаксационном операторе (1), (16), его естествен-

1 - cos(γ2cN_c/2Ω2c)

〈C^†C〉 = -γc

〈C^†C〉.

(23)

но назвать коллективным релаксационным сдвигом.

(γ2cN_c/2Ω2c)²

Авторам не известны работы, в которых бы кол-

лективный релаксационный сдвиг для осцилляторов

При записи двух последних выражений мы вновь

вычислялся и обсуждался. Авторам также не из-

вернулись к размерному времени. Решение приве-

вестны работы, выполненные в рамках глобально-

денного уравнения имеет отличительные особенно-

го подхода, где подобное явление обсуждалось. Для

сти, характерные для невинеровской динамики. Так,

504

ЖЭТФ, том 160, вып. 4 (10), 2021

Процессы второго порядка в излучении ансамбля...

константа распада γ_c по сравнению с обычной ви-

неровской динамикой приобретает дополнительный

осциллирующий множитель

1 - cos(γ2cN_c/2Ω2c)

(γ2cN_c/2Ω2c)²

зависящий от числа квантовых осцилляторов в ан-

самбле. Нетрудно видеть, что при определенных

значениях числа осцилляторов в ансамбле, Nc =

= 2nπ2Ω2c/γ2c, n

= 1, 2, 3, . . ., константа коллек-

тивной релаксации принимает значение, в точности

равное нулю. В этих ситуациях невинеровская ди-

намика ансамбля, производимая эффектами, учи-

тывающими второй порядок по взаимодействию ан-

самбля и вакуумного окружения и характеризуемая

учетом антивращающих слагаемых в операторе вза-

Рис. 1. Нормированное среднее число возбуждений ан-

имодействия, приводит к тому, что скорость кол-

самбля одинаковых квантовых осцилляторов. Время t —

безразмерная величина

лективной релаксации ансамбля обращается в нуль

и замораживается возбужденное состояние ансам-

бля осцилляторов. Этот эффект обусловлен кван-

товой интерференцией различных каналов взаимо-

случайным распределением фаз осцилляторов зна-

действия системы с окружением — квантовых пе-

чение среднего 〈C^†C〉₀ ∝ N_c, поскольку в этом слу-

реходов в системе с излучением реального кванта

чае 〈C^†〉₀ ∝ 〈C〉₀ ∝

√N_c.

и переизлучением виртуальных квантов с сохране-

На рис. 1 представлены графики зависимости

нием энергетического состояния открытой системы.

нормированного среднего числа возбуждений

Реальные переходы описываются квантовыми уни-

чтожающим B(t) и рождающим B⁺(t) процессами,

f (t, N_c) = 〈C^†C〉/〈C^†C〉₀

а переизлучение — считывающим процессом Λ(t).

Они имеют различные алгебраические свойства (см.

в зависимости от времени и числа осцилляторов в

соотношения алгебры Хадсона - Партасарати (11)).

системе. Среднее число возбуждений носит осцил-

Своеобразную интерференцию описывает считыва-

ляционный характер в зависимости от числа осцил-

ющее свойство dΛ(t) dB⁺(t) = dB⁺(t). Такая ин-

ляторов ансамбля. С увеличением числа последних

терпретация была дана ранее на примере ансамбля

среднее число возбуждений практически не меняет

атомных осцилляторов [24].

своего значения во времени, что определяется уче-

Решение уравнения (23), определяющее и вид

том процессов второго порядка по константе связи.

импульса сверхизлучения во времени,

Это — новый эффект, не встречающийся в теории

⎛

(

)

⎞

сверхизлучения ансамбля осцилляторов при приме-

γ2cN_c

1 - cos

нении обычного описания в рамках традиционной

⎜

⎟

⎜

2Ω²

⎟

〈C^†C〉 = 〈C^†C〉₀ exp

-γ_c

теории резонансного взаимодействия ансамбля с ва-

⎜

)₂

⎟

⎝

⁽γ2cN_c

⎠

куумным окружением в приближении вращающей-

2Ω²

ся волны.

На рис. 2 приведены графики зависимости нор-

существенным образом зависит от начального состо-

мированной интенсивности

яния осцилляторов, определяемого средним 〈C^†C〉₀,

или от способа приготовления коллективной систе-

I(t, N_c)

мы. Как и в случае винеровской динамики, значе-

g(t, N_c) =

ℏΩ_cγ_c〈C^†C〉₀

ние интенсивности оказывается пропорциональным

квадрату числа осцилляторов N2c только для слу-

импульсов сверхизлучения в зависимости от време-

чая сфазированно-приготовленного начального со-

ни и числа осцилляторов в системе. Видно, что мак-

стояния, когда 〈C^†C〉0 ∝ N2c. Для такого состоя-

симальное значение интенсивности отвечает именно

ния для средних справедливы соотношения 〈C^†〉₀ ∝

начальному моменту времени, что отличает систе-

∝ 〈C〉₀ ∝ N_c. В случае приготовления системы со

му квантовых осцилляторов от системы атомных ос-

505

ЖЭТФ, вып. 4 (10)

А. М. Башаров, А. И. Трубилко

ЖЭТФ, том 160, вып. 4 (10), 2021

A. I. Maimistov, Nonlinear Phenom. Complex Syst.

J. 19, 358 (2016).

Y. Kivshar, Low Temp. Phys. 45, 1201 (2019).

N. B. Plougonven, C. Minot, G. Bouwmans, A. Le-

venson, and J.-M. Moison, Opt. Express 22, 12379

(2014).

Xun-Wei Xu, Ai-Xi Chen, Yong Li, and Yu-xi Liu,

Phys. Rev. A 95, 063808 (2017).

K. Li, U. Krishnamoorthy, J. P. Heritage, and O. Sol-

gaard, Opt. Lett. 27, 366 (2002).

M. Hasan, I. V. Iorsh, O. V. Kibis, and I. A. Shelykh,

Phys. Rev. B 93, 125401 (2016).

Рис. 2. Нормированная интенсивность коллективного из-

лучения ансамбля возбужденных квантовых осциллято-

10.

S. Schmidt and G. Blatter, Phys. Rev. Lett. 103,

ров. Время t — безразмерная величина

086403 (2009).

11.

J. Perczel, J. Borregaard, D. E. Chang, S. F. Yelin,

and M. D. Lukin, Phys. Rev. Lett. 124, 083603

цилляторов. Однако на зависимости g(t, N_c) от чис-

(2020).

ла осцилляторов N_c наблюдаются колебания, а так-

же уменьшение времени затухания ансамбля с уве-

12.

S. Rojas-Rojas, E. Barriga, C. Munoz, P. Solano, and

личением N_c. Эти особенности сходны с аналогич-

C. Hermann-Avigliano, Phys. Rev. A 100, 023841

ными эффектами в ансамбле атомных осциллято-

(2019).

ров.

13.

А. М. Башаров, А. И. Маймистов, Э. А. Маныкин,

Для указанных зависимостей мы не учитывали

ЖЭТФ 84, 487 (1983).

малый частотный сдвиг частоты осциллятора,

полагая, что Ω^′′c ≈ Ω_c. Для исследования сдвигов

14.

А. М. Башаров, Фотоника, Метод унитарно-

частоты (18) и (20) хорошо разработаны спектраль-

го преобразования в нелинейной оптике, МИФИ,

ные методы, а различные зависимости от числа

Москва (1990).

осцилляторов N_c в ансамбле позволят отделять

15.

A. I. Maimistov and A. M. Basharov, Nonlinear Op-

один тип частотного сдвига ΔΩ_c от другого ΔΩ_R.

tical Waves, Kluwer Acad., Dordrecht (1999).

Финансирование. Работа выполнена при

16.

Л. Аллен, Д. Эберли, Оптический резонанс и

частичной финансовой поддержке Российского

двухуровневые атомы, Мир, Москва (1978).

фонда фундаментальных исследований (грант

№19-02-00234a).

17.

D. F. Walls, Z. Phys. 234, 231 (1970).

18.

B. Nachtergaele, B. Schlein, R. Sims, S. Starr, and

V. Zagrebnov, Rev. Math. Phys. 22, 207 (2010).

ЛИТЕРАТУРА

19.

J.-T.Hsiang and B.-L. Hu, Phys. Rev. D 101, 125003

(2020).

1. А. И. Трубилко, А. М. Башаров, ЖЭТФ 159, 262

20.

T. Chen, V. Balachandran, C. Guo, and D. Poletti,

(2021).

Phys. Rev. E 102, 012155 (2020).

2. B. W. Shore and P. L. Knight, J. Mod. Optics 40,

21.

A. S. Trushechkin and I. V. Volovich, Europhys. Lett.

1195 (2003).

113, 30005 (2016).

3. Л. Мандель, Э. Вольф, Оптическая когерент-

22.

A. E. Teretenkov, Infinite Dimensional Analysis,

ность и квантовая оптика, Физматлит, Москва

Quantum Probability and Related Topics

22,

(2000).

1930001 (2019).

506