ЖЭТФ, 2021, том 160, вып. 4 (10), стр. 491-497

NON-TRIVIAL DYNAMIC REGIMES OF SMALL (NANO-SCALE)

QUANTUM SYSTEMS

V. A. Benderskii^a, E. I. Katsb*

^a Institute of Problems of Chemical Physics, Russian Academy of Sciences

142432, Chernogolovka, Moscow Region, Russia

^b Landau Institute for Theoretical Physics, Russian Academy of Sciences

142432, Chernogolovka, Moscow Region, Russia

Received May 18, 2021,

revised version May 24, 2021.

Accepted for publication May 24, 2021

DOI: 10.31857/S0044451021100059

sults in the temperature dependent broadening and de-

cay of the echo components. Another generalization is

Abstract. Small (but still containing many,

to replace a single level by two states coupled to the

about 10²-10⁴, atoms) quantum systems (tradition-

Zwanzig reservoir. We anticipate that the basic ideas

ally termed nano-systems) are dramatically different

inspiring our work can be applied to a large variety of

from their macroscopic or genuine microscopic (atomic)

interesting for the applications nano-systems (e. g., dis-

cousins. Microscopic molecular systems (with a few

sipative free propagation of excitations along molecular

atoms) obey a regular quantum dynamics (described

chains, or as a model for exchange reactions).

by time dependent Schrödinger equation), whereas in

macroscopic systems with continuous energy spectra,

Introduction. There are materials which do not

one can expect regular dynamic behavior. The topic

exhibit unusual properties in the nano-scale regime.

of our paper is in-between these limits. Nano-scale

For example, simple non-polar hydrocarbon molecules

systems are characterized by small (but finite) mean

when aggregated are added merely additively. In other

interlevel spacing. In such a case with recurrence pe-

systems, that are under investigation in this work, the

riods in picosecond range, Loschmidt echo and dou-

properties may exhibit anomalous values (or behavior

ble resonance phenomena come into the game. Sys-

of a system is unusual) in the nano-regime. Common

tem behavior becomes non-trivial and manifests a sort

wisdom borrowed from textbooks on quantum mechan-

of transitions between regular and chaotic dynamics.

ics teaches that a population of somehow initially pre-

We show that such dynamic transitions occur when the

pared state of a macroscopic system monotonically de-

Loschmidt echo lifetime exceeds the typical recurrence

creases in time due to the energy flow from this ini-

cycle period. We illustrate this behavior in the frame-

tial state into the states of the reservoir (formed by

work of a few versions of the exactly solvable quan-

all continuous states of the macroscopic system under

tum problem, proposed long ago by Zwanzig [1]. It is

consideration). In the opposite limit (a small system

based on the study of time evolution of the initially

with a few degrees of freedom), system behavior is also

prepared vibrational state coupled to a reservoir with

well known. The system dynamics is reduced to the

a dense spectrum of its vibrational states. In the sim-

recurrence cycles, with their periods (according to the

plest version of the Zwanzig model, the reservoir has

famous Poincare theorem) determined by the lowest ra-

an equidistant spectrum, and the system reservoir cou-

tionally independent interlevel spacings. As it is often

pling matrix elements are independent of the reservoir

the case, an intermediate case (relatively large but not

states. We generalize the model to include into con-

macroscopically large quantum system) is the most dif-

sideration the coupling of the initially prepared single

ficult one for theoretical analysis. However, just such

state to system phonon excitations. The coupling re-

systems (generically termed as nano-systems) contain-

ing about several hundreds of atoms become more and

^* E-mail: efim.i.kats@gmail.com

more attractive for various applications.

491

V. A. Benderskii, E. I. Kats

ЖЭТФ, том 160, вып. 4 (10), 2021

a_s

1.0

0.5

–0.5

–1.0

a_s

1.0

0.5

S₀

–0.5

–1.0

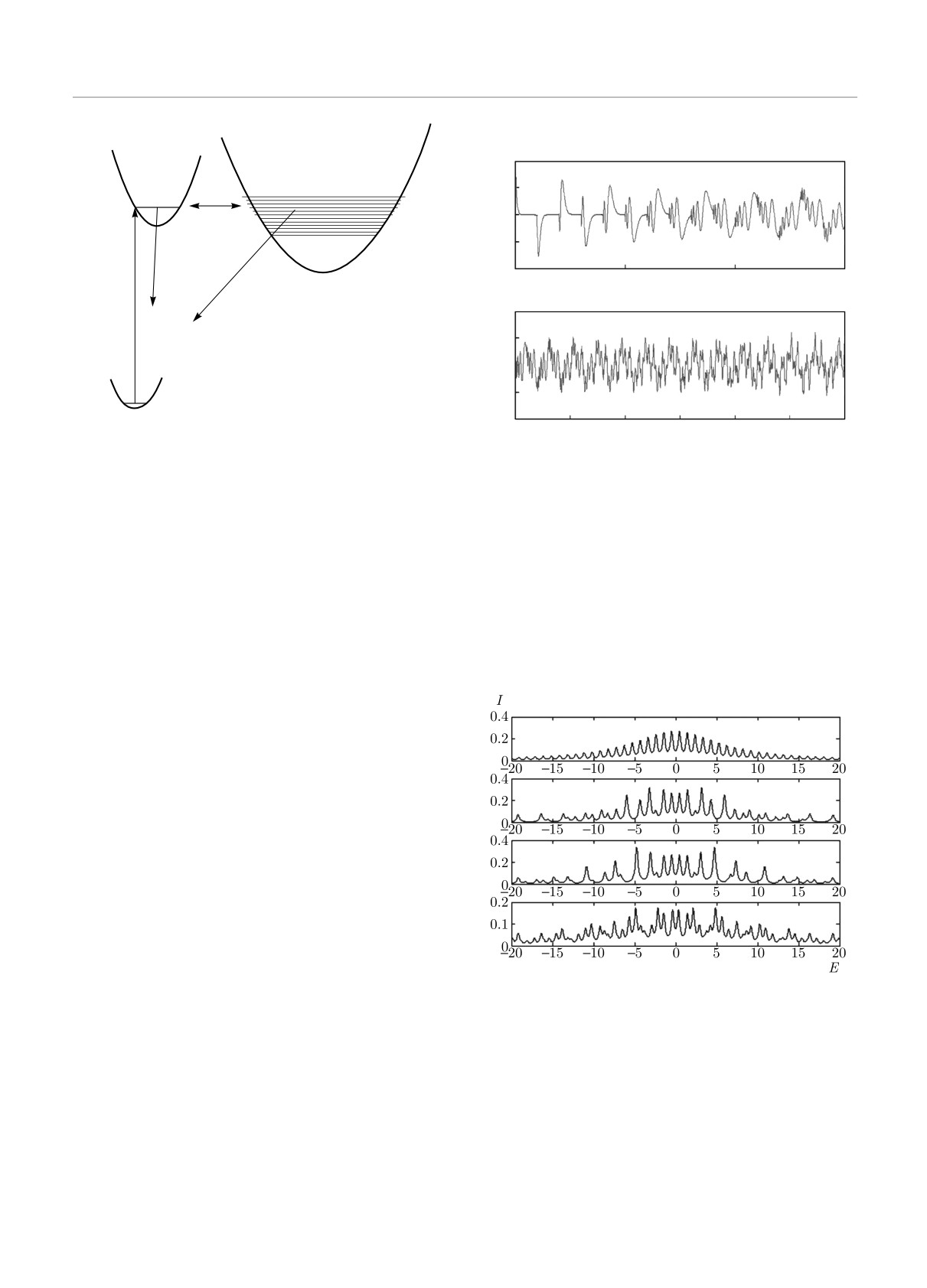
Fig. 1. Scheme of radiationless transitions {Rn} ← S accom-

panying by the optical transition S ← S0 from the ground to

initial state. Direct optical transitions {Rn} ← S0 are forbid-

Fig. 2. The initial state evolution for the bare Zwanzig model:

den. S is the state obtained by the optical pumping from the

as is the amplitude of the optically excited state, C is the SR

ground state S0, {Rn} are the final (reservoir) states, and ΓS

coupling constant, C² = 1, γs and γn are the widths of the

and ΓR are decay rates for the corresponding states

corresponding energy levels (in the figure, the both γ = 0).

Time is measured in the inverse interlevel spacing of the reser-

voir states. The upper panel shows the initial cycles with the

regular dynamics. The lower panel demonstrates chaotic-like

Our intent in this work is to investigate dynamic

long-time dynamics in the case of the overlapping recurrence

behavior of these intermediate nano-size quantum sys-

cycles

tems. In principle, the full information about the sys-

tem (both dynamics and statics) is naturally contained

in quantum mechanical solution of the corresponding

Schrödinger equation. In practice, however, the quan-

tum solution is unfeasible even for not too large (about

10²-10⁴ atoms) systems. Therefore, one has to rely

either on heavy ab initio numeric, or to look for ana-

lytically doable approximations. Luckily for us, many

years ago Robert Zwanzig in a remarkable work (al-

though published not in a regular and easy accessi-

ble journal [1]) proposed a simple (but not trivial) ex-

actly solvable model of quantum dynamics. Within

this model, an initially prepared single state of a quan-

tum system evenly couples to the dense but discrete

spectrum of the reservoir levels. Within the Zwanzig

model, the coupling strength is assumed to be a con-

stant independent of the reservoir levels. Surprisingly

enough that in spite of this evidently erroneous as-

sumption, Zwanzig approximation correctly identifies

Fig. 3. Crossover from the regular to quasi-random spectrum

the dynamic regimes and characteristic time scales in

of the mixed RS states upon the mixing deformation. I(E) is

the spectral density, and energy E is measured in the units of

the problem. Thus, although the Zwanzig model is a

the interlevel spacing; K is sublattices spectra regular splitting,

toy model (in the sense of caricaturing some physical

K = 3 in the computations; δ1 and δ2 are parameters which

features), when properly interpreted it can yield quite

determine the additional (with respect to regular) sublattices

reasonable values for a variety of essential (and prin-

splittings: δ1 = 0, 0.1, 0.4, 0.7 (from the top to the bottom),

cipally measured) quantities. That such a simple the-

and δ2 = 2δ1; C² = 0.1

ory can predict rather complex and subtle features for

nano-size quantum systems is remarkable.

492

ЖЭТФ, том 160, вып. 4 (10), 2021

Non-trivial dynamic regimes of small...

tems we have in mind. Our topic is nano-size quantum

objects, possessing discrete vibrational energy spectra.

Such objects are carbon nano-tubes, graphene flacks,

metallic clusters, some large organic molecules or their

clusters. Typical feature (relevant for everything what

follows in the paper) of such systems is that their vibra-

tional spectra are discrete and characteristic interlevel

spacing

Δ is on the order of 0.1-10 cm-1. This value

Δ is translated into the picosecond time scale for the

periods of the recurrence cycles

2π

T =

cΔ≃10-10-10-12 s^,

where c is the light speed. In turn, experimental stud-

ies of the excited state evolution in large (nano-size)

molecular systems [3-8] have established that the pro-

cesses of vibrational relaxation, energy transfer, and

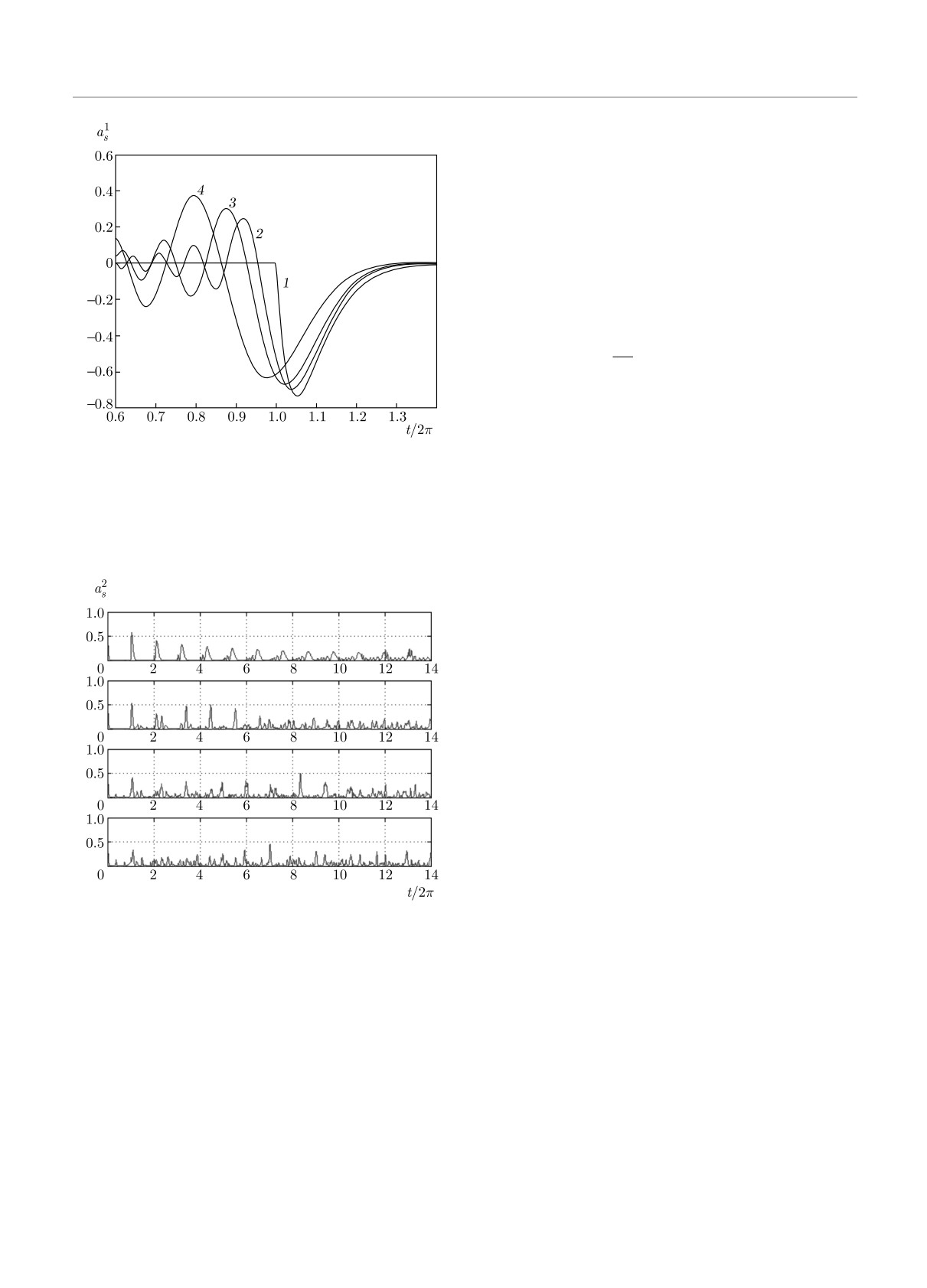
Fig. 4. Backward evolution of the initial state amplitude a1s

ultra-fast chemical reactions occur in the same picose-

for the cycle k = 1. The reservoir posses the increasing inter-

level spacings. C² = 1. The model parameters describing the

cond time range as recurrence cycles. Therefore, the re-

spectrum deformations are b = 0 and a = 0, 0.15, 0.25, 0.35

currence cycles are essential ingredients to be included

(curves 1-4, respectively)

to describe theoretically such features of the quantum

dynamics of nano-systems as irreversibility, chaotic be-

havior and loss-free distant energy transfer. These and

some other high-resolution experiments (which will be

cited and shortly discussed in our paper) demonstrate

that a system initial vibrational state evolution, as a

rule, has a complicated form with irregular oscillations.

The methods of double resonances in the non-linear

femtosecond spectroscopy [9-12] appear to be espe-

cially useful to observe these irregular oscillations of the

initial and final state populations simultaneously. The

phenomenon has been observed for the wide variety of

large-size molecules in liquid and solid solutions and on

interfaces [13-18]. Note to the point that irregular os-

cillations of the population of initially prepared excited

state have been confirmed by the numerous quantum

dynamical calculations [19-23].

The loss-free excitation energy transfer, observed

in linear molecules consisting of 12-26 CH₂ fragments

[20, 21], also belongs to a similar class of irregular in

Fig. 5. Time evolution of the initial state coupled to reservoir

time behavior. In such kind of experiments, the ini-

with spectral mixing for the cycle k = 1: C² = 1, K = 3,

tial excitation of the molecular terminal group pro-

δ2 = 2δ1, δ1 = 0, 0.019, 0.049, 0.079, a = 0, 0.15, 0.25, 0.5

(from the top to the bottom), and b = 0

duces the running wave with approximately constant

speed (about of 2 ps per one fragment). Even more

surprising is that instead of naively expected random

Here we compile a brief self-contained review that

distribution of the excitation energy over the total set of

we wish had existed when we first entered the field

intra-molecular modes, the wave propagation lasts dur-

[2]. In what follows in the frame work of generalized

ing several passages along the chain before the uniform

Zwanzig approach, we study a number of nano-size

distribution is established. The distant energy transfer

quantum systems. Since our work is primary about

occurs between localized vibrations of fragments sepa-

physics (and only then how it can be modeled theoret-

rated by about 1 nm distance during 20-40 ps whereas

ically), it is worth to note first what are physical sys-

the lifetime of these vibration excitations themselves

493

V. A. Benderskii, E. I. Kats

ЖЭТФ, том 160, вып. 4 (10), 2021

0.4

0.2

0.4

0.2

0.4

0.2

0.4

0.2

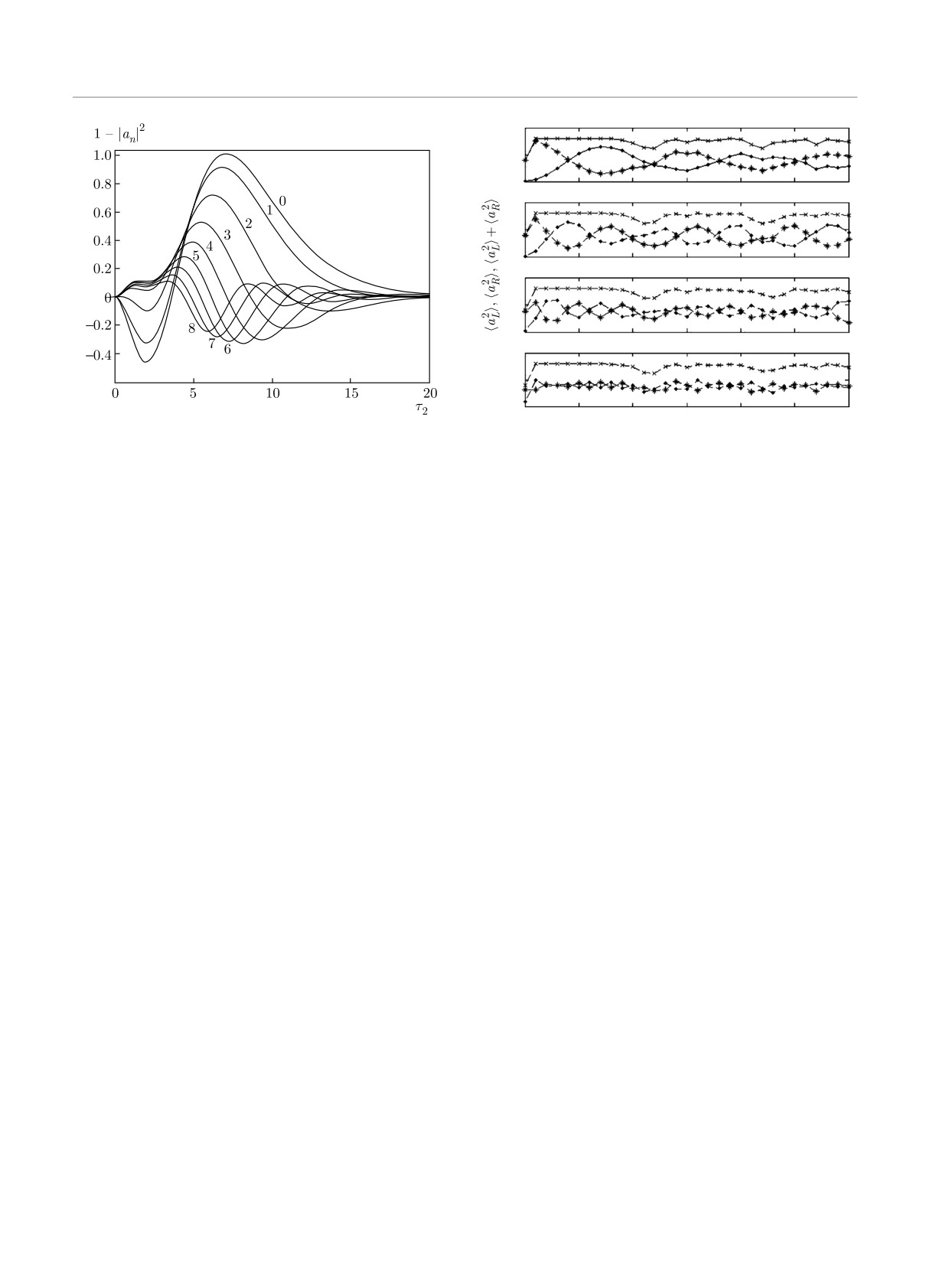
Fig. 6. Redistribution of the initial-state population over the

mixed reservoir states with the amplitudes an during the sec-

Fig. 7. Variation of the average per cycle populations of L0 (♦)

ond recurrence cycle k = 2 with duration τ2. The numbers of

and R0 (∗) states and the entire population of the two-level

the reservoir states are shown near the curves

systems (×) in the recurrence cycles versus the cycle num-

ber k: C² = 1 and the two-level splitting Δ = 0.4, 1.2, 2.7,

7.4 (from the top to the bottom)

does not exceed 3 ps. The matter is that the excita-

tion energy transfer includes intermediate excitations

of delocalized long-lived vibrations binding the initial

model. In these works, we also proposed a method

and final fragments [22-25].

which makes it possible to solve the dynamical prob-

These data permit to suggest that the irregular

lem analytically beyond the bare Zwanzig model ap-

evolution is the generic property of the systems with

proximations [27-32]. The main ingredient of our new

dense discrete spectra. Therefore, the role of the reser-

method (only schematically and briefly described in the

voir with a discrete spectrum is fundamentally differ-

previous papers) is the representation of the partial

ent from that with a continuous spectrum typical for

amplitudes of recurrence cycles. Unlike the standard

macroscopic systems. In the latter case (with the infi-

Fourier expansion over eigen-frequencies, this represen-

nite recurrence period time), the reservoir serves as a

tation reveals explicitly the time dependent exchange

sink for energy flow. Contrary in the case of the discrete

between intramolecular states in each recurrence cycle.

spectrum, repetitive reverse transitions from the reser-

The fine structure of the Loschmidt echo arises as a

voir to the initial state and in the opposite direction

result of the dephasing phenomena associated with the

determine the non-trivial and often irregular long-time

fact that the exchange of the different reservoir states

dynamics. The synchronization of these reverse tran-

with the initial state occurs not at the same instants

sitions results in the appearance of a multi-component

of time. The synchronization of the reverse transitions

Loschmidt echo phenomenon with a partial recovery

is destroyed when the Loschmidt echo components of

of the initial state population (at the frequency corre-

the different recurrence cycles start to overlap. The cy-

sponding to the initial excited state energy), and double

cle overlapping determines the critical recurrence cycle

resonances (at the frequencies of the reservoir states).

number. Then at larger time (cycle numbers), the sys-

Both effects are responsible for non-monotonic time

tem dynamics is expected to be in the stochastic-like

evolution. The counterpart of such behavior is the peri-

regime.

odic energy concentration in one of the vibration mode,

Since that time, we have realized that the quan-

arising as a result of the time-dependent exchange be-

tum dynamics of nano-size systems is much richer than

tween reservoir states far from equilibrium.

that predicted for the systems with continuous spec-

In a few of previous works of our group [2, 26-32],

tra, and that non-monotonous in time and irregular

we illustrated how such complex behavior might ap-

dynamics is a robust and generic feature of almost ar-

pear in the frame work of the simple Zwanzig model,

bitrary quantum system with 10²-10⁴ degrees of free-

and how the simplest version of the model can be gen-

dom. Moreover, the regular-stochastic dynamic transi-

eralized to relax some unphysical assumptions of the

tion (crossover) yields to a loss of the expected one-to-

494

ЖЭТФ, том 160, вып. 4 (10), 2021

Non-trivial dynamic regimes of small...

a₀

our method on a number of particular physical real-

izations (only partially overlapping with those in the

previous works). The aim to present this review arises

from the conviction that unifying our previous works

–1 0

supplemented by the new applications of the developed

theoretical approach and by new experimental data and

observations collected in very recent year, yield to a

–1 0

new stage of development of this field: dynamics of

nano-systems.

Our manuscript is divided into 7 sections. After this

Introduction, in Sec. 2 of the full text of this paper, we

–1 0

summarize shortly the results on quantum dynamics of

the bare Zwanzig model. A possible physical realiza-

tion most closely satisfying the model assumptions is

–1

also discussed. Section 2 contains also an extended list

t/T

of references to compensate partially its brevity. Then,

in Sec. 3 utilizing developed in our works [27-32] the-

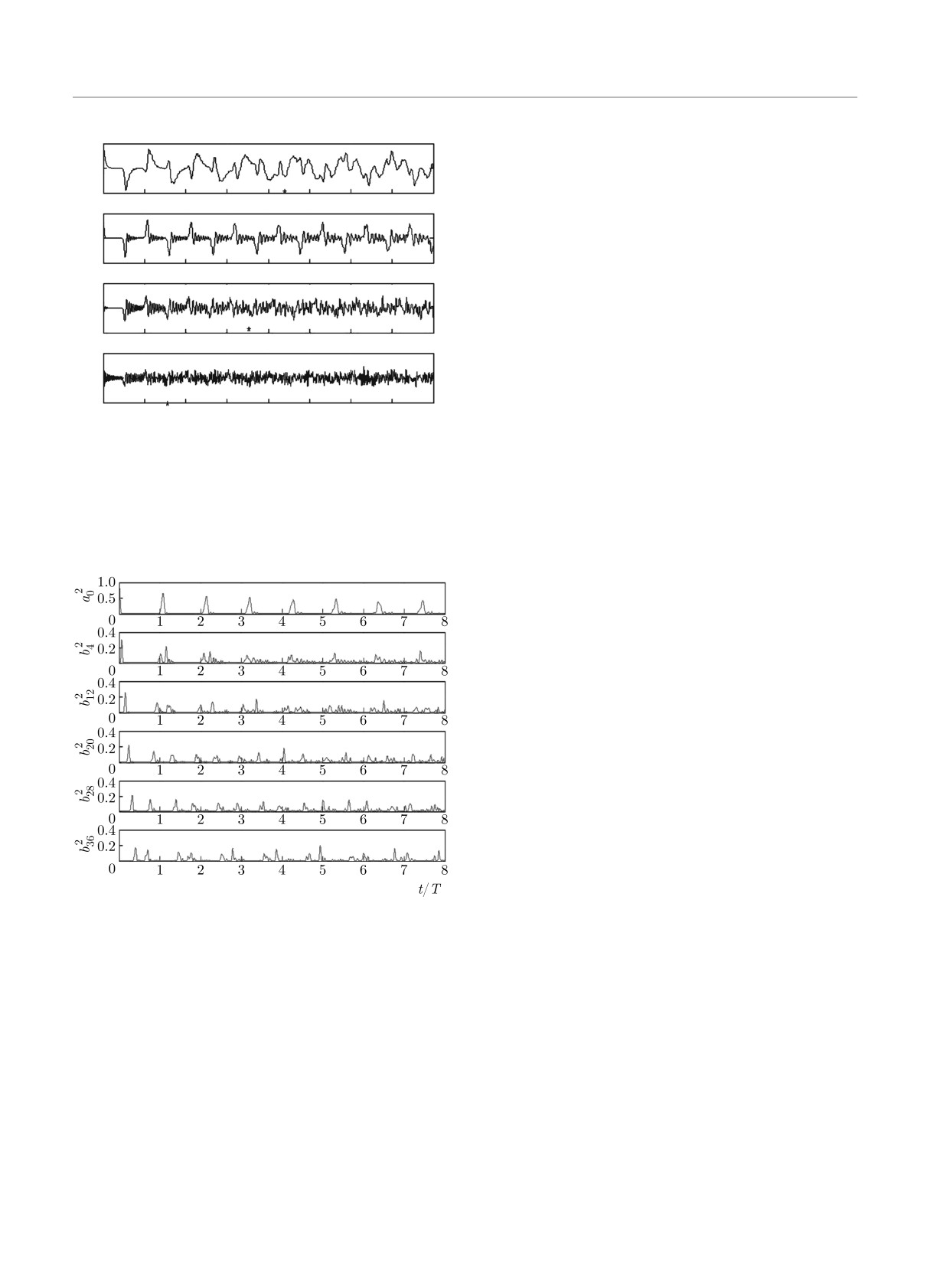
Fig. 8. Dynamics of the population at the excited impurity cite

located in the middle of the finite N = 49 size chain: a0 is

oretical approach, we investigate with all details the

the amplitude of the initially excited site; C² = 0.1, 0.25, 0.5,

evolution of the population of the initially prepared

0.95 from the top to the bottom; the critical cycle number

single state of the system. In Sec. 4, we analyze var-

kc is marked by the a star (kc = 23 for C² = 0.5); T is the

ious physically motivated generalizations of the bare

reccurence cycle period

Zwanzig model and how our analytical method should

be modified to describe theoretically these generaliza-

tions. In the same section, we show that on the similar

footing we can study dynamics not only for an indi-

vidual (single) nano-system but as well for the ensem-

ble of somehow distributed nano-systems. We investi-

gate the reservoir states evolution in Sec. 5. We collect

some already discussed in literature and new applica-

tions of our approach to physically interesting phenom-

ena in nano-systems, namely, two-level systems coupled

to reservoir, propagation of vibrational excitations in

nano-size chains (Sec. 6). The last Sec. 7 summarizes

the main findings of our work, with a discussion of pos-

sible physical consequences and interpretation of the

results.

The results from the list of Refs. [1-69] are used

or/and discussed in our work.

The figures illustrated our results are presented be-

Fig. 9. Impurity site excitation propagated along the chain.

low.

C² = 0.5, N = 49. The site numbers are indicated on the

panels as the subscripts of corresponding values along the ver-

Conclusion. Understanding all limitations of our

tical axes

simplified exactly solvable models, nevertheless we

hope that the results collected in this review capture

the essential peculiarities in nano-system dynamics.

one correspondence between system spectrum and its

Namely, the dense discrete spectra characteristic for

long-time dynamics. For all our examples, the spec-

nano-particles and large-size molecules are responsible

trum remains deterministic, while long-time dynamics

for appearance of recurrence cycles. By contrast to

eventually becomes stochastic. This unusual combina-

macroscopic systems with the continuous spectra,

tion is the specific feature of nano-systems.

where the initial state population decreases mono-

Motivated by this new understanding, we decided

tonically in time, the Loschmidt echo and double

to combine altogether our previous works to illustrate

resonances arise in each recurrence cycle. The revivals

495

V. A. Benderskii, E. I. Kats

ЖЭТФ, том 160, вып. 4 (10), 2021

in the time evolution makes it possible the emergence

13.

C. J. Fesko, J. D. Eaves, J. J. Loparo, A. Tokmakoff,

of new mechanisms of vibration stimulated processes

and P. L. Geissler, Science 301, 1698 (2003).

in single nano-particles and their ensembles as well.

14.

M. Khalil, N. Demirdoven, and A. Tokmakoff,

The regular behavior in the initial recurrence cycles

J. Chem. Phys. 121, 362 (2004).

transformed into chaotic-like long-time evolution is

an inherent characteristic of nano-world. The combi-

15.

A. V. Benderskii and K. B. Eisenthal, J. Phys. Chem.

A 106, 7482 (2002).

nation of the deterministic spectra with chaotic-like

long-time dynamics has no analogs in the quantum

16.

M. L. Cowan, B. D. Bruner, N. Huse, J. R. Dwyer,

dynamics of the macroscopic dissipative systems.

E. T. J. Nibbering, T. Elsaesser, and R. J. D. Miller,

Owing to specific mechanisms of energy transfer and

Nature 434, 199 (2005).

redistribution within the manifold of intramolecular

17.

F. Gai, K. C. Hanson, J. C. McDonald, and P. A. An-

modes, the loss-free and distant energy transfer be-

finrud, Science 279, 1886 (1998).

comes possible. The unique property of nano-systems

is the possibility for periodical accumulation of the

18.

S. Sportlein, H. Cartens, H. Satzger, C. Renner,

energy on the selected vibrational modes. The new

R. Beherendt, L. Moroder, P. Tavan, W. Zinth, and

fields for experimental studies and applications of this

J. Wachveitl, PNAS 99, 7998 (2002).

unusual effect are opened.

19.

D. M. Leitner and P. G. Wolynes, J. Phys. Chem.

A 101, 541 (1997).

The full text of this paper is published in the English

version of JETP.

20.

M. Ben-Nun, F. Molnar, H. Lu, J. C. Phillips,

T. J. Martinez, and K. Schulten, Farad. Discuss. 110,

447 (1998).

21.

G. K. Paramonov, H. Naundorf, and O. Kuhn, Eur.

REFERENCES

Phys. J. D 14, 205 (2001).

R. Zwanzig, Lect. Theor. Phys. 3, 106 (1960).

22.

S. Hayashi, E. Tajkhorshid, and K. Schulten, Bio-

phys. J. 85, 1440 (2003).

V. A. Benderskii, L. A. Falkovsky, and E. I. Kats,

JETP Lett. 86, 221 (2007).

23.

H. Fujisaki, Y. Zhang, and J. E. Straub, J. Chem.

Phys. 124, 144910 (2006).

T. User and W. H. Miller, Phys. Rep. 199, 7 (1991).

24.

Z. Wang, J. A. Carter, A. Laguchev, Y. K. Koh,

Time-resolved Vibrational Spectroscopy, ed. by S. Ta-

N.-H. Seong, D. C. Cahil, and D. D. Dlott, Science

kahashi, Springer, Berlin (1992).

317, 787 (2007).

A. H. Zewail, Femtochemistry: Ultrafast Dynamics of

25.

J. A. Carter, Z. Wang, and D. D. Dlott, Acc. Chem.

Chemical Bonds, World Sci., Singapore (1994).

Res. 42, 1343 (2009).

26.

V. A. Benderskii, L. N. Gak, and E. I. Kats, JETP

M. D. Feyer, Ultrafast Infrared and Raman Spectro-

scopy, Marcel Dekker, New York (2001).

108, 159 (2009).

27.

V. A. Benderskii, L. N. Gak, and E. I. Kats, JETP

A. H. Zewail, Phil. Trans. Roy. Soc. London A 364,

109, 505 (2009).

315 (2005).

28.

V. A. Benderskii and E. I. Kats, JETP Lett 88, 338

D. M. Leitner, Adv. Chem. Phys. B 130, 205 (2005).

(2008).

S. Mukamel, Principles of Nonlinear Spectroscopy,

29.

V. A. Benderskii and E. I. Kats, Eur. Phys. J. D 54,

Oxford Univ. Press, New York (1995).

597 (2009).

10.

R. M. Hochstrasser, PNAS 104, 14190 (2007).

30.

V. A. Benderskii and E. I. Kats, JETP Lett. 92, 370

(2010).

11.

J. Bredenbeck, A. Chosh, M. Smith, and M. Bohn,

J. Amer. Chem. Soc. 130, 2152 (2008).

31.

V. A. Benderskii and E. I. Kats, JETP 113, 562

(2011).

12.

J. B. Ashbury, T. Steinel, C. Stromberg, S. A. Or-

cell, C. P. Skinner, and M. D. Feyer, J. Phys. Chem.

32.

V. A. Benderskii and E. I. Kats, JETP Lett. 94. 459

A 108, 1107 (2004).

(2011).

496

ЖЭТФ, том 160, вып. 4 (10), 2021

Non-trivial dynamic regimes of small...

33.

R. D. Mattuck, A Guide to Feynmann Diagrams in

52.

O. Bohigas, S. Tomsovic, and D. Ulmo, Phys. Rep.

Many-Body Problem, McGraw-Hill, New York (1976).

223, 43 (1993).

53.

T. Papenbrock and H. A. Weidenmuller, Rev. Mod.

34.

G. M. Zaslavsky, Chaos in Dynamical Systems, Har-

Phys. 79, 997 (2007).

wood, New York (1985).

54.

W. Dietz and S. F. Fischer, J. Chem. Phys.113, 2741

35.

M. Tabor, Chaos and Integrability in Nonlinear Dy-

(2000).

namics, J. Wiley, New York (1989).

55.

D. V. Kurochkin, S. R. G. Naraharisetty, and

36.

M. E. Flatte and M. Holthaus, Ann. Phys. 245, 113

I. V. Rubtsov, PNAS 104, 14209 (2007).

(1996).

56.

S. G. Naraharisetty, V. M. Kysanenko, and I. V. Rub-

37.

F. M. Izrailev, Phys. Rep. 196, 299 (1990).

tsov, J. Chem. Phys. 128, 104502 (2008).

38.

W. H. Zurek, Phys. Rev. D 26, 1862 (1982).

57.

I. V. Rubtsov, Acc. Chem. Res. 42, 1385 (2009).

39.

P. Grigolini, Quantum Mechanical Irreversibility,

58.

Z. Smedarchina, W. Siebrand, and M. Z. Zgierski,

World Sci., Singapore (1993).

J. Chem. Phys. 103, 5326 (1995).

40.

Ya. G. Sinai, Introducrion to Ergodic Theory, Prince-

59.

V. A. Benderskii, A. V. Vetoshkin, L. von Laue, and

ton Univ. Press, Guilford (1977).

H. P. Trommsdorff, Chem. Phys. 219, 119 (1997).

41.

M. V. Berry, Chaotic Behavior in Deterministic Sys-

60.

V. A. Benderskii, V. A. Vetoshkin, and H. P. Tromm-

tems, ed. by G. Cassati, Plenum Press, New York

sdorff, Chem. Phys. 234, 173 (1998); 244, 273 (1999);

(1985).

262, 393 (2000).

42.

F. Haake, Quantum Signatures of Chaos, Springer,

61.

G. V. Milnikov and H. Nakamura, Phys. Chem.

Berlin (1990).

Chem. Phys. 10, 1374 (2008).

43.

C. Keating, B. A. McClure, J. J. Rack, and I. V. Rub-

62.

A. J. Leggett, S. Chakravarty, A. T. Dorsey,

tsov, J. Chem. Phys. 133, 144513 (2010).

M. P. A. Fisher, A. Garg, and M. Zwerger, Rev. Mod.

Phys. 59, 1 (1987).

44.

H. Kuzmany, B. Burger, A. Thess, and R. E. Smalley,

Carbon 36, 709 (1998).

63.

V. A. Benderskii, D. E. Makarov, and C. A. Wight,

Chemical Dynamics at Low Temperatures, J. Wiley,

45.

V. Schettino, H. Prigolini, and G. Cardini, J. Phys.

New York (1994).

Chem. A 106, 1815 (2002).

64.

A. O. Caldeira and A. J. Leggett, Ann. Phys. 149,

46.

S. Adhikari and R. Chowdhury, Phys. Lett. A 375,

374 (1983).

2166 (2011).

65.

A. I. Larkin and Yu. N. Ovchinnikov, JETP 58, 876

47.

T. Ishioka, W. Yan, H. L. Strauss, and R. G. Snyder,

(1983); 59, 420 (1984); 60, 1060 (1984).

Spectrochem. Acta A 59, 671 (2003).

66.

B. I. Ivlev and Yu. N. Ovchinnikov, JETP 66, 378

48.

L. Van Hove, Physica 21, 517 (1955).

(1987).

49.

L. D. Landau and E. M. Lifshitz, Statistical Physics,

67.

L. H. Yu, Phys. Rev. A 54, 3779 (1996).

Pt. 1, Pergamon, Oxford (1977).

68.

H. Bateman and A. Erdelyi, Higher Transcendental

50.

L. H. Yu and C. P. Sun, Phys. Rev. A 49, 592 (1994).

Functions, McGraw Hill, New York (1953).

51.

M. L. Mehta, Random Matrices, Acad. Press, New

69.

F. W. J. Olver, Asymptotics and Special Functions,

York (1968).

Acad. Press, New York (1974).

497