ЖЭТФ, 2021, том 160, вып. 1 (7), стр. 132-138

СВЯЗЬ ВЕЛИЧИН ПРОСТЫХ ЧИСЕЛ

С ИХ НОМЕРАМИ

Ю. Н. Овчинников^*

Max-Planck Institute for Physics of Complex Systems

01187, Dresden, Germany

Институт теоретической физики им. Л. Д. Ландау

Российской академии наук

142432, Черноголовка, Московская обл., Россия

Поступила в редакцию 18 февраля 2021 г.,

после переработки 18 февраля 2021 г.

Принята к публикации 18 февраля 2021 г.

Уравнение Эйлера порождает бесконечное число связей между величинами простых чисел и их номера-

ми. Эти связи осуществляются условно сходящимися рядами. Аналитическая функция, осуществляющая

эти связи, бесконечное число раз проходит через значение, равное единице. Расстояние между первой и

второй такими точками оказывается аномально большим.

DOI: 10.31857/S0044451021070142

2. ОСНОВНЫЕ УРАВНЕНИЯ

1. ВВЕДЕНИЕ

Для получения уравнений для функций {κ, ξ}

В работе [1] было показано, что в распределении

воспользуемся уравнением Эйлера для дзета-функ-

нулей дзета-функции Римана существует дальний

ции Римана [2], записанным в виде

порядок, что делает возможным установить номер

нуля с точностью ±1, если известно значение толь-

[ (

)

]

ко одного нуля, и однозначно, если известно значе-

∑

ние трех последовательных нулей. Формула Эйлера

ln ζ(z) =

(1)

P^z

устанавливает жесткую связь значений простых чи-

сел с дзета-функцией Римана [2].

где P — простые числа. Функция Римана имеет про-

стой полюс в точке z = 1. Используя разложение в

Точка z = 1 является простым полюсом дзе-

ряд дзета-функции Римана

та-функции. Это позволяет ввести две аналитиче-

ские функции {κ, ξ}, связывающие значение про-

стых чисел P с их номерами N. Полученная связь

{

}

позволяет восстановить значение функций {κ, ξ} на

∑

ζ(z) =

1+C(z-1) + C_k(z - 1)k+1

(2)

полуоси P > 0. В качестве примера мы приводим

z-1

k=1

значения функции κ в двух областях: P < 106 и

2.4 · 10⁷ < P < 5 · 10⁷. Функция κ бесконечное число

раз проходит через значение κ = 1. Значения функ-

ции ξ однозначно определены в целочисленных точ-

где C — константа Эйлера, получим из разложений

(1), (2) следующее уравнение:

ках {N, P (N)}. Среднее расстояние между просты-

ми числами δ равно ln(P/κ).

^* E-mail: ovc@itp.ac.ru

132

ЖЭТФ, том 160, вып. 1 (7), 2021

Связь величин простых чисел с их номерами

(

)

∑

ln P

= 2C +

N^z

P^z(P^z - 1)

N =1

(

)₂

∑

C_k(z - 1)^k(k + 2) + (z - 1)

C_k(z - 1)k

- C²(z - 1)

k=1

+ k⁼¹

(3)

∑

1 + C(z - 1) + C_k(z - 1)k+1

k=1

Ряды в правой части уравнения (3) быстро схо-

Из первого уравнения (4) следует всего лишь

∑

дятся в окрестности z = 1 и порождают бесконечное

условная сходимость ряда_N (1/N-ln P (N)/P (N)).

число связей на простые числа P как функцию их

Однако функция κ(P ), определяющая сходимость,

номера N. В частности, находим первые два равен-

является очень нетривиальной, и оценки для зави-

ства

симости N(P), полученные в работах [3-5], оказы-

)

ваются довольно грубыми.

∑

⁽1

ln P

Первое значение величины P₀, для которого

= 2C +

P (P - 1)

N =1

κ(P₀) = 1, оказывается достаточно большим, и для

его нахождения мы воспользуемся численными зна-

)

∑(ln2_P

ln N

чениями функции κ(P ), полученными в асимптоти-

(4)

ческом приближении в трех точках, соответствую-

N =1

щих значениям 〈N〉 равным 〈N〉 = {6, 5, 4}:

)

∑

ln² P

⁽1

+ 3C₁ - C².

= 9.33091735, κ = 1.436086,

P -1

= 8.3311375, κ = 1.2723356,

(7)

В результате оказывается возможным опреде-

лить две аналитические функции {κ, ξ} на полуоси

= 7.02868758, κ = 1.10973776.

P > 0:

⁽P⁾

P = N ln

+ ξ ln²

(5)

Интерполяция по трем точкам позволяет запи-

≤ P < 14 в неявном

сать функцию κ в интервале P₀

где κ — медленная функция от P , а ξ — быст-

виде:

ро осциллирующая неявная функция N, однозначно

(

)

определенная в целочисленных точках {N, P (N)}.

κ = 1.2723356+ α₁

- 8.3311375

Величина |ξ| ≲ 1.

Ряд в левой части k-го уравнения бесконечной

(

)₂

системы равенства (4) может быть записан в виде

+α₂

- 8.3311375

(8)

(

)

∑

ln^k N

lnk+1 P

где параметры α₁, α₂, P₀ равны

(6)

N =1

α₁ = 0.1468733, α₂ = 1.6916836 · 10-2,

(9)

Все эти ряды являются условно сходящимися. В

{κ = 1, P₀ = 5.6472442}.

результате функция {κ(P ), P > 0} бесконечное чис-

ло раз проходит через значение κ = 1. В области

Из уравнений (8), (9) находим значения первой

P ≫ 1 функция κ восстанавливается с помощью

и второй производных κ по P в точке P₀:

уравнения (5) и простых чисел в окрестности точ-



∂κ



ки P . Ниже мы приведем значения функции κ(P )



= 4.2584129 · 10-2,



∂P

в широкой области N < 5 · 10⁷, используя асимпто-

P =P0



(10)

тическое приближение и банк данных для простых

∂²κ



= 1.2069243 · 10-2.



чисел P (N).

∂P²

P =P0

133

Ю. Н. Овчинников

ЖЭТФ, том 160, вып. 1 (7), 2021

Таблица 1. Зависимость величины κ от ln(P/κ) в

интервале 5.35 < ln(P/κ) < 14.74

ln(P/κ)

5.35986733

2.532557395

6.361764094

2.7785552736

6.656853070

2.7376907868

7.138752753

2.7991641109

7.240179252

2.866279247

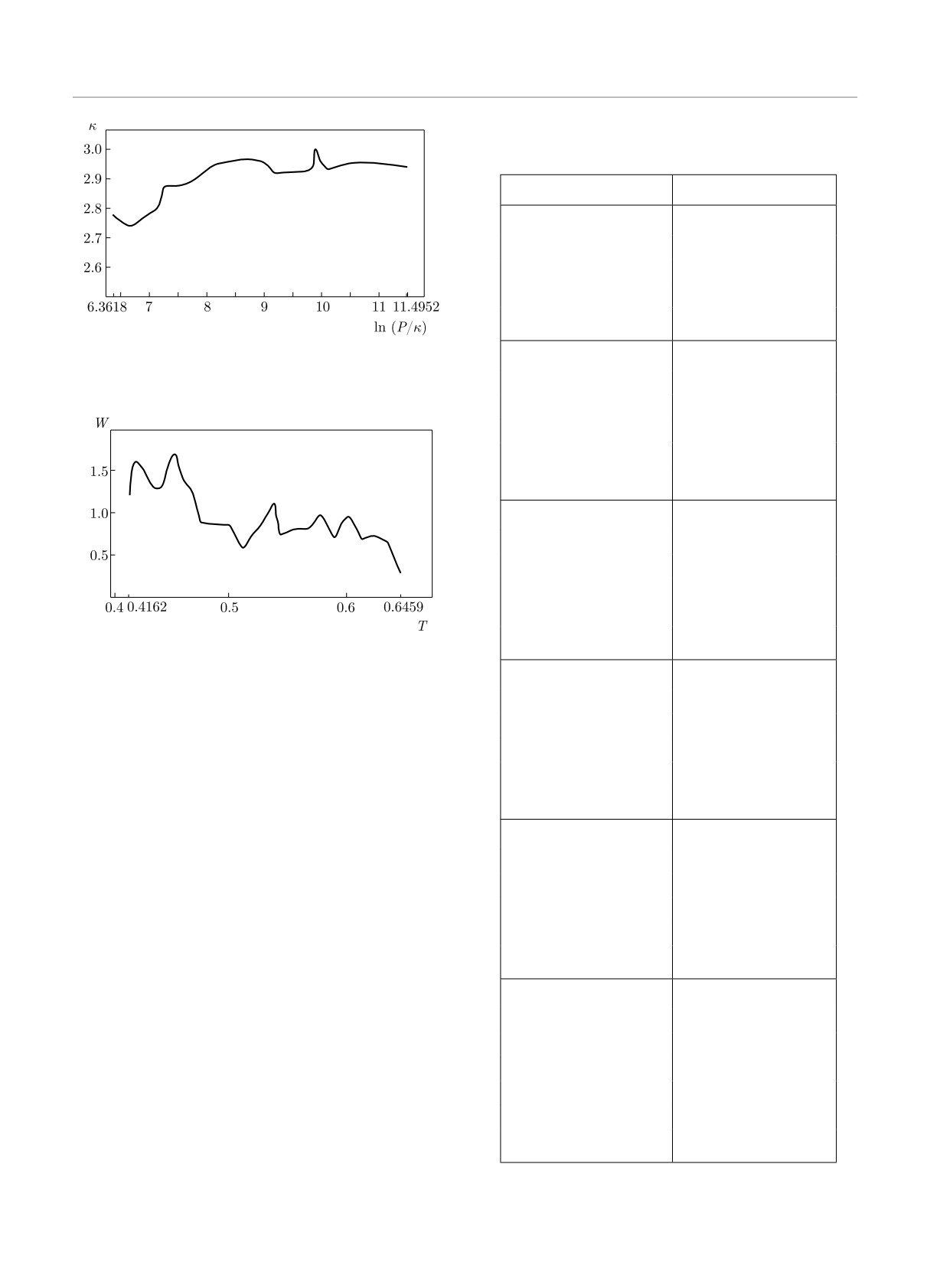
Рис. 1. Зависимость величины κ от ln(P/κ) в интервале

7.679349235

2.8825805393

6.35 < ln(P/κ) < 11.5

8.1531214638

2.9498744213

8.7361532971

2.96730411698

8.9738055746

2.9580785715

9.1078202553

2.935500058

9.1641636965

2.919485504

9.7288761507

2.925208492

9.8249648932

2.9342652576

9.8613751177

2.9442329767

9.8759351769

2.9947880488

9.900228354

3.0065822195

9.928897597

2.9770170407

Рис. 2. Зависимость величины κ от ln(P/κ) в интер-

вале

15.24

< ln(P/κ)

< 15.5; κ

= 2.911 + 10-2W ;

9.9451740301

2.97048106437

ln(P/κ) = 14.84 + T

9.9744924046

2.964698903

10.0983306239

2.9327967962

Используя формулы (9), (10), находим нечетную

10.4741457273

2.953829756

функцию κ(P) в области P ≤ P₀ (первые три члена

10.9297175937

2.9549719277

разложения):

11.4952340659

2.9401961334

κ=γ₁P +γ₂P³ +γ₃P⁵,

(11)

12.294175355

2.9401995052

где константы γ1,2,3 имеют следующие значения:

12.758840765

2.9490812862

γ₁ = 0.303279, γ₂ = -5.8058416 · 10-3,

12.9966888249

2.94683360385

(12)

γ₃ = 5.7965908 · 10-5.

13.00172510718

2.94625054098

В табл. 1 мы приводим значения величины κ как

13.2011721141

2.94050117017

неявной функции параметра P/κ в интервале 540 <

13.4388887258

2.9500020520

< P < 7.3 · 10⁶. Часть этих данных была использо-

вана для построения графика, представленного на

13.754458736

2.9360893117

рис. 1.

13.991422373

2.9338110441

Значение величины P , при котором функция κ

14.1882942799

2.93402098171

второй раз проходит через значение κ = 1, оказыва-

14.3527898788

2.9388529294

ется аномально большим, существенно превосходя-

14.5045135422

2.9247033152

щим величину P = 7.3 · 10⁶. Поэтому целесообразно

привести еще две таблицы значений функции κ в

14.628134333

2.9259205748

областях 8.16 · 10⁶ < P < 1.58 · 10⁷ и 9.2 · 10⁸ < P <

14.737507751

2.93074136764

< 9.825·10⁸ (табл. 2, 3), а также график зависимости

134

ЖЭТФ, том 160, вып. 1 (7), 2021

Связь величин простых чисел с их номерами

Таблица 2. Зависимость κ от ln(P/κ) в интервале

Таблица 3. Зависимость κ от величины ln(P/κ) в

14.84 < ln(P/κ) < 15.51

интервале 18.87 < ln(P/κ) < 19.65

ln(P/κ)

14.842012977

2.9243479799

18.872100641387

2.883917549832

14.8420644714

2.92476583005

18.88530470456

2.883821647853

14.8422005715

2.925043205288

18.898513188825

2.88385749774

14.93482165159

2.92766521445

18.915277601838

2.883709814489

15.0221175005

2.92412428438

19.5834048502

2.8775419576

15.105787376

2.9215655575

15.1768393655

2.92145015378

19.60644413388

2.876702036015

15.2446168534

2.9218232556

19.64044301007

2.87672022243

15.2561829441

2.923054851016

19.64099174063

2.87666572901

15.2616646486

2.92704088393

19.64148063226

2.87675655906

15.2696793082

2.9258098905

19.64207172507

2.87661380433

15.27669576

2.9238602422

19.64280973796

2.8764997721

15.2835251379

2.92398668898

19.6431621368

2.87653112677

15.2885691113

2.92648243034

19.6436317364

2.8766133494

15.2944510732

2.92793492459

19.6448815012

2.8765666246

15.3018253923

2.9248193697

19.645324773

2.8764057000

15.3089118352

2.9236628357

19.6458210148

2.87652288395

15.31630130749

2.91988575077

15.3230581547

2.91969750252

19.646377446

2.876417377328

15.3410729589

2.9195137771

19.6469020285

2.87642625346

15.35243137362

2.91685184742

19.646903686

2.87642507113

15.3748482399

2.9212716555

19.6474709814

2.876316271829

15.37861615754

2.92206461207

19.6479757649

2.8763774043

15.3809690351

2.9203751964

19.64851833796

2.87633459382

15.3817957353

2.91967658363

19.6490325534

2.87636853505

15.3841847891

2.91840517525

15.3956681915

2.91906708912

15.4072591843

2.91908981313

κ от ln(P/κ) в области 0.4 < ln(P/κ) - 14.84 <

2/3

15.41813991587

2.9207073572

(рис. 2). Эти данные позволяют провести хотя и гру-

15.4296689062

2.91809831012

бую, но важную и все еще разумную оценку второго

15.4355021939

2.919670940958

значения величины P , при которой κ = 1.

15.44077484115

2.920568271677

Величина κ является однозначной функцией P .

15.4454792496

2.919897317768

Но функция ln(P/κ) не является монотонно расту-

щей. Поэтому существуют узкие области, в которых

15.45287846854

2.917865400382

величина κ как функция ln(P/κ) не является одно-

15.45722005856

2.91806190337

значной. Одна из таких областей расположена внут-

15.46372783078

2.91827610925

. В табл. 4 мы

ри интервала 1.548·10⁷ < P < 1.549·10⁷

15.474893680726

2.917512899447

приводим значения величины {κ, ln(P/κ)} в двена-

15.4811222298

2.91525849714

дцати точках P , лежащих внутри этого интервала.

15.4859377749

2.9138585193

Используя значение величин {P, κ} в трех верх-

15.4882792369

2.9164619053

них строках табл. 2:

15.4912758845

2.918129923

15.4960674804

2.91782284429

{ln(P/κ) = (14.8420129777; 14.8420644714;

15.498561695

2.917669126

14.8422005715)},

15.502901555

2.9173601436

15.506369399

2.9159441886

135

Ю. Н. Овчинников

ЖЭТФ, том 160, вып. 1 (7), 2021

Таблица 4. P = 1.548 · 10⁷ + T ; κ = 2.91 · 10-3 κ;

Таблица 5. Значения ξ и κ (N — номер простого

ln(P/κ) = 15.4 + 10-2x

числа, P — простое число)

2011.42105263

4.351222317

8.554212465

550000

8163047

-0.289294796

2.92445623145

3796.68421052

3.997343055

8.57788639

550001

8163049

-0.347704066

2.9244568166

4883.14035087

3.74338389

8.593618401

550002

8163107

-0.155136627

2.92447367049

5519.6545455

3.858519304

8.593777486

550003

8163109

-0.2135527505

2.924474224764

5892.5438596

4.060487546

8.589254386

550004

8163121

-0.227172944

2.92447770492

6367.36363636

4.11998825

8.590278655

550005

8163131

-0.2497587709

2.92448057862

6815.350877193

4.2075043814 8.5901682678

7332.92982456

4.2858290451 8.5908226267

550006

8163139

-0.28130680031

2.92448287276

7676.368421052

4.2521941541 8.5941942923

550007

8163143

-0.33077031933

2.92448401822

7976.052631578

4.2475754424 8.5962877457

550008

8163191

-0.18326496992

2.92449768021

9534.754385964

4.2117179325 8.6003945486

550009

8163193

-0.241690687923

2.92449824612

11236.754385964 4.2944709531 8.6157294793

550010

8163227

-0.15694272000

2.92450782548

550011

8163241

-0.1616987974

2.924511747435

550012

8163251

-0.1843532127

2.92451454079

мы получаем следующую интерполяционную фор-

мулу для функции κ(P ) в интервале 8.1638 · 10⁶ <

550013

8163271

-0.1623029385

2.92452010742

< P < 8.1666 · 10⁶:

550014

8163283

-0.1760342491

2.9245234345

550015

8163313

-0.1093341666

2.924531710179

κ = 2.92 + 10-3κ,

(13)

550016

8163319

-0.1499013199143

2.92453335807

где

550017

8163329

-0.172600317414

2.9245360992

κ = 4.7658300529+2.102225195· 10-4(T-T₀)-

550018

8163359

-0.1059799123081

2.92454428245

−3.347544609· 10-8(T - T₀)²,

(14)

550019

8163401

1.41546012621 · 10-2

2.92455563775

550020

8163427

6.280542115015 · 10-2

2.9245626608043

P = 816 · 10⁴+T, T₀ = 4278.298245614.

550021

8163457

0.129258533298

2.9245709444

Подставляя в формулы (5), (12), (13) значения

550022

8163473

0.133236916658

2.92457482922

простых чисел из банка данных, получим значения

550023

8163479

9.26148988163 · 10-2

2.92457641284

функции ξ в целочисленных точках (N, P(N)), ле-

жащих в интервале 8.1638 · 10⁶ < P < 8.1666 · 10⁶.

550024

8163487

6.0907749269 · 10-2

2.92457852059

Эти значения приведены в табл. 5.

550025

8163497

3.8112724199 · 10-2

2.92458114925

Из табл. 1-4 следует очень нетривиальное пове-

дение функции κ даже в области значений P меж-

550026

8163503

-2.517521573681· 10-3

2.924582723234

ду двумя ближайшими точками, в которых κ обра-

550027

8163539

9.05388780683 · 10-2

2.9245921165

щается в единицу. Имеется очень широкая область,

550028

8163541

3.207341553 · 10-2

2.9245926358

важная для численных расчетов, в которой функ-

550029

8163557

3.597497581 · 10-2

2.9245967806

ция κ имеет плавную огибающую при наличии сла-

бых осцилляций. Данные, приведенные в табл. 2, 3,

550030

8163563

-4.6758427602· 10-3

2.92459833049

позволяют получить достаточно хорошую интерпо-

550031

8163583

1.7017722726 · 10-2

2.924603479

ляционную формулу в этой области:

550032

8163599

2.08808701541 · 10-2

2.924607579

κ = 2.883826627-9.8747968051· 10-3(ln(P/κ)-

550033

8163607

-1.08811450877· 10-2

2.9246096225

550034

8163613

-5.1549106935· 10-2

2.9246111524

− 18.892799033)+ 1.34071370507· 10-5 ×

550035

8163629

-4.7713395122· 10-2

2.92461522

× (ln(P/κ) - 18.892799033)²,

(15)

136

ЖЭТФ, том 160, вып. 1 (7), 2021

Связь величин простых чисел с их номерами

Таблица 5. (продолжение)

N P

550036

8163637

-7.948912575· 10-2

2.92461724749

550071 8164159 -0.12263288378

2.92474027445

550037

8163641

-0.129066461013

2.924618259589

550072 8164183 -8.3945836937· 10-2

2.9247454922

550038

8163647

-0.16974607895

2.92461977572

550073 8164201 -7.1796186709· 10-2

2.9247493802

550039

8163709

3.8621840882 · 10-2

2.92463530133

550074 8164213 -8.616540604 · 10-2

2.92475196015

550040

8163713

-1.097194955· 10-2

2.9246362941

550075 8164217 -0.1358743653

2.924752818

550041

8163737

2.83270265313 · 10-2

2.9246422285

550076 8164249 -6.1946370214· 10-2

2.924759642

550042

8163739

-3.01610440384· 10-2

2.9246427213

550077 8164259 -8.517693224 · 10-2

2.92476176066

550043

8163769

3.5756985394 · 10-2

2.924650081

550078 8164291 -1.1325784660407· 10-2 2.9247684948

550044

8163803

0.119385368367

2.924658349

550079 8164297 -5.222826795 · 10-2

2.9247697499

550045

8163817

0.114168334318

2.9246617313

550080 8164307 -7.5486266417· 10-2

2.9247718362

550046

8163821

6.4549862555 · 10-2

2.9246626952

550047

8163823

6.05220132773 · 10-3

2.9246631767

550048

8163829

-3.46898216005· 10-2

2.9246646198

где κ — огибающая функция κ. Формула (15) имеет

исключительно широкую область применимости. В

550049

8163833

-8.43110339885· 10-2

2.92466558047

частности, из нее следует, что вторая точка, в ко-

550050

8163839

-0.1250564841428

2.92466701947

торой функция κ обращается в единицу, находится

550051

8163847

-0.156928229725

2.9246689344

при значениях P около

550052

8163871

-0.1178130955035

2.924674653

P ∼ 3.27 · 10¹¹².

(16)

550053

8163917

1.88269990635 · 10-2

2.92468550726

550054

8163923

-2.19472538302· 10-2

2.9246869125

Это делает возможным сформулировать клас-

550055

8163929

-6.2723563236· 10-2

2.924688315

терно-обогатительный подход, позволяющий с вы-

550056

8163971

5.60415135045 · 10-2

2.9246980679

сокой скоростью находить простые числа.

550057

8163983

4.18300552139 · 10-2

2.9247008326

В настоящее время показано [6], что на множе-

550058

8163989

1.0331726483 · 10-3

2.92470221137

стве чисел вида M_n = 2ⁿ - 1 существует подмноже-

ство чисел ñ такое, что M_ñ есть простое число.

550059

8163997

-3.09071589937· 10-2

2.9247040459

550060

8164003

-7.17088403903· 10-2

2.924705419

550061

8164027

-3.28077521019· 10-2

2.92471088701

3. ЗАКЛЮЧЕНИЕ

550062

8164031

-8.2474210274· 10-2

2.92471179515

550063

8164033

-0.14099584436

2.92471224858

Зависимость величины простого числа от его

550064

8164069

-4.9030238574· 10-2

2.92472036443

номера определяется в основном аналитической

функцией κ, связанной с дзета-функцией Рима-

550065

8164073

-9.87062938677· 10-2

2.92472126083

на уравнением Эйлера. Показано, что функция

550066

8164099

-5.10543058019· 10-2

2.92472706136

κ бесконечное число раз проходит через значе-

550067

8164111

-6.5353559954· 10-2

2.92472972326

ние, равное единице. Средняя плотность простых

550068

8164127

-6.19733337456· 10-2

2.92473325746

чисел очень слабо зависит от величины P и

550069

8164141

-6.74496536088· 10-2

2.92473633583

лишь логарифмически мала по сравнению с еди-

ницей. Получено бесконечное число связей для

550070

8164147

-0.10830070674

2.9247376511

функции κ. Определяющую роль играет услов-

ная сходимость рядов в левой части уравнений (4).

137