ЖЭТФ, 2021, том 160, вып. 1 (7), стр. 88-94

УСЛОВИЯ РЕАЛИЗАЦИИ И МАГНИТОПОЛЕВАЯ

ЗАВИСИМОСТЬ УГЛОВЫХ ВОЗБУЖДЕНИЙ В

ТОПОЛОГИЧЕСКОМ ИЗОЛЯТОРЕ СО СВЕРХПРОВОДЯЩИМ

СПАРИВАНИЕМ НА ТРЕУГОЛЬНОЙ РЕШЕТКЕ

А. Д. Федосеев^*

Институт физики им. Л. В. Киренского, ФИЦ КНЦ Сибирского отделения Российской академии наук

660036, Красноярск, Россия

Поступила в редакцию 12 января 2021 г.,

после переработки 12 января 2021 г.

Принята к публикации 13 февраля 2021 г.

В последние годы исследования топологических свойств систем были расширены новой концепцией то-

пологических изоляторов и сверхпроводников высокого порядка. В то время как было предложено боль-

шое количество моделей двумерных систем на квадратной решетке, в которых могут возникать угловые

возбуждения, вопрос о реализации таких возбуждений в сверхпроводящих системах с треугольной кри-

сталлической решеткой остается слабо изучен. В данной работе на примере топологического изолятора

в форме треугольника с киральным сверхпроводящим параметром порядка показана возможность реа-

лизации угловых возбуждений в C3-симметричных системах. Несмотря на нетопологический характер,

эти возбуждения обладают значениями энергии внутри щели спектра краевых возбуждений первого по-

рядка в широком диапазоне параметров и хорошо локализованы в углах системы. Продемонстрировано

наличие бесщелевых угловых возбуждений в системе при определенных значениях параметров. Прило-

жение внешнего магнитного поля в плоскости системы приводит к снятию трехкратного вырождения

энергии угловых возбуждений и позволяет с помощью направления магнитного поля управлять положе-

нием углового возбуждения с минимальной энергией. В то же время изменение величины магнитного

поля позволяет сделать точную подстройку для реализации бесщелевого возбуждения в выбранном угле.

DOI: 10.31857/S0044451021070099

дексом, расположенных на открытой границе систе-

мы [2, 3].

1. ВВЕДЕНИЕ

Особый интерес топологические системы высо-

В последние годы исследования топологически

кого порядка вызывают в связи с возможностью ре-

нетривиальных систем получили новое направле-

ализации угловых майорановских состояний в дву-

ние, связанное с предложенной концепцией топо-

мерных топологических сверхпроводниках высоко-

логических изоляторов высокого порядка (ТИВП)

го порядка (ТСВП) [4, 5], поскольку снимают одну

[1]. В таких системах щелевым является не только

из проблем создания майорановских состояний на

спектр объемных состояний, но и спектр краевых со-

практике. Майорановские состояния первого поряд-

стояний первого порядка (обычных краевых состо-

ка требуют наличия чисто одномерной системы, что

яний), и при этом возникают краевые состояния на

сложно реализовать практически, в то время как

границах более высокого порядка: углов в двумер-

уширение цепочки приводит к возникновению бес-

ных системах, а также углов и ребер в трехмерных

щелевой зоны краевых возбуждений. В таком слу-

системах. Следует отметить, что еще до работы [1]

чае возбуждения с нулевой энергией хоть и остают-

была продемонстрирована возможность возникнове-

ся отделенными щелью от объемных возбуждений,

ния локализованных состояний на доменных стен-

но уже не отделены от других краевых возбужде-

ках между областями с разным топологическим ин-

ний. Кроме того, при уширении одномерной систе-

мы характер возбуждений меняется с чисто майора-

^* E-mail: fad@iph.krasn.ru

новского на киральный с изменением соотношения

ЖЭТФ, том 160, вып. 1 (7), 2021 Условия реализации и магнитополевая зависимость угловых возбуждений. . .

между длиной и шириной системы [6, 7]. Предска-

ки закрытием щели спектра краевых состояний. По

занные майорановские угловые состояния решают

предположению авторов такие состояния топологи-

эти проблемы. Во-первых, их энергия лежит в щели

чески защищены обобщенной киральной симметри-

спектра как объемных, так и краевых возбуждений.

ей [18,19]. Однако ключевой особенностью рассмат-

Во-вторых, их локализация строго в углах системы

риваемых систем являлось отсутствие электрон-ды-

препятствует смене характера, и они остаются майо-

рочной симметрии, а значит, подобный подход не

рановскими вне зависимости от соотношения разме-

применим для создания ТСВП. Кроме того, выво-

ров системы.

ды о топологической защищенности угловых состо-

Дополнительный интерес к ТСВП вызван воз-

яний в решетке Кагомэ впоследствии были оспоре-

можностью менять положение угловых возбужде-

ны [21, 22]. Более того, авторы работы [21] сделали

ний варьированием параметров системы [5,8,9]. Уг-

вывод о невозможности реализации топологически

ловые возбуждения в двумерных системах пред-

защищенных угловых состояний в C₃-симметричной

ставляются хорошими кандидатами для осуществ-

системе.

ления брейдинга, являющегося одним из ключевых

В то время как топологически защищенные уг-

требований при создании топологического кубита

ловые состояния в системах в форме треугольника,

[10]. Другим возможным практическим применени-

обладающих треугольной кристаллической решет-

ем таких систем является возможность создавать

кой, запрещены, эти системы все еще представля-

на их основе наноразмерные устройства с управля-

ют интерес для исследования. Во-первых, существу-

емыми транспортными характеристиками. Для та-

ют и другие проявления нетривиальной топологии

ких практических применений важна возможность

помимо возникновения бесщелевых угловых состоя-

управления угловыми возбуждениями с помощью

ний [16]. В частности, для C₃-симметричной систе-

внешних полей, которая была продемонстрирована

мы была продемонстрирована возможность возник-

в работах [5, 8].

новения зарядовой аномалии [23]. Во-вторых, крае-

Распространенный подход для получения ТСВП

вые состояния, в том числе бесщелевые, могут воз-

заключается в рассмотрении модели топологическо-

никать в системах, не обеспечивающих их тополо-

го изолятора при учете сверхпроводящего спарива-

гическую защищенность. Так, к примеру, краевые

ния, выбранного таким образом, чтобы спектр кра-

состояния были обнаружены в тривиальной фазе од-

евых возбуждений первого порядка стал щелевым,

номерной цепочки со спин-орбитальным взаимодей-

а масса Дирака для этих возбуждений имела про-

ствием и сверхпроводимостью s-типа [24,25], а так-

тивоположный знак на соприкасающихся границах

же экситонного диэлектрика со спин-орбитальным

[4]. В таком случае углы в системе будут выступать

взаимодействием [26]. Краевые возбуждения с ну-

в роли доменных границ, на которых будут возни-

левой энергией были найдены в тривиальной фа-

кать краевые возбуждения второго порядка, то есть

зе двумерного топологического изолятора с кираль-

бесщелевые угловые возбуждения. Этот подход хо-

ной сверхпроводимостью и 120-градусным магнит-

рошо работает в системах на квадратной кристал-

ным упорядочением [27, 28].

лической решетке, для которых предложено множе-

В связи с отсутствием в системах с треугольной

ство моделей ТИВП и ТСВП [11-15]. Однако он не

решеткой топологически защищенных угловых со-

применим для C₃-симметричных систем, поскольку

стояний представляется важным исследование воз-

в рамках описанного выше метода всегда возникает

можности реализации в такой системе угловых воз-

четное число топологически защищенных угловых

буждений нетопологического характера, в том чис-

состояний [16].

ле бесщелевых угловых возбуждений. Данная рабо-

Другой способ формирования угловых состояний

та посвящена исследованию условий возникновения

был предложен на примере решетки Кагомэ [17-19].

угловых возбуждений в двумерном топологическом

При определенных значениях параметров узлы, на-

изоляторе в форме треугольника с киральной сверх-

ходящиеся в углах системы с открытыми гранич-

проводимостью на треугольной решетке и их моди-

ными условиями в форме треугольника, становят-

фикации при приложении магнитного поля.

ся изолированными от остальной системы, форми-

2. МОДЕЛЬ ТОПОЛОГИЧЕСКОГО

руя угловые состояния (аналогично краевым со-

ИЗОЛЯТОРА С КИРАЛЬНОЙ

стояниям в модели Su-Schrieffer-Heeger или модели

СВЕРХПРОВОДИМОСТЬЮ НА

Китаева [20]). Эти состояния являются бесщелевы-

ТРЕУГОЛЬНОЙ РЕШЕТКЕ

ми и возникают во всей области параметров, ко-

Аналогично авторам работы

[4], рассмотрим

торая не отделена от особой параметрической точ-

двухуровневую модель в приближении сильной свя-

А. Д. Федосеев

ЖЭТФ, том 160, вып. 1 (7), 2021

√

(

)₂

E_k =

|Δ_k|² +

μ-E^TIk

(3)

где E^TIk обозначает спектр объемных состояний в

топологическом изоляторе:

√

E^TIk = ±

|t_k|² + |λ_kσ |²,

(

√

)

k_x

k_y

t_k = Δε - 2t + 4t cos

cos

+ cos

(

√

)

(4)

k_x

k_y

λkσ = 2iλσ sin

2 cos

+ cos

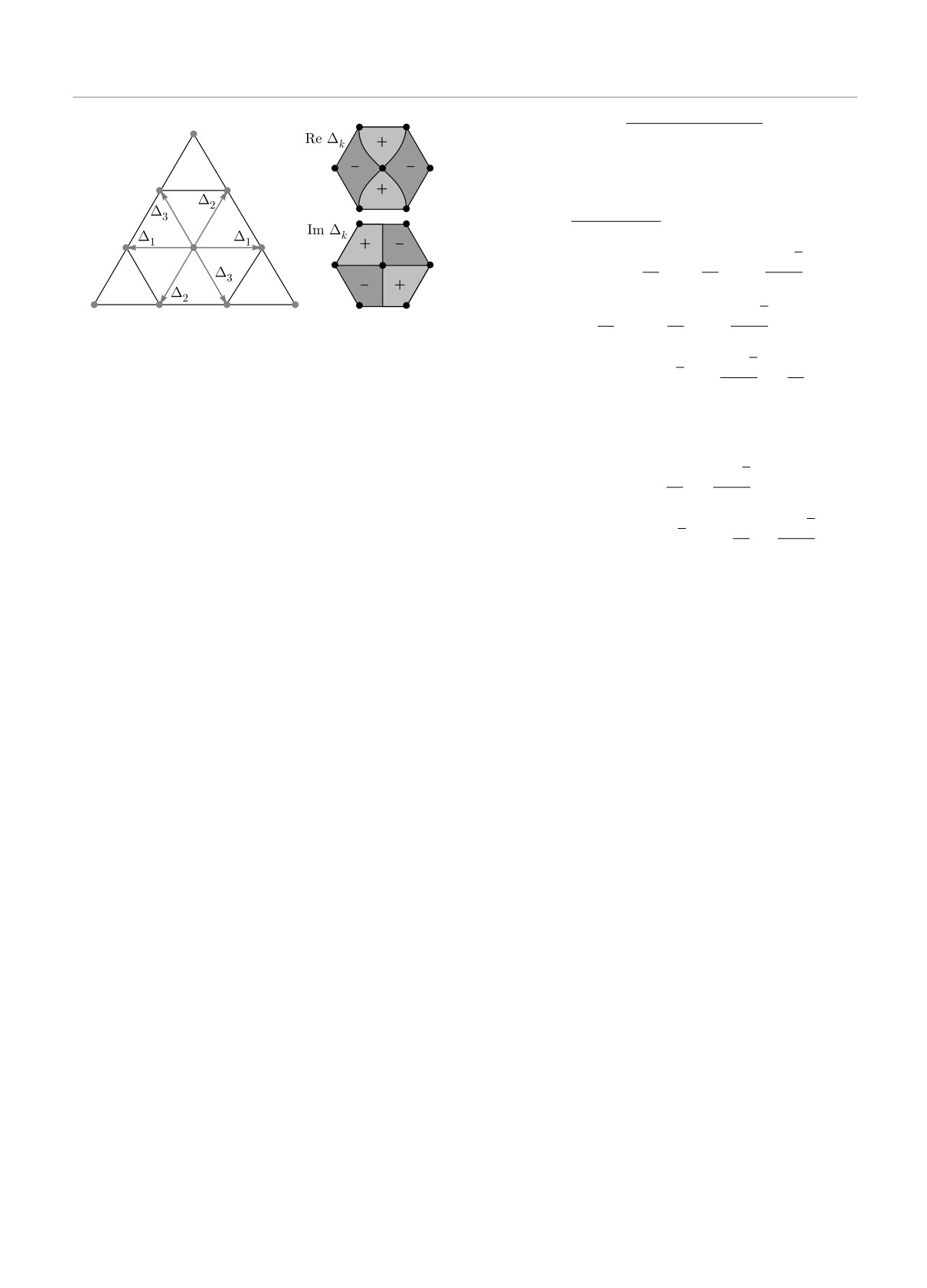
Рис. 1. (В цвете онлайн) Киральное сверхпроводящее спа-

ривание d + id-типа на треугольной решетке. Слева: на-

√

k_y

k_x

правление сверхпроводящего спаривания Δj (2). Справа:

−2

3λsin

cos

знак Re Δ_k и Im Δ_k [29]. Точками обозначены нодальные

точки Δ_k (3)

а Δ_k — сверхпроводящее спаривание, имеющее дву-

мерное представление

(

)

зи при учете гибридизации, индуцированной спин-

√

k_x

k_y

орбитальным взаимодействием Рашбы, и сверхпро-

Δ_k = 2Δ₁

cosk_x - cos

cos

водящего синглетного спаривания на соседних уз-

√

лах:

√

k_x

k_y

− 2i

3Δ₁ sin

sin

(5)

Ĥ= Ĥ₀ +

T +

Ĥ_so +

Ĥ_sc,

∑

Поскольку Δ_k имеет двумерное представление, оно

Ĥ₀ =

(νΔε - μ) c^†fνσc_fνσ,

обладает не нодальными линиями, как в работе [4], а

^fνσ∑

нодальными точками, как и спин-орбитальное взаи-

T =t

νc^†fνσc_mνσ,

модействие.

〈fm〉νσ

(1)

В отсутствие сверхпроводящего спаривания, га-

∑

мильтониан (1) описывает двумерный киральный

Ĥ_so = iλ

[σ_σσ′ × d_fm]_z c^†fνσc_m,-ν,σ′ ,

〈fm〉νσσ^′

топологический изолятор, характеризующийся спи-

∑

новым числом Черна [30]:

Ĥ_sc =

Δ_fmc^†fν↑c^†mν↓ + h.c.

〈fm〉ν

C_s = 1,

-6t < Δε < 2t,

(6)

C_s = 2,

2t < Δε < 3t.

Здесь сумма по f обозначает суммирование по уз-

лам решетки, 〈fm〉 отвечает суммированию по бли-

При отсутствии гибридизации между подзонами

жайшим соседям, d_fm — единичный вектор вдоль

рассматриваемая система является топологическим

направления от узла m к узлу f, μ — химический по-

сверхпроводником [31, 32] с числами Черна, проти-

тенциал системы, 2Δε — разница посадочных энер-

воположными для верхней и нижней подзон:

гий в двух подзонах, t — параметр перескока меж-

ду ближайшими соседями, λ — параметр спин-ор-

C_ν = 2ν,

-3t + Δε < νμ < 6t + Δε.

(7)

битального взаимодействия, σ_j — матрицы Паули в

Следует отметить, что поскольку числа Черна име-

спиновом пространстве, c^†fνσ — операторы рождения

электрона на узле f в разных подзонах, обозначен-

ют противоположный знак, на пересечении нетриви-

альных областей для верхней и нижней подзон пол-

ных индексом ν = ±1.

ное число Черна системы С = 0. Это делает систему

Будем рассматривать случай кирального сверх-

чувствительной к гибридизации между подзонами.

проводящего синглетного спаривания между элек-

При одновременном учете кирального сверхпро-

тронами на ближайших узлах, соответствующего

водящего спаривания и спин-орбитального взаимо-

симметрии треугольной решетки (рис. 1):

действия диаграмма топологических фаз остается

Δ_fm = Δ_j = Δ₁e2πi(j-1)/3, j = 1, 2, 3.

(2)

практически той же, что и в отсутствие спин-ор-

битального взаимодействия. Тривиальные области

Спектр объемных возбуждений рассматривае-

с C±1 = 0 остаются тривиальными, а области, в ко-

мой системы имеет вид

торых только одно из чисел Черна C±1 = 0, в то

ЖЭТФ, том 160, вып. 1 (7), 2021 Условия реализации и магнитополевая зависимость угловых возбуждений. . .

тора в форме треугольника с киральной сверхпро-

водимостью продемонстрировали, что в интересую-

щей области в зависимости от значений параметров

реализуются три ситуации (рис. 2 слева). В значи-

тельной части рассматриваемой области, хотя она

и является топологически тривиальной, в системе

возникают бесщелевые краевые возбуждения перво-

го порядка. Другая часть области отвечает наличию

угловых возбуждений нетопологического характера

с энергией внутри щели спектра краевых возбуж-

дений. Энергия таких возбуждений трехкратно вы-

рождена ввиду эквивалентности углов в системе.

Третий случай соответствует наличию в системе ще-

ли в спектре краевых возбуждений первого поряд-

ка, однако угловые возбуждения с энергией внутри

Рис. 2. (В цвете онлайн) Диаграмма параметров топо-

щели в системе отсутствуют.

логического изолятора в форме треугольника с кираль-

В одномерных системах существует взаимное со-

ной сверхпроводимостью на треугольной решетке. Слева:

ответствие между энергией краевых состояний и ха-

в отсутствие магнитного поля, справа: при наличии маг-

нитного поля в плоскости h = 0.3, φ_h = π/2. Красные

рактером этого состояния. Если энергия состояния

области соответствуют наличию бесщелевых краевых воз-

находится внутри щели объемного спектра, то состо-

буждений первого порядка, фиолетовые — объемных бес-

яние краевое, а если внутри значений спектра разре-

щелевых возбуждений. Синим обозначены области пара-

шенных объемных состояний, то состояние является

метров, при которых в системе возникают угловые воз-

объемным. В двумерных системах это соответствие

буждения со значением энергии, лежащим внутри щели

работает только в одну сторону. Если энергия состо-

спектра краевых возбуждений. Желтым — области пара-

яния находится внутри абсолютной щели спектра

метров, при которых спектр краевых возбуждений щеле-

объемных состояний, то такое состояние по-преж-

вой, однако угловые возбуждения с энергией внутри щели

нему является краевым. Однако обратное, вообще

отсутствуют. Белая линия соответствует параметрам, при

говоря, не верно. То же самое относится и к угло-

которых возникают бесщелевые угловые возбуждения, си-

вым возбуждениям в двумерных системах. Поэтому

няя линия — параметрам, при которых закрывается щель

спектра краевых возбуждений в магнитном поле. Параметр

для определения характера состояний в двумерных

спин-орбитального взаимодействия λ = 0.5t, сверхпрово-

случаях полезно рассчитать параметр IPR (inverse

дящего спаривания Δ1/t = 0.5

participation ratio) [33,34], характеризующей степень

локализации состояния, который хорошо зарекомен-

довал себя для обнаружения краевых состояний в

время как второе C∓1 = 0, остаются топологически

топологических изоляторах [35]:

нетривиальными. Обе эти области не представляют

∑

интереса для поиска угловых возбуждений. Область

(A_m(f))^q

Iq(m) (∑

)_q .

(8)

же, в которой оба числа Черна C±1 были отличны

A_m(f)

от нуля, формирует топологическую фазу с числом

Черна C = 0, которая более не содержит топологи-

Здесь A_m(f) — амплитуда возбуждения с номером

чески защищенных краевых возбуждений. Однако в

m на узле f, q > 1. Параметр I_q является отно-

ее границах все еще возможна реализация как крае-

сительно большим для локализованных состояний

вых возбуждений нетопологического характера, в

(Iq = 1 для состояния, локализованного на одном

том числе бесщелевых, так и угловых возбуждений.

узле), и имеет порядок 1/Vq-1 для делокализован-

Таким образом, именно эта область будет исследо-

ного состояния в системе с числом узлов V .

ваться в дальнейшем.

На рис. 3 представлена зависимость величины

I₄ от химпотенциала μ для различных собственных

возбуждений в системе. Как можно видеть, возбуж-

3. УГЛОВЫЕ ВОЗБУЖДЕНИЯ В СИСТЕМЕ

дения, характеризующиеся минимальной энергией

В ФОРМЕ ТРЕУГОЛЬНИКА

при μ = 0, остаются хорошо локализованными в уг-

Результаты численных расчетов спектра одно-

лах треугольника, даже когда их энергия оказыва-

электронных возбуждений топологического изоля-

ется за пределами щели спектра краевых возбужде-

А. Д. Федосеев

ЖЭТФ, том 160, вып. 1 (7), 2021

Рис. 3. (В цвете онлайн) a) Зависимость I4 (8) для собственных возбуждений в топологическом изоляторе в форме

треугольника с киральной сверхпроводимостью от величины химического потенциала. Синяя линия отвечает угловым

возбуждениям с минимальной энергией, красная линия обозначает величину химического потенциала μ, при котором

энергия угловых возбуждений пересекает границу зоны краевых возбуждений. б) Спектр системы при μ = 0. Точками

обозначены энергии краевых возбуждений, треугольниками — угловых, серые области обозначают зону краевых состо-

яний. в-д) Пространственное распределение угловых возбуждений при различных значениях химического потенциала,

отмеченных точками на a: при μ = 0 это угловое возбуждение с энергией внутри щели спектра краевых возбуждений,

при μ = 0.9t это угловое возбуждение с энергией внутри зоны краевых состояний, при μ = 1.5t возбуждение является

краевым с тенденцией к локализации в углах системы. Параметры системы: Δ1/t = 0.6, Δε = 0, λ/t = 0.5

ний в рассматриваемой системе (рис. 3г). Небольшие

4. ВЛИЯНИЕ МАГНИТНОГО ПОЛЯ НА

пики I₄ возникают из-за тенденции краевых возбуж-

УСЛОВИЯ РЕАЛИЗАЦИИ УГЛОВЫХ

дений первого порядка с энергиями в глубине ще-

ВОЗБУЖДЕНИЙ

ли спектра объемных возбуждений к локализации в

Рассмотрим влияние однородного магнитного

углах ограниченных систем [36]. Подобные возбуж-

поля, направленного в плоскости системы, на осо-

дения можно легко отличить от угловых возбужде-

бенности реализации угловых состояний в треуголь-

ний, изменяя размер системы. Поскольку краевые

ном топологическом изоляторе с киральной сверх-

возбуждения даже при наличии тенденции к лока-

проводимостью на треугольной решетке:

лизации в углах распределены по всей границе си-

∑

стемы, то их значения IPR уменьшаются с увели-

Ĥ_h = -

hσ_σσ′ c^†fνσc_fνσ′ ,

чением размеров системы, в то время как значения

fνσσ

′

(9)

IPR для угловых состояний остаются неизменными.

h = h(cosφ_h, sinφ_h, 0).

При определенных значениях параметров, фор-

мирующих линию на диаграмме параметров, в си-

Наличие магнитного поля приводит к измене-

стеме возможна реализация угловых возбуждений с

нию описанной в предыдущем параграфе диаграм-

нулевой энергией (рис. 2 слева). Эти линии нулевых

мы параметров (рис. 2 справа). Так, спектр объем-

мод не являются размерным эффектом в отличие от

ных возбуждений теперь закрывается не на лини-

ситуаций, рассмотренных в работах [25,37,38]. Нали-

ях, а в области параметров. Также внутри области

чие в системе беспорядка не влияет на возможность

параметров, соответствующих реализации угловых

реализации в ней нулевых угловых возбуждений, од-

возбуждений, возникает линия параметров, отвеча-

нако конкретные значения параметров, при которых

ющая закрытию щели в спектре краевых возбуж-

такие возбуждения возникают, оказались очень чув-

дений первого порядка. Линия реализации бесщеле-

ствительны к беспорядку непосредственно в углах

вых угловых мод при приложении магнитного поля

системы.

расщепляется на две. Однако сами области реали-

ЖЭТФ, том 160, вып. 1 (7), 2021 Условия реализации и магнитополевая зависимость угловых возбуждений. . .

5. ВЫВОДЫ

На примере двумерного топологического изо-

лятора в форме треугольника с киральной сверх-

проводимостью на треугольной решетке была

продемонстрирована возможность реализации уг-

ловых возбуждений в C₃-симметричных системах.

Было показано, что угловые возбуждения в такой

системе могут обладать энергиями как внутри щели

спектра краевых возбуждений первого порядка, так

и за ее пределами. При определенных значениях

параметров, формирующих линию на диаграмме

параметров, угловые возбуждения являются бес-

щелевыми. Включение магнитного поля в системе

снимает вырождение угловых возбуждений, при

этом энергия угловых возбуждений зависит как

от величины магнитного поля так и от его на-

правления в плоскости системы. Это позволяет не

Рис. 4. (В цвете онлайн) Сверху: зависимость энергии

только провести точную подстройку для получения

угловых возбуждений от направления магнитного поля

углового возбуждения с нулевой энергией, но и

h = 0.3t, направленного в плоскости системы. Снизу: про-

выбрать угол, в котором это угловое возбуждение

странственное распределение двух возбуждений с мини-

будет реализовываться.

мальной энергией при φ_h = π/2

Благодарности. Автор выражает благо-

зации угловых возбуждений остаются практически

дарность Д. М. Дзебисашвили, В. А. Мицкану,

без изменений.

М. С. Шустину, М. М. Коровушкину и С. В. Ак-

сенову за многочисленные дискуссии и внимание к

Поскольку в рассматриваемой системе вследст-

работе.

вие наличия спин-орбитального взаимодействия су-

Финансирование. Исследование выпол-

ществует связь между спиновыми и пространствен-

нено при финансовой поддержке Российского

ными степенями свободы, включение магнитного

фонда фундаментальных исследований (грант

поля, направленного в плоскости системы, приво-

№19-02-00348), Правительства Красноярского

дит к разрушению пространственной симметрии и

края, Красноярского краевого фонда поддержки

делает углы неэквивалентными. При этом энергия

научной и научно-технической деятельности в

возбуждений становится зависящей не только от

рамках научного проекта

№20-42-243005

«Изу-

величины, но и от направления магнитного поля

чение краевых состояний в одно- и двумерных

(рис. 4). Так, экстремальным значением энергии об-

топологических сверхпроводниках», №19-42-240011

ладает возбуждение, находящееся в том углу, на-

«Кулоновские взаимодействия в проблеме реа-

правление на который из центра треугольника сов-

лизации майорановских мод в низкоразмерных

падает с направлением магнитного поля. Таким об-

системах с нетривиальной топологией», а также

разом, с помощью магнитного поля можно осуще-

гранта Президента РФ МК-1641.2020.2.

ствить не только точную подстройку системы для

получения углового возбуждения с нулевой энерги-

ей, но и определить, в каком именно углу будет воз-

ЛИТЕРАТУРА

никать это возбуждение.

Поскольку полученные в магнитном поле воз-

1. W. A. Benalcazar, B. A. Bernevig, and T. L. Hughes,

буждения имеют нетопологический характер и не

Science 357, 61 (2017).

могут быть представлены в виде двух разнесенных

2. G. E. Volovik, Письма в ЖЭТФ 91, 201 (2010).

майорановских операторов, такая система не может

3. F. Zhang, C. L. Kane, and E. J. Mele, Phys. Rev.

быть использована для реализации брейдинга. Од-

Lett. 110, 046404 (2013).

нако она все еще может быть полезна для реализа-

ции устройства, транспортом через которое можно

4. Q. Wang, C.-C. Liu, Yu.-M. Lu, and F. Zhang, Phys.

управлять с помощью магнитного поля.

Rev. Lett. 121, 186801 (2018).

А. Д. Федосеев

ЖЭТФ, том 160, вып. 1 (7), 2021

X. Zhu, Phys. Rev. B 97, 205134 (2018).

21.

G. van Miert and C. Ortix, Quantum Mater. 5, 63

(2020).

A. C. Potter and P. A. Lee, Phys. Rev. Lett. 105,

227003 (2010).

22.

M. Jung, Y. Yu, and G. Shvets, arXiv:2010.10299

(2020).

N. Sedlmayr, J. M. Aguiar-Hualde, and C. Bena,

Phys. Rev. B 93, 155425 (2016).

23.

W. A. Benalcazar, T. Li, and T. L. Hughes, Phys.

Rev. B 99, 245151 (2019).

T. E. Pahomi, M. Sigrist, and A. A. Sluyanov, Phys.

Rev. Res. 2, 032068(R) (2020).

24.

M. Serina, D. Loss, and J. Klinovaja, Phys. Rev.

B 98, 035419 (2018).

S.-B. Zhang, A. Calzona, and B. Trauzettel, Phys.

Rev. B 102, 100503(R) (2020).

25.

А. Д. Федосеев, ЖЭТФ 155, 138 (2019).

10.

C. Nayak, S. H. Simon, A. Stern, M. Freedman, and

26.

В. В. Вальков, Письма в ЖЭТФ 111, 772 (2020).

S. D. Sarma, Rev. Mod. Phys. 80, 1083 (2008).

27.

V. V. Val’kov, A. O. Zlotnikov, A. D. Fedoseev, and

11.

A. Yoshida, Y. Otaki, R. Otaki, and T. Fukui, Phys.

M. S. Shustin, J. Magn. Magn. Mat. 440, 37 (2017).

Rev. B 100, 125125 (2019).

28.

V. V. Val’kov, A. O. Zlotnikov, and M. S. Shustin, J.

12.

J. Zou, Zh. He, and G. Xu, Phys. Rev. B 100, 235137

Magn. Magn. Mat. 459, 112 (2018).

(2019).

29.

A. M. Black-Schaffer and C. Honerkamp, J. Phys.:

13.

Q.-B. Zeng, Y.-B. Yang, and Y. Xu, Phys. Rev.

Condens. Matter 26, 423201 (2014).

B 101, 241104(R) (2020).

30.

M. Ezawa, Eur. Phys. J. B 85, 363 (2012).

14.

K. Asaga and T. Fukui, Phys. Rev. B 102, 115102

31.

T. Senthil, J. B. Marston, and M. P. A. Fisher, Phys.

(2020).

Rev. B 60, 4245 (1999).

15.

S.-B. Zhang, W. B. Rui, A. Calzona, S.-J. Choi,

32.

T. Chern, AIP Adv. 6, 085211 (2016).

A. P. Schnyder, and B. Trauzettel, Phys. Rev. Res.

2, 043025 (2020).

33.

D. J. Thouless, Phys. Rep. 13, 93 (1974).

16.

E. Khalaf, W. A. Benalcazar, T. L. Hughes, and

34.

N. C. Murphy, R. Wortis, and W. A. Atkinson, Phys.

R. Queiroz, arXiv:1908.00011 (2019).

Rev. B 83, 184206 (2011).

17.

M. Ezawa, Phys. Rev. Lett. 120, 026801 (2018).

35.

M. Calixto and E. Romera, J. Stat. Mech. 2015,

06029 (2015).

18.

X. Ni, M. Weiner, A. Alu, and B. Khanikaev, Nature

Mater. 18, 113 (2019).

36.

A. D. Fedoseev, J. Phys.: Condens. Matter 32, 215301

(2020).

19.

S. N. Kempkes, M. R. Slot, J. J. van den Broeke,

P. Capoid, W. A. Benalcazar, D. Vanmaekelbergh,

37.

В. В. Вальков, В. А. Мицкан, М. С. Шустин, Пись-

D. Cercioux, I. Swart, and C. M. Smith, Nature

ма в ЖЭТФ 106, 762 (2017).

Mater. 18, 1292 (2019).

38.

В. В. Вальков, В. А. Мицкан, М. С. Шустин,

20.

A. Yu. Kitaev, Phys. Usp. 44 (suppl), 131 (2001).

ЖЭТФ 156, 507 (2019).