ЖЭТФ, 2021, том 159, вып. 2, стр. 350-358

СТАТИСТИЧЕСКИЕ СВОЙСТВА СИСТЕМ МНОГИХ ЧАСТИЦ

С ИЕРАРХИЧЕСКОЙ СТРУКТУРОЙ

М. Ю. Романовский^*

Институт общей физики им. А. М. Прохорова Российской академии наук

119991, Москва, Россия

МИРЭА — Российский технологический университет

119454, Москва, Россия

Поступила в редакцию 21 апреля 2020 г.,

после переработки 9 октября 2020 г.

Принята к публикации 12 октября 2020 г.

Рассматриваются системы многих частиц, содержащихся внутри других частиц (задача 1), а также систе-

мы частиц, отграниченных внутри других частиц, которые, в свою очередь, отграничены внутри третьих

частиц (задача 2). При естественных предположениях о сохраняющихся величинах, таких как общее ко-

личество всех частиц, общей энергии и ряда других, изучается наивероятнейшие распределения частиц

по энергии — истинные (внутренние) и внешние — наблюдаемые. Результаты задач 1 и 2 могут тракто-

ваться как разделение частиц нижнего уровня на сорта с разными распределениями, наблюдаемыми в

разных экспериментах. В одночастичных наблюдениях в полной вероятностной задаче 1 непротиворечи-

вым образом возникает эффективный принцип Паули.

DOI: 10.31857/S0044451021020140

рактеристики конкретных физических систем нахо-

дятся как частные случаи применения этого общего

1. ВВЕДЕНИЕ

распределения (распределения Гиббса). Это дости-

Известно

[1, 2], что система тождественных

гается путем введения ограничений, вытекающих из

неразличимых частиц с дискретным энергетичес-

физических свойств рассматриваемых систем. На-

ким спектром при естественных предположениях

пример, функции распределения для идеальных га-

о конечном числе всех частиц и существова-

зов Ферми и Бозе получаются при учете перестано-

нии средней энергии частицы дает в качестве

вочной симметрии частиц. Назовем этот результат

наивероятнейшей экспоненциальную плотность

«задачей 0». Термодинамические величины и зако-

вероятности распределения¹⁾ нахождения частицы

ны в такой системе бесструктурных частиц хоро-

в определенном i-м энергетическом состоянии ϵ_i

шо известны. В настоящей работе в качестве кон-

вида

кретных объектов рассматриваются системы, состо-

W (ϵ_i) =

e-ϵi/τ ,

ящие из неразличимых частиц, имеющих внутрен-

нюю структуру.

где τ

— нормировочный коэффициент, имеющий

смысл некоторой средней энергии или эффективной

Такие более сложные системы, состоящие из

температуры системы частиц. Статистические ха-

неразличимых частиц, имеющих внутреннюю

структуру, во-первых, модифицируют термоди-

^* E-mail: slon@kapella.gpi.ru

намические соотношения, как, например, это

¹⁾ Далее для простоты мы будем именовать функции плот-

происходит для плазмы

[3], так и приводят к

ности вероятности распределения функциями распределения

новым эффектам типа «отрицательного трения» [4]

и просто распределением. Отметим также, что реально в ра-

боте под частицей понимается энергетическое состояние сис-

(такие частицы часто именуются «активными»).

темы, более точно — какая-нибудь наблюдаемая характери-

Поэтому естественно возникает вопрос, что будет

стика, определяемая этим состоянием — дипольный момент,

происходить с распределениями частиц по энергии,

магнитный момент, и т. д., см. ниже. По-видимому, рассмот-

рение может быть применено и вовсе не к физическим систе-

если определенные группы частиц отграничены

мам.

от других, или одни частицы (назовем их части-

350

ЖЭТФ, том 159, вып. 2, 2021

Статистические свойства систем многих частиц. ..

цами верхнего уровня) содержат другие (нижнего

Решение задачи 1 подсказывает комбинаторная

уровня, также неразличимые). Здесь термин «от-

проблема о количестве комбинаций при распреде-

граничение» представляется наиболее адекватным

лении одинаковых предметов по группам. Решение

для последующего анализа поведения иерархиче-

задачи 2 будет приведено далее.

ских систем частиц, аналогичным раскладыванию

по коробкам (и отдельных коробок по еще большим

2. ЗАДАЧА 1

коробкам, как в задаче 2, см. ниже), как это было

сделано в работах [1, 2].

Пусть имеется набор (m_i) частиц верхнего уров-

Эта задача также рассматривалась (см., напри-

ня таких, что в m₁ таких неразличимых частицах

мер, [1]). При дополнительном предположении об

содержится по p₁ частиц нижнего уровня²⁾, в m₂ —

a priori разном количестве частиц нижнего уров-

по p₂, и т. д. вплоть до N-й частицы нижнего уровня.

ня внутри частиц верхнего уровня, наивероятней-

Здесь n — общее количество различных расстановок

шее распределение дается большим каноническим

частиц нижнего уровня по частицам верхнего уров-

ансамблем. Условие тождественности частиц верх-

ня. Полное количество N частиц нижнего уровня

него уровня здесь не ставится. Назовем это «задачей

0^′». Дело не обязательно ограничивается частицами

∑

N = m_ip_i

(1)

и распределениями по энергии - можно рассматри-

i=1

вать, например, системы, имеющие внутри опреде-

ленные структуры, которые оказывают влияние на

распределено всего по M частицам верхнего уровня

внешние проявления системы, в этом случае роль

∑

«распределения по энергии» частиц нижнего уров-

M = m_i.

(2)

ня играет распределение по какому-то свойству (или

i=1

признаку) системы нижнего уровня.

При этом общее количество перестановок всех час-

Естественным является переход к задаче с уче-

тиц нижнего уровня по всем частицам верхнего

том наблюдаемой неразличимости частиц верхнего

уровня есть W₁₀ [5]:

уровня, назовем это «задачей 1». Здесь следует най-

ти наивероятнейшие распределения частиц нижне-

W₁₀ =

(3)

го уровня по энергии. Нельзя исключить, что таких

∏

распределений может быть несколько. Во-первых,

(p_i!)mi

это «истинные» распределения по энергии частиц

i=1

нижнего уровня в одной частице верхнего уровня.

а при условии упомянутой неразличимости частиц

Следует при этом выяснить, являются ли они на-

верхнего уровня

блюдаемыми, и если да, то в каких экспериментах.

Во-вторых, какие распределения будут наблюдае-

W₁₁ =

(4)

мыми, и в чем их отличие от истинных. Естествен-

∏

(p_i!)m

(m_i!)

ным пределом задачи 1 при наличии внутри части-

i=1

цы верхнего уровня только одной частицы нижнего

является (при определенных условиях) задача 0.

Обычно пользуются выражением ln W₁₁:

Постановка задачи может быть и более сложной,

∑

когда частицы имеют внутреннюю структуру в ви-

ln W₁₁ = ln N! - m_iln(p_i!) - ln(m_i!).

(5)

де других частиц, которые, в свою очередь, содер-

i=1

жат внутри себя еще и третьи частицы, это можно

Заметим, что, если здесь m_i≡1, то для задачи вы-

назвать задачей 2. Здесь также следует определить

числения наивероятнейшего распределения, опреде-

истинные и наблюдаемые наивероятнейшие распре-

ляемого условиями (1), (2), (4), мы имеем формули-

деления частиц нижнего уровня по энергии. Доста-

ровку, аналогичную формулировке задачи 0³⁾.

точно общепринятым является представление о час-

тицах, заключенных в коробки (см., например, [1]),

²⁾ Если вместо «частиц верхнего уровня» читать «связок»,

или в коробки с перегородками [2]. Последние мо-

вместо «частиц нижнего уровня» читать «грибов», то полу-

чится формулировка задачи о сушке грибов [5], или задача о

гут быть заключены в некоторые внешние коробки,

циклических перестановках [6].

тогда получается задача 2. Очевидные примеры за-

³⁾ Если в задаче о получении большого канонического ан-

дачи 2 (отнюдь не только физические) легко опре-

самбля допустить варьирование N, то ее можно свести к за-

делит читатель.

даче 1. Это не было сделано (см., например, [6]).

351

М. Ю. Романовский

ЖЭТФ, том 159, вып. 2, 2021

Пусть каждая частица нижнего уровня может

p_i = eα+γϵi

(11)

находиться в состоянии с какой-то энергией ϵ_i.

и, в свою очередь,

Для отыскания наивероятнейшего распределения по

этим энергиям при произвольном m_i следует учесть,

m_i = eβ+pi.

(12)

что, кроме выражения (3) или (4), и связей (1) и (2)

еще имеются условия конечности полной энергии

Таким образом, истинная функция наивероятней-

всей системы частиц

шего распределения частиц нижнего уровня по

энергии оказывается точно такой же, как и наиве-

∑

роятнейшая функция распределения в задаче 0 —

E= m_ip_iϵ_i,

(6)

это вероятность найти частицы нижнего уровня в

i=1

энергетическом состоянии ϵ_i.

которое практически означает, что существует сред-

Однако эта функция не является прямо наблю-

няя «энергия» одной частицы нижнего уровня 〈ϵ〉.

даемой и прямо измеримой. Для того чтобы изме-

Решим задачу 1. Для этого сначала образуем ва-

рить эту функцию распределения, следует иметь

риацию от выражения (5) с учетом простейших свя-

прибор, измеряющий p_i в зависимости от ϵ_i. Сделать

зей (1), (2) и (6). Для этого в уравнение (5) надо

это в какой-то одной определенной частице верхне-

в правую часть добавить члены αN + βM + γE с

го уровня нельзя в силу неразличимости частиц m_i.

лагранжевыми множителями α, β, и γ:

Какие функции будут наблюдаемыми? Для выясне-

ния этого перепишем систему (9) и (10), образовав

∑

ln W₁ = ln N! - m_iln(p_i!) - ln(m_i!) +

простейшие линейные комбинации уравнений

i=1

∑

ln p_i ± ln m_i = α ± β + γϵ_i ± p_i =

+α m_ip_i +β m_i +γ m_ip_iϵ_i.

(7)

=α±β+γϵ_i ±eα+γϵi,

(13)

i=1

Используем также первое приближение формулы

где мы воспользовались выражением (11). Таким

Стирлинга по m! и p!, и проведем варьирование по

образом, рассматриваться должны две функции —

δp_i и δm_i. Тогда получим для вариации наивероят-

p_im_i и p_i/m_i, которые являются решениями систе-

нейшего распределения ln W₁:

мы (9) и (10).

Для дальнейшего анализа нужно определить

∑

константы в (9) и (10). Определим константу β. Ве-

δ ln W₁ =

[-(δm_i)p_i(ln p_i - 1) -

личина m_i изменяется от некоторого положительно-

i=1

го значения eβ+eα при ϵ_i = 0 до e^β при ϵ_i → ∞. При

- (δp_i)m_i ln p_i-(δm_i) ln m_i+β(δm_i)+α(δm_i)p_i +

больших ϵ_i ввиду очевидной отрицательности γ

+ αm_i(δp_i) + γ(δm_i)p_iϵ_i + γ(δp_i)m_iϵ_i] = 0.

(8)

eeα+γϵi ≃ 1 + eα+γϵi

(14)

Соберем члены при независимых вариациях δp_i и

δm_i. Для первой вариации, сократив все слагаемые

По смыслу задачи при больших энергиях частицы

на ненулевые величины δp_i и m_i, получим первое

нижнего уровня вряд ли может быть много частиц

уравнение системы:

верхнего уровня, содержащих такую энергичную ча-

стицу нижнего уровня, и естественным образом для

ln p_i = α + γϵ_i.

(9)

задачи 1 можно положить, что β = 0 при ϵ_i → ∞, и

Для второй вариации, сократив на ненулевую вели-

m_i стремится к 1 при ϵ_i → ∞, т.е. β = 0.

чину δm_i и использовав уравнение (9), получим

Очевидно, что функция p_im_i потенциально

должна наблюдаться, поскольку она описывает

ln m_i = β + p_i.

(10)

распределение числа частиц (1). Эта функция зна-

Уравнения (9) и (10) дают решение задачи 1.

чительно отличается от p_i (см. рис. 1, определения

Решение уравнения

(9) точно соответствует

функций 1-4 на этом рисунке см. ниже):

обычному распределению Гиббса (см. Введение,

[1, 2]) и решению задачи 0. Отличия же от решения

p_im_i = eα+γϵieeα+γϵi .

(15)

задачи 0^′ заключаются в том, что в задаче 0^′ не

Нормированная функция этого распределения

осуществляется варьирование по числу частиц

верхнего уровня. Решения системы

(9) и

(10)

eα+γϵieeα+γϵi

очевидны:

(p_im_i)_norm = |γ|

(16)

eeα - 1

352

ЖЭТФ, том 159, вып. 2, 2021

Статистические свойства систем многих частиц. ..

Вторая функция, являющаяся решением (13) —

функция p_i/m_i — это распределение p_i в расчете на

одну частицу верхнего уровня из набора m_i, она так-

же представлена на рис. 1. Условия ее наблюдения

очевидно отличаются от p_im_i. По-видимому, наибо-

лее близкими по смыслу будут одночастичные изме-

рения энергетических спектров (в широком смысле

спектроскопические наблюдения).

Рассмотрим распределение частиц нижнего

уровня по энергиям в «среднем» на одну частицу

верхнего уровня p_i/m_i:

p_i

=eα+γϵie-eα+γϵi.

(17)

m_i

Здесь очевидно, что γ имеет смысл некоторой «об-

ратной температуры» системы; нормировка на 1

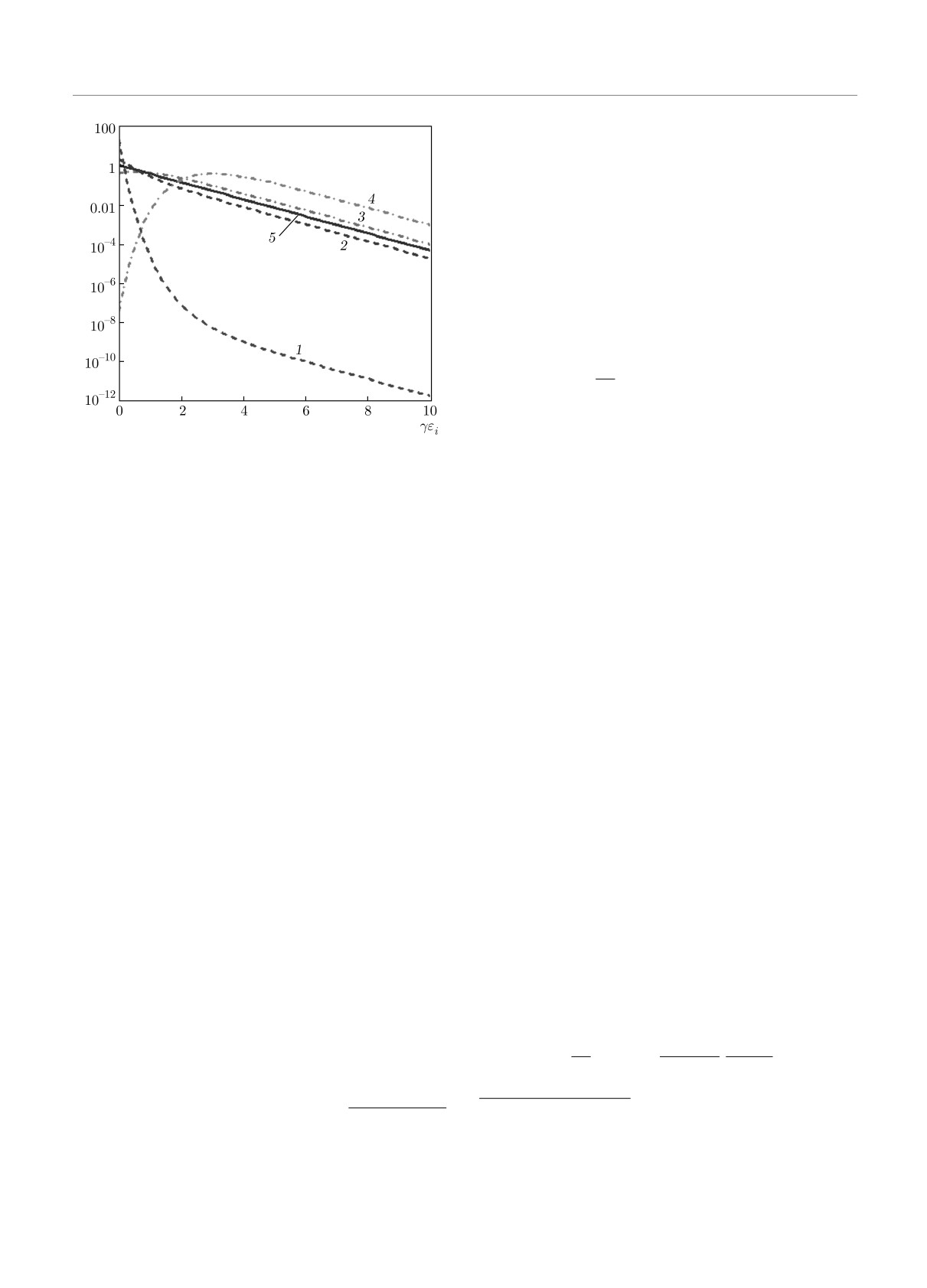
Рис.

1. Нормированные функции распределения pimi

распределения (17) дает множитель |γ|/(1 - e-eα ),

(штриховые кривые 1 и 2) и pi/mi (штрихпунктирные кри-

что уже при умеренном и тем более большом α прак-

вые 3 и 4) при различных параметрах нормировки α (для

тически совпадает с |γ|. Функция

(17) достигает

кривых 1 и 4 α = 3, для кривых 2 и 3 α = 0.5, приня-

максимума при ϵ_i = α/|γ|, а поскольку α является

то |γ| = 1), а также pi = |γ|eγϵi (сплошная прямая 5).

лагранжевым множителем при полном числе час-

Полулогарифмический масштаб

тиц (1), модельный «физический» смысл α (а точ-

нее, α/|γ|) может состоять в том, что это химиче-

ский потенциал частиц нижнего уровня μ, а α =

= |γ|μ. Заметим, что плотность вероятности (17)

совпадает с плотностью вероятности распределения

для α/|γ| = 0.5, 3 и кривых 1, 2 приведена на рис. 1

Гумбеля (типа I) [7].

в виде штриховых кривых. При увеличении α/|γ|,

Если продвинуться к физическим приложениям

т. е. например при уменьшении температуры при по-

рассматриваемой задачи 1, то, по-видимому, функ-

стоянном α, значение функции (16) в нуле по срав-

ции распределения (15) и (17) (а также нормирован-

нению с прямой 5 резко возрастает, а асимптотиче-

ные функции распределения и функции распределе-

ское при умеренных и больших ϵ_i — очень сильно

ния, возникающие в Задаче 2) следует понимать как

падает (см. рис. 1). Таким образом, распределение

распределение Гиббса (так как везде наличеству-

p_im_i (или (p_im_i)_norm) описывает, по-видимому, кон-

ет гиббсов фактор eγϵi), возникающее в системах

денсацию частиц нижнего уровня при малых энер-

с определенным взаимодействием — отграничением,

гиях, которая оказывается очень значительной при

неразличимостью частиц всех уровней и связанной

низких эффективных температурах (далее эффек-

с этим иерархией. Такое взаимодействие приводит к

тивную температуру будем именовать температу-

появлению дополнительного фактора в (15) и (17),

рой для краткости). Наблюдаемость этой функции

а также в функциях распределения, возникающих в

лучше всего реализуется в многочастичных эффек-

Задаче 2. Этот фактор может быть отнесен на со-

тах типа фазовых переходов, когда «все» частицы

ответствующий термодинамический потенциал (см.

(верхнего уровня) участвуют в процессе. Здесь ситу-

[1, 2])⁴⁾.

ация не зависит качественно от величины α. Следу-

Для удобства расчетов приведем нормированное

ет, тем не менее, обратить внимание на значительное

на 1 распределение p_i/m_i:

уменьшение p_im_i при умеренных значениях энергии

в сравнении с функцией p_i (на несколько порядков)

⁽p_i )

|γ|

eα+γϵi

уже при умеренных α. Для восстановления истин-

(18)

m_inorm

1-e-eα eeα+γϵi

ного распределения p_i по p_im_i и p_i/m_i следует при-

бегнуть к процедуре мультипликативного среднего

√

⁴⁾ Прозрачный способ получения функций распределений

(среднего геометрического): pi =

(p_im_i)(p_i/m_i),

в зависимости от определенного потенциала взаимодействия

что относительно несложно может быть реализова-

частиц, не такой, как в предлагаемой статье, рассмотрен, на-

но в том числе экспериментально.

пример, в работах [8, 9].

353

ЖЭТФ, вып. 2

М. Ю. Романовский

ЖЭТФ, том 159, вып. 2, 2021

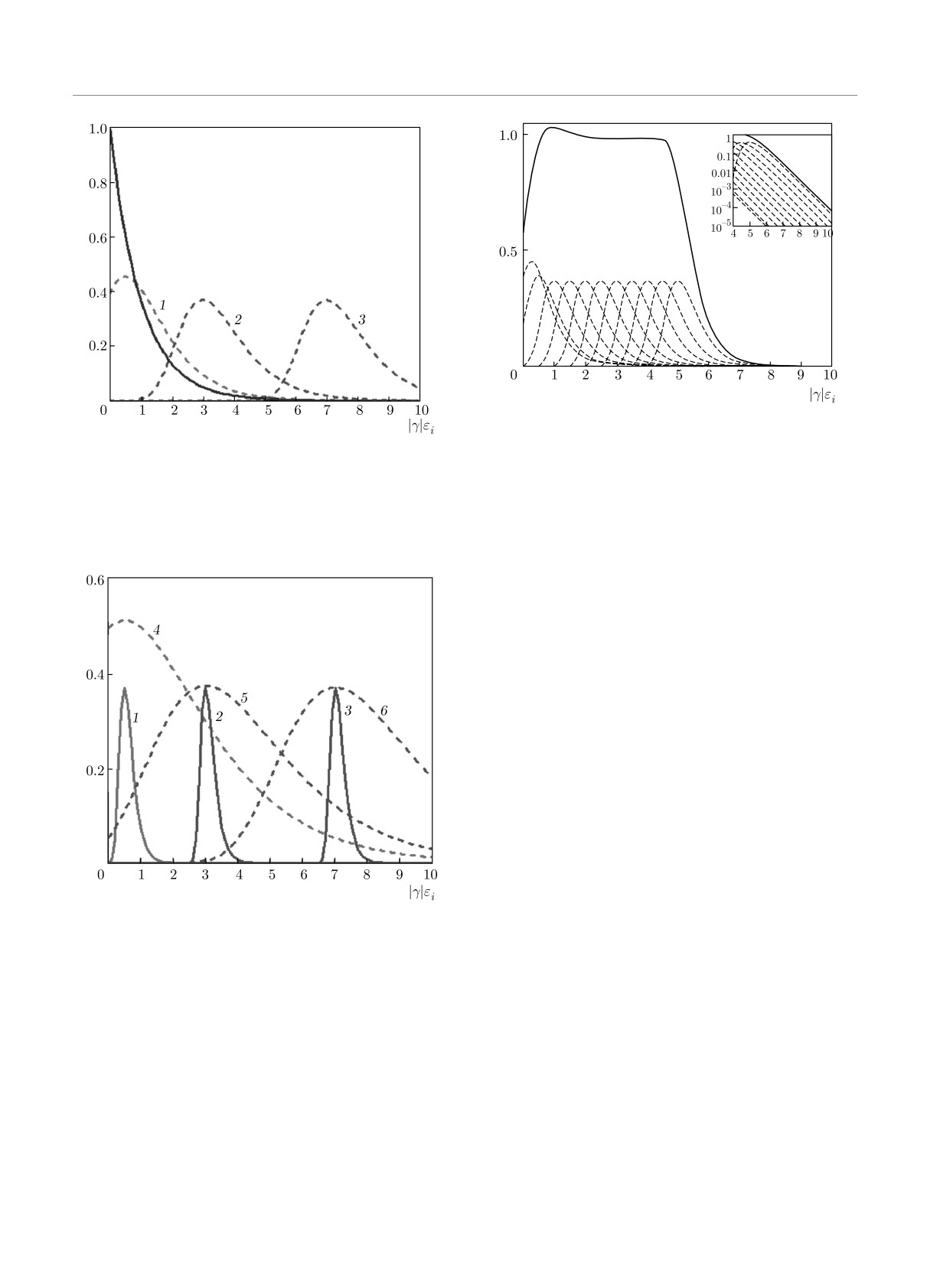
Рис. 4. Функции (pi/mi)norm (штриховые кривые) с α от

0.5 до 5 (через 0.5), а также сплошная кривая, представля-

Рис. 2. Нормированные на 1 функции от ϵi плотности веро-

ющая сумму всех этих (pi/mi)norm. На вставке в полуло-

ятности нормированного распределения (pi/mi)norm (18)

гарифмическом масштабе приведены значения этих функ-

при α = 0.5, 3, 7 (штриховые кривые 1-3 соответственно).

ций для больших аргументов — видна экспоненциальная

Сплошная кривая — распределение |γ|e(γϵi). Равномерный

асимптотика суммарной функции. Принято |γ| = 1

масштаб |γ| принята равной 1

на на рис. 3. Видно значительное «сужение» макси-

мумов (18) при увеличении |γ|, т. е. при уменьшении

эффективной температуры. Рисунки 2 и 3 показы-

вают, что распределение (17) (и (18)) имеет выра-

женный максимум распределения, совпадающий с

величиной химического потенциала ϵ_i = μ = α/|γ|.

Это означает, что при измерениях «на одну части-

цу» верхнего уровня частицы нижнего уровня мо-

гут присоединяться к (или отсоединяться от) части-

це верхнего уровня только в энергетические состоя-

ния, близкие μ. При понижении температуры шири-

на функции распределения уменьшается, и при ма-

лых температурах функция распределения может

стать настолько узкой, что в это состояние «помес-

тится» уже не более одной частицы нижнего уровня.

Закономерен вопрос, в какие состояния уходят

остальные частицы нижнего уровня. На рис. 4 изоб-

ражена модельная ситуация, где присутствует ан-

Рис. 3. Нормированные на 1 функции от ϵi плотности веро-

самбль частиц верхнего уровня с разными α (разны-

ятности нормированного распределения (pi/mi)norm (18)

при α = 0.5, 3, 7. Для штриховых кривых 1-3 |γ| = 0.5, для

ми химическими потенциалами для частиц нижнего

сплошных кривых 4-6 |γ| = 5. Равномерный масштаб

уровня).

В этом случае остальные частицы нижнего уров-

ня разместятся в энергетических состояниях соот-

На рис. 2 приведена функция (18) для нескольких

ветствующих распределений (штриховые кривые на

значений α. Вместе с возрастанием α (кривые 1-3

рис. 4) с одинаковыми максимумами. При плотном

соответственно) нормировочный множитель в (18)

распределении с αmin < α < αmax (αmin может

стремится к 1, и распределение (p_i/m_i)_norm просто

быть и нулем) суммарное распределение (сплошная

транслируется вдоль оси абсцисс в неизменном виде.

кривая на рис. 4) по энергии в этом случае будет

Зависимость (18) от коэффициента |γ|, т. е. от

выглядеть как постоянное до ϵ < α_max/|γ|, а за-

некоторой эффективной температуры, представле-

тем экспоненциально убывать (см. врезку рис. 4).

354

ЖЭТФ, том 159, вып. 2, 2021

Статистические свойства систем многих частиц. ..

Такое суммарное распределение будет практически

ственно определяются теперь общее количество час-

полностью совпадать с распределением Ферми с μ =

тиц нижнего уровня

= μ_max = α_max/|γ|. Этот результат наиболее оче-

∑

видно следует трактовать как проявление некото-

N = m_ip_it_i,

(20)

рого эффективного принципа Паули.

i=1

Для этого же вполне можно ограничиться, не

общее количество частиц среднего уровня

прибегая к сложным построениям рис. 4, тем сооб-

ражением, что при одночастичных измерениях со-

∑

стояния системы частиц всегда будет детектиро-

M = m_it_i

(21)

ваться некоторая энергия частицы нижнего уровня,

i=1

причем при малых температурах частиц эта энергия

и общее количество частиц верхнего уровня

может быть единственной — остальные значения мо-

гут просто не попасть «внутрь» кривых 1-3 рис. 3 в

∑

силу расстояния между уровнями дискретного энер-

T = t_i.

(22)

i=1

гетического спектра. Таким образом, одному энерге-

тическому состоянию будет соответствовать только

Выражение для полной энергии соответствует

одна частица: это также можно истолковать как осу-

ществление эффективного принципа Паули.

∑

E =

m_ip_it_iϵ_i.

(23)

i=1

По общему правилу образуем логарифм от этого ко-

3. ЗАДАЧА 2

личества расстановок

Как указывалось во Введении, возможна поста-

∑

новка задачи о распределении по энергиям час-

ln W₂₁ = ln N! - m_it_iln(p_i!) -

тиц нижнего уровня, содержащихся в наборе час-

i=1

тиц среднего уровня, которые, в свою очередь, со-

∑

держатся в наборе частиц верхнего уровня. На всех

− t_iln(m_i!) - ln(t_i!).

(24)

i=1

трех уровнях частицы являются неразличимыми⁵⁾.

Обозначим количество частиц нижнего уровня, со-

Соответственно, варьироваться должна величина

держащихся в частице среднего уровня, через p_i,

(24) с наложенными связями (20)-(23) с необходи-

количество частиц среднего уровня с таким коли-

мыми множителями Лагранжа α, β, γ, Δ, аналогич-

чеством частиц нижнего уровня в частицах средне-

ная (7):

го уровня m_i, и количество частиц верхнего уровня,

в которые сложены частицы среднего уровня в ко-

ln W₂ = ln W₂₁ + αN + βM + γE + ΔT.

(25)

личестве m_i, через t_i. В этом случае полное коли-

чество расстановок частиц нижнего уровня по всем

Переменные варьирования теперь p_i, m_i, t_i. При ва-

частицам среднего уровня, и последних по частицам

рьировании по p_i получаем первое уравнение, точно

верхнего уровня запишется как

совпадающее с уравнением (7) (и с решением зада-

чи 0):

ln p_i = α + γϵ_i.

(26)

W₂₁ =

(19)

∏

(p_i!)mitⁱ

(m_i!)ti

(t_i!)

Варьируя (25) по m_i и используя (26), имеем урав-

i=1

нение, точно совпадающее с уравнением (10):

Здесь n — снова полное число различных расстано-

ln m_i = β + p_i.

(27)

вок частиц нижнего уровня по частицам среднего

Наконец, варьируя (25) по t_i и используя (26) и (27),

уровня, а тех — по частицам верхнего уровня. Есте-

имеем третье уравнение задачи 2:

⁵⁾ На языке обобщенной «задачи о сушке грибов» это бу-

ln t_i = Δ + m_i.

(28)

дет подсчет распределения длин связок грибов, которые, в

свою очередь, объединены в пучки разной величины. Нераз-

личимыми теперь являются не только связки, но и пучки, не

Сделаем некоторые замечания относительно вели-

говоря уже о самих грибах.

чин β и Δ. Последняя входит во все выражения

355

11*

М. Ю. Романовский

ЖЭТФ, том 159, вып. 2, 2021

как простой множитель, т. е. нужна только в слу-

чае какой-то специальной нормировки, в первом же

приближении ее можно считать равной нулю, хотя

естественным было бы Δ = -1, тогда t_i стремилась

бы к 1 при ϵ_i → ∞ (см. выше).

Величину β в задаче 2 в первом приближении

можно считать совпадающей с β из задачи 1, т. е.

тоже равной нулю. Анализ показывает, что нерав-

ная нулю β меняет вид распределений задачи 2, но

только количественно. Она может описывать опре-

деленное число частиц нижнего уровня в частице

среднего (верхнего в задаче 1) уровня, существую-

щее при больших энергиях. Более полное выяснение

физического смысла β = 0 есть предмет отдельной

работы.

Создадим, как в задаче 1, простейшую линей-

ную комбинацию уравнений (26)-(28) и воспользу-

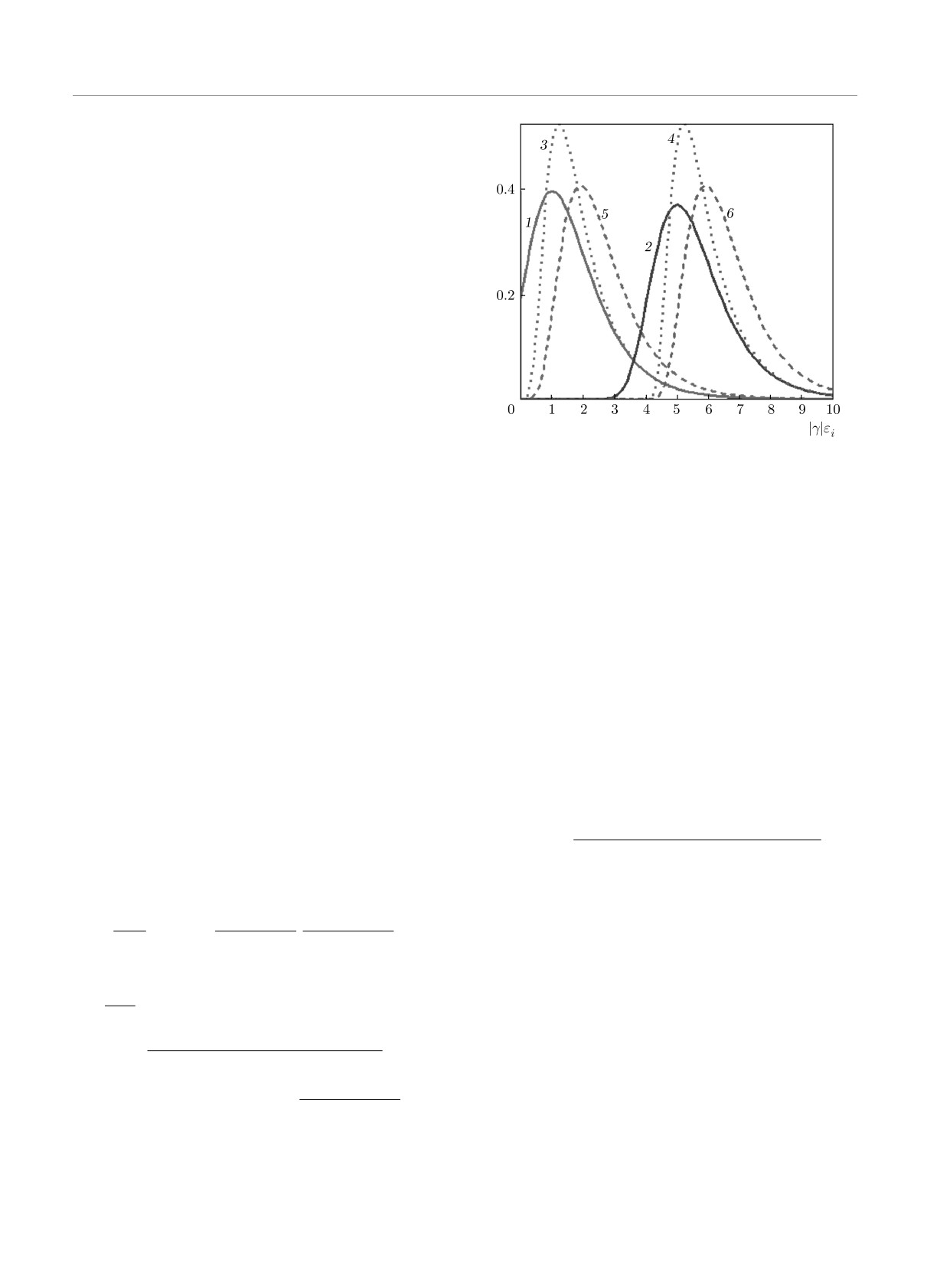
Рис. 5. Нормированные на 1 функции от ϵi плотности ве-

емся их решениями. Получим

роятности распределения pi/miti (кривая 5 для α = 1 и

кривая 6 для α = 5), pimi/ti (кривая 3 для α = 1 и кри-

ln p_i ± ln m_i ± ln t_i = α ± β ± Δ + γϵ_i±

вая 4 для α = 5). Для сравнения приведены распределе-

±eα+γϵi ±eβ+eα+γϵi.

(29)

ния (18) (кривая 1 для α = 1 и кривая 2 для α = 5).

Равномерный масштаб, |γ| принята равной 1

По аналогии с задачей 1, решениями (29) и функ-

циями распределения теперь являются выражения

p_i/m_it_i, p_im_i/t_i, p_im_it_i, а также p_it_i/m_i. Третья

и 6 для (31)). Так же, как и для задачи 1, функ-

функция описывает рассмотренные многочастич-

ции (30) и (31) являются некоторыми измеренны-

ные измерения с эффектом конденсации частиц при

ми на одну частицу верхнего уровня «средними»

малых энергиях, еще более сильной, чем аналогич-

функциями. На рис. 6 представлено поведение нор-

ная конденсация в задаче 1. Первые же два соотно-

мированных распределений (30), (31) в зависимо-

шения описывают некоторые, измеренные либо на

сти от эффективной температуры, кривые 1 и 3 —

одну частицу среднего уровня, либо на одну частицу

для сравнительно более малой температуры |γ| =

верхнего уровня, функции, имеющие выраженный

= 5, кривые 2 и 4 — для большей |γ|

= 0.5.

максимум. Теперь, однако, этот максимум не сов-

Видно превышение абсцисс максимумов распреде-

падает с величиной α, а превышает ее: для p_i/m_it_i

лений (30), (31) над величиной химического потен-

примерно на 1 в условиях рис. 5 (соответствует при-

циала. Истинная функция распределения p_i опять

метно одной единице эффективной температуры), и

выражается через среднее геометрическое наблюда-

√

на 0.2 (соответствует приметно 0.2 единиц эффек-

емых p_i =⁴

(p_i/m_it_i)(p_im_i/t_i)(p_im_it_i)(p_it_i/m_i).

тивной температуры) для p_im_i/t_i.

Нормированные распределения суть

4. ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

⁽p_im_i)

|γ|

eα+γϵieeα+γϵi

(30)

Результаты задач 1 и 2 можно интерпретировать

t_i

norm

1/e - e-eeα eeeα+γϵi

как зависящие от способа наблюдения. Все наблю-

дения в спектроскопических экспериментах (не обя-

(

)

p_i

зательно оптических, вообще большинства измере-

m_it_inorm

ний спектров энергии) дают некоторые отнесенные

|γ|

к одной частице верхнего уровня функции распре-

1/e - E₁(eeα) + E₁(1) - eeαe-eeα

деления. Основным результатом задачи 1 является

обнаружение максимума распределения частиц по

-eα+γϵi

eα+γϵi e

(31)

энергиям при одночастичном наблюдении. В самом

eeeα+γϵi

простом подходе к описанию этот максимум сов-

где E₁(x) — интегральная показательная функция,

падает с химическим потенциалом частиц нижнего

изображены на рис. 5 (кривые 3 и 4 для (30) и 5

уровня в частицах верхнего уровня — энергией при-

356

ЖЭТФ, том 159, вып. 2, 2021

Статистические свойства систем многих частиц. ..

Поведение другой наблюдаемой функции зада-

чи 1, p_im_i, также определяется температурой. Уже

при умеренных значениях α ≃ 6 доля частиц нор-

мированного распределения (13) с энергиями боль-

шими соответствующего значения химического по-

тенциала

10-180, т. е. таких (свободных?) частиц,

весьма вероятно нет во всей Вселенной. Вообще на-

ивная интерпретация результатов задачи 1 с двумя

функциями распределения, p_im_i и p_i/m_i, состоит в

том, что мы имеем дело с частицами двух сортов —

псевдобозонов для первой функции (так как она да-

ет конденсацию в низкоэнергетических состояниях

при малой температуре), и псевдофермионов (так

как при малых температурах одно энергетическое

состояние занимает одна такая частица).

Такая же интерпретация результатов задачи 2

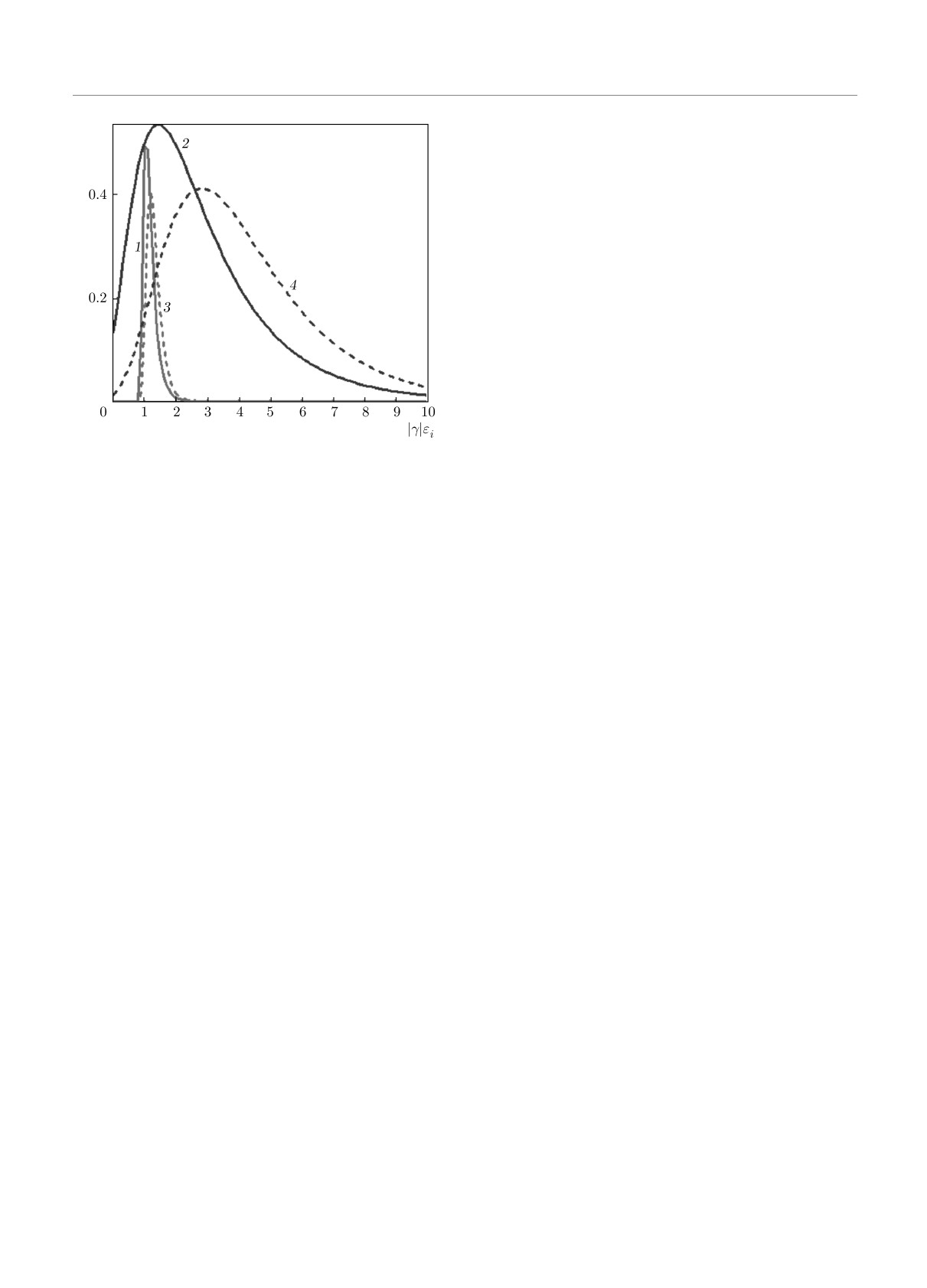
Рис. 6. Нормированные на 1 функции от ϵi плотности ве-

приводит к 4 сортам частиц. Псевдобозоны с еще

роятности распределения (pimi/ti)norm (30) при α = 1,

более выраженным эффектом конденсации описы-

для сплошной кривой 1 |γ| = 5, для сплошной кривой 2

ваются функцией p_im_it_i, частиц с энергиями боль-

|γ|

= 0.5. Вероятности нормированного распределения

шими химического потенциала здесь нет вовсе. По-

(pi/miti)norm (31) при α = 1, для штриховой кривой 3

хожие результаты дает функция p_it_i/m_i, но эф-

|γ| = 5, для штриховой кривой 4 |γ| = 0.5

фект конденсации в ней выражен меньше. Напро-

тив, частицы верхнего уровня, описываемые функ-

циями p_i/m_it_i, p_im_i/t_i, в основном содержат час-

тицы нижнего уровня в энергетических состояниях

соединения/отсоединения частицы нижнего уровня

выше химического потенциала. Простейшая интер-

от остальных таких частиц в частице верхнего уров-

претация этого — они не связаны в частицах сред-

ня. При этом простом подходе все частицы нижне-

него уровня, но связаны и «обобщены» в частицах

го уровня с энергиями меньше химического потен-

верхнего уровня.

циала должны интерпретироваться как связанные.

Отношение доли связанных состояний к несвязан-

Несомненно, распределение по энергетическим

ным состояниям в общем количестве всех состояний

уровням полной системы, объединяющей частицы

частиц нижнего уровня описывается соотношением

всех уровней, подчиняется распределению Гиббса.

(1 - e1-eα )/(e - 1).

Однако, как отмечалось выше, эти вероятности —

совсем не те величины, которые наблюдаются в

Как уже указывалось, при малых эффективных

реальных экспериментах. Наблюдаемые характери-

температурах функция плотности вероятности най-

стики системы — дипольный момент, магнитный мо-

ти частицу нижнего уровня в одночастичном изме-

мент, момент инерции или, возможно, в ряде слу-

рении в состоянии ϵ_i имеет очень узкий максимум

чаев, частота излучения — как раз и определяются

(см. рис. 3). Это значит, что при определенной малой

распределениями высшего уровня, рассмотренными

(и еще меньшей) температуре это состояние занима-

в данной работе. Очевидно, что это коллективные

ет не более одной частицы. Подобный результат мо-

характеристики, и говорить о «чистых» бозонах или

жет быть истолкован как реализация эффективно-

фермионах не следует. С другой стороны, ферми-

го принципа Паули — когда одно энергетическое со-

подобные функции распределения возникают в ста-

стояние занимает одна частица определенного сор-

тистической физике вполне классических систем с

та, соответствующая знаку «-» в левой части (13).

большим числом локальных минимумов энергии, са-

Некоторая модификация задачи 1, в которой воз-

мая известная — это так называемая KPZ (струна

никает набор функций p_i/m_i с различными α, при-

на случайном рельефе), сводящаяся к уравнению

водит при суммировании этих функций к функции,

Бюргерса со случайным шумом, в которой возни-

практически точно совпадающей с распределением

кает нечто вроде ударных волн в пространстве ве-

Ферми. Это еще одна возможная реализация эффек-

роятностей. Проследить за явным возникновением

тивного принципа Паули, появляющаяся в результа-

такой функции можно в работе [10].

те решения задачи 1.

357