БИОФИЗИКА, 2023, том 68, № 5, с. 1038-1045

БИОФИЗИКА CЛОЖНЫX CИCТЕМ

УДК 577.354

МОДЕЛИРОВАНИЕ КРИТИЧЕСКОЙ ЧАСТОТЫ СЛИЯНИЯ МЕЛЬКАНИЙ

В ЗРИТЕЛЬНОЙ СИСТЕМЕ ЧЕЛОВЕКА

*Институт общей физики им. А.М. Прохорова РАН, ул. Вавилова, 38, Москва, 119991, Россия

^#E-mail: dc.cetsil@gmail.com

**Институт когнитивных исследований Санкт-Петербургского государственного университета,

Университетская наб., 7/9, Санкт-Петербург, 199034, Россия

^##E-mail: shoshinaii@mail.ru

Поступила в редакцию 05.03.2023 г.

После доработки 01.05.2023 г.

Принята к публикации 17.05.2023 г.

Временная разрешающая способность зрительной системы имеет важное значение для восприятия

объективного мира. Наименьшая частота дискретизации последовательности изображений, при

которой восприятие становится слитным, называется критической частотой слияния мельканий.

Многообразие экспериментальных данных о порогах критической частоты может найти

объяснение с позиций предложенной модели контрастной чувствительности зрительной системы,

основанной на треморном модуляционном сигнале. Модель описывает зависимость критической

частоты слияния мельканий от яркости стимула, яркости адаптации, длительности и углового

размера стимула. Модель демонстрирует, что для ярких стимулов с малой длительностью и

большим угловым размером значения критической частоты лежат в диапазоне до 1000 Гц;

оптимальной для зрительной системы следует считать кадровую частоту 300-500 Гц; для

малоразмерных угловых стимулов критическая частота лежит в области низких частот. Различия в

скорости слияния мерцаний могут быть объяснены временной чувствительностью нейронов магно-

и парвоцеллюлярной зрительных подсистем.

Ключевые слова: критическая частота слияния мельканий, треморный модуляционный сигнал,

динамическая световая нагрузка, яркость адаптации, магноцеллюлярная система, парвоцеллюлярная

система.

DOI: 10.31857/S0006302923050253, EDN: NHUUMD

В качестве теста для определения КЧСМ

Скорость, с которой мозг обрабатывает визу-

обычно используется диск на равномерном фоне,

альную информацию, имеет важное значение для

яркость которого модулирована меандром с ам-

мозга, обеспечивающего построение внутренней

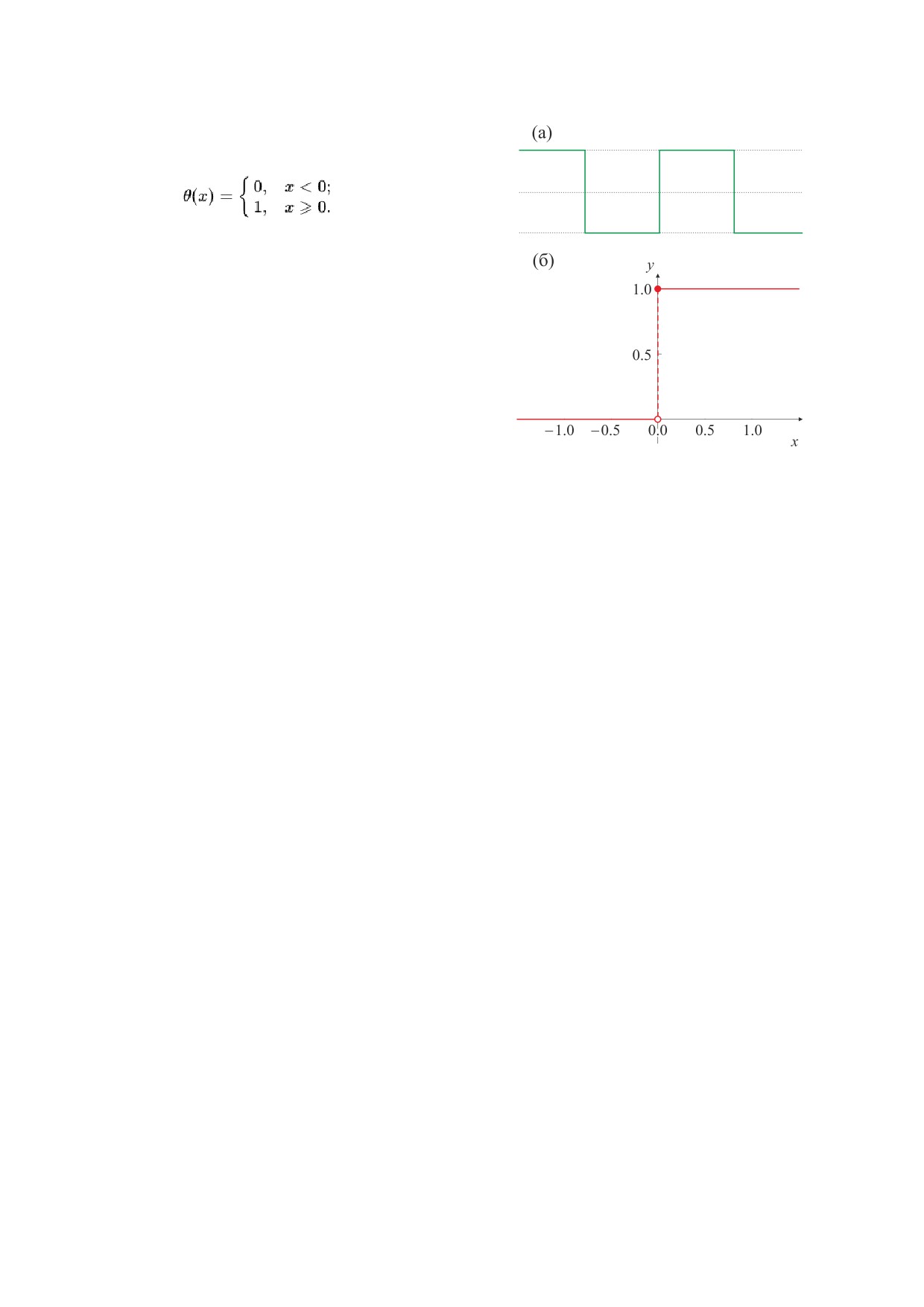
плитудой 0 и 1. Меандр - периодический сигнал

картины внешнего мира и адаптацию к его изме-

прямоугольной формы (рис. 1а), у которого дли-

нениям. Зрительная система характеризуется раз-

тельности положительной и отрицательной полу-

решающей способностью в пространственной и

волн равны. Аналитически меандр может быть за-

временной областях. Пространственное разреше-

писан с помощью функции Хевисайда, широко

ние в зрительной системе определяется как спо-

используемой для представления сигналов, пере-

ходящих в определенный момент времени из од-

собность различать в пространстве два соседних

ного состояния в другое:

объекта, временное разрешение - способность

различать изменения яркости во времени. Наи-

(1)

меньшая частота дискретизации (различения)

последовательности изображений, при которой

где S - скважность или отношение периода сле-

восприятие становится слитным, называется

дования (повторения) импульсов к длительности

критической частотой слияния мельканий

импульса, t - время, Т - период. Меандр описы-

(КЧСМ).

вается как S = 2.

Сокращения: КЧСМ

- критическая частота слияния

Функция Хевисайда - функция единичного

мельканий, ТМС - треморный модуляционный сигнал.

скачка [1] (рис. 1б), равная нулю для отрицатель-

1038

МОДЕЛИРОВАНИЕ КРИТИЧЕСКОЙ ЧАСТОТЫ СЛИЯНИЯ МЕЛЬКАНИЙ

1039

ных значений аргумента и единице - для поло-

жительных:

(2)

Показано, что КЧСМ зависит от яркости адап-

тации, яркости стимула, углового размера стиму-

ла и локализации его проекции на сетчатке, спек-

трального состава излучения и скважности ме-

андра

- соотношения периода повторения

световых импульсов к их длительности [2].

Регистрация КЧСМ находит приложение в ме-

дицине для оценки состояния центральной нерв-

ной системы, особенностей восприятия у лиц с

различными расстройствами [3-6]. Технический

аспект ее применения распространяется на обла-

сти от проектирования проблесковых маячков до

эргономики источников света и мониторов [7-

12].

Рис. 1. Сигнал прямоугольной формы - меандр (а) и

Для проблесковых источников света с ярко-

описывающая его единичная функция Хэвисайда (б),

которая при x = 0 доопределена значением 1.

стью до 1000 кд/м² КЧСМ определяется следую-

щим выражением [7]:

f_c = 12log(Lp) + 35,

(3)

ухудшающими пространственное разрешение и

контрастную чувствительность зрительной си-

что ограничивает КЧСМ значением 71 Гц.

стемы. Это означает, что на данных угловых ско-

По мере развития техники телевизионные

ростях зрительная система накапливает отноше-

стандарты кадровой частоты, связанные с

ние сигнал/шум без потерь. Во-вторых, тремор и

КЧСМ, демонстрируют увеличивающиеся значе-

дрейф составляют пару ортогональных движений

ния: 25, 30, 60 и 90 Гц, а производители монито-

и имеют соизмеримую угловую скорость, что

ров компьютеров и смартфонов успешно осваи-

обеспечивает двухкоординатную модуляцию сиг-

вают кадровые частоты 90, 120, 144, 240 и даже

нала.

360 Гц. Показано, что среди источников света

глаз регистрирует мерцание ламп дневного света

Сущность модели ТМС была подробно изло-

на частотах 100 и 120 Гц [9]. Авторы относительно

жена в серии работ [14-17]. В качестве меры ТМС

недавней работы [11] продемонстрировали, что

принята нормированная разность концентрации

человек способен различать модулированный и

фотореагента в фоторецепторе в крайних точках

постоянный свет с частотой до 500 Гц.

тремора [14]. Из этого следует, что источником

ТМС являются перепады и градиенты яркости.

Многообразие экспериментальных данных

Постоянная яркость или малые ее изменения в

может найти объяснение с позиций модели кон-

пределах шума спонтанной генерации импульсов

трастной чувствительности зрительной системы,

ганглиозными клетками или порога возбуждения

основанной на треморном модуляционном сиг-

нейрона дают нулевое значение сигнала. На пере-

нале.

паде или градиенте яркости ТМС может суще-

ствовать бесконечно долго. Согласно модели

МОДЕЛИРОВАНИЕ КЧСМ С ПОЗИЦИЙ

именно длительный ТМС является основанием

ТЕОРИИ ТРЕМОРНОГО

для автоформирования линий возбуждения, ко-

МОДУЛЯЦИОННОГО СИГНАЛА

торые впоследствии селектируются (повторяют-

ся) в высших отделах зрительной системы. Адек-

В основу модели треморного модуляционного

ватность модели была подтверждена в работах

сигнала (ТМС) положен факт исчезновения вос-

[14-17] для центрального и периферического зре-

приятия при остановке изображения на сетчатке,

ния в большом диапазоне внешних условий - яр-

полученный и подробно описанный в работе [13].

кости адаптации (10^-3-10³кд/м²), угловых раз-

Из всех движений, совершаемых глазом, в каче-

меров (1-300 угловых минут) и формы тестовых

стве основных движений в модели ТМС приняты

стимулов (диски, кольца Ландольта, миры Фуко,

тремор и дрейф. Есть две причины этого выбора.

синусоидальные решетки), времени их предъяв-

Во-первых, из всех движений, осуществляемых

глазом, тремор и дрейф являются самыми низко-

ления (10^-5-5 с). Модель не содержит поправоч-

скоростными (угловая скорость до 0.4 град/с), не

ных коэффициентов и функций во всем диапазо-

БИОФИЗИКА том 68

№ 5

2023

1040

ЛЯПУНОВ и др.

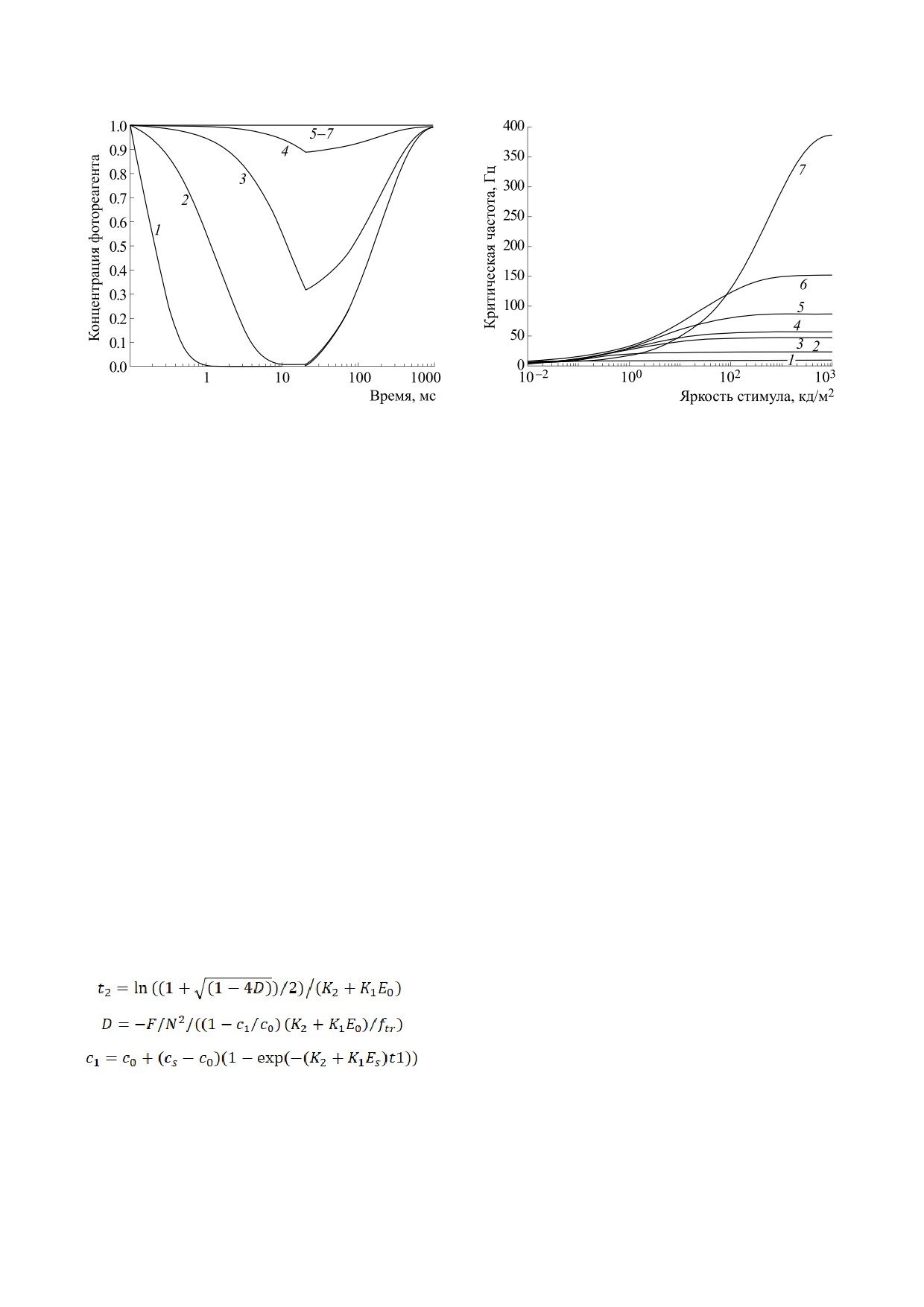
Рис. 2. Динамика переходных процессов концентра-

ции фотореагента во время воздействия первого

Рис.

3. Зависимость КЧСМ от яркости и дли-

светового импульса и после него для яркости адапта-

тельности стимула при яркости адаптации

ции 0.001 кд/м² и длительности стимула 0.02 с. Циф-

0.001 кд/м² и угловом размере стимула 1 град.

рами 1-7 обозначены кривые для яркостей стимула

Цифрами 1-7 обозначены кривые зависимостей для

L_s = [10000; 1000; 100; 10; 1; 0,1; 0,01] кд/м².

длительности стимула t₁ = [100; 40; 20; 16; 10; 5; 1] мс.

не внешних условий при восприятии различных

ния первого светового импульса длительностью

тестовых стимулов в пороговых и надпороговых

1; E - значение освещенности в плоскости сет-

условиях.

чатки; K₁ - концентрация разложения фотореа-

Значения КЧСМ в основном определяются

гента; K₂ - концентрация восстановления фото-

переходными фотохимическими процессами в

реагента; D - диаметр; F - порог нейронного воз-

рецепторе, описание которых приведено в При-

буждения. Более подробные пояснения к

ложении 1. С позиций модели ТМС задача опре-

формулам (4)-(7) приведены в Приложении 1.

деления КЧСМ сводится к пороговой постанов-

На рис. 2 представлена временная динамика

ке, когда после окончания воздействия первого

переходных процессов концентрации фотореа-

светового импульса определяется время переход-

гента во время воздействия первого светового им-

ного процесса концентрации фотореагента, в те-

пульса и после него для условий темновой адапта-

чение которого формируется ощущение, превы-

ции. Для яркостей стимула менее 1000 кд/м²

шающее пороговое значение. Иначе говоря, зри-

концентрация фотореагента не достигает устано-

тельная система между первым и вторым

вившегося значения, о чем говорит отсутствие

световыми импульсами формирует пороговое

участка сглаженного приближения к постоянно-

ощущение прерывания (дискретизации) цельно-

му уровню.

сти восприятия.

Очевидно, что при длительности стимула ме-

Модель ТМС позволяет получить численное

нее 1 мс это будет справедливо для всех приведен-

итерационное решение для КЧСМ:

ных на рис. 2 яркостей стимула. С точки зрения

f_c = 1/(t₁ + t₂),

(4)

эффективного накопления сигнала в зрительной

системе длительность стимула должна составлять

где t₁ - длительность светового импульса; t₂ -

10-20 мс.

критическая длительность паузы;

Результаты ТМС моделирования зависимости

КЧСМ от яркости стимула для различных дли-

(5)

тельностей стимула в условиях темновой адапта-

ции (при яркости адаптации 0.001 кд/м²) приве-

(6)

дены на рис. 3. С позиций модели ТМС опти-

мальная длительность стимула составляет 1 мс,

(7)

что соответствует времени перехода реакции фо-

где c₀ - концентрация адаптации; c_s - установив-

тотрансдукции в необратимое состояние.

шийся уровень концентрации при воздействии

Однако при данных длительностях для малых

первого светового импульса для t = ∞; c₁ - теку-

яркостей стимула эффективность накопления

щий уровень концентрации на момент оконча-

сигнала не достигает установившихся значений.

БИОФИЗИКА том 68

№ 5

2023

МОДЕЛИРОВАНИЕ КРИТИЧЕСКОЙ ЧАСТОТЫ СЛИЯНИЯ МЕЛЬКАНИЙ

1041

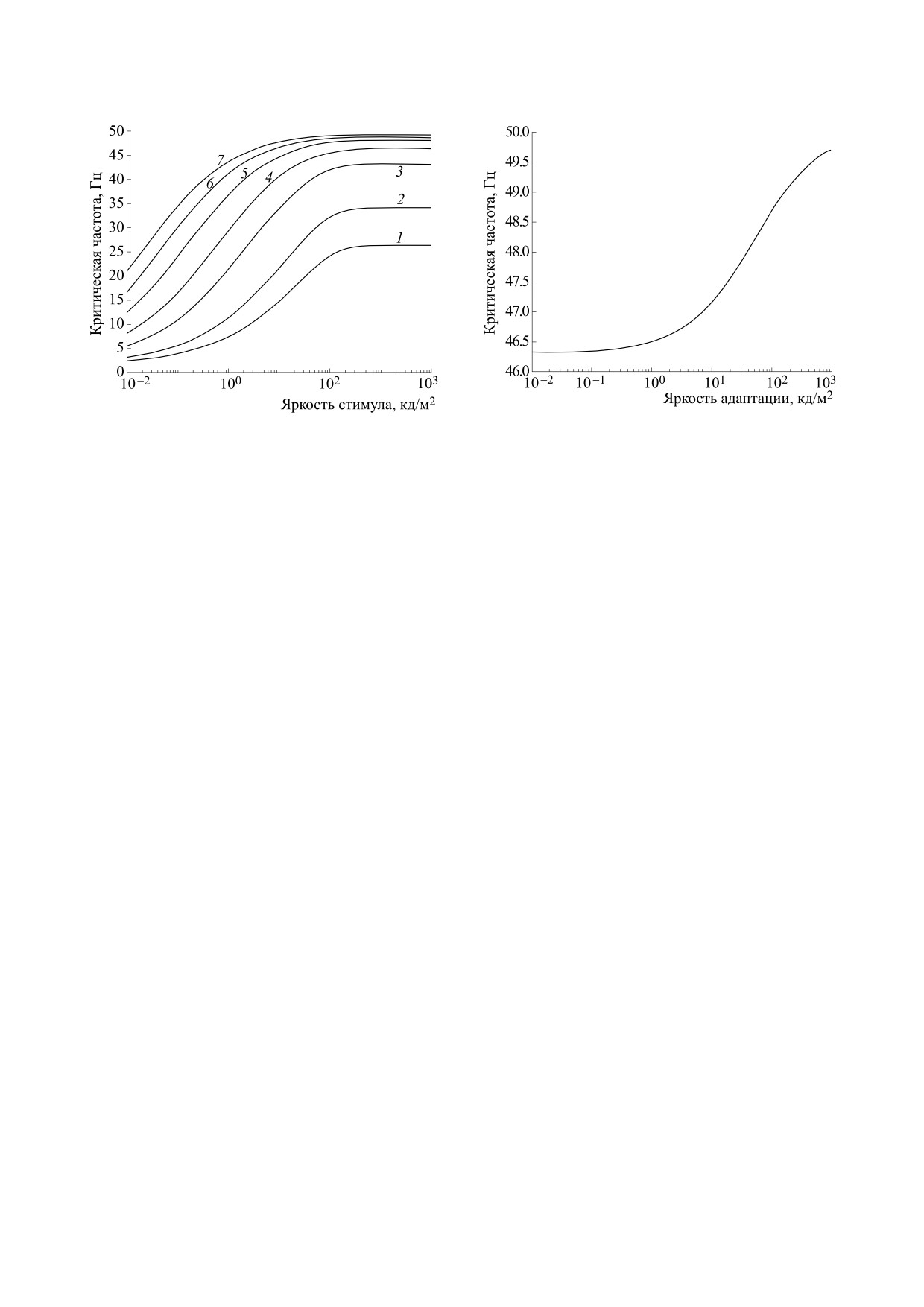
Рис. 5. Зависимость КЧСМ от яркости адаптации при

Рис. 4. Зависимость КЧСМ от яркости и углового

яркости стимула 10000 кд/м², длительности 20 мс и

размера стимула при яркости адаптации 0.001 кд/м² и

угловом размере 1 град.

длительности стимула

20 мс. Цифрами

1-7

обозначены кривые для угловых размеров стимула

N = [5; 10; 30; 60; 120; 200; 300] угл. мин.

определять значение КЧСМ. Малые угловые раз-

меры стимула имеют существенно меньшие зна-

Для недопущения взаимодействия с треморной

чения КЧСМ и могут быть исключены из рас-

модуляцией оптимальной длительностью стиму-

смотрения.

ла следует считать 2-3 мс (кадровая частота 300-

При увеличении яркости адаптации уменьша-

500 Гц).

ется критическое время паузы (t₂ становится мно-

Согласно модели ТМС диапазон кадровой ча-

го меньше t₁, см.формулу (4)) и значение КЧСМ

стоты 90 ± 20 Гц, соизмеримый с физиологиче-

стремится к уровню 1/t₁ (рис. 5). Можно видеть,

ской частотой тремора глаза, физиологически

что значение КЧСМ практически не зависит от

опасен, так как может приводить к перенапряже-

яркости адаптации.

нию зрительной системы и снижению ее кон-

Таким образом, зависимость КЧСМ от ярко-

трастной чувствительности за счет высокой до-

сти стимула носит нелинейный характер; для сти-

ступности ЦНС для внешних стимулов данной

мулов с большими угловыми размерами макси-

частоты и возможной принудительной внешней

мальные значения КЧСМ лежат в диапазоне до

синхронизации альфа-мотонейронов. Результаты

1000 Гц; оптимальной для зрительной системы

исследований влияния пульсирующих источни-

следует считать кадровую частоту 300-500 Гц; для

ков света на электрическую активность мозга че-

малоразмерных угловых стимулов КЧСМ лежит в

ловека свидетельствуют о том, что видимые низ-

области низких частот.

кочастотные (до 90 Гц) пульсации светового по-

тока вызывают зрительный дискомфорт,

зрительное и общее утомление, тогда как невиди-

НЕЙРОФИЗИОЛОГИЧЕСКИЕ

мые пульсации светового потока приводят к пе-

ОСНОВАНИЯ КЧСМ

регрузке зрительной системы и изменению есте-

ственной электрической активности мозга [18,

Различия в скорости слияния мерцания могут

19].

быть объяснены временной чувствительностью

магно- и парвоцеллюлярной зрительных подси-

Результаты ТМС-моделирования зависимости

стем, берущих начало от ганглиозных клеток сет-

КЧСМ от яркости стимула для различных угло-

чатки и дающих проекции, соответственно, к

вых размеров стимула в условиях темновой адап-

крупноклеточным магноцеллюлярным слоям и

тации (при яркости адаптации 0.001 кд/м²) при-

мелкоклеточным парвоцеллюлярным слоям ла-

ведены на рис. 4. Верхний предел моделирования

терального коленчатого тела таламуса. Отростки

ограничивается тем, что максимальный размер

нейронов этих слоев направляются к различным

поля площадной суммации составляет 5 угловых

слоям первичной зрительной коры и формируют

градусов. Типовое значение приборных полей со-

два потока информации из каудальных во фрон-

ставляет 2-3 размера макулы (40-60 градусов).

тальные зоны коры головного мозга [20-27].

При таком угловом размере крупноразмерных

Нейроны магноцеллюлярной и парвоцеллюляр-

стимулов будет достаточно много, и они будут

ной систем отличаются физиологически и психо-

БИОФИЗИКА том 68

№ 5

2023

1042

ЛЯПУНОВ и др.

физически: чувствительностью к восприятию

лее эффективной (меньшие ядра второго поряд-

контраста, цвета, движения стимулов, скоростью

ка) M-системой. Ни один из пиков, связанных с

передачи информации [24, 28, 29].

активностью P-системы, не показал значитель-

ной корреляции. Полученные результаты позво-

Разница в скорости слияния хроматических и

ляют рассматривать пороги мерцания как функ-

ахроматических мерцаний обычно приписывает-

циональный коррелят функции М-пути, что

ся различным путям: либо медленному, чувстви-

можно наблюдать при нелинейном анализе по-

тельному к красному/зеленому цвету парвоцел-

тенциалов mfVEP.

люлярному - P-пути, либо быстрому ахроматиче-

скому магноцеллюлярному

- M-пути

[22].

Логично, что временная способность обработ-

Показано, что пороги слияния ахроматического

ки и чувствительность магноцеллюлярных (M) и

мерцания находятся в диапазоне от 35 до 60 Гц

парвоцеллюлярных (P) подкорковых путей долж-

[30] в зависимости от глубины модуляции мерца-

ны частично зависеть от скорости восстановле-

ния, в то время как слияние цветов из красно-

ния нейронов после визуальной стимуляции. В

го/зеленого изолюминатного мерцания происхо-

соответствии с этим пороги слияния мерцаний

дит на гораздо более низких частотах (10-15 Гц)

для быстро модулированной яркости [30] уже

[31].

давно используются клинически в качестве меры

Исследования у приматов временной структу-

скорости перцептивной обработки [2]. Измере-

ры корковых зрительных вызванных потенциа-

ние порога КЧСМ используется для изучения ви-

лов с помощью псевдослучайной ахроматической

зуального временного разрешения и при патоло-

стимуляции показали нелинейность отклика на

гических состояниях. Авторы работы [35] показа-

изменения яркостного контраста: преобладание

ли, что КЧСМ является источником измененного

волнового комплекса P100-N115 при низких и

зрительного восприятия при высокой склонно-

средних контрастах (<60%), тогда как на высоких

сти к аутизму. Полученные данные рассматрива-

контрастах - комплекса N100-P120-N160 [32].

ются авторами, как свидетельства изменения ак-

Различия во времени адаптации нейронных гене-

тивности магноцеллюлярной системы при аутиз-

раторов этих двух компонент зрительных вызван-

ме. Эффективность использования метода

ных потенциалов обуславливают разделение сре-

регистрации порога КЧСМ в диагностике болез-

зов отклика ядер второго порядка. Второй срез

ни Альцгеймера, включая ранние этапы ее разви-

ядер второго порядка показывает пиковую за-

тия, показана в работе [36].

держку ~25 мс по сравнению с первым срезом.

Эти временно отделимые основные вклады в пер-

Таким образом, изучение КЧСМ имеет широ-

вый и второй срезы ядер второго порядка были

кое прикладное значение как в технике, так и в

идентифицированы как генерируемые нейрона-

медицине. Понимание природы КЧСМ и ее осо-

ми M- и P-путей на основе сходства с функциями

бенностей дает возможности для изучения рабо-

ахроматического контрастного ответа магно- и

ты мозга не только при различных функциональ-

парвоклеток, зарегистрированными в латераль-

ных состояниях в пределах нормы, но и при раз-

ном коленчатом теле (LGN) таламуса приматов

ного рода патологиях; разработки методов

[22, 33].

объективной диагностики и мониторинга состоя-

ния; развития возможностей трансляционной

Авторы работы [34] исследовали взаимосвязь

медицины в неврологии и психиатрии.

между частотой слияния ахроматических мерца-

ний и временным анализом крупноклеточного

(M) и парвоцеллюлярного (P) вклада в ахромати-

ческие нелинейные мультифокальные зритель-

ВЫВОДЫ

ные вызванные потенциалы (mfVEP), зареги-

Предпринято моделирование КЧСМ с пози-

стрированные в затылочной части головы (Oz) у

ций теории треморного модуляционного сигнала.

72 типично развивающихся молодых людей, ис-

Модель согласуется с эмпирическими фактами и

пользующих четырехстороннюю задачу слияния

предлагает их возможное объяснение, демон-

синусоидальных мерцаний с принудительным

выбором. Амплитуды всех нелинейностей, кото-

стрирует, что для ярких стимулов с малой дли-

тельностью и большим угловым размером значе-

рые демонстрировали компонент, генерируемый

ния КЧСМ лежат в диапазоне до 1000 Гц; опти-

М-клетками, отрицательно коррелировали с по-

рогами мерцания. Наиболее сильные из этих кор-

мальной для зрительной системы следует считать

реляций были продемонстрированы главной со-

кадровую частоту 300-500 Гц; для малоразмер-

ставляющей нелинейности M (первый срез ядер

ных угловых стимулов КЧСМ лежит в области

второго порядка K2.1N70-P100) как для высоко-

низких частот. Различия в КЧСМ могут быть объ-

контрастных, так и для низкоконтрастных усло-

яснены временной чувствительностью нейронов

вий, что указывает на то, что более высокий порог

магно- и парвоцеллюлярной зрительных подси-

слияния ахроматических мерцаний связан с бо-

стем.

БИОФИЗИКА том 68

№ 5

2023

МОДЕЛИРОВАНИЕ КРИТИЧЕСКОЙ ЧАСТОТЫ СЛИЯНИЯ МЕЛЬКАНИЙ

1043

Приложение 1

ДОПОЛНИТЕЛЬНЫЙ МАТЕРИАЛ

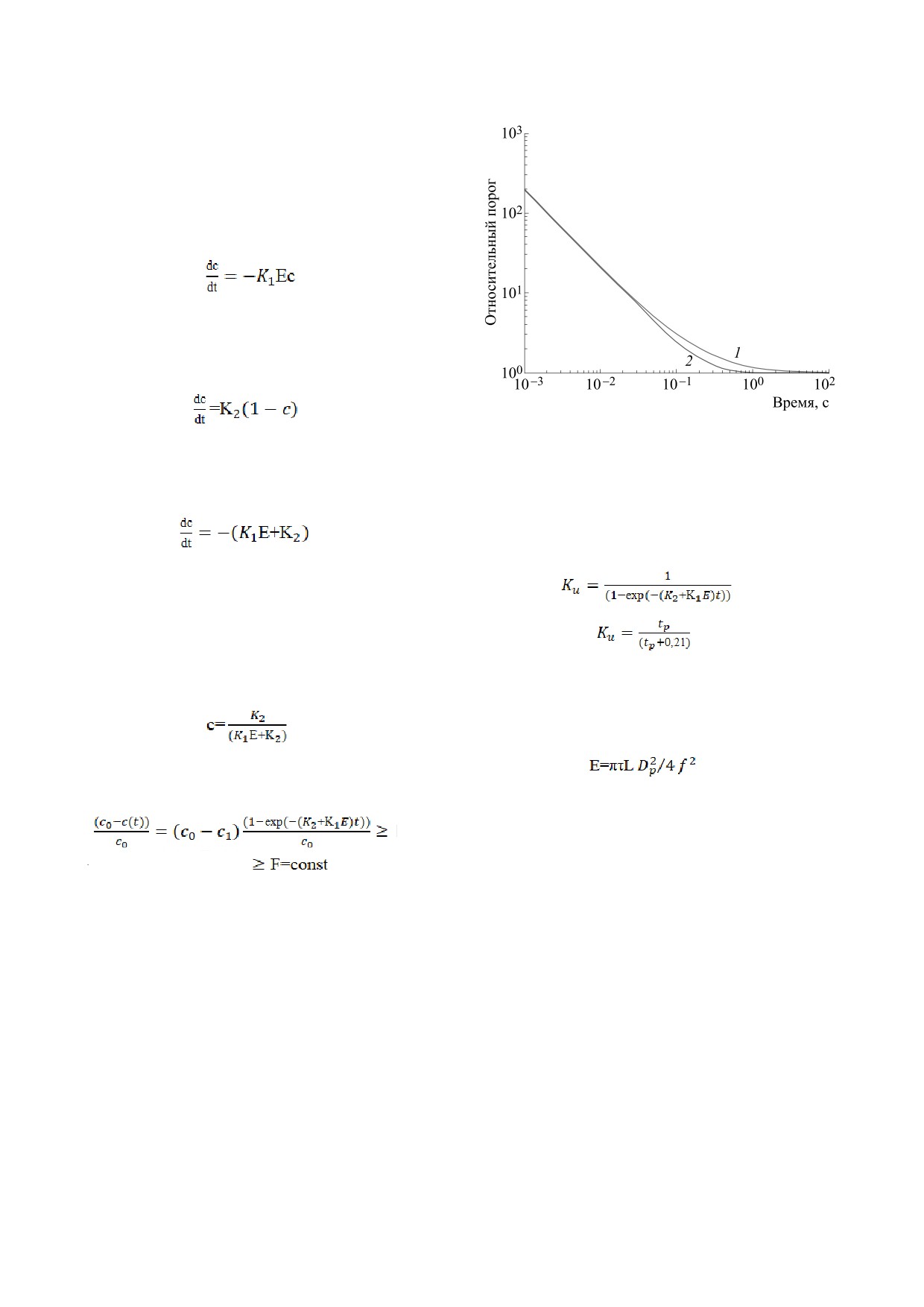
Скорость уменьшения концентрации (разло-

жения) фотореагента пропорциональна освещен-

ности E и текущей концентрации фотореагента с

(п. 1)

Скорость увеличения концентрации (восста-

новления) фотореагента пропорциональна его

концентрации в неактивной фазе (1 - c)

(п. 2)

Суммарный процесс, описывающий текущую

Рис. п1. Зависимость относительного порога восприя-

концентрацию фотореагента, как балансное со-

тия от времени предъявления стимула. Кривые отра-

жают: 1 - закон Блонделя-Рэя и Блоха-Шарпантье,

стояние конкурирующих процессов распада и

2 - результаты расчета по уравнению (7).

восстановления, имеет вид:

(п. 3)

жение для закона Блонделя-Рея и Блоха-Шар-

пантье (п. 8).

Числовые значения коэффициентов фотохи-

мической реакции вычисляются для круглого

(п. 7)

стимула с размером, равным 1 угловой минуте, и

постоянны во всех внешних условиях восприя-

тия. Решение уравнения (п. 3) имеет вид:

(п. 8)

c(t) = c₀ + (c₁ - c₀)exp(-(K₂ + K₁E₁)t), (п. 4)

- время предъявления стимула.

где t_p

где концентрация c определяется по формуле:

Значение освещенности E в плоскости сетчат-

ки, создаваемой яркостью L находим по следую-

(п. 5)

щим зависимостям:

Нормированное приращение концентрации

(п. 9)

должно быть больше порога нейронного возбуж-

дения F:

где D_p - диаметр зрачка глаза, определяется по

формуле Крауфорда:

D_p = 5 - 3th(0.4lgL_a).(п. 10)

(п. 10)

. (п. 6)

Результаты расчета зависимости относитель-

ного порога восприятия от времени предъявле-

Переход от начального значения c₀ к значению

ния стимула представлены на рис. п. 1.

c₁ не происходит мгновенно, а требует определен-

Выражение (6) имеет важную физическую и

ного времени для достижения балансного состоя-

физиологическую трактовку. Физическая трак-

ния конкурирующих процессов распада и восста-

товка проливает свет на формирование отноше-

новления. При этом время распада фотореагента

ния сигнал/шум в зрительной системе. Преобра-

в необратимое состояние характеризуется значе-

зуем выражение следующим образом:

нием порядка 1 мс и переходные процессы в ос-

новном определяются временем восстановления

dc(t)/c₀ = dc/c₀(1 - exp(-(K₂ + K₁E)t)), (п. 11)

фотореагента.

tms(t) = tms_max(1 - exp(-(K₂ + K₁E)t)). (п. 12)

Если соотнести приращение концентрации

для бесконечно большого и текущего времени,

Максимальное, предельное значение ТМС со-

можно получить выражение для относительного

ответствует перепаду яркости физического сти-

порога восприятия от времени предъявления сти-

мула в крайних точках тремора, преобразованно-

мула. Для сравнения представлены выражение,

му в пространство концентрации фотореагента.

полученное согласно модели ТМС (п. 7), и выра-

Функция SN(t) описывает временную динамику

БИОФИЗИКА том 68

№ 5

2023

1044

ЛЯПУНОВ и др.

накопление отношения сигнал/шум в зрительной

tau = 1/f_tr.

(п. 71)

системе:

SN(t) = 1 - exp(-(K₂ + K₁E)t).

(п. 13)

ФИНАНСИРОВАНИЕ РАБОТЫ

Из формулы (п. 11) получены выражения для

Данное исследование не получало какого-ли-

порогового восприятия дисков (массив Блекуэл-

бо специального гранта от финансирующих

ла), мир Фуко и синусоидальных решеток (мас-

агентств в государственном, коммерческом или

сив Маккена, Савоя, Кемпбела), колец Ландоль-

некоммерческом секторах.

та (массив остроты зрения). Формула (п. 11) опи-

сывает переход от точки один яркости адаптации

к точке два яркости объекта в пространстве кон-

КОНФЛИКТ ИНТЕРЕСОВ

центрации фотореагента в рецепторе. При этом

Авторы заявляют об отсутствии явных и по-

полагается, что в точке объекта фоторецептор на-

тенциальных конфликтов интересов, связанных с

ходится бесконечно долго. В интерпретации мо-

публикацией данной статьи.

дели ТМС фоторецептор в процессе тремора в

крайних точках попеременно экспонируется то

яркостью адаптации, то яркостью объекта за вре-

СОБЛЮДЕНИЕ ЭТИЧЕСКИХ СТАНДАРТОВ

мя равное 1/f_tr. Согласно модели, нормированная

Настоящая работа не содержит описания ка-

разность концентрации представляет собой тре-

ких-либо исследований с использованием людей

морный модуляционный согнал. Процесс попе-

и животных в качестве объектов.

ременного экспонирования повторяется на каж-

дом периоде тремора и ТМС накапливается со-

гласно выражению (п. 13).

СПИСОК ЛИТЕРАТУРЫ

Такая интерпретация сохраняет все ранее по-

К. А. Пупков и Н. Д. Егупов, Математические мо-

лученные результаты и одновременно позволяет

дели, динамические характеристики и анализ си-

получить выражение для площадного сигнала пе-

стем автоматического управления (Изд-во МГТУ

реходного процесса, который мы ощущаем как

им. Н.Э. Баумана, М., 2004).

послеобраз.

R. S. Brenton, H. S. Thompson, and C. Maxner, In

Поскольку послеобраз пространственно при-

New Methods of Sensory Visual Testing (Springer, NY,

вязан к фоторецептору, то очевидно, что тремор-

1989), pp 29-52.

ные колебания не формируют ТМС. При воздей-

A. C. Brown, J. L. Peters, C. Parsons, et al., Front.

ствии первого светового импульса длительностью

Hum. Neurosci., 14, 49 (2020).

t₁ концентрация в фоторецепторе будет равна:

J. I. Thompson, C. E. Peck, G. Karvelas, et al., Neuro-

psychologia, 69, 148 (2015).

c₁ = c₀ + (c_s - c₀)(1 - exp(-(K₂ - K₁E_s)t)). (п. 14)

Y. Chen, D. Norton, and C. Stromeyer, Schizophrenia

В период паузы между импульсами концентра-

Res., 156 (2-3), 190 (2014).

ция в фоторецепторе примет вид:

B. D. Parsons, S. Gandhi, E. L. Aurbach, et al., Neu-

ropsychologia, 51 (2), 372 (2013).

c₂ = c₁ + (c₀ - c₁)(1 - exp(-(K₂ - K₁E₀)t)). (п. 51)

С. В. Кравков, Глаз и его работа (Изд-во АН СССР,

Но в поле послеобраза есть временная модуля-

М., 1950).

ция площадного сигнала, обусловленная пере-

K. R. Boff and J. E. Lincoln, Engineering Data Compen-

ходным процессом от уровня c0 к уровню с₁. За

dium: Human Perception and Performance (Wright-Pat-

временной интервал tau концентрация фотореа-

terson AFB, OH: USAF Harry G. Armstrong Aero-

гента в тестирующем поле хоть и незначительно,

space Medical Research Laboratory, 1988).

но меняется. Приращение сигнала переходного

R. Küller and T. Laike, Ergonomics, 41 (4), 433 (2010).

процесса равно произведению производной пе-

10.

O. de Bruijn and R. Spence, In Proc. Int. Conf. on Ad-

реходного процесса на время tau:

vanced Visual Interfaces AVI-2000 (2000), p. 189.

11.

J. Davis, Y.-H. Hsieh, and H.-C. Lee, Sci. Rep., 5

dc_t(t) = (c₀ - c₁)(N - 2)²exp(-(K₂ + K₁E₁)t)×

(2015).

(п. 16)

×(K₂ + K₁E₁)tau(1 - exp(-(K₂ + K₁E₁)t)).

12.

J. Melzer and C. Spitzer, Digital avionics handbook,

22, 3 (2017).

Поскольку в треморном модуляционном сиг-

13.

А. Л. Ярбус, Роль движений глаз в процессе зрения

нале сравниваются значения концентрации фо-

(Наука, М., 1965).

тореагента в крайних точках тремора, то времен-

14.

S. I. Lyapunov, J. Optic. Technol., 81 (6), 349 (2014).

ной интервал tau для временной модуляции вы-

15.

S. I. Lyapunov, J. Optic. Technol., 84 (9), 613 (2017a).

бирается равным временному периоду тремора,

что для нормальной частоты тремора 87 Гц соста-

16.

S. I. Lyapunov, J. Optic. Technol., 84 (1), 16 (2017b).

вит 11.5 мс:

17.

S. I. Lyapunov, J. Optic. Technol., 85 (2), 100 (2018).

БИОФИЗИКА том 68

№ 5

2023

МОДЕЛИРОВАНИЕ КРИТИЧЕСКОЙ ЧАСТОТЫ СЛИЯНИЯ МЕЛЬКАНИЙ

1045

18. В. А. Ильянок и В. Г. Самсонова, Светотехника, 5

28. J. J. Nassi and E. M. Callaway, Nat. Rev. Neurosci., 10

(1963).

(5), 360 (2009).

19. C. Herrmann, Exp. Brain Res., 137, 346 (2001).

29. M. Edwards, S. C. Goodhew, and D. R. Badcock,

20. L. G. Ungerleider and M. Mishkin, In Analysis of visual

Psych. Bull. Rev., 28, 1029 (2021).

behavior (MIT Press., Cambridge, 1982).

30. D. H. de Lange, JOSA, 44, 380 (1954).

21. V. H. Perry, R. Oehler, and A. Cowey, Neuroscience,

31. P. H. Schiller, N. K. Logothetis, and E. R. Charles,

12, 1101 (1984).

Neuropsychologia, 29, 433 (1991).

22. A. M. Derrington and P. Lennie, J. Physiol., 357, 219

32. A. Klistorner, D. P. Crewther, and S. G. Crewther, Vi-

(1984).

sion Res., 37, 2161 (1997).

23. W. H. Merigan, L. M. Katz, and J. H. Maunsell, J.

33. E. Kaplan and R. M. Shapley, Proc. Natl. Acad. Sci.

Neurosci., 11, (4), 994 (1991).

USA, 83, 2755 (1986).

24. W. H. Merigan and J. H. R. Maunsell, Ann. Rev. Neu-

34. A. Brown, M. Corner, D. P. Crewther, and

rosci., 16, 369 (1993).

S. G. Crewther, Front. Hum. Neurosci.,

12,

176

25. L. J. Croner and E. Kaplan, Vision Res., 35, 7 (1995).

(2018).

26. E. H. F.de Haan, S. R. Jackson, and T. Schenk, Cortex.

35. J. I. R. Thompson, C. E. Peck, G. Karvelas, et al., Neu-

98, 1 (2018).

ropsychologia, 69, 148 (2015).

27. E. Freud, M. Behrmann, and J. C. Snow, Open Mind:

36. A. Abiyev, F. D. Yakaryılmaz, and Z. A. Öztürk, De-

Discoveries in Cognitive Science, 4, 40 (2020).

mentia & Neuropsychologia, 16 (1), 89 (2022).

Modeling the Critical Fliker Fusion Frequency in the Human Visual System

S.I. Lyapunov*, I.I. Shoshina**, and I.S. Lyapunov*

*Prokhorov General Physics Institute, Russian Academy of Sciences, ul. Vavilova 38, Moscow, 119991 Russia

**Institute for Cognitive Research, Saint Petersburg State University, Universitetskaya nab. 7/9, St. Petersburg, 199034 Russia

The temporal resolving power of the visual system is essential for the perception of the objective world. The

lowest sampling rate of a sequence of images at which perception becomes fused is called the critical flicker

fusion frequency. The variety of experimental data on critical frequency thresholds can be explained from a

point of view of a model of the contrast sensitivity of the visual system that based on the tremor modulation

signal. The model describes the dependence of critical frequency on stimulus brightness, adaptation bright-

ness, duration, and the angular size of the stimulus. This model demonstrates that for bright stimuli with short

duration and a large angular size, critical frequency values lie in the range up to 1000 Hz; the frame rate of

300-500 Hz should be considered optimal for the visual system; for small-sized angular stimuli, the critical

frequency lies in the low-frequency region. Differences in the rate of flicker fusion can be explained by tem-

poral sensitivity of magno- and parvocellular neurons.

Keywords: critical flicker fusion frequency, tremor modulation signal, dynamic light load, adaptation brightness,

magnocellular system, parvocellular system

БИОФИЗИКА том 68

№ 5

2023