БИОФИЗИКА, 2023, том 68, № 5, с. 1022-1030

БИОФИЗИКА CЛОЖНЫX CИCТЕМ

УДК 57.05, 577.353, 539.3

МИНИМАЛЬНАЯ МОДЕЛЬ ЗАВИСИМОСТИ НАПРЯЖЕНИЙ

В СТЕНКЕ ЦЕРЕБРАЛЬНОГО СОСУДА ОТ ПАРАМЕТРОВ

ГЛАДКОМЫШЕЧНОЙ КЛЕТКИ

*Институт физиологии им. И.П. Павлова РАН, наб. Макарова, 6, Санкт-Петербург, 199034, Россия

^#E-mail: nkhsh@yandex.ru

Поступила в редакцию 27.04.2023 г.

После доработки 18.05.2023 г.

Принята к публикации 07.06.2023 г.

Описана минимальная математическая модель стенки малого артериального сосуда, построенная

на основе опубликованных результатов экспериментов на церебральных сосудах крыс. Полагается,

что активная составляющая напряжений имеет только окружную компоненту и зависит от

окружного растяжения, концентрации кальция в цитоплазме и мембранного потенциала

гладкомышечных клеток. Представленная модель стенки малой артерии качественно

воспроизводит и результаты более сложных моделей других сосудов в условиях физиологической

нормы. В отличие от аналогичной модели, учитывающей лишь один клеточный параметр, введение

мембранного потенциала в число аргументов позволило выявить качественное изменение

зависимости окружного напряжения от растяжения и радиальной координаты с изменением

сосудистого тонуса. При фиксированных значениях мембранного потенциала и концентрации

кальция в фазе развития сосудистого тонуса напряжение убывает по мере приближения к наружной

стенке сосуда и увеличивается с ростом растяжения, а после того, как он сформируется,

направленность изменений окружного напряжения меняется на противоположную.

Ключевые слова: миогенная регуляция, резистивный сосуд, напряжение сосудистой стенки, кальций,

мембранный потенциал.

DOI: 10.31857/S000630292305023X, EDN: NARCNP

Сосудистая стенка состоит из трех основных

относящегося к разряду резистивных, на которые

слоев: внутреннего (интимы), среднего и наруж-

приходится наибольшая часть сосудистого со-

ного (адвентиции). Адвентиция состоит преиму-

противления. Повышение внутрисосудистого

щественно из волокон коллагена и эластина. Их

давления сопровождается деполяризацией мем-

соотношение, ориентация волокон зависят от ти-

браны гладкомышечных клеток и ростом концен-

па сосуда и его расположения. В интиму входят

трации ионов кальция в цитоплазме, что приво-

коллаген в небольшом количестве, эндотелиаль-

дит к увеличению степени активации и сокраще-

ные клетки, гликокаликс на границе между цир-

нию гладкомышечных клеток, в результате чего

кулирующей кровью и эндотелием. Наиболее

просвет сосуда сужается (см. работу [2]). Этот эф-

важной особенностью среднего слоя является

фект называют миогенной сосудистой реакцией.

Сокращение гладкомышечных клеток - резуль-

присутствие, помимо коллагена и эластина, глад-

комышечных клеток, за счет которых развивают-

тат сложных процессов взаимодействия ионных

каналов плазматической мембраны и эндоплаз-

ся активные напряжения. Их сокращение может

матического ретикулума [2, 3].

вызываться нервными, гуморальными, а также

механическими воздействиями. Гладкомышеч-

В математических моделях последних трех де-

ные клетки вместе с эндотелиальным слоем и

сятилетий, уделяющих основное внимание стро-

гликокаликсом являются основными регулятора-

ению артериальной стенки крупных артерий, ча-

ми сосудистого тонуса [1], физический смысл ко-

сто полагалось, что активная часть напряжения

торого можно определить как напряжение сосу-

пропорциональна параметру активации. Без

дистой стенки, обусловленное сократимостью

уточнения названия этого параметра расчеты де-

гладкомышечных клеток. В статье рассматрива-

лались для крупных сосудов при двух предельных

ется регуляция напряжения гладкомышечными

значениях этого параметра - нуле и единице [4-

клетками в стенке малого артериального сосуда,

6]. Иногда дополнительно вводилось некоторое

1022

МИНИМАЛЬНАЯ МОДЕЛЬ ЗАВИСИМОСТИ НАПРЯЖЕНИЙ

1023

промежуточное значение, соответствующее по-

чать до нескольких десятков уравнений, содержа-

ведению сосуда в норме [7, 8]. Материал стенки в

щих множество параметров, значения которых

целом считался всегда гиперупругим, а зависи-

неизвестны [18, 19]. Значения параметров берутся

мость напряжений от растяжений определялась

либо из данных, полученных на другом экспери-

экспериментально при двухосном растяжении

ментальном материале, либо подбираются мето-

сосудистых сегментов. Степень подробности

дами оптимизации и из соображений правдопо-

описания строения стенки варьировалась, рас-

добности результатов. Громоздкость такого под-

сматривались однослойные [9], двухслойные [4] и

хода практически сводит к нулю их

трехлойные [5] модели, учитывалось распределе-

использование для практических расчетов.

ние и ориентация гладкомышечных клеток и во-

Ранее нами была предложена [22] достаточно

локон коллагена и эластина [4, 10]. Для описания

простая модель стенки малого артериального со-

механических свойств стенки использовалась мо-

суда для описания экспериментов [23] по разду-

дель Хилла, материал стенки считался несжимае-

ванию сегмента малого церебрального сосуда сту-

мым.

пенчатым повышением внутрисосудистого дав-

Общепризнано (см. работу [11]), что регулято-

ления. В модели активное напряжение

ром сократительной активности гладкомышеч-

полагалось зависящим от растяжений стенки и

ных клеток являются ионы кальция в цитоплаз-

концентрации Са²⁺ в цитоплазме гладкомышеч-

ме. Впервые концентрация ионов кальция в каче-

ных клеток. Была получена зависимость актив-

стве параметра, регулирующего диаметр сосуда,

ной составляющей окружного напряжения от

была введена С.А. Регирером и его учениками в

концентрации Са²⁺. Основным источником по-

1975 г. [12]. В большинстве современных работ

ступления кальция в клетку являются потенциал-

[10, 11, 13-15], рассматривающих концентрацию

зависимые кальциевые каналы, вероятность от-

ионов кальция в качестве основного параметра,

крытия которых регулируется мембранным по-

от которого зависят сокращения гладкомышеч-

тенциалом. В то же время ионные каналы способ-

ных клеток, используется модифицированная

ствуют установлению и регулированию мембран-

модель Hai & Murphy [16], описывающая динами-

ного потенциала (см. работы

[2,

3]). Таким

ку изменения доли свободных и присоединенных

образом, оба эти параметра (концентрация каль-

мостиков между актиновыми и миозиновыми ни-

ция и потенциал) взаимозависимы и влияют на

тями. В этих публикациях активная часть напря-

формирование сосудистого тонуса. Вследствие

жений полагается пропорциональной коэффи-

этого в данной работе в число аргументов актив-

циентам фосфорилирования миозина из уравне-

ной составляющей напряжения вводится второй

ний Hai & Murphy, зависящим от концентрации

независимый клеточный параметр, мембранный

Са²⁺. Скорости дефосфорилирования обычно

потенциал гладкомышечной клетки (V_m).

полагаются константами, лишь в работе [11] для

них вводится зависимость от растяжений. Часто

ПОСТАНОВКА ЗАДАЧИ

концентрация Са²⁺ задавалась как функции вре-

мени [10, 13-15]. В работе [11] увеличение поступ-

Как и в работе [22], предполагается, что форма

ления концентрации Са²⁺ извне при растяжени-

сосуда близка к цилиндрической, материал стен-

ях стенки напрямую зависит от растяжений. По-

ки однородный, гиперупругий. Деформации

этому при расчетах оба эти параметра являются

стенки осесимметричны, описываются тензором

искомыми величинами. Растяжения стенки сосу-

деформаций Грина и в цилиндрических коорди-

да характеризовались удлинениями самой глад-

натах записываются как

комышечной клетки [10, 17] или сократительной

−1

r, θ,z, ε

≡

0 при

≠

(1)

единицы [14, 15], изменениями длины участков

(

)

«перекрытия» нитей миозина и актина [13].

В меньшей части публикаций дополнительно

≡

, λ

≡

, λ

≡

(2)

θθ

привлекаются уравнения, связывающие концен-

трацию кальция в цитоплазме гладкомышечной

где r,θ,z - радиальная, окружная и продольная

клетки и саркоплазматическом ретикулуме, мем-

координаты, λ_ii (i = r,θ,z) - растяжения в соответ-

бранный потенциал и ионные токи через мембра-

ствующем направлении, r₀ и z₀ - координаты точ-

ну [18-21]. При этом не рассматривается влияние

ки в ненагруженном ненапряженном состоянии.

внутриклеточных параметров на диаметр сосуда,

Поскольку для малых артерий соответствующие

макропараметр, определяемый в острых экспери-

данные отсутствуют, остаточные напряжения не

ментах на животных, прослеживаются лишь сме-

рассматриваются, по той же причине продольные

щения миозиновых и актиновых нитей. В публи-

растяжения λ_zz полагаются равными единице.

кациях, оценивающих изменения радиуса, его

считают пропорциональным длине гладкомы-

Полное напряжение стенки представляется

шечной клетки [19]. Такие модели могут вклю-

суммой пассивной и активной составляющих.

БИОФИЗИКА том 68

№ 5

2023

1024

ШАДРИНА

Активное напряжение развивается вследствие со-

тированы преимущественно в окружном направ-

кращения гладкомышечных клеток. Поскольку в

лении [24,25], считали, что активное напряжение

малых артериях гладкомышечные клетки ориен-

имеет только окружную составляющую:

σ_rr ≡ σ_r = q + σr(p), σ_θθ ≡ σ_θ = q + σ_θ(p) + σ_θ(a), σ_zz ≡ σ_z = q + σr(p),

(3)

где σ_rr, σ_θθ, σ_zz - радиальная, окружная и продоль-

ющие напряжения. Пассивные напряжения σ^(p)

ная составляющие напряжения соответственно,

находятся из функции энергии деформаций W_pas,

q - множитель Лагранжа. Верхние индексы (p) и

представляемой экспонентой от квадратичной

(a) обозначают пассивную и активную составля-

формы [26]

pas

[exp(Q)-1],

θθ

ε εrr

θθ

(4)

(p)

∂W

pas

(p)

∂

pas

(p)

, σ

≡

(5)

∂ε

θθ

Заметим, что ε_zz ≡ 0. Активная составляющая

шечный слой, S_sm = 0.694 (см. работу [22]). Функ-

ция f(λ_r,λ_θ), как и прежде [22], записывается в

напряжения σ_θ(a) полагается функцией растяже-

ний, концентрации кальция в цитоплазме глад-

виде

комышечных клеток (C_m) и мембранного потен-

циала (V_m):





λ



exp-



(7)









g



⁾ =

(λ ,λ

)

Ψ(

) Φ

(

(6)





где S_sm - доля площади поперечного сечения со-

Вместо уравнения (6) можно ввести единую

судистой стенки, приходящаяся на гладкомы- функцию энергии деформаций

W = W_pas + W_act,



λ





const ·Ψ

) Φ

)

Erf

-1

act











g





Вид зависимостей Ψ(C_m) и Φ(V_m) задается ис-

(a)

∂

act

где

const

Тогда

ходя из экспериментальных кривых C_m(p) и

∂ε

θθ

Vm(p), приведенных в работе [23]:

Ψ(

; Φ

asinh

(

·V

)

(8)

Коэффициент k = 300 нМ;

A a

A, a_i (i = 1,2,3)

∂

σ σ

(9)

в уравнении (4) и g_i (i = 1,..,9) в уравнениях (6)-

∂

(8) - постоянные, подлежащие определению.

λ_rλ_θλ_z = 1.

(10)

В соответствии с условиями экспериментов,

Не теряя общности, можно считать, что давле-

описанных в работе [23], рассматривается стати-

ние на внешней стенке равно нулю, а граничные

ческая задача распределения напряжений в сосу-

условия сводятся к

дистой стенке при нагружении трансмуральным

давлением. Уравнения равновесия и несжимае-

σ_r = -p, r = r_i,

(11)

мости для стенки имеют следующий вид:

σ_r = 0, r = r_i + h,

БИОФИЗИКА том 68

№ 5

2023

МИНИМАЛЬНАЯ МОДЕЛЬ ЗАВИСИМОСТИ НАПРЯЖЕНИЙ

1025

где p - внутрисосудистое давление, r_i и h - внут-

сутствии нагрузки: h₀ = 12.7 мкм. В качестве ха-

ренний радиус и толщина стенки соответственно.

рактерных значений для линейных величин, C_m,

V_m, давления и напряжений при приведении си-

стемы уравнений к безразмерному виду исполь-

ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ МОДЕЛИ

И МЕТОД РЕШЕНИЯ

зовали соответственно r^* = h^* = 98 мкм, C_m* =

Вычисления проводили с использованием

= 300 нМ, V_m = 100 мВ, p^* = σ^* = 100 мм рт. ст. =

экспериментальных данных, полученных на сег-

= 13.3322 кПа.

ментах задней мозговой артерии крыс [23], где в

Из уравнений (2) и условия несжимаемости

диапазоне давлений 10÷100 мм рт. ст. одновре-

материала стенки (10) следует соотношение

менно регистрировались сосудистый радиус,

концентрация кальция в цитоплазме и мембран-

ный потенциал гладкомышечной клетки в стенке

+C,

(12)

сосуда. Площадь поперечного сечения сосуди-

где C - константа, которую предстоит опреде-

стой стенки (S_w) определяли по микрофотогра-

лить. Уравнение (9) решается в конечных инте-

фиям, приведенным в работе [23], S_w = 3790 мкм².

гралах. Способ нахождения коэффициентов A и a_i

Диаметр пассивного сосуда при отсутствии на-

(i = 1,2,3) из решения задачи для пассивного сосу-

грузки вычисляли после аппроксимации статиче-

да был описан подробно в работе [27]. После пе-

ской зависимости «диаметр-давление» для пас-

репроверки измерений радиуса по эксперимен-

сивного сосуда из работы [23] рациональной и

тальным кривым получили следующие значения:

экспоненциальной функциями. Среднее двух по-

A = 54.5 кПа, a₁ = 0.247, a₂ = 0. 025, a₃ = 0.078.

лученных значений диаметра в точке p = 0 ис-

пользовали в вычислениях. Таким способом по-

Для нахождения коэффициентов, входящих в

лучили значение наружного диаметра ненагру-

функции f, Ψ и Φ, уравнение (9) решали для ак-

женного пассивного сосуда, равное 108 мкм. Зная

тивного сосуда с использованием уже найденных

коэффициентов A и a_i. Решение для радиальной

Sw^{и внешний диаметр, можно вычислить толщи-}

ну стенки в неактивированном состоянии при от-

компоненты напряжения имеет вид:

r₀





(p)

λ



−

Ψ(C

)Φ(V

)

exp-

dr











g







+h0



(p)



(

)

exp

(Q(

))

−

exp(Q r ))

−

exp

(Q r ))

,















Q y)

y

y2(y2 +C



(

y2 +C

)





Здесь r0i и h₀ - внутренний радиус и толщина

Для окружного напряжения получили соотно-

стенки при ненагруженном, ненапряженном со-

шение

стоянии сосуда.









exp(Q r ))

−

Ψ(C

) Φ

)

exp

-

,

































=σ -

−

exp(Q(

))





(

)





Коэффициенты g_i (i = 1,..,9) определяли мини-

рованного сосуда от давления с противополож-

мизацией суммы квадратов отклонений радиаль-

ным знаком при 9 значениях давления. Значения

ного напряжения на внутренней стенке активи-

коэффициентов приведены в табл. 1. После на-

БИОФИЗИКА том 68

№ 5

2023

1026

ШАДРИНА

Таблица

1. Значения параметров, входящих в

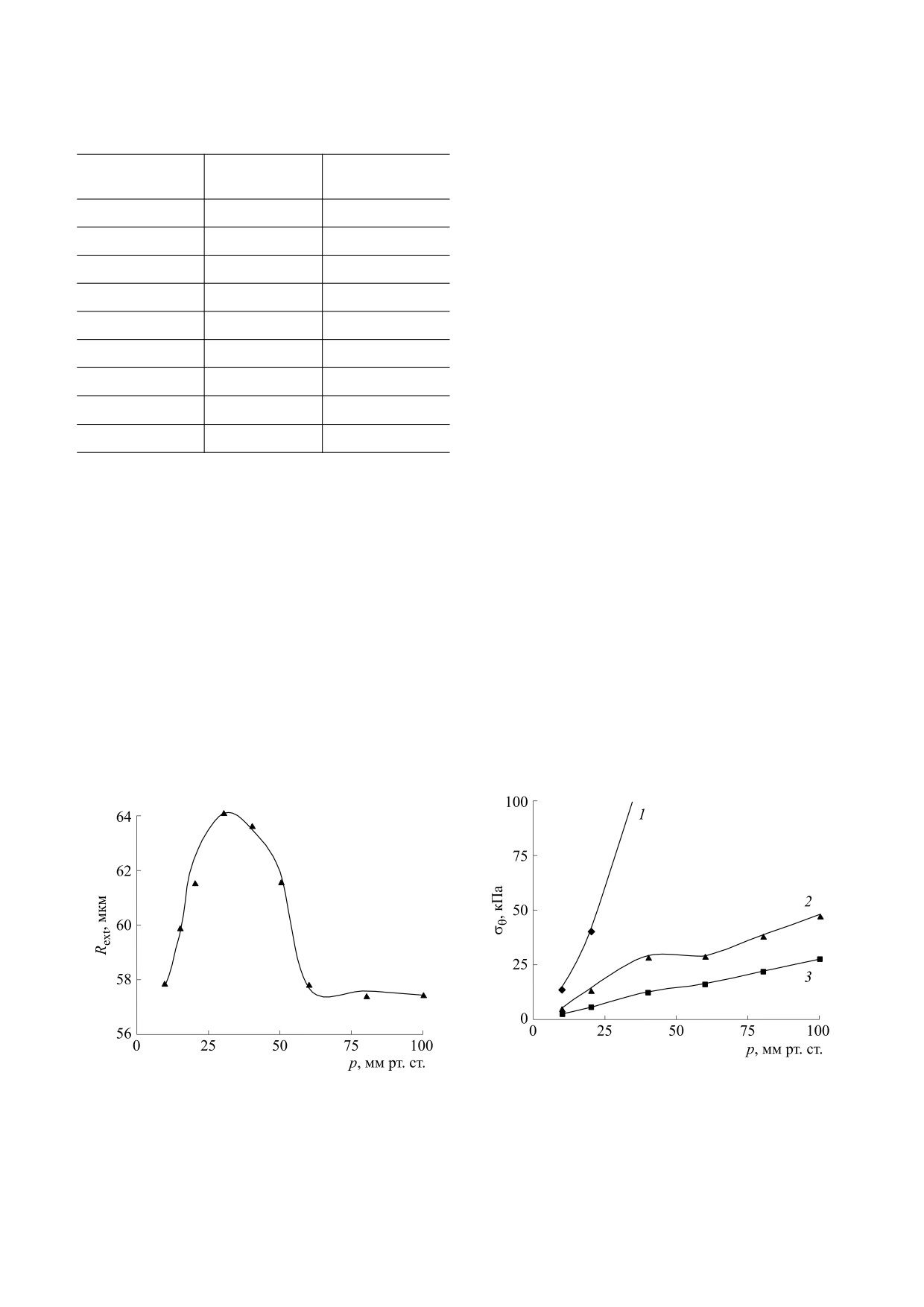
рис. 1). Как следует из результатов эксперимен-

активную составляющую напряжения

тов на сосудах [28], аналогичных рассмотренным

в работе [23], диапазон давлений, в котором ради-

Единица

Параметр

Значение

ус практически не меняет свое значение с ростом

измерения

давления, составляет 60÷140 мм рт. ст.

g₁

кПа

Окружное напряжение в активированном со-

g₂

3.9

б/р

суде (рис. 2, кривая 2) значительно ниже по срав-

нению с пассивным (рис. 2, кривая 1), что отме-

g₃

22.85

б/р

чалось и во многих других публикациях (см. на-

g₄

2.33

б/р

пример, работы

[5,

22]). При изменении

внутрисосудистого давления от 40 до 60 мм рт. ст.

g₅

2.72

б/р

окружное напряжение в стенке практически не

g₆

8.28

б/р

меняется (рис. 2, кривая 2). Однако этот эффект от-

сутствует (рис. 2, кривая 3), если не учитывать зави-

g₇

1.69

б/р

симость активного напряжения от мембранного

потенциала [22]. Диапазон давлений, в котором

g₈

11.62

мВ^-1

поддерживается постоянный уровень окружного

g₉

5.58

б/р

напряжения, соответствует падающему участку за-

висимости радиуса от давления (рис. 1), участку

Примечание. б/р - Безразмерная величина.

формирования сосудистого тонуса. После развития

сосудистого тонуса (p ≥ 60 мм рт. ст.) окружное на-

пряжение практически линейно зависит от давле-

хождения всех неизвестных коэффициентов из

ния. Добавление второго клеточного параметра в

граничного условия (11) вычисляли значения С

число параметров σ_θ(a) количественно сокращает

для давлений из рассматриваемого диапазона

разницу между напряжениями в активном и пас-

давлений при соответствующих эксперименталь-

сивном сосуде, этот результат соответствует вы-

ных значениях C_m и V_m. Зная C, можно

числениям для крупных сосудов [4].

определить радиальную координату из соотноше-

ния (12) и механические напряжения в любой

Как показали расчеты, при фиксированных

точке сосудистой стенки.

значениях C_m и V_m окружное напряжение в ради-

альном направлении изменяется монотонно, но

направление его изменения зависит от величины

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

трансмурального давления (рис. 3а). В фазе раз-

Вычисленные с использованием полученных

вития сосудистого тонуса напряжение убывает по

коэффициентов значения радиуса достаточно хо-

мере приближения к наружной стенке сосуда, а

рошо воспроизводят экспериментальные измере-

после того, как он сформируется, наименьшее

ния в рассмотренном диапазоне давлений (см.

Рис. 2. Зависимости окружного напряжения от давле-

Рис. 1. Статическая зависимость внешнего радиуса со-

ния, вычисленные для пассивного (кривая 1) и акти-

суда от трансмурального давления: сплошная линия -

вированного сосудов с учетом (кривая 2) и без учета

вычисленные значения, маркеры экспериментальные

(кривая 3) мембранного потенциала. Маркеры соот-

точки [23].

ветствуют точкам, для которых проводили расчеты.

БИОФИЗИКА том 68

№ 5

2023

МИНИМАЛЬНАЯ МОДЕЛЬ ЗАВИСИМОСТИ НАПРЯЖЕНИЙ

1027

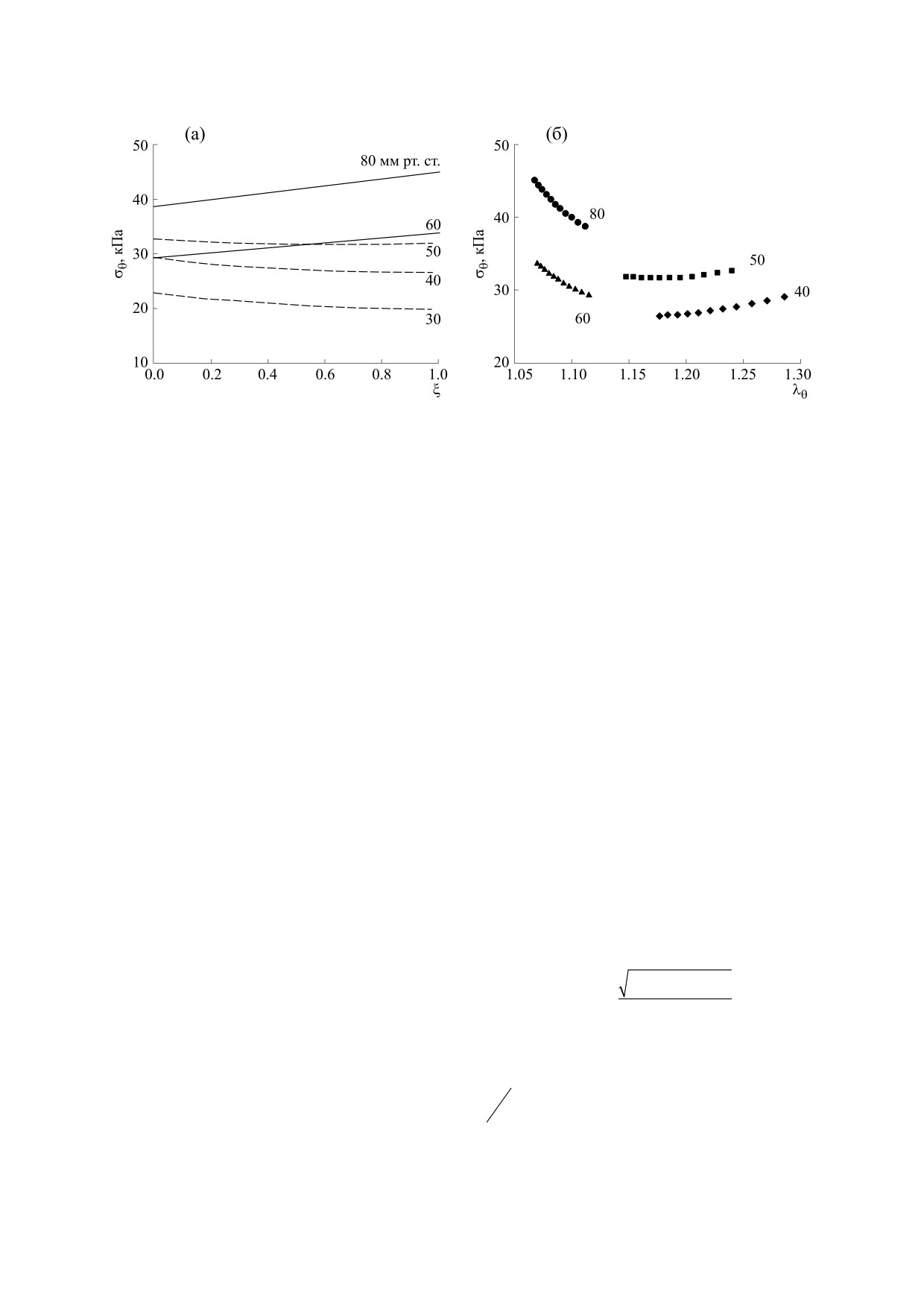
Рис. 3. Изменения окружного напряжения в радиальном направлении (а) и при изменении окружного растяжения (б).

По оси абсцисс - нормированное расстояние от внутренней стенки, цифры справа от линий - значение давления в

мм рт. ст.

окружное напряжение испытывает внутренняя

вающей распределение и ориентацию гладкомы-

стенка. Зависимость окружного напряжения от

шечных клеток и волокон эластина и коллагена в

растяжений также меняет свое поведение при

каждом из двух слоев сосудистой стенки, были

разном состоянии сосудистого тонуса (рис. 3б). В

проведены расчеты для двух разных значений

фазе развития сосудистого тонуса σ_θ по мере рас-

окружного растяжения максимально активиро-

ванного сосуда [4]. Оказалось, что в зависимости

тяжения растет, при сформированном тонусе -

снижается. Если в первой фазе различие напря-

от величины окружного растяжения зависимость

жений при минимальном и максимальном растя-

σ_θ(ξ) ведет себя по-разному: при меньшем значе-

жении относительно невелико, то во второй оно

нии (λ_θ

=1.24) она растущая, при большем

увеличивается (рис. 3б).

(λ_θ = 1.8) убывающая. На первый взгляд этот ре-

зультат не согласуется с представленным на

Такое различие в поведении окружного напря-

рис. 3. Однако в максимально активированном

жения в зависимости от тонуса сосуда не удается

сосуде изменение напряжения обусловлено толь-

описать, вводя в активное напряжение только

ко растяжениями, с увеличением растяжения,

один клеточный параметр C_m (см. работу [22]). В

возможно, сосуд начинает вести себя как пассив-

этом случае во всем рассмотренном диапазоне

ная трубка. В той же работе показано, что при

давлений σ_θ - растущая функция от растяжения и

λ_θ = 1.8 пассивная часть окружного напряжения

убывающая - от радиальной координаты.

также уменьшается по мере удаления от внутрен-

Результаты публикаций, рассматривающих

ней стенки. Можно предположить, что при ка-

только максимальную степень активации, свиде-

ком-то значении 1.24 < λ_θ < 1.8 в таких артериях

тельствуют о росте окружного напряжения в ра-

происходит переход от «активного» поведения к

диальном направлении [4 ,9], что соответствует

«пассивному».

нашим расчетам для сосуда при более высоких

Используя соотношения (2) и (12), окружные

давлениях из рассмотренного диапазона, т.е. при

растяжения сосудистой стенки при отсутствии

большей степени активации. Влияние степени

продольных деформаций, можно записать в виде

активации сократительного аппарата гладких

мышц на изменения окружного напряжения в ра-

(

) +

диальном направлении отмечали и в работе [7].

Сравнивали результаты вычислений окружного

напряжения при базальном тонусе аорты кролика

и после увеличения степени активации вдвое. В

где ξ - нормированная по толщине стенки ради-

первом случае зависимость напряжения от ради-

альная координата; на внутренней стенке ξ = 0,

альной координаты была убывающей, а после

на внешней ξ

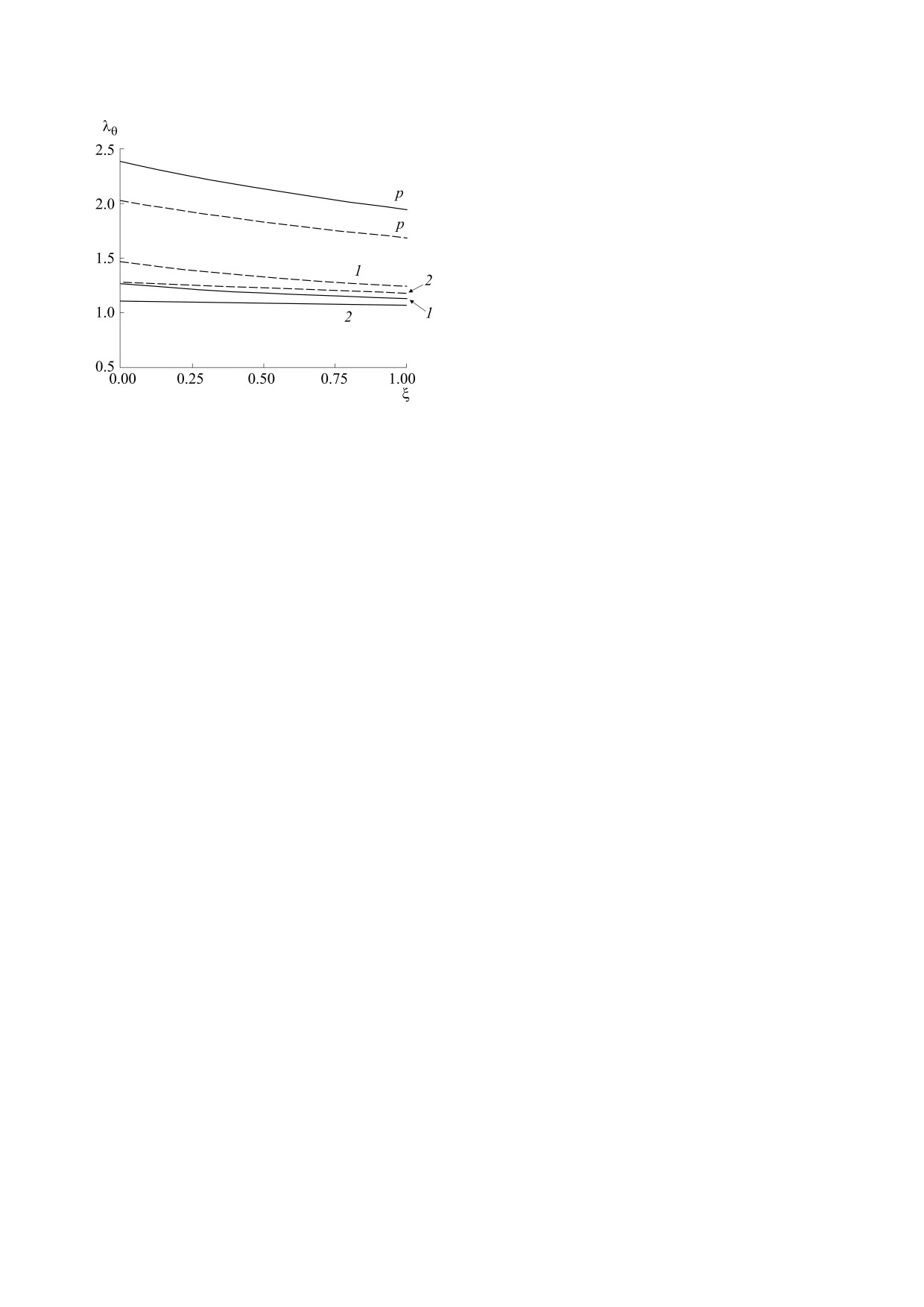
= 1. Поскольку производная

увеличения степени активации стала растущей,

∂λ

зависимость окружного растяжения от

что качественно совпадает с результатом, пред-

∂ξ

ставленным на рис. 3а. Для свиной коронарной

радиальной координаты всегда убывающая

артерии с помощью трехмерной модели, учиты-

(рис. 4).

БИОФИЗИКА том 68

№ 5

2023

1028

ШАДРИНА

артерий сведения об остаточных напряжениях в

литературе отсутствуют, поскольку их определе-

ние в сосудах диаметром порядка 100 мкм на сего-

дняшний день практически невозможно. Вслед-

ствие этого значение радиуса ненагруженного не-

активированного сосуда в представленной

модели было получено в результате аппроксима-

ции экспериментальной статической зависимо-

сти r(p) для пассивного сосуда (см. раздел «Опре-

деление параметров модели и метод решения»).

Как отмечалось, активные напряжения в мо-

дели полагали зависящими от трех параметров.

Коэффициенты функциональных соотношений

подбирали минимизацией суммы квадратов от-

клонений радиального напряжения на внутрен-

ней стенке от модуля давления. Зависимость ак-

тивного напряжения от растяжений в модели,

Рис. 4. Расчетные изменения окружного растяжения

учитывающей два клеточных параметра, пред-

в радиальном направлении в пассивном (p) сосуде и

ставляли такой же, как и при рассмотрении толь-

активном при учете одного (кривые 1) и двух (кривые

ко одного клеточного параметра, концентрации

2) клеточных параметров. Штриховые линии

кальция [22], отличие сводилось лишь к значени-

вычисления для p = 40 мм рт. ст., сплошные - для

p = 100 мм рт. ст.

ям коэффициентов. Функциональное же соотно-

шение, связывающее активное напряжение и C_m

в одном и том же диапазоне значений концентра-

В пассивном сосуде растяжения почти вдвое

ции кальция, после введения V_m имеет другой

превышают растяжения стенки активного сосуда,

вид. Что касается экспериментальной базы, дан-

большему давлению соответствуют и большие

ные такой зависимости были получены лишь на

растяжения (рис. 4, верхняя и нижняя кривые p).

гладкомышечных клетках толстой кишки мор-

В активированном сосуде распределение растя-

ской свинки в диапазоне C_m = 10²÷15∙10^-4 нМ

жений становится более однородным. Стенка ак-

[30]. В представленной модели Ψ(C_m) качествен-

тивного сосуда при большей нагрузке (p = 100 мм

рт.ст.) подвергается более слабому растяжению

но воспроизводит начальный участок экспери-

(рис. 4, сплошные и штриховые кривые 2) и одно-

ментальной зависимости из этой работы в диапа-

родность распределения становится более выра-

зоне C_m =50÷250 нМ, т.е. при значениях, соответ-

женной. При сравнении двух подходов к описа-

ствующих измерениям C_m на церебральных

нию активного напряжения оказывается, что учет

сосудах [23]. В модели [22] качественно воспроиз-

мембранного потенциала способствует получе-

водится зависимость Ψ(C_m) на всем диапазоне из

нию большей однородности растяжений вдоль

работы [30], тогда как в экспериментах на сегмен-

сосуда (рис. 4, сравни кривые 1 и 2). При давле-

тах церебральных артерий диапазон изменений

нии 100 мм рт. ст. растяжение практически оди-

концентрации кальция был существенно меньше.

наково по сечению сосуда (рис. 4,сплошная ли-

Предложенная модель позволяет рассчитать

ния 2). Уменьшение окружного растяжения по

мере удаления от внутренней стенки и увеличе-

напряженное состояние стенки и сосудистый

диаметр в физиологическом диапазоне измене-

ние степени однородности распределения растя-

ний давления при известных значениях внутри-

жения в радиальном направлении с ростом степе-

клеточных параметров в норме. Сопоставление

ни активации гладкомышечного слоя отмечали и

расчетов по модели с результатами эксперимен-

при расчетах для коронарного сосуда с использо-

тов на аналогичных сосудах [31] показало, что при

ванием трехслойной модели [29]. В описываемой

тех же значениях давления, концентрации каль-

модели, как и в работе [29], остаточные деформа-

ция и мембранного потенциала вычисленные

ции в стенке и продольные растяжения не рас-

значения радиуса находятся в диапазоне изме-

сматривали. Учет последних дает слабое увеличе-

ренных в эксперименте.

ние растяжений в радиальном направлении по

мере удаления от внутренней стенки [5, 7]. Как

Для описания поведения сосудистой стенки

уже указывалось [27], это можно объяснить раз-

после введения блокаторов мембранных каналов

личием локальных радиальных координат r₀ в

требуется введение в модель дополнительных со-

стенке ненагруженного сосуда до и после про-

отношений, связывающих изменения C_m и V_m с

дольного разреза сосуда, производимого для

проводимостью основных каналов, регулирую-

определения остаточных напряжений. Для малых

щих поступление кальция.

БИОФИЗИКА том 68

№ 5

2023

МИНИМАЛЬНАЯ МОДЕЛЬ ЗАВИСИМОСТИ НАПРЯЖЕНИЙ

1029

ЗАКЛЮЧЕНИЕ

СПИСОК ЛИТЕРАТУРЫ

И.В. Гончар, С.А. Балашов, И.А. Валиев и др.,

На основе экспериментальных данных для ма-

Труды МФТИ, 9 (1), 101 (2017).

лого церебрального сосуда получена простая ма-

N. R. Tykocki, E. M. Boerman, and W. F. Jackson,

тематическая модель поведения стенки малого

Compr. Physiol.,

(2),

485

(2018).

резистивного сосуда в статике, включающая мак-

DOI:10.1002/cphy.c160011

ро и микро параметры. Поскольку в малых арте-

W. F. Jackson, Front. Physiol., 12, 770450 (2021).

риях гладкомышечные клетки ориентированы в

DOI: 10.3389/fphys.2021.770450

окружном направлении, рассматривается только

H. Chen and G. S. Kassab, Sci. Rep., 7 (1), 9339

окружная составляющая активного напряжения.

(2017). DOI: 10.1038/s41598-017-08748-7

Получена функциональная зависимость актив-

ного напряжения от растяжений, концентрации

Y. Lu, J. Wu, Y. Li, et al., Sci. Rep., 7 (1), 13911 (2017).

кальция в цитоплазме гладкомышечных клеток и

DOI: 10.1038/s41598-017-14276-1

мембранного потенциала. Результаты вычисле-

K. Takamizawa, Cardiovasc. Eng. Tech., 10 (4), 604

ний показывают существенное снижение окруж-

(2019). DOI: 10.1007/s13239-019-00434-1

ного напряжения в стенке в результате активации

A. Rachev and K. Hayashi, Ann. Biomed. Eng. 27, 459

гладкомышечных клеток, увеличение степени од-

(1999). DOI: 10.1114/1.19

нородности распределения окружных растяже-

M. A. Zulliger, A. Rachev, and N. Stergiopulos, Am. J.

ний. В отличие от предыдущей, где напряжение

Physiol. Heart Circ. Physiol., 287, H1335 (2004). DOI:

является функцией только одного клеточного па-

10.1152/ajpheart.00094.2004

раметра, концентрации кальция, представленная

B. Zhou, A. Rachev, N. Shazly, J. Mech. Behav.

модель выявила изменение характера зависимо-

Biomed. Mater.,

48,

(2015).

DOI:

сти окружного напряжения от растяжений и ра-

10.1016/j.jmbbm.2015.04.004

диальной координаты с изменением степени ак-

10.

M. Böl, A. Schmitz, G. Nowak, and T. Siebert, J.

тивации гладкомышечных клеток. В процессе

Mech. Behav. Biomed. Mater., 13, 215 (2012). DOI:

формирования сосудистого тонуса напряжение

10.1016/j.jtbi.2011.11.012

растет (убывает) с ростом растяжения (радиаль-

11.

K. Uhlmann and D. Balzani, Biomech. Model. Mech-

ной координаты), при сформированном тонусе

anobiol., 22, 1049 (2023). DOI: 10.1007/s10237-023-

эта зависимость убывающая (растущая). Модель

01700-x

качественно воспроизводит результаты практи-

12.

С. А. Регирер, И. М. Руткевич и П. И Усик, Меха-

чески всех доступных теоретических работ, опи-

ника полимеров, № 4, 585 (1975).

сывающих поведение сосудистой стенки в усло-

13.

S. Murtada, A. Arner, and G. A. Holzapfel, J. Theor.

виях физиологической нормы. Дальнейшее раз-

Biol., 297, 176 (2012). DOI: 10.1016/j.jtbi.2011.11.012

витие модели состоит во введении минимального

14.

S. Murtada and G. A. Holzapfel, J. Theor. Biol., 358

числа параметров, характеризующих состояние

(7), 1 (2014). DOI: 10.1016/j.jtbi.2014.04.028

мембранных каналов, через которые кальций по-

15.

Á. Navarrete, P. Varela, M. López, et al., Front. Bio-

ступает в гладкомышечную клетку.

eng. Biotechnol.,

10,

924019

(2022).

DOI:

10.3389/fbioe.2022.924019

16.

C. Hai, and R. A. Murphy, Am. J. Physiol., 255, 86

ФИНАНСИРОВАНИЕ РАБОТЫ

(1988).

Работа выполнена в рамках Государственной

17.

J. Stälhand and G. A. Holzapfel, J. Theor. Biol., 397, 13

программы 47 ГП «Научно-технологическое раз-

(2016). DOI: 10.1016/j.jtbi.2016.02.028

витие Российской Федерации» (2019-2030), тема

18.

J. Yang, J. W. Clark, R. M. Bryan, and C. A. Robertson,

64.1 «Раскрытие механизмов взаимодействия мо-

Med. Engineer. & Physics, 25, 691 (2003). DOI:

лекулярно-клеточных и системных регуляций

10.1016/s1350-4533(03)00100-0

функций внутренних органов» (№ 0134-2019-

19.

J. Yang, J. W. Clark, R. M. Bryan, and C. A. Robertson,

0001).

Med. Engineer. & Physics, 25,

711

(2003). DOI:

10.1016/s1350-4533(03)00101-2

20. M. Koenigsberger, R. Sauser, D. Seppey, et al., Bophys.

КОНФЛИКТ ИНТЕРЕСОВ

J.,

(6),

2728

(2008). DOI:

10.1529/bio-

physj.108.131136

Авторы заявляют об отсутствии конфликта

21. A. Coccarelli, D. H. Edwards, A. Aggarwal, et al., J.

интересов.

Roy. Soc. Interface,

15,

20170732

(2018). DOI:

10.1098/rsif.2017.0732

22. Н. Х. Шадрина, Биофизика, 66 (1), 157 (2021).

СОБЛЮДЕНИЕ ЭТИЧЕСКИХ СТАНДАРТОВ

23. H. J. Knot and M. T. Nelson, J. Physiol., 508 (1), 199

Настоящая работа не содержит описания ка-

(1998). DOI: 10.1111/j.1469-7793.1998.199br.x

ких-либо исследований с использованием людей

24. G. Gabella, J. Ultrastruct. Res., 84 (1), 24 (1983).

и животных в качестве объектов.

DOI:10.1016/s0022-5320(83)90083-7

БИОФИЗИКА том 68

№ 5

2023

1030

ШАДРИНА

25. G. E. Sleek and B. R. Duling, Circ. Res., 59, 620

29. R. Sanft, A. Power, and C. Nicholson, Math. Biosci.,

(1986). DOI: 10.1161/01.res.59.6.620

315, 108223 (2019). DOI: 10.1016/j.mbs.2019.108223

26. Y. Fung, Biomechanics (Springer-Verlag, N.-Y., 1981).

30. A. Arner, Eur. J. Physiol., 395, 277 (1982). DOI:

27. Н. Х. Шадрина, Изв. РАН. Мех. жидк. и газа, № 2,

10.1007/BF00580790.

3 (2020). DOI: 10.31857/S0568528120020115

28. G. Osol, J. F. Brekke, K. McElroy-Yaggy, and

31. H. J. Knot, N. B. Standen, and M. T. Nelson, J. Physi-

N. I. Gokina, Am. J. Physiol. Heart Circ. Physiol.,

ol.,

508

(1),

211

(1998). DOI:

10.1111/j.1469-

283, H2260 (2002). DOI: 10.1152/ajpheart.00634.2002

7793.1998.211br.x

Minimal Model for the Dependence of Stresses in the Wall of a Cerebral Vessel

on the Parameters of a Smooth Muscle Cell

N.Kh. Shadrina*

*Pavlov Institute of Physiology, Russian Academy of Sciences, nab. Makarova 6, Saint-Petersburg, 199034 Russia

A minimal mathematical model of the wall of a small arterial vessel is described. This model is created based

on the published results of experiments performed on rat cerebral vessels. It is assumed that the active stress

has only a circumferential component and depends on the circumferential stretch, calcium concentration in

the cytoplasm, and the membrane potential of smooth muscle cells. The presented model for a small artery

сan qualitatively reproduce the results of more sophisticated models for other vessels under normal physio-

logical conditions. Unlike a similar model, that accounts for only one cellular parameter, the addition of

membrane potential as one of the main parameters was crucial to reveal a qualitative change in the depen-

dency of circumferential stress on stretch and the radial coordinate with an alteration in vascular tone. At

fixed values of membrane potential and calcium concentration in the phase of a development of vascular

tone, stress decreases as it approaches the outer wall of the vessel and increases as stretch increases, and after

it is formed, the direction of changes in the circumferential stress reverses.

Keywords: myogenic regulation, resistance vessel, vascular wall tension, calcium, membrane potential

БИОФИЗИКА том 68

№ 5

2023