БИОФИЗИКА, 2022, том 67, № 3, с. 587-595

БИОФИЗИКА CЛОЖНЫX CИCТЕМ

УДК 573.1

РЕГРЕССИОННЫЙ АНАЛИЗ И МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

ФЛУКТУАЦИЙ ПОКАЗАТЕЛЕЙ МИКРОЦИРКУЛЯЦИИ

СИММЕТРИЧНЫХ ОБЛАСТЕЙ ВЕРХНИХ КОНЕЧНОСТЕЙ ЧЕЛОВЕКА

НИИ нормальной физиологии им. П.К. Анохина, 125315, Москва, Балтийская ул., 8

E-mail: l.v.mezentseva@mail.ru

Поступила в редакцию 07.04.2022 г.

После доработки 07.04.2022 г.

Принята к публикации 11.04.2022 г.

Предложена новая расчетно-экспериментальная методика оценки устойчивости колебательных

процессов в системе регионарного кровообращения, основанная на анализе флуктуаций показате-

лей микроциркуляции крови симметричных областей верхних конечностей человека. Синхронные

измерения показателей микроциркуляции симметричных областей верхних конечностей проведе-

ны у пяти здоровых добровольцев методом лазерной допплеровской флоуметрии. Датчики фикси-

ровали на наружной поверхности симметричных областей нижних частей правого и левого плеча в

точках, расположенных на 3 см выше локтевого сгиба. Представлены регрессионные уравнения,

описывающие взаимосвязи между синхронными изменениями показателей микроциркуляции

симметричных областей верхних конечностей и их исходными значениями левой и правой сторон

измерения. Установлено, что изменения амплитуд флуктуаций микрокровотока симметричных об-

ластей верхних конечностей зависят от исходных значений этих показателей не только одноимен-

ной, но и противоположной стороны наблюдения. Показано, что изменения показателей микро-

циркуляции коррелируют отрицательно с мгновенными значениями перфузии той же стороны из-

мерения и положительно с мгновенными значениями перфузии противоположной стороны

измерения. Рассчитаны диапазоны числовых значений параметров модели, при которых имеют ме-

сто устойчивые режимы функционирования системы регионарного кровообращения. Результаты

исследований могут найти применение в медицинской практике, так как модель позволяет оцени-

вать состояние системы регионарного кровообращения у пациента и прогнозировать вероятности

перехода этой системы в патологические режимы и критические состояния.

Ключевые слова: микроциркуляция, асимметрия, лазерная допплеровская флоуметрия, математиче-

ская модель, устойчивость.

DOI: 10.31857/S000630292203019X, EDN: APVZOX

экспериментальных записей лишь позволяют на-

Флуктуации параметров физиологических си-

капливать описательные знания об изучаемых

стем являются условием их нормального функци-

объектах. Но для понимания физиологических

онирования, а результаты их адекватного матема-

тического анализа открывают возможности для

механизмов, лежащих в основе изучаемых явле-

ний, этого недостаточно. Понять механизм про-

построения математических моделей, описываю-

цесса - значит построить математическую мо-

щих регуляторные процессы в этих системах. В

настоящее время для анализа процессов флуктуа-

дель, описывающую регуляцию его основных па-

ции перфузии в различных органах и тканях на-

раметров, оценить диапазоны ее устойчивости и

ряду со стандартными статистическими подхода-

критические точки перехода в неустойчивые со-

стояния. В практической медицине проблема

ми широко применяются различные математиче-

ские методы: корреляционно-спектральный и

прогнозирования течения того или иного заболе-

вейвлет-анализ, методы нелинейной динамики

вания, четкой формулировки условий, при кото-

(оценка таких показателей, как энтропия, экспо-

рых возможны переходы из нормы в патологию

нента Ляпунова, индекс Хёрста, показатель Хау-

различной степени тяжести вплоть до критиче-

сдорфа и др.) [1-5]. Однако совершенствование

ских состояний, является особенно актуальной.

математических методов обработки и анализа

Для этого в распоряжении исследователя должна

быть не сумма разрозненных экспериментальных

Сокращение: ЛДФ - лазерная допплеровская флоуметрия.

данных, а математическая модель изучаемого яв-

587

588

МЕЗЕНЦЕВА

ления и точные математические методы оценки

как одноименной, так и противоположной сторо-

ее устойчивости. В настоящее время предприни-

ны наблюдения. С этой целью для каждого испы-

маются попытки построения математических мо-

туемого рассчитывались параметры a₀, a₁, a₂, b₀,

делей, описывающих колебательные процессы в

b₁, b₂ регрессионных уравнений

сердечно-сосудистой системе [6-11], однако при

их формулировке не учитываются обнаруженные

Δx





(1)

разными исследователями в последние годы фун-

Δx

даментальные закономерности лево-правосто-

ронней асимметрии [12-17]. Установлено, что в

Значимость результатов регрессионного ана-

механизмах регуляции колебательных процессов

лиза оценивали стандартными статистическими

перфузии в различных органах и тканях важную

методами. Полученная регрессионная модель

роль играют корреляционные взаимосвязи между

была положена в основу математической модели,

показателями микроциркуляции симметричных

сформулированной в виде системы линейных

областей [13-17]. Показано [17], что реакция по-

дифференциальных уравнений (см. описание

казателей микроциркуляции верхних конечно-

ниже).

стей на возмущающее воздействие в виде асим-

Дальнейшие исследования решений этой си-

метричных физических нагрузок зависит от ис-

стемы и их устойчивости проводили с использо-

ходных значений показателей микроциркуляции

ванием известных математических методов [20].

не только одноименной, но и противоположной

Расчеты проводили в условных (перфузионных)

стороны измерения. При этом оказалось, что ис-

единицах с помощью программного обеспече-

ходные и возмущенные временные ряды микро-

ния, входящего в пакеты прикладных программ

циркуляции характеризуются и инверсной дина-

Statistica и Excel for Windows (v. 6.0).

микой лево-правосторонней асимметрии геомет-

рических форм аттракторов [18].

РЕЗУЛЬТАТЫ

Однако механизмы, лежащие в основе этих

процессов, не ясны, также как не сформулирова-

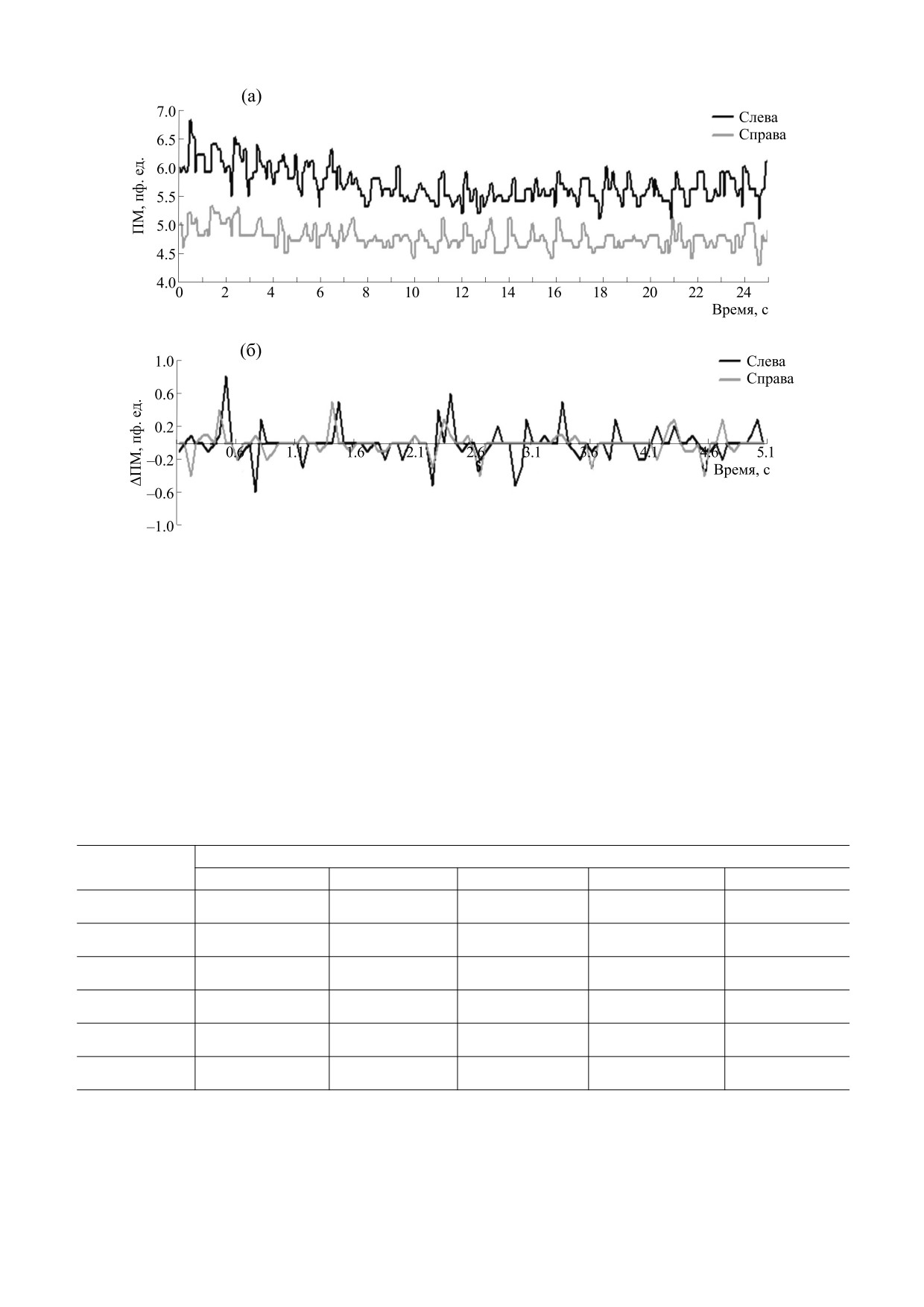
Регрессионный анализ. На рис. 1 представлены

на математическая модель, позволяющая рассчи-

временные ряды, отражающие динамику син-

тывать критические точки перехода системы в

хронных измерений показателей микроциркуля-

неустойчивые состояния и патологические ре-

ции слева (x₁ = ПМ_лев) и справа (x₂ = ПМ_прав) у

жимы.

одного из испытуемых. Можно видеть, что флук-

туации показателей микроциркуляции слева и

Целью настоящего исследования явилась раз-

справа - это разные, взаимно не накладывающи-

работка математической модели, описывающей

еся стохастические процессы. Статистический

экспериментальные закономерности лево-пра-

анализ этих процессов, выполненный для всех

восторонней асимметрии колебательных процес-

пяти испытуемых, показал, что среднее значение

сов в системе микроциркуляции, и исследование

величины ПМ слева (6.97 ± 0.94) немного выше,

условий устойчивости этой модели.

чем справа (5.48 ± 0.89), но эта разница была не

достоверна. Достоверных различий между сред-

МЕТОДИКА

ними значениями изменений Δx₁ и Δx₂ этих пока-

зателей слева и справа также не выявлено. Следу-

Измерения показателей микроциркуляции

ющим этапом исследований явилось изучение

проводились у пяти здоровых добровольцев

количественных закономерностей изменений

(мужчины 50-70 лет, правши) методом лазерной

показателей микроциркуляции слева и справа,

допплеровской флоуметрии (ЛДФ) с помощью

т. е. временных рядов

{Δx₁[i]} и

{Δx₂[i]},

двухканального прибора ЛАКК-02 (ООО НПП

i = 1,2,3,...,100. Для этой цели был использован

«ЛАЗМА», Москва) [20]. Датчики ЛДФ-сигнала

метод множественного регрессионного анализа:

фиксировали на наружной поверхности симмет-

была выполнена оценка коэффициентов регрес-

ричных областей нижних частей правого и левого

сии a₀, a₁, a₂, b₀, b₁, b₂ системы уравнений (1) для

плеча в точках, расположенных на 3 см выше лок-

тевого сгиба. Синхронные измерения показате-

всех фрагментов периодограмм по каждому ис-

лей микроциркуляции слева (ПМ_лев) и справа

пытуемому. Результаты расчетов представлены в

табл. 1. Из этой таблицы можно видеть, что рас-

(ПМ_прав) выполняли в дневное время суток через

четные значения величин коэффициентов ре-

каждые три часа (5 измерений в день) в течение

грессии a₂ у всех испытуемых достоверно отлича-

пяти дней. Записи ЛДФ-сигнала проведены с ча-

ются от 0 (p < 0.05). Это свидетельствует о том, что

стотой 20 Гц в течение 1 мин с интервалом отсче-

изменения показателя микроциркуляции слева

тов 0.05 с. Далее методом множественного регрес-

(Δx₁ = ΔПМ_лев) зависят не только от исходных

сионного анализа изучали взаимосвязи между из-

менениями перфузии каждой из сторон

значений этого показателя слева (х₁ = ПМ_лев), но

наблюдения и исходными значениями перфузии

также и от величины этого показателя справа

БИОФИЗИКА том 67

№ 3

2022

РЕГРЕССИОННЫЙ АНАЛИЗ И МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

589

Рис. 1. Динамика изменений у одного испытуемого: (а) - показателей микроциркуляции слева (x₁ = ПМ_лев) и справа

(x₂ = ПМ_прав), (б) - их изменений Δx₁ и Δx₂.

(х₂ = ПМ_прав). Аналогичная закономерность име-

(х₁ = ПМ_лев). Таким образом, результаты регрес-

ет место и для правой стороны наблюдения: рас-

сионного анализа свидетельствуют о том, что из-

четные значения величин коэффициентов ре-

менения амплитуд флуктуаций микрокровотока

грессии b₁ у всех испытуемых достоверно отлича-

симметричных областей верхних конечностей за-

висят от исходных значений этих показателей не

ются от 0 (p < 0.05). Это свидетельствует о том, что

только одноименной, но и противоположной

изменения показателя микроциркуляции справа

стороны наблюдения.

(Δx₂ = ΔПМ_прав) зависят не только от исходных

значений этого показателя справа (х₂ = ПМ_прав),

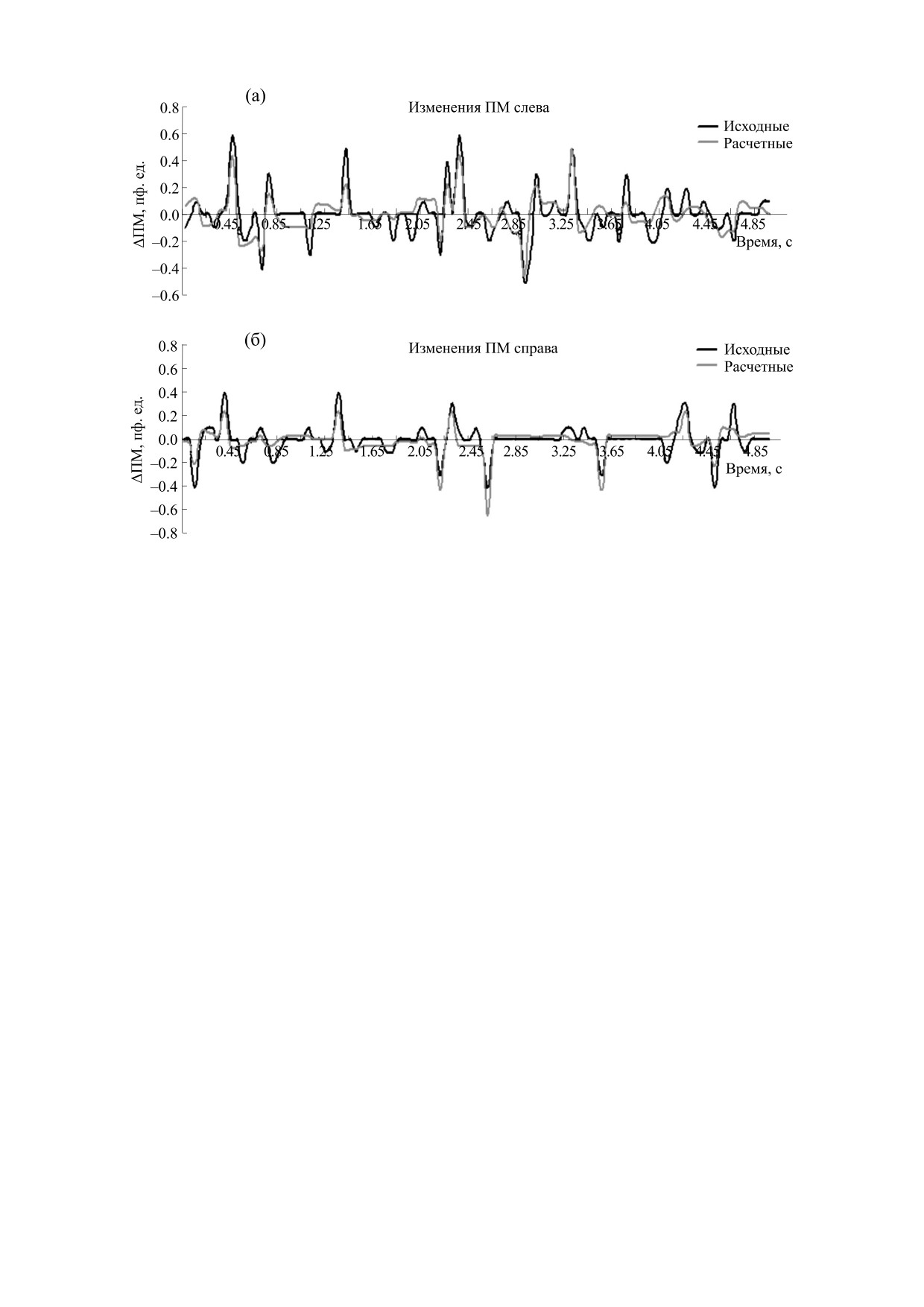
На рис. 2 показаны примеры исходных и рас-

но также и от величины этого показателя слева четных согласно регрессионным уравнениям (1)

Таблица 1. Расчетные значения средних величин коэффициентов регрессии (M ± m) для пяти испытуемых

Коэффициент

№ испытуемого

регрессии, усл.

а₂

0.143 ± 0.064*

0.187 ± 0.043*

0.139 ± 0.053*

0.135 ± 0.051*

0.184 ± 0.037*

а₁

-0.294 ± 0.021

-0.366 ± 0.027

-0.317 ± 0.048

-0.426 ± 0.032

-0.282 ± 0.018

а₀

1.024 ± 0.289

1.313 ± 0.222

1.651 ± 0.225

1.940 ± 0.342

0.534 ± 0.219

b₂

-0.363 ± 0.023

-0.318 ± 0.027

-0.303 ± 0.063

-0.284 ± 0.031

-0.307 ± 0.025

b₁

0.132 ± 0.031**

0.104 ± 0.024**

0.135 ± 0.044**

0.151 ± 0.037**

0.078 ± 0.021**

b₀

0.990 ± 0.110

1.421 ± 0.182

0.305 ± 0.059

1.305 ± 0.215

0.859 ± 0.193

Примечание. *- a₂ > 0, p < 0.05; **b₁ > 0, p < 0.05.

БИОФИЗИКА том 67

№ 3

2022

590

МЕЗЕНЦЕВА

Рис. 2. Исходные и расчетные временные ряды, описывающие мгновенные значения изменений Δx1 и Δx2

показателей микроциркуляции для одного испытуемого.

и (2) временных рядов, описывающих мгновен-

0, b₁ > 0). Следует также отметить, что абсолютная

ные значения изменений Δx₁ и Δx₂ показателей

величина коэффициента a₂ была, как правило,

микроциркуляции для одного из испытуемых.

меньше, чем величина коэффициента a₁, а абсо-

Можно видеть, что расчетные кривые изменений

лютная величина коэффициента b₁ - меньше,

Δx_{1 расч} и Δx_{2 расч} достаточно хорошо описывают

чем величина коэффициента b₂. Таким образом,

исходные кривые изменений показателей микро-

можно заключить, что изменения амплитуд

циркуляции. Дальнейшая проверка с помощью

флуктуаций микрокровотока коррелируют отри-

F-критерия Фишера показала статистическую до-

цательно с мгновенными значением амплитуд

стоверность выбранной регрессионной модели у

микрокровотока той же стороны измерения и по-

всех пяти испытуемых. Таким образом, использу-

ложительно с мгновенными значением амплитуд

емая в настоящем исследовании расчетно-экспе-

микрокровотока противоположной стороны из-

риментальная методика позволила сформулиро-

мерения. При этом с одноименной стороны на-

вать статистически значимую эмпирическую ре-

блюдения имеет место более сильное влияние,

грессионную модель, описывающую динамику

чем с противоположной стороны.

синхронных изменений показателей микроцир-

куляции симметричных областей верхних конеч-

Результаты проведенных исследований также

ностей человека.

показали, что геометрические области экспери-

) и

ментальных значений коэффициентов (a₁, a₂

Другая отличительная особенность, обнару-

(b₁, b₂) совпадают, что позволило их представить

женная в настоящем исследовании, касается ве-

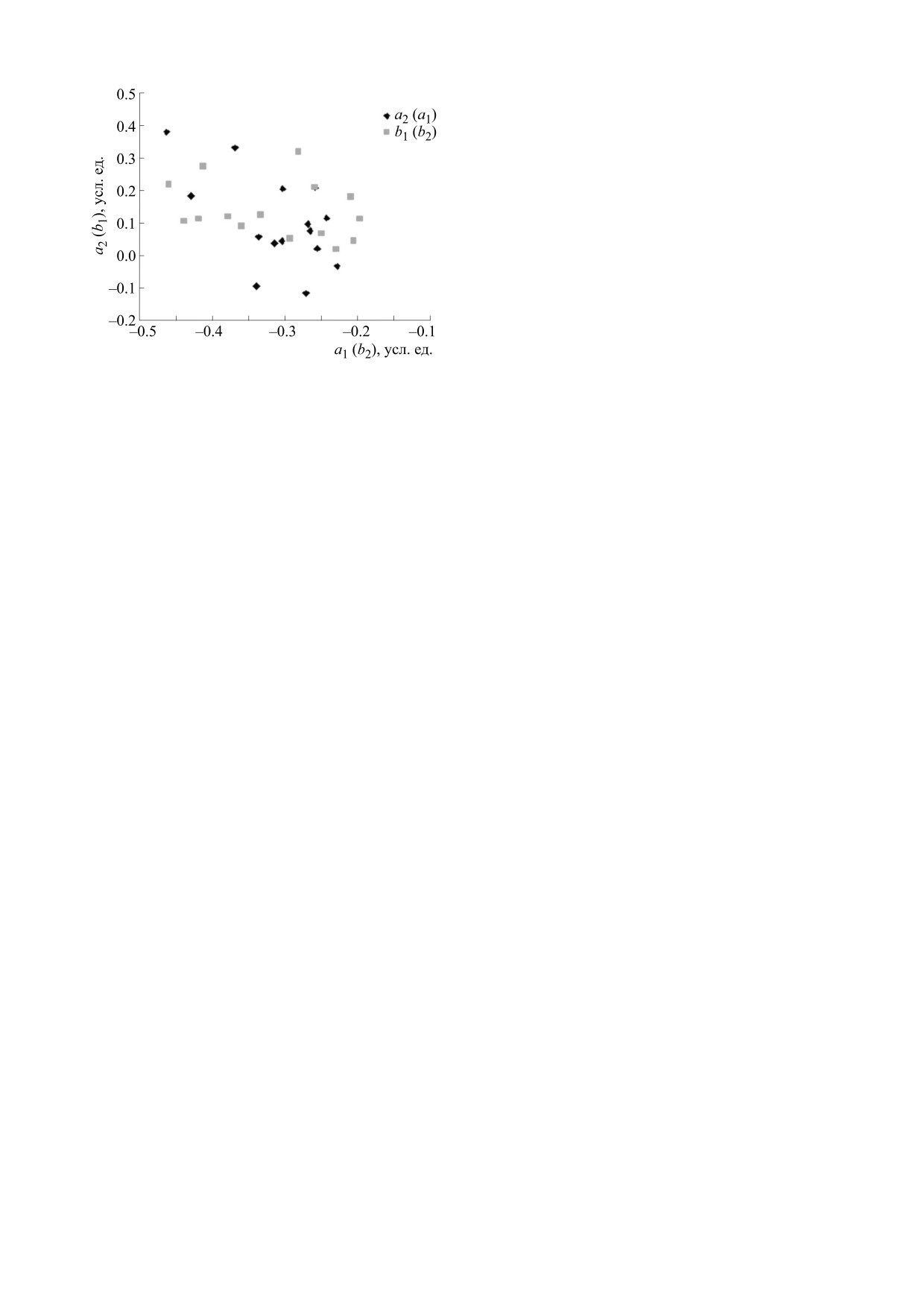
на одной фазовой плоскости. Это можно видеть

личин регрессионных коэффициентов a₁ и b₂. Ре-

на рис. 3, на котором показаны типичные приме-

зультаты расчетов показали, что для всех испыту-

ры геометрических областей экспериментальных

емых эти коэффициенты были отрицательные

значений коэффициентов (a₁, a₂) и (b₁, b₂) для од-

(a₁ < 0, b₂ < 0). Результаты регрессионного анали-

ного испытуемого. Подобная закономерность на-

за, выполненного по всем фрагментам выборки

блюдалась у всех пяти испытуемых. Указанная

(N = 1250) показали, что коэффициенты a₂ и b₁ в

особенность позволяет сделать предположение,

большинстве случаев были положительные (a₂ > что регрессионные коэффициенты {a1, a2} и

БИОФИЗИКА том 67

№ 3

2022

РЕГРЕССИОННЫЙ АНАЛИЗ И МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

591

(T₁ λ² + T₂ λ + 1)x₂ = 0.

(7)

Таким образом, математическая модель позво-

ляет получить общее решение {x₁(t), x₂(t)} систе-

мы линейных дифференциальных уравнений (2),

описывающих процессы регуляции показателей

микроциркуляции в симметричных областях пар-

ных органов человека.

Устойчивость процессов кровообращения в мик-

роциркуляторном русле. Одним из важных вопро-

сов, возникающих при исследовании физиологи-

ческих систем, является вопрос о механизмах

обеспечения устойчивости их функционирова-

ния. Результаты настоящего исследования свиде-

тельствуют о том, что функционирование систе-

мы микроциркуляции в симметричных отделах

парных органов человека подчиняется строгим

Рис. 3. Пример геометрических областей экспери-

математическим закономерностям, описывае-

ментальных значений коэффициентов (a₁, a₂) и (b₁

мым системой линейных дифференциальных

b₂) для одного испытуемого.

уравнений (2), поэтому исследование условий

устойчивости этой системы может быть выполне-

но стандартными математическими методами.

{b₁, b₂}, возможно, не являются независимыми.

Согласно критерию Гурвица [20], исследование

Для выяснения характера этих взаимосвязей тре-

на устойчивость системы линейных дифферен-

буются дальнейшие исследования.

циальных уравнений n-го порядка сводится к на-

Математическая модель. Закономерности из-

хождению условий отрицательности действи-

менения показателей микроциркуляции, описы-

тельных частей соответствующего характеристи-

ваемые системой регрессионных уравнений (1),

ческого уравнения. Применительно к нашему

дают основание полагать, что при малых измене-

случаю все корни характеристического уравне-

ниях {Δx₁[i]} и {Δx₂[i]} (а это действительно имело

ния (7) будут отрицательные, и система диффе-

место, поскольку интервал отсчета периодограм-

ренциальных уравнений (2) будет иметь устойчи-

мы Δt[i] = 0.05 с), систему регрессионных уравне-

вые решения в том случае, если

ний (1) можно заменить аналогичной системой

T₁ = 1/(a₁b₂ - b₁a₂) > 0,

(8)

дифференциальных уравнений:

T₂ = - (b₂ + a₁)/(a₁b₂ - b₁a₂) > 0.

(9)

dx

dt = a



(2)

При этом величины T₁ и T₂ связаны условием:

dx

dt = b

ζ = T₂/2T₁ < 1.

(10)

Эта система дифференциальных уравнений

была положена в основу математической модели.

Это условие означает, что корни характери-

Числовые значения регрессионных коэффициен-

стического уравнения (7) являются комплексны-

тов, определяющие параметры модели, представ-

ми. Поскольку система дифференциальных урав-

лены в табл. 1. Известно [20], что решение систе-

нений (2) описывает колебательный процесс, ха-

мы дифференциальных уравнений первого по-

рактеристики которого зависят от конкретных

рядка с постоянными коэффициентами может

числовых значений параметров a₀, a₁, a₂, b₀, b₁, b₂,

быть получено путем сведения этой системы к од-

то в зависимости от величины ζ возможны разные

ному линейному дифференциальному уравне-

варианты поведения исследуемой колебательной

нию более высокого порядка

системы. C ростом ζ колебательность переходно-

го процесса уменьшается, исчезая совсем при

(T₁ p² + T₂p + 1)x₂ = K,

(3)

ζ = 1.

где p - оператор дифференцирования, а коэффи-

Таким образом, математическая модель позво-

циенты T₁, T₂ и K равны соответственно:

ляет оценить устойчивость процессов кровообра-

щения в микроциркуляторном русле. В ходе на-

T₁= 1/(a₁b₂ - b₁a₂),

(4)

стоящих исследований нами были проведено те-

T₂ = (b₂ + a₁)/(b₁a₂ - a₁b₂),

(5)

стирование всех испытуемых на устойчивость

системы микроциркуляции. С этой целью для

K = (b₁a₀ - a₁b₀)/(a₁b₂ - b₁a₂),

(6)

всех испытуемых были рассчитаны числовые зна-

а поведение системы будет определяться корнями

чения параметров T₁, T₂ и ζ и выполнена провер-

характеристического уравнения

ка выполнения условий (8)-(10). Результаты те-

БИОФИЗИКА том 67

№ 3

2022

592

МЕЗЕНЦЕВА

Таблица 2. Числовые значения коэффициентов регрессии {a₁, a₂, b₁, b₂}, параметров {T₁, T₂, ζ}, а также

результаты проверки математической модели на устойчивость для всех испытуемых

Коэффициенты регрессии

Условия устойчивости

№ испытуемого

a_l

a₂

b_l

b₂

Т₁

Т₁ > 0

Т₂

T₂ > 0

T < i

-0.294

0.143

0.132

-0.363

11.384

TRUE

7.479

TRUE

0.329

TRUE

-0.366

0.187

0.104

-0.318

10.316

TRUE

7.056

TRUE

0.342

TRUE

-0.317

0.139

0.135

-0.303

12.939

TRUE

8.022

TRUE

0.310

TRUE

-0.426

0.135

0.151

-0.284

9.940

TRUE

7.058

TRUE

0.355

TRUE

-0.282

0.184

0.078

-0.307

13.846

TRUE

8.155

TRUE

0.295

TRUE

стирования представлены в табл. 2, из которой

a₁₂- 0.7a₁ - F₂ = 0.

(16)

можно видеть, что величины регрессионных ко-

эффициентов у всех испытуемых удовлетворяли

Поэтому имеем:

условиям устойчивости, неустойчивые состояния

не обнаружены.

a_{1(1 и 2)} = 0.35 ± 1/2

(0.49 + 4F

(17)

Упрощенная модель. Результаты настоящего

Это уравнение определяет две ветви парабол в

исследования показали, что геометрические об-

плоскости переменных {a₂, a₁}. Из них вторая па-

ласти экспериментальных значений коэффици-

рабола является не значимой, так как находится

ентов (a₁, a₂) и (b₁, b₂) совпадают, что позволило

вне диапазона реальных экспериментальных зна-

сделать предположение о наличии взаимосвязи

чений коэффициентов. Поэтому она не участвует

между регрессионными коэффициентами. Про-

в дальнейших расчетах. Для окончательного фор-

верка этого предположения была выполнена ме-

мирования области устойчивости в плоскости пе-

тодом регрессионного анализа. Результаты ана-

ременных {a₂, a₁} помимо первой параболы необ-

лиза подтвердили это предположение. Оказалось,

ходимо учитывать дополнительные ограничения

что коэффициент a₂ связан линейной зависимо-

стью с коэффициентом b₁, а коэффициент a₁ свя-

-0.65 < a₁ < 0 и a₂ > -0.3,

(18)

зан линейной зависимостью с коэффициентом

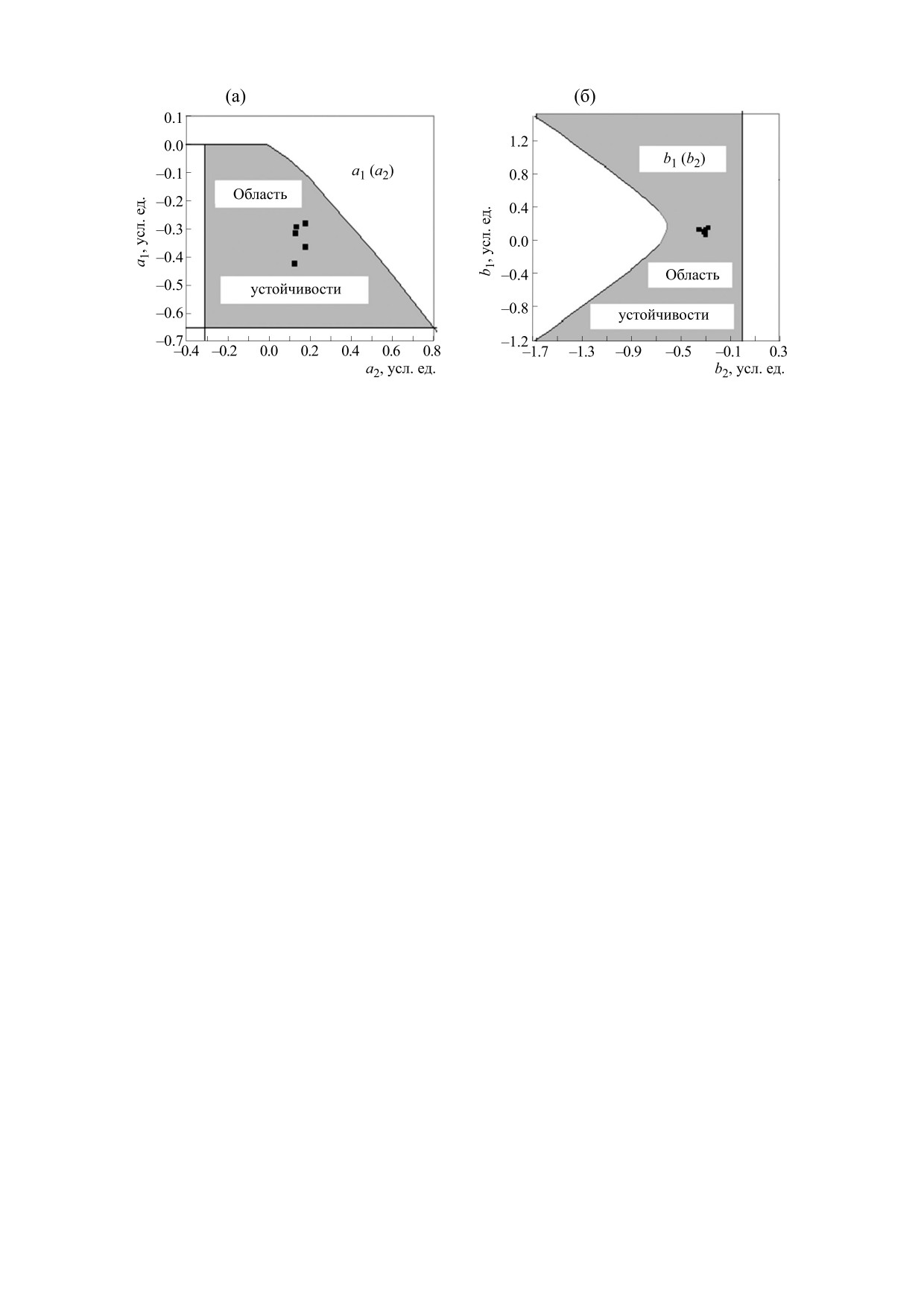
которые следуют из (10) и (15). Окончательный

b₂. Эти зависимости описываются регрессионны-

контур области устойчивости в плоскости пере-

ми уравнениями

менных {a₂, a₁} с учетом всех ограничений пока-

a₂ = -0.82b₁ + 0.26,

(11)

зан на рис. 4а. Аналогично рассчитываются кон-

туры геометрических областей устойчивости в

a₁ = -1.16b₂ - 0.70.

(12)

плоскости переменных {b₂, b₁}. Подставляя (13) и

Уравнения (11) и (12) позволяют упростить мо-

(14) в (8), получим, что условие устойчивости

дель. Снизив точность оценок коэффициентов

T₁ > 0 сводится к нахождению корней квадратно-

путем их округления, получим:

го уравнения

a₂ = -b₁ + 0.3,

(13)

b₁₂ - 0.3b₁ - FF₂ = 0,

(19)

a₁ = -b₂ - 0.7.

(14)

где мы ввели обозначение

Уравнения (13) и (14) положены в основу упро-

FF₂(b₂) = b₂₂+ 0.7b₂.

(20)

щенной модели. В этом случае условие устойчи-

вости (8) T₁> 0 сводится к неравенству

Поэтому имеем

a₁(a₁ - 0.7) - a₂(a₂ + 0.3) > 0.

(15)

b_{1(1 и 2)}

= 0.15 ± 1/2

(0.15 + 4FF

(21)

Если ввести обозначение F₂ = a₂(a₂ + 0.3), то

нахождение области устойчивости, удовлетворя-

Это уравнение определяет две ветви парабол в

ющей условию (15), сводится к нахождению кор-

плоскости переменных {b₂, b₁}. Для окончатель-

ней квадратного уравнения

ного формирования области устойчивости в

БИОФИЗИКА том 67

№ 3

2022

РЕГРЕССИОННЫЙ АНАЛИЗ И МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

593

Рис. 4. Области устойчивости параметров математической модели; (a) - в плоскости параметров (a₂, a₁), (б) - в плос-

кости параметров (b₂, b₁).

плоскости переменных {b₂, b₁} необходимо также

ричных регионов микроциркуляторного русла

учитывать дополнительные ограничения

определяется параметрами математической мо-

дели, описываемой системой дифференциальных

b₂ < 0 и |b₂| < 1.7,

(22)

уравнений (2). Сформулированные нами крите-

рии взаимосвязи между числовыми значениями

которые следуют из условий (10) и (15). Оконча-

этих параметров, выраженные в соотношениях

тельный контур области устойчивости в плоско-

(8)-(10), определяют условия устойчивости

сти переменных {b₂, b₁} с учетом всех ограниче-

функционирования целостной системы микро-

ний показан на рис. 4б. Результаты тестирования

циркуляции. Результаты настоящих исследова-

на устойчивость упрощенной модели показали,

ний подтверждают ранее сформулированный в

что величины регрессионных коэффициентов у

работах С.П. Ногиной (см. работу [21]) принцип

всех испытуемых находились внутри областей

право-левого гемодинамического баланса,

устойчивости, что можно видеть из рис. 4. На

определяющий пространственно-временную ор-

рис. 4а показаны локализации точек коэффици-

ганизацию гемодинамической системы и выяв-

ентов {a₁, a₂} по каждому испытуемому (табл. 1), а

ляющий ее интегративную роль в отношении

на рис. 4б - аналогичные локализации точек ко-

снабжаемых органов. Ею было показано, что ге-

эффициентов {b₁, b₂}. Можно видеть, что все ко-

модинамическая система представляет собой са-

эффициенты находятся в пределах контуров рас-

моорганизующуюся систему, устойчивость кото-

четных геометрических областей устойчивости,

рой обеспечивается право-левым гемодинамиче-

неустойчивые состояния не обнаружены.

ским балансом и пространственно-временной

Таким образом, разработанная нами матема-

организацией сосудистого русла. Сформулиро-

тическая модель позволяет определить количе-

ванный С.П. Ногиной принцип право-левого ге-

ственные критерии, разделяющие нормальные

модинамического баланса тесно связан с другим

(устойчивые) и патологические (неустойчивые)

фундаментальным свойством гемодинамической

режимы функционирования системы микроцир-

системы - свойством хиральности. Это одно из

куляции.

основополагающих свойств живых организмов,

проявляющихся на различных уровнях их орга-

низации, как на системном уровне, так и на реги-

ОБСУЖДЕНИЕ

онарном. Оказалось, что хиральность регионар-

Результаты настоящего исследования показа-

ного кровотока у животных проявляется с самого

ли, что определяющим фактором в поддержании

рождения и на всех дальнейших этапах их онтоге-

устойчивости функционировании системы реги-

нетического развития [15]. Полученные нами

онарного кровообращения человека является не

результаты, сформулированные в виде математи-

величина перфузии на той или другой стороне из-

ческой модели, не только подтверждают теорети-

мерения, а право-левосторонний баланс крово-

ческую концепцию С.П. Ногиной об определяю-

снабжения симметричных регионов. Степень

щей роли право-левого гемодинамического

сбалансированности кровоснабжения симмет-

баланса в обеспечении устойчивости функцио-

БИОФИЗИКА том 67

№ 3

2022

594

МЕЗЕНЦЕВА

нирования гемодинамической системы человека

СОБЛЮДЕНИЕ ЭТИЧЕСКИХ СТАНДАРТОВ

и животных, но и содержат практические реко-

Все процедуры, выполненные в исследовании

мендации по оценке устойчивости системы реги-

с участием людей, соответствовали этическим

онарного кровообращения исследуемых органов.

стандартам Хельсинкской декларации 1964 г. и ее

Результаты настоящего исследования могут

последующим изменениям. От всех участников

найти применение в практической медицине, так

предварительно было получено информирован-

как с помощью модели можно проводить персо-

ное добровольное согласие на участие в исследо-

нифицированные оценки состояния системы

вании.

микроциркуляции у различных групп населения

и прогнозировать вероятности перехода этой си-

стемы в патологические режимы и критические

СПИСОК ЛИТЕРАТУРЫ

состояния.

А. И. Крупаткин, В. В. Сидоров и И. А. Кутепов.

Регионарное кровообращение и микроциркуля-

ция 8 (3), 21 (2009).

ВЫВОДЫ

А. Н. Герасимов, Л. А. Михайличенко и

1. Впервые сформулированы регрессионные

М. И. Шпитанков, в кн. Исследование операций

уравнения, описывающие флуктуации показате-

(модели, системы, решения) (ВЦ РАН, М., 2008),

лей микроциркуляции симметричных областей

cс.140-146.

верхних конечностей человека.

L. A. Mikhailichenko and D. D. Matsievskii. Bull.

2. Установлено, что изменения амплитуд

Exp. Biol. Med. 152 (3), 382 (2012).

флуктуаций микрокровотока симметричных об-

ластей верхних конечностей зависят от исходных

A. Stefanovska, M. Bracic, and H. D. Kvernmo. IEEE

значений этих показателей не только одноимен-

Trans. Biomed. Eng. 46 (10), 1230 (1999).

ной, но и противоположной стороны наблю-

M. Thanaj, A. J. Chipperfield, and G. F. Clough.

дения.

Comput. Biol. Med. 102 (1), 157 (2018).

3. Показано, что изменения амплитуд флукту-

А. А. Гриневич, Регионарное кровообращение и

аций микрокровотока коррелируют отрицатель-

микроциркуляция 17 (68), 11 (2018).

но с мгновенными значениями амплитуд микро-

А. Grinevich, A. Tankanag, I. Tikhonova, and

кровотока той же стороны измерения и положи-

N. Chemeris, Microvasc. Res. 126, 103889 (2019).

тельно с мгновенными значениями амплитуд

A. J. Chipperfield, M. Thanaj, and G. F. Clough, 105

микрокровотока противоположной стороны из-

(9), 1452 (2020).

мерения.

4. Впервые сформулирована математическая

M. Thanaj and A. J. Chipperfield, in Proc. Annu. Int.

модель, описывающая флуктуации показателей

Conf. IEEE Eng. Med. Biol. Soc. (2019), p. 2281.

микроциркуляции симметричных областей верх-

10.

O. Forouzan, X. Yang, J. M. Sosa, et al., Microvasc.

них конечностей человека.

Res. 84 (2), 123 (2012).

5. Показано, что устойчивость функциониро-

11.

A. Goltsov, A. Anisimova, A. Zakharkina, et al.,

вания системы регионарного кровообращения

Front. Physiol. 8 (160), 1 (2017).

человека определяется параметрами математиче-

12.

M. Benedicic, A. Bernjak, A. Stefanovska, and R.

ской модели и сформулированы критерии взаи-

Bosnjak, Microvasc. Res. 7 (1), 45 (2007).

мосвязи между числовыми значениями этих па-

13.

Л. А. Михайличенко, Регионарное кровообраще-

раметров.

ние и микроциркуляция 28 (4), 71 (2008).

6. Впервые показано, что функционирование

14.

L. A. Mikhailichenko and I. A. Tikhomirova, Bull.

системы регионарного кровообращения описы-

Exp. Biol. Med. 151 (1), 16 (2011).

вается строгими математическими уравнениями,

определяющими сбалансированность кровоснаб-

15.

L. A. Mikhailichenko and L. V. Mezentseva, Bull.

жения правого и левого микроциркуляторного

Exp. Biol. Med. 158 (3), 308 (2015).

русла, направленную на поддержание устойчиво-

16.

L.V. Mezentseva and S. S. Pertsov. Bull. Exp. Biol.

сти всей системы.

Med. 166 (3), 301 (2019).

7. Результаты исследования могут быть ис-

17.

L. V. Mezentseva and S. S. Pertsov, Human Physiol.

пользованы в медицинской практике для разра-

46 (6), 671 (2020).

ботки методов персонализированной оценки на-

18.

L. V. Mezentseva, Biophysics 66 (1), 149 (2021).

рушений системы микроциркуляции и диффе-

19.

Лазерная допплеровская флоуметрия микроцирку-

ренцированных подходов к лечению пациентов с

ляции крови, под ред. А. И. Крупаткина и В. В. Си-

заболеваниями сердца и сосудов.

дорова (Медицина. М, 2005).

20.

Л. Э. Эльсгольц, Дифференциальные уравнения и

КОНФЛИКТ ИНТЕРЕСОВ

вариационное исчисление (Наука, М., 1969).

Автор заявляет об отсутствии конфликта инте-

21.

Л. В. Мезенцева, Евразийский союз ученых 11

ресов.

(56), 21 (2018).

БИОФИЗИКА том 67

№ 3

2022

РЕГРЕССИОННЫЙ АНАЛИЗ И МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

595

Regression Analysis and Mathematical Modeling of Fluctuations in Microcirculation

Parameters of Symmetrical Regions of the Human Upper Limbs

L.V. Mezentseva

P.K. Anokhin Research Institute of Normal Physiology, Baltyskaya ul. 8, Moscow, 125315 Russia

A new computational and experimental technique for assessing the stability of oscillatory processes in the re-

gional circulatory system based on the analysis of fluctuations in blood microcirculation indices of symmet-

rical regions of the human upper limbs is proposed. Synchronous measurements of microcirculatory param-

eters of the symmetrical regions of the upper limbs in 5 healthy volunteers were carried out by laser Doppler

f lowmetry. Sensors were fixed to the symmetrically located landmarks on shoulders (the anterior regions of

right and left upper arms) 3 cm from the point of the elbow bend. Regression equations are formulated that

describe the relationship between microcirculation parameters that changed synchronously for the symmet-

rical regions of the upper limbs and the initial measured values for the left and right shoulders. It is shown that

changes in the amplitudes of fluctuations in the microcirculatory flow in the symmetrical regions of the upper

limbs are caused not only by the processes in one shoulder but also by the processes in the other. It is shown

that changes in the microcirculation parameters are negatively correlated with instantaneous perfusion re-

sponse of one shoulder under observation but positively correlated with that of the other. The ranges of nu-

merical values of the model parameters are found; within these ranges, stable modes of functioning of the re-

gional blood circulation system are seen. The results of the research can be used in medical practice since the

model allows us to assess the state of the regional circulatory system in a patient and predict the likelihood of

the transition of this system to pathological regimes and critical conditions.

Keywords: microcirculation, asymmetry, laser Doppler flowmetry, mathematical model, stability

БИОФИЗИКА том 67

№ 3

2022