БИОФИЗИКА, 2022, том 67, № 3, с. 451-455

МОЛЕКУЛЯРНАЯ БИОФИЗИКА

УДК 541.11

ОПТИМИЗАЦИЯ ВЫЧИСЛЕНИЙ В ЗАДАЧЕ СТРУКТУРНОГО

МОДЕЛИРОВАНИЯ УРАВНЕНИЯМИ

ДЛЯ БИОИНФОРМАТИЧЕСКИХ ПРИЛОЖЕНИЙ

*Санкт-Петербургский политехнический университет Петра Великого, 195251, Санкт-Петербург,

Политехническая ул., 29

**Институт белка РАН, 142290, Пущино Московской области, Институтская ул., 4

E-mail: m.samsonova@spbstu.ru

Поступила в редакцию 14.03.2022 г.

После доработки 14.03.2022 г.

Принята к публикации 23.03.2022 г.

Структурное моделирование уравнениями - это метод для анализа линейных взаимодействий меж-

ду наблюдаемыми и латентными переменными, представленными в виде направленного причин-

но-следственного графа. Он является популярным инструментом в самых различных областях, от

гуманитарных до естественно-научных. За последнее десятилетие данный метод стал особенно ин-

тересен в областях, находящихся на стыке с биологией. Однако зачастую в биологических данных

нарушается распространенное предположение о независимости наблюдений, что необходимо учи-

тывать на этапе построения математической модели. Кроме того, в такой задаче, как, например,

полногеномный поиск ассоциаций, время оптимизации параметров модели является особенно

критичным фактором. В данной работе предлагается новая модель метода, а также быстрый способ

оценки ее параметров.

Ключевые слова: SEM, structural equation modelling, структурное моделирование уравнениями, semopy,

квадратуры гаусса, полногеномный поиск ассоциаций.

DOI: 10.31857/S0006302922030048, EDN: ANBULQ

их добавление позволяет более точно описать

Структурное моделирование уравнениями

процесс генерации данных и, как следствие, также

(Structural Equation Modelling - SEM) - это сово-

повысить статистическую мощность модели.

купность подходов к многомерному анализу при-

чинных отношений между наблюдаемыми и ла-

За последние годы возрос интерес к примене-

тентными переменными. Метод SEM находит

нию SEM в биоинформатических задачах, от ана-

применение в широком спектре областей: от пси-

лиза воздействия фотосинтеза в период вегетации

хологии и социологии до эконометрики и биоло-

на сроки старения листьев [2] до исследования

гии [1]. Одной из сильных сторон SEM является

поведения генных сетей у больных шизофренией

возможность в явном виде задавать причинно-

[3] и применения многоцелевой многолокусной

следственные связи между переменными (или,

модели, использующей моделирование структур-

другими словами, задавать структуру генератив-

ных уравнений для описания сложных ассоциа-

ной модели), что в случае, если предполагаемые

ций между однонуклеотидными полиморфизма-

связи соответствуют действительным, увеличива-

ми и признаками (multi-trait multi-locus Structural

ет статистическую мощность модели. Кроме того,

Equation Modelling - mtmlSEM) при полногеном-

зачастую сами причинно-следственные связи яв-

ном поиске ассоциаций (Genome-Wide Associa-

ляются объектом проверки гипотез, в частности,

tion Studies - GWAS) [4]. Однако, особенно в по-

в гуманитарных исследованиях. Другая сильная

следнем случае, применение SEM остается огра-

сторона SEM - это возможность учитывать в мо-

ниченным ввиду отсутствия возможности учесть

дели латентные переменные. Зачастую, разумное

общую дисперсию между наблюдениями, т. е. от-

бросить предположение о независимости наблю-

Сокращения: SEM - структурное моделирование уравнения-

ми, GWAS - полногеномный поиск ассоциаций, LMM -

дений, свойственное большинству линейных мо-

смешанная линейная модель, GP - гауссов процесс.

делей (и являющимся одним из условий теоремы

451

452

МЕЩЕРЯКОВ и др.

Гаусса-Маркова о независимости ошибок). Вза-

сотни образцов). В настоящей работе показано,

имозависимость в данных может быть обусловле-

что в общем случае сложность работы алгоритма

на либо наличием генетического сродства между

оптимизации зависит кубически от количества

образцами и/или их географической близостью.

образцов и использование алгоритма в такой

В первом случае, применительно к GWAS, суще-

форме представляется долгим процессом. Таким

ствуют известные подходы на основе смешанной

образом, целью данной работы являлось: 1) раз-

линейной модели (Linear Mixed Model - LMM)

работать SEM-модель, способную работать с за-

[5], а во втором - более общие методы на основе

висимыми данными подобно LMM/GP; 2) до-

гауссовых процессов (Gaussian Process - GP). Тем

биться меньшей асимптотической сложности,

не менее, ни LMM, ни GP не обобщены на случай

нежели O(n³).

SEM и работают лишь с простейшими линейны-

ми моделями.

Такие задачи, как GWAS, требуют высокую

МАТЕРИАЛЫ И МЕТОДЫ

скорость работы программ ввиду необходимости

обработки больших массивов данных (десятки и

Была взята модель из программного обеспече-

сотни тысяч однонуклеотидных полиморфизмов, ния semopy [6]:

H =ΒH +RG+E,

(0,Ψ In)



(1)

P =ΛH +ΠG

+Δ+U

,Δ

(0, Θ, I

),U

(0,

J + K)



где P - матрица фенотипов; H - матрица латент-

можно воспользоваться методом максимального

ных переменных; G - матрица генотипов/одно-

правдоподобия.

нуклеотидных полиморфизмов; B, Λ, П, R и Θ, Ψ,

Опуская прочие выкладки и выразив P из мо-

D, K - параметризованные матрицы загрузок и

дели (1):

ковариаций соответственно (подробнее см. в ис-

P = ΛC(RG + E) + ΠG + Δ + U,

(2)

ходной работе по mtmlSEM [4]), а MN - матрич-

но-нормальное распределение [7]. В отличие от

где С = (I - Β)^-1, посчитав M = E[P]:

оригинальной модели semopy мы, во-первых, пе-

M = (ΛCR+ Π)G,

(3)

решли от векторной нотации к матричной, а во-

V = cov[P]:

вторых, ввели слагаемое U, названное матрицей

случайных эффектов (англ. random effects), контро-

V = tr{Σ} I_n + tr{D}K,

(4)

лирующей общую дисперсию между наблюдени-

где Σ = ΛCΨC^TΛ^T+Θ, и T = cov[P^T]:

ями (таким образом, после вычета U из P можно

сказать, что наблюдения становятся независимы-

T = nΣ+tr{K}D,

(5)

ми). P как сумма линейных трансформаций мат-

а затем подставив выражения (3)-(5) в логарифм

рично-нормальных случайных величин также бу-

функции плотности матрично-нормального рас-

дет матрично-нормальной случайной величиной,

пределения и помножив на -1, получим следую-

и для оценки параметров в матрицах B, Λ, Θ, Ψ, K

щую функцию цели:

L(.) = tr{V^-1(Z - M)^TT^-1(Z - M)} + mln|V| + nln|T|,

(6)

где m - число фенотипов. Минимизация выраже-

обращения матрицы занимает O(n³) операций в

ния (6) дает оценку параметров модели методом

общем случае.

максимального правдоподобия. Однако, как вид-

Прежде всего заметим, что на практике очень

но из выражения, при каждом вызове целевой

важно найти правильную форму матрицы K, так

функции n необходимо считать V^-1 (размерность

как она определяет поведение слагаемого U. Яс-

V - n · n, где n - число наблюдений), а операция

но, что в общем случае K не может быть полно-

БИОФИЗИКА том 67

№ 3

2022

ОПТИМИЗАЦИЯ ВЫЧИСЛЕНИЙ

453

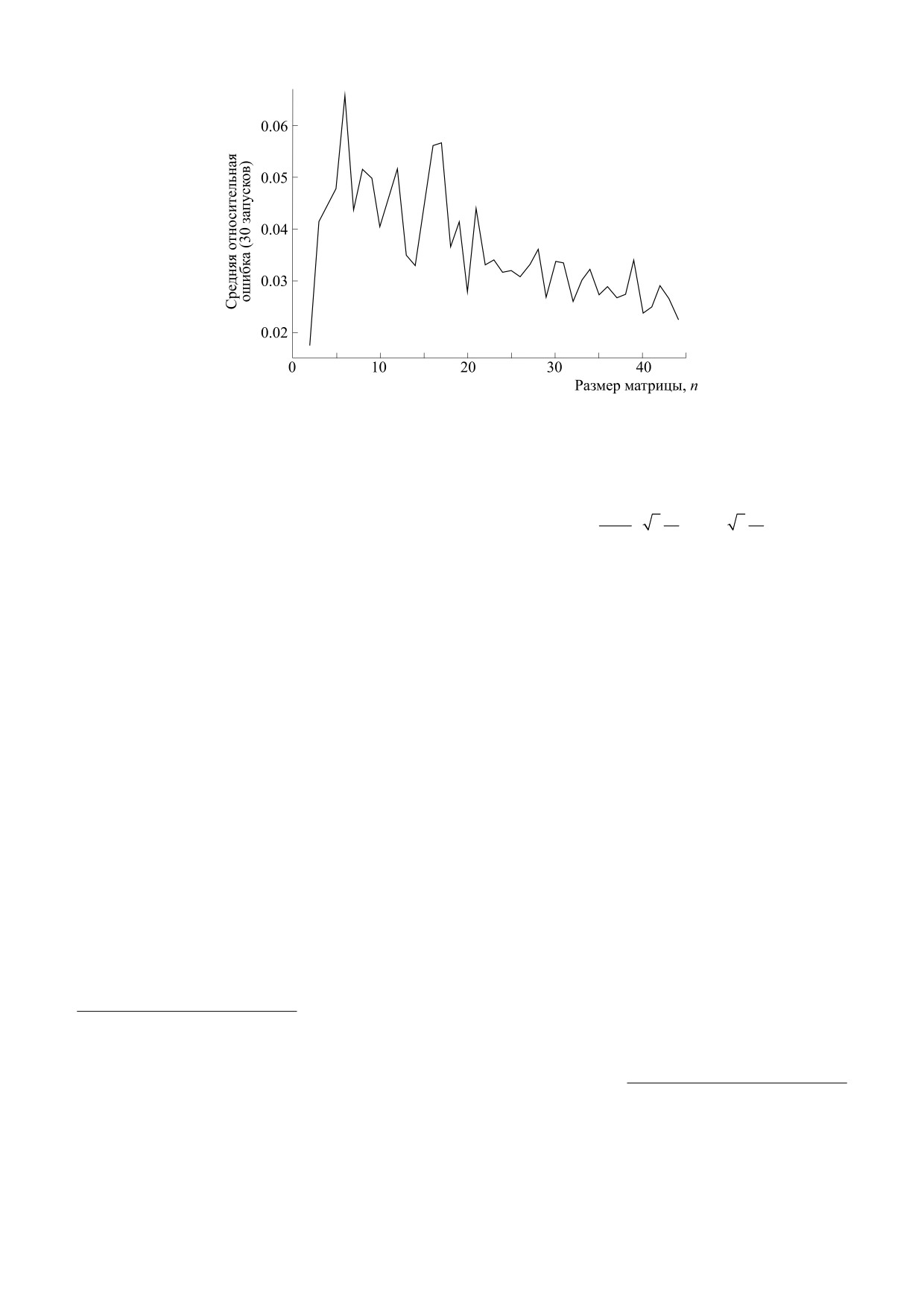
Рис. 1. Зависимость средней относительной точности от размера матрицы n.

стью параметризованной (так как в таком случае

1-ν









cov(i,

K_ν

(8)

число параметров будет порядка n², что намного









Γ(ν)







больше, чем число имеющихся наблюдений), и

мы вынуждено ограничены в свободе выбора K.

где ν и ρ - параметры, которые необходимо оце-

Иногда мы можем работать с полностью опреде-

нить, а d_ij - расстояние между двумя точками.

ленной K. В частности, так делают при необходи-

Так, учитывая то, что ν и ρ различны на

мости учета генетического родства, когда в нали-

каждом шаге оптимизационного алгоритма, раз-

чии имеется матрица генотипов G, а K считается

ложение (7) необходимо делать каждый раз, рав-

как ковариационная матрица по G [8]. Тогда, ис-

но как и поворот данных на новое Q, что делает

пользуя спектральное разложение K, имеем:

данный подход полностью бессмысленным. К со-

жалению, в общем случае, невозможно обращать

K = QSQ^T.

(7)

K быстрее чем за O(n³), но возможно считать

После этого, повернув данные на Q, при под-

«сложные» члены выражения (6) приближенно. В

счете выражения (4) видим, что от K остается

основе вычислительной схемы лежит процедура

только S, и V приобретает диагональную форму,

Гаусса-Ланшоца [10], ранее адаптированная к

обращение которой занимает O(n) операций.

LMM [11, 12] и находящая применение у GP в

Схожий подход использует инструмент для

рамках программного обеспечения LanczOs Vari-

GWAS FastLMM [5].

ance Estimates [13]. Процедура Гаусса-Ланшоца

позволяет приблизительно оценить квадратич-

Однако зачастую мы не можем знать K точно.

ную форму матрицы f(A), где f - любая матричная

Например, если мы хотим учесть сродство, обу-

аналитическая функция, без подсчета f (так, на-

словленное географическим положением образ-

цов, то, подобно тому, как это часто делают в GP

пример, f(A) = A^-1). Отбрасывая выкладки и дета-

[9], применяют ядро Матерна для подсчета кова-

ли, укажем, что процедура основана на стохасти-

риации между различными географическими

ческой оценке следа (так называемый трюк Хат-

точками:

чинсона):

∀x

E x]

0,Ex

 =

1 :

Ex

f A)x

 =

tr f (A)}

≈

f A)x

(9)











и представлении его через интеграл Римана-Стильетса:

БИОФИЗИКА том 67

№ 3

2022

454

МЕЩЕРЯКОВ и др.

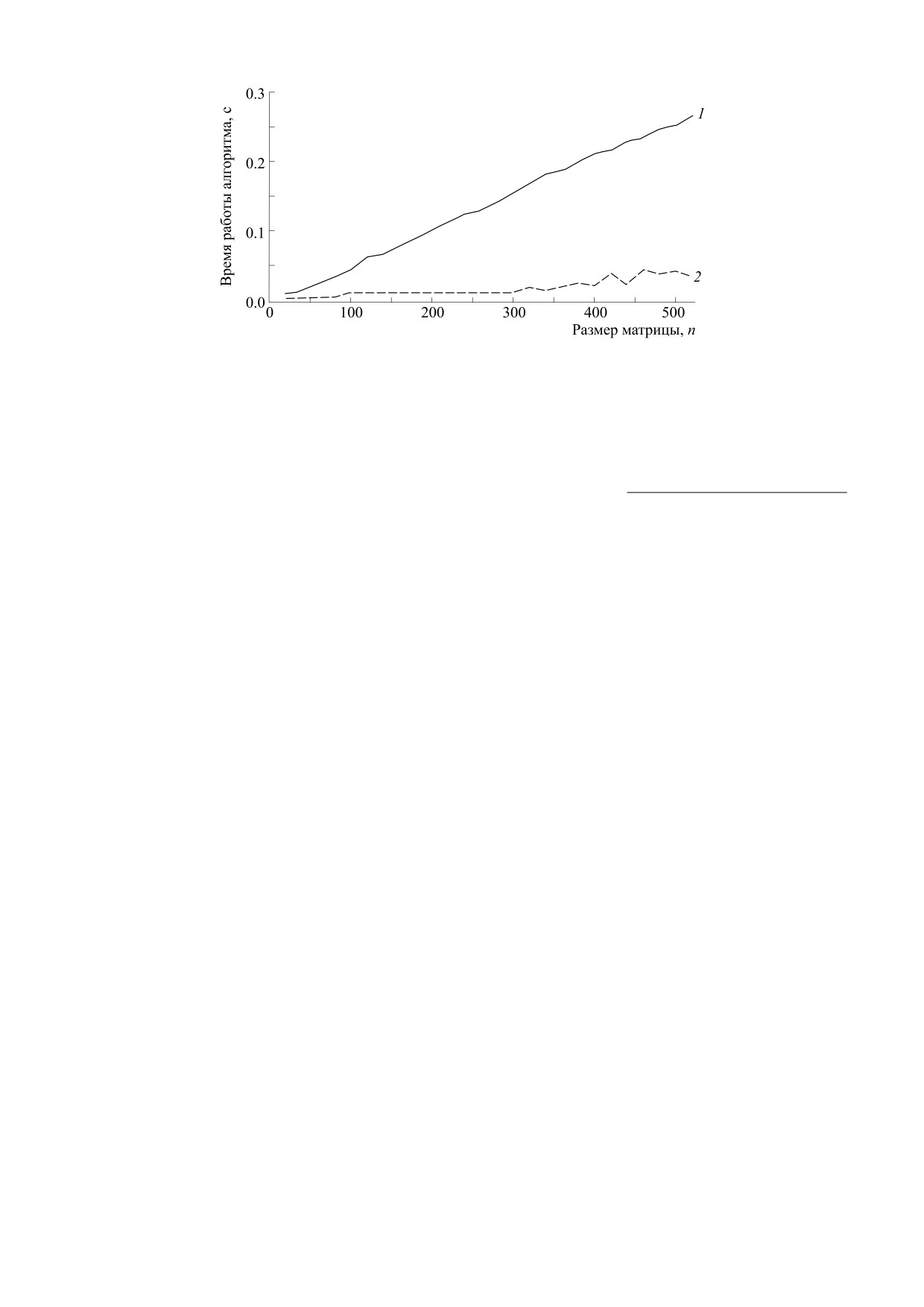
Рис. 2. Зависимость времени работы алгоритма в секундах от размера матрицы n: 1 - подсчет по модели (1), 2 - подсчет

по предложенному авторами методу.

T T

f A)x = x

(

)

x = x

Q f s)Qx

f s )

f t)

dμ t)

≈

)

(10)







i=1

Выражение

(10) считается приближенно

СОБЛЮДЕНИЕ ЭТИЧЕСКИХ СТАНДАРТОВ

квадратурами посредством ортогональных поли-

Настоящая работа не содержит описания ис-

номов Гаусса-Ланшоца. Чем выше L в выраже-

следований с использованием людей и животных

нии (9), тем больше точность алгоритма.

в качестве объектов.

СПИСОК ЛИТЕРАТУРЫ

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

1. А. А. Иголкина и М. Г. Самсонова, Биофизика 63

Предложенная модель (1) была успешно реа-

(2), 139 (2018).

лизована и интегрирована в программное обеспе-

2. X. Lu and T. F. Keenan, Global Change Biology 28

(9), 3083 (2022).

чение semopy (см. сайт semopy.com). Использо-

3. A. A. Igolkina, C. Armoskus, J. R. Newman, et al.,

ванная вычислительная схема дает приемлемую

Front. Mol. Neurosci. 11, 00192 (2018).

точность (средняя относительная ошибка не пре-

4. A. A. Igolkina, G. Meshcheryakov, M. V. Gretsova,

вышает 1% уже при L = 3, см. рис. 1) при значи-

et al., BMC Genomics 21, 490 (2020).

тельно меньшем времени работы (см. рис. 2).

5. C. Lippert, J. Listgarten, Y. Liu, et al., Nat. Methods

Кроме того, предложенная модель легко расши-

8, 833 (2011).

6. A. A. Igolkina and G. Meshcheryakov, Structural

ряется на случай нескольких случайных эффек-

Equation Modeling: A Multidisciplinary Journal, 27

тов с различными K, что дает возможность одно-

(6), 952 (2020).

временно учитывать генетическую и географиче-

7. A. K. Gupta and D. K. Nagar, Matrix Variate Distribu-

скую родственность образцов данных.

tions (Routledge, 1999).

8. J. Goudet, T. Kay, and B. S. Weir, Mol. Ecol. 27 (20),

4121 (2018).

ФИНАНСИРОВАНИЕ РАБОТЫ

9. C. E. Rasmussen, Gaussian Processes in Machine

Learning (Springer, Berlin, 2003).

Работа выполнена при финансовой поддержке

10. S. Ubaru, J. Chen, and Y. Saad, SIAM J. Matrix Anal-

ysis and Applications 38, 1075 (2017).

Российского фонда фундаментальных исследова-

11. R. Border and S. Becker, BMC Bioinformatics 20, 411

ний (грант № 18-29-13033).

(2019).

12. Г. А. Мещеряков, в сб. Тезисы XXI Всерос. конф.

молодых ученых по математич. моделированию и

КОНФЛИКТ ИНТЕРЕСОВ

информационным технологиям (2020), сс. 27-28.

13. G. Pleiss, J. Gardner, K. Weinberger, and A. Willson,

Авторы заявляют об отсутствии конфликта

In Proc. Int. Conf. Machine Learn. (2018). DOI:

интересов.

10.48550/arXiv.1803.06058

БИОФИЗИКА том 67

№ 3

2022

ОПТИМИЗАЦИЯ ВЫЧИСЛЕНИЙ

455

Optimization of Computations for Structural Equation Modeling

with Applications in Bionformatics

G.A. Meshcheryakov*^, **, V.A. Zuev*, A.A. Igolkina*, and M.G. Samsonova*

*Peter the Great St. Petersburg Polytechnic University, Polytekhnicheskaya ul. 29, St. Petersburg, 195251 Russia

**Institute of Protein Research, Russian Academy of Sciences, Institutskaya ul. 4, Pushchino, Moscow Region, 142290 Russia

Structural Equation Modeling (SEM) is a technique for analysis of linear relations represented as the causal

and correlational relationships between observed and latent variables. SEM is a popular tool in a wide range

of fields, from the humanities to the natural sciences. Over the past decade, this method has become espe-

cially interesting in areas that are at the interface with biology. However, a common assumption that obser-

vations are independent is often violated in biological data; it should be taken into account at the stage of con-

structing a mathematical model. In addition, in genome-wide association studies, the time of optimization

of model parameters is a particularly critical factor. In this paper, we propose a new SEM model, as well as a

fast way to estimate its parameters.

Keywords: SEM, structural equation modeling, semopy, Gauss quadrature, genome-wide association studies

БИОФИЗИКА том 67

№ 3

2022