БИОФИЗИКА, 2022, том 67, № 3, с. 444-450

МОЛЕКУЛЯРНАЯ БИОФИЗИКА

УДК 577.2.01:(57.052.2+577.322.23+577.322.54)

НОВАЯ МАТЕМАТИЧЕСКАЯ МОДЕЛЬ, ОПИСЫВАЮЩАЯ

ОКСИГЕНАЦИЮ ГЕМОГЛОБИНА

*Воронежский государственный университет, 394018, Воронеж, Университетская пл., 1

**Институт молекулярной биологии им. В.А. Энгельгардта РАН, 119991, Москва, ул. Вавилова, 32

***Севастопольский государственный университет, 299053, Севастополь, ул. Университетская, 33

E-mail: lavrinenko_ia@bio.vsu.ru

Поступила в редакцию 04.04.2022 г.

После доработки 06.04.2022 г.

Принята к публикации 08.04.2022 г.

Предложена модель оксигенации, основанная на уравнении Хилла, где одноименный коэффици-

ент представляет собой функцию от парциального давления кислорода (концентрации лиганда).

Показано, что уравнение Хилла с четырьмя параметрами хорошо аппроксимирует эксперименталь-

ную кривую диссоциации оксигемоглобина. Данные параметры, а также выводимые из них крите-

рии оценки оксигенации позволяют охарактеризовать положение максимума кооперативности, а

также границы минимальных и максимальных значений pO₂, при котором значение коэффициента

Хилла не выходит за установленный предел. Максимумы кооперативности для рассмотренных на-

боров экспериментальных данных лежат в области больших парциальных давлений кислорода от-

носительно значения p₅₀. Модифицированное уравнение Хилла может быть использовано не только

для анализа кислородсвязывающих свойств гемоглобина, но и при решении широкого круга задач,

связанных с кооперативностью, в частности, при оценке кинетических кривых ферментативных

реакций, различных зависимостях «доза-эффект», а также других приложений.

Ключевые слова: кооперативное связывание лигандов, кривая диссоциации оксигемоглобина, уравнение

Хилла, коэффициент Хилла, относительный коэффициент кооперативности.

DOI: 10.31857/S0006302922030036, EDN: AMZWVH

Как известно, функциональная активность

целью оптимизации согласованного протекания

белков возникает главным образом с формирова-

биохимических процессов [4].

нием третичной структуры этих биополимеров

Естественный ход эволюции привел к появле-

[1]. Для ферментов, обладающих такой структу-

нию четвертичной структуры ферментов, к кото-

рой, скорость ферментативной реакции может

рым относится и молекула гемоглобина, облада-

быть выведена из закона действующих масс и

ющая в окисленной форме каталитической ак-

описывается уравнением Михаэлиса-Ментен

тивностью [5-11]. Однако уравнения Гюфнера и,

(1913 г.). Эта скорость характеризуется констан-

в дальнейшем, Михаэлиса-Ментен из-за коопе-

той диссоциации фермент-субстратного ком-

ративного взаимодействия субъединиц не смогли

плекса (константа Михаэлиса, K_m) [2]. Вместе с

описать оксигенацию или кинетику фермента-

тивной реакции олигомеров. Применительно к

тем для миоглобина простетическую группу так-

гемоглобину Хилл (1910 г.) предложил зависи-

же можно рассматривать как аналог активного

мость, базирующуюся на уравнении Гюфнера, но

центра фермента, где зависимость степени окси-

представляющую оксигенацию как химическую

генации данного гем-белка от парциального дав-

реакцию n-го порядка. Коэффициент Хилла (h),

ления кислорода (pO₂) определяется уравнением

сопряженный с числом субъединиц макромоле-

Гюфнера (1890 г.). В этом уравнении величина p₅₀

кулы (n), позволил оценивать степень их коопе-

характеризует полунасыщение гембелка кисло-

ративного взаимодействия в составе олигомера

родом при некотором pO₂ и аналогична K_m [3].

[12].

Однако с физиологической точки зрения функ-

Вместе с тем уравнение Хилла недостаточно

ционирование ферментов, ограниченных только

хорошо аппроксимирует экспериментальные за-

лишь третичной структурой, не позволяет реали-

висимости, в частности, кривые диссоциации ок-

зовать более тонкую регуляцию и подстройку с

сигемоглобина, в областях низких и высоких зна-

444

НОВАЯ МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

445

чений парциального давления кислорода (а в об-

величина h для соответствующей кривой оксиге-

щем случае

- концентрации субстрата)

[13].

нации имеет постоянное значение и не зависит от

Уравнение Эдера (1925), основанное на идее по-

степени насыщения гембелка кислородом. В

следовательного присоединения молекул кисло-

приведенном уравнении: y - степень насыщения

рода к тетрамеру гемоглобина, обладает высокой

гемоглобина кислородом, p - парциальное давле-

аппроксимирующей способностью, в том числе

ние O₂, p₅₀ - давление O₂, при котором половина

благодаря большему количеству управляющих

макромолекул насыщена лигандом (также из-

параметров - четырех равновесных макроскопи-

вестное как константа Хилла K_h [26], аналогично

ческих констант [14]. Однако это уравнение не

константе Михаэлиса K_m) и h - коэффициент

дает представление о величине кооперативности,

Хилла.

а из его констант неясно, каково при этом значе-

ние p₅₀ [15]. Полученное Бернардом уравнение

В данной работе мы предлагаем рассматривать

оксигенации (1960 г.) [16] основано на представ-

коэффициент Хилла как функцию от парциаль-

лении об одновременном присоединении двух

ного давления кислорода. Такая зависимость бы-

молекул кислорода и лучше аппроксимирует кри-

ла продемонстрирована авторами работ [27, 28].

Однако функциональная зависимость, позволя-

вую оксигенации, чем уравнение Хилла. Уравне-

ющая аппроксимировать эмпирическую кривую,

ние имеет два параметра: p₅₀ и подгоночный

не предлагалась. Следует заметить, что в литера-

кинетический коэффициент a. Однако и это

туре существует ряд работ, в которых константы

уравнение не позволяет оценить степень коопе-

связывания макромолекулы рассматриваются

ративности молекулы гемоглобина в ходе ее ок-

как функции от заполнения макромолекулы ли-

сигенации.

гандом [29-31].

Хотя уравнение Хилла несколько хуже аппрок-

Для исходного уравнения Хилла величина h

симирует экспериментальные данные, чем урав-

нения Бернарда и Эдера [17], но может характери-

представляется как:

зовать кооперативность макромолекулы - и по-

=h =h

const,

(2)

тому не утратило своей актуальности. Оно

max

широко используется не только в энзимологии

где h_max - максимально возможное значение ко-

[18], но и в фармакологии [19], задачах моделиро-

эффициента Хилла в заданном диапазоне pO₂,

вания регуляции транскрипции гена [20], а также

hi - коэффициент Хилла при определенном pO2

различных зависимостях типа

«доза-эффект»

[21].

- среднее значение коэффициента Хилла.

В настоящей работе предпринята попытка мо-

Мы предлагаем моделировать зависимость ко-

дифицировать уравнение Хилла с целью повыше-

эффициента Хилла от парциального давления

ния его аппроксимирующей способности, сохра-

кислорода при помощи функции Гаусса:

няя при этом его преимущества в описании ко-

оперативности и простоте вычислений.

max

(3)

exp

[(

p - p

)

]

МЕТОДЫ ИССЛЕДОВАНИЙ

где s - параметр масштаба по оси абсцисс.

В качестве объекта исследования была исполь-

Так как в уравнении Хилла одноименный ко-

зована модель Хилла и набор экспериментальных

эффициент в отсутствие кооперативности равен

данных, полученных Р. Уинслоу с соавт. [22] и

единице, то уравнение (3) можно привести к сле-

Дж. Северингхаусом [23]. Оптимизация парамет-

дующему виду:

ров моделей проведена методом наименьших

квадратов [24]. Оценка степени соответствия мо-

max

(

−1)

(4)

(

−1

)

дели экспериментальным данным осуществлена

exp

[(

p - p

)

]

через коэффициент детерминации [25]. Необхо-

димые вычисления выполнены в программе MS

тем самым смещая аппроксимирующую функ-

Excel.

цию на единицу по оси ординат.

Логарифмирование оси абсцисс (рис. 1) пред-

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

ставляет кривую диссоциации оксигемоглобина

практически симметричной относительно p₅₀.

Представление коэффициента Хилла как функ-

Поэтому в выражении (5) используется логарифм

ции парциального давления кислорода. Как следует

давления O₂:

из уравнения Хилла:

max

(

−1)

(1)

i(−1)

(5)

exp

[(

(

p/p

)

)]

БИОФИЗИКА том 67

№ 3

2022

446

ЛАВРИНЕНКО и др.

Принимая во внимание тот факт, что значение

давления для h_max не обязано соответствовать ве-

личине p₅₀, мы вводим четвертый параметр -

ln p_max, парциальное давление кислорода, при ко-

тором коэффициент Хилла максимален. При

этом выражение (5) трансформируется следую-

щим образом:

max

(

−1

)

i(−1)

(6)

exp

[(

(

max

)

)]

Оценка эффективности аппроксимации модифи-

цированными уравнениями Хилла. По эксперимен-

тальным данным, представленным в работах [22,

23], были получены аппроксимирующие кривые

диссоциации оксигемоглобина при помощи

уравнений Хилла с двумя (исходное уравнение),

тремя и четырьмя параметрами, а также посред-

ством уравнений Бернарда и Эдера.

Для этих уравнений определены коэффициен-

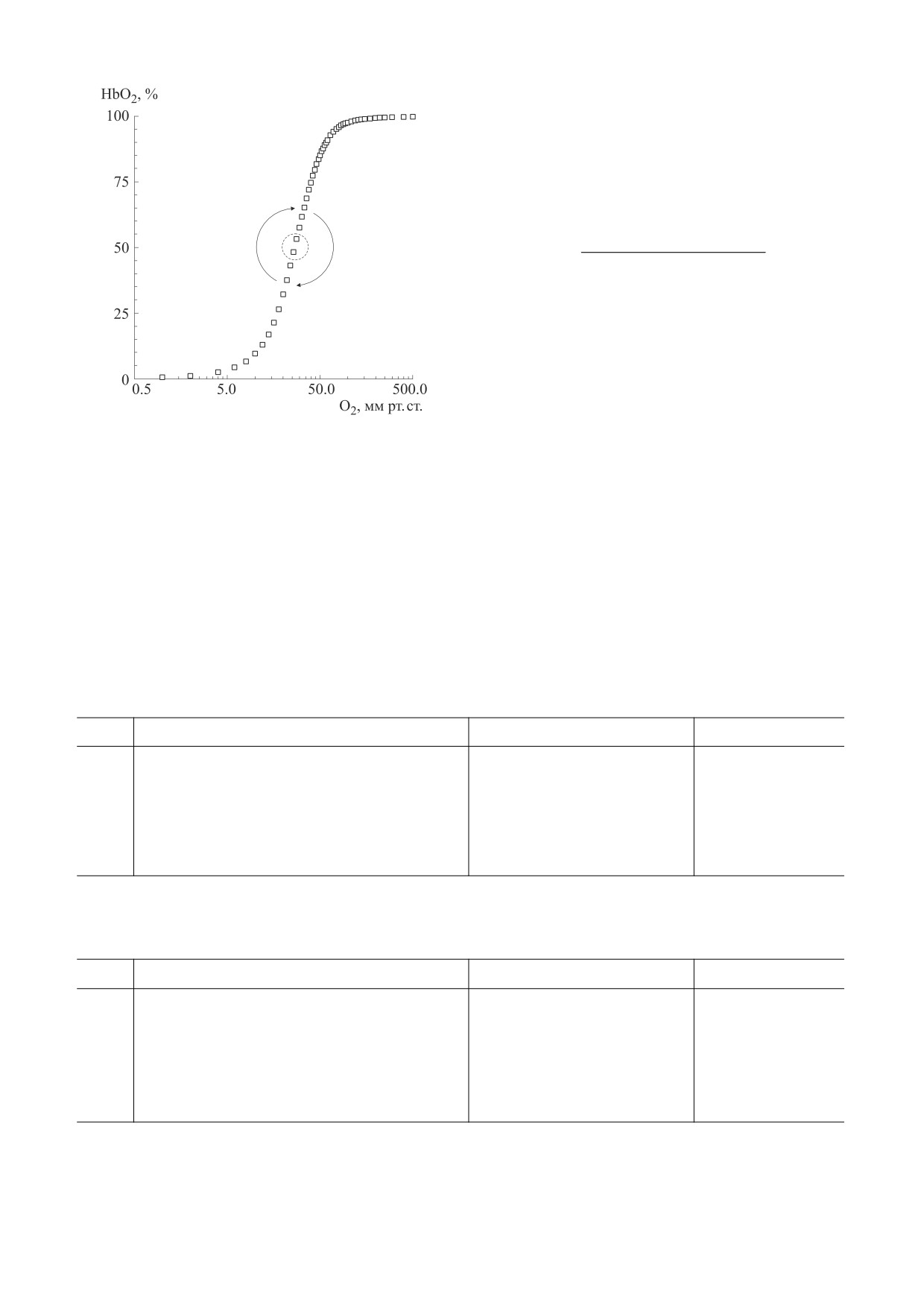
Рис. 1. Экспериментальные точки кривой диссоциа-

ты детерминации (R²) (табл. 1 и 2). Ранжирование

ции оксигемоглобина по Дж. Северингхаусу [23]:

функций выполнено по степени убывания R².

HbO₂ - степень оксигенации гемоглобина, pO₂ -

Как следует из представленных данных, уравне-

парциальное давление кислорода; стрелками и

ние Хилла с четырьмя параметрами (h_max(-1), s,

пунктирным кругом показана точка (p₅₀)

центральной симметрии данной кривой.

p₅₀ и ln p_max) по своим аппроксимирующим свой-

ствам сопоставимо с уравнением Эдера (рис. 2).

Вместе с тем параметры модифицированного

Таким образом, модифицированное уравне-

уравнения Хилла дают возможность более точно

ние Хилла имеет три параметра: h_max(-1), ln p₅₀ и s,

(хотя и формально) описать кооперативность

где h_max = h_max(-1) +1, а h_i = hi(-1) +1.

связывания лигандов. Однако и такие общепри-

Таблица 1. Аппроксимирующие кривые диссоциации оксигемоглобина функции, имеющие физический смысл

(по экспериментальным данным Р. Уинслоу и др. [22])

№

Уравнение

R², ppm

Число параметров

Уравнение Эдера

999953

Уравнение Хилла (4)

999944

Уравнение Хилла (3)

999778

Уравнение Бернарда

999745

Уравнение Хилла (2)

999603

Примечание. Здесь и в табл. 2 значения R² приведены в миллионных долях (ppm).

Таблица 2. Аппроксимирующие кривые диссоциации оксигемоглобина функции, имеющие физический смысл

(по экспериментальным данным Дж. Северингхауса [23])

№

Уравнение

R², ppm

Число параметров

Уравнение Хилла (4)

999943

Уравнение Эдера

999907

Уравнение Хилла (2)

999446

Уравнение Хилла (3)

999377

Уравнение Бернарда

999376

БИОФИЗИКА том 67

№ 3

2022

НОВАЯ МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

447

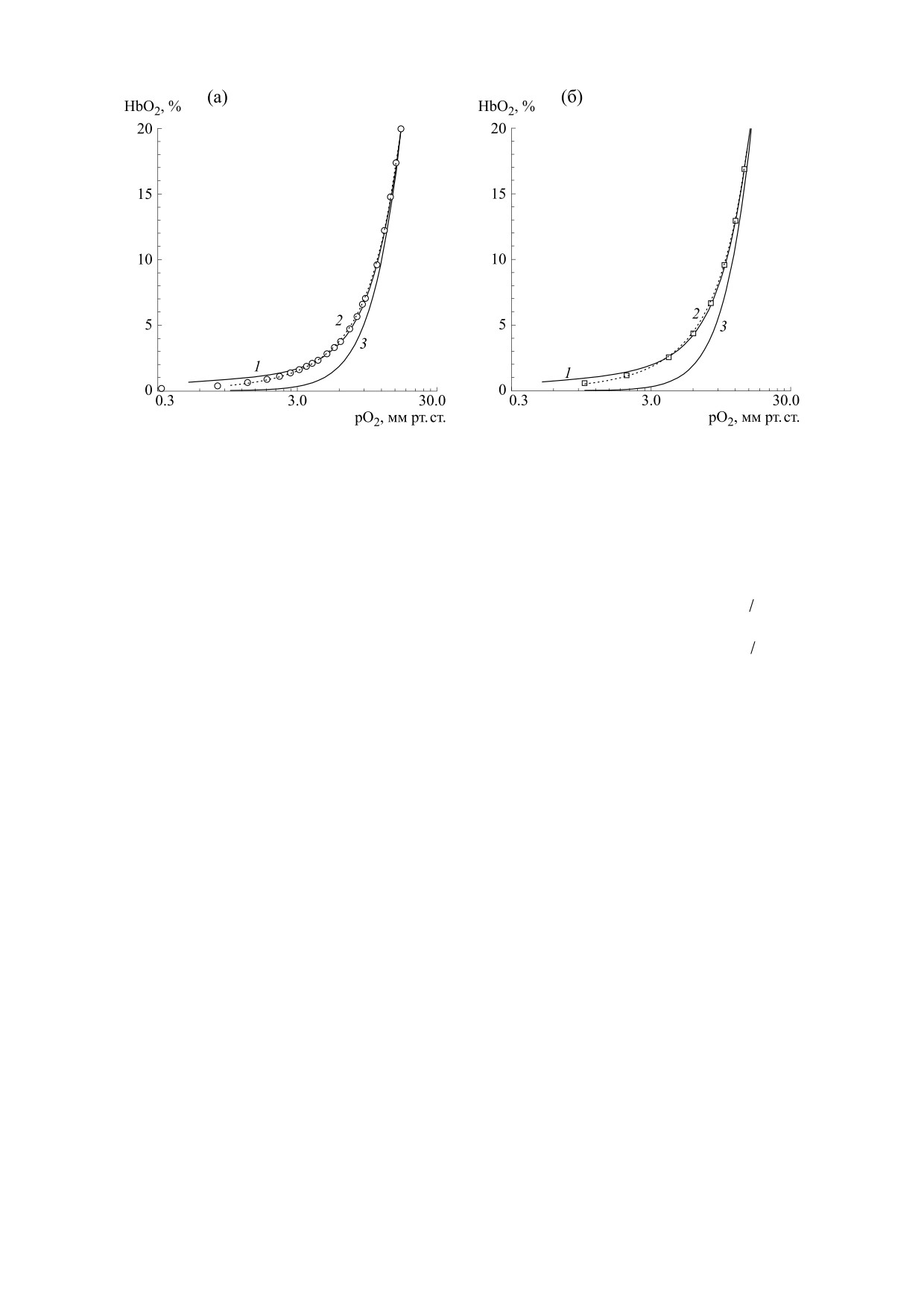
Рис. 2. Аппроксимация экспериментальных точек кривой диссоциации оксигемоглобина: (а) - по Р. Уинслоу и др.

[22] уравнением Хилла (4) (кривая 1), уравнением Эдера (кривая 2, пунктирная линия), уравнением Хилла (2)

(кривая 3); (б) - по Дж. Северингхаусу [23] уравнением Хилла (4) (кривая 1), уравнением Эдера (кривая 2, пунктирная

линия), уравнением Хилла (2) (кривая 3).

нятые константы, как p₅₀ (K_h), K_m, EC₅₀ [32], IC₅₀

значение диапазона pO₂ (а также его размах ΔpO₂)

[32], являются удобной, но формальной характе-

с заданной долей кооперативности от h_max(-1):

ристикой оценки полумаксимальной величины

соответствующей функции. В принципе, в урав-

expln

−

−lnω

,

(8)

2low

max

(

)¹²





нениях они могут быть заменены на любые кон-

станты, выраженные в процентах, например, p₉₅

expln

s(−lnω)12,

(9)

2high

max

(зарядное напряжение, представленное как кон-





станта), или в долях (1/exp, 1/π и т.д.).

Δp

= p

− p

(10)

high

low

Параметр h_max(-1), переводимый в h_max, поз-

где pO2low и pO2high - нижняя и верхняя граница

воляет оценить соответственно максимально воз-

можную относительную кооперативность взаи-

значений парциального давления кислорода, за

модействия субъединиц, используя уравнение (7)

которыми hi(-1) < ωh_max, ω - доля, выражаемая от

[33]:

0 до 1 (для 0.5 - более известная, как полуширина

на полувысоте, half width at half maximum).

h_max = θ(n)(n - 1),

(7)

Приведены параметры уравнений Хилла, ха-

где θ(n) - относительный коэффициент коопера-

рактеризующих процесс оксигенации для экспе-

тивности, n - число субъединиц олигомера.

риментальных кривых по данным Р. Уинслоу [22]

(табл. 3) и Дж. Северингхауза [23] (табл. 4).

Вычисленная разность Δh между h_max и h поз-

Как следует из табл. 3 и 4, вычисленные пара-

воляет косвенно охарактеризовать дисперсию ко-

оперативности.

метры и их производные величины дают возмож-

ность более детально проводить анализ кисло-

Величина p_max вычисляется экспонированием

родсвязывающих свойств гембелка. В частности,

параметра ln p_max и отмечает проекцию экстрему-

следует отметить, что положение максимумов ко-

ма на ось абсцисс, для которой по уравнениям (1)

оперативности смещено в сторону более высоких

и (6) можно найти степень насыщения гемогло-

значений парциального давления кислорода.

бина кислородом. Разность (и ее знак) между p_max

Возможно, это связано с определенной физиоло-

гической ролью макромолекулы гемоглобина

и p₅₀ указывает на смещение максимума коопера-

(это гетеротетрамер, субъединицы которого, не-

тивности и требует физической интерпретации.

смотря на свою структурную симметрию, облада-

При помощи параметра s по формулам (8) и (9)

ют функциональной асимметрией). Это предпо-

можно оценить минимальное и максимальное ложение подтверждается различием в равновес-

БИОФИЗИКА том 67

№ 3

2022

448

ЛАВРИНЕНКО и др.

Таблица 3. Значения параметров и их производных, получаемых из уравнений Хилла в различных модификациях

(по экспериментальным данным Р. Уинслоу и др. [22])

№

Параметры уравнения

Уравнение Хилла (2)

Уравнение Хилла (3)

Уравнение Хилла (4)

p₅₀, мм рт. ст.

28.82*

28.85*

29.08*

h (для уравнения Хилла (3) и

2.52*

2.26

2.30

уравнения Хилла (4): h^- )

h_max(-1)

1.60*

1.66*

h_max (h_max(-1) + 1)

2.60

2.66

0.34

0.36

Δh (h_max - h^-)

p_max, мм рт. ст.

52.92*

3.11*

3.33*

pO2low (для ω = 0.99), мм рт. ст.

21.08

37.95

pO2high (для ω = 0.99), мм рт. ст.

39.32

73.98

ΔpO₂ (pO2high - pO2low), мм рт. ст.

18.24

36.03

HbO₂ (при p_max), %

83.10

Примечание. Знаком «*» отмечены подгоночные параметры в соответствующих уравнениях.

Таблица 4. Значения параметров и их производных, получаемых из уравнений Хилла в различных модификациях

(по экспериментальным данным Дж. Северингхауса [23])

№

Параметры уравнения

Уравнение Хилла (2)

Уравнение Хилла (3)

Уравнение Хилла (4)

p₅₀, мм рт. ст.

26.38*

26.40*

26.82*

h (для уравнения Хилла (3) и

2.65*

2.60

2.62

уравнения Хилла (4): h

^-)

h_max(-1)

1.67*

1.82*

h_max (h_max(-1) + 1)

2.67

2.82

0.08

0.20

Δh (h_max - h

^-)

p_max, мм рт. ст.

80.84*

5.94*

3.59*

pO2low (для ω = 0.99), мм рт. ст.

14.51

56.27

pO2high (для ω = 0.99), мм рт. ст.

47.73

115.57

ΔpO₂ (pO2high - pO2low), мм рт. ст.

33.22

59.30

HbO₂ (при p_max), %

88.16

Примечание. Знаком «*» отмечены подгоночные параметры в соответствующих уравнениях.

ных константах связывания кислорода для этих

ЗАКЛЮЧЕНИЕ

субъединиц [34].

Предложена модель оксигенации, основанная

Видимо, функциональная асимметричность

на уравнении Хилла, где одноименный коэффи-

этой макромолекулы не может быть эффективно

циент представляет собой функцию от логарифма

реализована в случае одинаковых субъединиц

парциального давления кислорода (концентра-

(например, в случае гемоглобина H, состоящего

ции лиганда). Несмотря на то, что эта функция

только из четырех β-субъединиц) [35].

имеет осевую симметрию относительно максиму-

БИОФИЗИКА том 67

№ 3

2022

НОВАЯ МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

449

ма кооперативности, она позволяет улучшить ап-

СПИСОК ЛИТЕРАТУРЫ

проксимирующие свойства базового уравнения

Л. Страйер, Биохимия (Мир, М., 1984).

Хилла.

L. Michaelis and M. L. Menten, Biochem. Z. 49, 333

Так, уравнение Хилла с четырьмя подгоноч-

(1913).

ными параметрами аппроксимирует экспери-

G. Hüfner, Arch. ges Physiol. 31, 28 (1890).

ментальную кривую диссоциации оксигемогло-

П. Хочачка и Д. Сомеро, Биохимическая адапта-

бина не хуже уравнения Эдера. Данные парамет-

ция (Мир, М., 1988).

ры, а также выводимые из них критерии оценки

M. F. Perutz, M. G. Rossmann, A. F. Cullis, et al.,

оксигенации позволяют охарактеризовать поло-

Nature

185

(4711),

416

(1960). DOI:

10.1038/

жение максимума кооперативности, можно так-

185416A0

же определить минимальные и максимальные

M. F. Perutz, Nature 228 (5273), 726 (1970). DOI:

значения pO₂, для которых значение коэффици-

10.1038/228726A0

ента Хилла соответствует заданной доле от его

R. W. Carrell, C. C. Winterbourn, and J. K. French,

экстремума.

Hemoglobin

(8),

815

(1977). DOI:

10.3109/

03630267709003909

Максимумы кооперативности для рассмот-

M. Perutz, Annu. Rev. Biochem. 48 (1), 327 (1979).

ренных наборов экспериментальных данных ле-

DOI: 10.1146/ANNUREV.BI.48.070179.001551

жат в области больших парциальных давлений

M. F. Perutz, Quart. Rev. Biophys. 22 (2), 139 (1989).

кислорода относительно значения p₅₀. Примеча-

DOI: 10.1017/s0033583500003826

телен тот факт, что степень насыщения гемогло-

10.

B. Giardina, I. Messana, R. Scatena, et al., Crit. Rev.

бина кислородом для этих наборов данных сопо-

Biochem. Mol. Biol.

(3),

165

(1995). DOI:

ставима в максимуме кооперативности.

10.3109/10409239509085142

Таким образом, модифицированное уравне-

11.

M. Berenbrink, Nature 581 (7809), 388 (2020). DOI:

ние Хилла может быть использовано не только

10.1038/d41586-020-01287-8

при анализе кислородсвязывающих свойств ге-

12.

A. V. Hill, J. Physiol. 40, i (1910).

моглобина, но и при решении широкого круга за-

13.

Z. Konkoli, Theor. Biol. Medical Model. 8 (1), 10

дач, связанных с кооперативностью [36], в част-

(2011). DOI: 10.1186/1742-4682-8-10

ности, при оценке кинетических кривых фермен-

14.

G. S. Adair, A. V. Bock, and H. Jr. Field, J. Biol.

тативных реакций [37], различных зависимостях

Chem. 63, 529 (1925).

«доза-эффект» [38], а также других приложений

15.

T. Yonetani, S. I. Park, A. Tsuneshige, et al., J. Biol.

[39].

Chem.

277

(37),

34508

(2002).

DOI:

10.1074/jbc.M203135200

16.

S. S. R. Bernard, Bull. Math. Biophys. 22, 391 (1960).

БЛАГОДАРНОСТИ

DOI: 10.1007/BF02476722

17.

И. А. Лавриненко, Г. А. Вашанов, В. Ю. Сулин и

Авторы считают своим приятным долгом вы-

др., Биофизика

(6)

1065

(2021). DOI:

разить благодарность рецензентам за критиче-

10.31857/S000630292106003X

ский анализ рукописи и ценные замечания.

18.

A. K. Bordbar, Z. Saadati, and N. Sohrabi, Acta Bio-

chim. Pol.

(4),

963

(2004). DOI: 10.18388/

abp.2004_3529

ФИНАНСИРОВАНИЕ РАБОТЫ

19.

S. Goutelle, M. Maurin, F. Rougier, et al., Fundam.

Работа выполнена при частичной финансовой

Clin. Pharmacol.

(6),

633

(2008). DOI:

поддержке Программы фундаментальных науч-

10.1111/j.1472-8206.2008.00633.x

ных исследований в Российской Федерации на

20.

H. Aramaki, H. Kabata, S. Takeda, et al., Genes Cells

долгосрочный период (2021-2030 годы) (тема

(12),

1200

(2011).

DOI:

10.1111/j.1365-

121052600299-1).

2443.2011.01563.x

21.

S. Srinivasan, F. H. Waghu, S. Idicula-Thomas, et al.,

Biochim. Biophys. Acta - Biomembranes 1862 (4),

КОНФЛИКТ ИНТЕРЕСОВ

183242 (2020). DOI: 10.1016/j.bbamem.2020.183242

22.

R. M. Winslow, M. Swenberg, R. L. Berger, et al., J.

Авторы заявляют об отсутствии конфликта

Biol. Chem. 252, 2331 (1977). DOI: 10.1016/S0021-

интересов.

9258(17)40559-X

23.

J. W. Severinghaus, J. Appl. Physiol. 46 (3), 599

(1979). DOI: 10.1152/jappl.1979.46.3.599

СОБЛЮДЕНИЕ ЭТИЧЕСКИХ СТАНДАРТОВ

24.

F. M. Dekking, C. Kraaikamp, H. P. Lopuhaä, et al.,

Настоящая статья не содержит каких-либо ис-

A Modern Introduction to Probability and Statistics: Un-

следований с участием людей или животных в ка-

derstanding Why and How (Springer-Verlag, Lond.,

честве объектов исследований.

2005). DOI: 10.1007/1-84628-168-7

БИОФИЗИКА том 67

№ 3

2022

450

ЛАВРИНЕНКО и др.

25.

M. H. Katz, Multivariable Analysis: A Practical Guide

33. И. А. Лавриненко, Г. А. Вашанов и Ю. Д. Нечипу-

for Clinicians and Public Health Researchers (Cam-

ренко, Биофизика

(2),

229

(2022). DOI:

bridge University Press, Cambridge, 2011). DOI:

10.31857/S000630292202003X

10.1017/CBO9780511974175

34. G. Weber, Nature 300 (5893), 603 (1982). DOI:

26.

A. G. Marangoni, Enzyme Kinetics: a Modern Ap-

10.1038/300603a0

proach (John Wiley & Sons, New York, 2003).

35. R. Galanello and A. Cao, Genet. Med. 13 (2), 83

27.

Ч. Кантор и П. Шиммел, Биофизическая химия

(2011). DOI: 10.1097/GIM.0b013e3181fcb468

(Мир, М., 1984).

36. N. Kaihnsa, Y. Ren, M. Safey El Din, et al., J. Math.

28.

J. Wyman, S. J. Gill, Binding and Linkage: Functional

Biol. 81 (4), 1169 (2020). DOI: 10.1007/s00285-020-

Chemistry of Biological Macromolecules (University

01540-8

Science Books, Mill Valley CA, 1990).

37. J. Ricard and G. Noat, FEBS J. 152 (3), 557 (1985).

29.

Ю. Д. Нечипуренко, Биофизика 30, 231 (1985).

DOI: 10.1111/j.1432-1033.1985.tb09231.x

30.

А. В. Сиволоб и С. Н. Храпунов, Биофизика 34, 28

(1989).

38. T.-C. Chou, Integr. Biol. 3 (5), 548 (2011). DOI:

31.

И. А. Лавриненко, Г. А. Вашанов, А. С. Бучельни-

10.1039/c0ib00130a

ков и Ю. Д. Нечипуренко, Биофизика 67 (3), 421.

39. J. J. Maguire, R. E. Kuc, and A. P. Davenport, in Re-

(2022).

ceptor Binding Techniques, Ed. by A. P. Davenport

32.

J. B. Chang, K. M. Quinnies, R. Realubit, et al., Sci.

(Humana Press, Totowa, NJ, 2012), pp. 31-77. DOI:

Rep. 6 (1), 29387 (2016). DOI: 10.1038/srep29387

10.1007/978-1-61779-909-9_3

New Mathematical Model Describing Hemoglobin Oxygenation

I.A. Lavrinenko*, G.A. Vashanov*, and Yu.D. Nechipurenko**^, ***

*Voronezh State University, Universitetskaya pl. 1, Voronezh, 394018 Russia

**Engelhardt Institute of Molecular Biology, Russian Academy of Sciences, ul. Vavilova 32, Moscow, 119991 Russia

***Sevastopol State University, Universitetskaya ul. 33, Sevastopol, 299053 Russia

A model of oxygenation based on the Hill equation is proposed, where the Hill coefficient is a function of the

partial pressure of oxygen (ligand binding). It is shown that the Hill equation with four parameters is a rea-

sonable approximation to the experimental curve obtained for oxygen-hemoglobin dissociation. These pa-

rameters and the criteria for oxygenation assessment derived from the said parameters make it possible to

characterize the maximum cooperativity point, as well as the boundaries of the minimum and maximum pO₂

values at which the values of the Hill coefficient are not outside the limits specified. The maximum cooper-

ativity points for the considered sets of experimental data are in the region of higher oxygen partial pressures

relative to the p₅₀value. The modified Hill equation can be used not only for the analysis of the oxygen-bind-

ing properties of hemoglobin, but also for carrying out a wide range of tasks that are linked around coopera-

tivity, particularly, for kinetic analysis of enzymatic reactions, various dose-effect relationships, and many

others.

Keywords: cooperative ligand binding, oxygen-hemoglobin dissociation curve, Hill equation, Hill coefficient, rel-

ative coefficient of cooperativity

БИОФИЗИКА том 67

№ 3

2022