Коллоидный журнал, 2019, T. 81, № 4, стр. 411-440
Статистическая термодинамика обратных микроэмульсий, стабилизированных ионогенным поверхностно-активным веществом
В. Ф. Разумов 1, 2, 3, *, С. А. Товстун 1, 2
1 Институт проблем химической физики РАН
142432 Московская обл., Черноголовка, просп. Академика Семенова, 1, Россия
2 Федеральное государственное автономное образовательное учреждение высшего образования
“Московский физико-технический институт (национальный исследовательский университет)”
141701 Московская обл., Долгопрудный, Институтский пер., 9, , Россия
3 Московский государственный университет им. М.В. Ломоносова,
факультет фундаментальной физико-химической инженерии
119991 Москва, Ленинские горы, Россия
* E-mail: razumov@icp.ac.ru
Поступила в редакцию 10.01.2019
После доработки 11.02.2019
Принята к публикации 13.02.2019
Аннотация
Авторами приводится обзор своих теоретических исследований по статистической термодинамике обратных микроэмульсий и их применению для синтеза наночастиц. Дается общая теория флуктуаций состава обратных мицелл. Для обратных микроэмульсий на основе ионогенных поверхностно-активных веществ (ПАВ) излагается модель, позволяющая объяснить экспериментально наблюдаемую сферическую форму обратных мицелл, рассчитать энтальпию солюбилизации воды, химические потенциалы воды и ПАВ, а также фазовые диаграммы микроэмульсии. Описываются две модели ограничения роста наночастиц в обратных микроэмульсиях: термодинамическая, основанная на поиске минимума свободной энергии микроэмульсии с наночастицами, и кинетическая, основанная на рассмотрении зависимости энергии активации коагуляции наночастиц от их размеров и молярного соотношения воды и ПАВ.
ВВЕДЕНИЕ
В середине прошлого века было открыто явление самопроизвольного диспергирования воды в неполярных растворителях в присутствии поверхностно-активных веществ [1–3]. Обычно предполагается, что структура образующихся при этом термодинамически стабильных растворов представляет собой дисперсию наноразмерных капель воды, покрытых монослоем поверхностно-активного вещества (ПАВ), причем размер капель является линейной функцией отношения количеств воды и ПАВ. Для обратных микроэмульсий на основе бис-(2-этилгексил)сульфосукцината натрия (Aerosol OT, AOT) это предположение было убедительно подтверждено экспериментально [4–7]. Теперь такие капли, размер которых составляет всего несколько нанометров, обычно называют обратными мицеллами, а содержащие их растворы – обратными микроэмульсиями или микроэмульсиями типа “вода в масле”.
В начале 80-х годов прошлого века уникальную капельную структуру обратных микроэмульсий было предложено использовать для синтеза наночастиц [8]. Спустя некоторое время сложилось представление об обратных мицеллах, как о нанореакторах, способных ограничивать рост частиц и тем самым добиваться их малого размера и низкой степени полидисперсности, что необходимо для ряда приложений [9]. Со временем метод стал очень популярным и с его помощью были синтезированы наночастицы самых различных веществ: металлов, солей, оксидов [10]. Было опубликовано несколько тысяч работ по обратным микроэмульсиям, однако на ряд принципиальных вопросов, касающихся термодинамической устойчивости и способности обратных микроэмульсий ограничивать рост наночастиц, не было дано исчерпывающих ответов.
В данном обзоре кратко изложены наиболее важные результаты исследований по статистической термодинамике обратных микроэмульсий, полученные авторами за последние 5 лет. Они представляют собой новый взгляд на проблему термодинамической стабильности обратных микроэмульсий и процессов стабилизации наночастиц в таких системах.
В основе этой новой теории лежит тот факт, что в обратной мицелле существует расклинивающее давление, обусловленное наличием внутри нее двойного электрического слоя (ДЭС), образующегося в результате диссоциации молекул ПАВ. Роль расклинивающего давления в термодинамической стабилизации обратной мицеллы в некотором смысле аналогична роли расклинивающего давления в агрегативной устойчивости лиофобных коллоидных дисперсий, описываемой известной теорией Дерягина–Ландау–Фервея–Овербека (ДЛФО) [11]. Разница состоит в том, что для обратной мицеллы важно внутреннее расклинивающее давление, а для частицы в водном коллоиде – внешнее. Последовательное применение этой концепции позволило дать количественное объяснение сферической формы микроэмульсионных частиц и показать, что общепринятый до этого подход на основе уравнения Хелфриха [12], определяющего зависимость поверхностной энергии монослоя ПАВ от локальной кривизны, является ошибочным [13].
ОБЩИЕ ПОЛОЖЕНИЯ И ОПРЕДЕЛЕНИЯ
Многие ПАВ в неполярном растворителе (масле) при превышении некоторой критической концентрации образуют агрегаты, называемые обратными мицеллами. В обратной мицелле молекулы ПАВ ориентированы полярными головными группами в центр агрегата, а неполярными “хвостами” – наружу. При добавлении полярной жидкости (воды) в раствор, содержащий обратные мицеллы, последние “набухают”: молекулы воды солюбилизируются в центральной части агрегата, образуя так называемый водный пул. Такие мицеллы называют набухшими обратными мицеллами. Растворы, содержащие набухшие обратные мицеллы, называют обратными микроэмульсиями или микроэмульсиями типа “вода-в-масле”. Обратные мицеллы могут солюбилизировать только ограниченное количество воды. При добавлении большего количества образуется двухфазная система. Обратные микроэмульсии являются термодинамически стабильными гомогенными однофазными жидкостями. Размер мицелл определяется главным образом отношением молярных концентраций воды и ПАВ, обозначаемым обычно как W. Во многих случаях для формирования обратной микроэмульсии необходимы вспомогательные вещества – так называемые со-ПАВ, в качестве которых, как правило, используют различные спирты.
Одним из самых широко исследованных ПАВ, применяемых для получения обратных микроэмульсий, является AOT. Обратные микроэмульсии на основе AOT способны солюбилизировать довольно большое количество воды [14] (вплоть до W ≈ 125 в н-гексане при 17°C [15]), при этом не требуется введение со-ПАВ. Мицеллы на основе AOT имеют сферическую форму. Численные оценки в настоящей работе приведены для этого ПАВ.
При теоретическом описании микроэмульсий можно выделить несколько масштабов энергии. Первый масштаб соответствует разнице энергий ПАВ между состояниями на границе фаз вода–масло и вне такой границы. От этой энергии существенно зависит доля ПАВ, находящегося на границе фаз вода–масло. Мы будем считать, что почти все ПАВ находится на этой границе. Второй масштаб соответствует минимизации энергии границы фаз вода–масло за счет оптимизации площади a, приходящейся на одну молекулу ПАВ. Такую оптимизацию можно представить следующим образом. Если площадь a велика, то наличием ПАВ можно пренебречь и за счет обычного поверхностного натяжения между водой и маслом поверхность будет сокращаться. Если площадь a мала, то молекулы ПАВ будут отталкиваться, и поверхность будет увеличиваться. Таким образом, должно существовать некоторое равновесное значение площади a0. На этом масштабе, наверняка, необходимо учитывать притяжение между молекулами ПАВ. Третий масштаб соответствует минимизации энергии пленки ПАВ за счет изменения ее кривизны и взаимодействия между различными участками образовавшейся пленки со стороны водной фазы. Этот третий масштаб энергии определяет топологию пленки ПАВ и многообразие возможных фаз. Четвертый масштаб соответствует взаимодействию между различными участками образовавшейся пленки со стороны масляной фазы, что в случае обратных микроэмульсий есть межмицеллярное взаимодействие.
Большинство теоретических работ по статистической термодинамике обратных мицелл опираются на априорное выражение для зависимости энергии единицы поверхности мицеллярной оболочки от ее кривизны, предложенное в работе Хелфриха [12] для описания везикул. Для сферической поверхности радиуса R эта энергия σ записывается в виде [16]
(1)
$\sigma = {{\sigma }_{0}} + \frac{{\bar {\kappa }}}{{{{R}^{2}}}} + 2\kappa {{\left( {\frac{1}{R} - \frac{1}{{{{R}_{{\text{S}}}}}}} \right)}^{2}},$ТЕОРИЯ ФЛУКТУАЦИЙ СОСТАВА ОБРАТНЫХ МИЦЕЛЛ
Приводимые в литературе экспериментальные данные о полидисперсности обратных мицелл весьма противоречивы. Теоретические работы сводятся к использованию априорного выражения (1) для свободной энергии искривленной пленки ПАВ. Такой подход обладает рядом серьезных недостатков, связанных с тем, что существующие модельные представления оказываются недостаточно точными для описания обратных мицелл.
Распределение сферических обратных мицелл по радиусам их водных пулов может быть вычислено путем минимизации свободной энергии единицы объема микроэмульсии
(2)
$\begin{gathered} F = \sum\limits_{i,j} {c\left( {i,j} \right)f\left( {i,j} \right) + } \\ + \,\,c\left( {i,j} \right){{k}_{{\text{B}}}}T\ln \left( {c\left( {i,j} \right)l_{{ij}}^{3}} \right) + {\text{const}} \\ \end{gathered} $(3)
$\left\{ {\begin{array}{*{20}{c}} {{{c}_{{\text{W}}}} = \sum\limits_{i,j} {ic\left( {i,j} \right)} } \\ {{{c}_{{\text{S}}}} = \sum\limits_{i,j} {jc\left( {i,j} \right),} } \end{array}} \right.$(4)
$c\left( {i,j} \right) = l_{{ij}}^{{ - 3}}\exp \left( {\frac{{{{\mu }_{{\text{W}}}}i + {{\mu }_{{\text{S}}}}j - f\left( {i,j} \right)}}{{{{k}_{{\text{B}}}}T}}} \right),$(5)
$\rho (R) = \frac{{8\pi R}}{{{{a}_{0}}l_{R}^{3}}}\exp \left( {\frac{{4\pi {{\mu }_{{\text{W}}}}}}{{3\text{v}{{k}_{{\text{B}}}}T}}{{R}^{3}} + \frac{{4\pi {{\mu }_{{\text{S}}}}}}{{{{a}_{0}}{{k}_{{\text{B}}}}T}}{{R}^{2}} - \frac{{\varphi (R)}}{{{{k}_{{\text{B}}}}T}}} \right),$(6)
$\begin{array}{*{20}{c}} {{{\mu }_{{\text{W}}}} = 3\text{v}\sigma {\text{'}}\left( {{{R}_{0}}} \right) - \frac{{3\text{v}{{k}_{{\text{B}}}}T{{S}_{0}}}}{{2\pi R_{0}^{3}}},} \\ {{{\mu }_{{\text{S}}}} = {{a}_{0}}\sigma \left( {{{R}_{0}}} \right) - {{a}_{0}}\sigma {\text{'}}\left( {{{R}_{0}}} \right){{R}_{0}} + \frac{{3{{a}_{0}}{{k}_{{\text{B}}}}T{{S}_{0}}}}{{4\pi R_{0}^{2}}}.} \end{array}$Ширину распределения $\rho (R)$ определяет вторая производная S ''(R) в точке R = R0, которая с учетом выражений (6) равна
В гауссовом приближении имеем
Относительная ширина распределения получается равной
где θR – стандартное отклонение радиуса R. Осталось заметить, что S0 ≈ ln(cmicl 3), где cmic – концентрация мицелл. Если полидисперсность (7) выразить через химический потенциал воды (6), то получится:Большинство теоретических работ по полидисперсности обратных мицелл опираются на формулу Хелфриха (1). Подстановка выражения (1) в формулу (7) дает следующее выражение для полидисперсности (в предположении $\bar {\kappa } = 0$):
(8)
$\frac{{{{\theta }_{R}}}}{{{{R}_{0}}}} = \sqrt {\frac{{{{k}_{{\text{B}}}}T}}{{48\pi \kappa \left( {1 - \frac{2}{3}\frac{{{{R}_{0}}}}{{{{R}_{{\text{S}}}}}}} \right) + 6{{S}_{0}}}}} .$Результаты, близкие к формуле (8), были получены в работах [17–19]. Отличия состоят в следующем. В работе [17] вычислялась энергия малой деформации сферической капли на основе выражения, близкого к формуле Хелфриха (1). При этом выражение (8) может быть получено из энергии деформации, соответствующей изменению размера капли при сохранении ею сферической формы. В работах [18, 19] учитывается ряд поправок, в основном связанных с предэкспоненциальным множителем.
Для того чтобы иметь возможность применить формулу (8) для вычисления полидисперсности, необходимо знать величину κ, характеризующую жесткость мицеллярной оболочки. Есть несколько работ, в которых измерялась жесткость мицеллярной оболочки. В работе [20] использовали эффект Керра для определения величины флуктуаций формы обратных мицелл, что позволило получить оценку κ ≈ 0.5kBT. В работе [18] рассчитанные на основе этих данных значения полидисперсности лежат примерно в интервале 20–30%.
В работах Эрикссона и др. [16, 21, 22] также на основе выражения типа (1) выведены формулы для полидисперсности обратных мицелл в системе типа Winsor II (обратная микроэмульсия в равновесии с отделяющейся водной фазой). В самом простом виде, без учета некоторых поправок, результат записывается следующим образом:
где σ∞ = σ0 + ${{{\text{2}}\kappa } \mathord{\left/ {\vphantom {{{\text{2}}\kappa } {R_{{\text{S}}}^{{\text{2}}}}}} \right. \kern-0em} {R_{{\text{S}}}^{{\text{2}}}}}$ – поверхностное натяжение плоской границы вода–масло в системе Winsor II. По формуле (9) в работе [16] для полидисперсности получена оценка 15%. Для системы Winsor II (без учета несущественных сейчас поправок и в предположении $\bar {\kappa } = 0$) R0 = RS, а поверхностное натяжение между масляной и водной фазами связано [23, 24] с жесткостью пленки:Нетрудно видеть, что формула (9) есть следствие формул (8) и (10) в пренебрежении членом S0, учитывающим трансляционное движение мицелл. Выражение (10) для системы Winsor II получается из уравнения Δp = 0, где
(11)
$\Delta p = \frac{{2\sigma {\text{(}}R{\text{)}}}}{R} + \frac{{\partial \sigma {\text{(}}R{\text{)}}}}{{\partial R}}$На основе формулы Хелфриха (1) полидисперсность вычислена также в работе Овербека [25] для микроэмульсий типа Winsor II на основе лаурилсульфата натрия. Поученное значение лежит в пределах 12–21% и зависит от используемых в расчете констант жесткости пленки ПАВ. Аналогичные вычисления приведены в работе [26].
Подходы, использованные в упомянутых выше теоретических работах, не позволяют в полной мере решить вопрос о полидисперсности обратных мицелл. Во-первых, в настоящее время нет согласия относительно того, каким образом вычислять энтропию смешения, что в данной работе выражается в неопределенности масштаба длины lij [24]. Во-вторых, разброс экспериментальных данных о жесткости пленки и полидисперсности мицелл не позволяет проверить теорию [24]. В-третьих, использование энергии Хелфриха и предположения о постоянстве площади, занимаемой одной молекулой ПАВ в мицеллярной оболочке, допустимо только для достаточно больших капелек. В-четвертых, зависимость энергии пленки от кривизны, предложенная Хелфрихом, может оказаться неподходящей для описания обратных мицелл, особенно, в случае ионогенных ПАВ [24]. И, наконец, не принимается во внимание тот факт, что распределение обратных мицелл должно быть двумерным. Обратная мицелла представляет собой агрегат, состоящий из двух компонентов, поэтому ее состав задается двумя числами, в качестве которых можно выбрать количества молекул ПАВ и воды. Для задания распределения двумерной случайной величины в самом простейшем приближении (распределении Гаусса) требуются три параметра, не считая средних значений. В качестве таких параметров можно выбрать, например, стандартные отклонения количеств молекул воды и ПАВ и коэффициент корреляции между этими количествами. С этой точки зрения в упомянутых выше работах искалась только одна величина: стандартное отклонение количества молекул воды в обратной мицелле. При этом, поскольку не принималось во внимание то, что параметров должно быть три, возникает вопрос о том, насколько верны полученные в цитируемых выше работах результаты.
В нашей работе [27] был развит другой – феноменологический – подход к термодинамическому описанию обратных мицелл. Суть подхода заключается в утверждении о том, что вся интересующая нас информация об обратных мицеллах заключается в их стандартном химическом потенциале μ0(i, j), рассматриваемом как функция чисел агрегации i и j. При этом используется двумерное распределение по числам агрегации i и j и отсутствуют какие-либо априорные положения или подгоночные коэффициенты. Предполагается, что вся необходимая численная информация доступна из экспериментов по определению размеров обратных мицелл и по измерению значений давления насыщенных водяных паров над поверхностью микроэмульсии.
Считая мицеллы невзаимодействующими, для их химического потенциала можно записать:
(12)
$\mu \left( {i,j} \right) = {{\mu }^{0}}\left( {i,j} \right) + {{k}_{{\text{B}}}}T\ln c\left( {i,j} \right),$Предполагается, что с достаточно большими числами агрегации i и j можно обращаться как с действительными числами, а функция μ0(i, j) является достаточно хорошей с математической точки зрения, то есть дифференцируемой необходимое число раз. Функция μ0(i, j) является при этом связующим звеном между различными свойствами обратных мицелл: средними числами агрегации и величиной их флуктуаций, химическими потенциалами воды и ПАВ. Поэтому удается без каких-либо априорных предположений относительно энергии или состава мицеллы выразить параметры флуктуаций через величины, доступные экспериментально: давление водяных паров над микроэмульсией и средние количества молекул воды и ПАВ в мицелле. Существенно, что рассматриваются флуктуации не размера, а состава, представляющего собой двумерную случайную величину. Химические потенциалы μW и μS определяются полными концентрациями воды cW и ПАВ cS через систему уравнений (3). В качестве двух переменных, однозначно описывающих состояние рассматриваемой системы, можно выбрать либо концентрации cW и cS, либо химические потенциалы μW и μS, либо наиболее вероятные числа агрегации мицелл i0 и j0. Пусть
(14)
$S\left( {i,j} \right) = \ln c\left( {i,j} \right) = \frac{{i{{\mu }_{{\text{W}}}} + j{{\mu }_{{\text{S}}}} - {{\mu }^{0}}\left( {i,j} \right)}}{{{{k}_{{\text{B}}}}T}}.$Из того, что при i = i0, j = j0 концентрация мицелл имеет максимум, дифференцированием выражения (14) получаем
(15)
${{\mu }_{{\text{W}}}} = \frac{{\partial {{\mu }^{0}}\left( {{{i}_{0}},{{j}_{0}}} \right)}}{{\partial i}},\,\,\,\,{{\mu }_{{\text{S}}}} = \frac{{\partial {{\mu }^{0}}\left( {{{i}_{0}},{{j}_{0}}} \right)}}{{\partial j}}.$Будем считать, что числа агрегации велики по сравнению с единицей, и обращаться с ними, как с действительными числами. Распределение по числам агрегации будем искать приближенно в виде распределения Гаусса. Для этого рассмотрим отклонение S как функции i и j от максимального значения при i = i0, j = j0:
(16)
$\Delta S = - \frac{1}{{2{{k}_{{\text{B}}}}T}}\left( {{{\mu }_{{ii}}}\Delta {{i}^{2}} + 2{{\mu }_{{ij}}}\Delta i\Delta j + {{\mu }_{{jj}}}\Delta {{j}^{2}}} \right),$(17)
$\begin{gathered} {{\mu }_{{ii}}} = \frac{{{{\partial }^{2}}{{\mu }^{0}}\left( {{{i}_{0}},{{j}_{0}}} \right)}}{{\partial {{i}^{2}}}},\,\,\,\,{{\mu }_{{ij}}} = \frac{{{{\partial }^{2}}{{\mu }^{0}}\left( {{{i}_{0}},{{j}_{0}}} \right)}}{{\partial i\partial j}}, \\ {{\mu }_{{jj}}} = \frac{{{{\partial }^{2}}{{\mu }^{0}}\left( {{{i}_{0}},{{j}_{0}}} \right)}}{{\partial {{j}^{2}}}}. \\ \end{gathered} $Из сравнения квадратичной формы (16) с общим выражением для двумерного нормального распределения
(18)
$\begin{gathered} {{\mu }_{{ii}}} = \frac{{{{k}_{{\text{B}}}}T}}{{(1 - {{r}^{2}})\theta _{i}^{2}}},\,\,\,\,{{\mu }_{{ij}}} = \frac{{ - r{{k}_{{\text{B}}}}T}}{{(1 - {{r}^{2}}){{\theta }_{i}}{{\theta }_{j}}}}, \\ {{\mu }_{{jj}}} = \frac{{{{k}_{{\text{B}}}}T}}{{(1 - {{r}^{2}})\theta _{j}^{2}}}, \\ \end{gathered} $(19)
$\theta _{i}^{2} = \frac{{{{k}_{{\text{B}}}}T{{\mu }_{{jj}}}}}{{{{\mu }_{{ii}}}{{\mu }_{{jj}}} - \mu _{{ij}}^{2}}},\,\,\,\,\theta _{j}^{2} = \frac{{{{k}_{{\text{B}}}}T{{\mu }_{{ii}}}}}{{{{\mu }_{{ii}}}{{\mu }_{{jj}}} - \mu _{{ij}}^{2}}},\,\,\,\,r = \frac{{ - {{\mu }_{{ij}}}}}{{\sqrt {{{\mu }_{{ii}}}{{\mu }_{{jj}}}} }}.$Пусть S0 – логарифм концентрации наиболее вероятных мицелл, тогда из выражения (14) находим:
(20)
${{k}_{{\text{B}}}}T{{S}_{0}} = {{i}_{0}}{{\mu }_{{\text{W}}}} + {{j}_{0}}{{\mu }_{{\text{S}}}} - {{\mu }^{0}}({{i}_{0}},{{j}_{0}}).$Дифференцируя выражение (20) с учетом уравнений (15), получаем
(21)
${{k}_{{\text{B}}}}Td{{S}_{0}} = {{i}_{0}}d{{\mu }_{{\text{W}}}} + {{j}_{0}}d{{\mu }_{{\text{S}}}},$(22)
${{k}_{{\text{B}}}}Td{{S}_{0}} = {{i}_{0}}\left( {{{\mu }_{{ii}}}d{{i}_{0}} + {{\mu }_{{ij}}}d{{j}_{0}}} \right) + {{j}_{0}}\left( {{{\mu }_{{ij}}}d{{i}_{0}} + {{\mu }_{{jj}}}d{{j}_{0}}} \right).$Поскольку W = cW/cS = i0/j0, то
Для дифференциала μW имеем
Из выражений для дифференциалов (21)–(24) легко получить следующие частные производные:
(25)
$n \equiv {{\left( {\frac{{\partial \ln {{j}_{0}}}}{{\partial \ln {{i}_{0}}}}} \right)}_{{{{S}_{0}}}}} = - \frac{{i_{0}^{2}{{\mu }_{{ii}}} + {{i}_{0}}{{j}_{0}}{{\mu }_{{ij}}}}}{{{{i}_{0}}{{j}_{0}}{{\mu }_{{ij}}} + j_{0}^{2}{{\mu }_{{jj}}}}},$(26)
${{\left( {\frac{{\partial {{\mu }_{{\text{W}}}}}}{{\partial W}}} \right)}_{{{{S}_{0}}}}} = j_{0}^{3}\frac{{{{\mu }_{{ii}}}{{\mu }_{{jj}}} - \mu _{{ij}}^{2}}}{{i_{0}^{2}{{\mu }_{{ii}}} + 2{{i}_{0}}{{j}_{0}}{{\mu }_{{ij}}} + j_{0}^{2}{{\mu }_{{jj}}}}},$(27)
${{\left( {\frac{{\partial {{\mu }_{{\text{W}}}}}}{{\partial {{S}_{0}}}}} \right)}_{W}} = \frac{{{{k}_{{\text{B}}}}T}}{{{{i}_{0}}}}\frac{n}{{n - 1}},$(28)
${{\left( {\frac{{\partial \ln {{i}_{0}}}}{{\partial {{S}_{0}}}}} \right)}_{W}} = {{\left( {\frac{{\partial \ln {{j}_{0}}}}{{\partial {{S}_{0}}}}} \right)}_{W}} = \frac{{{{k}_{{\text{B}}}}T}}{{i_{0}^{2}{{\mu }_{{ii}}} + 2{{i}_{0}}{{j}_{0}}{{\mu }_{{ij}}} + j_{0}^{2}{{\mu }_{{jj}}}}},$(29)
$W{{\left( {\frac{{\partial {{\mu }_{{\text{W}}}}}}{{\partial {{\mu }_{{\text{S}}}}}}} \right)}_{{{{S}_{0}}}}} = - 1.$Из уравнений (25), (26) и (28) можно получить, что
(30)
$\begin{gathered} {{\mu }_{{ii}}} = \frac{1}{{{{j}_{0}}}}{{\left( {\frac{{\partial {{\mu }_{{\text{W}}}}}}{{\partial W}}} \right)}_{{{{S}_{0}}}}} + \frac{{{{n}^{2}}{{k}_{{\text{B}}}}T}}{{i_{0}^{2}{{{\left( {1 - n} \right)}}^{2}}{{{\left( {\frac{{\partial \ln {{i}_{0}}}}{{\partial {{S}_{0}}}}} \right)}}_{W}}}}, \\ {{\mu }_{{ij}}} = - \frac{{{{i}_{0}}}}{{j_{0}^{2}}}{{\left( {\frac{{\partial {{\mu }_{{\text{W}}}}}}{{\partial W}}} \right)}_{{{{S}_{0}}}}} - \frac{{n{{k}_{{\text{B}}}}T}}{{{{i}_{0}}{{j}_{0}}{{{\left( {1 - n} \right)}}^{2}}{{{\left( {\frac{{\partial \ln {{i}_{0}}}}{{\partial {{S}_{0}}}}} \right)}}_{W}}}}, \\ {{\mu }_{{jj}}} = \frac{{i_{0}^{2}}}{{j_{0}^{3}}}{{\left( {\frac{{\partial {{\mu }_{{\text{W}}}}}}{{\partial W}}} \right)}_{{{{S}_{0}}}}} + \frac{{{{k}_{{\text{B}}}}T}}{{j_{0}^{2}{{{\left( {1 - n} \right)}}^{2}}{{{\left( {\frac{{\partial \ln {{i}_{0}}}}{{\partial {{S}_{0}}}}} \right)}}_{W}}}}. \\ \end{gathered} $Подставляя выражения (30) в формулы (19), получаем
(31)
$\begin{gathered} \frac{{\theta _{i}^{2}}}{{i_{0}^{2}}} = \frac{{{{k}_{{\text{B}}}}T}}{{{{j}_{0}}{{W}^{2}}{{{\left( {\frac{{\partial {{\mu }_{{\text{W}}}}}}{{\partial W}}} \right)}}_{{{{S}_{0}}}}}{{{\left( {1 - n} \right)}}^{2}}}} + {{\left( {\frac{{\partial \ln {{i}_{0}}}}{{\partial {{S}_{0}}}}} \right)}_{W}}, \\ \frac{{\theta _{j}^{2}}}{{j_{0}^{2}}} = \frac{{{{k}_{{\text{B}}}}T}}{{{{j}_{0}}{{W}^{2}}{{{\left( {\frac{{\partial {{\mu }_{{\text{W}}}}}}{{\partial W}}} \right)}}_{{{{S}_{0}}}}}{{{\left( {1 - \frac{1}{n}} \right)}}^{2}}}} + {{\left( {\frac{{\partial \ln {{i}_{0}}}}{{\partial {{S}_{0}}}}} \right)}_{W}}, \\ {{r}^{2}} = \frac{{{{{\left( {1 + nx} \right)}}^{2}}}}{{\left( {1 + x} \right)(1 + x{{n}^{2}})}}, \\ \end{gathered} $Таким образом, видно, что распределение мицелл по числам агрегации определяется производными (25), (26) и (28). Концентрация всех мицелл равна
(32)
${{c}_{{{\text{mic}}}}} = \iint {{{e}^{S}}didj = {{e}^{{{{S}_{0}}}}}\frac{{2\pi {{k}_{{\text{B}}}}T}}{{\sqrt {{{\mu }_{{ii}}}{{\mu }_{{jj}}} - \mu _{{ij}}^{2}} }}}.$Пусть Smic – логарифм концентрации всех мицелл. Тогда из уравнения (32) следует, что
(33)
$d{{S}_{{{\text{mic}}}}} = d{{S}_{0}} - \frac{1}{2}d\left[ {\ln \left( {{{\mu }_{{jj}}}{{\mu }_{{ii}}} - \mu _{{ij}}^{2}} \right)} \right].$В выражении (33) мы будем пренебрегать логарифмическим членом и считать, что dSmic ≈ dS0. Таким образом, в частных производных (25)–(29) можно заменить S0 на Smic. Рассмотрим эти частные производные.
Производные (25) и (28) отражают изменение среднего состава мицеллы при изменении концентраций воды и ПАВ. Из выражения (28) видно, что средний размер мицелл слабо растет с ростом их концентрации, поскольку его правая часть имеет порядок квадрата полидисперсности. В эксперименте такая слабая зависимость в силу ряда причин была не замечена. Таким образом, сложилось мнение, что размер мицелл не зависит от их концентрации, но зависит от отношения концентраций воды и ПАВ W = i0/j0 [5, 6]. При этом для типичных концентраций ПАВ и воды наиболее вероятные числа агрегации с хорошей точностью лежат на некоторой кривой
Из такой экспериментально измеряемой кривой (34) получается значение производной (25). Заметим, что для больших сферических мицелл, когда площадь, занимаемая одной молекулой ПАВ на поверхности пула, не зависит от W, зависимость (34) является степенно'й с показателем степени n = 2/3. Для малых мицелл n = 0, поскольку при W = 0 в выражении (25) i0 = 0.
Производные (26) и (27) отражают изменение химического потенциала воды при изменении концентраций воды и ПАВ. Химический потенциал воды зависит очень слабо от концентрации мицелл и сильно – от параметра W. Производная (26) может быть экспериментально получена из зависимости давления p насыщенных водяных паров над обратной микроэмульсией от отношения W в соответствии с формулой μW = kВT ln(p/p0), где p0 – давление насыщенного водяного пара над поверхностью воды при той же температуре, за точку отсчета химического потенциала воды выбирается чистая вода. Таким образом, при максимально возможном параметре W, когда микроэмульсия может находиться в равновесии с водной фазой, оказывается что μW = 0. Подставив в уравнение (26) выражения (18), получим
(35)
${{\left( {\frac{{\partial {{\mu }_{{\text{W}}}}}}{{\partial w}}} \right)}_{{{{S}_{0}}}}} = \frac{{{{j}_{0}}{{k}_{{\text{B}}}}T}}{{i_{0}^{2}}}{{\left( {\frac{{\theta _{i}^{2}}}{{i_{0}^{2}}} - 2r\frac{{{{\theta }_{i}}}}{{{{i}_{0}}{{j}_{0}}}} + \frac{{\theta _{j}^{2}}}{{j_{0}^{2}}}} \right)}^{{ - 1}}}.$Найдем теперь относительное стандартное отклонение величины w = i/j, имеющей смысл для каждого отдельно взятого агрегата. Заметим, что среднее значение величины w равно W. Из уравнения для вариации δw/w = δi/i − δj/j, общего выражения для дисперсии суммы двух случайных величин x и y $\theta _{{x + y}}^{2}$ = $\theta _{x}^{2}$ + $2r{{\theta }_{x}}{{\theta }_{y}}$ + $\theta _{y}^{2}$ и выражения (35) получаем квадрат относительного стандартного отклонения величины w:
(36)
${{\left( {\frac{{{{\theta }_{w}}}}{W}} \right)}^{2}} = \frac{{{{k}_{{\text{B}}}}T}}{{{{j}_{0}}{{W}^{2}}{{{\left( {\frac{{\partial {{\mu }_{{\text{W}}}}}}{{\partial W}}} \right)}}_{{{{S}_{0}}}}}}}.$Таким образом, производная химического потенциала воды по W определяет величину флуктуаций отношения w, характеризующего состав отдельной мицеллы.
Выражение для производной (29) позволяет вычислить химический потенциал ПАВ по известному химическому потенциалу воды.
Линии уровня функции распределения обратных мицелл по числам агрегации в гауссовом приближении представляют собой эллипсы с центром в точке (i0, j0). В качестве параметров эллипса можно использовать либо величины (30), либо величины (31). Несложно показать, что если в выражениях (30) доминируют слагаемые с производной химического потенциала воды по параметру W, то эллипсы вытянуты в направлении, определяемым вектором (i0, j0). Если же доминируют слагаемые с (∂ ln i0/∂S0)W, то эллипсы вытянуты вдоль направления (1, (∂j0/∂i0)S0), то есть по касательной к кривой (34).
Для расчета распределения обратных мицелл по числам агрегации согласно формулам (31) и (36) необходимы экспериментальные данные для производных (25), (26) и (28). То есть необходимо знать зависимости среднего числа молекул ПАВ и давления насыщенного водяного пара над поверхностью микроэмульсии от параметра W, а также зависимость размера мицелл от их концентрации при постоянном параметре W.
Зависимость чисел агрегации обратных мицелл на основе AOT от параметра W находилась нами на основе экспериментальных данных, имеющихся в литературе [4, 5, 28–33]. При этом были отброшены сильно заниженные числа агрегации из работ [28, 31, 32], имеющие большой разброс, и завышенные числа агрегации для мицелл в декане из работы [30]. Оказалось, что за исключением данных работы [4] при W < 20 и данных работы [5] для мицелл в толуоле при W < 4 связь числа агрегации с параметром W хорошо приближается формулой
(37)
$\sqrt {{{N}_{{{\text{AOT}}}}}} = \sqrt {36\pi a_{0}^{{ - 3}}} \left( {{{\text{v}}_{{\text{W}}}}W + {{\text{v}}_{{\text{H}}}}} \right),$(38)
$R = \frac{{3{{\text{v}}_{{\text{W}}}}}}{{{{a}_{0}}}}W + \frac{{3{{\text{v}}_{{\text{H}}}}}}{{{{a}_{0}}}}.$Подбор коэффициентов в формуле (37) методом наименьших квадратов дает: a0 = 63 Å2 и vH = = 222 Å3. Количество молекул AOT в сухой обратной мицелле (W = 0) при этом оказывается равным 22, что согласуется с результатами работ [35–37] в пределах имеющегося в них разброса данных. Также имеется согласие между размерами водных пулов, вычисленными по формуле (38) и приведенными в работах [7, 38, 39] (кроме значений при W < 5, когда методы, примененные в указанных работах, дают большую ошибку). Если учесть, что длина неполярного хвоста молекулы ПАВ составляет примерно 1 нм, то при W > 1 имеется также удовлетворительное согласие с формулой для гидродинамического радиуса обратных мицелл в гептане (Rh = 0.175W + 1.5 нм, 0 ≤ W ≤ 30), полученной в работе [40]. В то же время, в работе [6] методом фотонной корреляционной спектроскопии получены несколько бо'льшие значения гидродинамических радиуса обратных мицелл в изооктане: Rh = 0.21W + 1.6 нм, 0 ≤ W ≤ 30 (наша аппроксимация). Из формулы (37) можно получить функцию (34) и производную (25):
Давление насыщенных водяных паров над микроэмульсией на основе AOT измерялось в работах [31, 32, 41–45]. При этом данные работ [31, 32, 44, 45] количественно совпадают при W < 6 и качественно совпадают при W > 6. Данные работ [41–43] не совпадают с данными работ [31, 32, 44, 45] (совпадения можно добиться удвоением значений параметра W в первой серии работ). Для расчета мы выбрали данные работы [32] для микроэмульсий в изооктане при 37°C для диапазона W = 0–18 (рис. 1). Давление насыщенного водяного пара над поверхностью микроэмульсии равно нулю при W = 0 и давлению насыщенных водяных паров над чистой водой при той же температуре при максимально возможном значении W для рассматриваемой микроэмульсии. При этом согласно данным работ [31, 32, 45] при W < 18 эти давления почти не зависят от природы растворителя (бензол, циклогексан, изооктан и др.). При W > 18 давление очень слабо зависит от W и поэтому в указанных работах не исследовано ввиду недостаточной точности использованных экспериментальных методик (при больших значениях W для наших расчетов необходима точность измерения давления не хуже 0.1%). Заметим, что для системы AOT/вода/изооктан при 37°C максимальное значение параметра W составляет примерно 50.
Рис. 1.
Зависимость давления p насыщенных водяных паров над обратной микроэмульсией AOT/вода/изооктан от параметра W при 37°C; p0 – давление насыщенных водяных паров над чистой водой при той же температуре [32].

На основании формул (31) и (36) и экспериментальных данных по давлению паров для системы AOT/вода/изооктан при 37°C можно получить (рис. 2) относительные среднеквадратичные отклонения отношения w и радиуса R водного пула, задаваемого через количество молекул воды NW в мицелле соотношением 4πR3/3 = NWVw. Величина флуктуаций радиуса водного пула при этом определяется в пренебрежении зависимостью состава мицелл от их концентрации, т.е. производной (28). Таким образом, это расчетное значение следует рассматривать как нижнюю границу.
Рис. 2.
Относительные стандартные отклонения отношения w количества молекул воды к количеству молекул ПАВ в мицелле (1) и радиуса водного пула R (2).

Эффект изменения среднего состава мицелл с изменением их концентрации измерить трудно, поскольку он маскируется другими эффектами. Во-первых, при большом разбавлении микроэмульсии растворителем нельзя пренебрегать концентрацией ПАВ, находящегося в неполярной среде в виде отдельных молекул и не участвующего в образовании мицелл [46–49]. Разбавление микроэмульсии ведет к высвобождению части ПАВ из состава мицелл в объем растворителя, тем самым увеличивая эффективный параметр Weff:
Рис. 3.
Линия уровня функции распределения на полувысоте (сплошная линия) при W = 15. Эта линия уровня представляет собой эллипс, в пределах которого находится половина всех мицелл. Пунктирной линией показана зависимость (39) между средними числами молекул AOT и воды в обратной мицелле для диапазона W = 0–20. NW – количество молекул воды, NAOT – количество молекул AOT.

Заметим, что хотя мы и получили распределение, слабо отклоняющееся от кривой (34), отклонения формы мицеллы от сферической, тем не менее, могут быть значительными – того же порядка, что и отклонение радиуса. Если разложить флуктуации формы мицеллы на сферические гармоники [17], то гармоника с l = 0 будет соответствовать изменению радиуса мицеллы без изменения формы, то есть изменению числа агрегации вдоль кривой (34), гармоники с l = 1 – перемещению мицеллы, как целого, а высшие гармоники с l ≥ 2 – изменению формы мицеллы. Расчет показывает, что отклонения количеств молекул воды и ПАВ от их средних значений для гармоник с l ≥ 2 являются квадратичными по амплитудам, т.е. малыми величинами. Таким образом, существенные флуктуации формы совместимы с малым отклонением распределения от кривой (34).
С помощью формулы (29) и известной зависимости давления водяных паров над микроэмульсией от W можно вычислить с точностью до произвольного множителя зависимость концентрации c0 неагрегированного ПАВ от W:
Так, из зависимости, изображенной на рис. 1, мы получили, что в системе AOT/вода/изооктан при 37°C в диапазоне W = 0–18 концентрация неагрегированного AOT примерно обратно пропорциональна W. Отметим, что похожая зависимость концентрации c0 от W наблюдалась в работе [49] для системы нонилфениловый эфир пентаэтиленгликоля/вода/циклогексан.
Таким образом, для микроэмульсии AOT/вода/изооктан при 37°C в диапазоне W = 0–18 на основе полученных формул и соответствующих литературных данных удалось оценить флуктуации состава и размера обратных мицелл: среднеквадратичное отклонение отношения количества молекул воды к количеству молекул ПАВ составляет примерно 10%, а полидисперсность пула мицеллы лежит в интервале 8–12%. Кроме того, можно вычислить зависимость от параметра W концентрации неагрегированного ПАВ.
МЕХАНИЗМ ОГРАНИЧЕНИЯ РОСТА НАНОЧАСТИЦ ОБОЛОЧКАМИ ОБРАТНЫХ МИЦЕЛЛ
Как уже было сказано в вводной части, с начала 80-х гг. прошлого века обратные микроэмульсии стали применяться для синтеза наночастиц [53]. Существуют несколько вариантов такого синтеза. В самом распространенном варианте смешивают две микроэмульсии, в водных псевдофазах которых растворены вещества, реагирующие с образованием наночастиц. Использование обратных микроэмульсий для синтеза наночастиц обычно мотивировалось предположением о том, что оболочки обратных мицелл останавливают рост частиц, когда их размер становится равным размеру пулов [54–57]. Такое ограничение роста, как предполагалось, позволяет управлять размером синтезируемых частиц посредством изменения молярного отношения W. При этом, поскольку обратные мицеллы предполагались монодисперсными, ожидалось также, что и синтезируемые в них частицы должны быть монодисперсными [57–61]. Однако как показал детальный анализ, проведенный в нашем обзоре [10], такие представления об ограничении роста частиц оболочками обратных мицелл противоречат экспериментальным данным.
Рассмотрим более подробно возможный механизм ограничения роста наночастиц обратными мицеллами и сделаем соответствующие численные оценки для обратных микроэмульсий на основе AOT. Растущие наночастицы будем считать сферическими и монодисперсными. Рост частиц будем рассматривать при уменьшении их количества и сохранении их суммарной массы, что имеет место при оствальдовском созревании и коагуляции. Таким образом, движущей силой роста частиц в нашем рассмотрении является уменьшение их суммарной поверхностной энергии. Пока частицы меньше размеров водных пулов обратных мицелл, их рост ничем не ограничен. Как только размер частиц достигает размеров пулов, их дальнейшему росту начинают препятствовать мицеллярные оболочки. Поскольку мицеллярные оболочки не являются абсолютно жесткими, обратные мицеллы под давлением растущих в них частиц должны увеличиваться в размерах за счет обмена молекулами воды и ПАВ с другими мицеллами. В результате распределение мицелл отклоняется от равновесного, становясь бимодальным, что приводит к увеличению их суммарного термодинамического потенциала Гиббса. Таким образом, рост частиц уменьшает поверхностную энергию частиц, но увеличивает термодинамический потенциал обратных мицелл. Рост частиц должен прекратиться при таком их размере, при котором суммарный термодинамический потенциал системы минимален.
Изменение термодинамического потенциала Гиббса системы обратных мицелл вместе с растущими в них частицами ΔGfull можно представить как сумму независимо вычисляемых слагаемых:
(39)
$\Delta {{G}_{{{\text{full}}}}} = \Delta {{G}_{{{\text{mic}}}}} + \Delta {{G}_{{{\text{part}}}}},$Рис. 4.
Термодинамическая цепочка, иллюстрирующая возможность независимого рассмотрения изменений термодинамических потенциалов Гиббса обратных мицелл и растущих в них частиц. Серый цвет обозначает воду; большие черные кружки – частицы, серые прямоугольники – резервуары с водой, серые кружки – водные пулы обратных мицелл. Цифрами обозначены гипотетические стадии, на которые разбит процесс роста частиц в обратных мицеллах.

На первой стадии имеются обратные мицеллы, в водных пулах которых находятся частицы. При переходе ко второй стадии частицы переносятся в резервуар с водой, а на их место переносится вода из резервуара. На третьей стадии распределение мицелл становится бимодальным. При переходе на четвертую стадию растут частицы. На пятой стадии выросшие частицы переносятся в большие мицеллы, а лишняя вода из обратных мицелл переносится в резервуар. При переходах от второй к третьей стадии и от третьей к четвертой термодинамический потенциал изменяется на ΔGmic и ΔGpart соответственно. При переходах от стадии 1 к стадии 2 и от стадии 4 к стадии 5 термодинамический потенциал не изменяется. Последнее утверждение обосновывается следующим образом. Вода в обратной мицелле, за исключением тонкого слоя вблизи мицеллярной оболочки, имеет такие же свойства, как и обычная вода, но при отрицательном давлении. Отрицательное давление возникает из-за стремления мицеллярной оболочки иметь естественную кривизну и по абсолютной величине убывает с ростом размера мицелл. Это давление влияет на термодинамический потенциал в соответствии общим с уравнением
где G – термодинамический потенциал Гиббса, S – энтропия, T – абсолютная температура, V – объем, P – давление. Из уравнения (40) при постоянной температуре и с учетом несжимаемости воды получаем, что вклад некоторого объема воды в пуле обратной мицеллы в ее термодинамический потенциал Гиббса равен произведению этого объема на давление в пуле. При замене некоторого объема воды V в водном пуле мицеллы на частицу того же объема из резервуара с водой термодинамический потенциал воды изменяется на величину –PV, но зато термодинамический потенциал частицы изменяется на обратную величину PV, поэтому суммарный термодинамический потенциал Гиббса не изменяется. Таким образом, оказывается, что при переходах от стадии 1 к стадии 2 и от стадии 4 к стадии 5 термодинамический потенциал системы не изменяется. Сум-мируя изменения термодинамического потенциала Гиббса на всех стадиях, получаем уравнение (39). Найдем изменение термодинамического потенциала мицелл ΔGmic. Будем считать, что частицы начали расти в мицеллах, размер которых соответствует молярному отношению W0, и что частиц при этом гораздо меньше, чем мицелл. По мере роста частицы как бы “растягивают” те мицеллы, в которых растут.Это приводит к бимодальному распределению мицелл по размерам (рис. 5): часть из них имеет размер, соответствующий молярному отношению W0, а часть – некоторому большему значению W > W0. Для краткости будем называть обратные мицеллы с молярным отношением W0 маленькими, а с молярным отношением W – большими.
Рис. 5.
Бимодальное распределение обратных мицелл по размерам, возникающее в процессе роста частиц. Штриховкой внутри больших мицелл показаны растущие частицы.

Из небольшой части молекул воды и ПАВ, составляющих маленькие мицеллы, необходимо сформировать большие мицеллы. Связанное с этим изменение термодинамического потенциала Гиббса равно
(41)
$\Delta {{G}_{{{\text{mic}}}}} = {{N}_{{\text{S}}}}\Delta {{\mu }_{{\text{S}}}} + {{N}_{{\text{W}}}}\Delta {{\mu }_{{\text{W}}}},$(42)
$\begin{gathered} \Delta {{\mu }_{{\text{W}}}} = {{\mu }_{{\text{W}}}}\left( W \right) - {{\mu }_{{\text{W}}}}\left( {{{W}_{0}}} \right), \\ \Delta {{\mu }_{{\text{S}}}} = {{\mu }_{{\text{S}}}}\left( W \right) - {{\mu }_{{\text{S}}}}\left( {{{W}_{0}}} \right), \\ \end{gathered} $(43)
${{N}_{{\text{W}}}}d{{\mu }_{{\text{W}}}} + {{N}_{{\text{S}}}}d{{\mu }_{{\text{S}}}} + {{N}_{{{\text{solv}}}}}d{{\mu }_{{{\text{solv}}}}} = 0,$Действительно, дифференциалы dμW и dμS в уравнении (43) имеют порядки kBTdNW/NW и kBTdNS/NS соответственно, а дифференциал химического потенциала растворителя в соответствии с теорией слабых растворов равен kВTdNmic/Nsolv, где Nmic – число обратных мицелл. Из этих оценок с учетом того, что при больших числах агрегации число обратных мицелл много меньше числа молекул воды и ПАВ, следует, что в уравнении (43) можно пренебречь последним слагаемым.
Из определения молярного отношения W имеем:
(45)
$W = {{{{N}_{{\text{W}}}}} \mathord{\left/ {\vphantom {{{{N}_{{\text{W}}}}} {{{N}_{{\text{S}}}}}}} \right. \kern-0em} {{{N}_{{\text{S}}}}}}.$Уравнения (44) и (45) позволяют выразить один химический потенциал через другой:
(46)
${{\mu }_{{\text{S}}}} = - \int {Wd{{\mu }_{{\text{W}}}}} = - \int W \mu _{{\text{W}}}^{'}\left( W \right)dW,$(47)
${{\mu }_{{\text{W}}}} = - \int {{{W}^{{ - 1}}}d{{\mu }_{{\text{S}}}}} = - \int {{{W}^{{ - 1}}}\mu _{{\text{S}}}^{'}\left( W \right)dW} .$С учетом уравнения (47) для изменения химического потенциала воды можно записать
(48)
$\Delta {{\mu }_{{\text{W}}}} = - \int\limits_{{{W}_{0}}}^W {{{W}^{{ - 1}}}\mu _{{\text{S}}}^{'}\left( W \right)dW} .$Из уравнений (41), (42), (45) и (48) получаем выражение для изменения термодинамического потенциала системы обратных мицелл:
(49)
$\begin{gathered} \Delta {{G}_{{{\text{mic}}}}} = \frac{{{{N}_{{\text{W}}}}}}{W}\left( {{{\mu }_{{\text{S}}}}\left( W \right) - {{\mu }_{{\text{S}}}}\left( {{{W}_{0}}} \right)} \right) - \\ - \,\,{{N}_{{\text{W}}}}\int\limits_{{{W}_{0}}}^W {{{W}^{{ - 1}}}\mu _{{\text{S}}}^{'}\left( W \right)dW} . \\ \end{gathered} $Для изменения поверхностной энергии частиц имеем:
(50)
$\begin{gathered} \Delta {{G}_{{{\text{part}}}}} = \left( {\Omega - {{\Omega }_{0}}} \right)\sigma = \frac{{3V\sigma }}{R} - {{\Omega }_{0}}\sigma \approx \\ \approx \frac{{3{{\text{v}}_{{\text{W}}}}{{N}_{{\text{W}}}}\sigma }}{{\frac{{3{{\text{v}}_{{\text{W}}}}}}{{{{a}_{0}}}}W}} - {{\Omega }_{0}}\sigma = {{N}_{{\text{W}}}}\frac{{{{a}_{0}}\sigma }}{W} - {{\Omega }_{0}}\sigma , \\ \end{gathered} $(51)
$\begin{gathered} \Delta {{G}_{{{\text{full}}}}} = \frac{{{{N}_{{\text{W}}}}}}{W}\left( {{{\mu }_{{\text{S}}}}\left( W \right) - {{\mu }_{{\text{S}}}}\left( {{{W}_{0}}} \right)} \right) - \\ - \,\,{{N}_{{\text{W}}}}\int\limits_{{{W}_{0}}}^W {{{W}^{{ - 1}}}\mu _{{\text{S}}}^{'}\left( W \right)dW + {{N}_{{\text{W}}}}\frac{{{{a}_{0}}\sigma }}{W} - {{\Omega }_{0}}\sigma {\kern 1pt} } . \\ \end{gathered} $Рост частиц прекращается при значении молярного отношения для больших мицелл W = Wmax, при котором изменение термодинамического потенциала (51) минимально (рис. 6), т.е. при условии
(52)
${{\left. {\frac{{d\Delta {{G}_{{{\text{full}}}}}}}{{dW}}} \right|}_{{W = {{W}_{{\max }}}}}} = 0.$Рис. 6.
Качественная зависимость изменения термодинамического потенциала Гиббса от молярного отношения W в больших мицеллах. 1 –зависимость поверхностной энергии частиц от W, 2 – зависимость термодинамического потенциала мицелл от W, 3 – суммарное изменение термодинамического потенциала.

Из уравнений (51) и (52) с учетом того, что NW = const (следует из постоянного суммарного объема растущих частиц), получаем
(53)
${{\mu }_{{\text{S}}}}\left( {{{W}_{0}}} \right) - {{\mu }_{{\text{S}}}}\left( {{{W}_{{\max }}}} \right) = \sigma {{a}_{0}}.$Уравнение (53) позволяет вычислить равновесное значение размера частиц (с помощью уравнения (38)) или установить, что такового не имеется. Зависимость μS(W), входящую в уравнение (53), можно получить из зависимости μW(W) с помощью уравнения (46). Химический потенциал воды μW, в свою очередь, можно найти из давления водяных паров над микроэмульсией в соответствии с формулой μW = kBT ln(p/p0), где p и p0 определены выше, и за точку отсчета химического потенциала воды выбирается чистая вода. Для расчета мы выбрали данные, представленные на рис. 1. Таким образом, для этой системы получаем зависимость химического потенциала AOT от молярного отношения W (рис. 7).
Рис. 7.
Зависимость химического потенциала AOT от молярного отношения W, вычисленная на основе данных рис. 1.

За точку отсчета химического потенциала AOT при этом мы выбрали состояние при W = 50 (максимально возможное значение W для рассматриваемой системы при данной температуре [14, 62]). На рис. 7 видно, что при изменении молярного отношения W от 0.75 до 50 химический потенциал AOT уменьшается на 3.9kВT. Для обратных мицелл на основе AOT a0 ≈ 63 Å2. Отсюда следует, что для рассматриваемой микроэмульсии уравнение (53) не может иметь решений при σ > 26 мДж/м2. Отсутствие решения означает невозможность ограничения роста частиц. При меньших значениях поверхностного натяжения ограничение возможно. При этом равновесный размер оказывается зависящим от поверхностного натяжения (рис. 8) и молярного отношения W0 (рис. 9).
Рис. 8.
Зависимость равновесного молярного отношения Wmax для больших мицелл в бимодальном распределении от поверхностного натяжения частиц σ для значений молярного отношения W0 = 0.75 (1) и 5 (2).
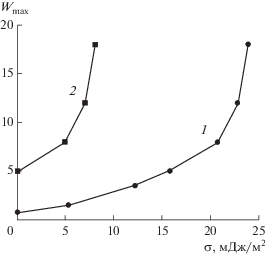
Рис. 9.
Зависимость равновесного молярного отношения Wmax для больших мицелл в бимодальном распределении от молярного отношения W0 для σ = 10 (1), 15 (2) и 20 мДж/м (3).

В пределе нулевого поверхностного натяжения получается, что Wmax = W0. Для каждого значения W0 существует значение поверхностного натяжения, выше которого ограничение роста невозможно. И, наоборот, для каждого значения поверхностного натяжения существует значение W0, выше которого ограничение роста наночастиц невозможно.
Только что мы рассмотрели термодинамический механизм ограничения роста наночастиц в обратных микроэмульсиях, основанный на предположении о том, что минимум свободной энергии системы может соответствовать некоторому конечному размеру частиц. Однако гораздо более вероятным является кинетическое ограничение роста. Рассмотрим один из механизмов роста, при котором реализуется такое ограничение, – коагуляционный механизм [63].
Прежде всего, отметим, что согласно литературным данным коагуляционный механизм роста в обратных мицеллах можно считать установленным для ряда материалов в случае использования AOT в качестве ПАВ. Как правило, кинетика роста наночастиц в обратных мицеллах, по крайней мере, на поздних стадиях является гораздо более медленной, чем та, которая должна была бы быть при быстрой коагуляции, когда слияние частиц не связано с преодолением энергетического барьера. Это означает, что коагуляция должна быть медленной, то есть – с активационным барьером. Есть две причины, приводящие к появлению такого барьера: ДЭС и адсорбция ПАВ на поверхности частиц. Барьер за счет ДЭС больше характерен для водного раствора. Барьер за счет адсорбированных на поверхности частиц молекул ПАВ имеет место при синтезе в обратных мицеллах. Естественно ожидать, что скорость коагуляционного роста частиц в обратных мицеллах зависит от того, насколько плотно на них адсорбировано ПАВ.
Покажем теперь, каким образом при коагуляционном механизме роста молярное отношение W концентраций воды к ПАВ может влиять на размер синтезируемых частиц. Как мы видели выше, химический потенциал ПАВ и, соответственно, его концентрация в неполярной среде в неагрегированном виде, убывают с ростом W. Для случая AOT в качестве ПАВ его концентрация в неагрегированном виде примерно обратно пропорциональна W. В случае если адсорбция не очень близка к максимально возможной, то вполне вероятно, что количество адсорбированного AOT будет пропорционально его концентрации в неагрегированном виде, то есть оно будет обратно пропорционально W. А это означает, что и величина активационного барьера при слиянии частиц будет обратно пропорциональна W. Зависимость величины активационного барьера для двух сферических частиц от их радиусов R1 и R2 можно оценить с помощью приближения Дерягина для случая короткодействующих сил [11]:
где C – некоторая величина, независящая от радиусов R1 и R2. Для случая равных радиусов получаем, что величина активационного барьера прямо пропорциональна радиусу. Строго говоря, коагуляционный рост никогда не заканчивается, но по мере увеличения радиуса частиц активационный барьер, преодолеваемый при их слиянии, возрастает, поэтому рост замедляется: скорость роста экспоненциально падает с увеличением радиуса, зависимость радиуса от времени при этом является логарифмической. Поскольку эксперимент по синтезу частиц, как правило, идет некоторое фиксированное время, не превышающее нескольких суток, то можно говорить о зависимости размера синтезированных частиц от каких-либо параметров синтеза. Из сказанного следует, что фиксированное время синтеза означает фиксированную величину конечного активационного барьера. А поскольку величина этого барьера, по крайней мере, для случая AOT обратно пропорциональна W, то получается, что конечный размер частиц пропорционален W. И действительно, в экспериментах по синтезу наночастиц в обратных мицеллах часто наблюдается линейная зависимость конечного размера частиц от W.НЕПРИМЕНИМОСТЬ УРАВНЕНИЯ ХЕЛФРИХА ДЛЯ ОБЪЯСНЕНИЯ УСТОЙЧИВОСТИ ОБРАТНЫХ МИЦЕЛЛ СФЕРИЧЕСКОЙ ФОРМЫ
Монослой ПАВ на границе фаз вода–масло в обратных микроэмульсиях является плотноупакованным из-за стягивающего межфазного натяжения между водой и маслом. Поэтому площадь, приходящаяся на одну молекулу ПАВ на границе фаз, практически не зависит от состава обратной микроэмульсии и определяется геометрией молекул ПАВ. Из этого следует, что количество ПАВ в обратной микроэмульсии однозначно определяет площадь поверхности раздела вода–масло. При этом эта поверхность ограничивает объем, равный суммарному объему воды в микроэмульсии.
При заданных ограничениях на общий объем и суммарную площадь межфазной поверхности гипотетически возможны самые различные ее пространственные конфигурации. Кроме того, возможно также выделение части воды в отдельную фазу. Однако в действительности реализуется лишь та конфигурация, которая обладает наименьшей свободной энергией. Поэтому для понимания структуры обратных микроэмульсий ключевым является вопрос о том, каким образом и почему свободная энергия системы масло/вода/ПАВ зависит от формы межфазной поверхности и соответственно от формы монослоя ПАВ.
Традиционно для ответа на этот вопрос используется представление о зависимости свободной энергии единицы поверхности от ее кривизны [64–69]. Локальные свойства любой достаточно гладкой поверхности в каждой ее точке могут быть описаны с помощью двух параметров: так называемых главных кривизн с1 = 1/r1 и с2 = 1/r2 (r1 и r2 – главные радиусы кривизны). Мы будем считать кривизну положительной для обратных мицелл (в литературе обычно используется противоположное соглашение о знаке кривизны). Свободную энергию σ единицы поверхности можно разложить по степеням этих параметров с точностью до второго порядка включительно относительно плоской поверхности, для которой с1 = с2 = 0:
(54)
$\begin{gathered} \sigma \left( {{{c}_{1}},{{c}_{2}}} \right) = \sigma \left( {0,0} \right) + \frac{{\partial \sigma \left( {0,0} \right)}}{{\partial {{c}_{1}}}}{{c}_{1}} + \frac{{\partial \sigma \left( {0,0} \right)}}{{\partial {{c}_{2}}}}{{c}_{2}} + \\ + \,\,\frac{1}{2}\frac{{{{\partial }^{2}}\sigma \left( {0,0} \right)}}{{\partial c_{1}^{2}}}c_{1}^{2} + \frac{1}{2}\frac{{{{\partial }^{2}}\sigma \left( {0,0} \right)}}{{\partial c_{2}^{2}}}c_{2}^{2} + \frac{{{{\partial }^{2}}\sigma \left( {0,0} \right)}}{{\partial {{c}_{1}}\partial {{c}_{2}}}}{{c}_{1}}{{c}_{2}}. \\ \end{gathered} $В уравнении (54) в предположении отсутствия выделенных направлений на поверхности в силу симметрии необходимо положить равными коэффициенты перед кривизнами c1 и c2, а также перед их квадратами. Если ввести обозначения
(55)
$\sigma = {{\sigma }_{0}} + \frac{\kappa }{2}{{\left( {{{c}_{1}} + {{c}_{2}} - 2{{c}_{0}}} \right)}^{2}} + \bar {\kappa }{{c}_{1}}{{c}_{2}}.$Приведенное во Введении уравнение (1) является частным случаем уравнения (55) для сферической поверхности. В таком виде эта формула была впервые получена Хелфрихом в работе [12]. Входящие в формулу (55) константы κ и κ̄ называются, соответственно, жесткостью и гауссовой жесткостью поверхности и характеризуют сопротивляемость поверхности деформациям; c0 = 1/rS – так называемая спонтанная кривизна (rS – так называемый радиус спонтанной кривизны). Второе слагаемое в формуле (55) характеризует зависимость поверхностной энергии от средней кривизны (с1 + с2)/2, а третье – от гауссовой кривизны c1c2.
Заметим, что при применении формулы (55) к искривленному монослою ПАВ конечной толщины, возникает проблема, состоящая в том, что в пределах этого монослоя поверхность можно провести различными способами. Эта проблема решается, если учесть, что применение форму-лы (55) подразумевает условие постоянства площади, приходящейся на одну молекулу ПАВ. Та-ким образом, в формуле (55) нужно использовать так называемую поверхность нерастяжения [70, 71], т.е. такую поверхность, площадь сечения молекулы ПАВ которой не изменяется при малых изменениях главных кривизн поверхности. Положение поверхности нерастяжения может зависеть от главных кривизн поверхности [70]. Приближенно можно считать, что поверхность нерастяжения проходит через наиболее “толстые” части молекул ПАВ.
Уравнение (55) можно переписать в виде
(56)
$\begin{gathered} \sigma = {{\sigma }_{0}} + \frac{{2\kappa \bar {\kappa }c_{0}^{2}}}{{2\kappa + \bar {\kappa }}} + \frac{{2\kappa + \bar {\kappa }}}{4}{{\left( {{{c}_{1}} + {{c}_{2}} - \frac{{2{{c}_{0}}}}{{1 + \frac{{\bar {\kappa }}}{{2\kappa }}}}} \right)}^{2}} - \\ - \,\,\frac{{\bar {\kappa }}}{4}{{\left( {{{c}_{2}} - {{c}_{1}}} \right)}^{2}}, \\ \end{gathered} $(57)
${{c}_{1}} = {{c}_{2}} = \frac{{{{c}_{0}}}}{{{{1 + \bar {\kappa }} \mathord{\left/ {\vphantom {{1 + \bar {\kappa }} {\left( {2\kappa } \right)}}} \right. \kern-0em} {\left( {2\kappa } \right)}}}}.$Нетрудно понять, что при с0 ≠ 0 это соответствует сфере [70–73]. Устоявшееся за величиной c0 название спонтанной кривизны является не вполне логичным. Из формулы (57) мы видим, что величина c0 могла бы иметь смысл спонтанной кривизны только при κ̄ = 0, но в этом случае, ввиду равенства нулю последнего слагаемого в формуле (56), не существовало бы минимума свободной энергии поверхности как функции главных кривизн. Частичным оправданием закрепления за величиной c0 названия спонтанной кривизны является только то обстоятельство, что по теореме Гаусса–Бонне интеграл от гауссовой кривизны c1c2 по произвольной замкнутой поверхности Ω зависит только от ее топологии, но не от формы или размеров:
где p – количество несвязанных частей поверхности, g – род поверхности (так называемое в топологии число “ручек” поверхности; например, для тора g = 1). Тогда при нахождении поверхности с фиксированной топологией и минимальной свободной энергией в формуле (55) можно было бы не учитывать гауссову кривизну и соответственно гауссову жесткость κ̄.Если для обратной микроэмульсии ограничиться рассмотрением только сферических обратных мицелл, считая другие формы невозможными, то получится следующая картина. Для обратных мицелл малого размера кривизна монослоя ПАВ является очень высокой. Если привести такую микроэмульсию в контакт с водной фазой, то за счет стремления монослоя ПАВ принять спонтанную кривизну вода будет солюбилизироваться до тех пор, пока либо она не закончится, либо не будет достигнута спонтанная кривизна. В последнем случае образуется двухфазная система типа “обратная микроэмульсия + вода”. Такая трактовка процесса солюбилизации встречается, например, в работах [16, 18, 21, 24].
Однако искусственно ограничиваться рассмотрением лишь сферических обратных мицелл некорректно, поскольку, в принципе, в рамках формулы Хелфриха другие формы могут обладать меньшей свободной энергией. В нашей работе [13] было показано, что это так и есть на самом деле, то есть сферическая форма мицелл в рамках уравнения Хелфриха не соответствует минимуму свободной энергии микроэмульсионной системы.
Были рассмотрены три формы обратных мицелл: сферы, цилиндры и ламеллы, для которых формула (55) принимает следующий вид:
(58)
${{\sigma }_{{{\text{sph}}}}} = {{\sigma }_{0}} + 2\kappa {{\left( {\frac{1}{{{{r}_{0}}}} - \frac{1}{{{{r}_{{\text{S}}}}}}} \right)}^{2}} + \frac{{\bar {\kappa }}}{{r_{0}^{2}}},$(59)
${{\sigma }_{{{\text{cyl}}}}} = {{\sigma }_{0}} + \frac{\kappa }{2}{{\left( {\frac{1}{{{{r}_{0}}}} - \frac{2}{{{{r}_{{\text{S}}}}}}} \right)}^{2}},$Радиус сферических, цилиндрических и ламеллярных обратных мицелл приближенно определяется молярным соотношением W = [вода]/[ПАВ] из геометрических условий, накладываемых на их суммарные объем и площадь. При этом для достаточно больших обратных мицелл, когда можно пренебречь объемом ПАВ, получается следующая формула:
где n = 1, 2 и 3 для ламеллярных, цилиндрических и сферических обратных мицелл соответственно, v – объем одной молекулы воды (30 Å3), a0 – площадь, приходящаяся на одну молекулу ПАВ на границе фаз вода–масло.В соответствии с уравнениями (58), (59), (60), (61), минимизируя свободную энергию при заданном составе с помощью метода общих касательных, можно построить фазовую диаграмму обратной микроэмульсии (рис. 10). На этой фазовой диаграмме для каждого значения κ̄/κ и определенного значения содержания воды в микроэмульсии (т.е. для заданного W) приведены оптимальные формы обратных мицелл. При некоторых значениях состава и отношения κ̄/κ оказывается возможным сосуществование различных форм. При достаточно большом молярном отношении W образуется двухфазная система типа “обратная микроэмульсия со сферическими обратными мицеллами + вода”. На построенной фазовой диаграмме можно выделить три области значений отношения κ̄/κ с качественно различной картиной фаз.
Рис. 10.
Фазовая диаграмма обратной микроэмульсии в соответствии с формулой Хелфриха (66). По горизонтали отложено содержание воды, выраженное в виде отношения rsphere/rS, где rsphere – радиус сферических обратных мицелл, соответствующий гипотетической ситуации, когда есть только сферические обратные мицеллы, и они солюбилизировали всю воду. Соединительные линии для двухфазных систем являются горизонтальными. Под фазами на этом рисунке понимаются, в том числе, и мезофазы трех рассматриваемых форм обратных мицелл в составе одной микроэмульсии.

При –κ̄/κ > 2 свободная энергия единицы поверхности в соответствии с уравнением (56) стремится к минус бесконечности при стремлении главных кривизн к бесконечности, что соответствует сферическим обратным мицеллам минимального размера, условно названных на рис. 10 сухими. Поскольку вода при этом не солюбилизируется, она существует в виде отдельной фазы.
При 0.268 ≈ 2 – 31/2 < –κ̄/κ < 2 по мере увеличения содержания воды имеет место следующая последовательность фазовых переходов: сухие ламеллярные обратные мицеллы + сферические обратные мицеллы → сферические обратные мицеллы → сферические обратные мицеллы + + отдельная водная фаза. Сухие ламеллярные обратные мицеллы получились, с одной стороны, потому, что их свободная энергия не зависит от содержания воды в них, а с другой стороны, потому, что энергетически выгоднее имеющуюся воду использовать для образования сферических обратных мицелл, чем ламеллярных.
При 0 < –κ̄/κ < 2 – 31/2 ≈ 0.268 последовательность фаз такова: сухие ламеллярные обратные мицеллы + цилиндрические обратные мицеллы → → сосуществующие цилиндрические и сферические обратные мицеллы → сферические обратные мицеллы → сферические обратные мицеллы + + отдельная водная фаза.
Полученная таким образом фазовая диаграмма не согласуется с экспериментом. Во-первых, она дает гораздо более узкий диапазон содержания воды, при котором обратные мицеллы являются сферическими. Во-вторых, она предсказывает наличие сухих ламеллярных обратных мицелл при малом содержании воды, что представляется совершенно несоответствующим действительности. Причины, по которым при малом содержании воды в таком расчете возникают ламеллярные мицеллы, можно качественно понять из следующих рассуждений. Если термодинамически возможно образование больших сферических обратных мицелл, то это означает, что спонтанная кривизна монослоя ПАВ c0 близка к нулю. При малой спонтанной кривизне и малом количестве воды образование ламеллярных обратных мицелл энергетически выгоднее, чем сферических, поскольку для первых кривизна ближе к равновесной.
Одной из причин несоответствия полученных по формуле Хелфриха фазовых диаграмм экспериментальным является ошибочное предположение о том, что спонтанная кривизна может быть выражена через первые и вторые производные зависимости свободной энергии от кривизны. Конечно, разложение в ряд Тейлора (54) всегда можно представить в виде (55), но это вовсе не означает, что c0 является спонтанной кривизной, то есть соответствует абсолютному минимуму разлагаемой в ряд функции. По той же причине и при разложении свободной энергии единицы поверхности по главным кривизнам нет большого смысла учитывать квадратичные слагаемые. Таким образом, для произвольной поверхности формула Хелфриха неприменима, но она может быть применима к поверхностям, свободная энергия которых определяется только двумя независимыми физическими параметрами, один из которых дает малый линейный член, а другой – квадратичный. Тогда сумма этих членов будет давать свободную энергию в форме уравнения Хелфриха, которое будет иметь определенный физический смысл, а не являться разложением в ряд Тейлора некоторой произвольной функции. Например, формула Хелфриха верна для симметричного липидного бислоя, для которого она изначально и выводилась [12]. Для такого бислоя существует обеспечивающий устойчивость квадратичный член, связанный с упаковкой алкильных хвостов и наличием ионогенных групп на поверхности. Ввиду симметрии линейный член для симметричного бислоя равен нулю. Если каким-либо образом немного нарушить симметрию, то к свободной энергии добавится небольшой ненулевой линейный член, что приведет к зависимости свободной энергии от кривизны, описываемой формулой Хелфриха. Нарушить симметрию можно, например, создав различные поверхностные плотности заряда по разные стороны бислоя [74]. В отличие от бислоя, для монослоя ПАВ применение формулы Хелфриха совершенно необоснованно. Так, если формально с использованием формулы Хелфриха вычислить радиус спонтанной кривизны монослоя ионогенного ПАВ, рассматривая лишь свободную энергию его ДЭС, то получится некоторая абсурдно малая величина порядка длины дебаевского экранирования вблизи поверхности (несколько ангстрем) [75–77]. Однако на самом деле такая поверхность вообще не имеет никакой спонтанной кривизны, а ее свободная энергия является монотонной функцией средней кривизны.
ВНУТРЕННЕЕ РАСКЛИНИВАЮЩЕЕ ДАВЛЕНИЕ ДЕРЯГИНА
Из сказанного выше можно было бы сделать вывод, что если вместо формулы Хелфриха, выведенной из разложения в ряд Тейлора, использовать некоторую произвольную функцию главных кривизн или увеличить порядок разложения, добавив следующие члены ряда Тейлора, то можно было бы добиться согласия между расчетными фазовыми диаграммами и экспериментальными данными. Однако это не так, поскольку неверно само предположение о том, что свободная энергия микроэмульсии сводится к поверхностному интегралу по границе фаз от некоторой функции главных кривизн. В действительности необходимо учитывать также наличие расклинивающего давления внутри микроэмульсионных капель. Для обратных микроэмульсий ионогенных ПАВ с одновалентным противоионом это расклинивающее давление является положительным и связано с ДЭС, образовавшимся в результате диссоциации ПАВ. На качественном уровне можно считать, что расклинивающее давление возникает в результате перекрытия ДЭС с противоположных сторон обратной мицеллы. Следовательно, результат такого перекрытия зависит главным образом от размера обратной мицеллы. Отсюда, в частности, следует, что свободная энергия ламеллярной обратной мицеллы должна зависеть от ее толщины, что в принципе не может описываться формулой Хелфриха. Неприменимость формулы Хелфриха в случае перекрытия ДЭС в отсутствие фонового электролита обсуждалось также в работах [78, 70 ]. Таким образом, свободная энергия микроэмульсии должна определяться не только поверхностным интегралом от некоторой функции, зависящей от кривизны межфазной границы, но и учитывать некоторым образом расстояние между частями межфазной границы, расположенными противоположно друг другу. Первый из этих вкладов можно условно назвать поверхностным, а второй – объемным.
Фактически, следуя Дерягину, это есть разделение поверхностных сил на силы первого и второго рода [11]. Силы, определяющие расклинивающее давление, Дерягин относил к поверхностным силам второго рода. Хорошо известно, что эта идея разделения поверхностных сил привела к созданию теории агрегативной устойчивости лиофобных дисперсных систем, получившей название теории ДЛФО.
Одновременный учет поверхностного и объемного вкладов позволяет наиболее правильным образом описать зависимость свободной энергии обратной микроэмульсии от формы межфазной границы. Упрощенно это выглядит следующим образом. Объемный вклад обеспечивает стремление обратных мицелл неограниченно увеличивать свой размер за счет солюбилизации воды, а поверхностный вклад определяет наиболее выгодную форму. Так, если свободная энергия монослоя будет уменьшаться с увеличением его кривизны, то можно ожидать, что сферические обратные мицеллы будут более выгодными, чем цилиндрические и ламеллярные. При этом поверхностный вклад в свободную энергию не должен быть слишком большим, чтобы не пересилить объемный вклад, отвечающий за солюбилизацию. Однако это предположение требует тщательной проверки путем проведения соответствующих расчетов и численных оценок с привлечением достоверных экспериментальных данных. Далее будут приведены основные результаты такого расчета свободной энергии микроэмульсионной системы, состоящей из обратных мицелл сферической, цилиндрической или ламеллярной формы, выполненные нами в работе [13].
Будем полагать, что радиус обратных мицелл определяeтся формулой (61), и молярное отношение вода/ПАВ представим в виде
(62)
$W = {{{{N}_{{\text{W}}}}} \mathord{\left/ {\vphantom {{{{N}_{{\text{W}}}}} {{{N}_{{\text{S}}}}}}} \right. \kern-0em} {{{N}_{{\text{S}}}}}},$Уравнение Пуассона при постоянной в пространстве скалярной диэлектрической проницаемости имеет вид
где Δ – оператор Лапласа, а ρ(r) – объемная плотность заряда, связанная с концентрацией противоионов:Напряженность электрического поля определяется градиентом электрического потенциала:
В приближении среднего поля распределение противоионов внутри обратной мицеллы является распределением Больцмана:
где c0 – концентрация противоионов в центре обратной мицеллы. Из уравнений (68), (69) и (71) следует уравнение Пуассона–Больцмана(72)
$\Delta \varphi (r) = \frac{{ - q{{c}_{0}}}}{{\varepsilon {{\varepsilon }_{0}}}}\exp \left( { - \frac{{q\varphi (r)}}{{{{k}_{{\text{B}}}}T}}} \right).$Для рассматриваемых форм обратных мицелл граничное условие для уравнения Пуассона–Больцмана (72) получается по теореме Гаусса (66) с использованием уравнений (64), (65), (67), (70) и имеет следующий вид:
(73)
${{\left. {\frac{{\partial \varphi }}{{\partial r}}} \right|}_{{r = {{r}_{0}}}}} = \frac{{ - q}}{{{{a}_{0}}\varepsilon {{\varepsilon }_{0}}}}.$Потенциал электрического поля без ограничения общности положим равным нулю в центре обратной мицеллы:
Свободная энергия ДЭС складывается из свободной энергии электрического поля
(76)
${{G}_{{{\text{el}}}}} = \frac{{\varepsilon {{\varepsilon }_{0}}}}{2}\int {{{{\left( {\nabla \varphi } \right)}}^{2}}dV} $(77)
${{G}_{{{\text{mix}}}}} = {{k}_{{\text{B}}}}T\int {c(r)\ln \frac{{c(r)}}{{{{c}_{{{\text{ref}}}}}}}dV} ,$(79)
${{c}_{\Omega }} = {{c}_{0}}\exp \left( {\frac{{ - q{{\varphi }_{\Omega }}}}{{{{k}_{{\text{B}}}}T}}} \right),$Подставляя в формулу для свободной энергии смешения (77) выражение для концентрации (71) и учитывая уравнения (79) и (63), получаем:
(80)
$\begin{gathered} {{G}_{{{\text{mix}}}}} = {{k}_{{\text{B}}}}T{{N}_{{\text{S}}}}\ln \frac{{{{c}_{\Omega }}}}{{{{c}_{{{\text{ref}}}}}}} - \\ - \,\,2\left( {\frac{1}{2}\int {c(r)q\varphi (r)dV - \frac{1}{2}q{{\varphi }_{\Omega }}{{N}_{{\text{S}}}}} } \right). \\ \end{gathered} $Из электростатики известно [79], что в уравнении (80) выражение в скобках представляет собой энергию взаимодействия рассматриваемой системы зарядов, причем оно в точности равно энергии электрического поля (76). Поэтому уравнение (80) можно переписать в виде
(81)
${{G}_{{{\text{mix}}}}} = {{k}_{{\text{B}}}}T{{N}_{{\text{S}}}}\ln \frac{{{{c}_{\Omega }}}}{{{{c}_{{{\text{ref}}}}}}} - 2{{G}_{{{\text{el}}}}}.$Из уравнений (81) и (78) получаем, что
(82)
${{G}_{{{\text{PB}}}}} = {{k}_{{\text{B}}}}T{{N}_{{\text{S}}}}\ln \frac{{{{c}_{\Omega }}}}{{{{c}_{{{\text{ref}}}}}}} - {{G}_{{{\text{el}}}}}.$Уравнения Пуассона–Больцмана для сферической, цилиндрической и ламеллярной обратных мицелл имеют один и тот же вид (72), но отличаются только лишь оператором Лапласа. Для всех рассматриваемых форм мицелл в уравнении Пуассона–Больцмана (72) можно осуществить следующую замену переменных:
(84)
$r = \sqrt {\frac{{2\varepsilon {{\varepsilon }_{0}}{{k}_{{\text{B}}}}T}}{{{{c}_{0}}{{q}^{2}}}}} y.$В результате такой замены получится уравнение
Граничные условия (73), (74), (75) в результате замены (83), (84), примут вид
где через y0 обозначено значение y, связанное по формуле (84) с радиусом водного ядра обратной мицеллы r0,(89)
${{y}_{0}} = \sqrt {\frac{{{{c}_{0}}{{q}^{2}}}}{{2\varepsilon {{\varepsilon }_{0}}{{k}_{{\text{B}}}}T}}} {\kern 1pt} {{r}_{0}},$(90)
$z = \frac{{{{q}^{2}}{{r}_{0}}}}{{2{{a}_{0}}\varepsilon {{\varepsilon }_{0}}{{k}_{{\text{B}}}}T}}.$(92)
${{W}_{0}} = \frac{{2{{k}_{{\text{B}}}}Ta_{0}^{2}\varepsilon {{\varepsilon }_{0}}}}{{{{q}^{2}}\text{v}}}.$Для обратных мицелл AOT формула (92) дает W0 = 3. Для концентрации противоионов на границе обратной мицеллы с учетом уравнений (71), (83), (91), (86) и (92) можно записать:
(93)
${{c}_{\Omega }} = \frac{1}{{\text{v}{{W}_{0}}{{{\left( {h{\text{'}}({{y}_{0}})} \right)}}^{2}}}}.$Из уравнений (90), (61) и (92) следует
где введено обозначение $\tilde {W}$ = W/W0, удобное в последующих формулах.Вычислим электростатическую часть свободной энергии ДЭС обратной мицеллы. Согласно уравнению (76) имеем:
(95)
${{G}_{{{\text{el}}}}} = \frac{{\varepsilon {{\varepsilon }_{0}}}}{2}{{A}_{\Omega }}\int\limits_0^{{{r}_{0}}} {{{{\left( {\frac{r}{{{{r}_{0}}}}} \right)}}^{{n\, - \,\,1}}}{{{\left( {\frac{{d\varphi }}{{dr}}} \right)}}^{2}}dr} .$Подставляя (83), (84), (65), (89), (91) и (92) в (95), получаем:
(96)
${{G}_{{{\text{el}}}}} = {{k}_{{\text{B}}}}T{{N}_{{\text{S}}}}\frac{{{{y}_{0}}}}{z}\int\limits_0^{{{y}_{0}}} {{{{\left( {\frac{y}{{{{y}_{0}}}}} \right)}}^{{n\,\, - \,\,1}}}{{{\left( {\frac{{h{\text{'}}}}{h}} \right)}}^{2}}dy} .$Для того чтобы взять интеграл в уравнении (96), можно воспользоваться равенством
которое следует из уравнения (85). При n ≠ 2 равенство (97) позволяет взять интеграл в выражении (96):Выписав необходимые формулы, перейдем к рассмотрению случаев ламеллярной, цилиндрической и сферической обратных мицелл. Для первых двух случаев решения известны [80, 81], но мы получим их заново, чтобы в явном и единообразном виде иметь выражения для свободной энергии мицелл различных форм.
Для ламеллярной обратной мицеллы (n = 1) решение дифференциального уравнения (85) с начальными условиями (87), (88) имеет вид:
Поскольку, согласно определению (83), функция h(y) должна быть положительной, то из уравнения (99) следует, что y < π/2. С учетом (99) и (94) граничное условие (86) приводится к виду
Решение уравнения (100) не выражается в элементарных функциях. Однако можно получить асимптотические решения
(101)
${{y}_{0}} = \frac{\pi }{2}\frac{{\tilde {W}}}{{\tilde {W} + 1}} + o\left( {\frac{1}{{{{{\tilde {W}}}^{2}}}}} \right),\,\,\,\,\tilde {W} \to \infty ,$(102)
${{y}_{0}} = \sqrt {\tilde {W}} \left( {\frac{1}{{{{1 + \tilde {W}} \mathord{\left/ {\vphantom {{1 + \tilde {W}} 6}} \right. \kern-0em} 6}}} + o\left( {\tilde {W}} \right)} \right),\,\,\,\,\tilde {W} \to 0.$Подставляя (99) в (98), можно получить:
(103)
${{G}_{{{\text{el}}}}} = {{k}_{{\text{B}}}}T{{N}_{{\text{S}}}}\left( {1 - {{y}_{0}}{\text{ctg}}{\kern 1pt} {{y}_{0}}} \right).$Подставляя (103) и (93) в уравнение (82) и учитывая (99), получаем выражение для свободной энергии ДЭС ламеллярной обратной мицеллы:
(104)
$\begin{gathered} {{G}_{{{\text{PB}}}}} = {{k}_{{\text{B}}}}T{{N}_{{\text{S}}}}\left( { - \ln \left( {\text{v}{{c}_{{{\text{ref}}}}}{{W}_{0}}} \right) - } \right. \\ \left. { - \,\,2\ln \sin {{y}_{0}} + {{y}_{0}}{\kern 1pt} {\text{ctg }}{{y}_{0}}} \right). \\ \end{gathered} $Уравнение (104) является точным, однако не совсем наглядным, поскольку в него входит y0, которое еще надо выразить через $\tilde {W}$ из трансцендентного уравнения (100). Воспользовавшись асимптотическими решениями (101) и (102), можно записать асимптотические выражения для свободной энергии:
(105)
$\begin{gathered} {{G}_{{{\text{PB}}}}} = {{k}_{{\text{B}}}}T{{N}_{{{\text{ion}}}}}\left( { - \ln \left( {\text{v}{{c}_{{{\text{ref}}}}}{{W}_{0}}} \right){{ + }^{{^{{^{{^{{^{{^{{}}}}}}}}}}}}}} \right. \\ \left. { + \,\,\frac{{{{\pi }^{2}}}}{{4\left( {\tilde {W} + 1} \right)}} + o\left( {\frac{1}{{{{{\tilde {W}}}^{3}}}}} \right)} \right),\,\,\,\,\tilde {W} \to \infty , \\ {{G}_{{{\text{PB}}}}} = {{k}_{{\text{B}}}}T{{N}_{{{\text{ion}}}}}\left( { - \ln \left( {\text{v}{{c}_{{{\text{ref}}}}}{{W}_{0}}} \right) + \ln \left( {\frac{1}{3} + \frac{1}{{\tilde {W}}}} \right) + } \right. \\ \left. {^{{^{{^{{^{{}}}}}}}} + \,\,1 + o\left( {\tilde {W}} \right)} \right),\,\,\,\,\tilde {W} \to 0. \\ \end{gathered} $Заметим, что, дифференцируя асимптотику (105) по расстоянию между монослоями 2r0, можно получить известное уравнение Ленгмюра для расклинивающего давления P [80]:
Для цилиндрической обратной мицеллы (n = 2) решение дифференциального уравнения (85) с начальными условиями (87), (88) имеет вид:
Поскольку функция h(y) должна быть положительной, из уравнения (106) следует, что y < 2. С учетом (106) и (94) граничное условие (86) приводится к уравнению
(107)
${{y}_{0}} = 2{{\left( {1 + {{{\tilde {W}}}^{{ - 1}}}} \right)}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}.$Подставив (106) и (107) в (96), для электростатической части свободной энергии можно получить:
(108)
${{G}_{{{\text{el}}}}} = {{k}_{{\text{B}}}}T{{N}_{{\text{S}}}}\left( {1 - {{{\tilde {W}}}^{{ - 1}}}\ln \left( {1 + \tilde {W}} \right)} \right).$Подставляя (108) и (93) в (82) и учитывая (106) и (107), находим выражение для свободной энергии ДЭС цилиндрической обратной мицеллы:
(109)
$\begin{gathered} {{G}_{{{\text{PB}}}}} = {{k}_{{\text{B}}}}T{{N}_{{\text{S}}}}\left( { - \ln \left( {\text{v}{{c}_{{{\text{ref}}}}}{{W}_{0}}} \right) + } \right. \\ \left. { + \,\,\ln \left( {1 + {{{\tilde {W}}}^{{ - 1}}}} \right) + {{{\tilde {W}}}^{{ - 1}}}\ln \left( {1 + \tilde {W}} \right)} \right). \\ \end{gathered} $Для сферической обратной мицеллы (n = 3) дифференциальное уравнение (85) имеет вид:
Решить уравнение (110) аналитически не удалось, поэтому это было сделано численно. Кроме того, аналитически были получены следующие асимптотики для свободной энергии:
(111)
$\begin{gathered} \frac{{{{G}_{{{\text{PB}}}}}}}{{{{k}_{{\text{B}}}}T{{N}_{{\text{S}}}}}} + \ln \left( {\text{v}{{c}_{{{\text{ref}}}}}{{W}_{0}}} \right) = \frac{{4\ln \left( {3\tilde {W}} \right) - K + 4}}{{3\tilde {W}}} + \\ + \,\,O\left( {\frac{{{{{\ln }}^{2}}\tilde {W}}}{{{{{\tilde {W}}}^{2}}}}} \right),\,\,\,\,\tilde {W} \to \infty , \\ \frac{{{{G}_{{{\text{PB}}}}}}}{{{{k}_{{\text{B}}}}T{{N}_{{\text{S}}}}}} + \ln \left( {\text{v}{{c}_{{{\text{ref}}}}}{{W}_{0}}} \right) = 1 - \ln \left( {\tilde {W}} \right) + \\ + \,\,\frac{{3\tilde {W}}}{5} + O\left( {{{{\tilde {W}}}^{2}}} \right),\,\,\,\,\tilde {W} \to 0, \\ \end{gathered} $(112)
$\begin{gathered} \frac{{{{G}_{{{\text{PB}}}}}}}{{{{k}_{{\text{B}}}}T{{N}_{{\text{S}}}}}} + \ln \left( {\text{v}{{c}_{{{\text{ref}}}}}{{W}_{0}}} \right) = \ln \left( {1 + \frac{{1.48371699}}{{\tilde {W}}}} \right) + \\ + \,\,\frac{{4\ln \left( {{\text{1}} + {\text{0}}{\text{.45408719}}\tilde {W}} \right)}}{{3\tilde {W}}}, \\ \end{gathered} $Численные расчеты зависимости свободной энергии ДЭС обратных мицелл различных форм от W по формулам (104), (109) и (112) показали, что свободная энергия для каждого фиксированного значения W возрастает в ряду ламеллы–цилиндры–сферы. Таким образом, самыми энергетически выгодными являются ламеллярные обратные мицеллы, и для них зависимость свободной энергии ДЭС от молярного отношения W весьма существенна. Эту зависимость свободной энергии ДЭС для ламеллярной обратной мицеллы и можно считать тем самым объемным вкладом, о котором говорилось ранее.
Для того, чтобы нагляднее представить соотношение свободных энергий мицелл разной формы, на рис. 11 показаны зависимости их разностей для сферической и ламеллярной и цилиндрической и ламеллярной мицелл, а на рис. 12 – отношение этих разностей.
Рис. 11.
Разности значений свободной энергии ДЭС сферической и ламеллярной мицелл (кривая 1) и цилиндрической и ламеллярной мицелл (кривая 2).

Рис. 12.
Отношение вклада кривизны в свободную энергию для сферических и цилиндрических обратных мицелл.

Отметим, что с точки зрения качественного понимания полученные зависимости свободной энергии ДЭС обратной мицеллы можно трактовать как результат стремления противоионов раствориться в как можно большем количестве воды. Для ламеллярных обратных мицелл это происходит за счет увеличения расстояния между противолежащими монослоями. Для цилиндрических или сферических обратных мицелл по сравнению с ламеллярными кривизна монослоя ведет к эффективному уменьшению доступного объема для противоионов, сосредоточенных вблизи поверхности, что, в свою очередь, ведет к возрастанию свободной энергии по сравнению со случаем ламеллярных обратных мицелл.
Представленные на рис. 11 и 12 зависимости позволяют более наглядно выделить влияние кривизны на свободную энергию ДЭС. На рис. 11 видно, что разности свободных энергий примерно пропорциональны, а на рис. 12 видно, что для больших $\tilde {W}$ (примерно, начиная с $\tilde {W}$ = 2) отношение вкладов кривизны в свободную энергию для сферических и цилиндрических обратных мицелл равно 4/3. Это значение согласуется с разложением свободной энергии по степеням кривизны (54), оборванным на линейных членах:
(113)
$\sigma \left( {{{c}_{1}},{{c}_{2}}} \right) = \sigma \left( {0,0} \right) + \frac{{\partial \sigma \left( {0,0} \right)}}{{\partial {{c}_{1}}}}\left( {{{c}_{1}} + {{c}_{2}}} \right).$Действительно, в соответствии с формулой (61) для отношения свободных энергий сферической и цилиндрической обратных мицелл в этом случае имеем:
(114)
$\frac{{\frac{1}{{{{r}_{{{\text{sphere}}}}}}} + \frac{1}{{{{r}_{{{\text{sphere}}}}}}}}}{{\frac{1}{{{{r}_{{{\text{cylinder}}}}}}} + \frac{1}{\infty }}} = 2\frac{{{{r}_{{{\text{cylinder}}}}}}}{{{{r}_{{{\text{sphere}}}}}}} = 2\frac{{{{2\text{v}W} \mathord{\left/ {\vphantom {{2\text{v}W} {{{a}_{0}}}}} \right. \kern-0em} {{{a}_{0}}}}}}{{{{3\text{v}W} \mathord{\left/ {\vphantom {{3\text{v}W} {{{a}_{0}}}}} \right. \kern-0em} {{{a}_{0}}}}}} = \frac{4}{3}.$Отношение (114) следует также из выражений для свободной энергии ДЭС цилиндрической и сферической обратных мицелл (109) и (111). Та-ким образом, с некоторой точностью можно разложить свободную энергию ДЭС обратной мицеллы на объемную и поверхностную части. Однако, несмотря на выполнение соотношения (114), для поверхностной части понятие о зависимости свободной энергии от кривизны работает не в полной мере: коэффициент перед c1 + c2 в уравнении (113) оказывается непостоянным. В соответствии с уравнениями (109) и (111) он логарифмически возрастает с увеличением $\tilde {W}$:
(115)
$\frac{{\partial \sigma \left( {0,0} \right)}}{{\partial {{c}_{1}}}} = 2{{k}_{{\text{B}}}}T{{W}_{0}}\ln (\tilde {W}),\,\,\,\,\tilde {W} \to \infty .$К похожему выводу о зависимости константы жесткости от соотношения вода/ПАВ пришли также в работах [77, 82–84] при рассмотрении ундулирующих мембран в ламеллярных фазах. Это важно отметить, поскольку существует ряд работ [72, 74–76, 85], где вычисляются константы жесткости заряженных мембран и монослоев в избытке электролита, когда расклинивающее давление экранируется и, соответственно, не возникает зависимостей, подобных (115).
Представленные выше формулы для ДЭС позволяют проверить, может ли равновесная площадь a0, приходящаяся на одну молекулу ионогенного ПАВ в его монослое, определяться балансом сил межфазного натяжения γ на границе вода–масло и сил электростатического отталкивания одноименно заряженных полярных групп молекул ПАВ:
(116)
${{\left( {\frac{{\partial \left( {{{G}_{{{\text{PB}}}}} + \gamma {{A}_{\Omega }}} \right)}}{{\partial {{a}_{0}}}}} \right)}_{{{{N}_{{\text{W}}}},\,\,{{N}_{{\text{S}}}}}}} = 0.$Можно показать (см. [81] или дополнительные материалы к [13]), что уравнение для нахождения a0 (116) преобразуется к более простому виду:
Уравнение (117) также непосредственно следует из того, что связанное с ДЭС поверхностное давление равно удвоенной электростатической свободной энергии ДЭС в расчете на единицу поверхности [86].
Для всех трех форм обратных мицелл Gel < < kBTNS, поэтому с учетом уравнений (117) и (65) следует, что a0 < 2kBT/γ ≈ 16 Å2 (здесь для оценки использовано характерное значение межфазного натяжения вода–масло 50 мДж/м2 [87]). В реальности площадь a0 существенно больше 16 Å2 (для AOT a0 = 63 Å2 [27]), поэтому можно сделать вывод, что исходная предпосылка (116) о том, что равновесная площадь a0 определяется балансом электростатических сил и сил межфазного натяжения, неверна. На самом деле эта площадь определяется упаковкой молекул ПАВ в монослое.
Таким образом, мы приходим к выводу, что объяснить устойчивость сферической формы обратных мицелл в сколь-нибудь широком диапазоне молярных отношений вода/ПАВ не удается ни в рамках уравнения Хелфриха, ни на основе внутреннего расклинивающего давления Дерягина, учитывая лишь свободную энергию ДЭС. Однако можно предположить, что одновременный учет и кривизны, и ДЭС позволит объяснить сферическую форму обратных мицелл.
Действительно, предположим, что свободная энергия монослоя ПАВ уменьшается с увеличением его средней кривизны. Ограничимся простейшим случаем линейной зависимости (113) с коэффициентом перед c1 + c2, равным –k0. Тогда, при достаточной силе этой зависимости, добавление ее к свободной энергии ДЭС может изменить соотношение между свободными энергиями различных форм, сделав более выгодными сферические обратные мицеллы. То есть, внутренняя зависимость свободной энергии монослоя ПАВ от кривизны как бы компенсирует и пересиливает ту зависимость от кривизны, которая связана с ДЭС. Однако необходимо учитывать, что зависимость от кривизны, связанная с ДЭС, эффективно характеризуется переменной константой (115), возрастающей с $\tilde {W}$. Это означает, что при фиксированном k0 всегда найдется такое значение $\tilde {W}$, выше которого компенсация невозможна и более выгодными являются ламеллярные мицеллы. Таким образом, при k0 = 0 наиболее выгодны ламеллярные обратные мицеллы, при достаточно большом k0 наиболее выгодны сферические обратные мицеллы вплоть до определенного $\tilde {W} = {{\tilde {W}}_{0}}$ и ламеллярные – при большем $\tilde {W}$. При этом с ростом k0 значение ${{\tilde {W}}_{0}}$ должно возрастать. На самом деле, при более строгом рассмотрении, резкого перехода от сфер к ламеллам не будет – будет некоторая переходная область сосуществования мицелл двух форм, количества которых определяются методом общей касательной к свободным энергиям. Переход к ламеллярным структурам при больших молярных отношениях вода/ПАВ, действительно, имеет место для обратных мицелл AOT [88].
Описанный здесь механизм, допускающий существование сферических обратных мицелл, как оптимальной геометрии монослоя ПАВ в обратной микроэмульсии, может быть качественно получен при комбинации объемного и поверхностного вкладов в свободную энергию обратной микроэмульсии. Объемный вклад, представляющий собой свободную энергию ламеллярной обратной мицеллы, обеспечивает солюбилизацию воды, а поверхностный вклад, формирующийся частично за счет ДЭС и частично за счет внутренних сил в монослое ПАВ, отвечает за оптимальную форму обратных мицелл.
Заметим, что здесь мы в качестве возможных альтернативных форм обратных мицелл рассматривали лишь сферы, цилиндры и ламеллы – максимально симметричные формы с точки зрения эквивалентности всех точек поверхности. Заранее не очевидно, ведет ли асимметрия к увеличению свободной энергии. В недавней работе [89] мы провели численные расчеты свободной энергии обратной мицеллы в форме вытянутого эллипсоида вращения. Анализ решения уравнения Пуассона–Больцмана для этой формы позволил сделать вывод, что неэквивалентность точек поверхности обратной мицеллы должна приводить к росту свободной энергии и, следовательно, к термодинамической невыгодности несимметричных форм. Отсюда следует, что в нашем анализе обратных микроэмульсий достаточно рассматривать лишь симметричные формы.
Рассмотрим более детальную модель строения обратной мицеллы. Первое уточнение касается локализации в водном ядре обратной мицеллы отрицательных зарядов молекул ПАВ. Поскольку бо'льшая часть противоионов сосредоточена именно вблизи этих зарядов, представляется целесообразным более точно рассмотреть строение ДЭС в этой области. Для этого, прежде всего, необходимо заметить, что отрицательные заряды диссоциированных молекул ПАВ не могут находиться строго на границе водного ядра: они должны быть погружены в него на некоторую глубину, по крайней мере, из-за сил электростатического изображения, стремящихся оттолкнуть заряд в сторону среды с большей диэлектрической проницаемостью. При погружении отрицательных зарядов вглубь водного ядра можно ожидать, как минимум, двух эффектов. Во-первых, при этом поверхностная плотность зарядов перестает быть постоянной и начинает зависеть от радиуса мицеллы. Во-вторых, ДЭС теперь становится двухсторонним: противоионы распределяются и внутри, и снаружи поверхности отрицательных зарядов. Для рассматриваемых в данной работе обратных мицелл AOT глубина “залегания” отрицательных зарядов в водном ядре (2.3 Å) определена из результатов молекулярно-динамических расчетов, проведенных в работах [34, 90]. Отрицательные заряды диссоциированной молекулы AOT расположены главным образом на трех кислородах сульфогруппы, размер которой и определяет глубину их залегания.
Второе уточнение касается связи радиуса водного ядра обратной мицеллы с молярным соотношением воды и ПАВ W. Экспериментально установлено, что эта зависимость является линейной [7, 33]. При этом эта линейная зависимость обычно интерпретируется [27, 91–93] в рамках следующей формулы:
(118)
${{r}_{0}} = \frac{{n\text{v}}}{{{{a}_{0}}}}W + \frac{{n{{\text{v}}_{{\text{H}}}}}}{{{{a}_{0}}}},$(119)
${{r}_{{{\text{inext}}}}} = \frac{{n\text{v}}}{{{{a}_{0}}}}W + \frac{{n\left( {{{\text{v}}_{{{\text{H1}}}}} + {{\text{v}}_{{{\text{H2}}}}}} \right)}}{{{{a}_{0}}}}.$Расстояние между поверхностью нерастяжения и границей полярного ядра примерно равно vH2/a0. Вычитая это расстояние из радиуса поверхности нерастяжения (119), получаем следующую формулу для радиуса полярного ядра:
(120)
${{r}_{0}} = \frac{{n\text{v}}}{{{{a}_{0}}}}W + \frac{{n{{\text{v}}_{{{\text{H1}}}}} + \left( {n - 1} \right){{\text{v}}_{{{\text{H2}}}}}}}{{{{a}_{0}}}},$Не вызывает сомнений, что сульфогруппа находится в воде ввиду своей ионогенности, а этилгексильные хвосты в ней не находятся ввиду своей гидрофобности. Спорным является вопрос о местонахождении промежуточных атомов. Заметим, что они структурно похожи на пару молекул метилацетата, растворимость которого в воде составляет всего 25 мас. % [94]. Если бы эти промежуточные атомы находились в водном ядре, то в соответствии с данным значением растворимости их массовая доля в приповерхностном слое должна была бы быть не более 25%, но это несовместимо с упаковкой этих промежуточных атомов. Действительно, объем указанных атомов в молекуле АОТ составляет примерно 200 Å3. Если бы эти атомы были в воде, то в соответствии с указанным значением растворимости на одну молекулу ПАВ приходился бы объем 200 Å3/0.25 = = 800 Å3 раствора, но такой объем при площади на одну молекулу ПАВ 63 Å2 имел бы длину 13 Å, что слишком много для указанной группы атомов. Это означает, что эти промежуточные атомы не могут находиться в водном ядре, но должны располагаться на его поверхности.
Таким образом, полярной группой молекулы AOT является сульфогруппа вместе с противоионом. Объем, приходящийся на эти атомы, можно оценить как 62 Å3 в приближении плотной упаковки, исходя из плотности и молярной массы дигидрата дитионата натрия (SO3Na)2 · 2H2O (242 г/моль, 2.19 г/см3) [94]. Теперь величина vH2 в формуле (120) может быть оценена как (222 – 62) × × 3/(3 – 1) Å3 = 240 Å3. Отсюда следует, что поверхность нерастяжения находится на расстоянии vH2/a0 = 3.8 Å от поверхности полярного ядра.
Несовпадение поверхности нерастяжения и границы полярного ядра имеет очень большое значение для энергетики обратных мицелл, поскольку оно приводит к зависимости площади полярного ядра в расчете на одну молекулу ПАВ от размера мицеллы. Действительно, если эта площадь не является постоянной, то в зависимости свободной энергии мицеллы от размера должен появиться член, учитывающий межфазное натяжение на поверхности полярного ядра (γcore):
(121)
${{G}_{{{\text{full}}}}} = {{G}_{{{\text{PB}}}}} + {{\gamma }_{{{\text{core}}}}}{{A}_{\Omega }},$В моделях обратных мицелл, описываемых формулами (61) и (118), площадь поверхности полярного ядра в расчете на одну молекулу ПАВ была постоянной, поэтому в учете межфазного натяжения не было необходимости.
Заметим, что в полную свободную энергию обратной мицеллы (121) мы не включаем свободную энергию смешения обратных мицелл с неполярным растворителем, которой на самом деле можно пренебречь.
Схематически уточненная модель обратной мицеллы показана на рис. 13. Глядя на этот рисунок, баланс сил в обратной мицелле можно качественно представить, рассматривая две соседние молекулы ПАВ как две палочки, шарнирно связанные в месте контакта на поверхности нерастяжения. Угол, образуемый этими палочками, зависит от кривизны поверхности и, соответственно, от размера мицеллы. На эти палочки действуют стягивающие силы межфазного натяжения и расталкивающие силы между отрицательными зарядами. Эти силы в какой-то степени скомпенсированы и приводят в конечном итоге к зависимости свободной энергии монослоя ПАВ от его кривизны. Заметим, что в этой модели только стягивающие силы межфазного натяжения способствуют образованию сферических обратных мицелл, поскольку среди всех рассматриваемых форм сфера обладает при заданном W максимальной кривизной поверхности и, соответственно, минимальной площадью межфазной поверхности. Без межфазного натяжения сферические обратные мицеллы не могли бы быть устойчивыми.
Рис. 13.
Уточненная модель обратной мицеллы AOT. На границе полярного ядра действует стягивающее межфазное натяжение. В окрестности поверхности отрицательных зарядов действуют электростатические силы отталкивания между полярными головными группами молекул ПАВ. На поверхности нерастяжения, обозначенной штриховой линией, площадь сечения молекулы ПАВ не зависит от размера мицеллы.

В действительности, на зависимость свободной энергии монослоя ПАВ от его кривизны, помимо межфазного натяжения и ДЭС, могут влиять и другие факторы, которые мы не будем учитывать, полагая их для обратных мицелл AOT несущественными.
Например, такое влияние может оказывать изменение упаковки неполярных хвостов молекул ПАВ с изменением кривизны монослоя [71, 95]. Этот фактор не может быть слишком существенным по следующим соображениям. Примерно посередине неполярных хвостов (на расстоянии 3.8 Å от поверхности полярного ядра) проходит поверхность нерастяжения, где упаковка с изменением кривизны не меняется. Концы же неполярных хвостов находятся от поверхности нерастяжения на расстояниях 3.8 Å и примерно 6 Å. Поскольку эти расстояния, по крайней мере, при W > 10 много меньше радиуса кривизны монослоя ПАВ, то и упаковка на концах неполярных хвостов не может существенно изменяться.
Также на зависимость свободной энергии монослоя ПАВ от его кривизны может влиять межфазное натяжение на внешней границе обратной мицеллы – между неполярной оболочкой и растворителем. Однако устойчивость обратных мицелл к агрегации подразумевает использование хорошего растворителя, для которого это межфазное натяжение должно быть очень малым.
Для численного расчета свободной энергии обратных мицелл AOT более-менее точно известны все необходимые параметры, кроме одного – межфазной энергии на поверхности полярного ядра. Таким образом, этот параметр является свободным и должен подбираться таким образом, чтобы удовлетворить экспериментальным данным. Тем не менее, можно оценить допустимый диапазон его изменения, учтя, что фрагменты молекулы ПАВ, находящиеся над поверхностью полярного ядра, похожи на молекулы метилацетата или этилацетата. Известно, что межфазное натяжение в системе вода–этилацетат составляет 6.8 мДж/м2, а в системе вода–алкан – 50 мДж/м2 [87]. Интересующее нас межфазное натяжение в обратных мицеллах AOT должно лежать между этими значениями. Перебор значений этого параметра показал, что близким к оптимальному с точки зрения совпадения с экспериментом (сферические мицеллы при W примерно меньше ста) является значение 22 мДж/м2. Для этого межфазного натяжения сравнение свободных энергий обратных мицелл различной геометрии показано на рис. 14. Видно, что при малых W устойчивы сферические обратные мицеллы, а при больших – ламеллярные. Как ведет себя свободная энергия мицелл для других значений межфазного натяжения, можно увидеть на рис. 15 и 16.
Рис. 14.
Сравнение свободных энергий для трех форм обратных мицелл при межфазном натяжении полярного ядра 22 мДж/м2. Видно, что сферические обратные мицеллы устойчивы при W < 48 (область I), ламеллярные – при W > 83 (область III). При промежуточных значениях W сосуществуют сферические и ламеллярные мицеллы (область II). Область сосуществования определяется общей касательной к зависимостям свободной энергии от состава фаз.

Рис. 15.
Сравнение свободных энергий для трех форм обратных мицелл при межфазном натяжении полярного ядра 15 мДж/м2. Сферические обратные мицеллы устойчивы при W < 3 (область I), цилиндрические – при 3 < W < 14 (область II), ламеллярные – при W > 19 (область IV). При 14 < W < 19 сосуществуют цилиндрические и ламеллярные мицеллы (область III). Если в данном расчете энергия цилиндрической мицеллы лишь не на много (~ 0.01kBT в расчете на молекулу ПАВ) меньше, чем сферической, то из-за энтропии трансляционного движения мицелл выгоднее может оказаться все же сферическая геометрия. Из-за малой разницы в значениях свободной энергии цилиндрических и сферических обратных мицелл переходная область между ними не показана.

Рис. 16.
Сравнение свободных энергий для трех форм обратных мицелл при межфазном натяжении полярного ядра 26 мДж/м2. Видно, что устойчивы только сферические обратные мицеллы, причем только при W < 9 (при дальнейшем увеличении W свободная энергия возрастает, что означает невыгодность процесса солюбилизации воды, при W > 9 здесь образовалась бы двухфазная система).

Итак, в соответствии с рис. 14, результаты моделирования говорят о том, что при определенных параметрах модели могут быть устойчивыми сферические обратные мицеллы. В этом случае моделирование предсказывает переход к ламеллярным мицеллам при больших молярных отношениях воды и ПАВ W. Экспериментально такая картина наблюдается для обратных микроэмульсий на основе очищенного AOT [14, 88, 96, 97].
В рамках сформулированной выше модели обратных мицелл AOT можно находить различные термодинамические характеристики обратной микроэмульсии. Так, представленные на рис. 14 данные позволяют вычислить химические потенциалы воды (μW) и ПАВ (μS) для обратных мицелл различной геометрии. Это можно сделать с помощью следующих формул:
Рис. 17.
Зависимость химического потенциала воды от молярного отношения W для сферических, цилиндрических и ламеллярных обратных мицелл AOT в соответствии с данными рис. 8.

Рис. 18.
Зависимость химического потенциала ПАВ от молярного отношения W для сферических, цилиндрических и ламеллярных обратных мицелл AOT в соответствии с данными рис. 8.

В рамках описанной модели обратных мицелл можно вычислить зависимость от W энтальпии солюбилизации (ΔHfull) воды раствором AOT в масле. В соответствии с уравнением Гиббса–Гельмгольца имеем:
(122)
$\Delta {{H}_{{{\text{full}}}}} = {{G}_{{{\text{full}}}}} - T{{\left( {\frac{{\partial {{G}_{{{\text{full}}}}}}}{{\partial T}}} \right)}_{P}}.$При расчете энтальпии солюбилизации по формуле (122) необходимо учесть, что диэлектрическая проницаемость воды сильно зависит от температуры. При 298.15 K из справочных данных имеем [94]:
Также необходимо учесть зависимость межфазного натяжения от температуры. Для межфазной границы вода/н-алкан (от гексана до додекана) при 298.15 K имеем [98]:
В нашем случае, строго говоря, полярное ядро не граничит с чистым н-алканом. Однако, тем не менее, межфазное натяжение на границе полярного ядра (22 мДж/м2) определяется главным образом именно контактами между водой и алкановыми фрагментами молекул AOT. Поэтому равенство (124) можно считать применимым в нашем случае. Кроме того, при расчете энтальпии оно входит в результат лишь как поправка к собственно межфазному натяжению. Результаты расчета в соответствии с формулами (122), (123) и (124) вместе с литературными экспериментальными данными [99, 100] представлены на рис. 19.
ЗАКЛЮЧЕНИЕ
В результате проведенных нами исследований разработана теория флуктуаций состава обратных мицелл. Выведены уравнения, связывающие параметры флуктуаций количеств молекул воды и ПАВ в обратной мицелле с зависимостью давления насыщенных водяных паров над поверхностью микроэмульсии от молярного отношения вода/ПАВ и с зависимостью среднего состава обратной мицеллы от концентраций воды и ПАВ [27].
Выведено уравнение, определяющее равновесный размер стабилизируемых в обратных мицеллах наночастиц в зависимости от жесткости мицеллярных оболочек и удельной поверхностной энергии наночастиц. Согласно этому уравнению в обратных микроэмульсиях АОТ стабилизация наночастиц невозможна, если их удельная поверхностная энергия превышает 30 мДж/м2. При меньших значениях удельной поверхностной энергии стабилизация возможна, но размер частиц, образующихся в таких микроэмульсиях, существенно превышает размер обратных мицелл [101].
Проведен анализ различных механизмов стабилизации наночастиц в обратных микроэмульсиях. Предложен коагуляционный механизм роста частиц в обратных микроэмульсиях, учитывающий адсорбцию ПАВ на поверхности частиц и зависимость энергии активации процесса коагуляции от радиуса частиц в приближении Дерягина. Показано, что молярное отношение вода/ПАВ влияет на величину адсорбции, и это приводит к зависимости размера синтезируемых частиц от этого отношения [63].
Показано, что при вычислении свободной энергии обратных микроэмульсий на основе AOT необходимо в первую очередь учитывать ДЭС, межфазное натяжение на границе полярного ядра и несовпадение границы полярного ядра с поверхностью нерастяжения. Этого, по крайней мере, на качественном уровне достаточно для описания основных свойств обратной микроэмульсии: оптимальной формы обратных мицелл, химических потенциалов воды и ПАВ, полидисперсности мицелл, энтальпии солюбилизации, фазовой диаграммы (в том числе в присутствии соли).
Важным является то обстоятельство, что вклад ДЭС в свободную энергию является ключевым и при этом принципиально не может быть интерпретирован в рамках формулы Хелфриха, традиционно применяемой для описания обратных микроэмульсий, в том числе и на основе AOT. Это означает, что многие результаты относительно обратных микроэмульсий AOT, полученные с использованием формулы Хелфриха, должны быть пересмотрены.
В заключение отметим, что при рассмотрении ДЭС предполагалась полная диссоциация ПАВ. В принципе, при тех высоких концентрациях противоионов, которые имеют место вблизи границы полярного ядра, диссоциация может быть неполной и зависеть от размера обратной мицеллы. Нам не удалось найти в литературе соответствующей количественной информации, применимой к обратным мицеллам AOT. Однако поскольку расчеты, проведенные без учета неполной диссоциации, привели к количественно более-менее верным результатам, то можно предположить, что диссоциация AOT близка к полной.
ФИНАНСИРОВАНИЕ РАБОТЫ
Работа выполнена по теме государственного задания (номер государственной регистрации 0089-2019-0003) и при финансовой поддержке Министерства образования и науки РФ по Программе повышения конкурентоспособности МФТИ “5–100” среди ведущих мировых научно-образовательных центров на 2016–2020 гг. (Соглашение № 074-02-2018-286).
Список литературы
Mattoon R.W., Mathews M.B. // J. Chem. Phys. 1949. V. 17. P. 497.
Mathews M.B., Hirschhorn E. // J. Colloid Sci. 1953. V. 8. P. 86.
Schulman J.H., Stoeckenius W., Prince L.M. // J. Phys. Chem. 1959. V. 63. P. 1677.
Cabos P.C., Delord P. // J. Appl. Cryst. 1979. V. 12. P. 502.
Day R.A., Robinson B.H., Clarke J.H.R., Doherty J.V. // J. Chem. Soc. Faraday Trans. 1. 1979. V. 75. P. 132.
Zulauf M., Eicke H.F. // J. Phys. Chem. 1979. V. 83. P. 480.
Kotlarchyk M., Chen S.H., Huang J.S. // J. Phys. Chem. 1982. V. 86. P. 3273.
Boutonnet M., Kizling J., Stenius P., Maire G. // Colloids Surf. 1982. V. 5. P. 209.
Fendler J.H. // Chem. Rev. 1987. V. 87. P. 877.
Товстун С.А., Разумов В.Ф. // Успехи химии. 2011. Т. 80. С. 996.
Дерягин Б.В., Чураев Н.В., Муллер В.М. Поверхностные силы. М.: Наука, 1985.
Helfrich W. // Z. Naturforsch. C. 1973. V. 28. P. 693.
Tovstun S.A., Razumov V.F. // Colloid Polym. Sci. 2015. V. 293. P. 165.
Fletcher P.D.I., Howe A.M., Robinson B.H. // J. Chem. Soc., Faraday Trans. 1. 1987. V. 83. P. 985.
Rička J., Borkovec M., Hofmeier U. // J. Chem. Phys. 1991. V. 94. P. 8503.
Eriksson J.C., Ljunggren S. // Progr. Colloid Polym. Sci. 1990. V. 81. P. 41.
Safran S.A. // J. Chem. Phys. 1983. V. 78. P. 2073.
Borkovec M. // J. Chem. Phys. 1989. V. 91. P. 6268.
Borkovec M., Eicke H.F., Ricka J. // J. Colloid Interface Sci. 1989. V. 131. P. 366.
Borkovec M., Eicke H.F. // Chem. Phys. Lett. 1989. V. 157. P. 457.
Eriksson J.C., Ljunggren S. // Langmuir. 1995. V. 11. № 4. P. 1145.
Eriksson J.C., Ljunggren S., Kegel W.K., Lekkerkerker H.N.W. // Colloids Surf. A. 2001. V. 183–185. P. 347.
De Gennes P.G., Taupin C. // J. Phys. Chem. 1982. V. 86. P. 2294.
Borkovec M. // Adv. Colloid Interface Sci. 1992. V. 37. P. 195.
Overbeek J.T.G. // Progr. Colloid Polym. Sci. 1990. V. 83. P. 1.
Kegel W.K., Overbeek J.T.G., Lekkerkerker H.N.W. // Handbook of Microemulsions Science and Technology / Ed. by Kumar P., Mittal K.L. New York: Marcel Dekker, 1999. P. 13.
Tovstun S.A., Razumov V.F. // J. Colloid Interface Sci. 2010. V. 351. P. 485.
Menger F.M., Donohue J.A., Williams R.F. // J. Am. Chem. Soc. 1973. V. 95. P. 286.
Eicke H.F., Rehak J. // Helv. Chim. Acta. 1976. V. 59. P. 2883.
Lang J., Jada A., Malliaris A. // J. Phys. Chem. 1988. V. 92. P. 1946.
Ueda M., Schelly Z.A. // J. Colloid Interface Sci. 1988. V. 124. P. 673.
Ueda M., Schelly Z.A. // Langmuir. 1988. V. 4. P. 653.
Amararene A., Gindre M., Le Huérou J.Y., Urbach W., Valdez D., Waks M. // Phys. Rev. E. 2000. V. 61. P. 682.
Nevidimov A.V., Razumov V.F. // Mol. Phys. 2009. V. 107. P. 2169.
Peri J.B. // J. Colloid Interface Sci. 1969. V. 29. P. 6.
Kon-No K., Kitahara A. // J. Colloid Interface Sci. 1971. V. 35. P. 636.
Kotlarchyk M., Huang J.S., Chen S.H. // J. Phys. Chem. 1985. V. 89. P. 4382.
Robinson B.H., Toprakcioglu C., Dore J.C., Chieux P. // J. Chem. Soc. Faraday Trans. 1. 1984. V. 80. P. 13.
Kotlarchyk M., Stephens R.B., Huang J.S. // J. Phys. Chem. 1988. V. 92. P. 1533.
Nicholson J.D., Clarke J.H.R. // Surfactants in Solutions, V. 3 / Ed. by Mittal K.L., Lindman B. New York: Plenum Press, 1984. P. 1663.
Kitahara A., Ishikawa T., Tanimori S. // J. Colloid Interface Sci. 1967. V. 23. P. 243.
Kon-No K., Kitahara A. // J. Colloid Interface Sci. 1971. V. 35. P. 409.
Kon-No K., Kitahara A. // J. Colloid Interface Sci. 1972. V. 41. № 1. P. 86.
Kubik R., Eicke H.F., Jönsson B. // Helv. Chim. Acta. 1982. V. 65. P. 170.
Chew C.H., Wong M.K. // J. Dispersion. Sci. Technol. 1991. V. 12. P. 495.
Kotlarchyk M., Chen S.H., Huang J.S., Kim M.W. // Phys. Rev. A. 1984. V. 29. P. 2054.
Huang J.S. // J. Chem. Phys. 1985. V. 82. P. 480.
Assih T., Larché F., Delord P. // J. Colloid Interface Sci. 1982. V. 89. P. 35.
Lemyre J.L., Lamarre S., Beaupré A., Ritcey A.M. // Langmuir. 2010. V. 26. P. 10524.
Chatenay D., Urbach W., Nicot C., Vacher M., Waks M. // J. Phys. Chem. 1987. V. 91. P. 2198.
Cassin G., Illy S., Pileni M.P. // Chem. Phys. Lett. 1994. V. 221. P. 205.
Jain T.K., Cassin G., Badiali J.P., Pileni M.P. // Langmuir. 1996. V. 12. P. 2408.
Eastoe J., Hollamby M.J., Hudson L. // Adv. Colloid Interface Sci. 2006. V. 128–130. P. 5.
Pillai V., Kumar P., Hou M.J., Ayyub P., Shah D.O. // Adv. Colloid Interface Sci. 1995. V. 55. P. 241.
Khiew P.S., Radiman S., Huang N.M., Soot Ahmad Md. // J. Cryst. Growth. 2003. V. 254. P. 235.
Holmberg K. // J. Colloid Interface Sci. 2004. V. 274. P. 355.
Uskoković V., Drofenik M. // Adv. Colloid Interface Sci. 2007. V. 133. P. 23.
Gobe M., Kon-No K., Kandori K., Kitahara A. // J. Colloid Interface Sci. 1983. V. 93. P. 293.
Kandori K., Kon-No K., Kitahara A. // J. Colloid Interface Sci. 1987. V. 115. P. 579.
Ayyub P., Maitra A.N., Shah D.O. // Physica C. 1990. V. 168. P. 571.
Chhabra V., Pillai V., Mishra B.K., Morrone A., Shah D.O. // Langmuir. 1995. V. 11. P. 3307.
Maitra A., Sarangi A. // J. Biosci. 1986. V. 10. P. 403.
Товстун С.А. Анализ процессов зарождения и роста наночастиц в истинных и обратно-мицеллярных растворах. Дис. … канд. физ.-мат. наук, Черноголовка: Институт проблем химической физики РАН, 2010.
Wennerström H. // Curr. Opin. Colloid Interface Sci. 1996. V. 1. P. 370.
Strey R. // Curr. Opin. Colloid Interface Sci. 1996. V. 1. P. 402.
Hellweg T. // Curr. Opin. Colloid Interface Sci. 2002. V. 7. P. 50.
Gradzielski M. // Curr. Opin. Colloid Interface Sci. 2002. V. 13. P. 263.
Kellay H., Binks B.P., Hendrikx Y., Lee L.T., Meunier J. // Adv. Colloid Interface Sci. 1994. V. 49. P. 85.
Sjöblom J., Lindberg R., Friberg S.E. // Adv. Colloid Interface Sci. 1996. V. 65. P. 125.
Ennis J. // J. Chem. Phys. 1992. V. 97. P. 663.
Szleifer I., Kramer D., Ben Shaul A., Gelbart W.M., Safran S.A. // J. Chem. Phys. 1990. V. 92. P. 6800.
Mitchell D.J., Ninham B.W. // Langmuir. 1989. V. 5. P. 1121.
Fogden A., Hyde S.T., Lundberg G. // J. Chem. Soc. Faraday Trans. 1991. V. 87. P. 949.
Winterhalter M., Helfrich W. // J. Phys. Chem. 1988. V. 92. P. 6865.
Lekkerkerker H.N.W. // Physica A. 1990. V. 167. P. 384.
Duplantier B., Goldstein R.E., Romero-Rochín V., Pesci A.I. // Phys. Rev. Lett. 1990. V. 65. P. 508.
Daicic J., Fogden A., Carlsson I., Wennerström H., Jönsson B. // Phys. Rev. E. 1996. V. 54. P. 3984.
Fogden A., Mitchell D.J., Ninham B.W. // Langmuir. 1990. V. 6. P. 159.
Landau L.D., Lifshitz E.M. The Classical Theory of Fields. 3rd ed. Oxford: Pergamon Press, 1971. Sec. 37.
Israelachvili J.N. Intermolecular and Surface Forces. London: Academic Press, 1997.
Jönsson B., Wennerström H. // J. Colloid Interface Sci. 1981. V. 80. P. 482.
Higgs P.G., Joanny J. F. // J. Phys. France. 1990. V. 51. P. 2307.
Fogden A., Daicic J., Mitchell D.J., Ninham B.W. // Physica A. 1996. V. 234. P. 167.
Harden J.L., Marques C., Joanny J.F., Andelman D. // Langmuir. 1992. V. 8. P. 1170.
Lekkerkerker H.N.W. // Physica A. 1989. V. 159. P. 319.
Jähnig F. // Biophys. Chem. 1976. V. 4. P. 309.
Donahue D.J., Bartell F.E. // J. Phys. Chem. 1952. V. 56. P. 480.
Kunieda H., Shinoda K. // J. Colloid Interface Sci. 1979. V. 70. P. 577.
Tovstun S.A., Razumov V.F. // J. Mol. Liq. 2019. V. 275. P. 578.
Невидимов А.В., Разумов В.Ф. // Коллоид. журн. 2013. Т. 75. С. 213.
Bordi F., Cametti C. // Colloid Polym. Sci. 1998. V. 276. P. 1044.
Nave S., Eastoe J., Heenan R.K., Steytler D., Grillo I. // Langmuir. 2000. V. 16. P. 8741.
Luan Y., Xu G., Dai G., Sun Z., Liang H. // Colloid Polym. Sci. 2003. V. 282. P. 110.
CRC Handbook of Chemistry and Physics / Ed. by D.R. Lide, 84th ed., 2003–2004.
Szleifer I., Ben-Shaul A., Gelbart W.M. // J. Phys. Chem. 1990. V. 94. P. 5081.
Tamamushi B., Watanabe N. // Colloid Polymer Sci. 1980. V. 258. P. 174.
Hall A.C., Tekle E., Schelly Z.A. // Langmuir. 1989. V. 5. P. 1263.
Aveyard R., Haydon D.A. // Trans. Faraday Soc. 1965. V. 61. P. 2255.
Rouviere J., Couret J.M., Lindheimer A., Lindheimer M., Brun B. // J. Chim. Phys. 1979. V. 76. P. 297.
D’Aprano A., Lizzio A., Turco Liveri V. // J. Phys. Chem. 1987. V. 91. P. 4749.
Товстун С.А., Разумов В.Ф. // Изв. Акад. наук, сер. хим. 2011. С. 1177.
Дополнительные материалы отсутствуют.
Инструменты
Коллоидный журнал










